Abstract
Atmospheric particulate matter (PM) has major threats to global health, especially in urban regions around the world. Dhaka, Narayanganj and Gazipur of Bangladesh are positioned as top ranking polluted metropolitan cities in the world. This study assessed the performance of the application of hybrid models, that is, Autoregressive Integrated Moving Average (ARIMA)-Artificial Neural Network (ANN), ARIMA-Support Vector Machine (SVM) and Principle Component Regression (PCR) along with Decision Tree (DT) and CatBoost deep learning model to predict the ambient PM2.5 concentrations. The data from January 2013 to May 2019 with 2342 observations were utilized in this study. Eighty percent of the data was used as training and the rest of the dataset was employed as testing. The performance of the models was evaluated by R2, RMSE and MAE value. Among the models, CatBoost performed best for predicting PM2.5 for all the stations. The RMSE values during the test period were 12.39 µg m−3, 13.06 µg m−3 and 12.97 µg m−3 for Dhaka, Narayanganj and Gazipur, respectively. Nonetheless, the ARIMA-ANN and DT methods also provided acceptable results. The study suggests adopting deep learning models for predicting atmospheric PM2.5 in Bangladesh.
1. Introduction
Atmospheric pollution is one of the greatest threats that the world has been suffering. It is accountable for a major portion of the global burden of diseases from environmental factors [1]. Several published works elaborately documented the six ambient criteria air pollutants (i.e., particulate matter (PM), sulfur oxides (SOx), nitrogen oxides (NOx), carbon mono oxide (CO), ozone (O3) etc.) and their relationship with multi-dimensional acute and chronic health effects of human [2,3]. Among the most important atmospheric pollutants, particulate matter, that is, coarse PM (PM10) and fine PM (PM2.5) are getting most attention for their adverse effects on local and regional air quality, visibility of the atmosphere and finally, global climate [4,5]. From several epidemiological and clinical studies, it has already been proven that there is a strong association of high PM10 and PM2.5 concentration and different acute and chronic health hazards such as respiratory disease [6], cancer [7], metabolic disease [8], cardiovascular diseases [9], skin diseases [10], kidney disease [11] and so forth. A clinical meta-analysis regarding the health issues from PM exposure revealed that a 10 μgm−3 increase of PM2.5 concentration could accelerate the mortality up to 2% [12]. Another similar study [13] found that, globally, about 3% of cardiopulmonary and 5% of lung cancer deaths are attributable to PM exposure. The study also argued that the existence of PM in the atmosphere poses more threat to public health than that of other ambient air pollutants. Moreover, a new study conducted in TH Chan School of Public Health, Harvard University, found the association between the exposure of PM and the novel coronavirus disease 2019 (COVID-19). The study revealed that an increase of 1 g.m−3 in PM2.5 could accelerate the death rate of the new pandemic COVID-19 by 15% [14]. Thus, numerous scientific studies have illustrated strong evidence of the association between health hazards and PM concentration.
According to the World Health Organization (WHO) database of 2018, almost 98% of the lower and middle-income countries do not maintain the air quality guidelines on account of focusing more on the rapid progress of industrialization, technological advancements and the increasing trend of transportation. Moreover, people from these areas are exposed to poor air quality levels. The WHO reported 3.7 million premature death worldwide which are derived from exposure to atmospheric pollutants and it is assumed to be doubled in 2050 [15]. Bangladesh, as a lower-middle-income country, is no exception to that. The country is facing severe air pollution problems over the last two decades [16]. The WHO included Narayanganj, Dhaka and Gazipur among the top 50 cities out of 2975 cities in the world having the worst air quality level [17]. Several studies argued that most of the pollution had been increased because of the substantial number of transportations, municipal constructions, industrial and manufacturing operations and other adjacent brick kilns around the cities in Bangladesh [16,18,19]. Moreover, it is projected that half of the population is about to migrate in urban areas in Bangladesh by 2050 [16]. Consequently, congestion of population in urban areas has become the major concern as well. Multiple chemical speciation studies of PM have stated that secondary aerosols include ammonium bi-sulfate, ammonium sulfate, and, ammonium nitrate as a result of the chemical transformation of gaseous emission of different precursor gases, which is evidence that gaseous pollutants contribute significantly to the PM pollution in the metropolitan areas [20,21,22]. Apart from these anthropogenic activities, meteorological parameters with the topographical condition have also a significant contribution on affecting the concentration, dispersion and, finally, the transportation of pollutants [23].
The development of air pollution modeling and forecasting is, therefore, necessary to develop the controlling mechanism for abating the effects of pollutants. There are different types of air pollution modeling techniques, such as physical models, dispersion models and statistical models. In particular, Gaussian models (i.e., AERMOD, PLUME, etc.), Lagrangian models, that is, NAME, Eulerian models, (i.e., Unified Model) and Chemical Transport Models (CTMs) (e.g., GEOS-Chem, CMAQ, WRF-Chem, etc.) are the most popular physical process models. These models incorporate atmospheric science and multi-processing computational approaches, including the real-time updated emission inventory inputs and meteorological records [24]. However, the application of these models is further limited by some complexities in terms of geophysical characteristics, that is, land use and terrain [25,26]. Recent studies found that the traditional deterministic models struggle to capture the non-linearity among pollutants’ concentration, meteorology, land use and emission and dispersion sources [27,28]. On the other hand, machine learning algorithms seem promising in several studies to minimize and tackle the complexities of the models [24,29]. Some hybrid machine learning models, such as Principle Component Analysis (PCA)-SVM, ARIMA-ANN, ARIMA-SVM, fuzzy logic-ANN, have been performed as the most popular classifiers to overcome the nonlinear uncertainties and trends to accomplish better forecasting accuracy [30,31]. Numerous studies have been conducted in different countries to assess machine learning and hybrid models’ performance on air quality modeling and forecasting [32]. However, based on relevant literature, the study of machine learning in air pollution modeling was limited in Bangladesh, though multiple studies were performed to investigate and estimate the particle pollution in different metropolitans [16,33]. To simulate the pollutants’ concentration, a CTM—namely WRF-CMAQ—was used by few studies [20].
On the other hand, the most used statistical technique to forecast air quality in Bangladesh was Seasonal ARIMA [34]. A recent study in Bangladesh on machine learning applications in particle pollution suggested to use hybrid models to get better prediction performance [35]. The study used ANN, Linear-SVM, Medium gaussian-SVM, GPR, Random Forest Regression (RFR) and PROPHET to check their applicability in particle pollution modeling. Therefore, keeping in view of these observations, the study sets three objectives to investigate. Firstly, the study will evaluate the performance of hybrid models, that is, ARIMA-ANN, ARIMA-SVM and PCR on particle pollution modeling in three air pollution hotspots in Bangladesh. Secondly, it will draw the relationships among the meteorological variables and air pollutants throughout the study period. Thirdly, the study will compare the results of hybrid models with a machine learning model, that is, Decision Tree and a gradient boosting deep learning model, namely CatBoost.
2. Air Monitoring Stations
The study conducted in Dhaka, Gazipur and Narayanganj City Corporation in Bangladesh. Every metropolitan area has specific importance for considering as study area in this research. Dhaka is the capital of Bangladesh which is situated in the central part (23°41′ N latitude and 90°22′ E longitude) of the country with an area of 306.38 km2. In terms of population density and fast-growing urban sprawling, it is ranked 19th among 47 megacities in the world [17]. Moreover, the city is exposed to air pollution problems at a higher rate among the cities worldwide [36]. On the other hand, Narayanganj is the most polluted city in Bangladesh at the moment, as it is one of the industrial zones in the country [17]. The city, with an area of 687.7 km2, is located in between 23°33′ and 23°57′ north latitudes and in between 90°26′ and 90°45′ east longitudes. Gazipur is also an industrial zone in Bangladesh, with an area of 1741.5 km2. The city is located in between 23°53′ and 24°21′ north latitudes and in between 90°09′ and 92°39′ east longitudes (Figure 1). The study areas experience a hot, wet and humid tropical climate.
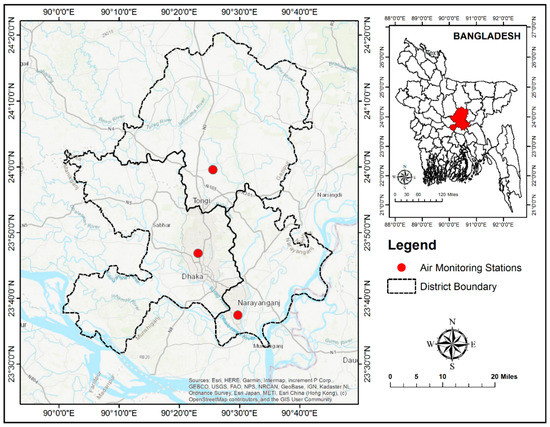
Figure 1.
Air monitoring sites in Dhaka, Narayanganj and Gazipur in Bangladesh. The red dots represent the location of air quality monitoring stations.
3. Methodology
The overall methodology of this study is divided into four parts: (a) data pre-processing, that involves the collection of pollutants and meteorological data and the correction of missing values; (b) investigation of the relations among meteorological parameters and pollutants; (c) feature importance, that involves the screening of features among meteorological variables and air pollutants before operating the models; (d) application of the models namely ARIMA-ANN, ARIMA-SVM, PCR, DT and CatBoost. Figure 2 represents the overall methodological framework of the study.
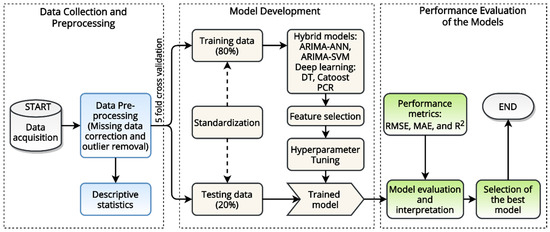
Figure 2.
Framework of the study; from data collection and pre-processing, data splitting and model development to model evaluation and interpretation.
3.1. Pre-Processing
This study used continuous air quality data from three Air Monitoring Stations established by Department of Environment (DoE), Ministry of Environment, Forest and Climate Change (MoEFCC), Government of Bangladesh under the Clean Air and Sustainable Environment (CASE) project. For measuring concentrations of PM2.5 and PM10 an automatic and real-time suspended particulate monitor (Beta Gauge 101M; ENVIRONMENT SA, France) was installed in every three stations. The data generation at the monitoring stations is centrally retrieved into Central Data Station at the DoE Head Office. EnVIEW 2000 software and SQL were used to retrieve data and database, respectively. To maintain quality assurance and control, calibration was routinely performed. Servicing and repair of instruments were also checked properly during the data generation. Calibration of the analyzers is performed using NIST traceable calibration gases usually quarterly or after repair. Particulate monitors based on beta gauge attenuation are calibrated using standard foils of known areal mass density. While processing the data were checked for outliers and if 75% of the data in a day were not available for any parameter due to power failure or equipment’s nonoperational, values were considered as non-representative and excluded from the analysis. Meteorological variables (Temperature, relative humidity, rainfall and wind speed) consisted of the daily mean for the same periods were collected from DoE also.
The amount of total captured data for Dhaka, Narayanganj and Gazipur were 90.4, 86.3 and 89.7% from January 2013 to May 2019. The study used the nearest neighbor method (NN) to correct the missing values, which was also used in previous studies [36]. The NN aims to provide unbiased and valid estimates of associations based on information from the available data. The NN is widely known as the standard method to deal with missing data in many areas of research. The algorithm is similarity-based concept that relies on distance metrics. In this work, we used the Minkowski norm (D) given by Equation (1) as metric to evaluate distance in form of the Euclidean, when p = 2,
where, and are the test sample and training data, respectively. To run the overall process of missing value correction, the XLSTAT18 was used. On the other hand, to process the checking and removal of spatiotemporal outliers from raw data, the Z scores method was used before the calculation of statistical parameters, in consistency with previous studies [37]. The removal criterion consisted of three conditions. Initially, the raw data were transformed into Z-scores. The observations in the transformed series were excluded from the original series meeting the following three conditions: (i) having absolute Z score is greater than 4 (); (ii) the increment from the previous value of the series is larger than 9 (); and (iii) the ratio of the Z-score value to its centered mean of order 3 (MA3) being greater than 2 ().
After the pre-processing, the dataset consists of 2342 observations which covered the daily 24-h mean concentration of particulate matter. Before the implementation of the following models, data splitting was executed. This was performed by splitting data into two subsets, that is, training data (80%) and testing (20%) data. The training data was used to develop the model and the test data was used for model evaluation. K-fold (K = 5) cross validation (CV) method was implemented to evaluate the models in consistence with our previous study [35]. The CV method is illustrated in Figure 3.
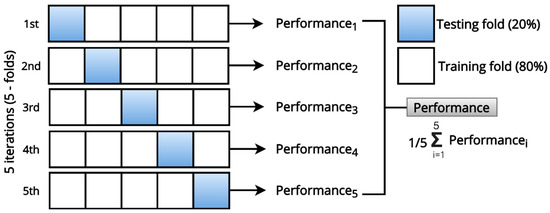
Figure 3.
The architecture of five-fold cross validation for the evaluation of the models.
3.2. ARIMA
Autoregressive Integrated Moving Average (ARIMA) is basically comprised of inclusive Autoregressive (AR) models, the Integrated (I) models and the Moving Average (MA) models. For operating the ARIMA model by the Box-Jenkins methodology, there are three steps that should be considered that is, identification, estimation parameters and forecasting [38,39]. In the identification step, firstly, stationarity check is performed on time series data (PM2.5 concentration). If stationarity is found absent in times series data after the first attempt, differencing (or power transformation) method is performed continuously till non-stationarity is disposed. If this operation is performed d times, the integration order of the model is set to be d. Thereafter, when , an autoregressive moving average (ARMA) is applied on the resultant data as follows: Let the actual data value be and random error t at any given time t. This actual value is considered as a linear function of the past p observation values, say and q random errors, say .
In Equation (2), the coefficients from to are Autoregression coefficients, to are Moving Average coefficients. Note that random errors t are identically distributed with a mean of zero and a constant variance. Similar to the d parameter, p and q coefficients are referred to as the orders of the model. When q equals to zero, the model is reduced to AR model of order p. If p is equal to zero, the model becomes MA model of order q. The main issue in ARIMA modeling is to determine the appropriate model orders (p, d, q). In order to estimate order of the ARIMA model, Box and Jenkins proposed to use correlation analyses tools, such as the autocorrelation function (ACF) and the partial autocorrelation function (PACF). When model coefficient estimation is finalized, the future values of the time series data are forecasted using available past data values and estimated model coefficients [38].
3.3. Artificial Neural Network (ANN)
ANN is the widely used machine learning algorithm that generally investigates the complex relationships between predictors and predictand [35]. Due to its flexible architecture, number of layers and the neurons at each layer can be easily varied. In addition, ANN does not require any prior assumption, such as data stationarity, in model building process. Therefore, the network model is largely determined by the characteristics of the data. The architecture of the most widely used ANN model in time series forecasting, which is also called as multilayer perceptrons, contains three-layers. The neurons of the processing units are cyclically linked. In order to model time series data using such a network, nonlinear function f of sequence from to is constructed as shown in the following Equation (3):
where, at any given time t, and are model weights and H and N are the number of hidden and input nodes, respectively. In this Equation, corresponds to a noise or error term. The transfer function of the hidden layers f in ANN architecture is generally a sigmoid function. The power of ANN comes from its flexibility to approximate any continuous function by changing the number of layers N and hidden nodes H. The choice of number of layers and the nodes at each of them play important role in ANNs’ forecasting performance. Large numbers of N and H can give very high training accuracies but since it tends to memorize the training data, it suffers from overfitting. On the other hand, a too simple network of ANN leads to poor generalization. Unfortunately, there is no systematic set of rules to decide the value of these parameters. Thus, extensive number of experiments are required to tune functions and the parameters. In this study, Multilayer Perceptrons (MLP) was used as it is the most classical type of ANN. The architecture of the MLP-ANN model is illustrated in Figure 4. After experimenting on several MLP structures, the study decided to utilize two hidden layers. The model has N inputs of meteorological variables and PM. Between the two hidden layers, the first layer was composed of N neurons where the second layer was N/2 neurons. To avoid overfitting, “early stopping” regularization was used.
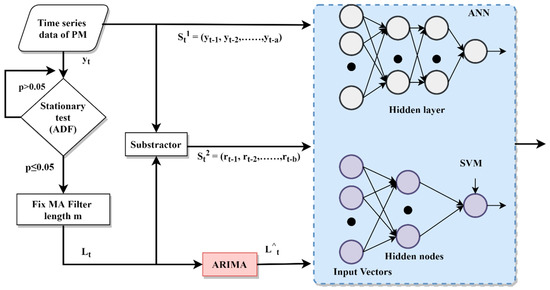
Figure 4.
Architecture of proposed (moving average-filter) hybrid models that is, Auto Regressive Integrated Moving Average-Artificial Neural Network (ARIMA-ANN) and ARIMA-Support Vector Machine (ARIMA-SVM). The time series data is considered as a combination of linear () and nonlinear components (). After the stationary test, two components are separated from the original data by using moving average (MA) filter with the length of M. Then, the linear and nonlinear component was modelled by ARIMA, and ANN and SVM, respectively.
3.4. Support Vector Machine (SVM)
The fundamental theory of SVM was centered on the principle of structured risk minimization (SRM). The usage of SVM has received attention in the field of atmospheric pollution modeling due to its promising empirical performance [35]. Let be a training dataset, where represents the explanatory variables and the response variable. In the -SV linear regression the aim is to find a function that has at most a deviation from for all training data. The solution of this problem is formulated as the following minimization problem with restrictions.
where ‖·‖ = the Euclidean norm, and = slack variables and > 0 estimates the trade-off between the evenness of and the value of such deviations. The evenness of depends on (the smaller the elements of are, the flatter is. The quality of the estimation is determined by the -insensitive loss function :
The slack variables explain the deviations of the solution beyond the ε-sensitive zone. If value is too higher, then the objective is to lessen the average loss, which is called empirical risk, without regard to model complexity. The optimization problem in Equation (4) is computationally simpler to solve in its Lagrange dual formulation (LDF) [34]. The solution is a linear combination of a subset of sample points called support vectors (SV).
where , and the Lagrange multipliers. The SV corresponds to the observations for which . The LDF allows extending the solution to nonlinear functions by substituting the dot product with a positive definition function (kernel) as follows:
where is a transformation that maps into a high dimensional space which is also known as feature space. The explicit coordinates in the feature space and even the mapping function become unnecessary when we define a kernel. The advantage of this procedure, known as the kernel trick, is that the complexity of the optimization problem remains dependent only on the dimensionality of the input space and not on the feature. The solution of the optimization problem is analogous to
Using this method, nonlinear SVM finds the optimal function in the transformed predictor space. There are many types of kernels in existing literature, polynomial and tangent hyperbolic kernels being two of the most cited [35]. In this study, medium gaussian SVM was implemented.
3.5. Hybrid Model
In this study, we proposed a hybrid method for time series forecasting, which aims to overcome the limitations of traditional hybrid methods by eliminating strong assumptions. The architecture of the proposed hybrid method is shown in Figure 4. The algorithm starts with data decomposition. In this method time-series data is considered as a function of linear Lt and nonlinear Nt components in the same way as given in Equation (9).
These two components are separated from the original data by using moving average (MA) filter with the length of m, as given in Equation (10).
While the linear component lt has low volatility, the residual rt, which is the difference between the original data and the decomposed linear data in Equation (11), shows high fluctuation.
After the linear component is achieved with MA filter, a linear model is constructed as shown in Equation (12). The stationary component l is modelled as a linear function of past values of the data series and random error series in Equation (2) using the ARIMA model.
where g is a linear function of ARIMA. Finally, nonlinear modeling ANN and SVM are used to implement functional relationship between components as indicated in Equation (5). The past observed data present ARIMA forecast result of the decomposed stationary data and residuals of the data decomposition
are fed to ANN and SVM as indicated in Equations (13)–(16):
where f is the nonlinear function of ANN and SVM, a and b are parameters of the model which show how much we will go back in time to use as features to ANN and SVM.
3.6. Decision Trees
Decision tree (DT) is a convenient method for data mining. It is also used as a suitable and rampant decision-making tool. In decision analysis, a DT, specifically the diagram of the decision, denotes a visible tool for more comprehensible and analytical decision-making [40]. This method categorizes the test datasets from root up to branches and leaves. Every leaf of the tree embodies a particular class. A well-developed tree can handle manifold parameters with frequent data for each variable. Three kinds of nodes are available in the architecture of DT, which are decision node, chance node and end node. Every inner node resembles an input data and the edges to children for each of the likely values of that input variable. A leaf illustrates a value of the target variable given the values of the input variables denoted by the path from the root to the leaf [41]. In this study, a tree was developed where 9 predictors (Mean temperature, relative humidity, rainfall, wind speed, O3, NOx, SO2, PM10 and CO) were assumed as the input values and PM2.5 plays the target parameter’s role. The rationale behind the selection of predictors is their correlation to PM2.5. Generally, both PM2.5 and PM10 are constituted by other subclasses of atmospheric pollutants with the major ones being water-soluble ions, that is, sulfates (SO42), nitrates (NO3−), ammonium (NH4+) and minor constituents such as sea salts, metal ions, organic and elemental carbon and volatile organics [35].
An extended and wide tree may encounter with overfitting problem and a limited one probably cannot consider the all variables, where pruning the tree is a tool to keep the tree size in a satisfactory and optimal range. Overfitting can occur when the machine learning memorizes the dataset and produces very similar outcomes to inputs [40]. Therefore, to avoid the overfitting, predictors were examined by Boruta Algorithm feature selection process like the previous study [35]. The method utilizes a wrapper algorithm and capable of working with any classification methodology that can produce variable importance measure as an output. By default, BA utilizes the random forest (RF) algorithm to find out the most effective predictors. In this study, BA was operated in the R working environment. The number of estimators was set to be ‘auto’ since BA offers an automatic number of estimator’s selection.
3.7. CatBoost
CatBoost is a gradient boosting library that can work with categorical data. This deep learning method works based on improved gradient boosting decision tree (GBDT), which can solve problems with noisy data, heterogeneous features and complex dependencies. This algorithm can handle the categorical features well. In general, traditional GBDT algorithm can replace categorical features with corresponding average label value. The average label value used as the criterion for node splitting, which is known as Greedy Target-based Statistics (Greedy TBS), The GTBS is defined as the follows [42]:
Usually, features include more information than labels. If average label value is utilized to denote features forcefully, it will lead to a conditional shift. CatBoost adds an initial value to Greedy TBS. Assume that a given dataset of observations D = {Xi, Yi} I = 1, …, n, if a permutation is σ = (σ1, …, σn), xσp,k is substituted with [42]:
where p is a prior value, a is the weight of prior value. This method contributes to reducing the noise obtained from the low-frequency category. CatBoost combines multiple categorical features. Generally, it utilizes a greedy way to integrate all categorical features and their combinations in the current tree with all categorical features in the dataset (Figure 5). Moreover, it can overcome gradient bias found in traditional GBDT by utilizing a method to change the gradient estimation in the classic algorithm, which is named as ordered boosting. This method can overcome the limitation, that is, prediction shift caused by gradient bias and enhance the generalization ability of the model.
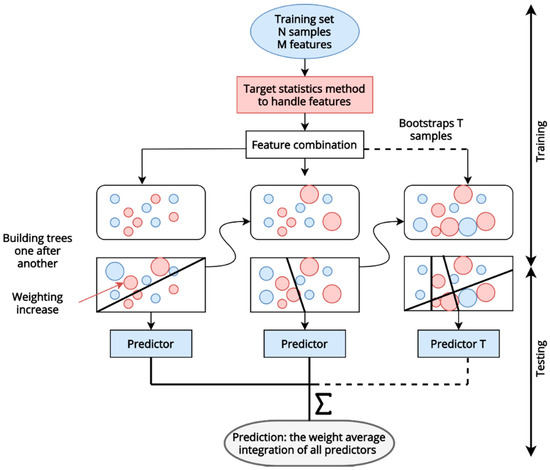
Figure 5.
The structure of the CatBoost algorithm.
3.8. Principle Component Regression
Principal component regression (PCR) analysis is a integration of Principle component analysis (PCA) and Ordinary Least Squares (OLS) regression. PCR analysis can reduce the multicollinearity in datasets. The existence of multicollinearity among the explanatory variables may produce invalid results in terms of the model’s predictions and determination of the significant independent variables. PCA, an integral part of PCR analysis, minimizes the dataset’s dimensionality by carrying out a covariance analysis between the factors. The PCA maximizes the correlation between the original and new uncorrelated covariates that are mutually orthogonal. Thus, it can produce a new set of variables, that is, principle components (PCs) where the number of PCs is less than or equal to the number of original covariates, which provides the linear combination of the original set of data. PCA is generally written as:
where, is the ith principal component and is the loading of the observed variable . The PC associated with the greatest eigenvalue (PC1) accounts for the maximum variability in the data. All components with eigenvalue ≥1 will be considered for the significant factors. Then, the significant factors, consisting of independent variables obtained from the PCA, were regressed against the dependent variables using OLS regression analysis. The general equation of the model is as follows:
where, are the regression coefficients, are the principle components and is stochastic error associated with the regression.
3.9. Empirical Results
In this study, the performance of the models was evaluated based on some quantitative statistics such as and root mean square error (RMSE), mean absolute error (MAE) and coefficient of determination (R2).
where, n = number of data used for estimation, = actual value of the i-th element of the data set, = predicted value of the i-th element of the data set.
4. Results and Discussion
4.1. Descriptive Statistics
Table 1 shows the summary statistics of air pollutants’ data from January 2013 to June 2019 in Dhaka, Gazipur and Narayanganj city in Bangladesh. Among the three stations, Narayanganj and Gazipur showed the highest and lowest emission of particulate matter, respectively. Table 1 depicts the overall statistics across the years. For Dhaka, the mean concentration of PM2.5 and PM10 ranged from 7.1 to 351.2 μgm−3 and 15.5 to 617.8 μgm−3 respectively from 2013 to 2019. On the other hand, meteorological parameters, that is, temperature (temp), relative humidity (RH), rainfall (R) and wind speed (WS) ranged from 11.1 to 34.5 °C, 37.9–93.9 %, 0.1–8.9 mm, 991.5–1019.1 mb,15.1–562.9 Wm−2 and 0.13–12.9 ms−1 respectively. For Gazipur, the daily mean concentration of PM2.5 and PM10 ranged from 4.9 to 313.5 μgm−3 and 9.9 to 501.1 μgm−3 respectively from 2013 to 2019. The atmospheric parameters, that is, temp, RH, R and WS ranged from 9.01 to 35.7 °C, 10.2–90.4%, 0.1–8.9 mm and 0.1–11.9 ms−1, respectively. For Narayanganj, daily the mean concentration of PM2.5 and PM10 ranged from 4.9 to 313.5 μgm−3 and 9.9–501.1 μgm−3 respectively from 2013 to 2019. On the other hand, meteorological parameters, that is, temperature, relative humidity, rainfall and wind speed ranged from 11.11 to 44.1 °C, 10.2–99.9%, 0.01–4.2 mm and 0.17–42.8 ms−1 respectively. Table 1 illustrates the summary statistics of the variables with annual mean, standard error and standard deviation. It demonstrated that annual averages of the PM2.5 and PM10 concentration in the air of the Dhaka, Gazipur and Narayanganj are greater than the standards of WHO. In Dhaka, it is about six times greater than the standard. Moreover, the annual PM concentration of stations surpassed the value of Bangladesh Air Quality Standard (BNAAQS- 150 μgm−3 for PM10 and 65 μgm−3 for PM2.5).

Table 1.
Summary statistics of air pollutants and meteorological data in air pollution monitoring sites in Bangladesh during 2013–2019.
4.2. Local Meteorology and Their Relation to Pollutants
Climatologically, the climate of air monitoring areas is subtropical monsoon. In general, the seasons are broadly categorized as cool and dry winter (December–February), hot and rainless pre-monsoon or summer (March–May) with recurring drought occurrence and rainy days or monsoon (June–September) and post-monsoon (October–November). However, there is a significant variation in terms of meteorological conditions such as mean temperature, rainfall, RH, solar radiation, WS and so forth. Scanty rainfall, low RH and low northwesterly prevailing winds usually occur in the winter season. The pattern of the meteorological variables slowly increases in the pre-monsoon season when moderately increased rainfall, WS and RH can be observed. In monsoon, the WS increases more and the air becomes purely marine. However, the speed of the wind and the intensity of rain gradually falls in the post-monsoon season [23]. The central of Bangladesh, Dhaka city experienced adequate rainfall, high cloud coverage and south-easterly wind during May to October. However, in November to April, the city experienced low rainfall, low cloud coverage and mainly north-westerly wind [33]. The wet season was also characterized with high temperature and high RH. Local meteorology during dry season was not uniform. December and January were characterized with low temperature, high RH, weak solar radiation and rare rainfall. Solar radiation and temperature increased from February to April, while RH gradually decreased. Cloud coverage and rainfall in April were remarkably greater than those in other months in the winter season. The other two cities Gazipur and Narayanganj, being located in close vicinity of Dhaka, were expected to have the same meteorology as Dhaka in different seasons as the whole region has very flat terrain, similar topography and the same climatic condition.
The overall statistics of the seasonal and daily pattern of particulate matter across the air monitoring stations are illustrated in Figure 6 and, Supplementary Materials Figure S1. It is clear from the figures that the concentration of PM10 and PM2.5 across the stations was the highest in winter whereas it was lowest in the monsoon season. The fluctuation pattern with the seasonal variation throughout the stations was almost the same. In winter, the highest mean concentration of PM2.5 and PM10 was observed in Narayanganj (201.3 µg m−3 and 347.1 µg m−3, respectively) and the lowest in Dhaka (153.0 µg m−3 and 270.5 µg m−3). However, in monsoon, it was found the highest PM2.5 concentrations in Narayanganj (31.4 µg m−3) and lowest in Gazipur (26.4 µg m−3). From the above statistics, it is clear that there is a relation among the particulate matters and meteorological variables throughout the seasons. Many studies identified the relationship among PM2.5, PM10 and meteorological parameters across different countries in the world that is, Bangladesh [23]; Malaysia [43], China [44], India [45] and Australia [46]. The study [23,35] illustrated the relationship among the air pollutants and meteorological parameters (mean temperature, relative humidity, rainfall, solar radiation, barometric pressure, wind speed and wind direction) in Dhaka, Sylhet, Rajshahi and Chattogram in Bangladesh. To study the local meteorology and their influence on the concentration of air pollutants across the Dhaka, Narayanganj and Gazipur, Spearman correlation analysis was examined among the variables.
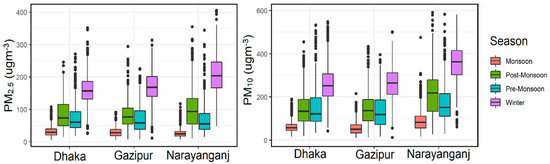
Figure 6.
Seasonal pattern of particulate matter throughout the air monitoring stations.
The overall correlation among the meteorological parameters and the air pollutants is illustrated in Figure 7. It revealed that PM10 and PM2.5 had a negative correlation with air temperature, RH, rainfall and WS during most of the seasons across the stations. The seasonal pattern of the correlation among them is illustrated in Supplementary Materials Figure S2. It was observed that the concentration of particulate matter was found highest in the winter season. In winter, the atmospheric inversion is one of the most important reasons for the highest concentration of the pollutants. By the process of accumulation and condensation, the atmospheric inversion can maximize the concentration of PM [45]. The study areas that is, Dhaka, Gazipur and Narayanganj, generally, exhibit the industrial-prone cities in the country. Brick-kilns industries around the corner of the cities are fully operational in winter. Studies revealed that this industry is mostly responsible for the highest concentration of PM around the cities during winter. The north-western wind of the winter season is dominant in the study region, which can transport the PMs from the brick-kilns. On the other hand, in monsoon, the heavy rainfall throughout the cities is the key factor for the low concentration of pollutants. According to the study [44], particulate matter absorbs water vapors in the atmosphere and deposits to the ground since it is made of soil and dust. Moreover, vegetation, that is, leaves can act as an instrumental factor in changing the pattern of particulate matter concentration. In monsoon, the presence of green leaves is abundant, which can minimize the particles from the atmosphere [23]. However, a positive correlation was observed among particulate matter, mean temperature and wind speed in this season. It is mainly because of the high summer temperature and maximum wind speed in that season which can combinedly accelerate the concentration of the pollutant [23,45].
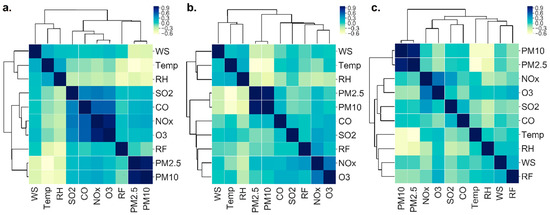
Figure 7.
Correlation among the pollutants and meteorological variables at air monitoring sites (a). Dhaka; (b). Narayanganj; (c). Gazipur.
Apart from the correlation with meteorological variables, PM is also highly correlated with other gaseous air pollutants. The study found that PMs had a significant correlation with CO, NOx, SO2 and O3. At late pre-monsoon and early monsoon, for PM2.5 and PM10, the highest correlation was found with CO because of the on-road traffic congestion. On the other hand, in the pre-monsoon and post-monsoon period, the SO2 was found highly correlated with NOx in every air monitoring stations. It can be addressed by high construction activities due to favorable weather conditions. During that period, for the NOx emission, traffic and construction were not the only significant sources but rather a considerable amount of NOx was emitted to the atmosphere from the main source of SO2 emissions. It was found that the main sources of SO2 emissions in study areas are brick-kilns.
4.3. Results of ARIMA-ANN and ARIMA-SVM
Before implementing the ARIMA model, it is necessary to employ the test of stationarity of the dataset. The study utilized Augmented Dicky Fuller (ADF) test to examine the stationarity of dataset. The ADF stationarity test result of the time series of daily mean PM2.5 concentration showed 0.01 for Dhaka and Narayanganj, whereas it showed 0.02 for Gazipur air monitoring station. The values found by the ADF test were lower than the threshold 0.05 (Table 2). That implies that the dataset is stationary and, unit root is not present on the dataset. Supplementary Materials Figure S3 represents the overall time series plot of the PM2.5 concentration throughout the stations.

Table 2.
Augmented Dicky Fuller (Unit-root) test of stationarity (alternative hypothesis: stationary).
To determine the order of the model, the graph of sample auto correlation function (ACF) and partial autocorrelation function (PACF) should be observed. The ACF and PACF graphs of PM2.5 time series values at Dhaka, Narayanganj and Gazipur, as shown in Supplementary Materials Figure S4, infer seasonality of data which required to be de-seasonalized. For de-seasonalization, first difference in log of PM2.5 time series data with a seasonal first difference at lag 10 was found satisfactory for Dhaka, Narayanganj and Gazipur. Figure 8 illustrates ACF and PACF of deseasonalized and stationary PM2.5 data of air monitoring stations. The figure shows vanishing spikes of ACF and PACF over lag implying non-seasonality of the time series data. Therefore, ARIMA(p,0,q) (P,1,Q), ARIMA(p,0,q) (P,0,Q) and ARIMA (p,0,q) (P,0,Q) process is appropriate to model PM2.5 data of Dhaka, Narayanganj and Gazipur, respectively. Based on minimum AIC, ARIMA (3,0,2) (2,0,2)10, (3,0,2) (2,0,1)10 and (3,0,2) (1,0,1)10 are identified as the best models for modeling PM2.5 concentration of Dhaka, Narayanganj and Gazipur, respectively.
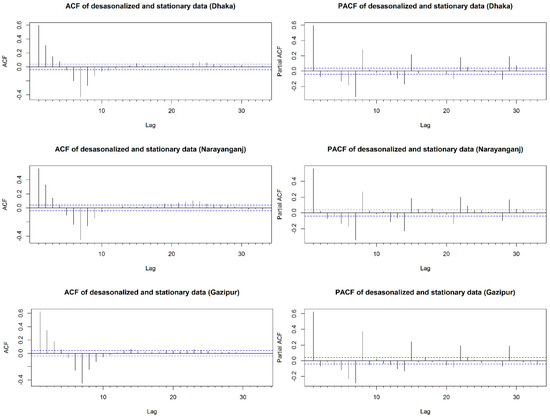
Figure 8.
Auto correlation function (ACF) and partial autocorrelation function (PACF) plot of de-seasonalized PM2.5 value of Dhaka, Narayanganj and Gazipur.
Table 3 represents the coefficients of fitted ARIMA models for Dhaka, Narayanganj and Gazipur with AIC 14,329.3, 15,371.32 and 13,842.38, respectively. All autoregressive (AR), moving average (MA), seasonal autoregressive (SAR) and seasonal moving average parameters are found significant in the models for Dhaka, Narayanganj and Gazipur. Supplementary Materials Figure S4 illustrates residuals produced from the above models for every station. The residual plots illustrate uniform fluctuations over the period and they exhibit normal distribution. Moreover, small p-values (at 5% level of significance) of the Box-Pierce tests, for all the models, find no dependency in residuals, which infers nothing remaining to capture further. Supplementary Materials Figure S5 represents the diagnostic plot of the residuals, including residual plot and normal Q-Q plot of residuals.

Table 3.
Parameter estimation of fitted ARIMA models during training session.
In the proposed method of the hybrid model, the linear component was extracted from the dataset when the MA filter length was 5. As the ADF test result interprets a certain level of stationarity in the dataset across the air monitoring stations, the relatively short MA filter length was expected. Because of the MA filter, the stationary test result was found less than 0.01 for the achieved linear component, which shows even more stationarity to be properly modeled by ARIMA. The best fitted artificial neural network in the last step of the proposed hybrid model has 9 nodes in the input layer where 5 of them were observed values, 3 of them were residuals and one node was assigned for the result of linear component forecast. According to our tuning experiments in MATLAB, when the number of hidden nodes were adjusted to the best possible outputs in terms of RMSE value. The best fitted ANN model was accomplished for Dhaka, Narayanganj and Gazipur was 9 × 2 × 1, where 9 denotes the number of input nodes, 2 denotes the hidden layers and 1 is the output layer. Like the process of ANN, the SVM was executed in the similar way where observed values (n = 5), residuals (n = 3) and linear component forecast (n = 1) were counted as the covariates for the model. The SVM parameters were tuned using υ-regression type. Accordingly, υ value was set to 1, the chosen kernel was medium gaussian with degree 3, γ = 2 and the independent parameter α0 = 5. Regarding the general parameters of the model, the cost was set at C = 1.1 and ε = 0.1. As the time series of the PM2.5 concentration across the air monitoring stations have the similarity, the model architecture of SVM and ANN was set same for the stations.
The overall training and test results of the ARIMA-ANN and ARIMA-SVM with the comparison of other models, that is, DT and CatBoost are represented in Table 4 and Figure 7 respectively. In this study, the performance was estimated, employing the root mean square error (RMSE) and mean absolute error (MAE). All the hybrid models performed better than the individual ARIMA model implemented across the air monitoring stations. Between ARIMA-ANN and ARIMA-SVM, ARIMA-ANN performed better. The RMSE values for predicting PM2.5 using ARIMA-ANN during the model training were 11.96 µg m−3, 12.86 µg m−3 and 12.34 µg m−3 for Dhaka, Narayanganj and Gazipur, respectively. On the hand, in terms of using ARIMA-SVM, the lowest RMSE value was found for Gazipur air monitoring station (RMSE = 12.68 µg m−3). During the test session, like the training result, ARIMA-ANN outperformed the individual ARIMA and ARIMA-SVM. The RMSE values obtained from ARIMA-ANN model during the test session were 14.04 µg m−3, 13.08 µg m−3 and 14.17 µg m−3 for Dhaka, Narayanganj and Gazipur, respectively. A study in Bangladesh used the seasonal ARIMA model for AQI forecasting weekly in Dhaka, where the RMSE value was 30.36 using individual model [34]. Another study in Chile, which utilized the Zhang’s hybrid model of ARIMA-ANN and found the higher RMSE value for ARIMA (28.39 µg m−3) and lower RMSE value (8.89 µg m−3) using hybrid model [47]. The study [35] used six machine learning models, including ANN and SVM at four air monitoring stations in Bangladesh. The individual ANN and SVM model did not perform well for the prediction of PM2.5. The overall numerical results given in Table 3 and Table 4, Figure 9 and the previous study [35] denote that individual methods such as ARIMA, ANN, SVM have apparently lowest performance as compared to hybrid models. This infers that either ARIMA or ANN, when individually utilized in predicting PM2.5 in the cities of Bangladesh, do not capture all patterns in the data series. Therefore, combining two methods, making the hybrid model, by taking advantage of each of them can be an effective way to overcome this limitation.

Table 4.
Performance of the models across the air monitoring stations during the training session.
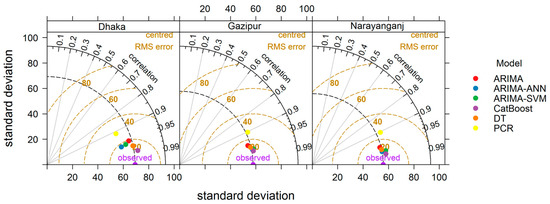
Figure 9.
Taylor Diagram of the test results of the models implemented in this study. Among the models, ARIMA-ANN and CatBoost showed the best performance.
4.4. Result of Decision Tree (DT) and CatBoost
Before implementing the machine learning models, that is, DT and CatBoost, it is important to screen the predictors. The predictors used in this study was daily mean temperature, relative humidity, rainfall, wind speed, NOx, SO2, CO and O3. Boruta Algorithm was used like previous studies to select the most important variables before running the models [34]. In general, BA uses a wrapper algorithm and it can work with any classification methodology that creates feature importance measure as output. By default, BA utilizes the random forest algorithm to find out the most effective features. The overall results regarding the importance of variables are illustrated in Supplementary Materials Figure S6. The results showed that RH and Temperature are the most important predictors among the meteorological variables. The variable importance of RH for PM2.5 prediction in Dhaka, Narayanganj and Gazipur was 13.8, 13.92 and 14.19, respectively. On the other hand, the importance score for temperature across the stations was 13.75, 13.78 and 14.27, respectively. By using BA, the first seven important covariates were selected for the model training and testing later to avoid the overfitting of the models.
Between the models, deep learning model, that is, CatBoost performed better in terms of lower RMSE and MAE values. In this study, the best model architecture of CatBoost found when the iterations = 1500, learning rate = 0.01, random seed = 55, metric period = 1 and depth = 10. During the training period, CatBoost showed lower RMSE and MAE values than the DT. For PM2.5 prediction of Dhaka, Narayanganj and Gazipur, the RMSE value of the CatBoost were 11.41 µg m−3, 12.56 µg m−3 and 12.07 µg m−3, respectively whereas for DT, they were 12.27 µg m−3, 13.07 µg m−3 and 14.21 µg m−3, respectively. Figure 7 indicates that the results of CatBoost and DT was acceptable. During the test period, The RMSE values were 12.39 µg m−3, 13.06 µg m−3 and 12.97 µg m−3 for Dhaka, Narayanganj and Gazipur, respectively. Over-fitting or over-training was controlled in this study during the model execution. A study in Tehran [48], similar to this study, utilized DT model to predict the PM2.5 concentration. It used CO, O3, NO2, SO2, average nebulosity, wind speed, sunshine, maximum and minimum air temperature, relative humidity and precipitation as the covariates. The RMSE value was 0.0591, which was much better than this study. On the other hand, the study related to the application of the CatBoost deep learning model in terms of air pollution modeling is limited. A recent study recommends the application of CatBoost [49]. Among the models, that is, the M5Tree, RF, XGBoost, CatBoost and SVM, Catboost showed satisfactory generalization capability and high computational efficiency.
4.5. Results of PCR
The explanatory variables were transformed into PCs through the variables’ eigenvalue matrix, which would explain most of the variation of the PM2.5 dataset. The PCR models for all the air monitoring stations were developed with the PCs and analyzed statistically. The study utilized t-test (95% confidence interval) to examine the significance of the variables. The statistically insignificant PCs were removed from the final model development. It was observed that 6 PCs (PM10, SO2, WS, Temp, RH and RF) were found statistically significant for Dhaka. Like Dhaka, the study found similar number of PCs for Gazipur to model PM2.5 concentration, which are PM10, SO2, NOx, WS, Temp and RH. However, only 4 PCs, that is, PM10, CO, NOx and Temp, were found statistically significant for Narayanganj air monitoring station. The equations for the Dhaka (Equation (24)), Gazipur (Equation (25)) and Narayanganj (Equation (26)) are given below:
Using PCR, the best prediction result was found for Dhaka and Gazipur. To predict the PM2.5, the lowest RMSE value (=25.31 µg m−3) and MAE (=14.23 µg m−3) was found in Dhaka during the training period. On the other hand, the worst performance observed in Narayanganj using the PCR equation (R2 = 0.78, RMSE = 26.87 µg m−3, MAE = 18.73 µg m−3) [Table 4]. A study [50], in Delhi, utilized the PCR approach to predict the AQI value. The found a higher RMSE (on average of 40.28 µg m−3) throughout the seasons.
4.6. Comparison of Model Performance
The study utilized DT and CatBoost to compare them to hybrid models. Comparatively, CatBoost deep learning model performed best among the models for the prediction of PM2.5 as it showed higher R2 and lower RMSE and MAE value. From Table 4 and Figure 9, it is apparent that CatBoost and proposed ARIMA-ANN model is the best performer in terms of predicting PM2.5 concentration across Dhaka, Narayanganj and Gazipur. On the other hand, a linear model, that is, PCR did not perform well throughout the stations in terms of predicting PM2.5 concentration.
Besides, there are some important results attained in the experiments of this study. Firstly, when individual methods’ results, that is, ARIMA were compared among other studies, it showed relatively similar results with it and other machine learning models. On the other hand, the proposed hybrid methods presented better performance as compared to individual ones, especially for these datasets. Finally, the assumptions made by other hybrid methods like Zhang’s hybrid method [51], Khashei and Bijari’s hybrid method [52], Babu and Reddy’s hybrid method [53] degenerate the performance of the forecasting when unexpected situations occur in the dataset. However, this hybrid model avoids these assumptions apparently and thus, creates more general models and outperforms the other individual examined models.
5. Conclusions
The present study assessed the performance of two hybrid models (ARIMA-ANN and ARIMA-SVM) and two tree-based soft computing models (Decision Tree and CatBoost) for predicting daily PM2.5 concentration in three air pollution hotspots in Bangladesh data in terms of prediction accuracy and computational efficiency. The result indicated that, among the models, CatBoost showed the best performance in terms of higher R2 value and lower RMSE and MAE value. Besides, the second-best performer among the models was ARIMA-ANN. ANN offered the best combination with ARIMA to predict accuracy and generalization capability in all three air monitoring stations, followed by the CatBoost deep learning model. Therefore, the study recommends further research on developing deep learning model for forecasting air pollution in Bangladesh. Finally, the obtained results from the study revealed that the efficiency of ARIMA-ANN and deep learning models could deliver useful information for the government officials and policymakers to take immediate actions understanding the early alerts of the pollution.
Supplementary Materials
The following are available online at https://www.mdpi.com/2073-4433/12/1/100/s1, Figure S1: Monthly and daily pattern of particulate matters across the air monitoring stations from 2013–2019. Figure S2: Season-wise correlation among the meteorological variables and atmospheric pollutants in Dhaka, Narayanganj and Gazipur. Figure S3: ACF and PACF plot of daily PM2.5 concentration at the air monitoring stations. Figure S4: Residual plot of the models. Figure S5: Diagnostic test of residuals from the model (Normal Q-Q plot). Figure S6. Variable importance for predicting PM2.5 across A. Dhaka, B. Narayanganj and C. Gazipur.
Author Contributions
Conceptualization, S.A.S., M.A.S., I.K.; methodology, S.A.S., I.K. and R.I.; software, S.A.S., K.H., R.I.; validation, M.A.S., I.K.; formal analysis, I.K., K.H., M.H.; investigation, M.A.S., A.E.R., Z.H., N.R.A.; resources, I.K., M.H., K.H.; data curation, S.A.S., I.K., K.H., M.H.; writing—original draft preparation, S.A.S., K.H., M.H.; writing—review and editing, I.K., M.A.S., N.R.A., Z.H., A.E.R.; visualization, S.A.S.; supervision, M.A.S., I.K.; project administration, M.A.S., A.E.R., Z.H., N.R.A.; All authors have read and agreed to the published version of the manuscript.
Funding
This research received partial funding from the Ministry of Higher Education, Malaysia, under the Fundamental Research Grant Scheme (FRGS), Project no. R/FRGS/A0800/01525A003/2018/00554.
Acknowledgments
We, highly, acknowledge the support from Department of Environment, Ministry of Environment, Forest and Climate Change, Government of Bangladesh.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Manisalidis, I.; Stavropoulou, E.; Stavropoulos, A.; Bezirtzoglou, E. Environmental and Health Impacts of Air Pollution: A Review. Front. Public Health 2020, 8, 14. [Google Scholar] [CrossRef]
- Lv, D.; Chen, Y.; Zhu, T.; Li, T.; Shen, F.; Li, X.; Mehmood, T.; Ying, C. The pollution characteristics of PM10 and PM2.5 during summer and winter in Beijing, Suning and Islamabad. Atmos. Pollut. Res. 2019, 10, 1159–1164. [Google Scholar] [CrossRef]
- Bo, M.; Salizzoni, P.; Clerico, M.; Buccolieri, R. Assessment of Indoor-Outdoor Particulate Matter Air Pollution: A Review. Atmosphere 2017, 8, 136. [Google Scholar] [CrossRef]
- Fuzzi, S.; Baltensperger, U.; Carslaw, K.S.; Decesari, S.; Van Der Gon, H.D.; Facchini, M.C.; Fowler, D.; Koren, I.; Langford, B.; Lohmann, U.; et al. Particulate matter, air quality and climate: Lessons learned and future needs. Atmos. Chem. Phys. Discuss. 2015, 15, 8217–8299. [Google Scholar] [CrossRef]
- Cesari, D.; De Benedetto, G.; Bonasoni, P.; Busetto, M.; Dinoi, A.; Merico, E.; Chirizzi, D.; Cristofanelli, P.; Donateo, A.; Grasso, F.; et al. Seasonal variability of PM2.5 and PM10 composition and sources in an urban background site in Southern Italy. Sci. Total Environ. 2018, 612, 202–213. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.-Y.; Dunea, D.; Iordache, S.; Pohoata, A. A Review of Airborne Particulate Matter Effects on Young Children’s Respiratory Symptoms and Diseases. Atmosphere 2018, 9, 150. [Google Scholar] [CrossRef]
- Choi, S.; Kim, K.H.; Kim, K.; Chang, J.; Kim, S.M.; Kim, S.R.; Cho, Y.; Lee, G.; Son, J.S.; Park, S.M. Association between Post-Diagnosis Particulate Matter Exposure among 5-Year Cancer Survivors and Cardiovascular Disease Risk in Three Metropolitan Areas from South Korea. Int. J. Environ. Res. Public Health 2020, 17, 2841. [Google Scholar] [CrossRef]
- Jaganathan, S.; Jaacks, L.M.; Magsumbol, M.; Walia, G.K.; Sieber, N.L.; Shivashankar, R.; Dhillon, P.K.; Shahulhameed, S.; Schwartz, J.D.; Prabhakaran, D. Association of Long-Term Exposure to Fine Particulate Matter and Cardio-Metabolic Diseases in Low- and Middle-Income Countries: A Systematic Review. Int. J. Environ. Res. Public Health 2019, 16, 2541. [Google Scholar] [CrossRef]
- Yin, P.; Guo, J.; Wang, L.; Fan, W.; Lu, F.; Guo, M.; Moreno, S.B.R.; Wang, Y.; Wang, H.; Zhou, M.; et al. Higher Risk of Cardiovascular Disease Associated with Smaller Size-Fractioned Particulate Matter. Environ. Sci. Technol. Lett. 2020, 7, 95–101. [Google Scholar] [CrossRef]
- Bae, J.-E.; Choi, H.; Shin, D.W.; Na, H.-W.; Park, N.Y.; Kim, J.B.; Jo, D.S.; Cho, M.J.; Lyu, J.H.; Chang, J.H.; et al. Fine particulate matter (PM2.5) inhibits ciliogenesis by increasing SPRR3 expression via c-Jun activation in RPE cells and skin keratinocytes. Sci. Rep. 2019, 9, 3994. [Google Scholar] [CrossRef]
- Bowe, B.; Xie, Y.; Li, T.; Yan, Y.; Xian, H.; Al Aly, Z. Estimates of the 2016 global burden of kidney disease attributable to ambient fine particulate matter air pollution. BMJ Open 2019, 9, e022450. [Google Scholar] [CrossRef] [PubMed]
- Atkinson, R.; Kang, S.; Anderson, R.; Mills, I.; Walton, H. Epidemiological time series studies of PM2.5 and daily mortality and hospital admissions: A systematic review and meta-analysis. Thorax 2014, 69, 660–665. [Google Scholar] [CrossRef] [PubMed]
- Kim, K.-H.; Kabir, E.; Kabir, S. A review on the human health impact of airborne particulate matter. Environ. Int. 2015, 74, 136–143. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.; Nethery, R.C.; Sabath, B.M.; Braun, D.; Dominici, F. Exposure to air pollution and COVID-19 mortality in the United States. medRxiv 2020. [Google Scholar] [CrossRef]
- Lelieveld, J.; Evans, J.S.; Fnais, M.; Giannadaki, D.; Pozzer, A. The contribution of outdoor air pollution sources to premature mortality on a global scale. Nat. Cell Biol. 2015, 525, 367–371. [Google Scholar] [CrossRef]
- Begum, B.A.; Hopke, P.K. Ambient Air Quality in Dhaka Bangladesh over Two Decades: Impacts of Policy on Air Quality. Aerosol Air Qual. Res. 2018, 18, 1910–1920. [Google Scholar] [CrossRef]
- Mahmood, A.; Hu, Y.; Nasreen, S.; Hopke, P.K. Airborne Particulate Pollution Measured in Bangladesh from 2014 to 2017. Aerosol Air Qual. Res. 2019, 19, 272–281. [Google Scholar] [CrossRef]
- Begum, B.A.; Biswas, S.K.; Hopke, P.K. Assessment of trends and present ambient concentrations of PM2.2 and PM10 in Dhaka, Bangladesh. Air Qual. Atmos. Health 2008, 1, 125–133. [Google Scholar] [CrossRef]
- Mitra, N.; Shahriar, S.A.; Lovely, N.; Khan, S.; Rak, A.; Kar, S.; Khaleque, A.; Amin, M.F.M.; Kayes, I.; Salam, M.A. Assessing Energy-Based CO2 Emission and Workers’ Health Risks at the Shipbreaking Industries in Bangladesh. Environment 2020, 7, 35. [Google Scholar] [CrossRef]
- Ibn Azkar, M.A.M.B.; Chatani, S.; Sudo, K. Simulation of urban and regional air pollution in Bangladesh. J. Geophys. Res. Space Phys. 2012, 117, 1–23. [Google Scholar] [CrossRef]
- Salam, M.A.; Shirasuna, Y.; Hirano, K.; Masunaga, S. Particle associated polycyclic aromatic hydrocarbons in the atmospheric environment of urban and suburban residential area. Int. J. Environ. Sci. Technol. 2011, 8, 255–266. [Google Scholar] [CrossRef]
- Ab Kadir, Z.; Yusoff, M.; Awang, N.R.; Jani, M.; Arieff, M.; Selvam, B.; Sulaiman, M.A.; Salam, M.A. Identification of Cation Elements in PM10 Concentration in Industrial Area of Penang. J. Trop. Resour. Sustain. Sci. 2017, 5, 46–50. [Google Scholar]
- Kayes, I.; Shahriar, S.A.; Hasan, K.; Akhter, M.; Kabir, M.M.; Salam, M.A. The relationships between meteorological parameters and air pollutants in an urban environment. Glob. J. Environ. Sci. Manag. 2019, 5, 265–278. [Google Scholar] [CrossRef]
- Rybarczyk, Y.; Zalakeviciute, R. Machine Learning Approaches for Outdoor Air Quality Modelling: A Systematic Review. Appl. Sci. 2018, 8, 2570. [Google Scholar] [CrossRef]
- Jiménez, P.A.; Dudhia, J. On the Ability of the WRF Model to Reproduce the Surface Wind Direction over Complex Terrain. J. Appl. Meteorol. Clim. 2013, 52, 1610–1617. [Google Scholar] [CrossRef]
- Chen, Q.; Taylor, D. Transboundary atmospheric pollution in Southeast Asia: Current methods, limitations and future developments. Crit. Rev. Environ. Sci. Technol. 2018, 48, 997–1029. [Google Scholar] [CrossRef]
- Shimadera, H.; Kojima, T.; Kondo, A. Evaluation of Air Quality Model Performance for Simulating Long-Range Transport and Local Pollution of PM2.5 in Japan. Adv. Meteorol. 2016, 2016, 1–13. [Google Scholar] [CrossRef]
- Chen, J.; Chen, J.Y.; Wu, Z.; Hu, D.; Pan, J.Z. Forecasting smog-related health hazard based on social media and physical sensor. Inf. Syst. 2017, 64, 281–291. [Google Scholar] [CrossRef]
- Yang, G.; Lee, H.; Lee, G. A Hybrid Deep Learning Model to Forecast Particulate Matter Concentration Levels in Seoul, South Korea. Atmosphere 2020, 11, 348. [Google Scholar] [CrossRef]
- Suleiman, A.; Tight, M.; Quinn, A. Applying machine learning methods in managing urban concentrations of traffic-related particulate matter (PM10 and PM2.5). Atmos. Pollut. Res. 2019, 10, 134–144. [Google Scholar] [CrossRef]
- Pakrooh, P.; Pishbahar, E. Forecasting Air Pollution Concentrations in Iran, Using a Hybrid. Model. Pollut. 2019, 5, 739–747. [Google Scholar] [CrossRef]
- Kang, G.K.; Gao, J.; Chiao, S.; Lu, S.; Xie, G. Air Quality Prediction: Big Data and Machine Learning Approaches. Int. J. Environ. Sci. Dev. 2018, 9, 8–16. [Google Scholar] [CrossRef]
- Rana, M.; Sulaiman, N.; Sivertsen, B.; Khan, F.; Nasreen, S. Trends in atmospheric particulate matter in Dhaka, Bangladesh, and the vicinity. Environ. Sci. Pollut. Res. 2016, 23, 17393–17403. [Google Scholar] [CrossRef] [PubMed]
- Islam, M.; Sharmin, M.; Ahmed, F. Predicting air quality of Dhaka and Sylhet divisions in Bangladesh: A time series modeling approach. Air Qual. Atmos. Health 2020, 13, 607–615. [Google Scholar] [CrossRef]
- Shahriar, S.A.; Kayes, I.; Hasan, K.; Salam, M.A.; Chowdhury, S. Applicability of machine learning in modeling of atmospheric particle pollution in Bangladesh. Air Qual. Atmos. Health 2020, 13, 1247–1256. [Google Scholar] [CrossRef] [PubMed]
- Krzyzanowski, M.; Apte, J.S.; Bonjour, S.P.; Brauer, M.; Cohen, A.J.; Prüss-Ustun, A.M. Air Pollution in the Mega-cities. Curr. Environ. Health Rep. 2014, 1, 185–191. [Google Scholar] [CrossRef]
- Barzeghar, V.; Sarbakhsh, P.; Hassanvand, M.S.; Faridi, S.; Gholampour, A. Long-term trend of ambient air PM10, PM2.5, and O3 and their health effects in Tabriz city, Iran, during 2006–2017. Sustain. Cities Soc. 2020, 54, 101988. [Google Scholar] [CrossRef]
- Tang, R.; Zeng, F.; Chen, Z.; Jing-Song, W.; Huang, C.M.; Wu, Z. The Comparison of Predicting Storm-Time Ionospheric TEC by Three Methods: ARIMA, LSTM, and Seq2Seq. Atmosphere 2020, 11, 316. [Google Scholar] [CrossRef]
- Mossad, A.; Alazba, A. Drought Forecasting Using Stochastic Models in a Hyper-Arid Climate. Atmosphere 2015, 6, 410–430. [Google Scholar] [CrossRef]
- Kamiński, B.; Jakubczyk, M.; Szufel, P. A framework for sensitivity analysis of decision trees. Cent. Eur. J. Oper. Res. 2018, 26, 135–159. [Google Scholar] [CrossRef]
- Moret, B.M.E. Decision Trees and Diagrams. Acm Comput. Surv. 1982, 14, 593–623. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, Z.; Zheng, J. CatBoost: A new approach for estimating daily reference crop evapotranspiration in arid and semi-arid regions of Northern China. J. Hydrol. 2020, 588, 125087. [Google Scholar] [CrossRef]
- Mat Shukri, M.A.; Yusoff, M.; Awang, N.R.; Jani, M.; Ab Kadir, Z.; Selvam, B.; Sulaiman, M.A.; Salam, M.A. Investigation of relationship between particulate matter (PM2.5 and PM10) and meteorological parameters at Roadside Area of First Penang Bridge. J. Trop. Resour. Sustain. Sci. 2017, 5, 33–39. [Google Scholar]
- Zhang, H.; Wang, Y.; Hu, J.; Ying, Q.; Hu, X.-M. Relationships between meteorological parameters and criteria air pollutants in three megacities in China. Environ. Res. 2015, 140, 242–254. [Google Scholar] [CrossRef] [PubMed]
- Manju, A.; Kalaiselvi, K.; Dhananjayan, V.; Palanivel, M.; Banupriya, G.S.; Vidhya, M.H.; Panjakumar, K.; Ravichandran, B. Spatio-seasonal variation in ambient air pollutants and influence of meteorological factors in Coimbatore, Southern India. Air Qual. Atmos. Health 2018, 11, 1179–1189. [Google Scholar] [CrossRef]
- Haddad, K.; Vizakos, N. Air quality pollutants and their relationship with meteorological variables in four suburbs of Greater Sydney, Australia. Air Qual. Atmos. Health 2020, 1–13. [Google Scholar] [CrossRef]
- Díaz-Robles, L.A.; Ortega, J.C.; Fu, J.S.; Reed, G.D.; Chow, J.C.; Watson, J.G.; Moncada-Herrera, J.A. A hybrid ARIMA and artificial neural networks model to forecast particulate matter in urban areas: The case of Temuco, Chile. Atmos. Environ. 2008, 42, 8331–8340. [Google Scholar] [CrossRef]
- Mehdipour, V.; Stevenson, D.S.; Memarianfard, M.; Sihag, P. Comparing different methods for statistical modeling of particulate matter in Tehran, Iran. Air Qual. Atmos. Health 2018, 11, 1155–1165. [Google Scholar] [CrossRef]
- Fan, J.; Wang, X.; Zhang, F.; Ma, X.; Wu, L. Predicting daily diffuse horizontal solar radiation in various climatic regions of China using support vector machine and tree-based soft computing models with local and extrinsic climatic data. J. Clean. Prod. 2020, 248, 119264. [Google Scholar] [CrossRef]
- Kumar, A.; Goyal, P. Forecasting of air quality in Delhi using principal component regression technique. Atmos. Pollut. Res. 2011, 2, 436–444. [Google Scholar] [CrossRef]
- Zhang, G.P. Time series forecasting using a hybrid ARIMA and neural network model. Neurocomputing 2003, 50, 159–175. [Google Scholar] [CrossRef]
- Babu, C.N.; Reddy, B.E. A moving-average filter based hybrid ARIMA–ANN model for forecasting time series data. Appl. Soft Comput. 2014, 23, 27–38. [Google Scholar] [CrossRef]
- Khashei, M.; Bijari, M. A novel hybridization of artificial neural networks and ARIMA models for time series forecasting. Appl. Soft Comput. 2011, 11, 2664–2675. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).