Combining MWL and MSG SEVIRI Satellite Signals for Rainfall Detection and Estimation
Abstract
1. Introduction
2. Study Area and Dataset
2.1. Study Area
2.2. Data Set
2.2.1. Rain Gauge Data
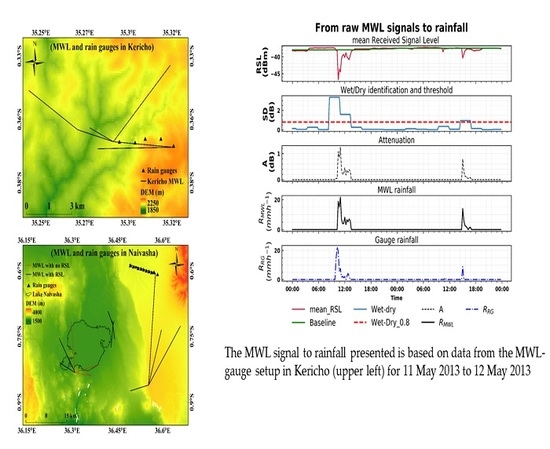
2.2.2. MWL Data
2.2.3. MSG Satellite Data
3. Method
3.1. Estimating Rainfall from Rain Gauges
3.2. Estimating Rainfall from MWL Data
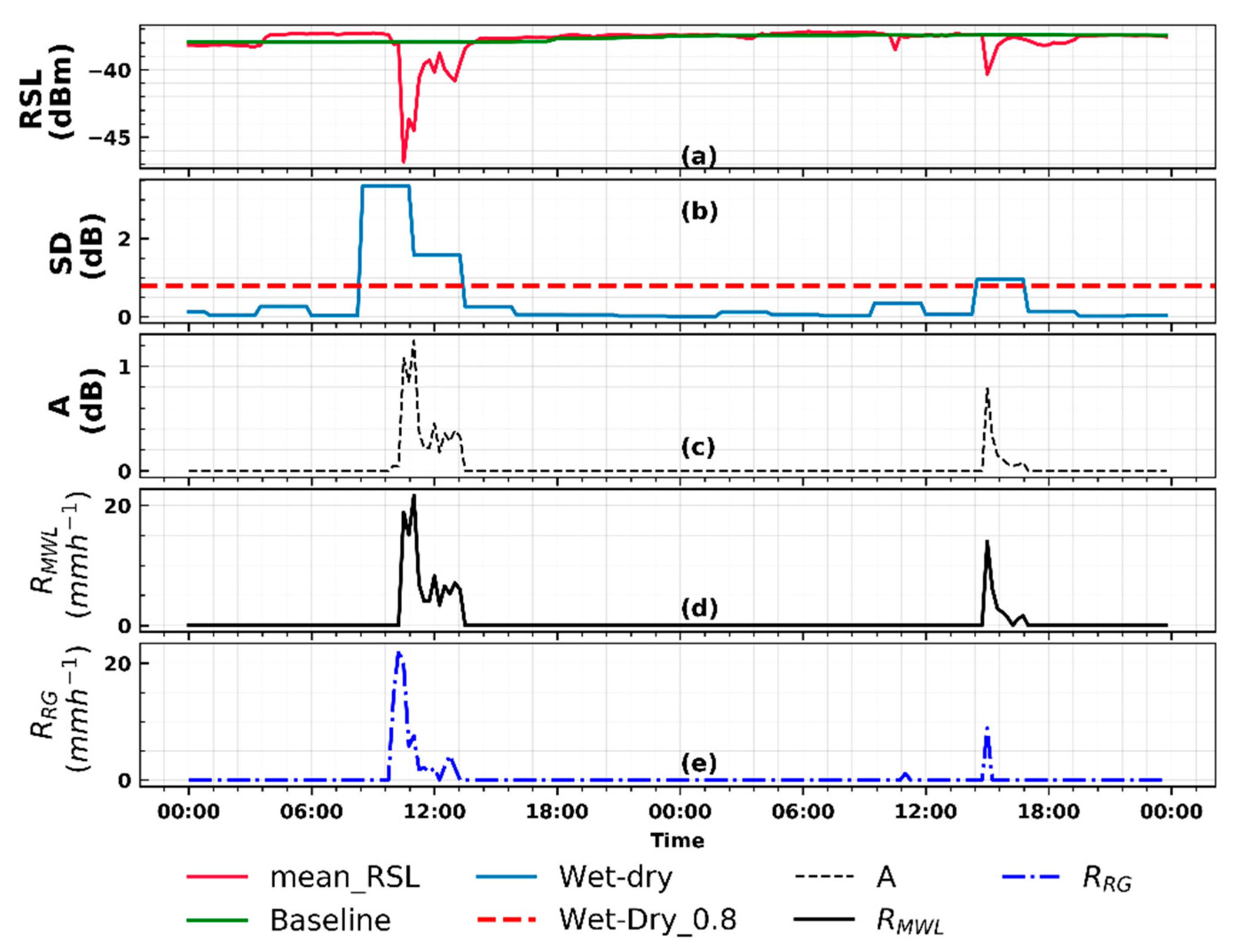
3.2.1. Wet/Dry Classification of RSL Data
3.2.2. Estimating the Reference RSL
3.2.3. Estimating R from Z
3.3. SEVIRI Data Retrieval and Processing
3.3.1. The Conceptual Model for Detecting Rainfall Using MSG SEVIRI Data
3.3.2. The Spatial and Temporal Differences between SEVIRI and Ground Data
3.4. Analysing MWL Rainfall and SEVIRI Data
3.5. Performance Measures
3.5.1. Evaluating MWL Rainfall Intensities
3.5.2. Evaluating the Performance of SEVIRI Based Rain Detection on MWL
4. Results and Discussion
4.1. Results
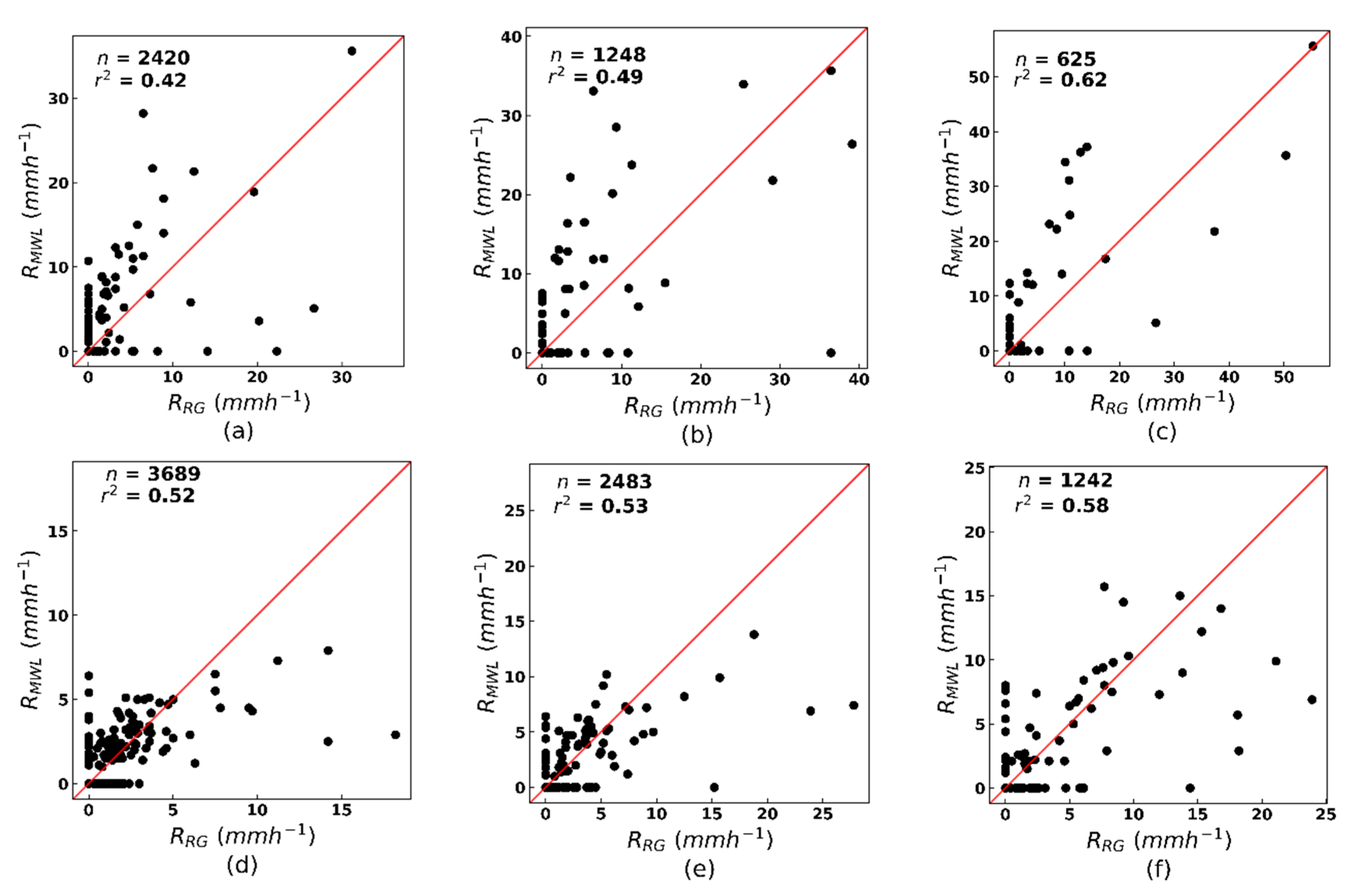
4.1.1. RMWL versus RRG
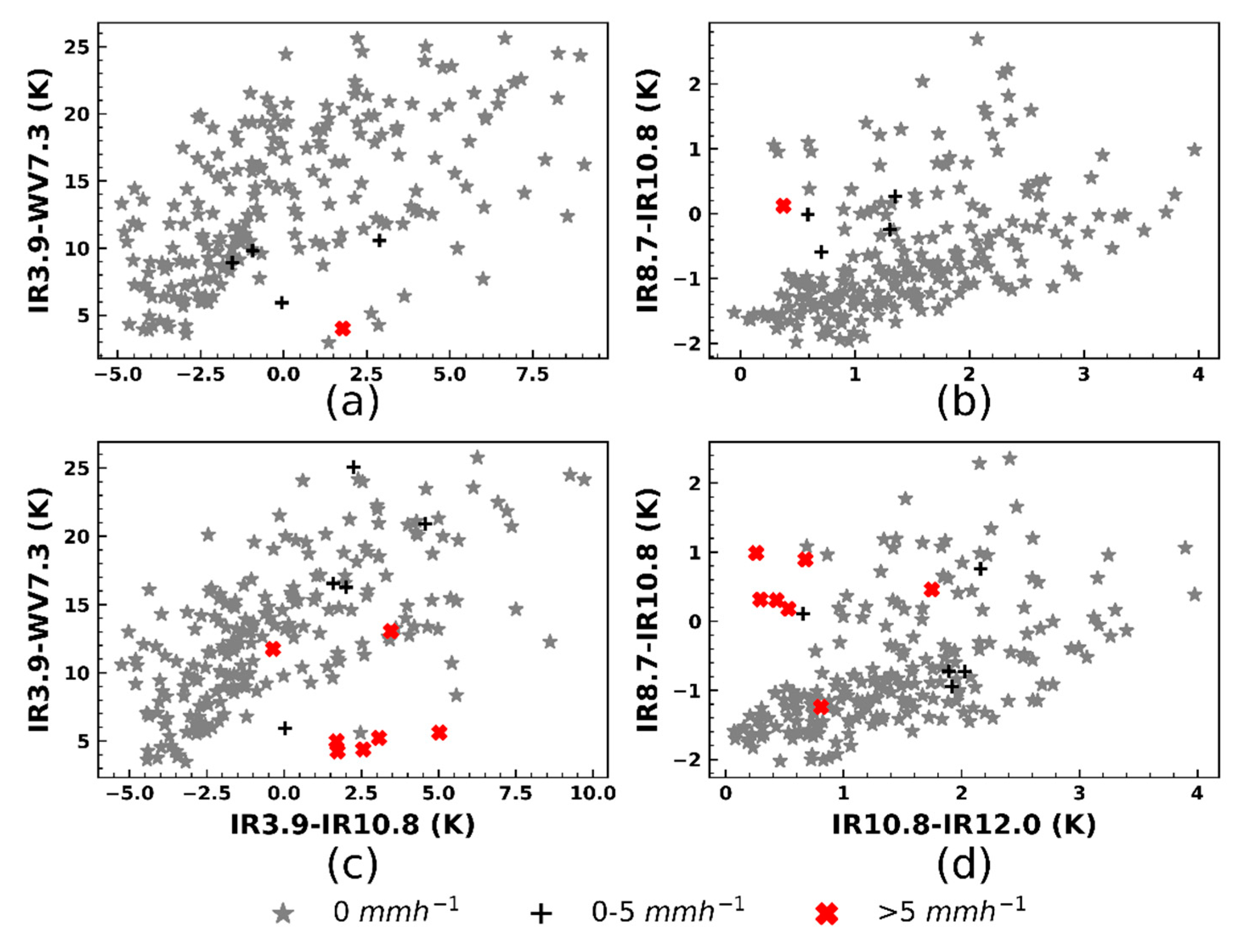
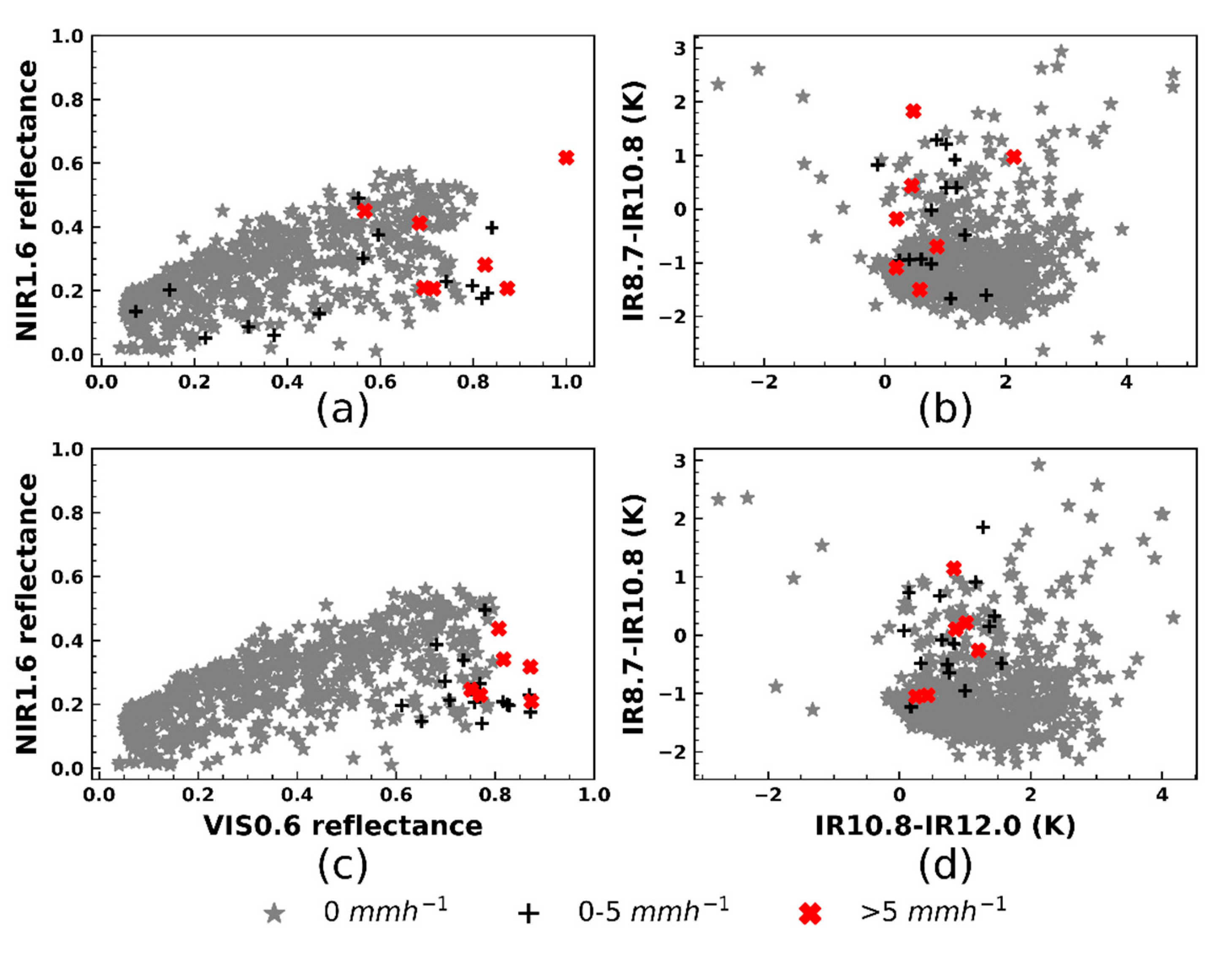
4.1.2. Joint Analysis of Rainfall and SEVIRI Satellite Data
4.1.3. Rainfall Detection with MSG SEVIRI Data
4.2. Discussion
4.2.1. Accuracy of the MWL Rainfall Estimates
4.2.2. The Analysis of RMWL with MSG SEVIRI Data
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| MSG Signal | RMWL (mm h−1) | Min | Max | Mean | Mode | Median | SD |
|---|---|---|---|---|---|---|---|
| Kericho Day time | |||||||
| VIS 0.6 μm | 0 | 0.073 | 0.886 | 0.417 | 0.3 | 0.38 | 0.215 |
| 0–5 | 0.562 | 0.972 | 0.74 | 0.8 | 0.77 | 0.15 | |
| >5 | 0.374 | 1 | 0.726 | 0.7 | 0.726 | 0.148 | |
| NIR 1.6 μm | 0 | 0.036 | 0.858 | 0.337 | 0.3 | 0.32 | 0.132 |
| 0–5 | 0.31 | 0.608 | 0.433 | 0.3 | 0.384 | 0.137 | |
| >5 | 0.178 | 0.536 | 0.304 | 0.3 | 0.296 | 0.09 | |
| ∆TIR8.7-IR10.8 | 0 | −2.357 | 2.177 | −0.613 | −1 | −0.756 | 0.88 |
| 0–5 | −1.826 | 1.417 | −0.453 | - | −0.57 | 1.10 | |
| >5 | −1.721 | 1.42 | −0.137 | −0.9 | −0.354 | 0.915 | |
| ∆TIR10.8-IR12.0 | 0 | −0.55 | 4.336 | 1.711 | 2.3 | 1.736 | 0.98 |
| 0–5 | −0.215 | 2.366 | 0.737 | 0.9 | 0.617 | 0.914 | |
| >5 | −1.836 | 2.064 | 0.469 | 0.8 | 0.561 | 0.749 | |
| Nighttime | |||||||
| ∆TIR3.9-IR10.8 | 0 | −5.252 | 9.709 | −0.204 | −1.6 | −1.166 | 3.194 |
| 0–5 | 0.033 | 4.57 | 2.087 | - | 1.998 | 1.633 | |
| >5 | −0.366 | 5.026 | 2.454 | 1.7 | 2.563 | 1.686 | |
| ∆TIR3.9-WV7.3 | 0 | 3.466 | 25.765 | 12.884 | 13.2 | 12.64 | 5.122 |
| 0–5 | 5.933 | 25.068 | 16.938 | - | 16.537 | 7.134 | |
| >5 | 4.234 | 13.046 | 7.033 | - | 5.226 | 3.711 | |
| ∆TIR8.7-IR10.8 | 0 | −2.024 | 2.354 | −0.702 | −1.1 | −0.959 | 0.894 |
| 0–5 | −0.944 | 0.76 | −0.306 | −0.7 | −0.724 | 0.72 | |
| >5 | −1.242 | 0.988 | 0.272 | 0.3 | 0.318 | 0.734 | |
| ∆TIR10.8-IR12.0 | 0 | 0.072 | 3.976 | 1.449 | 1.5 | 1.365 | 0.808 |
| 0–5 | 0.655 | 2.162 | 1.732 | 1.9 | 1.918 | 0.611 | |
| >5 | 0.258 | 1.748 | 0.678 | 0.3 | 0.532 | 0.511 | |
| Naivasha Day time | |||||||
| VIS 0.6 μm | 0 | 0.04 | 0.795 | 0.338 | 0.1 | 0.314 | 0.221 |
| 0–5 | 0.611 | 0.871 | 0.758 | 0.8 | 0.764 | 0.075 | |
| >5 | 0.751 | 0.873 | 0.815 | 0.8 | 0.812 | 0.05 | |
| NIR 1.6 μm | 0 | 0.01 | 0.561 | 0.256 | 0.2 | 0.239 | 0.124 |
| 0–5 | 0.14 | 0.495 | 0.244 | 0.2 | 0.21 | 0.093 | |
| >5 | 0.209 | 0.437 | 0.296 | 0.2 | 0.281 | 0.086 | |
| ∆TIR8.7-IR10.8 | 0 | −2.199 | 2.923 | −0.973 | −1.2 | −1.184 | 0.775 |
| 0–5 | −1.232 | 1.85 | −0.066 | −0.5 | 0.114 | 0.834 | |
| >5 | −1.054 | 1.146 | −0.146 | - | −0.077 | 0.835 | |
| ∆TIR10.8-IR12.0 | 0 | −2.76 | 4.17 | 1.31 | 1.8 | 1.282 | 0.859 |
| 0–5 | 0.073 | 1.556 | 0.786 | 0.1 | 0.748 | 0.497 | |
| >5 | 0.249 | 1.202 | 0.763 | - | 0.843 | 0.359 | |
| Nighttime | |||||||
| ∆TIR3.9-IR10.8 | 0 | −5.37 | 12.848 | −1.162 | −2.5 | −1.972 | 2.436 |
| 0–5 | −2.404 | 8.041 | 0.844 | - | 0.315 | 3.036 | |
| >5 | −2.4 | 6.999 | 0.537 | - | 0.166 | 2.42 | |
| ∆TIR3.9-WV7.3 | 0 | 3.834 | 22.985 | 13.495 | 11.7 | 13.33 | 4.015 |
| 0–5 | 3.648 | 13.04 | 8.537 | 13 | 9.44 | 2.967 | |
| >5 | 3.317 | 16.932 | 7.845 | - | 7.994 | 3.902 | |
| ∆TIR8.7-IR10.8 | 0 | −1.851 | 2.175 | −0.84 | −1.2 | −1.071 | 0.709 |
| 0–5 | −1.277 | 1.953 | −0.144 | −0.9 | −0.258 | 0.884 | |
| >5 | −1.246 | 1.239 | −0.171 | −0.1 | −0.145 | 0.697 | |
| ∆TIR10.8-IR12.0 | 0 | −0.181 | 4.008 | 0.945 | 0.9 | 0.851 | 0.715 |
| 0–5 | 0.017 | 2.504 | 0.809 | 0.5 | 0.674 | 0.514 | |
| >5 | 0.258 | 1.426 | 0.742 | 0.8 | 0.72 | 0.289 | |
References
- Hong, Y.; Adler, R.F.; Negri, A.; Huffman, G.J. Flood and landslide applications of near real-time satellite rainfall products. Nat. Hazards 2007, 43, 285–294. [Google Scholar] [CrossRef]
- Levizzani, V.; Bauer, P.; Turk, F.J. Measuring Precipitation from Space: EURAINSAT and the Future; Springer: Dordrecht, The Netherlands, 2007; Volume 28, p. 722. [Google Scholar]
- Cristiano, E.; ten Veldhuis, M.-C.; van de Giesen, N. Spatial and temporal variability of rainfall and their effects on hydrological response in urban areas—A review. Hydrol. Earth Syst. Sci. 2017, 21, 3859–3878. [Google Scholar] [CrossRef]
- Michaelides, S.; Levizzani, V.; Anagnostou, E.; Bauer, P.; Kasparis, T.; Lane, J.E. Precipitation: Measurement, remote sensing, climatology and modeling. Atmos. Res. 2009, 94, 512–533. [Google Scholar] [CrossRef]
- Rios, G.M.F.; Aart, O.; Hidde, L.; Marc, B.; Remko, U. Rainfall Field Estimation Using Simulated Microwave Link Information. Master’s Thesis, Faculty of Geosciences, Utrecht University, Utrecht, The Netherlands, 2012. [Google Scholar]
- Villarini, G.; Mandapaka, P.V.; Krajewski, W.F.; Moore, R.J. Rainfall and sampling uncertainties: A rain gauge perspective. J. Geophys. Res. Atmos. 2008, 113, 1–12. [Google Scholar] [CrossRef]
- Tang, G.Q.; Ma, Y.Z.; Long, D.; Zhong, L.Z.; Hong, Y. Evaluation of GPM Day-1 IMERG and TMPA Version-7 legacy products over Mainland China at multiple spatiotemporal scales. J. Hydrol. 2016, 533, 152–167. [Google Scholar] [CrossRef]
- Barthès, L.; Mallet, C. Rainfall measurement from the opportunistic use of an Earth-space link in the Ku band. Atmos. Meas. Tech. 2013, 6, 2181–2193. [Google Scholar] [CrossRef]
- Upton, G.J.G.; Holt, A.R.; Cummings, R.J.; Rahimi, A.R.; Goddard, J.W.F. Microwave Links: The Future For Urban Rainfall Measurement? Atmos. Res. 2005, 77, 300–312. [Google Scholar] [CrossRef]
- Dinku, T.; Chidzambwa, S.; Ceccato, P.; Connor, S.J.; Ropelewski, C.F. Validation of satellite rainfall products over East Africa’s complex topography. Int. J. Remote Sens. 2008, 29, 4097–4110. [Google Scholar] [CrossRef]
- Kidd, C.; Becker, A.; Huffman, G.J.; Muller, C.L.; Joe, P.; Skofronick-Jackson, G.; Kirschbaum, D.B. So, how much of the Earth’s surface is covered by rain gauges? Bull. Am. Meteorol. Soc. 2017, 98, 69–78. [Google Scholar] [CrossRef]
- Lengfeld, K.; Clemens, M.; Münster, H.; Ament, F. Performance of high-resolution X-band weather radar networks - The PATTERN example. Atmos. Meas. Tech. 2014, 7, 4151–4166. [Google Scholar] [CrossRef]
- Uijlenhoet, R.; Berne, A. Stochastic simulation experiment to assess radar rainfall retrieval uncertainties associated with attenuation and its correction. Hydrol. Earth Syst. Sci. 2008, 12, 587–601. [Google Scholar] [CrossRef]
- Villarini, G.; Krajewski, W.F. Review of the Different Sources of Uncertainty in Single Polarization Radar-Based Estimates of Rainfall. Surv. Geophys. 2010, 31, 107–129. [Google Scholar] [CrossRef]
- David, N.; Alpert, P.; Messer, H. The potential of cellular network infrastructures for sudden rainfall monitoring in dry climate regions. Atmos. Res. 2013, 131, 13–21. [Google Scholar] [CrossRef]
- Dinku, T.; Anagnostou, E.N.; Borga, M. Improving radar-based estimation of rainfall over complex terrain. J. Appl. Meteorol. 2002, 41, 1163–1178. [Google Scholar] [CrossRef]
- Hoedjes, J.C.B.; Kooiman, A.; Maathuis, B.H.P.; Said, M.Y.; Becht, R.; Limo, A.; Mumo, M.; Nduhiu-Mathenge, J.; Shaka, A.; Su, B. A Conceptual Flash Flood Early Warning System for Africa, Based on Terrestrial Microwave Links and Flash Flood Guidance. ISPRS Int. J. Geo-Inf. 2014, 3, 584–598. [Google Scholar] [CrossRef]
- Rosenfeld, D. Cloud Top Microphysics as a Tool for Precipitation Measurements. In Measuring Precipitation from Space; Levizzani, V., Bauer, P., Turk, F.J., Eds.; Springer: Dordrecht, The Netherlands, 2007; Volume 1, pp. 61–77. [Google Scholar]
- Kidd, C.; Levizzani, V.; Laviola, S.; Testik, F.Y.; Gebremichael, M. Section II: Rainfall Measurement and Estimation. In Extreme Events; American Geophysical Union (AGU): Washington, DC, USA, 2010; Volume 191, pp. 127–158. [Google Scholar]
- Paredes, T.J.F.; Álvarez, B.H.; Peñaloza-Murillo, M.A.; Moreno, M.A.; Farias, A. Intercomparison of improved satellite rainfall estimation with CHIRPS gridded product and rain gauge data over Venezuela. Atmósfera 2016, 29, 323–342. [Google Scholar] [CrossRef]
- Sohn, B.J.; Han, H.J.; Seo, E.K. Validation of satellite-based high-resolution rainfall products over the Korean Peninsula using data from a dense rain gauge network. J. Appl. Meteorol. Climatol. 2010, 49, 701–714. [Google Scholar] [CrossRef]
- Dezfuli, A.K.; Ichoku, C.M.; Huffman, G.J.; Mohr, K.I.; Selker, J.S.; van de Giesen, N.; Hochreutener, R.; Annor, F.O. Validation of IMERG Precipitation in Africa. J. Hydrometeorol. 2017, 18, 2817–2825. [Google Scholar] [CrossRef]
- Doumounia, A.; Gosset, M.; Cazenave, F.; Kacou, M.; Zougmore, F. Rainfall monitoring based on microwave links from cellular telecommunication networks: First results from a West African test bed. Geophys. Res. Lett. 2014, 41, 6016–6022. [Google Scholar] [CrossRef]
- Chwala, C.; Gmeiner, A.; Qiu, W.; Hipp, S.; Nienaber, D.; Siart, U.; Eibert, T.; Pohl, M.; Seltmann, J.; Fritz, J.; et al. Precipitation observation using microwave backhaul links in the alpine and pre-alpine region of Southern Germany. Hydrol. Earth Syst. Sci. 2012, 16, 2647–2661. [Google Scholar] [CrossRef]
- Leijnse, H.; Uijlenhoet, R.; Stricker, J.N.M. Hydrometeorological Application Of A Microwave Link: 2. Precipitation. Water Resour. Res. 2007, 43, 1–9. [Google Scholar] [CrossRef]
- Messer, H.; Zinevich, A.; Alpert, P. Environmental monitoring by wireless communication networks. Science 2006, 312, 713. [Google Scholar] [CrossRef] [PubMed]
- Overeem, A.; Leijnse, H.; Uijlenhoet, R. Retrieval algorithm for rainfall mapping from microwave links in a cellular communication network. Atmos. Meas. Tech. 2016, 9, 2425–2444. [Google Scholar] [CrossRef]
- Marielle, G.; Kunstmann, H.; Zougmore, F.; Cazenave, F.; Leijnse, H.; Uijlenhoet, R.; Chwala, C.; Keis, F.; Doumounia, A.; Boubacar, B.; et al. Improving Rainfall Measurement in Gauge Poor Regions Thanks to Mobile Telecommunication Networks. Bull. Am. Meteorol. Soc. 2016, 97, ES49–ES51. [Google Scholar] [CrossRef]
- Uijlenhoet, R.; Overeem, A.; Leijnse, H. Opportunistic remote sensing of rainfall using microwave links from cellular communication networks. Wires Water 2018, 5. [Google Scholar] [CrossRef]
- Chwala, C.; Kunstmann, H. Commercial microwave link networks for rainfall observation: Assessment of the current status and future challenges. Wires Water 2019, 6, e1337. [Google Scholar] [CrossRef]
- Sebastianelli, S.; Russo, F.; Napolitano, F.; Baldini, L. On precipitation measurements collected by a weather radar and a rain gauge network. Nat. Hazards Earth Syst. Sci. 2013, 13, 605–623. [Google Scholar] [CrossRef]
- Todini, E. A Bayesian technique for conditioning radar precipitation estimates to rain-gauge measurements. Hydrol. Earth Syst. Sci. 2001, 5, 187–199. [Google Scholar] [CrossRef]
- Long, Y.; Zhang, Y.; Ma, Q. A Merging Framework for Rainfall Estimation at High Spatiotemporal Resolution for Distributed Hydrological Modeling in a Data-Scarce Area. Remote Sens. 2016, 8, 599. [Google Scholar] [CrossRef]
- Bianchi, B.; Jan van Leeuwen, P.; Hogan, R.J.; Berne, A. A Variational Approach to Retrieve Rain Rate by Combining Information from Rain Gauges, Radars, and Microwave Links. J. Hydrometeorol. 2013, 14, 1897–1909. [Google Scholar] [CrossRef]
- Liberman, Y.; Samuels, R.; Alpert, P.; Messer, H. New algorithm for integration between wireless microwave sensor network and radar for improved rainfall measurement and mapping. Atmos. Meas. Tech. 2014, 7, 3549–3563. [Google Scholar] [CrossRef]
- Scheidegger, A.; Rieckermann, J. Bayesian Assimilation of Rainfall Sensors with Fundamentally Different Integration Characteristics. Available online: https://www.researchgate.net/publication/261586169_Bayesian_assimilation_of_rainfall_sensors_with_fundamentally_different_integration_characteristics (accessed on 16 August 2020).
- Kühnlein, M.; Thies, B.; Nauß, T.; Bendix, J. Rainfall-Rate Assignment Using MSG SEVIRI Data—A Promising Approach to Spaceborne Rainfall-Rate Retrieval for Midlatitudes. J. Appl. Meteorol. Climatol. 2010, 49, 1477–1495. [Google Scholar] [CrossRef]
- Thies, B.; Nauss, T.; Bendix, J. Discriminating raining from non-raining cloud areas at mid-latitudes using meteosat second generation SEVIRI night-time data. Meteorol. Appl. 2008, 15, 219–230. [Google Scholar] [CrossRef]
- Thies, B.; Nauss, T.; Bendix, J. Discriminating raining from non-raining clouds at mid-latitudes using meteosat second generation daytime data. Atmos. Chem. Phys. 2008, 8, 2341–2349. [Google Scholar] [CrossRef]
- Roebeling, R.A.; Holleman, I. SEVIRI rainfall retrieval and validation using weather radar observations. J. Geophys. Res. Atmos. 2009, 114, 1–13. [Google Scholar] [CrossRef]
- Schip, v.h.T.I.; Overeem, A.; Leijnse, H.; Uijlenhoet, R.; Meirink, J.F.; van Delden, A.J. Rainfall measurement using cell phone links: Classification of wet and dry periods using geostationary satellites. Hydrol. Sci. J. 2017, 62, 1343–1353. [Google Scholar] [CrossRef]
- Hoedjes, J.; Said, M.; Becht, R.; Kifugo, S.; Kooiman, A.; Limo, A.; Maathuis, B.; Moore, I.; Mumo, M.; Nduhiu Mathenge, J.; et al. Towards Near Real-time Convective Rainfall Observations over Kenya. EGUGA 2013, EGU2013-8082. [Google Scholar]
- Kimani, M.W.; Hoedjes, J.C.B.; Su, Z. An assessment of satellite-derived rainfall products relative to ground observations over East Africa. Remote Sens. 2017, 9, 430. [Google Scholar] [CrossRef]
- Schneider, T.; Bischoff, T.; Haug, G.H. Migrations and dynamics of the intertropical convergence zone. Nature 2014, 513, 45–53. [Google Scholar] [CrossRef]
- MoAlf. Climate Risk Profile for Kericho County. Kenya County Climate Risk Profile Series; MoAlf: Nairobi, Kenya, 2017. [Google Scholar]
- Odongo, V.O.; van der Tol, C.; van Oel, P.R.; Meins, F.M.; Becht, R.; Onyando, J.; Su, Z. Characterisation of hydroclimatological trends and variability in the Lake Naivasha basin, Kenya. Hydrol. Process. 2015, 29, 3276–3293. [Google Scholar] [CrossRef]
- Kenya, R.O. County Government of Kericho: Second Generation County Integrated Development Plan 2018–2022; Kenya, R.O.: Nairobi, Kenya, 2017. [Google Scholar]
- van de Giesen, N.; Hut, R.; Selker, J. The Trans-African Hydro-Meteorological Observatory (TAHMO). Wiley Interdiscip. Rev. Water 2014, 1, 341–348. [Google Scholar] [CrossRef]
- EROS, U. USGS EROS Archive—Digital Elevation—Shuttle Radar Topography Mission (SRTM) 1 Arc-Second Global. Available online: https://www.usgs.gov/centers/eros/science/usgs-eros-archive-digital-elevation-shuttle-radar-topography-mission-srtm-1-arc?qt-science_center_objects=0#qt-science_center_objects (accessed on 28 April 2020).
- Atlas, D.; Ulbrich, C.W. Path- and Area-Integrated Rainfall Measurement by Microwave Attenuation in the 1-3 cm Band. J. Appl. Meteorol. 1977, 16, 1322–1331. [Google Scholar] [CrossRef]
- Zinevich, A.; Messer, H.; Alpert, P. Prediction of rainfall intensity measurement errors using commercial microwave communication links. Atmos. Meas. Tech. 2010, 3, 1385–1402. [Google Scholar] [CrossRef]
- EUMETSAT. Meteosat Second Generation (MSG) Provides Images of the Full Earth disc, and Data for Weather Forecasts. Available online: https://www.eumetsat.int/website/home/Satellites/CurrentSatellites/Meteosat/index.html (accessed on 11 August 2020).
- Eumetsat. Meteosat-8 Satellite’s New Position of 41.5E Provides Weather and Climate View over the Indian Ocean. Available online: https://phys.org/news/2016-09-meteosat-satellite-position-415e-weather.html (accessed on 14 July 2020).
- Schmetz, J.; Pili, P.; Tjemkes, S.; Just, D.; Kerkmann, J.; Rota, S.; Ratier, A. An Introduction to Meteosat Second Generation (MSG). Bull. Am. Meteorol. Soc. 2002, 83, 977–992. [Google Scholar] [CrossRef]
- Maathuis, B.; Mannaerts, C.; Schouwenburg, M.; Retsios, B.; Lemmens, R. GEONETCAST Toolbox: Installation, Configuration and User Guide of the Geonetcast Toolbox Plug-In for Ilwis 3.7; University of Twente: Enschede, The Netherlands, 2014; pp. 1–143. [Google Scholar]
- Bergès, J.C.; Chopin, F.; Bessat, F.; Based, S. Satellite Based Downscaling Algorithm for Rainfall Estimation Hal. In Proceedings of the IV Colóquio Brasileiro de Ciências Geodésicas—IV CBCG, Curitiba, Brazil, 16–20 May 2005. [Google Scholar]
- Olsen, R.; Rogers, D.; Hodge, D. The aRb Relation in the Calculation of Rain Attenuation. IEEE Trans. Antennas Propag. 1978, 26, 318–329. [Google Scholar] [CrossRef]
- Itu, R. RECOMMENDATION ITU-R P.838-2 Specific Attenuation Model for Rain for Use in Prediction Methods; 1992199920032; ITU: Geneva, Switzerland, 2005; pp. 1–8. [Google Scholar]
- Ostrometzky, J.; Messer, H. Accumulated Rainfall Estimation Using Maximum Attenuation of Microwave Radio Signal. In Proceedings of the 2014 IEEE 8th Sensor Array and Multichannel Signal Processing Workshop (SAM), A Coruna, Spain, 22–25 June 2014; pp. 193–196. [Google Scholar]
- David, N.; Alpert, P.; Messer, H. Technical Note: Novel method for water vapour monitoring using wireless communication networks measurements. Atmos. Chem. Phys. 2009, 9, 2413–2418. [Google Scholar] [CrossRef]
- David, N.; Gao, H.O. Using Cell-Phone Tower Signals for Detecting the Precursors of Fog. J. Geophys. Res. Atmos. 2018, 123, 1325–1338. [Google Scholar] [CrossRef]
- Schleiss, M.; Berne, A. Identification of dry and rainy periods using telecommunication microwave links. IEEE Geosci. Remote Sens. Lett. 2010, 7, 611–615. [Google Scholar] [CrossRef]
- Wang, Z.; Schleiss, M.; Jaffrain, J.; Berne, A.; Rieckermann, J. Using Markov switching models to infer dry and rainy periods from telecommunication microwave link signals. Atmos. Meas. Tech. 2012, 5, 1847–1859. [Google Scholar] [CrossRef]
- Endris, H.S.; Omondi, P.; Jain, S.; Lennard, C.; Hewitson, B.; Chang’a, L.; Awange, J.L.; Dosio, A.; Ketiem, P.; Nikulin, G.; et al. Assessment of the Performance of CORDEX Regional Climate Models in Simulating East African Rainfall. J. Clim. 2013, 26, 8453–8475. [Google Scholar] [CrossRef]
- Wakachala, F.M.; Shilenje, Z.W.; Nguyo, J.; Shaka, S.; Apondo, W. Statistical Patterns of Rainfall Variability in the Great Rift Valley of Kenya. J. Environ. Agric. Sci. 2015, 5, 17–26. [Google Scholar]
- ITU. ITU-R Attenuation by Atmospheric Gases and Related Effects; ITU: Istanbul, Turkey, 2019. [Google Scholar]
- Schleiss, M.; Rieckermann, J.; Berne, A. Quantification and modeling of wet-antenna attenuation for commercial microwave links. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1195–1199. [Google Scholar] [CrossRef]
- Thies, B.; Nauss, T.; Bendix, J. First results on a process-oriented rain area classification technique using Meteosat Second Generation SEVIRI nighttime data. Adv. Geosci. 2008, 16, 63–72. [Google Scholar] [CrossRef][Green Version]
- Lensky, I.M.; Rosenfeld, D. A night-rain delineation algorithm for infrared satellite data based on microphysical considerations. J. Appl. Meteorol. 2003, 42, 1218–1226. [Google Scholar] [CrossRef]
- Thies, B.; Nauss, T.; Bendix, J. A new technique for detecting precipitation at mid-latitudes during daytime using Meteosat Second Generation SEVIRI. In Proceedings of the EUMETSAT Meteorological Satellite Conference, Darmstadt, Germany, 8–12 September 2008. [Google Scholar]
- Lensky, I.M.; Rosenfeld, D. Satellite-based insights into precipitation formation processes in continental and maritime convective clouds at nighttime. J. Appl. Meteorol. 2003, 42, 1227–1233. [Google Scholar] [CrossRef]
- Lazri, M.; Ameur, S.; Brucker, J.M.; Testud, J.; Hamadache, B.; Hameg, S.; Ouallouche, F.; Mohia, Y. Identification of raining clouds using a method based on optical and microphysical cloud properties from Meteosat second generation daytime and nighttime data. Appl. Water Sci. 2013, 3, 1–11. [Google Scholar] [CrossRef]
- Lazri, M.; Ameur, S.; Mohia, Y. Instantaneous rainfall estimation using neural network from multispectral observations of SEVIRI radiometer and its application in estimation of daily and monthly rainfall. Adv. Space Res. 2014, 53, 138–155. [Google Scholar] [CrossRef]
- Feidas, H.; Giannakos, A. Identifying precipitating clouds in Greece using multispectral infrared Meteosat Second Generation satellite data. Theor. Appl. Climatol. 2011, 104, 25–42. [Google Scholar] [CrossRef]
- Eumetsat. Cloud Mask Product: Product Guide; Eumetsat: Darmstadt, Germany, 2015; pp. 1–6. [Google Scholar]
- Baum, B.A.; Spinhirne, J.D. Remote sensing of cloud properties using MODIS airborne simulator imagery during SUCCESS: 3. Cloud Overlap. J. Geophys. Res. Atmos. 2000, 105, 11793–11804. [Google Scholar] [CrossRef]
- Kawamoto, K.; Nakajima, T.; Nakajima, T.Y. A global determination of cloud microphysics with AVHRR remote sensing. J. Clim. 2001, 14, 2054–2068. [Google Scholar] [CrossRef]
- Kokhanovsky, A.A. A semianalytical cloud retrieval algorithm using backscattered radiation in 0.4–2.4 μm spectral region. J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef]
- Thies, B.; Nauss, T. A New Technique for Detecting Precipitation at Mid-Latitudes during Daytime Using Meteosat Second Generation SEVIRI; Eumetsat: Darmstadt, Germany, 2008. [Google Scholar]
- Thies, B.; Nauss, T.; Bendix, J. Precipitation process and rainfall intensity differentiation using Meteosat Second Generation Spinning Enhanced Visible and Infrared Imager data. J. Geophys. Res. Atmos 2008, 113, D23206. [Google Scholar] [CrossRef]
- Strabala, K.I.; Ackerman, S.A.; Menzel, W.P. Cloud Properties inferred from 8–12-µm Data. J. Appl. Meteorol. 1994, 33, 212–229. [Google Scholar] [CrossRef]
- Wolters, E.L.A.; Roebeling, R.A.; Feijt, A.J. Evaluation of cloud-phase retrieval methods for SEVIRI on Meteosat-8 using ground-based lidar and cloud radar data. J. Appl. Meteorol. Climatol. 2008, 47, 1723–1738. [Google Scholar] [CrossRef]
- Inoue, T. An Instantaneous Delineation of Convective Rainfall Areas Using Split Window Data of Noaa-7 Avhrr. J. Meteorol. Soc. Jpn. 1987, 65, 469–481. [Google Scholar] [CrossRef][Green Version]
- Feidas, H.; Giannakos, A. Classifying convective and stratiform rain using multispectral infrared Meteosat Second Generation satellite data. Theor. Appl. Climatol. 2011, 108, 613–630. [Google Scholar] [CrossRef]
- Inoue, T.; Wu, X.; Bessho, K. Life Cycle of Convective Activity in Terms of Cloud Type Observed By Split Window. In Proceedings of the 11th Conference on Satellite Meteorology and Oceanography, Madison, WI, USA, 16 October 2001; pp. 3–4. [Google Scholar]
- Inoue, T. Day-to-night cloudiness change of cloud types inferred from split window measurements aboard NOAA polar-orbiting satellites. J. Meteorol. Soc. Jpn. 1997, 75, 59–66. [Google Scholar] [CrossRef][Green Version]
- Ha, E.; North, G.R.; Yoo, C.; Ha, K.J. Evaluation of some ground truth designs for satellite estimates of rain rate. J. Atmos. Ocean. Technol. 2002, 19, 65–73. [Google Scholar] [CrossRef]
- Roe, G.H. Orographic precipitation. Annu. Rev. Earth Planet. Sci. 2005, 33, 645–671. [Google Scholar] [CrossRef]
- Young, A.H.; Bates, J.J.; Curry, J.A. Application of cloud vertical structure from CloudSat to investigate MODIS-derived cloud properties of cirriform, anvil, and deep convective clouds. J. Geophys. Res. Atmos. 2013, 118, 4689–4699. [Google Scholar] [CrossRef]
- Kato, S.; Marshak, A. Solar zenith and viewing geometry-dependent errors in satellite retrieved cloud optical thickness: Marine stratocumulus case. J. Geophys. Res. Atmos. 2009, 114, 1–13. [Google Scholar] [CrossRef]
- Cattani, E.; Torricella, F.; Laviola, S.; Levizzani, V. On the statistical relationship between cloud optical and microphysical characteristics and rainfall intensity for convective storms over the Mediterranean. Nat. Hazards Earth Syst. Sci. 2009, 9, 2135–2142. [Google Scholar] [CrossRef]
- Walther, B.A.; Moore, J.L. The concepts a literature with of species richness the performance estimators, of estimator review performance precision. Ecography 2005, 28, 815–829. [Google Scholar] [CrossRef]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences; Academic Press: Cambridge, MA, USA, 2006; Volume 14, p. 627. [Google Scholar]
- Barnston, A.G. Correspondence among the Correlation, RMSE, and Heidke Forecast Verification Measures; Refinement of the Heidke Score. Weather Forecast. 1992, 7, 699–709. [Google Scholar] [CrossRef]
- Harold, B.; Barb, B.; Beth, E.; Chris, F.; Johannes, J.; Ian, J.; Tieh-Yong, K.; Paul, R.; David, S. WWRP/WGNE Joint Working Group on Forecast Verification Research; WMO: Geneva, Switzerland, 2015. [Google Scholar]
- Inoue, T.; Vila, D.; Rajendran, K.; Hamada, A.; Wu, X.Q.; Machado, L.A.T. Life Cycle of Deep Convective Systems over the Eastern Tropical Pacific Observed by TRMM and GOES-W. J. Meteorol. Soc. Jpn. 2009, 87a, 381–391. [Google Scholar] [CrossRef]
- Leijnse, H.; Uijlenhoet, R.; Berne, A. Errors and Uncertainties in Microwave Link Rainfall Estimation Explored Using Drop Size Measurements and High-Resolution Radar Data. J. Hydrometeorol. 2010, 11, 1330–1344. [Google Scholar] [CrossRef]
- Leijnse, H.; Uijlenhoet, R.; Stricker, J.N.M. Microwave link rainfall estimation: Effects of link length and frequency, temporal sampling, power resolution, and wet antenna attenuation. Adv. Water Resour. 2008, 31, 1481–1493. [Google Scholar] [CrossRef]
- Martin, F.; Vojtech, B. Quantifying Hardware Related Attenuation from the Analysis of Nearby Microwave Links. In Proceedings of the 2018 IEEE Workshop on Statistical Signal Processing (SSP), Freiburg, Germany, 10–13 June 2018; pp. 135–138. [Google Scholar]
- David, N.; Gao, H.O.; Kumah, K.K.; Hoedjes, J.C.B.; Su, Z.; Liu, Y. Microwave communication networks as a sustainable tool of rainfall monitoring for agriculture needs in Africa. In Proceedings of the 16th International Conference on Environmental Science and Technology, Rhodes, Greece, 4–7 September 2019. [Google Scholar]
- Safont, G.; Salazar, A.; Vergara, L. Multiclass Alpha Integration of Scores from Multiple Classifiers. Neural Comput. 2019, 31, 806–825. [Google Scholar] [CrossRef]
- Lahat, D.; Adali, T.; Jutten, C. Multimodal Data Fusion: An Overview of Methods, Challenges, and Prospects. Proc. IEEE 2015, 103, 1449–1477. [Google Scholar] [CrossRef]
- Kühnlein, M.; Appelhans, T.; Thies, B.; Nauß, T. Precipitation Estimates from MSG SEVIRI Daytime, Nighttime, and Twilight Data with Random Forests. J. Appl. Meteorol. Climatol. 2014, 53, 2457–2480. [Google Scholar] [CrossRef]
- Meyer, H.; Kühnlein, M.; Appelhans, T.; Nauss, T. Comparison of four machine learning algorithms for their applicability in satellite-based optical rainfall retrievals. Atmos. Res. 2016, 169, 424–433. [Google Scholar] [CrossRef]
- Watts, P.D.; Bennartz, R.; Fell, F. Retrieval of two-layer cloud properties from multispectral observations using optimal estimation. J. Geophys. Res. Atmos. 2011, 116, 1–22. [Google Scholar] [CrossRef]
- Lensky, I.; Rosenfeld, D. Estimation of Precipitation Area and Rain Intensity Based on the Microphysical Properties Retrieved from NOAA AVHRR Data. J. Appl. Meteorol. 1997, 36, 234–242. [Google Scholar] [CrossRef]
- Wang, J.Y.; Houze, R.A.; Fan, J.W.; Brodzik, S.R.; Feng, Z.; Hardin, J.C. The Detection of Mesoscale Convective Systems by the GPM Ku-Band Spaceborne Radar. J. Meteorol. Soc. Jpn. 2019, 97, 1059–1073. [Google Scholar] [CrossRef]
- Zipser, E.J.; Cecil, D.J.; Liu, C.; Nesbitt, S.W.; Yorty, D.P. Where Are the Most Intense Thunderstorms on Earth? Bull. Am. Meteorol. Soc. 2006, 87, 1057–1072. [Google Scholar] [CrossRef]
- Kober, K.; Tafferner, A. Tracking and nowcasting of convective cells using remote sensing data from radar and satellite. Meteorol. Z. 2009, 18, 75–84. [Google Scholar] [CrossRef]
- Turdukulov, U.D.; Kraak, M.J.; Blok, C.A. Designing a visual environment for exploration of time series of remote sensing data: In search for convective clouds. Comput. Graph. 2007, 31, 370–379. [Google Scholar] [CrossRef]
- Bell, T.L.; Kundu, P.K. Comparing satellite rainfall estimates with rain gauge data: Optimal strategies suggested by a spectral model. J. Geophys. Res. Atmos. 2003, 108. [Google Scholar] [CrossRef]
- Kühnlein, M.; Appelhans, T.; Thies, B.; Nauss, T. Improving the accuracy of rainfall rates from optical satellite sensors with machine learning—A random forests-based approach applied to MSG SEVIRI. Remote Sens. Environ. 2014, 141, 129–143. [Google Scholar] [CrossRef]
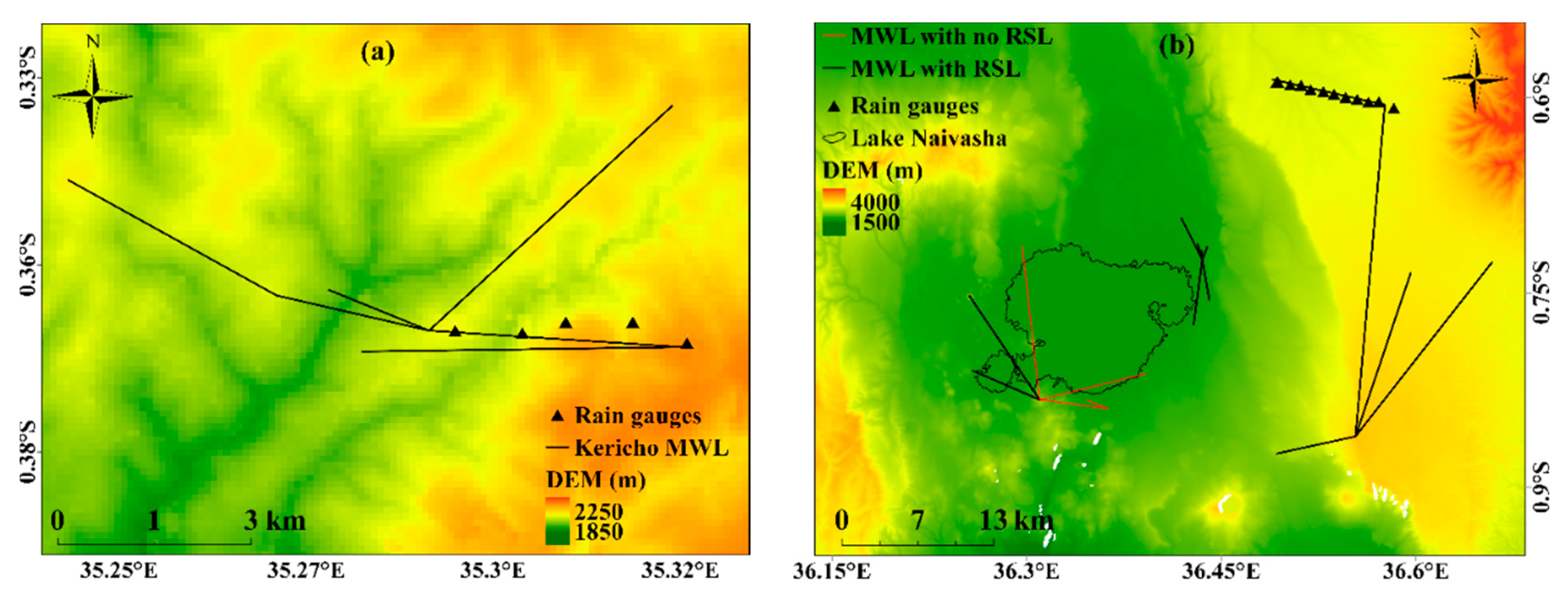



| Study Location | Evaluation Period | Number of MWL | Frequency (GHz) | Link Length (km) | |
|---|---|---|---|---|---|
| Year | Month | ||||
| Kericho | 2013 | May–June | 2 | 23 | <2 |
| 4 | 15 | 3.45–4.77 | |||
| Naivasha | 2014 | May–June | 3 | 23 | <2 |
| 9 | 15 | 3.47–18.95 | |||
| 1 | 8 | 28.4 | |||
| 2018 | 1 | 15 | 10 | ||
| Frequency (GHz) | Parameter | |
|---|---|---|
| a | b | |
| 15 | 0.05008 | 1.0440 |
| 23 | 0.1284 | 0.9630 |
| Performance Measure | Formula | Range |
|---|---|---|
| RB | −1 to + ∞ | |
| CV | 0 to ∞ | |
| r2 | 0 to 1 | |
| RMSE | 0 to + ∞ |
| Study Location | RB | CV | r2 | RSME (mm h−1) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 15 min | 30 min | 1 h | 15 min | 30 min | 1 h | 15 min | 30 min | 1 h | 15 min | 30 min | 1 h | |
| Kericho 1 | 0.50 | 0.32 | 0.32 | 9.87 | 7.18 | 5.09 | 0.42 | 0.49 | 0.62 | 1.22 | 1.96 | 2.77 |
| Naivasha 2 | −0.05 | −0.14 | −0.18 | 5.78 | 5.68 | 4.07 | 0.52 | 0.53 | 0.58 | 0.48 | 0.80 | 1.15 |
| Study Area | RMWL (mm h−1) | 1 Percentage of Data (%) | Accumulated RMWL (mm) | ||
|---|---|---|---|---|---|
| Day | Night | Day | Night | ||
| Kericho | 0 | 91.56 (93.81) | 94.5 (97.7) | 0 (0) | 0 (0) |
| 0–5 | 1.95 (2.61) | 2.29 (1.84) | 12.22 (24.92) | 13.57 (12.06) | |
| >5 | 6.49 (3.58) | 3.21 (0.46) | 314.25 (219.49) | 98.1 (39.40) | |
| Naivasha | 0 | 96.68 (96.84) | 95.34 (96.02) | 0 (0) | 0 (0) |
| 0–5 | 2.41 (2.11) | 2.61 (2.88) | 48.45 (34.74) | 61.92 (54.14) | |
| >5 | 0.90 (1.05) | 2.06 (1.1) | 43.02 (88.88) | 106.09 (61.41) | |
| Study Location | Time | Visthres | Nirthres | ∆TIR8.7-IR10.8 Range K | ∆TIR10.8-IR12.0 Range K |
|---|---|---|---|---|---|
| Kericho | Day | >0.70 | <0.43 | −1.0–1.42 | −1.0–1.0 |
| Naivasha | >0.70 | <0.50 | −1.10–1.15 | 0.0–1.2 | |
| ∆TIR3.9-IR10.8 range K | ∆TIR3.9-WV7.3 range K | ∆TIR8.7-IR10.8 range K | ∆TIR10.8-IR12.0 range K | ||
| Kericho | Night | 2.0–5.0 | 4.0–12.0 | −0.01–1.0 | 0.26–1.9 |
| Naivasha | −3.0–1.0 | 3.0–15.0 | −1.0–2.0 | 0.0–1.0 |
| MWL Name? | 1RMWL (mm) | Hits % | Miss % | False Alarms % | Correct Negatives % | POD | FAR | POFD | ACC | CSI | HSS |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Perfect score | - | - | - | - | 1 | 0 | 0 | 1 | 1 | 1 | |
| Kericho MWL | |||||||||||
| Day time | |||||||||||
| 13471368 | 311.32 | 58.1 | 41.9 | 29 | 96.4 | 0.58 | 0.33 | 0.04 | 0.92 | 0.45 | 0.58 |
| 13671368 | 230.87 | 78.6 | 21.4 | 28.6 | 98.4 | 0.79 | 0.27 | 0.02 | 0.97 | 0.61 | 0.75 |
| 30941368 | 331.15 | 57.1 | 42.9 | 17.9 | 98.4 | 0.57 | 0.24 | 0.02 | 0.94 | 0.49 | 0.62 |
| 30953094 | 83.53 | 66.7 | 33.3 | 66.7 | 98.1 | 0.67 | 0.50 | 0.03 | 0.96 | 0.40 | 0.55 |
| 34051368 | 437.98 | 65 | 35 | 50 | 96.3 | 0.65 | 0.44 | 0.04 | 0.94 | 0.43 | 0.57 |
| Nighttime | |||||||||||
| 13471368 | 124.62 | 50 | 50 | 30 | 98.5 | 0.50 | 0.38 | 0.02 | 0.96 | 0.39 | 0.5 |
| 13671368 | 138.43 | 25 | 75 | 6.2 | 99.5 | 0.25 | 0.2 | 0.01 | 0.94 | 0.24 | 0.4 |
| 30941368 | 112.65 | 41.7 | 58.3 | 8.3 | 99.5 | 0.42 | 0.18 | 0.01 | 0.96 | 0.39 | 0.5 |
| 30953094 | 68.72 | 50 | 50 | 12.5 | 99.5 | 0.50 | 0.2 | 0.01 | 0.98 | 0.44 | 0.6 |
| Naivasha MWL | |||||||||||
| Day time | |||||||||||
| 13201328 | 77.0 | 65 | 35 | 5 | 99.8 | 0.65 | 0.07 | 0.002 | 0.99 | 0.62 | 0.76 |
| 34101372 | 203.73 | 61.5 | 38.5 | 15.4 | 99.6 | 0.62 | 0.20 | 0.004 | 0.99 | 0.53 | 0.69 |
| 13723379 | 201.47 | 57.1 | 42.9 | 28.6 | 99.6 | 0.57 | 0.33 | 0.004 | 0.99 | 0.44 | 0.61 |
| 1372 | 187.10 | 62.5 | 37.5 | 25 | 99.6 | 0.63 | 0.29 | 0.004 | 0.99 | 0.50 | 0.66 |
| 13201327 | 80.22 | 60 | 40 | 5 | 99.8 | 0.6 | 0.08 | 0.02 | 0.98 | 0.57 | 0.72 |
| 13071372 | 232.91 | 61.5 | 38.5 | 15.4 | 99.6 | 0.62 | 0.20 | 0.004 | 0.99 | 0.53 | 0.69 |
| Nighttime | |||||||||||
| 13201328 | 42.10 | 91.7 | 8.3 | 58.3 | 98.9 | 0.92 | 0.39 | 0.011 | 0.99 | 0.58 | 0.73 |
| 13723365 | 169.10 | 57.1 | 42.9 | 78.6 | 97.7 | 0.57 | 0.58 | 0.023 | 0.97 | 0.32 | 0.47 |
| 13201327 | 21.57 | 30 | 70 | 120 | 98.2 | 0.3 | 0.8 | 0.018 | 0.97 | 0.14 | 0.23 |
| 13263035 | 46.46 | 60 | 40 | 100 | 98.9 | 0.6 | 0.63 | 0.011 | 0.99 | 0.3 | 0.46 |
| 13263302 | 55.34 | 45.5 | 54.5 | 54.5 | 98.7 | 0.46 | 0.55 | 0.013 | 0.97 | 0.29 | 0.44 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumah, K.K.; Hoedjes, J.C.B.; David, N.; Maathuis, B.H.P.; Gao, H.O.; Su, B.Z. Combining MWL and MSG SEVIRI Satellite Signals for Rainfall Detection and Estimation. Atmosphere 2020, 11, 884. https://doi.org/10.3390/atmos11090884
Kumah KK, Hoedjes JCB, David N, Maathuis BHP, Gao HO, Su BZ. Combining MWL and MSG SEVIRI Satellite Signals for Rainfall Detection and Estimation. Atmosphere. 2020; 11(9):884. https://doi.org/10.3390/atmos11090884
Chicago/Turabian StyleKumah, Kingsley K., Joost C. B. Hoedjes, Noam David, Ben H. P. Maathuis, H. Oliver Gao, and Bob Z. Su. 2020. "Combining MWL and MSG SEVIRI Satellite Signals for Rainfall Detection and Estimation" Atmosphere 11, no. 9: 884. https://doi.org/10.3390/atmos11090884
APA StyleKumah, K. K., Hoedjes, J. C. B., David, N., Maathuis, B. H. P., Gao, H. O., & Su, B. Z. (2020). Combining MWL and MSG SEVIRI Satellite Signals for Rainfall Detection and Estimation. Atmosphere, 11(9), 884. https://doi.org/10.3390/atmos11090884