Abstract
This contribution presents a comprehensive computational study on the reactions of secondary ozonide (SOZ) with ammonia and water molecules. The mechanisms were studied in both a vacuum and the aqueous medium. All the molecular geometries were optimized using the B3LYP functional in conjunction with several basis sets. M06-2X, APFD, and ωB97XD functionals with the full basis set were also used. In addition, single-point energy calculations were performed with the G4MP2 and G3MP2 methods. Five different mechanistic pathways were studied for the reaction of SOZ with ammonia and water molecules. The most plausible mechanism for the reaction of SOZ with ammonia yields HC(O)OH, NH3, and HCHO as products, with ammonia herein acting as a mediator. This pathway is exothermic and exergonic, with an overall barrier height of only 157 kJ mol−1 using the G3MP2 method. All the reaction pathways between SOZ and water molecules are endothermic and endergonic reactions. The most likely reaction pathway for the reaction of SOZ with water involves a water dimer, in which the second water molecule acts as a mediator, with an overall barrier height of only 135 kJ mol−1 using the G3MP2 method. Solvent effects were found to incur a significant reduction in activation energies. When the second H2O molecule acts as a mediator in the reaction of SOZ with water, the barrier height of the rate-determining step state decreases significantly.
1. Introduction
Simple alkenes are important constituents of the urban atmosphere and tropical forests. The unsaturated hydrocarbons of volatile organic compounds (VOCs) are continuously emitted into the earth’s atmosphere [1,2]. Ethene (C2H4) is one of the alkenes that endures a short chemical lifetime, and it originates from a variety of anthropogenic and natural sources. These natural sources include plants, microorganisms, volcanos, and forest fires. The anthropogenic sources are mainly the incomplete combustion of fossil fuels, the burning of agricultural wastes and vegetation for agriculture, and leakage from industrial ethylene plants [3,4]. Since the 1950s, the ozonolysis of ethene has been studied intensively through Criegee’s three-step mechanism. A schematic of the initial reaction pathways for the ozonolysis of ethene is depicted in Figure 1. Herein, primary ozonide (POZ), carbonyl oxide, and secondary ozonide (1,2,4-trioxolane, SOZ) are formed as transitory products of the reaction [5]. Carbonyl oxide and formaldehyde react to produce the ethene secondary ozonide that involves the formation of a van der Waals complex on the reaction coordinate before reaching the transition state. The process is exothermic and encounters no genuine reaction barrier [6]. SOZ is formed when a stabilized Criegee intermediate undergoes a 1,3-dipolar cycloaddition to the carbonyl compound, as shown in Figure 1. SOZ is more stable than primary ozonide and exhibits a sufficiently long lifetime [5,6,7].
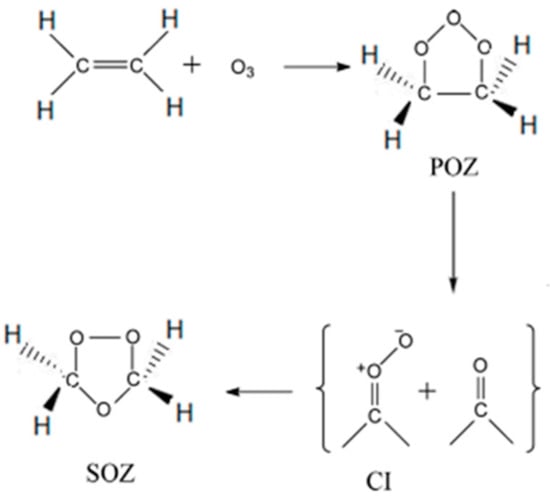
Figure 1.
The formation of secondary ozonide (SOZ) in the ozonolysis of ethene.
The formation of SOZ from alkenes has been reported in numerous studies [8,9] with a prime focus on the formation and relative stability of SOZs resulting from the ozonolysis of selected cyclic monoterpenes (C10H16) [10] taking place in both a gas and a liquid phase.
The SOZs of alkenes assume an important role in atmospheric chemical reactions. They react with atmospheric species, such as NH3 and H2O. Most importantly, they play an important role in the formation of secondary organic aerosol (SOA), which causes more environmental pollution than primary organic aerosol (POA) does. SOAs affect visibility, human health, and air quality. They participate in the complex physio-chemical phenomena of climate change [11,12].
As one of the most abundant, basic gases in the atmosphere, ammonia (NH3) plays a key role in atmospheric chemical processes. The major source of atmospheric ammonia is agriculture and mining-related activities, along with natural processes and human activities [13,14]. Ammonia also reacts rapidly with sulfuric and nitric acids in a process that enhances the levels of fine particles, such as ammonium sulfates (NH4HSO4 and (NH4)2SO4) and ammonium nitrate (NH4NO3). Depending on the availability of NH3, these reactions eventually lead to the generation of a secondary aerosol [13]. Naa and co-workers [12] studied the formation of aerosol particles due to the ozonolysis of styrene in the presence and absence of ammonia. Very recently, Banu and co-workers have theoretically explored the formation of SOA from the ozonolysis of styrene in the presence of ammonia and water [14]. Rousso et al. [15] studied the ozonolysis of ethylene and their results provide valuable information about plasma- and ozone-assisted combustion processes and atmospheric aerosol formation. Experimentally, a decrease in the number of aerosol particles was observed in comparison with the experimental results without ammonia. In a subsequent study, ozonolysis of α-pinene was investigated, revealing an opposite trend of α-pinene [12,16]. Furthermore, the effect of NH3 gas on the SOA formation of α-pinene by dark ozonolysis and photoxidation was investigated using the newly-developed flow reactor [17]. The theoretical work by Jørgensen and Gross afforded an insight into the experimental work of Naa and co-workers by surveying plausible, pertinent reaction mechanisms [18]. Moreover, our previous work on ozonolysis reactions provided good initial guesses that helped us attain a complete picture about the proposed mechanisms for this study [7,19,20,21,22,23].
To the best of our knowledge, literature presents no computational accounts on the reaction mechanism of SOZ with water or ammonia in a solvent. Therefore, a thorough computational study for the reactions of SOZ with ammonia and water molecules was performed (Scheme 1) in this work to map out the detailed reaction mechanisms. The thermodynamic and kinetic parameters were obtained at different levels of theory. It is hoped that this computational study would benefit experimentalists by providing a more detailed mechanistic understanding of the reactions that prevail during the SOZ formation, and that it will possibly aid in the design of new experiments for a further understanding of related atmospheric chemistry. Likewise, calculations at various theoretical levels would enable us to optimize a suitable theoretical framework tailored specifically for SOZ reactions.
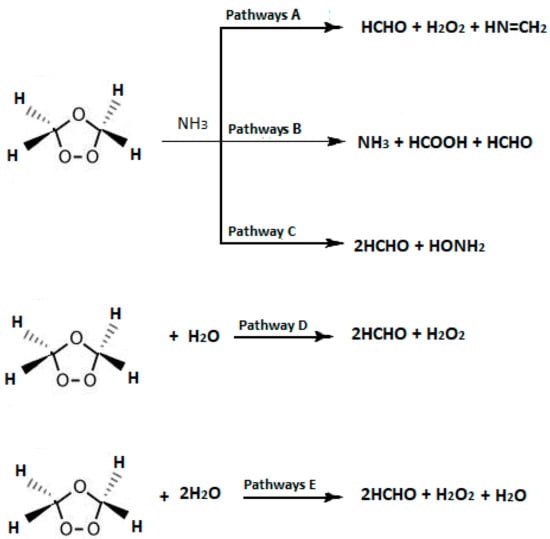
Scheme 1.
Proposed reactions of SOZ with NH3, H2O, and 2H2O.
2. Computational Methods
All calculations were performed using the Gaussian-16 (G16) software package [24]. The geometries of all reactants, transition states, intermediates, and products were fully optimized. Transition states and energy minima were confirmed with one and no imaginary frequencies, respectively, using the B3LYP [25,26] method with the 6-31G(d), 6-31G(2df,p), and 6-311++G(3df,3pd) basis sets [27]. Calculations were also performed using M06-2X and M11, and functionals that include dispersion terms, such as APFD (Austin-Frisch-Petersson functional with dispersion) and ωB97XD (uses a version of Grimme’s D2 dispersion model), were performed using a 6-311++G(3df,3pd) basis set. Single-point energy calculations were done using G4MP2 [28] and G3MP2 methods [29,30]. Reactions in the troposphere layer with abundant moist content were simulated via deploying a solvent model density (SMD) [31] at the B3LYP/6-311++G(3df,3pd) level of theory.
The relative energies of all stationary points were corrected with zero-point vibrational energies (ZPE). Furthermore, transition states were analyzed using the intrinsic reaction coordinate (IRC) method [32] at the B3LYP/6-31G(d) level of theory. The structures of the reactant, intermediate, and product were identified using the IRC to confirm the nature of stationary points and how they are connected to the potential energy diagrams (PED’s) for each proposed mechanism.
The APFD requests the Austin–Frisch–Petersson functional with dispersion, while ωB97XD includes empirical dispersion and also accounts for long-range corrected functionals, which were developed by Head-Gordon and coworkers. Other hybrid functionals that were used from the Truhlar Group include M11 and M06-2x. In general, density functional theory (DFT) is widely used to study different chemical systems, as it generally requires fewer (for nonhybrid functionals) or equivalent (for hybrid functionals) computer resources compared with other theories and it provides reasonably accurate results. The application of DFT is still facing a problem in describing the “long-range” electron correlation. Although H-bonded complexes are controlled by electrostatic forces, the traditional density functionals are still generally capable of computing reasonable binding energies. Therefore, it must be mentioned that the selection of a functional to use will have to depend on the type and property of the system or the problem in which one is interested, and on the availability and computational cost associated with performing the calculations.
3. Results and Discussion
3.1. SOZ with Ammonia
3.1.1. Pathway A
In Pathway A (Figure 2), the reactant (RA) reacts to produce CH2NH (methyleneimine), H2O2, and HCHO. In the first step, the ammonia molecule is weakly attached to the reactant. Following this weak adsorption, a hydrogen atom is transferred from the nitrogen atom to the oxygen atom, O1, leading to the formation of I1aA through TS1A followed by a conformational change to produce the second intermediate I1bA. These intermediates are conformers and share very similar geometries, differing mainly in the torsion of hydroxyl and amine groups, and their activation energies are very small. In the subsequent step, I1bA produces the reaction products through TS2A directly. Considering the four-centered transition state structure of TS2A, the bond length O4–C5 is significantly elongated by 0.40 Å with respect to I1bA, whereas the C–N bond is shortened to a double-bond distance. Concentric hydrogen transfer reactions via TS2A conclude the mechanism and form the final reaction products CH2NH, H2O2, and HCHO (PA).
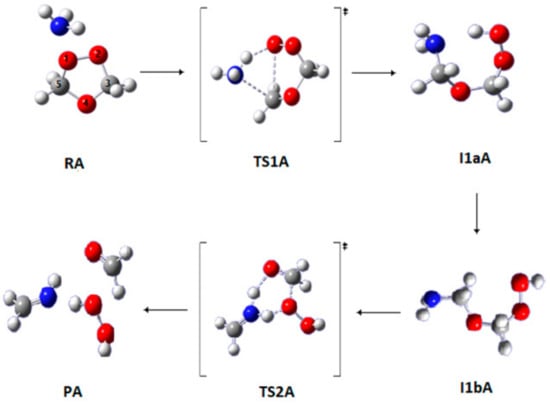
Figure 2.
Optimized geometries for the stationary points in Pathway A of the reaction between SOZ and ammonia. Calculated at the APFD/6-311++G(3df,3pd).
The barrier heights of the rate-determining steps of TS1A and TS2A are the lowest when calculated at B3LYP/6-311++G(3df,3pd) with the values of 189 and 140 kJ mol−1. The barrier heights for the first transition states for all proposed mechanisms were taken with respect to the separated species, as shown in the Supporting Information (SI), Figure S1. The corresponding energy barriers of TS1A and TS2A become noticeably lowered to 158 and 136 kJ mol−1 using SMD solvation models at B3LYP/6-311++G(3df,3pd) (Table 1). The Gibbs energies of activation of TS1A and TS2A are 228 and 137 kJ mol−1, respectively, at B3LYP/6-311++G(3df,3pd). The Gibbs energies of activation of the rate-determining step differ no more than 30 kJ mol−1 at all levels of theory.

Table 1.
Barrier Heights and Gibbs energies of activation (in kJ mol−1) at 298.15 K for Pathways A and B.
The use of functionals that include dispersion correction, such as APFD and ωB97XD, does not decrease the barrier height. The activation energies at APDF/6-311++G(3df,3pd) and ωB97XD/6-311++G(3df,3pd) levels of theory are 195 and 205 kJ mol−1, respectively. Furthermore, the activation energy calculated with high-accuracy energy G3MP2 is 203 kJ mol−1, which is very close to the barrier of B3LYP/6-311++G(3df,3pd) (Table 1). The barrier heights, with respect to the complex reactant, are also included in the Supporting Information in Tables S1–S3 for all proposed mechanisms.
3.1.2. Pathway B
Potential energy diagrams (PEDs) for all the reaction mechanisms are reported in the Supporting Information in Figures S1–S5 at the respective levels of theory. Relative energies are in kJ mol−1. In Pathway B (Figure 3), the reaction of SOZ with NH3 produces three different products: HC(O)OH, NH3, and HCHO. The NH3 molecule acts as a mediator to facilitate the transfer of the hydrogen atom in the complexes. In the first step, the reactant (RB) forms the I1aB adduct through TS1B followed by conformational change to give a second intermediate I1bB. In the ensuing step, the chemical bond between O4 and C5 is broken and a double hydrogen atom transfer occurs to generate the products via TS2B.
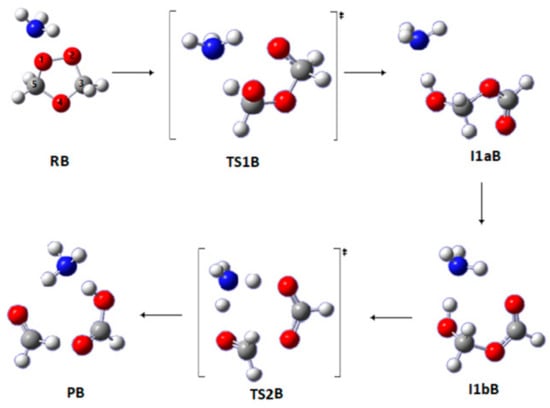
Figure 3.
Optimized geometries for the stationary points in Pathway B of the reaction between SOZ and ammonia. Calculated at the APFD/6-311++G(3df,3pd).
The barrier height for the conversion of the reactant as a complex to TS2B is 58 kJ mol−1 (see Table S1 in the SI). In comparison, the barrier height of the same step reported by Jorgensen and Gross is much higher, with a value of 81.2 kJ mol−1 using G2 and G3 methods. It becomes even higher with a value of 84 kJ mol−1 using the G3MP2 method. Analogous activation energies of TS2B are 63 and 70 kJ mol−1 at APFD and ωB97XD levels of theory, respectively. The energy barriers of TS2B, calculated by the B3LYP method with different basis sets, are scattered in the range 55–58 kJ mol−1 (Table 1). The highest energy barriers of TS2B are 84 kJ mol−1, calculated with the M06-2X and G3MP2 methods. The Gibbs energies of activation of TS1B are 151 and 102 kJ mol−1 in the gas and solution phases, respectively, at B3LYP/6-311++G(3df,3pd).
3.1.3. Pathway C
The first step of this pathway is similar to that of Pathway A. In the second step, a scission of the O1–O2 occurs, and the chemical bond between O1 and N is formed, leading to a new ring-like structure I2C that is formed via TS2C (Figure 4). Intermediate I2C is slightly less stable than I1bA1. In the last step, the molecular structure breaks into three moieties; the chemical bonds between C3–O4 and C5–N are broken, leading to the product structure (PC) via the transition state TS3C, as shown in Figure 4.
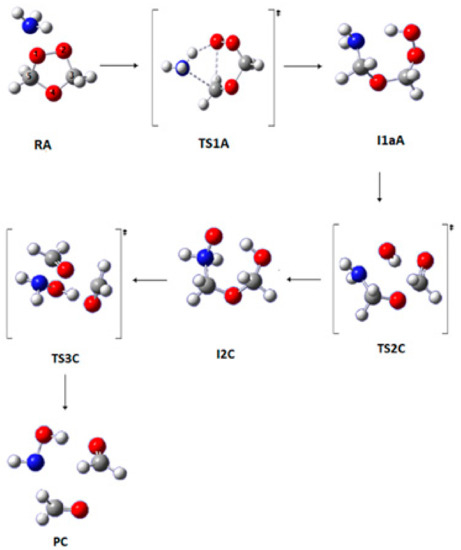
Figure 4.
Optimized geometries for the stationary points in Pathway C of the reaction between SOZ and ammonia. Calculated at the APFD/6-311++G(3df,3pd).
The overall barrier height of Pathway C is 189 kJ mol−1 at B3LYP/6-311++G(3df,3pd) with a Gibbs energy value of 228 kJ mol−1, while in the work of Jorgensen and Gross the same reaction was reported to have an overall barrier height of 234 kJ mol−1 calculated with G2 and G3 methods. The barrier heights of TS2C are 229 and 255 kJ mol−1 at APFD and ωB97XD methods, respectively. The application of the SMD model reduces the overall barrier height to 158 kJ mol−1 at B3LYP6-311++G(3df,3pd) (Table 2). This is due to the larger solvation effects on TS1A.

Table 2.
Barrier Heights and Gibbs energies of activation (in kJ mol−1) at 298.15 K for Pathway C.
In the reaction mechanisms, Pathways A and B, the conversion of SOZ into products requires overcoming two activation barriers, whereas in Pathway C the reaction involves three barriers with a barrier energy of 189 kJ mol−1. The enthalpy and Gibbs energies for Pathway A were found to be endothermic and endergonic, respectively, while for Pathway B they are exothermic and exergonic at all levels of theory and basis sets. In addition, the rate-determining step in the solvent model for Pathway A is 158 kJ mol−1, while for Pathway B it is 96 kJ mol−1, which makes Pathway B more favorable at all levels of theory, see Figures S1–S2. The SMD method dropped the barrier heights in the range 31–45 kJ mol−1 at B3LYP6-311++G(3df,3pd) and G3MP2. This is due to the fact that the transition state was stabilized more by the SMD model.
3.2. Reaction of SOZ with Water
3.2.1. Pathway D
This pathway represents the reaction with one water molecule, which is depicted in Figure 5. In the first step, a nucleophilic attack occurs from water on the carbon atom C5 of SOZ, and then a hydrogen atom is transferred from the oxygen in the water molecule to the oxygen atom O1 in the SOZ, leading to the formation of a I1D structure through TS1D. In the next step, a proton is transferred from the terminal oxygen to O4. The chemical bond between the C5 atom and terminal oxygen is noticeably shortened, leading to the formation of a double bond. Thus, two fragments are formed; one of them is the reaction product, HCHO, and the other one is HOCH2OOH formed via TS2D. In the last step, the fragment HOCH2OOH breaks down to form the reaction products H2O2 and HCHO, as shown in Figure 5.
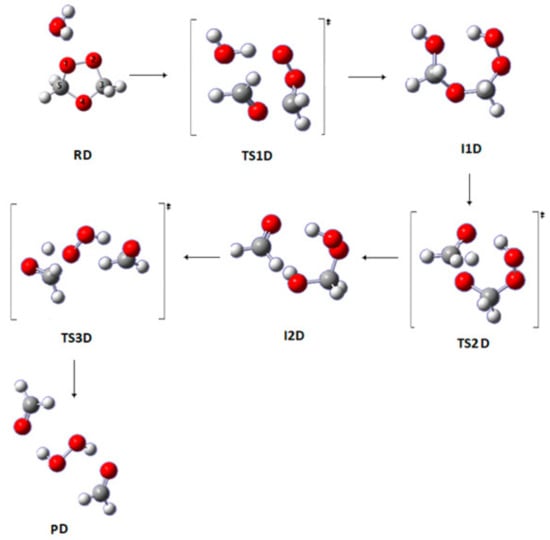
Figure 5.
Optimized geometries for the stationary points in Pathway D of the reaction between SOZ and water at the APFD/6-311++G(3df,3pd) for Pathway D.
The lowest barrier for the first step (TS1D) is 163 kJ mol−1 at G3MP2, but the highest barrier at M06-2X/6-311++G(3df,3pd) is 201 kJ mol−1. The effects of the solvent (SMD model) on this step slightly reduce the barrier height to 147 kJ mol−1 at B3LYP6-311++G(3df,3pd). The barrier height for the second step is 172 kJ mol−1 at B3LYP6-311++G(3df,3pd). The use of the SMD solvation model predicts high activation energies for this step (173 kJ mol−1). The barrier height of the last step amounts to 190 kJ mol−1 at B3LYP6-311 ++G(3df,3pd). The SMD solvation model decreases the barrier by 16 and 28 kJ mol−1 at G3MP2 and B3LYP6-311 ++G(3df,3pd), respectively, for the first step (Table 3) with reference to the gas phase process. This is due to the larger solvation effects on TS1A.

Table 3.
Barrier Heights and Gibbs energies of activation (in kJ mol−1) at 298.15 K for Pathways D and E.
3.2.2. Pathway E
This pathway is a reaction with two water molecules. The first step characterizes a nucleophilic attack from the water molecule on the carbon atom, followed by a hydrogen atom transfer from the oxygen in the water molecule to the oxygen atom in the SOZ. Then, a hydroxide group is transferred from the second water molecule to the terminal carbon atom in the SOZ, leading to the I1E intermediate through TS1E. The second step incorporates analogous reactions that are encountered in Pathway D. Subsequently, a conformational change produces I2bE. In the last step, the fragment HOCH2OOH breaks down to form H2O2, HCHO, and H2O via TS3E (see Figure 6).
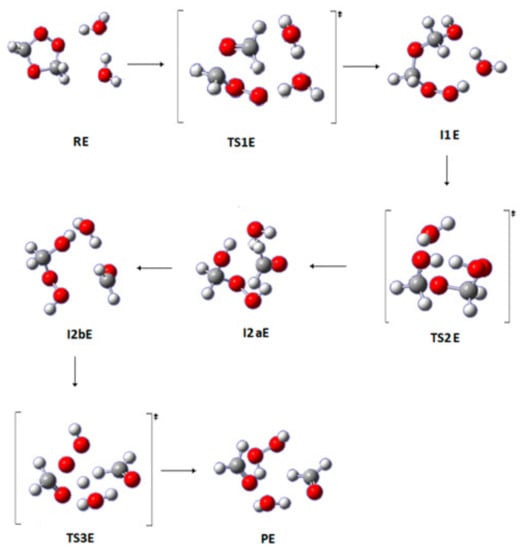
Figure 6.
Optimized geometries for the stationary points in Pathway E of the reaction between SOZ and 2H2O. Calculated at the APFD/6-311++G(3df,3pd).
The second water molecule in the reaction of SOZ with water acts as a mediator. Therefore, the barrier height of the water-mediated reaction dropped significantly to become 43 kJ mol−1.
The barrier height of the first step amounts to 117 and 135 kJ mol−1 SMD at B3LYP/6-311++G(3df,3pd) and G3MP2, while in Pathway D, it is 175 and 163 kJ mol−1, respectively. It should be noted here that the solvent effects have a significant role in this step. The water phase reduces the energy barrier of TS1E to 42 kJ mol−1 according to calculations made using SMD at B3LYP/6-311++G(3df,3pd). In the second step, the barrier height is 98 kJ mol−1. The analogous value in Pathway D is 172 kJ mol−1 of barrier height for the same step. The overall barrier for Pathway E in the aqueous phase using the SMD method attains a value of 75 kJ mol−1 at B3LYP/6-311++G(3df,3pd) (Table 3 and Figures S4–S5).
The enthalpy and Gibbs energies for the reaction of SOZ with water were found to be endothermic and endergonic, respectively, at all levels of theory for the two pathways (D and E). Thus, the reaction of SOZ with water incurs a thermodynamic penalty in the atmosphere.
4. Conclusions
In this work, a detailed computational study on the reactions of SOZ with NH3, H2O, and 2H2O in a vacuum and a solution was carried out. The dissociation reaction of SOZ with H2O that produces H2O2, H2O, and HCHO (Pathway E) is energetically favored over all other pathways, with an overall barrier height of only 117 and 135 kJ mol−1 at B3LYP/6-311++G(3df,3pd) and G3MP2. Interestingly, Pathway B attains the overall activation energy of 112 and 157 kJ mol−1 in a vacuum at B3LYP/6-311++G(3df,3pd) and G3MP2. The dissociation reaction of SOZ with two water molecules (Pathway E) is energetically favored compared with the analogous pathway that utilizes a single water molecule (Pathway D). The solvent effects play an important role in Pathway E, which shows a barrier substantially reduced, becoming 42 kJ mol−1 at the B3LYP/6-311++G(3df,3pd) level of theory.
It is worth noting here that the barrier heights and the Gibbs energy of activation calculated at B3LYP/6-311++G(3df,3pd) were very close to the G3MP2 method, differing by no more than 7 and 27 kJ mol−1 for all proposed pathways, respectively. This makes the B3LYP/6-311++G(3df,3pd) reliable and a good choice to study such systems compared with the most computationally expensive method, G4MP2. The entropy values for all proposed pathways are very small (ranging from −0.06 to 0.40 kJ mol−1) when using both complex and separated species. It is also worth noting here that the barrier heights and the Gibbs energy of activation calculated at B3LYP/6-311++G(3df,3pd) were very close to the G4MP2 method, differing by no more than 13 and 27 kJ mol−1 for all proposed pathways, respectively. This makes the B3LYP/6-311++G(3df,3pd) reliable and a good choice to study such systems compared to the most computationally expensive method, G4MP2.
Supplementary Materials
The following are available online at https://www.mdpi.com/2073-4433/11/1/100/s1, Figure S1: PED for the reaction of SOZ with ammonia (Pathway A) at the respective levels of theory. Relative energies are in kJ mol−1. Figure S2: PED for the reaction of SOZ with ammonia (Pathway B) at the respective levels of theory. Relative energies are in kJ mol−1. Figure S3: PED for the reaction of SOZ with ammonia (Pathway C) at the respective levels of theory. Relative energies are in kJ mol−1. Figure S4: PED for the reaction of SOZ with water (Pathway D) at the respective levels of theory. Relative energies are in kJ mol−1. Figure S5: PED for the reaction of SOZ with water (Pathway E) at the respective levels of theory. Relative energies are in kJ mol−1. Table S1: Barrier heights and Gibbs energies of activation (in kJ mol−1) at 298.15K for Pathways A and B. Relative energies with respect to the complex reactant. Table S1: Barrier heights and Gibbs energies of activation (in kJ mol−1) at 298.15K for Pathways A and B. Relative energies with respect to the complex reactant. Table S3. Barrier heights and Gibbs energies of activation (in kJ mol−1) at 298.15K for Pathways D and E. Relative energies with respect to the complex reactant.
Author Contributions
M.H.A. and S.F.A. conceived the idea and wrote the manuscript and analyzed the results. S.F.A. performed the calculations, collected the data, and data analysis. A.A.-A.A.-S. performed parts of DFT calculations and perform data analysis. M.A. provided theoretical and technical support and helped supervise the project. M.H.A. initiated discussions and collaborations with Y.Z. who contributed to the interpretation of the results, and provided critical feedback and helped shape the research, analysis, and manuscript. All authors discussed the results and contributed to the final version of the manuscript.
Acknowledgments
Mansour H. Almatarneh is grateful to the Deanship of Academic Research at the University of Jordan for the grant. We gratefully acknowledge Compute Canada for the computer time.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lamb, B.; Guenther, A.; Gay, D.; Westberg, H. A National Inventory of Biogenic Hydrocarbon Emissions. Atmos. Environ. 1987, 21, 1695–1705. [Google Scholar] [CrossRef]
- Almatarneh, M.H.; Elayan, I.A.; Poirier, R.A.; Altarawneh, M. The Ozonolysis of Cyclic Monoterpenes: A Computational Review. Can. J. Chem. 2017, 96, 281–292. [Google Scholar] [CrossRef]
- Aikin, A.C.; Herman, J.R.; Maier, E.J.; Mcquillan, C.J. Atmospheric Chemistry of Ethane and Ethylene. J. Geophys. Res. 1982, 87, 3105–3118. [Google Scholar] [CrossRef]
- Sawada, S.; Totsuka, T. Natural and Anthropogenic Sources and Fate of Atmospheric Ethylene. Atmos. Environ. 1967, 5, 821–832. [Google Scholar] [CrossRef]
- Bariseviciute, R.; Ceponkus, J.; Sablinskas, V. Matrix Isolation FTIR Spectroscopical Study of Ethene Secondary Ozonide. CEJC 2007, 5, 71–86. [Google Scholar] [CrossRef]
- Anglada, J.M.; Crehuet, R.; Bofill, M. The Ozonolysis of Ethylene: A Theoretical Study of the Gas-Phase Reaction Mechanism. Chem. Eur. J. 1999, 6, 1809–1822. [Google Scholar] [CrossRef]
- Almatarneh, M.H.; Alshamaileh, E.; Ahmad, Z.M.; Abu-Saleh, A.A.; Elayan, I.A. A Computational Study of the Ozonolysis of Phenanthrene. Acta Phys. Pol. A 2017, 132. [Google Scholar] [CrossRef]
- Neeb, N.; Horie, O.; Moortgat, G. Gas-phase Ozonolysis of Ethene in the Presence of Hydroxylic Compounds. Int. J. Chem. Kinet. 1996, 28, 721–730. [Google Scholar] [CrossRef]
- Aschmann, S.M.; Tuazon, E.C.; Arey, J.; Atkinson, R. Products of the Gas-phase Reaction of O3 with Cyclohexene. J. Phys. Chem. A 2003, 107, 2247–2255. [Google Scholar] [CrossRef]
- Vibenholt, A.; Nørgaard, A.W.; Clausen, P.A.; Wolkoff, P. Formation and Stability of Secondary Ozonides from Monoterpenes Studied by Mass Spectrometry. Chemosphere 2009, 76, 572–577. [Google Scholar] [CrossRef]
- Deng, J.; Chen, J.; Geng, C.; Liu, H.; Wang, W.; Bai, Z.; Xu, Y. The Overall Reaction Process of Ozone with Methacrolein and Isoprene in the Condensed Phase. J. Phys. Chem. A 2012, 116, 1710–1716. [Google Scholar] [CrossRef] [PubMed]
- Naa, K.; Songa, C.; Cocker, D.R. Formation of Secondary Organic Aerosol from the Reaction of Styrene with Ozone in the Presence and Absence of Ammonia and Water. Atmos. Environ. 2006, 40, 1889–1900. [Google Scholar] [CrossRef]
- Behera, S.B.; Sharma, M.; Aneja, V.P.; Balasubramanian, R. Ammonia in the Atmosphere: A Review on Emission Sources, Atmospheric Chemistry and Deposition on Terrestrial Bodies. Environ. Sci. Pollut. Res. 2013, 20, 8092–8131. [Google Scholar] [CrossRef] [PubMed]
- Banu, T.; Sen, K.; Das, A.K. Atmospheric Fate of Criegee Intermediate Formed During Ozonolysis of Styrene in the Presence of H2O and NH3: The Crucial Role of Stereochemistry. J. Phys. Chem. A 2018, 122, 8377–8389. [Google Scholar] [CrossRef] [PubMed]
- Rousso, A.C.; Hansen, N.; Jasper, A.W.; Ju, Y. Identification of the Criegee Intermediate Reaction Network in Ethylene Ozonolysis: Impact on Energy Conversion Strategies and Atmospheric Chemistry. Phys. Chem. Chem. Phys. 2019, 21, 7341–7357. [Google Scholar] [CrossRef]
- Na, K.; Song, C.; Switzer, C.; Cocker, D.R. Effect of Ammonia on Secondary Organic Aerosol Formation from α-Pinene Ozonolysis in Dry and Humid Conditions. Environ. Sci. Technol. 2007, 41, 6096–6102. [Google Scholar] [CrossRef]
- Babar, Z.B.; Park, J.H.; Lim, H.J. Influence of NH3 on Secondary Organic Aerosols from the Ozonolysis and Photooxidation of α-Pinene in a Flow Reactor. Atmos. Environ. 2017, 146, 71–84. [Google Scholar] [CrossRef]
- Jørgensen, S.; Gross, A. Theoretical Investigation of Reactions Between Ammonia and Precursors from the Ozonolysis of Ethane. Chem. Phys. 2009, 362, 8–15. [Google Scholar] [CrossRef]
- Almatarneh, M.H.; Elayan, I.A.; Altarawneh, M.; Hollett, J.W. A computational study of the ozonolysis of sabinene. Theor. Chem. Acc. 2019, 138, 30. [Google Scholar] [CrossRef]
- Elayan, I.A.; Almatarneh, M.H.; Hollett, J.W. Reactivity of the anti-Criegee intermediate of β-pinene with prevalent atmospheric species. Struct. Chem. 2019, 30, 1353–1364. [Google Scholar] [CrossRef]
- Almatarneh, M.H.; Elayan, I.A.; Abu-Saleh, A.A.; Altarawneh, M.; Aryia, P.A. The Gas-Phase Ozonolysis Reaction of MethylButenol: A Mechanistic Study. Int. J. Quantum Chem. 2019, 119, e25888. [Google Scholar] [CrossRef]
- Elayan, I.A.; Almatarneh, M.H.; Hollett, J.W. The bimolecular catalytic transformation of methyl vinyl ketone oxide: A DFT study. Chem. Phys. 2020, 530, 110649. [Google Scholar] [CrossRef]
- Almatarneh, M.H.; Elayan, I.A.; Altarawneh, M.; Hollett, J.W. Hydration and Secondary Ozonide of the Criegee Intermediate of Sabinene. ACS-OMEGA 2018, 3, 2417–2427. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian; Revision a.02; Gaussian. Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Becke, A.D. Density-functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti Correlation-energy Formula into A Functional of the Electron Density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Petersson, G.A.; Bennett, A.; Tensfeldt, T.G.; Al-Laham, M.A.; Shirley, W.A.; Mantzaris, J. A Complete Basis Set Mmodel Chemistry. I. The Total Energies of Closed-shell Atoms and Hydrides of the First-row Atoms. J. Chem. Phys 1988, 89, 2193–2218. [Google Scholar] [CrossRef]
- Curtiss, L.A.; Redfern, P.C.; Raghavachari, K. Gaussian-4 Theory Using Reduced Order Perturbation Theory. J. Chem. Phys 2007, 127, 124105. [Google Scholar] [CrossRef]
- Montgomery, J.A.; Frisch, M.J.; Ochterski, J.W.; Petersson, G.A. A Complete Basis Set Model Chemistry. VI. Use of Density Functional Geometries and Frequencies. J. Chem. Phys 1999, 110, 2822–2827. [Google Scholar] [CrossRef]
- Wood, G.P.F.; Radom, L.; Petersson, G.A.; Barnes, E.C.; Frisch, M.J.; Montgomery, J.A. A Restricted-open-shell Complete-basis-set Model Chemistry. J. Chem. Phys 2006, 125, 094106. [Google Scholar] [CrossRef]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef]
- Fukui, K. The Path of Chemical Reactions—The IRC Approach. Acc. Chem. Res. 1981, 14, 363–368. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).