The Spatiotemporal Dynamics and Socioeconomic Factors of SO2 Emissions in China: A Dynamic Spatial Econometric Design
Abstract
1. Introduction
2. Data and Methodology
2.1. Variables Selection and Data Resources
2.2. ESDA
2.2.1. Global Spatial Autocorrelation
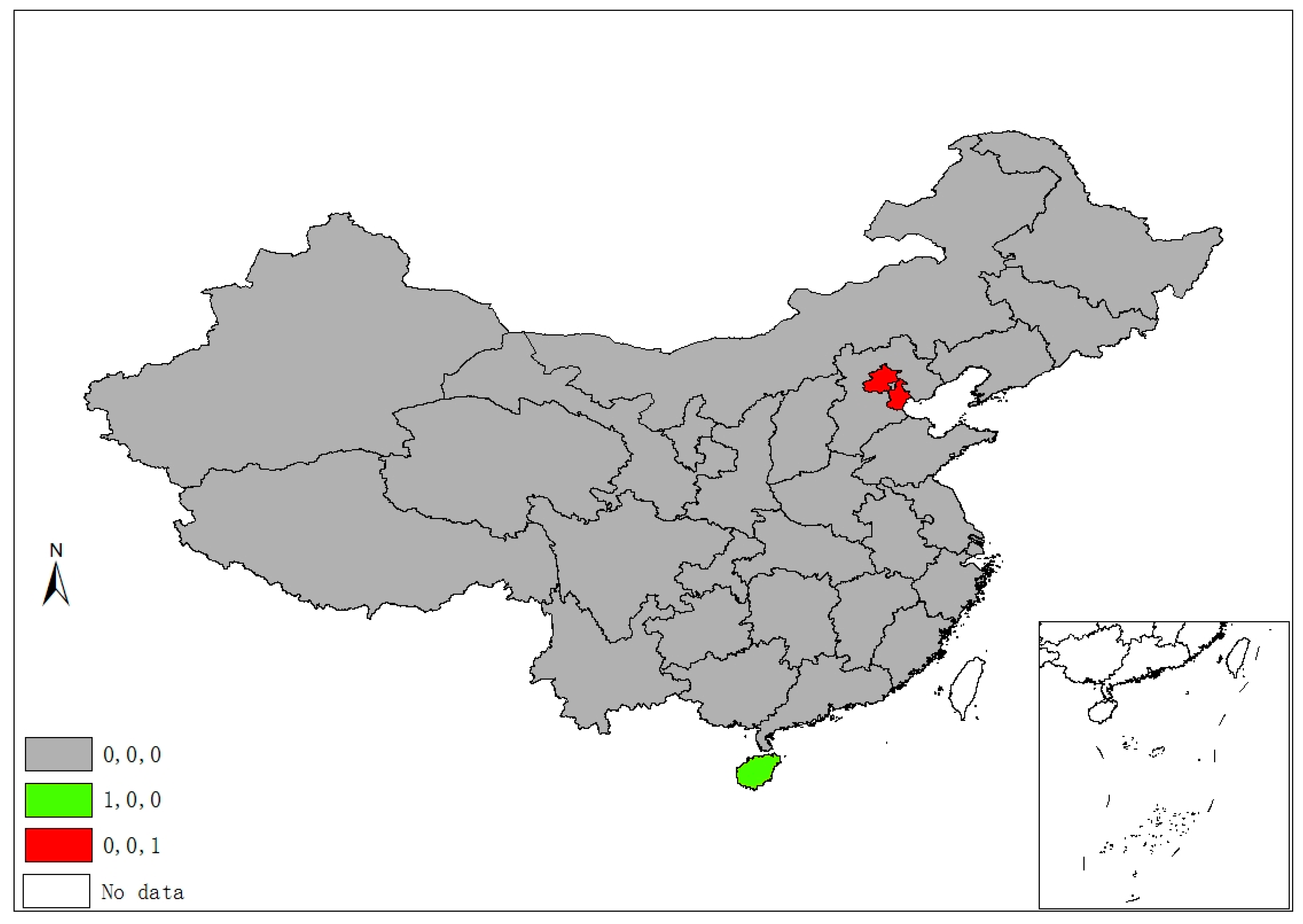
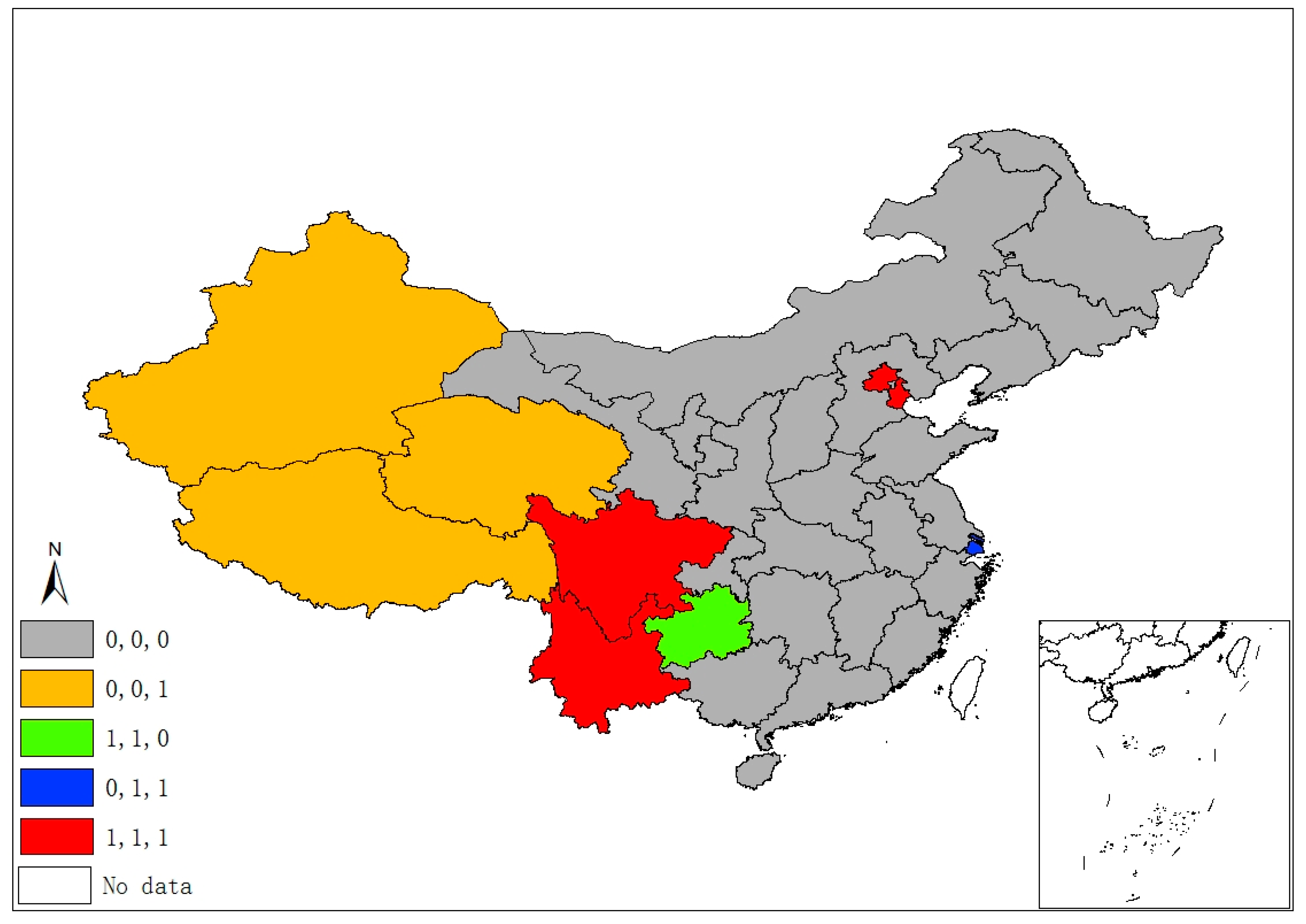
2.2.2. Local Spatial Agglomeration
2.3. Dynamic Spatial Panel Data Model
3. Findings and Interpretation
3.1. Spatiotemporal Characteristics of SO2 Emissions
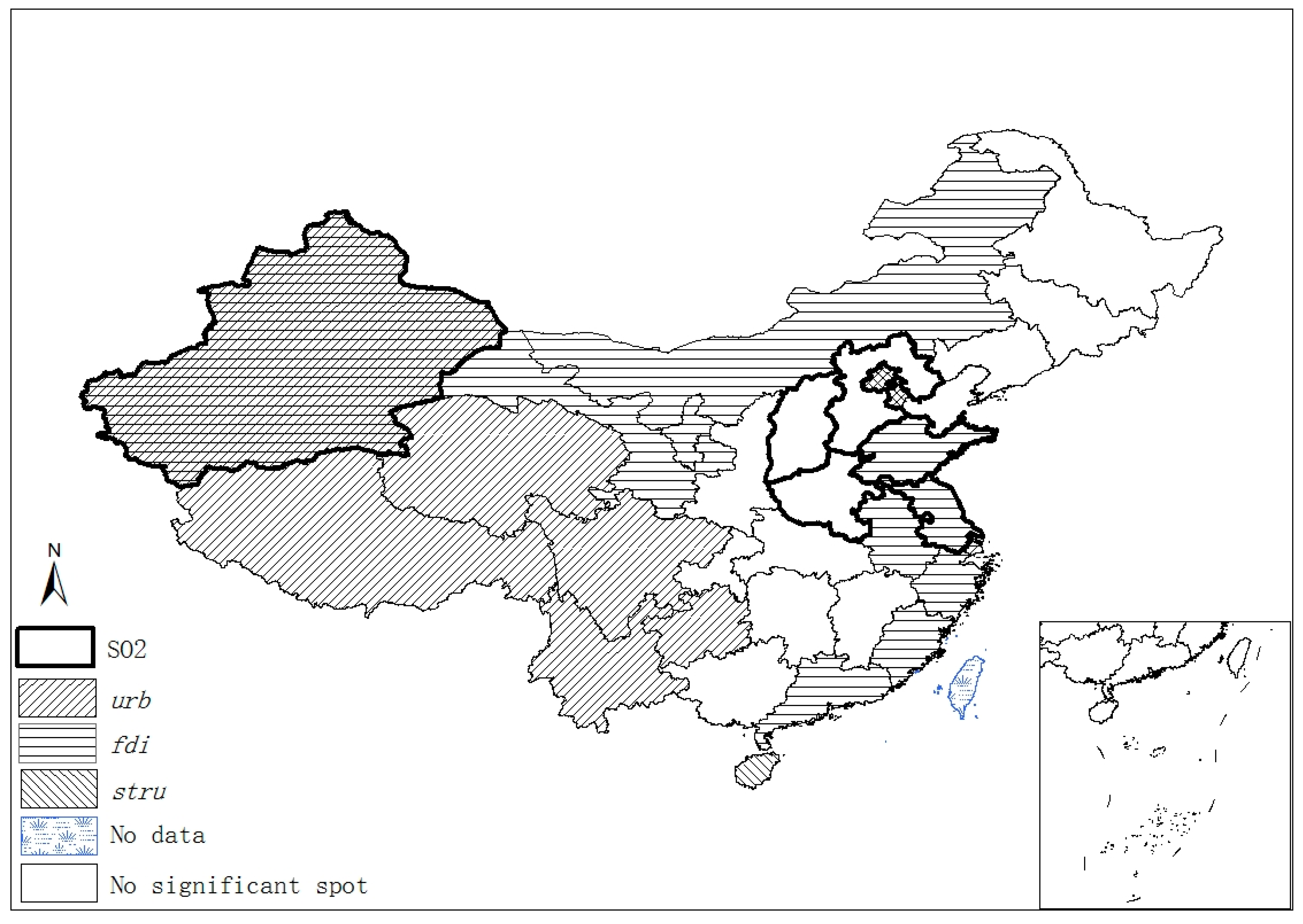
3.2. Space–Time Nexus between SO2 Emissions and Its Socioeconomic Determinants
3.3. Econometric Results and Interpretation
4. Discussion
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Wang, S.; Fang, C.; Ma, H.; Wang, Y.; Qin, J. Spatial differences and multi-mechanism of carbon footprint based on GWR model in provincial China. J. Geogr. Sci. 2014, 24, 612–630. [Google Scholar] [CrossRef]
- Wang, S.; Fang, C.; Wang, Y.; Huang, Y.; Ma, H. Quantifying the relationship between urban development intensity and carbon dioxide emissions using a panel data analysis. Ecol. Indic. 2015, 49, 121–131. [Google Scholar] [CrossRef]
- Wang, Q.; Zhou, P.; Shen, N.; Wang, S. Measuring carbon dioxide emission performance in Chinese provinces: A parametric approach. Renew. Sustain. Energy Rev. 2013, 21, 324–330. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, S. The Relationship between Urbanization, Economic Growth and Energy Consumption in China: An Econometric Perspective Analysis. Sustainability 2015, 7, 5609–5627. [Google Scholar] [CrossRef]
- Wang, S.; Zhou, C.; Li, G.; Feng, K. CO2, economic growth, and energy consumption in China’s provinces: Investigating the spatiotemporal and econometric characteristics of China’s CO2 emissions. Ecol. Indic. 2016, 69, 184–195. [Google Scholar] [CrossRef]
- Wang, Y.; Han, R.; Kubota, J. Is there an Environmental Kuznets Curve for SO2 emissions? A semi-parametric panel data analysis for China. Renew. Sustain. Energy Rev. 2016, 54, 1182–1188. [Google Scholar] [CrossRef]
- Boningari, T.; Smirniotis, P.G. Impact of nitrogen oxides on the environment and human health: Mn-based materials for the NOx abatement. Curr. Opin. Chem. Eng. 2016, 13, 133–141. [Google Scholar] [CrossRef]
- Cheng, Z.; Li, L.; Liu, J. Identifying the spatial effects and driving factors of urban PM2.5 pollution in China. Ecol. Indic. 2017, 82, 61–75. [Google Scholar] [CrossRef]
- Schreifels, J.J.; Fu, Y.; Wilson, E.J. Sulfur dioxide control in China: Policy evolution during the 10th and 11th Five-year Plans and lessons for the future. Energy Policy 2012, 48, 779–789. [Google Scholar] [CrossRef]
- Pui, D.Y.; Chen, S.-C.; Zuo, Z. PM 2.5 in China: Measurements, sources, visibility and health effects, and mitigation. Particuology 2014, 13, 1–26. [Google Scholar] [CrossRef]
- Su, S.; Li, B.; Cui, S.; Tao, S. Sulfur Dioxide Emissions from Combustion in China: From 1990 to 2007. Environ. Sci. Technol. 2011, 45, 8403–8410. [Google Scholar] [CrossRef] [PubMed]
- Wei, J.; Guo, X.; Marinova, D.; Fan, J. Industrial SO2 pollution and agricultural losses in China: Evidence from heavy air polluters. J. Clean. Prod. 2014, 64, 404–413. [Google Scholar] [CrossRef]
- Liu, C.; Hong, T.; Li, H.; Wang, L. From club convergence of per capita industrial pollutant emissions to industrial transfer effects: An empirical study across 285 cities in China. Energy Policy 2018, 121, 300–313. [Google Scholar] [CrossRef]
- Xu, Y.; Masui, T. Local air pollutant emission reduction and ancillary carbon benefits of SO2 control policies: Application of AIM/CGE model to China. Eur. J. Oper. Res. 2009, 198, 315–325. [Google Scholar] [CrossRef]
- Cheung, K.-Y.; Lin, P. Spillover effects of FDI on innovation in China: Evidence from the provincial data. China Econ. Rev. 2004, 15, 25–44. [Google Scholar] [CrossRef]
- Wang, H.; Jin, Y. Industrial Ownership and Environmental Performance: Evidence from China; The World Bank: Washington, DC, USA, 2002. [Google Scholar]
- Bao, Q.; Chen, Y.; Song, L. Foreign direct investment and environmental pollution in China: A simultaneous equations estimation. Environ. Dev. Econ. 2011, 16, 71–92. [Google Scholar] [CrossRef]
- Dean, J.M.; Lovely, M.E.; Wang, H. Are Foreign Investors Attracted to Weak Environmental Regulations? Evaluating the Evidence from China; The World Bank: Washington, DC, USA, 2005. [Google Scholar]
- Dinda, S. Environmental Kuznets Curve Hypothesis: A Survey. Ecol. Econ. 2004, 49, 431–455. [Google Scholar] [CrossRef]
- Stern, D.I. The Rise and Fall of the Environmental Kuznets Curve. World Dev. 2004, 32, 1419–1439. [Google Scholar] [CrossRef]
- Zhou, Z. The Underground Economy and Carbon Dioxide (CO2) Emissions in China. Sustainability 2019, 11, 2802. [Google Scholar] [CrossRef]
- Cole, M.A.; Neumayer, E. Examining the Impact of Demographic Factors on Air Pollution. Popul. Environ. 2004, 26, 5–21. [Google Scholar] [CrossRef]
- Parikh, J.; Shukla, V. Urbanization, energy use and greenhouse effects in economic development. Glob. Environ. Chang. 1995, 5, 87–103. [Google Scholar] [CrossRef]
- Chen, H.; Jia, B.; Lau, S. Sustainable urban form for Chinese compact cities: Challenges of a rapid urbanized economy. Habitat Int. 2008, 32, 28–40. [Google Scholar] [CrossRef]
- Yue, W.; Liu, Y.; Fan, P.; Ye, X.; Wu, C. Assessing spatial pattern of urban thermal environment in Shanghai, China. Stoch. Environ. Res. Risk Assess. 2012, 26, 899–911. [Google Scholar] [CrossRef]
- Ge, X.; Zhou, Z.; Zhou, Y.; Ye, X.; Liu, S. A Spatial Panel Data Analysis of Economic Growth, Urbanization, and NOx Emissions in China. Int. J. Environ. Res. Public Heal. 2018, 15, 725. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Fu, J.; Kong, Y.; Wu, R. How Foreign Direct Investment Influences Carbon Emissions, Based on the Empirical Analysis of Chinese Urban Data. Sustainability 2018, 10, 2163. [Google Scholar] [CrossRef]
- Riti, J.S.; Song, D.; Shu, Y.; Kamah, M. Decoupling CO2 emission and economic growth in China: Is there consistency in estimation results in analyzing environmental Kuznets curve? J. Clean. Prod. 2017, 166, 1448–1461. [Google Scholar] [CrossRef]
- Mahmood, H.; Furqan, M.; Bagais, O. Environmental accounting of financial development and foreign investment: Spatial analyses of East Asia. Sustainability 2019, 11, 13. [Google Scholar] [CrossRef]
- Koçak, E.; Ulucak, Z.S. The effect of energy R&D expenditures on CO2 emission reduction: Estimation of the STIRPAT model for OECD countries. Environ. Sci. Pollut. Res. 2019, 26, 14328–14338. [Google Scholar]
- Gong, X.; Mi, J.; Yang, R.; Sun, R. Chinese National Air Protection Policy Development: A Policy Network Theory Analysis. Int. J. Environ. Res. Public Heal. 2018, 15, 2257. [Google Scholar] [CrossRef]
- Gong, X.; Mi, J.; Wei, C.; Yang, R. Measuring Environmental and Economic Performance of Air Pollution Control for Province-Level Areas in China. Int. J. Environ. Res. Public Heal. 2019, 16, 1378. [Google Scholar] [CrossRef]
- Ding, Y.; Zhang, M.; Chen, S.; Wang, W.; Nie, R. The environmental Kuznets curve for PM2.5 pollution in Beijing-Tianjin-Hebei region of China: A spatial panel data approach. J. Clean. Prod. 2019, 220, 984–994. [Google Scholar] [CrossRef]
- Chen, X.; Yi, G.; Liu, J.; Liu, X.; Chen, Y. Evaluating Economic Growth, Industrial Structure, and Water Quality of the Xiangjiang River Basin in China Based on a Spatial Econometric Approach. Int. J. Environ. Res. Public Heal. 2018, 15, 2095. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.; Deng, C.; Huang, X.; Kwan, M.-P. Driving forces and the spatial patterns of industrial sulfur dioxide discharge in China. Sci. Total. Environ. 2017, 577, 279–288. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Z.; Ye, X.; Ge, X. The Impacts of Technical Progress on Sulfur Dioxide Kuznets Curve in China: A Spatial Panel Data Approach. Sustainability 2017, 9, 674. [Google Scholar] [CrossRef]
- Yang, X.; Wang, S.; Zhang, W.; Zhan, D.; Li, J. The impact of anthropogenic emissions and meteorological conditions on the spatial variation of ambient SO2 concentrations: A panel study of 113 Chinese cities. Sci. Total. Environ. 2017, 584, 318–328. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Guo, S.; Zhao, H. Impacts of GDP, Fossil Fuel Energy Consumption, Energy Consumption Intensity, and Economic Structure on SO2 Emissions: A Multi-Variate Panel Data Model Analysis on Selected Chinese Provinces. Sustainability 2018, 10, 657. [Google Scholar] [CrossRef]
- Li, R.; Fu, H.; Cui, L.; Li, J.; Wu, Y.; Meng, Y.; Wang, Y.; Chen, J. The spatiotemporal variation and key factors of SO2 in 336 cities across China. J. Clean. Prod. 2019, 210, 602–611. [Google Scholar] [CrossRef]
- Giacomini, R.; Granger, C.W. Aggregation of space-time processes. J. Econ. 2004, 118, 7–26. [Google Scholar] [CrossRef]
- Anselin, L. Spatial Effects in Econometric Practice in Environmental and Resource Economics. Am. J. Agric. Econ. 2001, 83, 705–710. [Google Scholar] [CrossRef]
- Belotti, F.; Hughes, G.; Mortari, A.P. Spatial Panel-data Models Using Stata. Stata J. Promot. Commun. Stat. Stata 2017, 17, 139–180. [Google Scholar] [CrossRef]
- Grossman, G.M.; Krueger, A.B. Economic Growth and the Environment. Q. J. Econ. 1995, 110, 353–377. [Google Scholar] [CrossRef]
- Martínez-Zarzoso, I.; Bengochea-Morancho, A.; Morales-Lage, R. The impact of population on CO2 emissions: Evidence from European countries. Environ. Resour. Econ. 2007, 38, 497–512. [Google Scholar] [CrossRef]
- York, R.; Rosa, E.A.; Dietz, T. STIRPAT, IPAT and ImPACT: Analytic tools for unpacking the driving forces of environmental impacts. Ecol. Econ. 2003, 46, 351–365. [Google Scholar] [CrossRef]
- Anselin, L.; Syabri, I.; Kho, Y. GeoDa: An Introduction to Spatial Data Analysis. Geogr. Anal. 2006, 38, 5–22. [Google Scholar] [CrossRef]
- Yu, D.; Wei, Y.D. Spatial data analysis of regional development in Greater Beijing, China, in a GIS environment. Pap. Reg. Sci. 2008, 87, 97–117. [Google Scholar] [CrossRef]
- Moran, P.A.P. Notes on Continuous Stochastic Phenomena. Biometrika 1950, 37, 17–23. [Google Scholar] [CrossRef]
- Ord, J.K.; Getis, A. Testing for Local Spatial Autocorrelation in the Presence of Global Autocorrelation. J. Reg. Sci. 2001, 41, 411–432. [Google Scholar] [CrossRef]
- Getis, A.; Ord, J.K. The Analysis of Spatial Association by Use of Distance Statistics. Geogr. Anal. 2010, 24, 189–206. [Google Scholar] [CrossRef]
- Ye, X.; Wu, L. Analyzing the dynamics of homicide patterns in Chicago: ESDA and spatial panel approaches. Appl. Geogr. 2011, 31, 800–807. [Google Scholar] [CrossRef]
- Elhorst, J.P. Spatial Econometrics from Cross-Sectional Data to Spatial Panels; Springer: Heidelberg, Germany, 2014. [Google Scholar] [CrossRef]
- Vega, S.H.; Elhorst, J.P. The slx model. J. Reg. Sci. 2015, 55, 339–363. [Google Scholar] [CrossRef]
- Baltagi, B. Econometric Analysis of Panel Data; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Lesage, J.; Pace, R.K. Introduction to Spatial Econometrics; Informa UK Limited; Chapman and Hall/CRC: Boca Raton, FL, USA, 2009. [Google Scholar]
- Rey, S.J.; Ye, X. Comparative spatial dynamics of regional systems. In Progress in Spatial Analysis; Springer: Berlin, Germany, 2010; pp. 441–463. [Google Scholar]
- Ye, X.; Rey, S. A framework for exploratory space-time analysis of economic data. Ann. Reg. Sci. 2013, 50, 315–339. [Google Scholar] [CrossRef]
- Sheng, P.; Guo, X. The Long-run and Short-run Impacts of Urbanization on Carbon Dioxide Emissions. Econ. Model. 2016, 53, 208–215. [Google Scholar] [CrossRef]
- Yu, J.; De Jong, R.; Lee, L.-F. Estimation for spatial dynamic panel data with fixed effects: The case of spatial cointegration. J. Econ. 2012, 167, 16–37. [Google Scholar] [CrossRef]
- Li, Q.; Song, J.; Wang, E.; Hu, H.; Zhang, J.; Wang, Y. Economic growth and pollutant emissions in China: A spatial econometric analysis. Stoch. Environ. Res. Risk Assess. 2013, 28, 429–442. [Google Scholar] [CrossRef]
- Cole, M.A. Trade, the pollution haven hypothesis and the environmental Kuznets curve: Examining the linkages. Ecol. Econ. 2004, 48, 71–81. [Google Scholar] [CrossRef]
- Ehrhardt-Martinez, K. Social Determinants of Deforestation in Developing Countries: A Cross-National Study. Soc. Forces 1998, 77, 567–586. [Google Scholar] [CrossRef]
- Martinez-Zarzoso, I.; Maruotti, A. The impact of urbanization on CO2 emissions: Evidence from developing countries. Ecol. Econ. 2011, 70, 1344–1353. [Google Scholar] [CrossRef]
- Liddle, B. Demographic Dynamics and Per Capita Environmental Impact: Using Panel Regressions and Household Decompositions to Examine Population and Transport. Popul. Environ. 2003, 26, 23–39. [Google Scholar] [CrossRef]
- Pachauri, S. An analysis of cross-sectional variations in total household energy requirements in India using micro survey data. Energy Policy 2004, 32, 1723–1735. [Google Scholar] [CrossRef]
- Pachauri, S.; Jiang, L. The household energy transition in India and China. Energy Policy 2008, 36, 4022–4035. [Google Scholar] [CrossRef]
- Torras, M.; Boyce, J.K. Income, inequality, and pollution: A reassessment of the environmental Kuznets Curve. Ecol. Econ. 1998, 25, 147–160. [Google Scholar] [CrossRef]
- Yu, S.; Hu, X.; Fan, J.-L.; Cheng, J. Convergence of carbon emissions intensity across Chinese industrial sectors. J. Clean. Prod. 2018, 194, 179–192. [Google Scholar] [CrossRef]
- Ministry of Ecology and Environment (MEE). Bulletin of National Environmental Statistics (2015); Ministry of Ecology and Environment of the People’s Republic of China: Beijing, China, 2017.
- Suri, V.; Chapman, D. Economic growth, trade and energy: Implications for the environmental Kuznets curve. Ecol. Econ. 1998, 25, 195–208. [Google Scholar] [CrossRef]
- Dinda, S.; Coondoo, D.; Pal, M. Air quality and economic growth: An empirical study. Ecol. Econ. 2000, 34, 409–423. [Google Scholar] [CrossRef]
- Zhang, C.; Lin, Y. Panel estimation for urbanization, energy consumption and CO2 emissions: A regional analysis in China. Energy Policy 2012, 49, 488–498. [Google Scholar] [CrossRef]
- REN21, P.S. Renewables 2014: Global Status Report; REN21 Secretariat: Paris, France, 2014. [Google Scholar]
- Galeotti, M.; Lanza, A. Richer and cleaner? A study on carbon dioxide emissions in developing countries. Energy Policy 1999, 27, 565–573. [Google Scholar] [CrossRef]
- Bruyn, D.S.M. Explaining the Kuznets curve. Structural change and international agreements in reducing sulphur emissions. Environ. Dev. Econ. 1997, 2, 485–502. [Google Scholar] [CrossRef]
- Krugman, P. Increasing Returns and Economic Geography. J. Politi. Econ. 1991, 99, 483–499. [Google Scholar] [CrossRef]
- Miao, F.U. Geographical Distance and Technological Spillover Effects: A Spatial Econometric Explanation of Technological and Economic Agglomeration Phenomena. China Econ. Q. 2009, 8, 1549–1566. [Google Scholar]
- Pirotte, A.; Mur, J. Neglected dynamics and spatial dependence on panel data: Consequences for convergence of the usual static model estimators. Spat. Econ. Anal. 2017, 12, 202–229. [Google Scholar] [CrossRef]
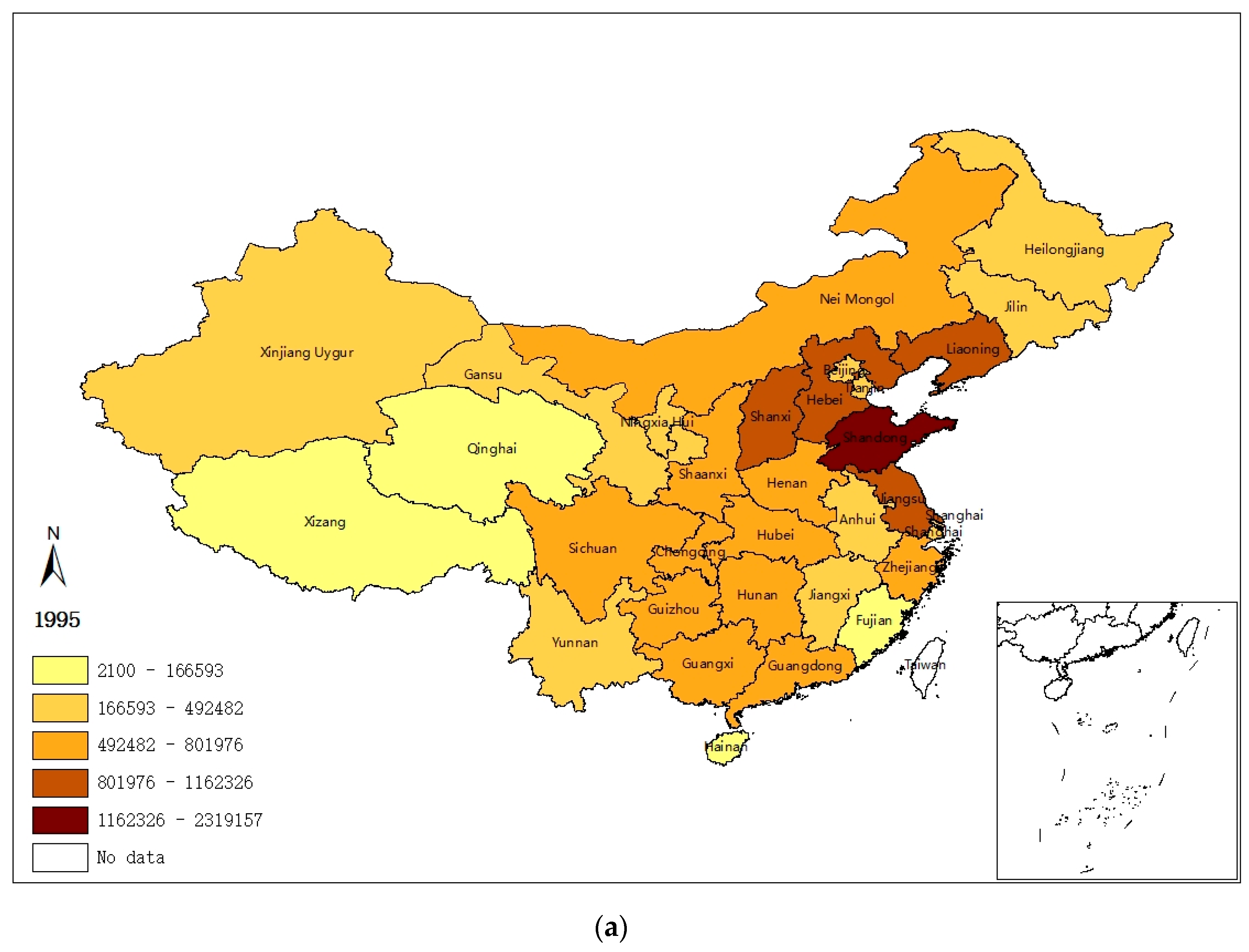
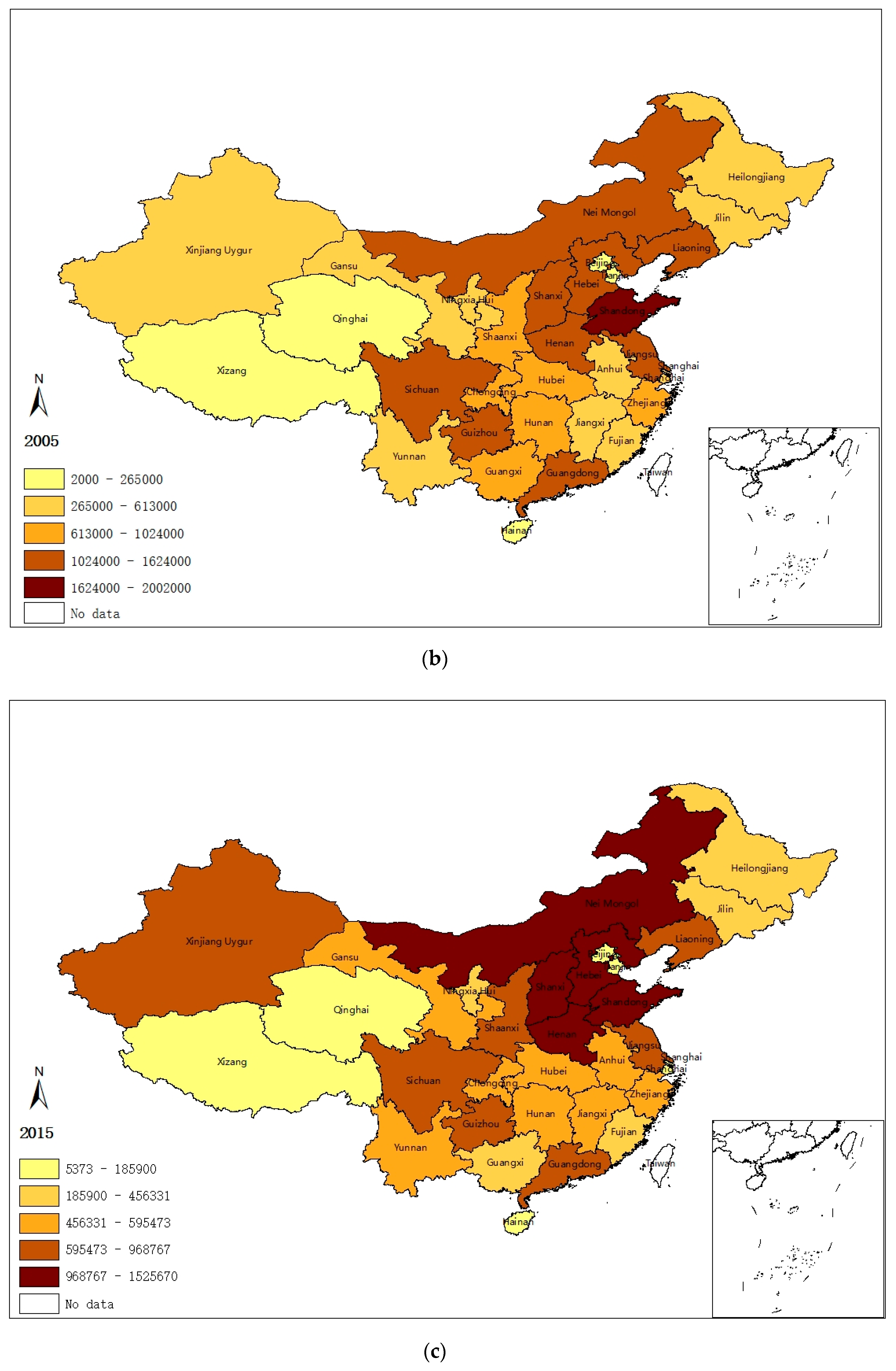
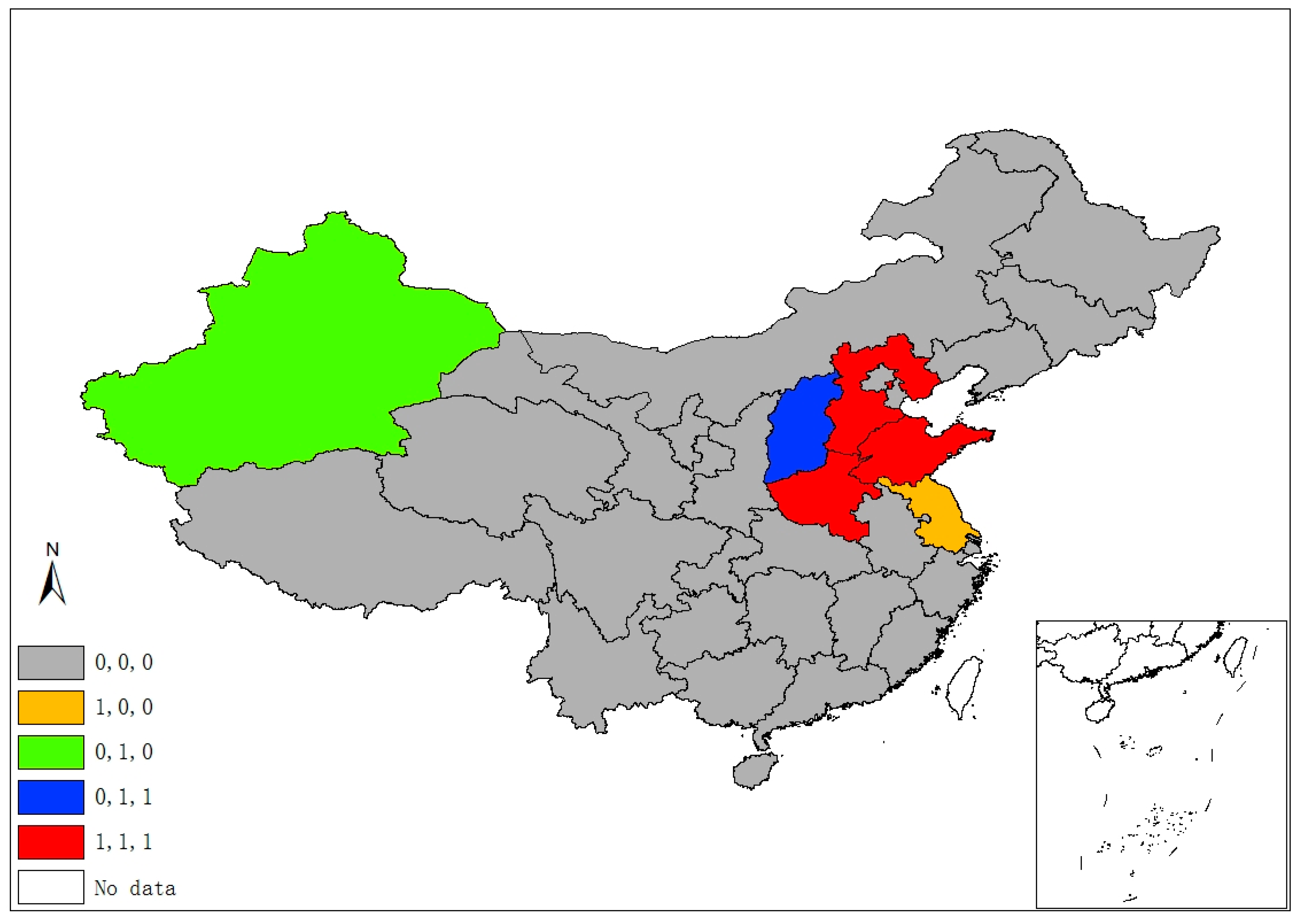
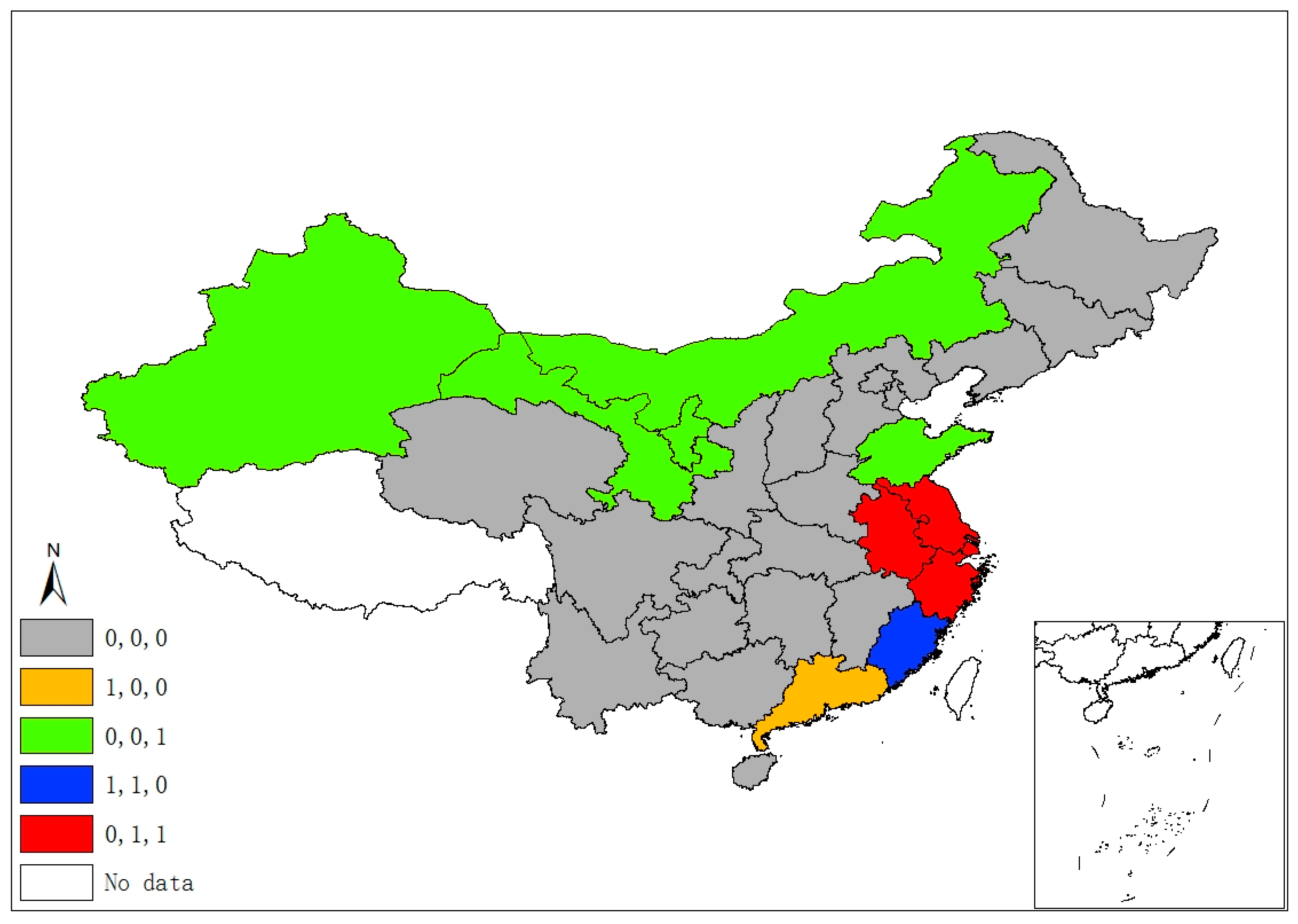
| Variables | Definition | Mean | Std. Dev. | Min | Max |
|---|---|---|---|---|---|
| lnSO2 | SO2 emissions (tons) in logarithm | 13.10 | 0.936 | 9.735 | 14.51 |
| urb | Proportion of population living in urban area (%) | 46.40 | 16.04 | 20.39 | 89.60 |
| fdi | Ratio of FDI to GDP (%) | 2.986 | 3.181 | 0.001 | 21.19 |
| stru | The ratio of the tertiary industry to the secondary industry (%) | 95.36 | 42.40 | 403.79 | 49.70 |
| lnPOP | population size (10 thousand) in logarithm | 8.127 | 0.770 | 6.176 | 9.292 |
| lnEI | energy intensity (tons of coal equivalent/billion Yuan) in logarithm | 9.715 | 0.511 | 8.706 | 11.27 |
| lnGDP | real per capita GDP (100 Yuan, in 1995 constant price) in logarithm | 4.867 | 0.855 | 2.905 | 7.170 |
| Year | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 |
| Moran’s I | 0.200 | 0.201 | 0.249 | 0.225 | 0.229 | 0.170 | 0.158 | 0.154 | 0.131 | 0.146 | 0.148 |
| z-statistics | 2.266 | 2.274 | 2.658 | 2.428 | 2.428 | 1.842 | 1.731 | 1.700 | 1.478 | 1.607 | 1.630 |
| p-value | 0.023 | 0.023 | 0.008 | 0.015 | 0.015 | 0.065 | 0.084 | 0.089 | 0.139 | 0.108 | 0.103 |
| Year | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | |
| Moran’s I | 0.148 | 0.165 | 0.166 | 0.148 | 0.116 | 0.230 | 0.222 | 0.226 | 0.208 | 0.210 | |
| z-statistics | 1.629 | 1.775 | 1.789 | 1.626 | 1.335 | 2.380 | 2.309 | 2.339 | 2.184 | 2.206 | |
| p-value | 0.103 | 0.076 | 0.074 | 0.104 | 0.182 | 0.017 | 0.021 | 0.019 | 0.029 | 0.027 |
| Year | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1995 | 1.00 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - |
| 1996 | 1.00 | 1.00 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - |
| 1997 | 0.99 | 0.99 | 1.00 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - |
| 1998 | 0.96 | 0.97 | 0.97 | 1.00 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - |
| 1999 | 0.95 | 0.95 | 0.94 | 0.96 | 1.00 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - |
| 2000 | 0.89 | 0.90 | 0.91 | 0.94 | 0.93 | 1.00 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - |
| 2001 | 0.88 | 0.90 | 0.91 | 0.95 | 0.94 | 1.00 | 1.00 | - | - | - | - | - | - | - | - | - | - | - | - | - | - |
| 2002 | 0.89 | 0.91 | 0.92 | 0.95 | 0.94 | 0.99 | 1.00 | 1.00 | - | - | - | - | - | - | - | - | - | - | - | - | - |
| 2003 | 0.87 | 0.88 | 0.91 | 0.93 | 0.92 | 0.96 | 0.96 | 0.98 | 1.00 | - | - | - | - | - | - | - | - | - | - | - | - |
| 2004 | 0.85 | 0.87 | 0.90 | 0.92 | 0.92 | 0.95 | 0.96 | 0.97 | 0.99 | 1.00 | - | - | - | - | - | - | - | - | - | - | - |
| 2005 | 0.86 | 0.87 | 0.90 | 0.91 | 0.91 | 0.92 | 0.94 | 0.95 | 0.98 | 0.99 | 1.00 | - | - | - | - | - | - | - | - | - | - |
| 2006 | 0.85 | 0.86 | 0.89 | 0.89 | 0.89 | 0.92 | 0.93 | 0.94 | 0.97 | 0.98 | 1.00 | 1.000 | - | - | - | - | - | - | - | - | - |
| 2007 | 0.83 | 0.84 | 0.88 | 0.88 | 0.89 | 0.91 | 0.92 | 0.94 | 0.97 | 0.99 | 1.00 | 1.00 | 1.00 | - | - | - | - | - | - | - | - |
| 2008 | 0.83 | 0.84 | 0.88 | 0.88 | 0.88 | 0.89 | 0.91 | 0.92 | 0.96 | 0.98 | 0.99 | 1.00 | 1.00 | 1.00 | - | - | - | - | - | - | - |
| 2009 | 0.82 | 0.83 | 0.87 | 0.87 | 0.88 | 0.89 | 0.91 | 0.93 | 0.96 | 0.97 | 0.99 | 1.00 | 1.00 | 1.00 | 1.00 | - | - | - | - | - | - |
| 2010 | 0.81 | 0.82 | 0.86 | 0.86 | 0.86 | 0.88 | 0.90 | 0.91 | 0.96 | 0.97 | 0.99 | 0.99 | 0.99 | 0.99 | 1.00 | 1.00 | - | - | - | - | - |
| 2011 | 0.82 | 0.83 | 0.87 | 0.87 | 0.86 | 0.83 | 0.86 | 0.88 | 0.91 | 0.92 | 0.95 | 0.95 | 0.95 | 0.96 | 0.96 | 0.95 | 1.00 | - | - | - | - |
| 2012 | 0.81 | 0.82 | 0.86 | 0.85 | 0.84 | 0.81 | 0.83 | 0.86 | 0.90 | 0.91 | 0.94 | 0.94 | 0.95 | 0.95 | 0.95 | 0.94 | 1.00 | 1.00 | - | - | - |
| 2013 | 0.78 | 0.79 | 0.83 | 0.83 | 0.82 | 0.80 | 0.82 | 0.84 | 0.89 | 0.90 | 0.93 | 0.94 | 0.94 | 0.94 | 0.95 | 0.94 | 1.00 | 1.00 | 1.00 | - | - |
| 2014 | 0.80 | 0.80 | 0.84 | 0.83 | 0.82 | 0.80 | 0.82 | 0.84 | 0.88 | 0.89 | 0.92 | 0.93 | 0.93 | 0.94 | 0.94 | 0.93 | 0.99 | 1.00 | 1.00 | 1.00 | - |
| 2015 | 0.80 | 0.80 | 0.84 | 0.83 | 0.82 | 0.79 | 0.81 | 0.84 | 0.88 | 0.89 | 0.92 | 0.93 | 0.93 | 0.94 | 0.94 | 0.93 | 0.99 | 1.00 | 1.00 | 1.00 | 1.00 |
| Variables | Equation (2) | Equation (3) | Equation (4) | |||
|---|---|---|---|---|---|---|
| x | Wx | x | Wx | x | Wx | |
| lnSO2 t − 1 (γ0) | 0.873 *** | 0.862 *** | ||||
| (35.99) | (35.81) | |||||
| WlnSO2 t − 1 (ρ0) | −0.156 ** | 0.243 *** | ||||
| (−2.45) | (2.60) | |||||
| urb | −0.004 ** | −0.009 ** | −0.013 *** | −0.051 *** | −0.004 * | −0.008 * |
| (−2.01) | (−2.18) | (−3.51) | (−7.59) | (−1.65) | (−1.88) | |
| fdi | 0.003 | 0.009 * | −0.006 | 0.033 *** | 0.003 | 0.009 * |
| (1.13) | (1.76) | (−1.28) | (3.74) | (1.10) | (1.67) | |
| stru | −0.001 *** | −0.001 ** | −0.003 *** | −0.003 ** | −0.001 *** | −0.001 |
| (−3.06) | (−2.01) | (−5.99) | (−2.40) | (−2.73) | (−1.47) | |
| lnGDP | 0.168 | 1.483 *** | 0.205 | |||
| (1.01) | (5.47) | (1.22) | ||||
| (lnGDP)2 | −0.020 * | −0.100 *** | −0.020 * | |||
| (−1.69) | (−5.12) | (−1.70) | ||||
| lnPOP | 0.255 * | 0.460 ** | 0.989 *** | −0.318 | 0.270 ** | 0.436 ** |
| (1.93) | (2.31) | (4.55) | (−0.96) | (2.04) | (2.17) | |
| lnEI | 0.101 ** | −0.125 | 0.525 *** | −0.083 | 0.098 ** | −0.161 |
| (2.23) | (−1.11) | (7.18) | (−0.45) | (2.15) | (−1.43) | |
| WlnSO2 t (λ0) | 0.132 ** | 0.074 | 0.057 | |||
| (2.40) | (1.07) | (1.38) | ||||
| Observations | 600 | 600 | 600 | |||
| Log-likelihood | 203.020 | −504.279 | 340.714 | |||
| R2 | 0.881 | 0.645 | 0.891 | |||
| N | 30 | 30 | 30 | |||
| lnSO2 | Direct Effects (Short-Term) | Spillover Effects (Short-Term) | Total Effects (Short-Term) | Direct Effects (Long-Term) | Spillover Effects (Long-Term) | Total Effects (Long-Term) |
|---|---|---|---|---|---|---|
| urb | −0.004 ** | −0.011 ** | −0.015 *** | −0.032 | −0.065 | −0.097 |
| (−2.15) | (−2.34) | (−3.07) | (−1.57) | (−0.26) | (−0.38) | |
| fdi | 0.004 | 0.011 * | 0.014 ** | 0.024 | 0.068 | 0.092 |
| (1.28) | (1.88) | (2.35) | (0.94) | (0.52) | (0.69) | |
| stru | −0.001 *** | −0.002 ** | −0.003 *** | −0.008 *** | −0.009 | −0.017 |
| (−3.17) | (−2.04) | (−2.78) | (−2.72) | (−0.24) | (−0.45) | |
| lnPOP | 0.275 ** | 0.541 ** | 0.817 *** | 2.015 * | 3.066 | 5.081 |
| (2.10) | (2.46) | (3.31) | (1.67) | (0.23) | (0.38) | |
| lnEI | 0.099 ** | −0.124 | −0.025 | 0.878 ** | −0.967 | −0.089 |
| (2.24) | (−0.94) | (−0.18) | (2.08) | (−0.32) | (−0.03) |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Z. The Spatiotemporal Dynamics and Socioeconomic Factors of SO2 Emissions in China: A Dynamic Spatial Econometric Design. Atmosphere 2019, 10, 534. https://doi.org/10.3390/atmos10090534
Zhou Z. The Spatiotemporal Dynamics and Socioeconomic Factors of SO2 Emissions in China: A Dynamic Spatial Econometric Design. Atmosphere. 2019; 10(9):534. https://doi.org/10.3390/atmos10090534
Chicago/Turabian StyleZhou, Zhimin. 2019. "The Spatiotemporal Dynamics and Socioeconomic Factors of SO2 Emissions in China: A Dynamic Spatial Econometric Design" Atmosphere 10, no. 9: 534. https://doi.org/10.3390/atmos10090534
APA StyleZhou, Z. (2019). The Spatiotemporal Dynamics and Socioeconomic Factors of SO2 Emissions in China: A Dynamic Spatial Econometric Design. Atmosphere, 10(9), 534. https://doi.org/10.3390/atmos10090534





