On the ‘Divergence Problem’ in the Alatau Mountains, Central Asia: A Study of the Responses of Schrenk Spruce Tree-Ring Width to Climate under the Recent Warming and Wetting Trend
Abstract
1. Introduction
2. Materials and Methods
2.1. Sample Collection
2.2. Tree-Ring Core Treatments and Ring-Width Measurements
2.3. Tree-Ring Width Chronology Development
2.4. Climatic Data
2.5. Statistical Analysis
3. Results
3.1. Variation Characteristics of the Meteorological Data
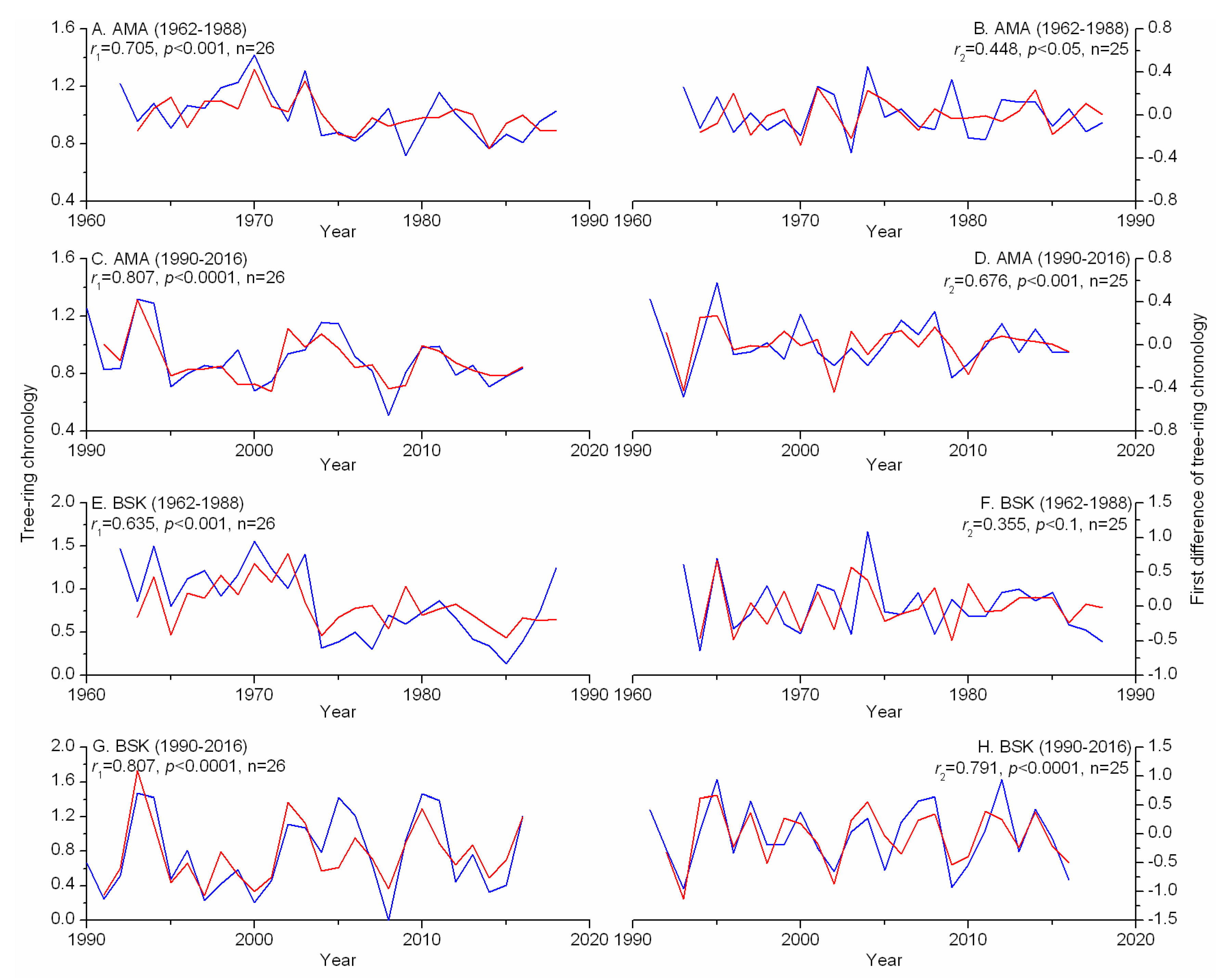
3.2. Comparative Analysis between Tree-Ring Chronologies
3.3. Correlations between Chronologies and Climatic Data
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Nabuurs, G.J.; Pussinen, A.; van Bruselen, J.; Schelhaas, M.J. Future harvesting pressure on European forests. Eur. J. For. Res. 2007, 126, 391–400. [Google Scholar] [CrossRef]
- Kolström, M.; Lindner, M.; Vilén, T.; Maroschek, M.; Seidl, R.; Lexer, M.J.; Netherer, S.; Kremer, A.; Delzon, S.; Barbati, A.; et al. Reviewing the Science and Implementation of Climate Change Adaptation Measures in European Forestry. Forests 2011, 2, 961–982. [Google Scholar] [CrossRef]
- Machar, I.; Vlckova, V.; Bucek, A.; Vozenilek, V.; Salek, L.; Jerabkova, L. Modelling of Climate Conditions in Forest Vegetation Zones as a Support Tool for Forest Management Strategy in European Beech Dominated Forests. Forests 2017, 8, 82. [Google Scholar] [CrossRef]
- Jacoby, G.C.; D’Arrigo, R.D. Tree ring width and density evidence of climatic and potential forest change in Alaska. Glob. Biogeochem. Cycles 1995, 9, 227–234. [Google Scholar] [CrossRef]
- Büntgen, U.; Frank, D.C.; Schmidhalter, M.; Neuwirth, B.; Seifert, M.; Esper, J. Growth/climate response shift in a long subalpine spruce chronology. Trees-Struct. Funct. 2006, 20, 99–110. [Google Scholar] [CrossRef]
- Pisaric, M.F.J.; Carey, S.K.; Kokelj, S.V.; Youngblut, D. Anomalous 20th century tree growth, Mackenzie Delta, Northwest Territories, Canada. Geophys. Res. Lett. 2007, 34, 247–260. [Google Scholar] [CrossRef]
- Briffa, K.R.; Jones, P.D.; Schweingruber, F.H.; Osborn, T.J. Influence of volcanic eruptions on Northern Hemisphere summer temperature over the past 600 years. Nature 1998, 393, 450–455. [Google Scholar] [CrossRef]
- Yonenobu, H.; Eckstein, D. Reconstruction of early spring temperature for central Japan from the tree-ring widths of Hinoki cypress and its verification by other proxy records. Geophys. Res. Lett. 2006, 33, 328–340. [Google Scholar] [CrossRef]
- Esper, J.; Frank, D.; Büntgen, U.; Verstege, A.; Hantemirov, A.M.; Kirdyanov, L.V. Trends and uncertainties in Siberian indicators of 20th century warming. Glob. Chang. Biol. 2010, 16, 386–398. [Google Scholar] [CrossRef]
- D’Arrigo, R.D.; Wilson, R.; Liepert, B.; Cherubini, P. On the ‘Divergence Problem’ in Northern Forests: A review of the tree-ring evidence and possible causes. Glob. Planet. Chang. 2008, 60, 289–305. [Google Scholar] [CrossRef]
- Davi, N.K.; Jacoby, G.C.; Wiles, G.C. Boreal temperature variability inferred from maximum latewood density and tree-ring width data, Wrangell Mountain region, Alaska. Quat. Res. 2003, 60, 252–262. [Google Scholar] [CrossRef]
- Driscoll, W.W.; Wiles, G.C.; D’Arrigo, R.D.; Wilmking, M. Divergent tree growth response to recent climatic warming, Lake Clark National Park and Preserve, Alaska. Geophys. Res. Lett. 2005, 32, 423–436. [Google Scholar] [CrossRef]
- Barber, V.A.; Juday, G.P.; Finney, B.P. Reduced growth of Alaskan white spruce in the twentieth century from temperature-induced drought stress. Nature 2000, 405, 668–673. [Google Scholar] [CrossRef] [PubMed]
- Cook, E.R.; Peters, K. Calculating unbiased tree-ring indices for the study of climatic and environmental change. Holocene 1997, 7, 361–370. [Google Scholar] [CrossRef]
- Becker, F.; Li, Z.L. Towards a local split window method over land surface. Int. J. Remote Sens. 1990, 11, 369–393. [Google Scholar] [CrossRef]
- Esper, J.; Frank, D.C.; Wilson, R.J.S.; Büntgen, U.; Treydte, K. Uniform growth trends among central Asian low- and high-elevation juniper tree sites. Trees-Struct. Funct. 2007, 21, 141–150. [Google Scholar] [CrossRef]
- Yang, C.Y.; Shen, K.M.; Mao, Z.M. Flora Xinjiangensis: Tomus 1; Xinjiang Science & Technology & Hygiene Publishing House: Urumqi, China, 1992. (In Chinese) [Google Scholar]
- Esper, J. Long-term tree-ring variations in Juniperus at the upper timber-line in the Karakorum (Pakistan). Holocene 2000, 10, 253–260. [Google Scholar] [CrossRef]
- Opała, M.; Niedźwiedź, T.; Rahmonov, O.; Owczarek, P.; Małarzewski, Ł. Towards improving the Central Asian dendrochronological network—New data from Tajikistan, Pamir-Alay. Dendrochronologia 2017, 41, 10–23. [Google Scholar] [CrossRef]
- Opała-Owczarek, M.; Owczarek, P.; Rahmonov, O.; Niedźwiedź, T. The first dendrochronological dating of timber from Tajikistan–Potential for developing a millennial tree-ring record. Tree-Ring Res. 2018, 74, 50–62. [Google Scholar] [CrossRef]
- Esper, J.; Shiyatov, S.G.; Mazepa, V.S.; Wilson, R.J.S.; Graybill, D.A.; Funkhouser, G. Temperature-sensitive Tien Shan tree ring chronologies show multi-centennial growth trends. Clim. Dynam. 2003, 21, 699–706. [Google Scholar] [CrossRef]
- Winter, M.B.; WolV, B.; Gottschling, H.; Cherubini, P. The impact of climate on radial growth and nut production of Persian walnut (Juglans regia L.) in Southern Kyrgyzstan. Eur. J. For. Res. 2009, 128, 531–542. [Google Scholar] [CrossRef]
- Zhang, T.W.; Yuan, Y.J.; He, Q.; Wei, W.S.; Diushen, M.; Shang, H.M.; Zhang, R.B. Development of tree-ring width chronologies and tree-growth response to climate in the mountains surrounding the Issyk-Kul Lake, Central Asia. Dendrochronologia 2014, 32, 230–236. [Google Scholar] [CrossRef]
- Fang, K.Y.; Davi, N.; Gou, X.H.; Chen, F.H.; Cook, E.; Li, J.B.; D’Arrigo, R. Spatial drought reconstructions for central High Asia based on tree rings. Clim. Dynam. 2010, 35, 941–951. [Google Scholar] [CrossRef]
- Chen, F.; He, Q.; Bakytbek, E.; Yu, S.L.; Zhang, R.B. Reconstruction of a long streamflow record using tree rings in the upper Kurshab River (Pamir-Alai Mountains) and its application to water resources management. Int. J. Water Resour. D 2017, 33, 976–986. [Google Scholar] [CrossRef]
- Panyushkina, I.P.; Meko, D.M.; Macklin, M.G.; Toonen, W.H.J.; Mukhamadiev, N.S.; Konovalov, V.G.; Ashikbaev, N.Z.; Sagitov, A.O. Runoff variations in Lake Balkhash Basin, Central Asia, 1779–2015, inferred from tree rings. Clim. Dynam. 2018, 51, 3161–3177. [Google Scholar] [CrossRef]
- Chen, F.H.; Huang, W.; Jin, L.Y.; Chen, J.H.; Wang, J.S. Spaiotemporal precipitation variations in the arid Central Asia in the context of global warming. Sci. China Earth Sci. 2011, 54, 1812–1821. [Google Scholar] [CrossRef]
- Huang, W.; Wu, X.; Chen, J.H.; Chen, F.H. Tropospheric biennial oscillations and abrupt changes of precipitation in the arid Central Asia. Adv. Clim. Chang. Res. 2012, 8, 448–455, (In Chinese, with English abstract). [Google Scholar]
- Wang, J.S.; Chen, F.H.; Jin, L.Y.; Wei, F. The response to two global warming periods in the 20th century over the arid Central Asia. J. Glaciol. Geocryol. 2008, 30, 224–233, (In Chinese, with English abstract). [Google Scholar]
- Shen, W.F.; Miao, Q.L.; Wei, T.X.; Kong, C.C. Analysis of temperature variation in recent 130 years in Central Asia. J. Arid Meteorol. 2013, 31, 32–36, (In Chinese, with English abstract). [Google Scholar]
- Lu, P.; Yan, G.X. Xinjiang Forests; Xinjiang People’s Press: Urumqi, China; China Forestry Publishing House: Beijing, China, 1989. (In Chinese) [Google Scholar]
- Pan, Y.F.; Yan, S.; Mu, G.J.; Kong, Z.C.; Ni, J.; Yang, Z.J. Changes in the concentrations of airborne Picea schrenkiana pollen in response to temperature changes in the Tianshan Mountain area. Acta. Ecol. Sin. 2011, 31, 6999–7006, (In Chinese, with English abstract). [Google Scholar]
- Sang, W.G.; Wang, Y.X.; Su, H.X.; Lu, Z.H. Response of tree-ring width to rainfall gradient along the Tianshan Mountains of northwestern China. Chin. Sci. Bull. 2007, 52, 2954–2962. [Google Scholar] [CrossRef]
- FAO; IIASA; ISRIC; ISSCAS; JRC. Harmonized World Soil Database (version 1.2); FAO: Rome, Italy; IIASA: Laxenburg, Austia, 2012. [Google Scholar]
- Speer, J.H. Fundamentals of Tree-Ring Research; The University of Arizona Press: Tucson, AZ, USA, 2010. [Google Scholar]
- Schöngart, J.; Piedade, M.T.F.; Wittmann, F.; Junk, W.J.; Worbes, M. Wood growth patterns of Macrolobium acaciifolium (Benth.) Benth. (Fabaceae) in Amazonian black-water and white-water floodplain forests. Oecologia 2005, 145, 454–461. [Google Scholar] [CrossRef] [PubMed]
- Grissino-Mayer, H.D. Evaluating crossdating accuracy: A manual and tutorial for the computer program COFECHA. Tree-Ring Res. 2001, 57, 205–221. [Google Scholar]
- Cook, E.R.; Krusic, P.J. Program ARSTAN: A Tree-Ring Standardization Program Based on Detrending and Autoregressive Time Series Modeling, with Interactive Graphics; Lamont-Doherty Earth Observatory, Columbia University: New York, NY, USA, 2005. [Google Scholar]
- Liu, Y.; Tian, H.; Song, H.M.; Liang, J.M. Tree ring precipitation reconstruction in the Chifeng-Weichang region, China, and East Asian summer monsoon variation since A.D. 1777. J. Geophys. Res. 2010, 115, 620–631. [Google Scholar] [CrossRef]
- Cook, E.R.; Kairiukstis, L.A. Methods of Dendrochronology: Applications in the Environmental Sciences; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1990. [Google Scholar]
- Wigley, T.M.L.; Briffa, K.R.; Jones, P.D. On the average value of correlated time series, with applications in dendroclimatology and hydrometeorology. J. Clim. Appl. Meteorol. 1984, 23, 201–213. [Google Scholar] [CrossRef]
- Harris, I.; Jones, P.D.; Osborn, T.J.; Lister, D.H. Updated high-resolution grids of monthly climatic observations—The CRU TS3.10 Dataset. Int. J. Climatol. 2014, 34, 623–642. [Google Scholar] [CrossRef]
- D’Arrigo, R.; Mashig, E.; Frank, D.; Wilson, R.; Jacoby, G. Temperature variability over the past millennium inferred from Northwestern Alaska tree rings. Clim. Dynam. 2005, 24, 227–236. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, C.Y.; Hao, W.J.; Song, H.M.; Cai, Q.F.; Tian, H.; Sun, B.; Linderholm, H.W. Tree-ring-based annual precipitation reconstruction in Kalaqin, Inner Mongolia for the last 238 years. Chin. Sci. Bull. 2011, 56, 2995–3002. [Google Scholar] [CrossRef]
- Opała, M.; Mendecki, M.J. An attempt to dendroclimatic reconstruction of winter temperature based on multispecies tree-ring widths and extreme years chronologies (example of Upper Silesia, Southern Poland). Theor. Appl. Climatol. 2014, 115, 73–89. [Google Scholar] [CrossRef]
- Wei, F.Y. Modern Climate Statistical Diagnosis and Prediction Technology; China Meteorological Press: Beijing, China, 2007. (In Chinese) [Google Scholar]
- Yuan, Y.J.; Zhang, T.W.; Wei, W.S.; Nievergelt, D.; Verstege, A.; Yu, S.L.; Zhang, R.B.; Esper, J. Development of tree-ring maximum latewood density chronologies for the western Tien Shan Mountains, China: Influence of detrending method and climate response. Dendrochronologia 2013, 31, 192–197. [Google Scholar] [CrossRef]
- Schweingruber, F.H.; Briffa, K.R.; Nogler, P. A tree-ring densitometric transect from Alaska to Labrador. Int. J. Biometeorol. 1993, 37, 151–169. [Google Scholar] [CrossRef]
- Wang, H.; Shao, X.M.; Jiang, Y.; Fang, X.Q.; Wu, S.H. The impacts of climate change on the radial growth of Pinus koraiensis along elevations of Changbai Mountain in northeastern China. For. Ecol. Manag. 2013, 289, 333–340. [Google Scholar] [CrossRef]
- Shi, Y.F.; Shen, Y.P.; Kang, E.S.; Li, D.L.; Ding, Y.J.; Zhang, G.W.; Hu, R.J. Recent and future climate change in northwest China. Clim. Chang. 2007, 80, 379–393. [Google Scholar] [CrossRef]
- Cook, E.R. A Time-Series Analysis Approach to Tree-Ring Standardization. Ph.D. Thesis, The University of Arizona, Tucson, AZ, USA, 1985. [Google Scholar]
- Li, J.B.; Gou, X.H.; Cook, E.R.; Chen, F.H. Tree-ring based drought reconstruction for the central Tien Shan area in northwest China. Geophys. Res. Lett. 2006, 33, L07715. [Google Scholar] [CrossRef]
- Zhang, T.W.; Zhang, R.B.; Yuan, Y.J.; Gao, Y.Q.; Wei, W.S.; Diushen, M.; He, Q.; Shang, H.M.; Wang, J. Reconstructed precipitation on a centennial timescale from tree rings in the western Tien Shan Mountains, Central Asia. Quat. Int. 2015, 358, 58–67. [Google Scholar] [CrossRef]
- Jiao, L.; Jiang, Y.; Wang, M.; Zhang, W.; Zhang, Y. Age-effect radial growth responses of Picea schrenkiana to climate change in the eastern Tianshan Mountains, Northwest China. Forests 2017, 8, 294. [Google Scholar] [CrossRef]
- Wilson, R.; D’Arrigo, R.; Buckley, B.; Büntgen, U.; Esper, J.; Frank, D.; Luckman, B.; Payette, S.; Vose, R.; Youngblut, D. A matter of divergence: Tracking recent warming at hemispheric scales using tree ring data. J. Geophys. Res. Atmos. 2007, 112, 107–114. [Google Scholar] [CrossRef]
- Sidorova, O.V.; Siegwolf, R.T.W.; Myglan, V.S.; Ovchinnikov, D.V.; Shishov, V.V.; Helle, G.; Loader, N.J.; Saurer, M. The application of tree-rings and stable isotopes for reconstructions of climate conditions in the Russian Altai. Clim. Chang. 2013, 120, 153–167. [Google Scholar] [CrossRef]
- Seim, A.; Tulyaganov, T.; Omurova, G.; Nikolyai, L.; Botman, E.; Linderholm, H.W. Dendroclimatological potential of three juniper species from the Turkestan range, northwestern Pamir-Alay Mountains, Uzbekistan. Trees-Struct. Funct. 2016, 30, 733–748. [Google Scholar] [CrossRef]
- Liang, E.; Shao, X.; Hu, Y.; Lin, J. Dendroclimatic evaluation of climate-growth relationships of Meyer spruce (Picea meyeri) on a sandy substrate in semi-arid grassland, north China. Trees-Struct. Funct. 2001, 15, 230–235. [Google Scholar] [CrossRef]
- Gou, X.; Gao, L.; Deng, Y.; Chen, F.; Yang, M.; Still, C. An 850-year tree-ring-based reconstruction of drought history in the western Qilian Mountains of northwestern China. Int. J. Climatol. 2015, 35, 3308–3319. [Google Scholar] [CrossRef]
- Fritts, H.C. Tree Rings and Climate; Academic Press, Inc. (London), Ltd.: New York, NY, USA, 1976. [Google Scholar]
- Liu, Y.; Shi, J.F.; Shishov, V.; Vaganov, E.; Yang, Y.K.; Cai, Q.F.; Sun, J.Y.; Wang, L.; Djanseitov, I. Reconstruction of May–July precipitation in the north Helan Mountain, Inner Mongolia since A.D. 1726 from tree-ring late-wood widths. Chin. Sci. Bull. 2004, 49, 405–409. [Google Scholar] [CrossRef]
- Yu, D.; Wang, G.G.; Dai, L.; Wang, Q. Dendroclimatic analysis of Betula ermanii forests at their upper limit of distribution in Changbai Mountain, Northeast China. For. Ecol. Manag. 2007, 240, 105–113. [Google Scholar] [CrossRef]
- Dittmar, C.; Zech, W.; Elling, W. Growth variations of Common beech (Fagus sylvatica L.) under different climatic and environmental conditions in Europe—A dendroecological study. For. Ecol. Manag. 2003, 173, 63–78. [Google Scholar] [CrossRef]
- Affolter, P.; Büntgen, U.; Esper, J.; Rigling, A.; Weber, P.; Luterbacher, J.; Frank, D. Inner Alpine conifer response to 20th century drought swings. Eur. J. For. Res. 2009, 129, 289–298. [Google Scholar] [CrossRef]
- Brookhouse, M.T.; Bi, H. Elevation-dependent climate sensitivity in Eucalyptus pauciflora Sieb. ex Spreng. Trees-Struct. Funct. 2009, 23, 1309–1320. [Google Scholar] [CrossRef]
- Lo, Y.-H.; Blanco, J.A.; Seely, B.; Welham, C.; Kimmins, J.P. (Hamish). Relationships between climate and tree radial growth in interior British Columbia, Canada. For. Ecol. Manag. 2010, 259, 932–942. [Google Scholar] [CrossRef]
- Kienast, F.; Schweingruber, F.H.; Bräker, O.U.; Schär, E. Tree-ring studies on conifers along ecological gradients and the potential of single-year analyses. Can. J. For. Res. 1987, 17, 683–696. [Google Scholar] [CrossRef]
- Grace, J.; Norton, D.A. Climate and growth of Pinus Sylvestris at its upper altitudinal limit in Scotland: Evidence from tree growth-rings. J. Ecol. 1990, 78, 601–610. [Google Scholar] [CrossRef]
- Jacoby, G.C.; Lovelius, N.V.; Shumilov, O.I.; Raspopov, O.M.; Karbainov, J.M.; Frank, D.C. Long-term temperature trends and tree growth in the Taymir region of northern Siberia. Quat. Res. 2000, 53, 312–318. [Google Scholar] [CrossRef]
- Büntgen, U.; Frank, D.; Trouet, V.; Esper, J. Diverse climate sensitivity of Mediterranean tree-ring width and density. Trees-Struct. Funct. 2009, 24, 261–273. [Google Scholar] [CrossRef]
- Shi, C.; Masson-Delmotte, V.; Daux, V.; Li, Z.; Zhang, Q.B. An unstable tree-growth response to climate in two 500 year chronologies, North Eastern Qinghai-Tibetan Plateau. Dendrochronologia 2010, 28, 225–237. [Google Scholar] [CrossRef]
- Yu, D.; Liu, J.; Lewis, B.J.; Zhou, L.; Zhou, W.; Fang, X.; Wei, Y.; Jiang, S.; Dai, L. Spatial variation and temporal instability in the climate–growth relationship of Korean pine in the Changbai Mountain region of Northeast China. For. Ecol. Manag. 2013, 300, 96–105. [Google Scholar] [CrossRef]
- Zhang, W.T.; Jiang, Y.; Wang, M.C.; Zhang, L.N.; Dong, M.Y.; Gou, Y.Y. Responses of radial growth to climate warming in Picea meyeri trees growing at different elevations on the southern slope of Luya Mountain. Chin. J. Plant. Ecol. 2013, 37, 1142–1152, (In Chinese, with English abstract). [Google Scholar] [CrossRef]
- Babushkina, E.; Belokopytova, L.; Zhirnova, D.; Barabantsova, A.; Vaganov, E. Divergent growth trends and climatic response of Picea obovata along elevational gradient in Western Sayan mountains, Siberia. J. Mt. Sci. 2018, 15, 2378–2397. [Google Scholar] [CrossRef]
- Jiao, L.; Jiang, Y.; Zhang, W.T.; Wang, M.C.; Zhang, L.N.; Zhao, S.D. Divergent responses to climate factors in the radial growth of Larix sibirica in the eastern Tianshan Mountains, northwest China. Trees-Struct. Funct. 2015, 29, 1673–1686. [Google Scholar] [CrossRef]
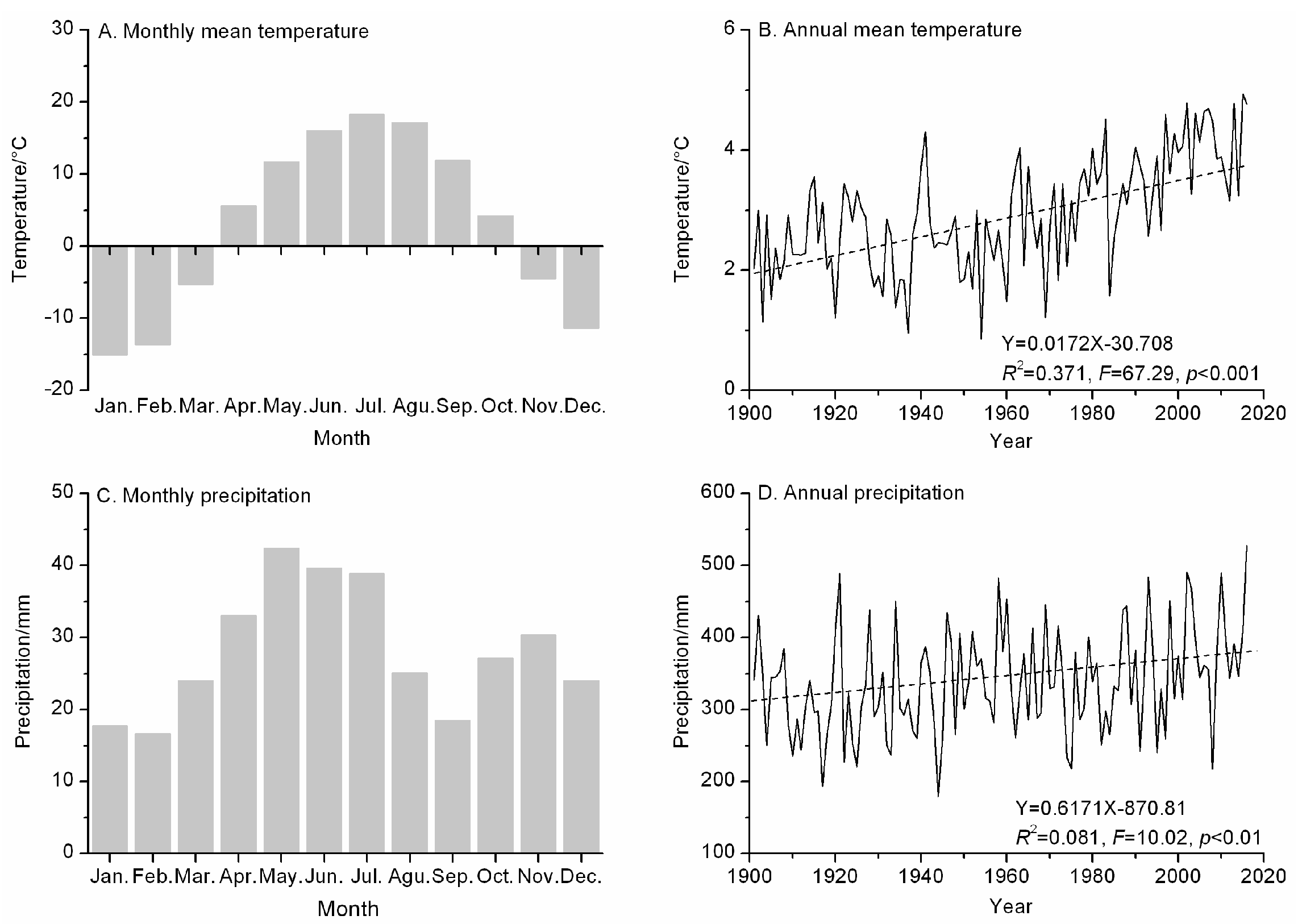
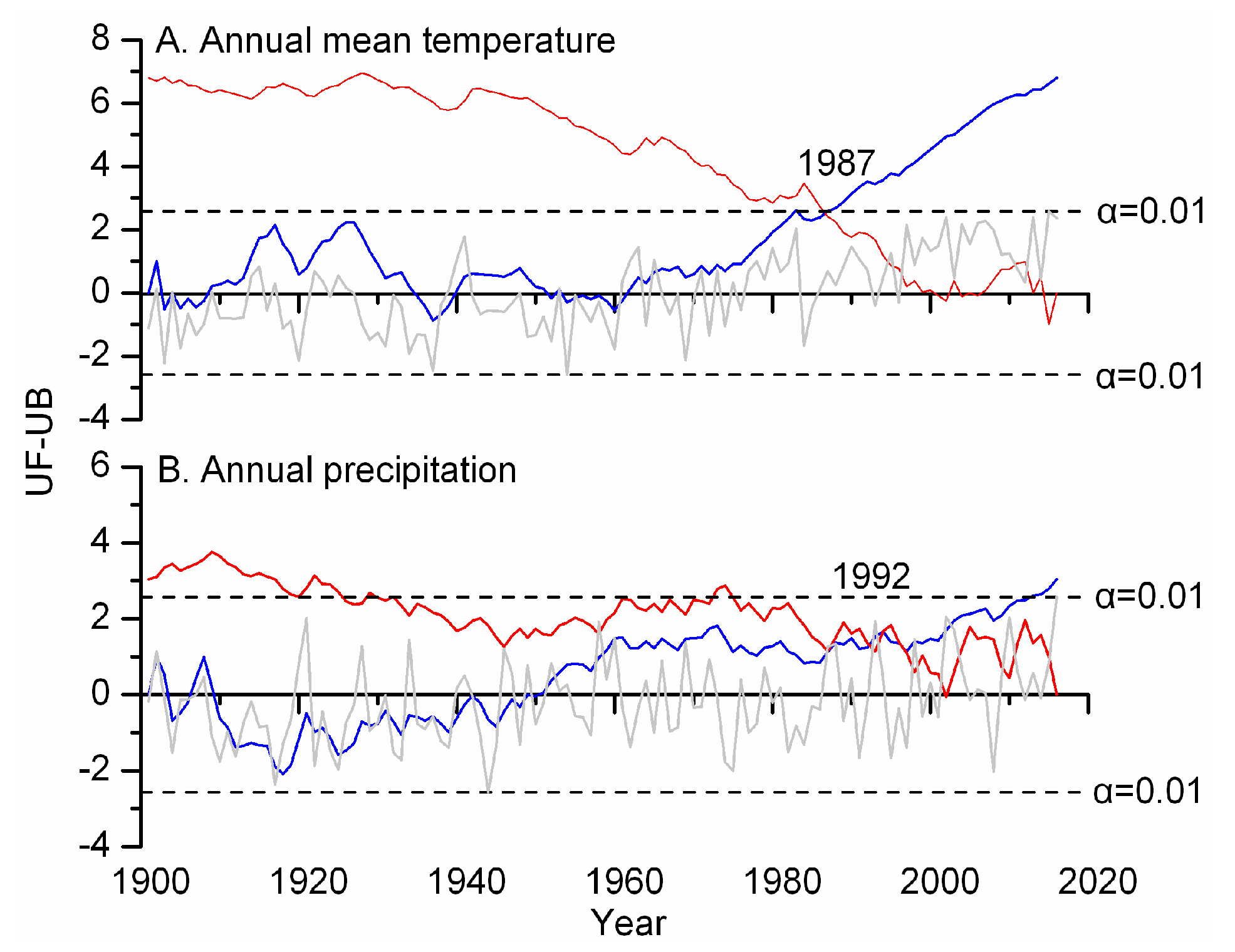

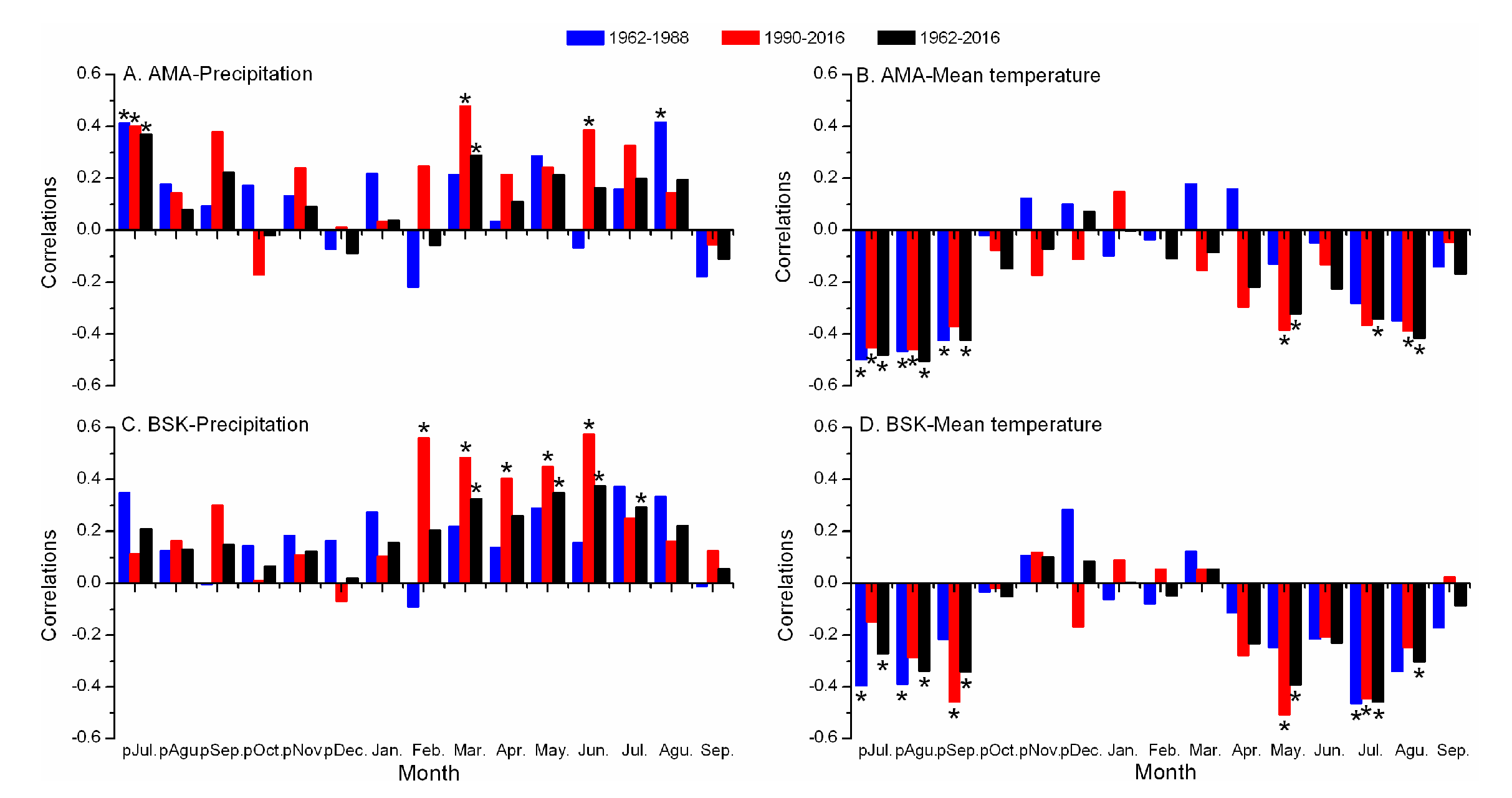
| Study Area | Site Code | Latitude (N) | Longitude (E) | Trees/Cores | Elevation (m) | Aspect | Slope | Maximum Tree Age | The Rate of Absent Rings (%) |
|---|---|---|---|---|---|---|---|---|---|
| Alatau Mountain | AMA | 45.26° | 80.08° | 28/50 | ~2050 | N | 20° | 175 (1842–2016) | 0.246 |
| BSK | 45.25° | 80.15° | 23/45 | ~1450 | N | 20° | 161 (1856–2016) | 0.514 |
| Statistic | AMA | BSK |
|---|---|---|
| Standard deviation (SD) | 0.198 | 0.414 |
| Mean sensitivity (MS) | 0.180 | 0.379 |
| First-order autocorrelation (AC1) | 0.396 | 0.577 |
| Interseries correlation (trees) | 0.466 | 0.698 |
| Interseries correlation (all series) | 0.477 | 0.705 |
| Mean within-tree correlation | 0.695 | 0.771 |
| Signal-to-noise ratio (SNR) | 13.681 | 16.705 |
| Expressed population signal (EPS) | 0.932 | 0.944 |
| The first principal component (PC#1) | 0.519 | 0.749 |
| First year EPS > 0.8 | 1880 | 1880 |
| AMA | BSK | ||||||
|---|---|---|---|---|---|---|---|
| 10 Highest-Value Years | 10 Lowest-Value Years | 10 HIGHEST-Value Years | 10 Lowest-Value Years | ||||
| Year | Value | Year | Value | Year | Value | Year | Value |
| 1891 | 1.459 | 2008 | 0.511 | 1929 | 1.678 | 2008 | 0.001 |
| 1924 | 1.452 | 1945 | 0.607 | 1909 | 1.654 | 1985 | 0.137 |
| 1970 | 1.421 | 1913 | 0.614 | 1935 | 1.573 | 2000 | 0.211 |
| 1993 | 1.319 | 1885 | 0.621 | 1970 | 1.556 | 1997 | 0.226 |
| 1973 | 1.307 | 1917 | 0.625 | 1890 | 1.536 | 1991 | 0.249 |
| 1994 | 1.292 | 1914 | 0.632 | 1952 | 1.517 | 1927 | 0.249 |
| 1888 | 1.291 | 1911 | 0.645 | 1964 | 1.502 | 1917 | 0.286 |
| 1950 | 1.282 | 2000 | 0.675 | 1960 | 1.473 | 1977 | 0.304 |
| 1951 | 1.275 | 1900 | 0.678 | 1962 | 1.473 | 1974 | 0.322 |
| 1923 | 1.27 | 1927 | 0.694 | 1993 | 1.467 | 2014 | 0.334 |
| BSK | AMA | |||
|---|---|---|---|---|
| Precipitation | Temperature | Precipitation | Temperature | |
| pJul. | 0.829 | −0.893 | 0.05 | −0.196 |
| pAgu. | −0.132 | −0.392 | 0.111 | −0.035 |
| pSep. | −1.048 | 0.912 | −1.016 | −0.214 |
| pOct. | 0.443 | −0.046 | 1.158 | 0.201 |
| pNov. | 0.254 | −0.049 | −0.375 | 0.996 |
| pDec. | 0.781 | 1.534 | −0.283 | 0.71 |
| January | 0.598 | −0.517 | 0.643 | −0.843 |
| February | −2.455 * | −0.457 | −1.613 | −0.131 |
| March | −1.040 | 0.242 | −1.019 | 1.144 |
| April | −0.981 | 0.595 | −0.622 | 1.584 |
| May | −0.632 | 1.046 | 0.164 | 0.935 |
| June | −1.684 | −0.030 | −1.620 | 0.282 |
| July | 0.461 | −0.084 | −0.613 | 0.317 |
| August | 0.627 | −0.353 | 1.018 | 0.158 |
| September | −0.465 | −0.676 | −0.430 | −0.312 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, T.; Zhang, R.; Jiang, S.; Bagila, M.; Ainur, U.; Yu, S. On the ‘Divergence Problem’ in the Alatau Mountains, Central Asia: A Study of the Responses of Schrenk Spruce Tree-Ring Width to Climate under the Recent Warming and Wetting Trend. Atmosphere 2019, 10, 473. https://doi.org/10.3390/atmos10080473
Zhang T, Zhang R, Jiang S, Bagila M, Ainur U, Yu S. On the ‘Divergence Problem’ in the Alatau Mountains, Central Asia: A Study of the Responses of Schrenk Spruce Tree-Ring Width to Climate under the Recent Warming and Wetting Trend. Atmosphere. 2019; 10(8):473. https://doi.org/10.3390/atmos10080473
Chicago/Turabian StyleZhang, Tongwen, Ruibo Zhang, Shengxia Jiang, Maisupova Bagila, Utebekova Ainur, and Shulong Yu. 2019. "On the ‘Divergence Problem’ in the Alatau Mountains, Central Asia: A Study of the Responses of Schrenk Spruce Tree-Ring Width to Climate under the Recent Warming and Wetting Trend" Atmosphere 10, no. 8: 473. https://doi.org/10.3390/atmos10080473
APA StyleZhang, T., Zhang, R., Jiang, S., Bagila, M., Ainur, U., & Yu, S. (2019). On the ‘Divergence Problem’ in the Alatau Mountains, Central Asia: A Study of the Responses of Schrenk Spruce Tree-Ring Width to Climate under the Recent Warming and Wetting Trend. Atmosphere, 10(8), 473. https://doi.org/10.3390/atmos10080473






