The Collective Contribution of Atmospheric and Oceanic Components to ENSO Asymmetry
Abstract
1. Introduction
2. Models and Datasets
2.1. Model Description and Experiment Design
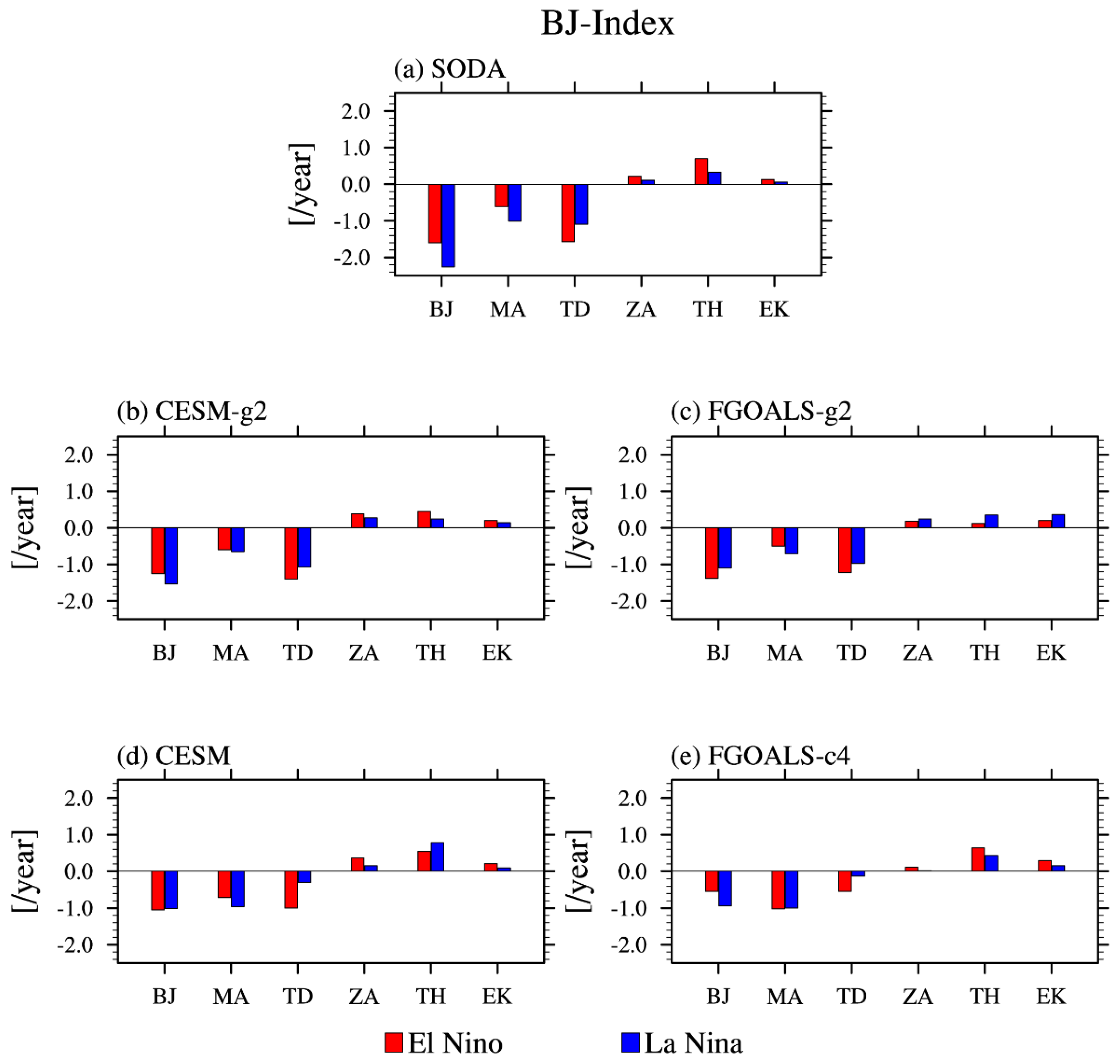
2.2. Validation Datasets and BJ Stability Index Analysis
3. Results and Analysis
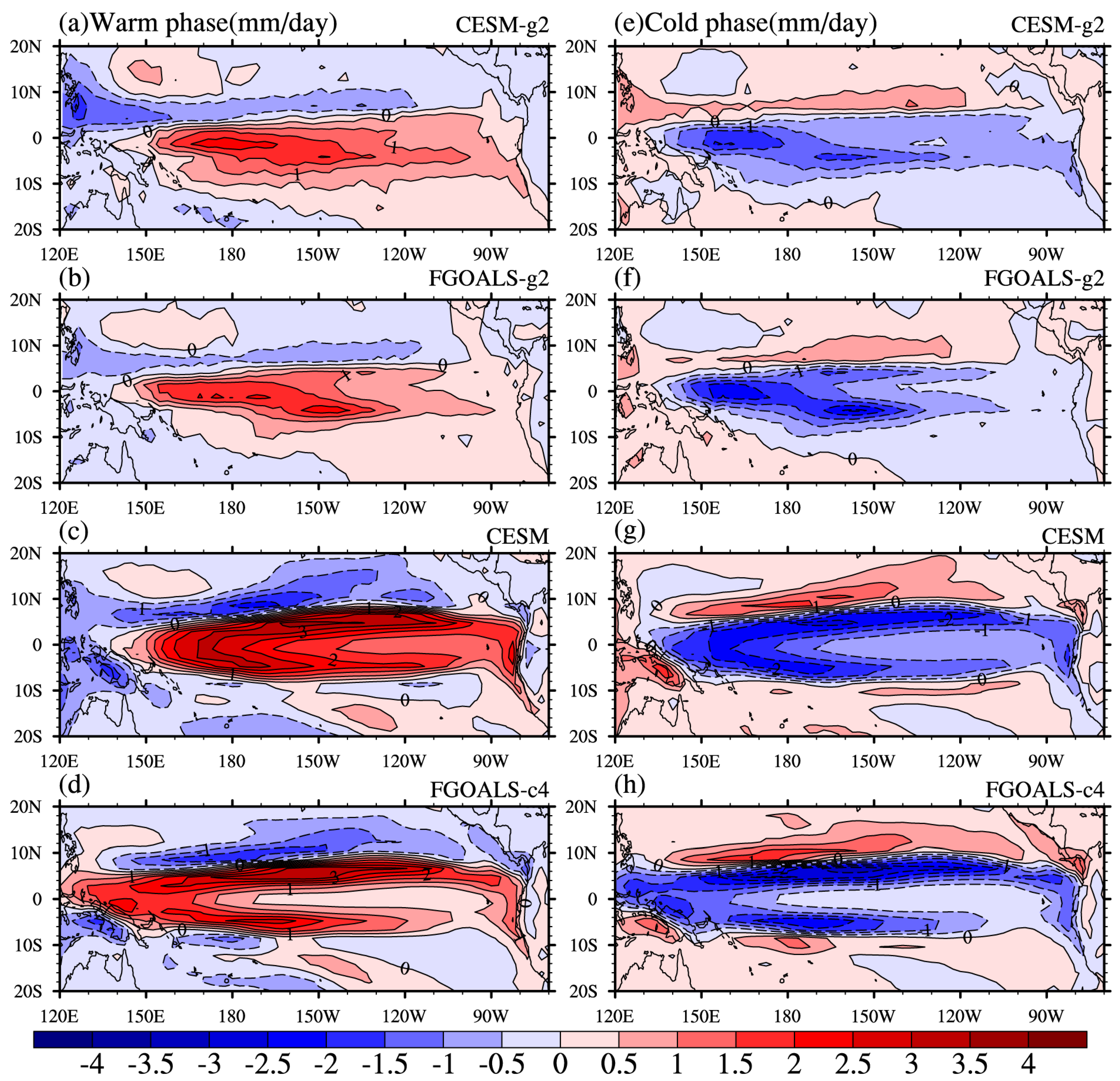
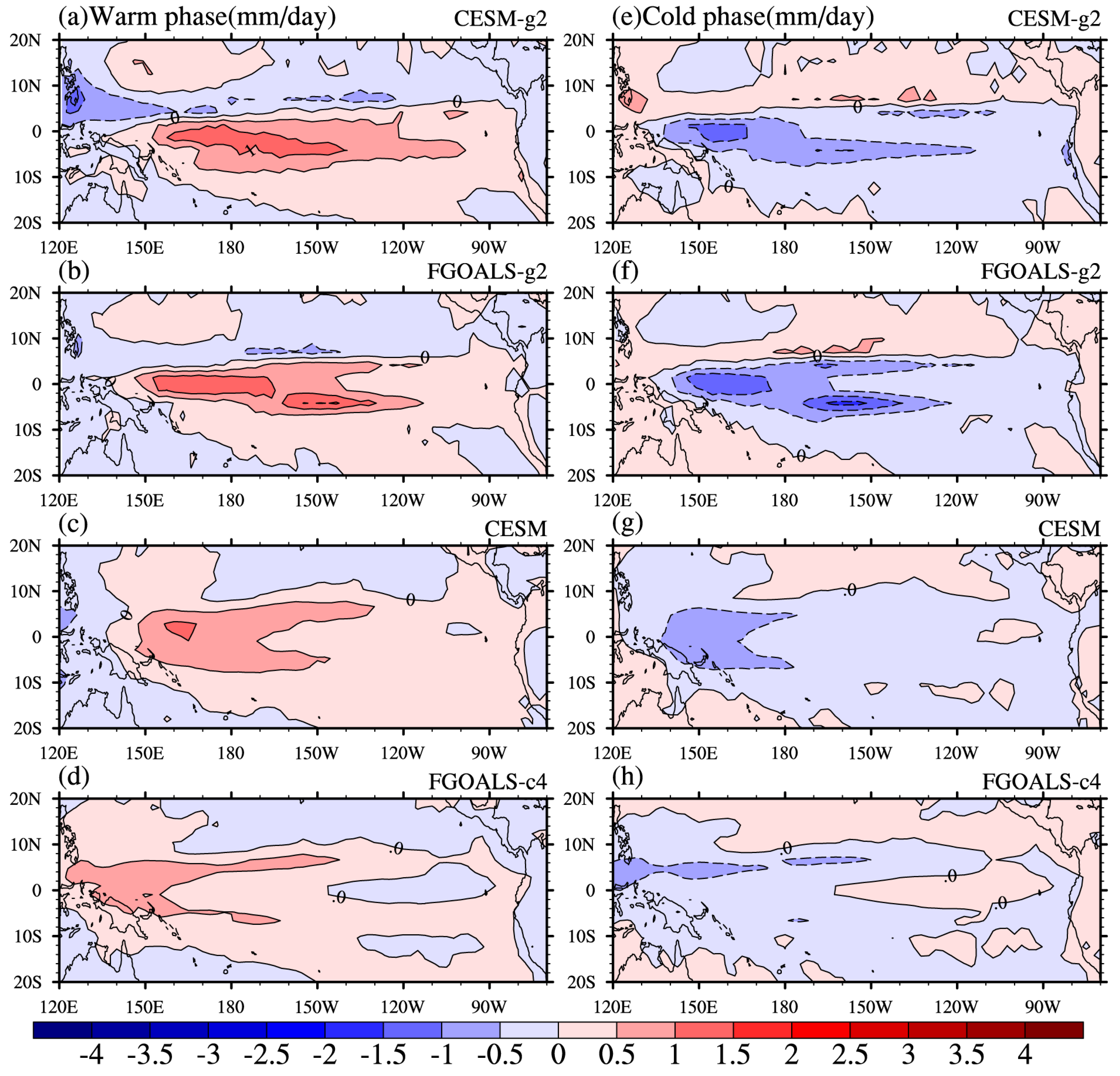
3.1. Asymmetry in the SST Fields
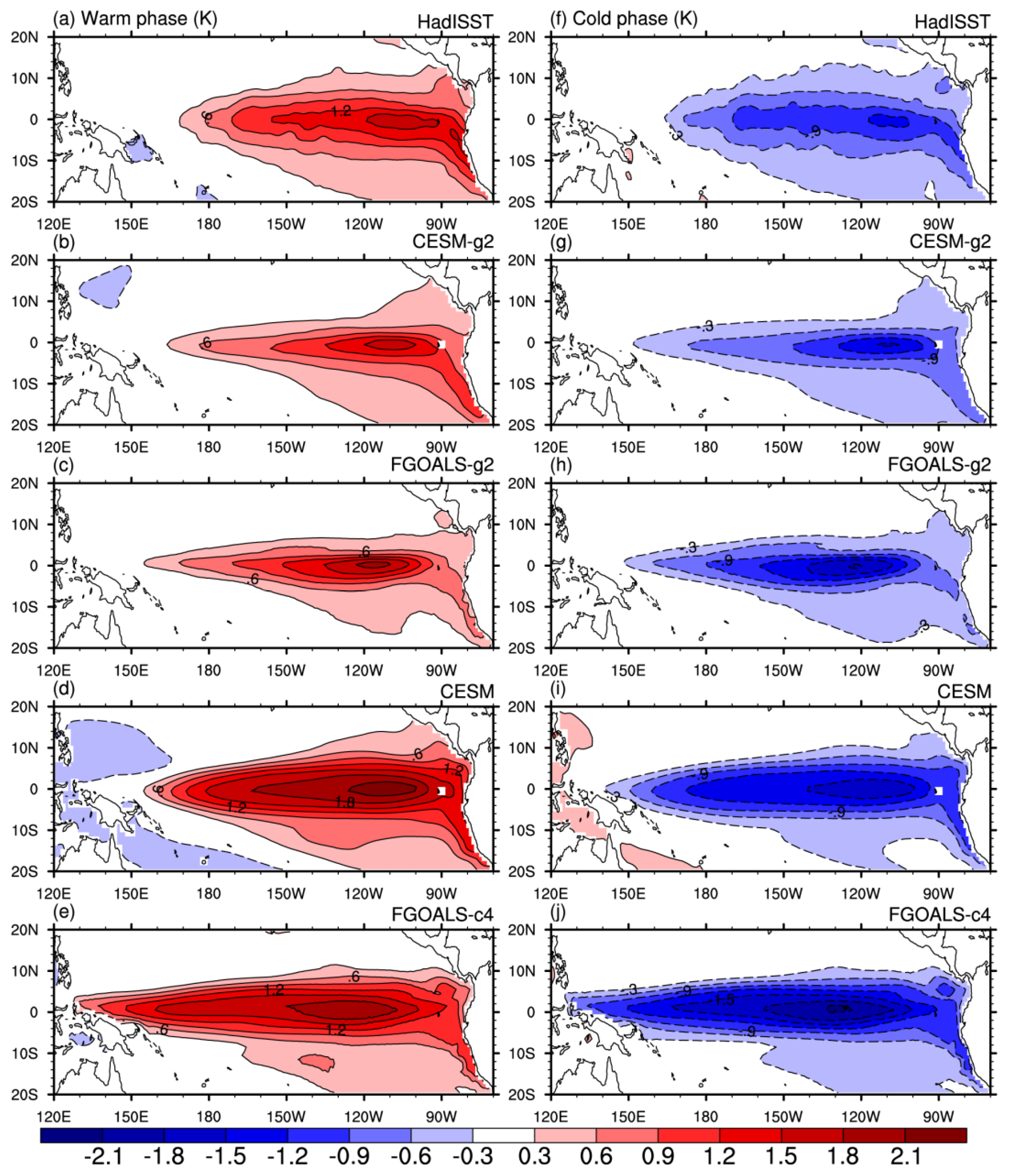
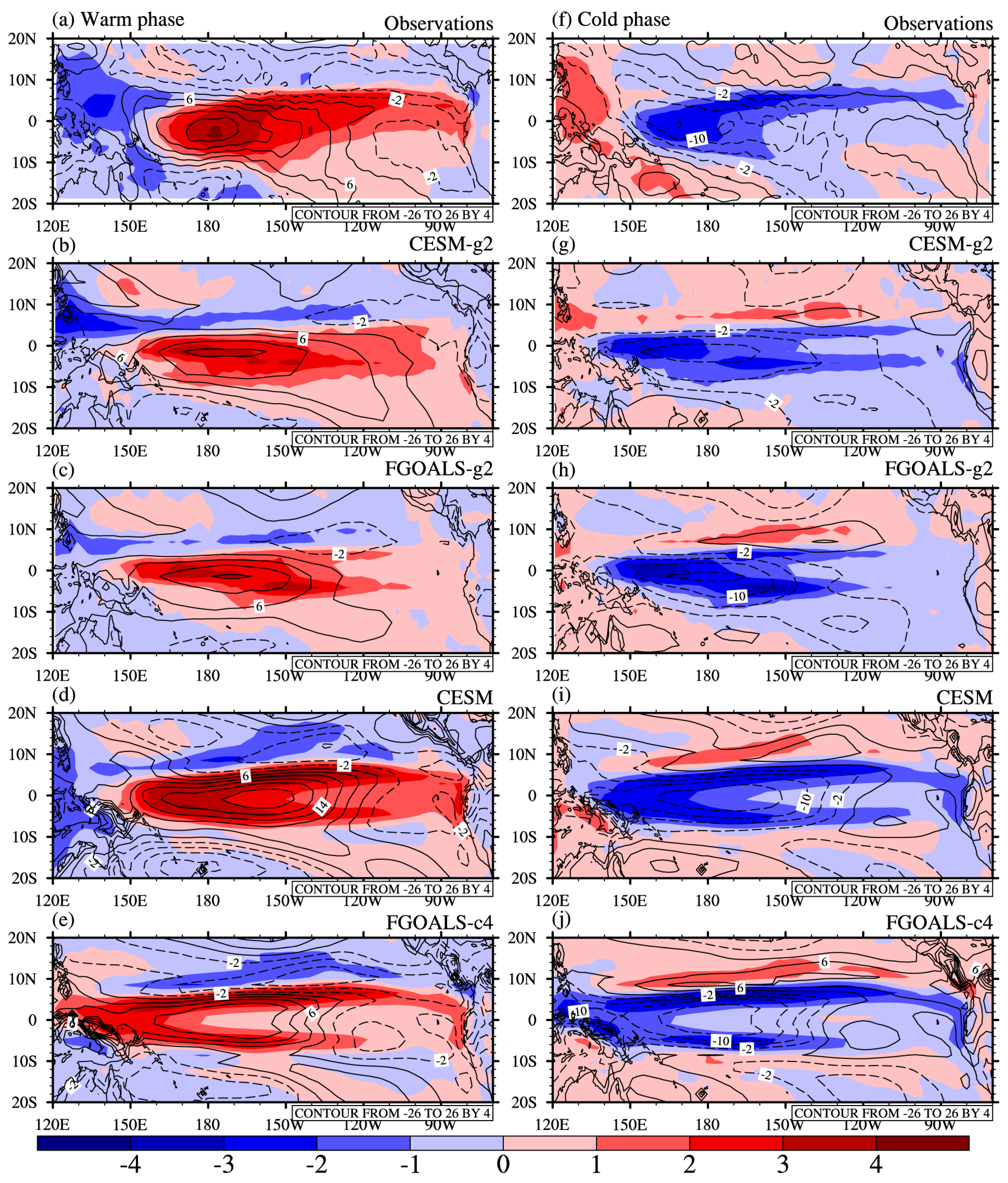
3.2. The Factors Affecting the Asymmetry of the SST Anomalies
4. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Choi, K.Y.; Vecchi, G.A.; Wittenberg, A.T. ENSO transition, duration, and amplitude asymmetries: Role of the nonlinear wind stress coupling in a conceptual model. J. Clim. 2013, 26, 9462–9476. [Google Scholar] [CrossRef]
- Rodgers, K.B.; Friederichs, P.; Latif, M. Tropical pacific decadal variability and its relation to decadal modulations of ENSO. J. Clim. 2004, 17, 3761–3774. [Google Scholar] [CrossRef]
- Schopf, P.S.; Burgman, R.J. A simple mechanism for ENSO residuals and asymmetry. J. Clim. 2006, 19, 3167–3179. [Google Scholar] [CrossRef]
- Dommenget, D.; Bayr, T.; Frauen, C. Analysis of the non-linearity in the pattern and time evolution of El Niño southern oscillation. Clim. Dyn. 2013, 40, 2825–2847. [Google Scholar] [CrossRef]
- An, S.; Jin, F.F. Nonlinearity and asymmetry of ENSO. J. Clim. 2004, 17, 2399–2412. [Google Scholar] [CrossRef]
- Su, J.; Zhang, R.; Li, T.; Rong, X.; Kug, J.S.; Hong, C.C. Causes of the El Niño and La Niña amplitude asymmetry in the equatorial eastern Pacific. J. Clim. 2010, 23, 605–617. [Google Scholar] [CrossRef]
- Graham, N.E.; Barnett, T.P. Sea surface temperature, surface wind divergence, and convection over tropical oceans. Science 1987, 238, 657–659. [Google Scholar] [CrossRef]
- Hoerling, M.P.; Kumar, A.; Zhong, M. El Niño, La Niña, and the nonlinearity of their teleconnections. J. Clim. 1997, 10, 1769–1786. [Google Scholar] [CrossRef]
- Kang, I.S.; Kug, J.S. El Niño and La Niña sea surface temperature anomalies: Asymmetry characteristics associated with their wind stress anomalies. J. Geophys. Res. 2002, 107(D19), 4372. [Google Scholar] [CrossRef]
- Zhang, T.; Sun, D.Z.; Neale, R.; Rasch, P.J. An evaluation of ENSO asymmetry in the community climate system models: A view from the subsurface. J. Clim. 2009, 22, 5933–5961. [Google Scholar] [CrossRef]
- Zhang, T.; Sun, D.Z. ENSO asymmetry in CMIP5 models. J. Clim. 2014, 27, 4070–4093. [Google Scholar] [CrossRef]
- Ham, Y.G. A reduction in the asymmetry of ENSO amplitude due to global warming: The role of atmospheric feedback. Geophys. Res. Lett. 2017, 44, 8576–8584. [Google Scholar] [CrossRef]
- Tang, Y.; Li, L.; Dong, W.; Wang, B. Tracing the source of ENSO simulation differences to the atmospheric component of two CGCMs. Atmos. Sci. Let. 2016, 17, 155–161. [Google Scholar] [CrossRef]
- Tang, Y.; Li, L.; Wang, B.; Lin, P.; Chen, L.; Xie, F.; Dong, W.; Xia, K. The dominant role of the atmospheric component of coupled models in ENSO amplitude simulations. Clim. Dyn. 2019, 52, 4833–4847. [Google Scholar] [CrossRef]
- Neale, R.B.; Richter, J.; Park, S.; Lauritzen, P.H.; Vavrus, S.J.; Rasch, P.J.; Zhang, M. The mean climate of the community atmosphere model (CAM4) in forced SST and fully coupled experiments. J. Clim. 2013, 26, 5150–5168. [Google Scholar] [CrossRef]
- Smith, R.D.; Jones, P.; Briegleb, B.; Bryan, F.; Danabasoglu, G.; Dennis, J.; Dukowicz, J.; Eden, C.; Fox-Kemper, B.; Gent, P.; et al. The Parallel Ocean Program (POP) Reference Manual; Technical Report for Los Alamos National Laboratory LAUR-10-01853; Los Alamos National Laboratory: Los Alamos, NM, USA, 2010; p. 140.
- Wang, B.; Wan, H.; Ji, Z.Z.; Zhang, X.; Yu, R.C.; Yu, Y.Q.; Liu, H.T. Design of a new dynamical core for global atmospheric models based on some efficient numerical methods. Sci. China Math. 2004, 47, 4–21. [Google Scholar] [CrossRef]
- Li, L.J.; Wang, B.; Dong, L.; Liu, L.; Shen, S.; Hu, N.; Sun, W.Q.; Wang, Y.; Huang, W.Y.; Shi, X.J.; et al. Evaluation of gridpoint atmospheric model of IAP LASG Version 2 (GAMIL2). Adv. Atmos. Sci. 2013, 30, 855–867. [Google Scholar] [CrossRef]
- Liu, H.L.; Lin, P.F.; Yu, Y.Q.; Zhang, X.H. The baseline evaluation of LASG/IAP climate system ocean model (LICOM) version 2.0. Acta Meteorol. Sin. 2012, 26, 318–329. [Google Scholar] [CrossRef]
- Wu, F.; Liu, H.; Li, W.; Zhang, X. Effect of adjusting vertical resolution on the eastern equatorial Pacific cold tongue. Acta Meteorol. Sin. 2005, 24, 1–12. [Google Scholar]
- Tang, Y.; Li, L.; Dong, W.; Wang, B. Reducing the climate shift in a new coupled model. Sci Bull. 2016, 61, 488–494. [Google Scholar] [CrossRef]
- Lin, P.F.; Liu, H.L.; Xue, W.; Li, H.M.; Jiang, J.R.; Song, M.R.; Song, Y.; Wang, F.C.; Zhang, M.H. A coupled experiment with LICOM2 as the ocean component of CESM1. J. Meteor. Res. 2016, 30, 76–92. [Google Scholar] [CrossRef]
- Hurrell, J.W.; Hack, J.J.; Shea, D.; Caron, J.M.; Rosinski, J. A new sea surface temperature and sea ice boundary dataset for the community atmosphere model. J. Clim. 2008, 21, 5145–5153. [Google Scholar] [CrossRef]
- Uppala, S.M.; Kållberg, P.W.; Simmons, A.J.; Andrae, U.; Bechtold, V.D.C.; Fiorino, M.; Gibson, J.K.; Haseler, J.; Angeles, H.C.; Kelly, G.A.; et al. The ERA-40 re-analysis. Q. J. Roy. Meteor. Soc. 2005, 131, 2961–3012. [Google Scholar] [CrossRef]
- Adler, R.F.; Huffman, G.J.; Chang, A.; Ferraro, R.; Xie, P.P.; Janowiak, J.; Rudolf, B.; Schneider, U.; Curtis, S.; Bolvin, D.; et al. The version-2 global precipitation climatology project (GPCP) monthly precipitation analysis (1979–Present). J. Hydrometeor. 2003, 4, 1147–1167. [Google Scholar] [CrossRef]
- Carton, J.A.; Giese, B.S. A reanalysis of ocean climate using simple ocean data assimilation. Mon. Weather Rev. 2008, 136, 2999–3017. [Google Scholar] [CrossRef]
- Giese, B.S.; Ray, S. El Niño variability in simple ocean data assimilation (SODA), 1871–2008. J. Geophys. Res. 2011, 116, C02024. [Google Scholar] [CrossRef]
- Kim, S.T.; Jin, F.F. An ENSO stability analysis. Part I: Results from a hybrid coupled model. Clim. Dyn. 2011, 36, 1593–1607. [Google Scholar] [CrossRef]
- Jin, F.F.; Kim, S.T.; Bejarano, L. A coupled stability index for ENSO. Geophys. Res. Lett. 2006, 33, L23708. [Google Scholar] [CrossRef]
- Chen, L.; Yu, Y.; Zheng, W. Improved ENSO simulation from climate system model FGOALS-g1.0 to FGOALS-g2. Clim. Dyn. 2016, 47, 2617–2634. [Google Scholar] [CrossRef]
- Im, S.H.; An, S.I.; Kim, S.T.; Jin, F.F. Feedback processes responsible for El Niño-La Niña amplitude asymmetry. Geophys. Res. Lett. 2015, 42, 5556–5563. [Google Scholar] [CrossRef]
- Chen, L.; Wang, L.; Li, T.; Sun, D.Z. Contrasting cloud radiative feedbacks during warm pool and cold tongue El Niños. SOLA 2018, 14, 126–131. [Google Scholar] [CrossRef]
- Chen, L.; Sun, D.Z.; Wang, L.; Li, T. A further study on the simulation of cloud-radiative feedbacks in the ENSO cycle in the tropical pacific with a focus on the asymmetry. Asia-Pacific. J. Atmos. Sci. 2019, 55, 303–316. [Google Scholar] [CrossRef]
- Ham, Y.G.; Kug, J.S.; Kim, D.; Kim, Y.H.; Kim, D.H. What controls phase-locking of ENSO to boreal winter in coupled GCMs? Clim. Dyn. 2013, 40, 1551–1568. [Google Scholar] [CrossRef]
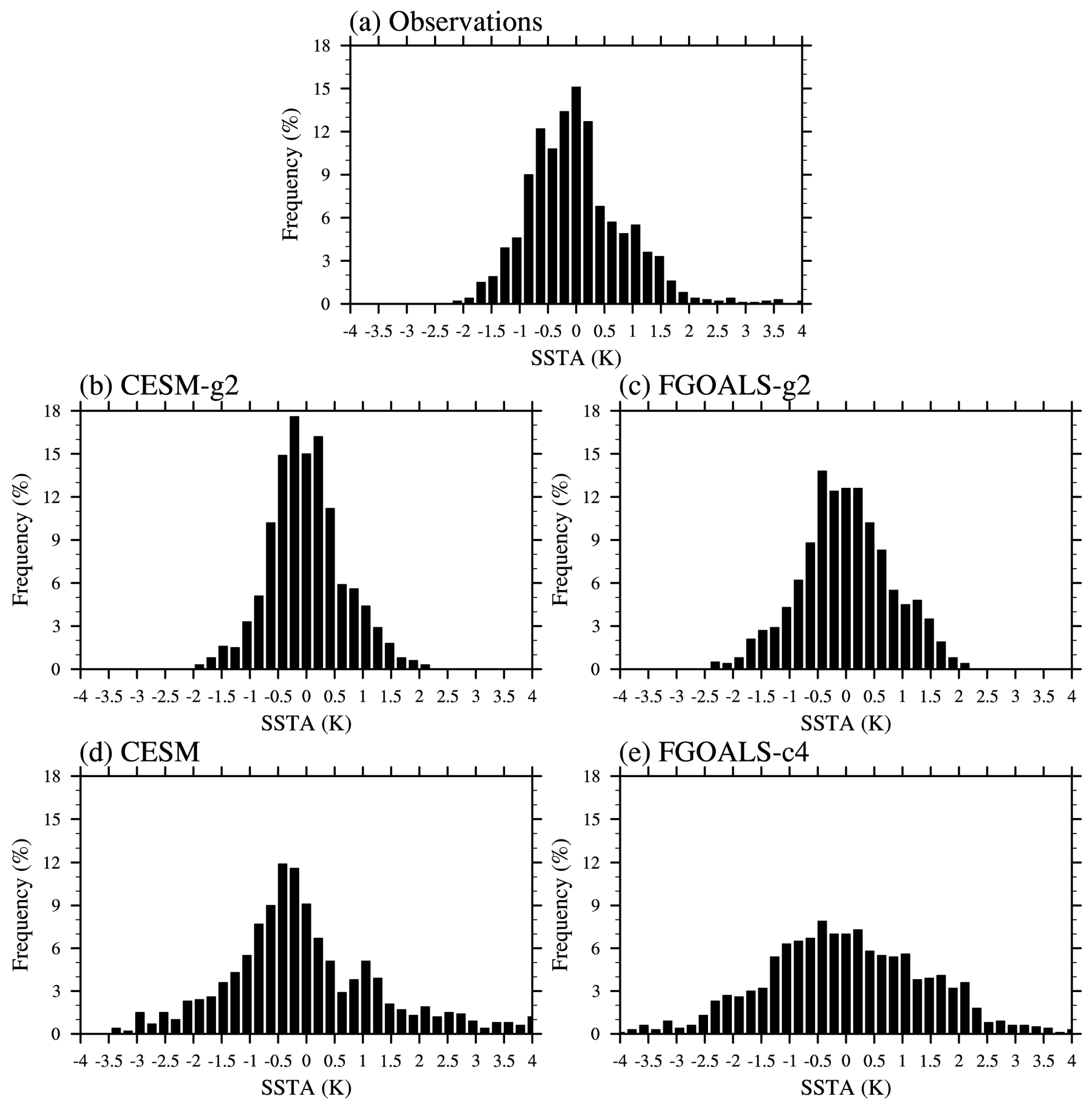
| Standard Deviation | Skewness | ||||
|---|---|---|---|---|---|
| Observations | 0.81 | 0.603 | |||
| Years | 401–500 | 401–500 | 301–400 | 201–300 | 101–200 |
| CESM-g2 | 0.63 | 0.103 | −0.27 | −0.11 | 0.20 |
| FGOALS-g2 | 0.77 | −0.246 | −0.18 | −0.22 | −0.07 |
| CESM | 1.37 | 0.625 | 0.60 | 0.52 | 0.40 |
| FGOALS-c4 | 1.37 | 0.016 | 0.35 | 0.41 | −0.19 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, Y.; Li, L.; Wang, B.; Lin, P.; Dong, W.; Xia, K. The Collective Contribution of Atmospheric and Oceanic Components to ENSO Asymmetry. Atmosphere 2019, 10, 469. https://doi.org/10.3390/atmos10080469
Tang Y, Li L, Wang B, Lin P, Dong W, Xia K. The Collective Contribution of Atmospheric and Oceanic Components to ENSO Asymmetry. Atmosphere. 2019; 10(8):469. https://doi.org/10.3390/atmos10080469
Chicago/Turabian StyleTang, Yanli, Lijuan Li, Bin Wang, Pengfei Lin, Wenjie Dong, and Kun Xia. 2019. "The Collective Contribution of Atmospheric and Oceanic Components to ENSO Asymmetry" Atmosphere 10, no. 8: 469. https://doi.org/10.3390/atmos10080469
APA StyleTang, Y., Li, L., Wang, B., Lin, P., Dong, W., & Xia, K. (2019). The Collective Contribution of Atmospheric and Oceanic Components to ENSO Asymmetry. Atmosphere, 10(8), 469. https://doi.org/10.3390/atmos10080469






