A Study of Objective Prediction for Summer Precipitation Patterns Over Eastern China Based on a Multinomial Logistic Regression Model
Abstract
1. Introduction
2. Data and Machine Learning Method
2.1. Data
2.2. Multinomial Logistic Regression
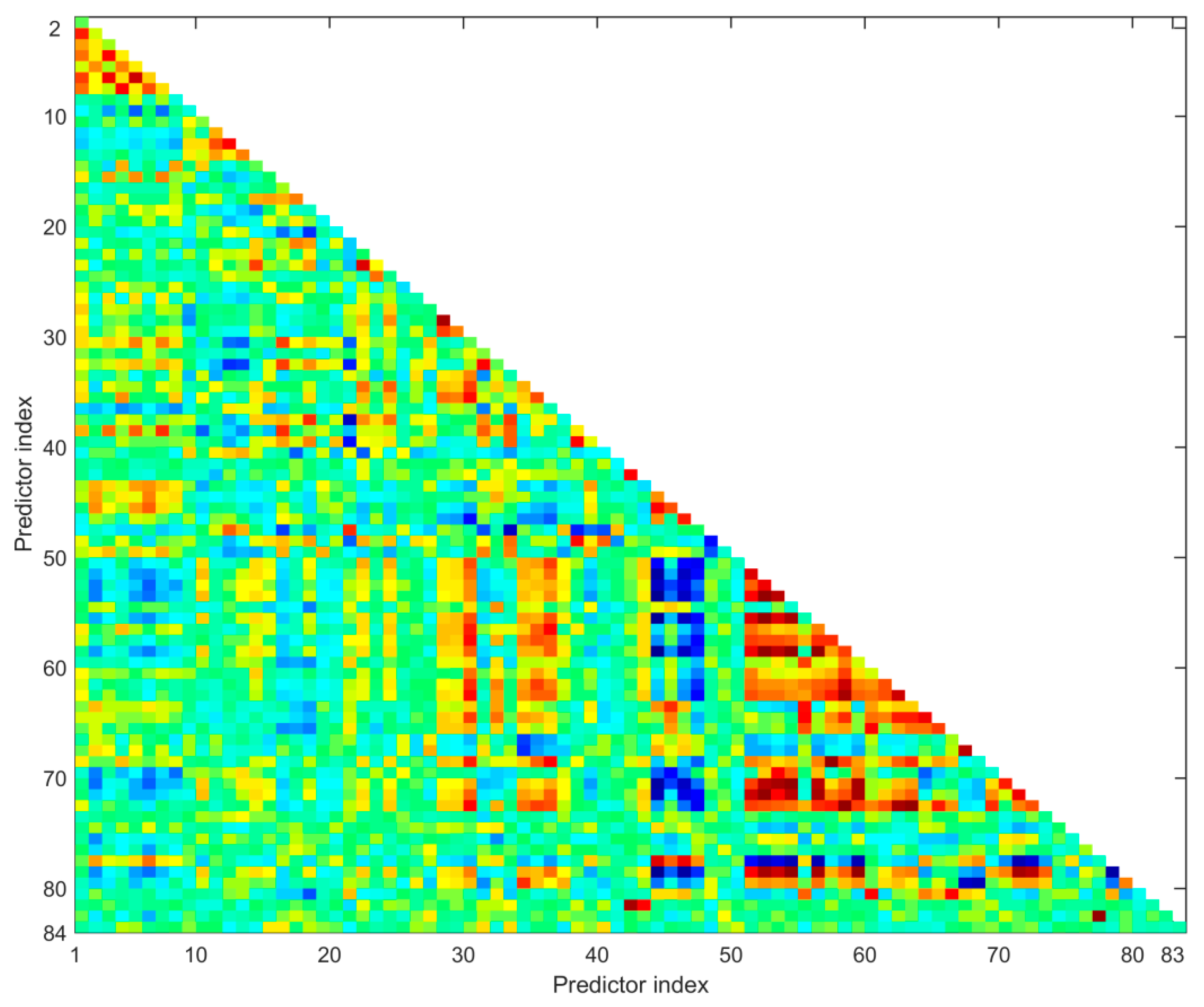
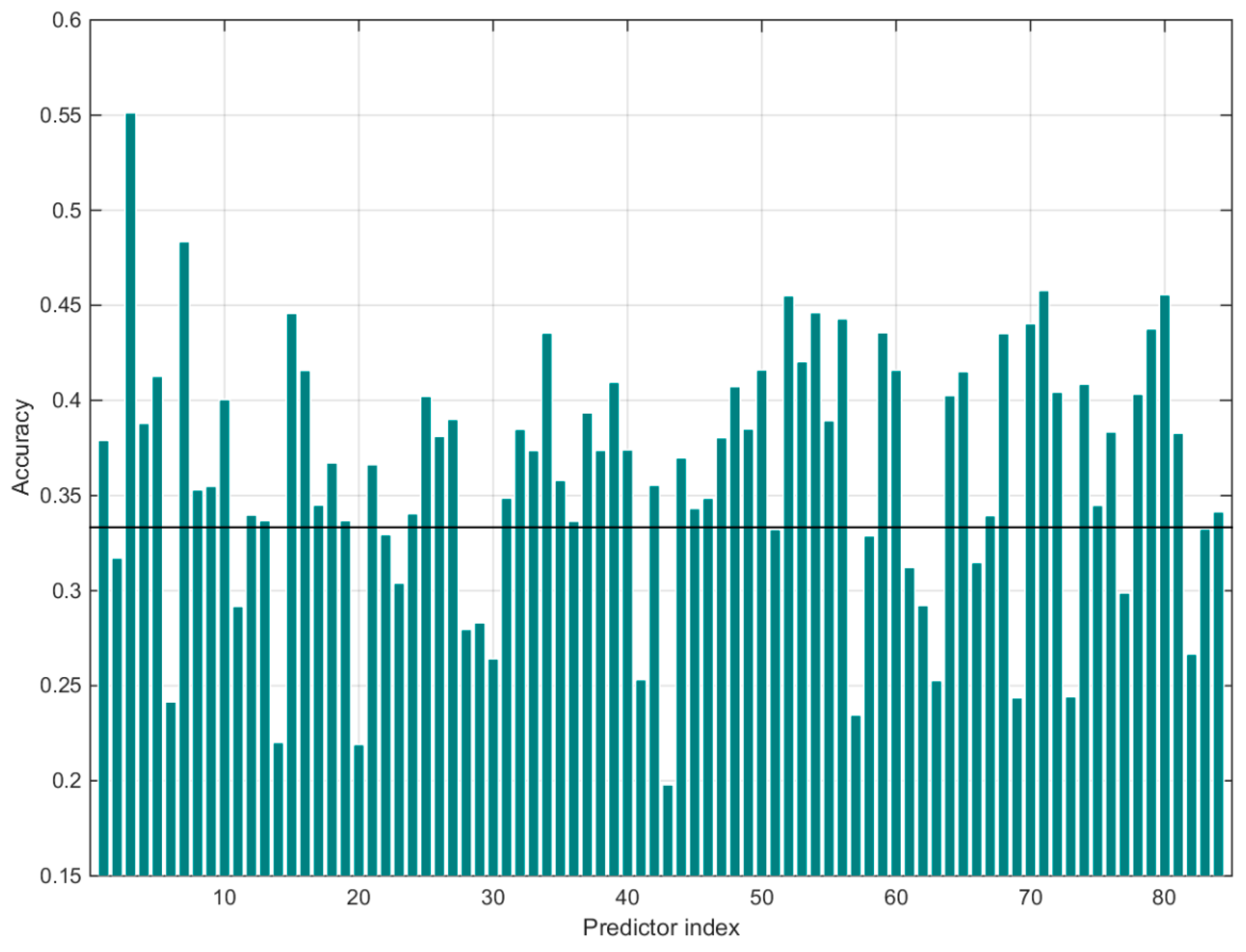
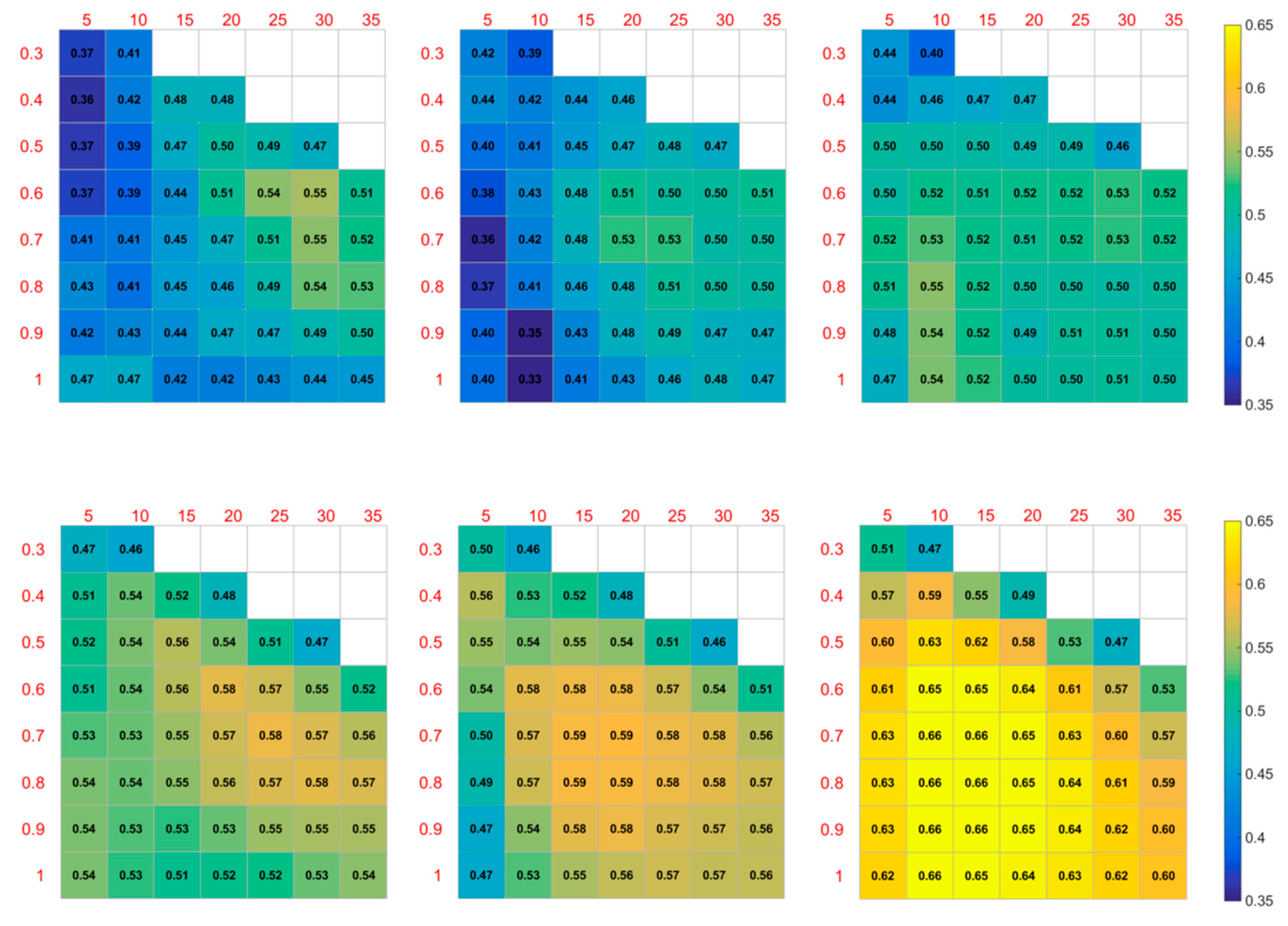
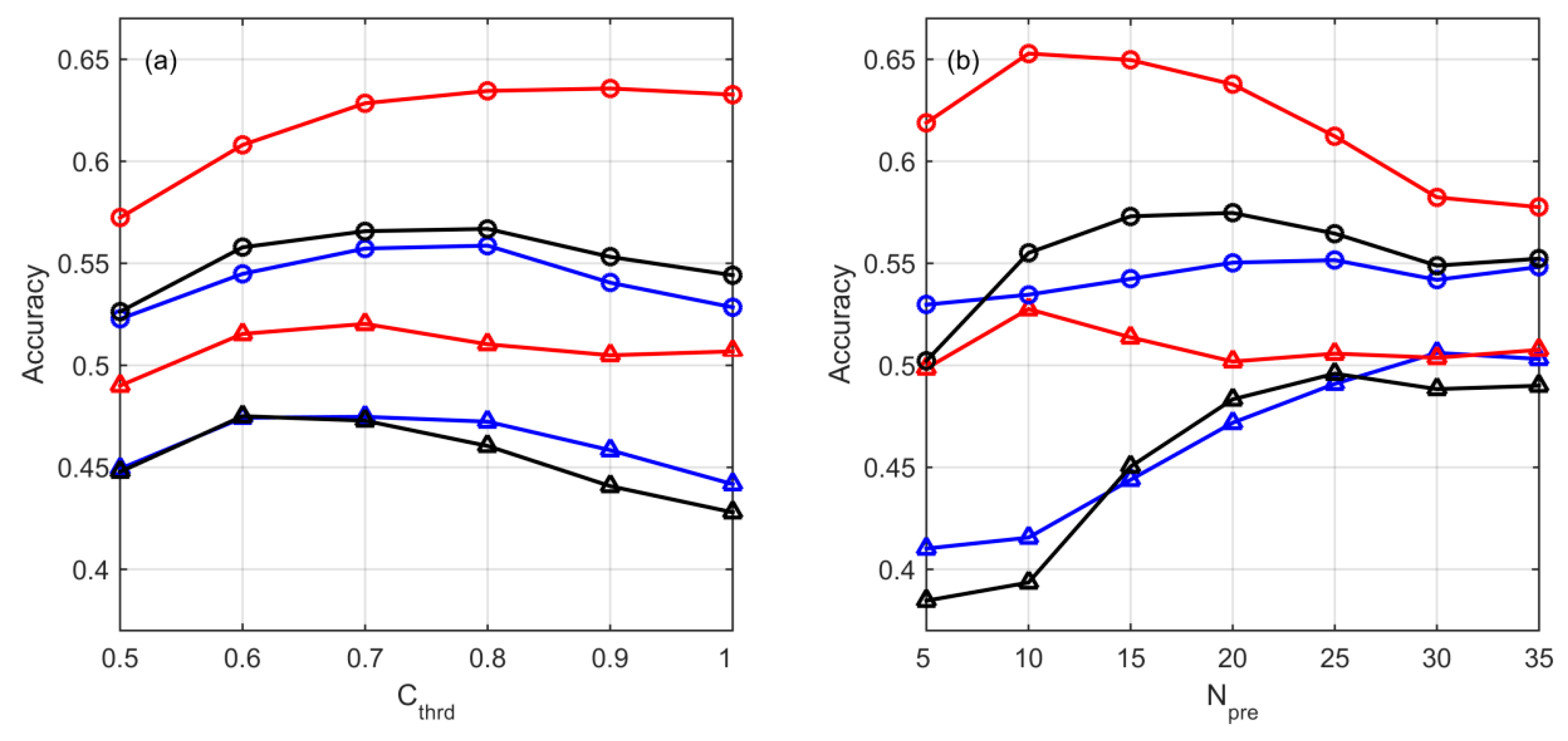
3. Objective Selection of Predictors
- Calculate the Pearson CC matrix of all predictors;
- Find the minimum absolute CC between predictor and in the matrix. Terminate the process if the minimum absolute CC is less than the threshold Cthrd;
- Calculate the average absolute CC between and all other predictors, and do the same with ;
- Remove the predictor with a larger average CC;
- Repeat 2-4.
4. Results
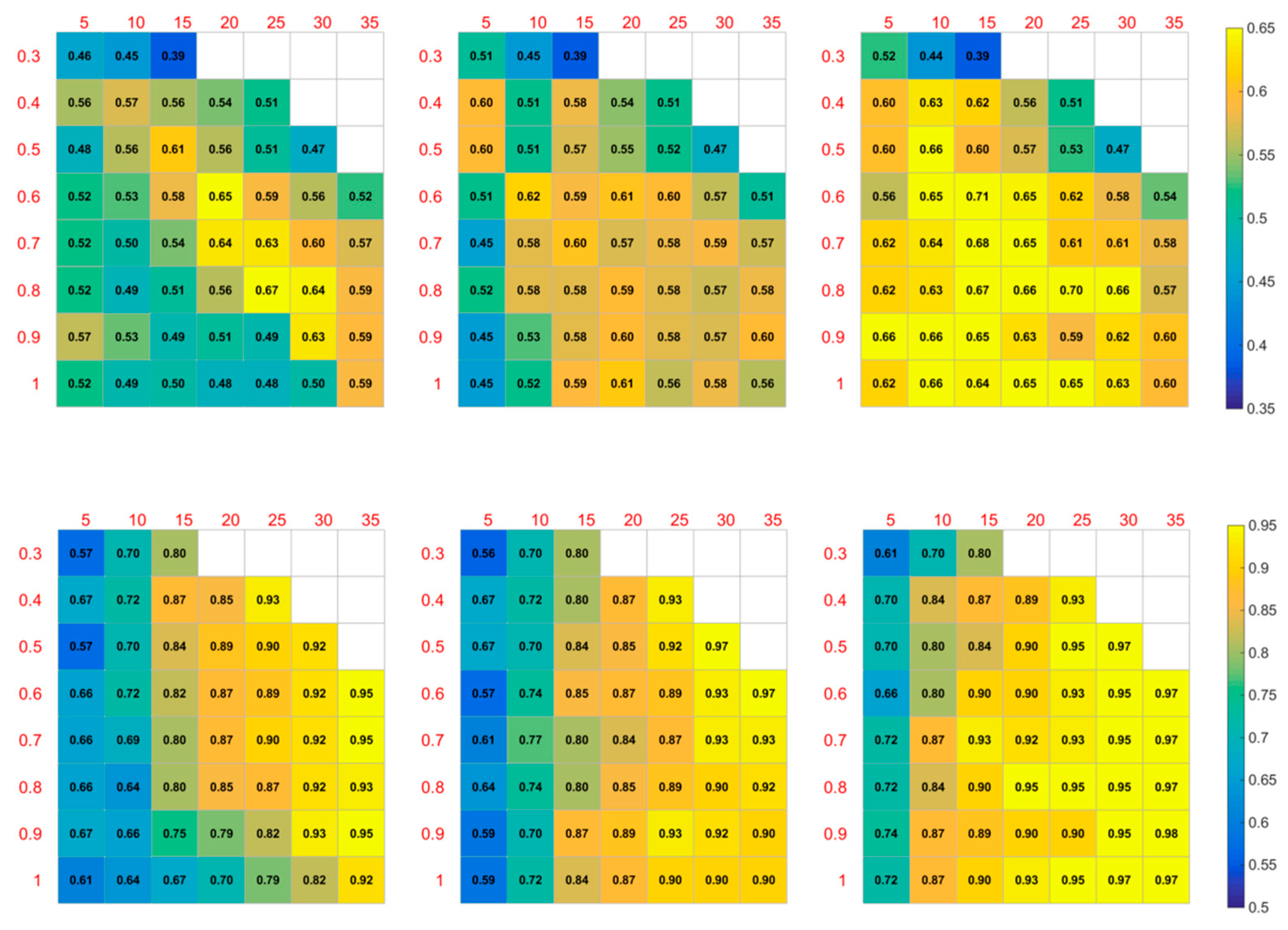
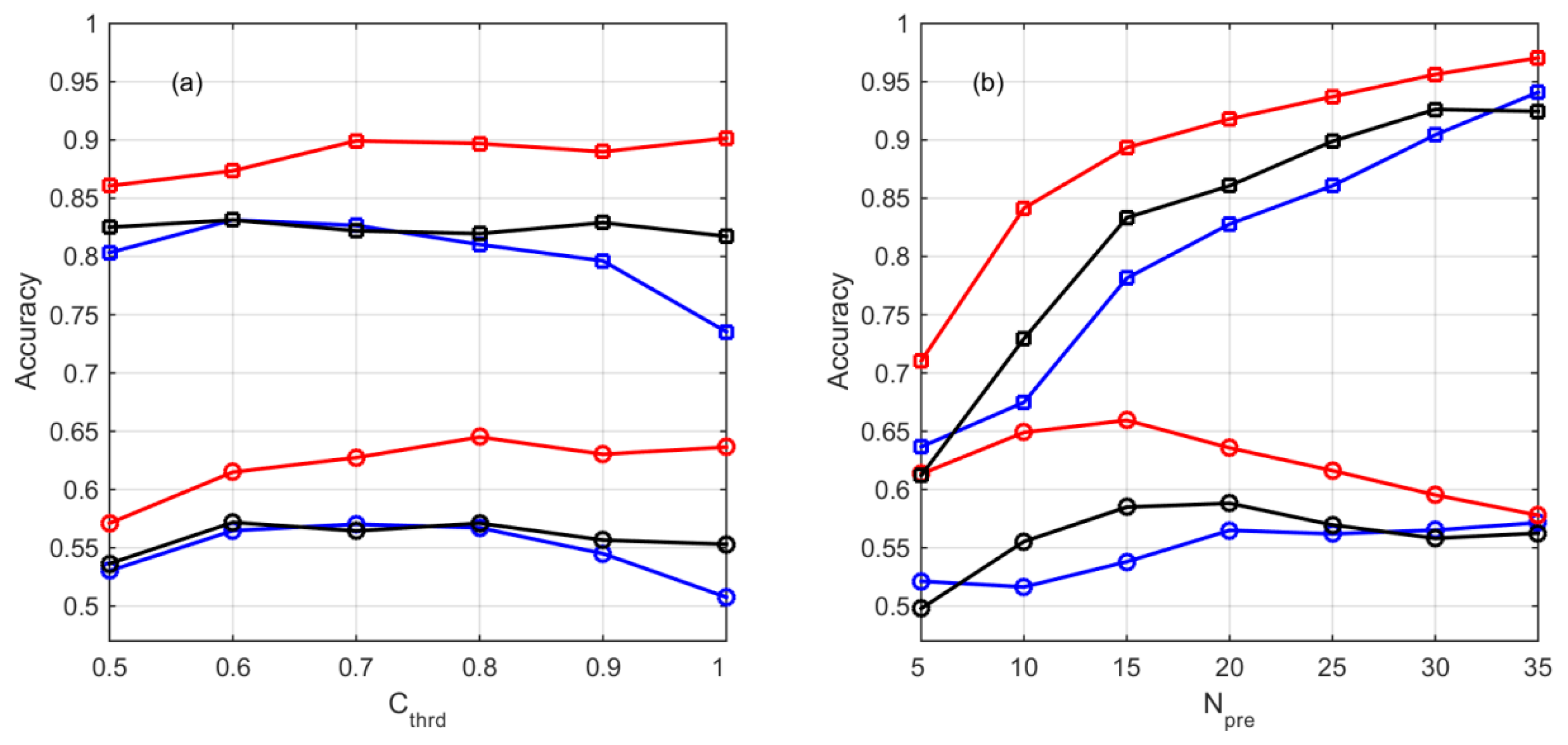
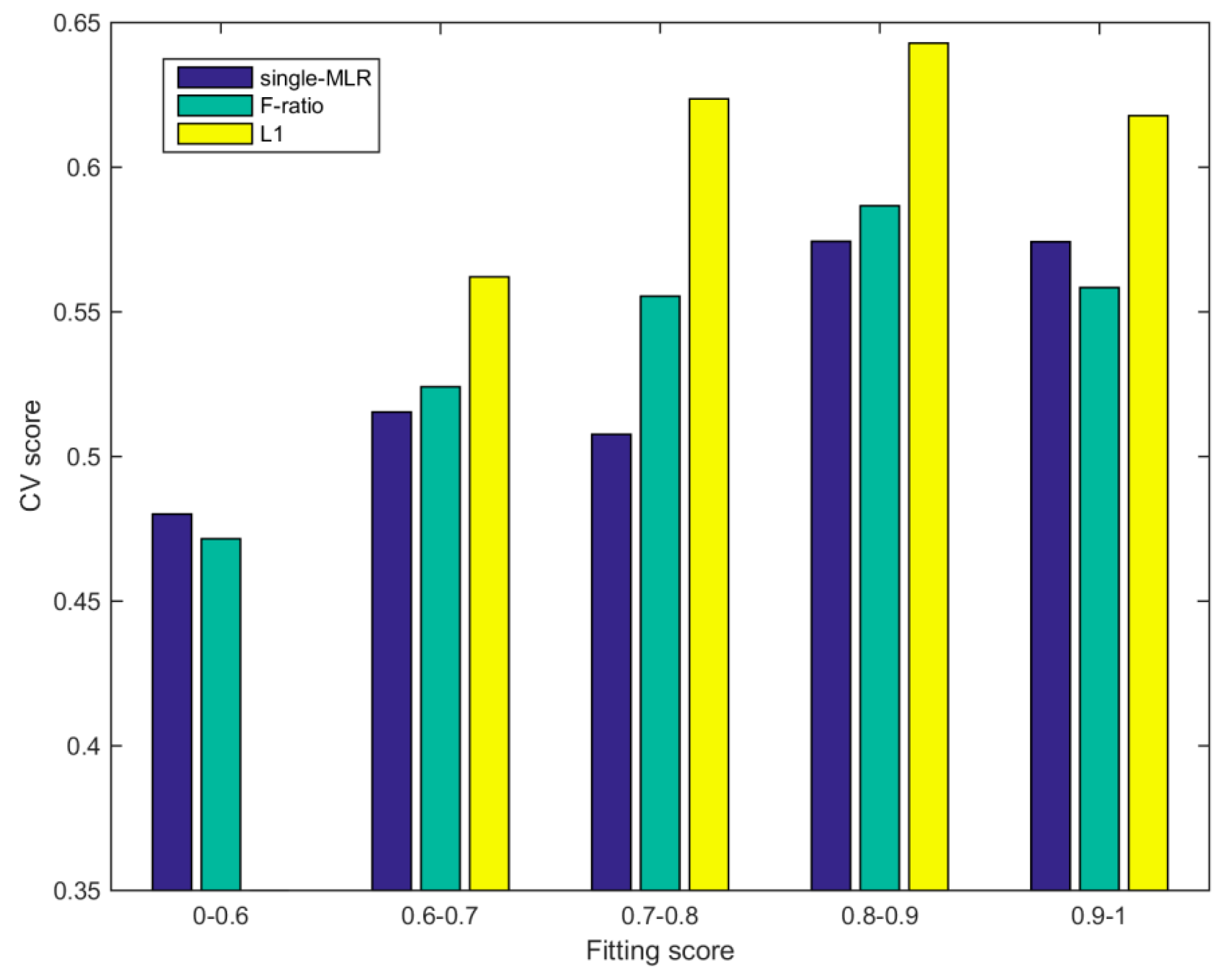
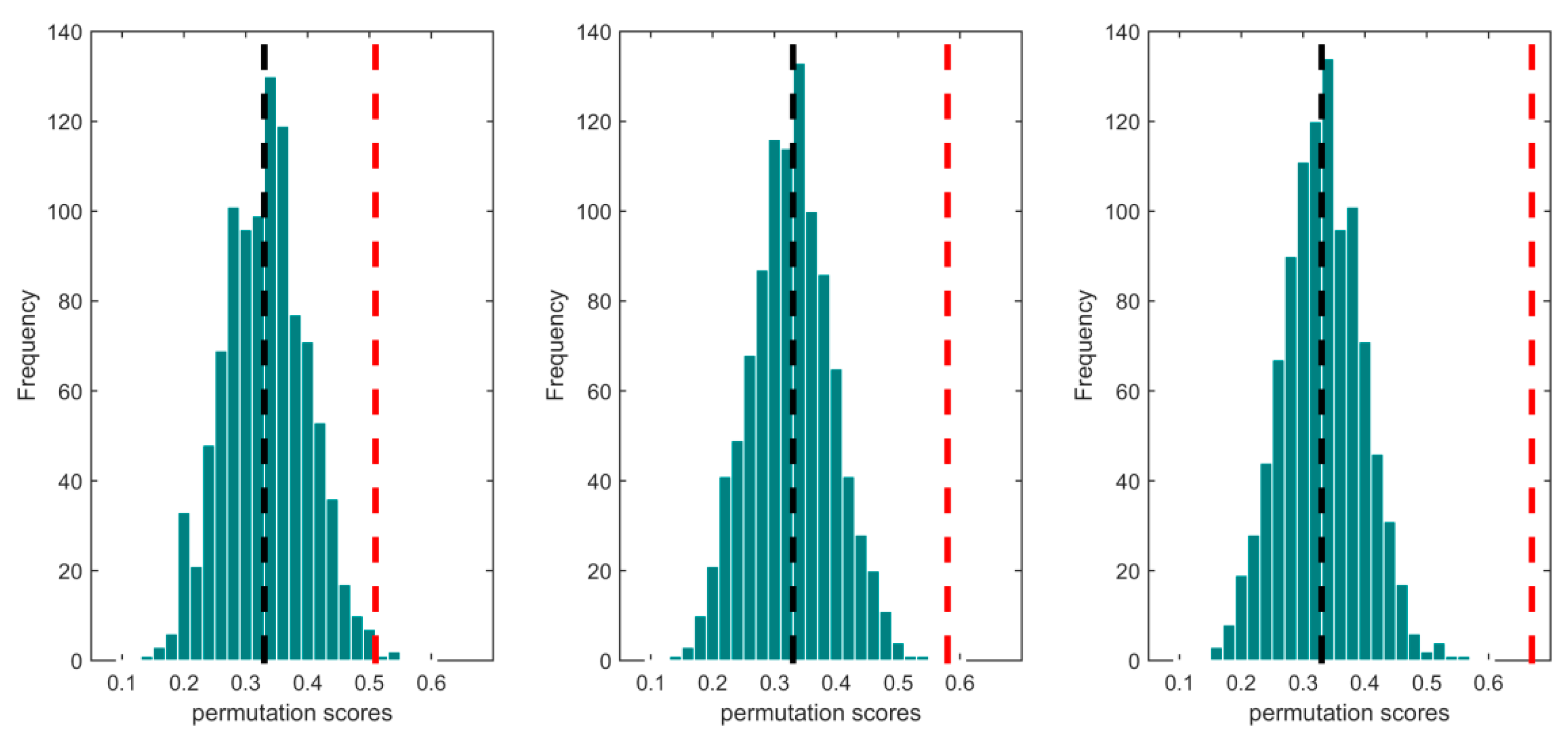
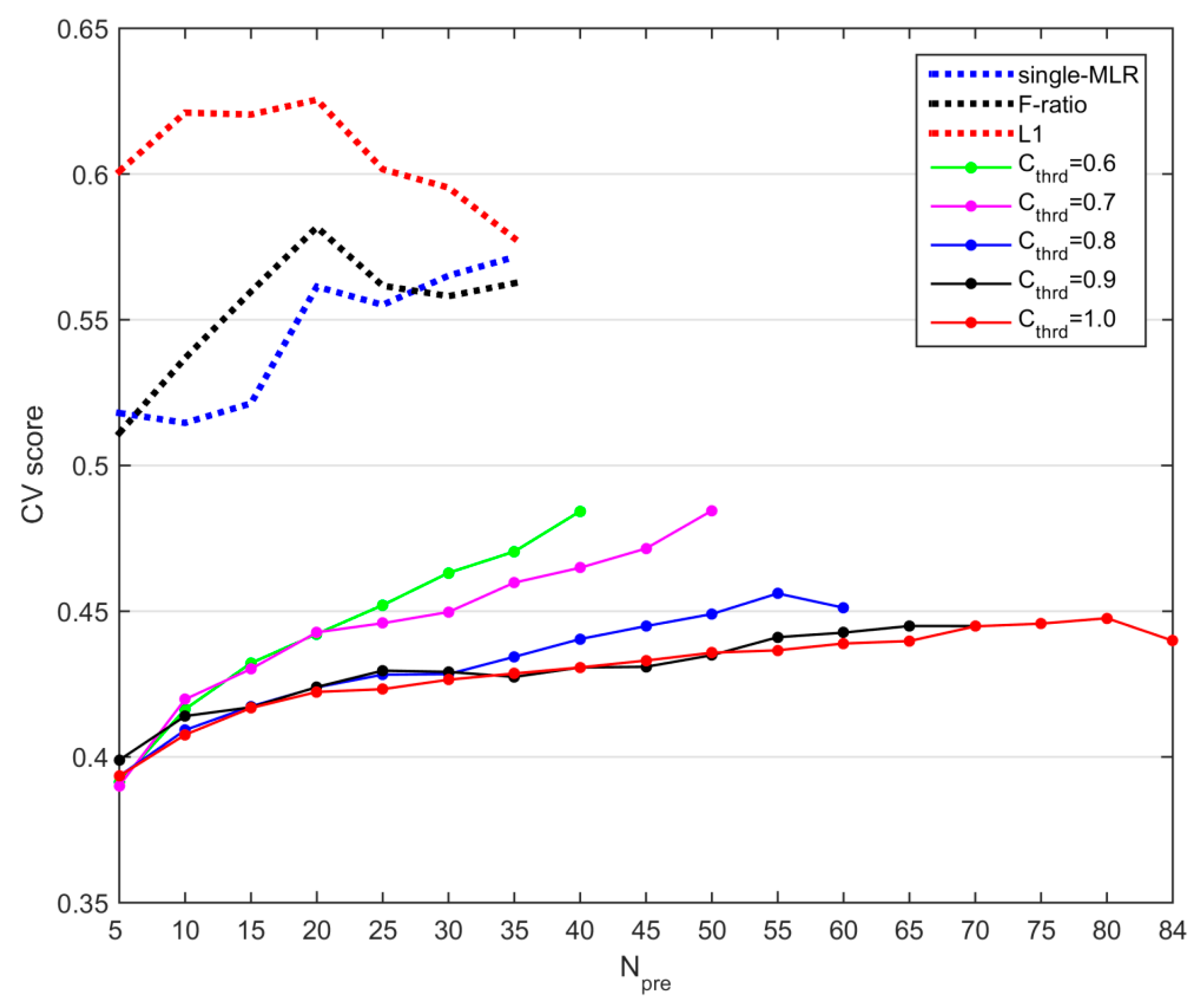
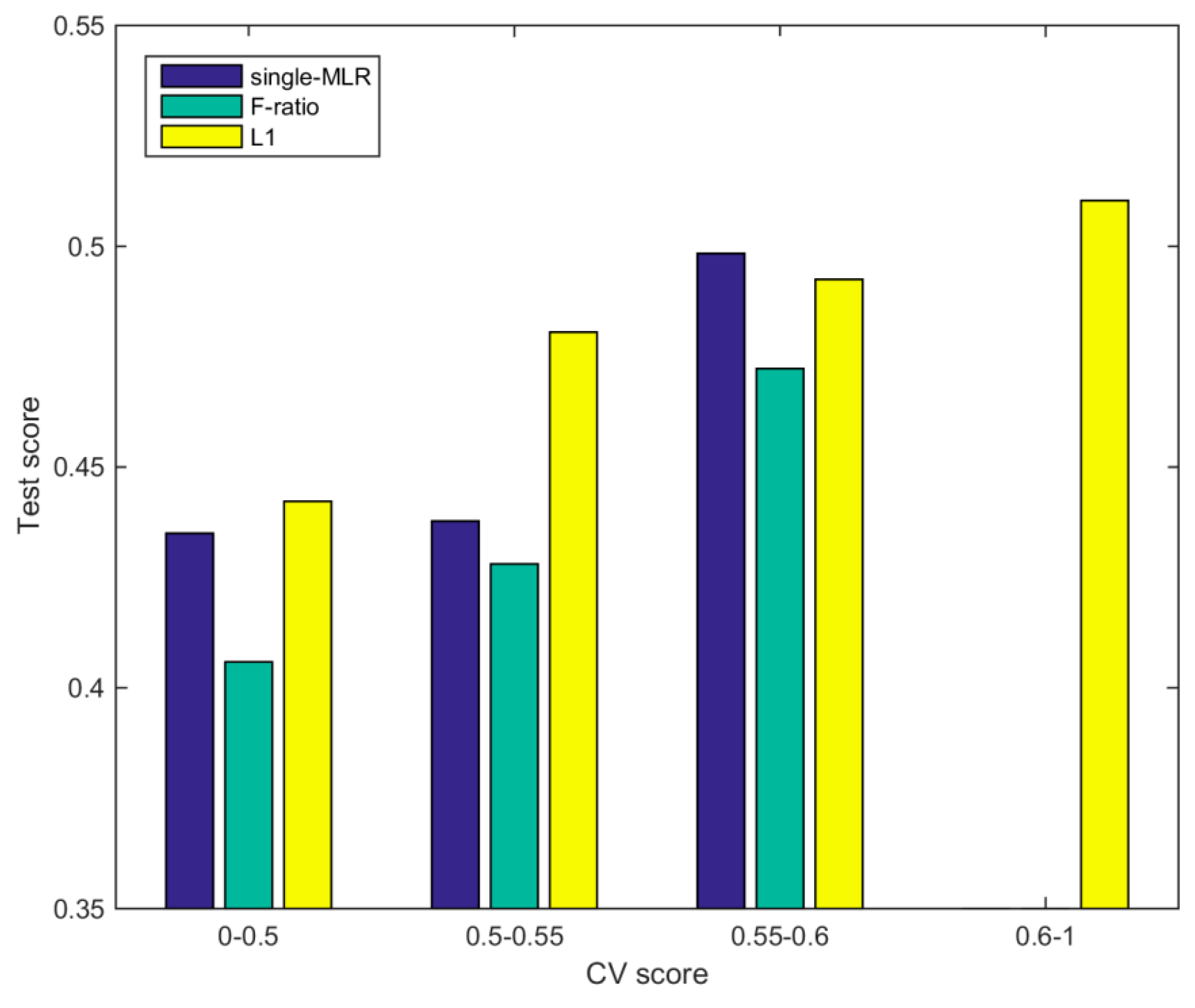
4.1. Training and Validation of the Objective Prediction Model
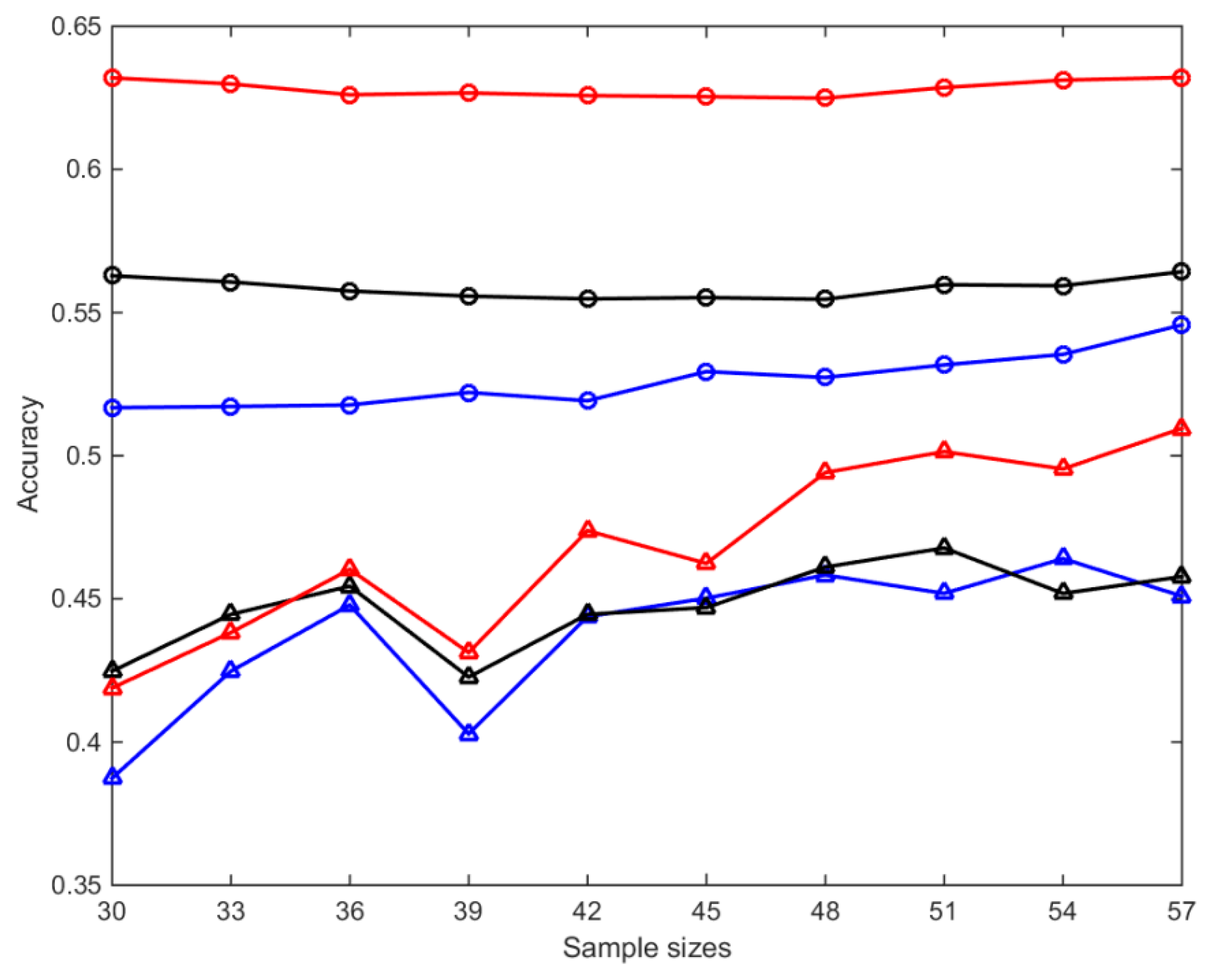
4.2. Generalization Ability of the Objective Prediction Model
5. Summary and Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
- Northern Hemisphere Subtropical High Ridge Position Index
- North African Subtropical High Ridge Position Index
- North African-North Atlantic-North American Subtropical High Ridge Position Index
- Western Pacific Subtropical High Ridge Position Index
- North American Subtropical High Ridge Position Index
- South China Sea Subtropical High Ridge Position Index
- North American-North Atlantic Subtropical High Ridge Position Index
- Pacific Subtropical High Ridge Position Index
- Asia Polar Vortex Area Index
- Pacific Polar Vortex Area Index
- North American Polar Vortex Area Index
- Atlantic-European Polar Vortex Area Index
- Northern Hemisphere Polar Vortex Area Index
- Asia Polar Vortex Intensity Index
- Pacific Polar Vortex Intensity Index
- North American Polar Vortex Intensity Index
- Atlantic-European Polar Vortex Intensity Index
- Northern Hemisphere Polar Vortex Intensity Index
- Northern Hemisphere Polar Vortex Central Longitude Index
- Northern Hemisphere Polar Vortex Central Latitude Index)
- Northern Hemisphere Polar Vortex Central Intensity Index
- Eurasian Zonal Circulation Index
- Eurasian Meridional Circulation Index
- Asian Zonal Circulation Index
- Asian Meridional Circulation Index
- East Asian Trough Position Index
- East Asian Trough Intensity Index
- Tibet Plateau Region 1 Index
- Tibet Plateau Region 2 Index
- India-Burma Trough Intensity Index
- Arctic Oscillation, AO
- Antarctic Oscillation, AAO
- North Atlantic Oscillation, NAO
- Pacific/ North American Pattern, PNA
- East Atlantic Pattern, EA
- West Pacific Pattern, WP
- North Pacific Pattern, NP
- East Atlantic-West Russia Pattern, EA/WR
- Tropical-Northern Hemisphere Pattern, TNH
- Polar-Eurasia Pattern, POL
- Scandinavia Pattern, SCA
- 30 hPa zonal wind Index
- 50 hPa zonal wind Index
- Mid-Eastern Pacific 200mb Zonal Wind Index
- West Pacific 850mb Trade Wind Index
- Central Pacific 850mb Trade Wind Index
- East Pacific 850mb Trade Wind Index
- Atlantic-European Circulation W Pattern Index
- Atlantic-European Circulation C Pattern Index
- Atlantic-European Circulation E Pattern Index
- NINO 1+2 SSTA Index
- NINO 3 SSTA Index
- NINO 4 SSTA Index
- NINO 3.4 SSTA Index
- NINO W SSTA Index
- NINO C SSTA Index
- NINO A SSTA Index
- NINO B SSTA Index
- NINO Z SSTA Index
- Tropical Northern Atlantic SST Index
- Tropical Southern Atlantic SST Index
- Indian Ocean Warm Pool Area Index)
- Indian Ocean Warm Pool Strength Index
- Western Pacific Warm Pool Area Index
- Western Pacific Warm Pool Strength index
- Atlantic Multi-decadal Oscillation Index
- Oyashio Current SST Index
- West Wind Drift Current SST Index
- Kuroshio Current SST Index
- ENSO Modoki Index
- Warm-pool ENSO Index
- Cold-tongue ENSO Index
- Indian Ocean Basin-Wide Index
- Tropic Indian Ocean Dipole Index
- South Indian Ocean Dipole Index
- Cold Air Activity Index
- Total Sunspot Number Index
- Southern Oscillation Index
- Multivariate ENSO Index
- Pacific Decadal Oscillation Index
- Atlantic Meridional Mode SST Index
- Quasi-Biennial Oscillation Index
- Solar Flux Index
- Average snow depth over Tibet Plateau.
References
- Song, J. Changes in dryness/wetness in China during the last 529 years. Int. J. Climatol. 2000, 20, 1003–1015. [Google Scholar] [CrossRef]
- Wei, F.Y. An integrative estimation model of summer rainfall-band patterns in China. Prog. Nat. Sci. Mater. 2007, 17, 280–288. [Google Scholar]
- Huang, J.P.; Yi, Y.H.; Wang, S.W.; Chou, J.F. An analogue-dynamical long-range numerical weather prediction system incorporating historical evolution. Q. J. R. Meteorol. Soc. 1993, 119, 547–565. [Google Scholar] [CrossRef]
- Wang, B.; Ding, Q.H.; Fu, X.H.; Kang, I.S.; Jin, K.; Shukla, J.; Doblas-Reyes, F. Fundamental challenge in simulation and prediction of summer monsoon rainfall. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Wang, H.J.; Fan, K.; Sun, J.Q.; Li, S.L.; Lin, Z.H.; Zhou, G.Q.; Chen, L.J.; Lang, X.M.; Li, F.; Zhu, Y.L.; et al. A Review of Seasonal Climate Prediction Research in China. Adv. Atmos. Sci. 2015, 32, 149–168. [Google Scholar] [CrossRef]
- Yang, Y.M.; Wang, B.; Li, J. Improving Seasonal Prediction of East Asian Summer Rainfall Using NESM3.0: Preliminary Results. Atmosphere 2018, 9, 487. [Google Scholar] [CrossRef]
- Liu, Y.; Fan, K. Improve the prediction of summer precipitation in the Southeastern China by a hybrid statistical downscaling model. Meteorol. Atmos. Phys. 2012, 117, 121–134. [Google Scholar] [CrossRef]
- Wang, H.J.; Fan, K. A New Scheme for Improving the Seasonal Prediction of Summer Precipitation Anomalies. Weather. Forecast. 2009, 24, 548–554. [Google Scholar] [CrossRef]
- Ding, Y.H.; Chan, J.C.L. The East Asian summer monsoon: An overview. Meteorol. Atmos. Phys. 2005, 89, 117–142. [Google Scholar] [CrossRef]
- Zhou, T.J.; Yu, R.C. Atmospheric water vapor transport associated with typical anomalous summer rainfall patterns in China. J. Geophys. Res. Atmos. 2005, 110. [Google Scholar] [CrossRef]
- Wang, B.; Xiang, B.Q.; Lee, J.Y. Subtropical High predictability establishes a promising way for monsoon and tropical storm predictions. Proc. Natl. Acad. Sci. USA 2013, 110, 2718–2722. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.J.; Xue, F.; Zhou, G.Q. The spring monsoon in South China and its relationship to large-scale circulation features. Adv. Atmos. Sci. 2002, 19, 651–664. [Google Scholar]
- Liu, X.F.; Yuan, H.Z.; Guan, Z.Y. Effects of Enso on the Relationship between Iod and Summer Rainfall in China. J. Trop. Meteorol. 2009, 15, 59–62. [Google Scholar] [CrossRef]
- Storch, H.V.; Zorita, E.; Cubasch, U. Downscaling of Global Climate Change Estimates to Regional Scales: An Application to Iberian Rainfall in Wintertime. J. Clim. 1993, 6, 1161–1171. [Google Scholar] [CrossRef]
- Wu, Z.W.; Wang, B.; Li, J.P.; Jin, F.F. An empirical seasonal prediction model of the east Asian summer monsoon using ENSO and NAO. J. Geophys. Res. Atmos. 2009, 114. [Google Scholar] [CrossRef]
- Cao, Q.; Hao, Z.C.; Yuan, F.F.; Su, Z.K.; Berndtsson, R. ENSO Influence on Rainy Season Precipitation over the Yangtze River Basin. Water 2017, 9, 469. [Google Scholar] [CrossRef]
- Huang, R.H.; Wu, Y.F. The influence of ENSO on the summer climate change in China and its mechanism. Adv. Atmos. Sci. 1989, 6, 21–32. [Google Scholar] [CrossRef]
- Wu, Z.W.; Li, J.P.; Jiang, Z.H.; He, J.H.; Zhu, X.Y. Possible effects of the North Atlantic Oscillation on the strengthening relationship between the East Asian Summer monsoon and ENSO. Int. J. Climatol. 2012, 32, 794–800. [Google Scholar] [CrossRef]
- Zhao, P.; Zhou, Z.J.; Liu, J.P. Variability of Tibetan spring snow and its associations with the hemispheric extratropical circulation and East Asian summer monsoon rainfall: An observational investigation. J. Clim. 2007, 20, 3942–3955. [Google Scholar] [CrossRef]
- Wu, Z.W.; Li, J.P.; Jiang, Z.H.; Ma, T.T. Modulation of the Tibetan Plateau Snow Cover on the ENSO Teleconnections: From the East Asian Summer Monsoon Perspective. J. Clim. 2012, 25, 2481–2489. [Google Scholar] [CrossRef]
- Sung, M.K.; Kwon, W.T.; Baek, H.J.; Boo, K.O.; Lim, G.H.; Kug, J.S. A possible impact of the North Atlantic Oscillation on the east Asian summer monsoon precipitation. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Gu, W.; Li, C.; Li, W.; Zhou, W.; Chan, J.C.L. Interdecadal unstationary relationship between NAO and east China’s summer precipitation patterns. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Liao, Q.S.; Zhao, Z.G. A seasonal forecasting scheme on precipitation distribution in summer in China. Quart. J. Appl. Meteor. 1992, 3 (Suppl. 1), 1–9. (In Chinese) [Google Scholar]
- Fan, K.; Lin, M.; Gao, Y. Forecasting the summer rainfall in North China using the year-to-year increment approach. Sci. China Earth Sci. 2009, 52, 532–539. [Google Scholar] [CrossRef]
- Yim, S.-Y.; Wang, B.; Xing, W.J. Prediction of early summer rainfall over South China by a physical-empirical model. Clim. Dyn. 2014, 43, 1883–1891. [Google Scholar] [CrossRef]
- Chen, X.F.; Zhao, Z.G. The Application and Research on Predication of China Rainy Season Rainfall; Meteorological Press: Beijing, China, 2000. (In Chinese) [Google Scholar]
- Zhao, J.H.; Feng, G.L. Reconstruction of conceptual prediction model for the Three Rainfall Patterns in the summer of eastern China under global warming. Sci. China Earth Sci. 2014, 57, 3047–3061. [Google Scholar] [CrossRef]
- Liao, Q.S.; Chen, G.Y.; Chen, G.Z. Collection of Long Time Weather Forecast; China Meteorological Press: Beijing, China, 1981; pp. 103–114. (In Chinese) [Google Scholar]
- Wei, F.Y.; Zhang, X.G. The classification and forecasting of summer rain-belt in the east part of China. Meteorol. Mon. 1988, 14, 15–19. (In Chinese) [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006. [Google Scholar]
- Yan, H.S.; Yang, S.Y.; Hu, J.; Chen, J.G. A Study of the relationship between the winter middle-high latitude atmospheric circulation change and the principal rain patterns in rainy season over China. Chin. J. Atmos. Sci. 2006, 30, 285–292. (In Chinese) [Google Scholar]
- Sanderson, M.G.; Economou, T.; Salmon, K.H.; Jones, S.E.O. Historical Trends and Variability in Heat Waves in the United Kingdom. Atmosphere 2017, 8, 191. [Google Scholar] [CrossRef]
- Pour, S.H.; Bin Harun, S.; Shahid, S. Genetic Programming for the Downscaling of Extreme Rainfall Events on the East Coast of Peninsular Malaysia. Atmosphere 2014, 5, 914–936. [Google Scholar] [CrossRef]
- Seo, J.H.; Lee, Y.H.; Kim, Y.H. Feature Selection for Very Short-Term Heavy Rainfall Prediction Using Evolutionary Computation. Adv. Meteorol. 2014, 203545. [Google Scholar] [CrossRef]
- Wei, C.C.; Peng, P.C.; Tsai, C.H.; Huang, C.L. Regional Forecasting of Wind Speeds during Typhoon Landfall in Taiwan: A Case Study of Westward-Moving Typhoons. Atmosphere 2018, 9, 141. [Google Scholar] [CrossRef]
- Lyu, B.L.; Zhang, Y.H.; Hu, Y.T. Improving PM2.5 Air Quality Model Forecasts in China Using a Bias-Correction Framework. Atmosphere 2017, 8, 147. [Google Scholar] [CrossRef]
- Alin, A. Multicollinearity. WIREs Comp. Stat. 2010, 2, 370–374. [Google Scholar] [CrossRef]
- Jin, L.; Huang, X.Y.; Shi, X.M. A Study on Influence of Predictor Multicollinearity on Performance of the Stepwise Regression Prediction Equation. Acta Meteorol. Sin. 2010, 24, 593–601. [Google Scholar]
- Dormann, C.F.; Elith, J.; Bacher, S.; Buchmann, C.; Carl, G.; Carre, G.; Marquez, J.R.G.; Gruber, B.; Lafourcade, B.; Leitao, P.J.; et al. Collinearity: A review of methods to deal with it and a simulation study evaluating their performance. Ecography 2013, 36, 27–46. [Google Scholar] [CrossRef]
- Hogg, R.V.; Craig, A.T. Introduction to Mathematical Statistics, 5th ed.; Prentice Hall: Upper Saddle River, NJ, USA, 1995. [Google Scholar]
- Ojala, M.; Garriga, G.C. Permutation Tests for Studying Classifier Performance. J. Mach. Learn. Res. 2010, 11, 1833–1863. [Google Scholar]
- Wang, S.W. Advances in Modern Climatology; China Meteorological Press: Beijing, China, 2002. (In Chinese) [Google Scholar]

| Class | Year |
|---|---|
| I | 1953 1958 1959 1960 1961 1964 1966 1967 1973 1976 1977 1978 1981 1985 1988 1992 1994 1995 2004 2012 |
| II | 1956 1957 1962 1963 1965 1971 1972 1975 1979 1982 1984 1987 1989 1990 1991 2000 2003 2005 2007 2008 2009 |
| III | 1952 1954 1955 1968 1969 1970 1974 1980 1983 1986 1993 1996 1997 1998 1999 2001 2002 2006 2010 2011 |
| Predictor index | 28 | 41 | 51 | 53 | 55 | 56 | 57 |
| 58 | 67 | 70 | 72 | 76 | 78 | ||
| CCs | 0.99 | 0.89 | 0.97 | 0.97 | 0.99 | 0.97 | 0.81 |
| 0.96 | 0.95 | 0.95 | 0.94 | 0.93 | 0.93 |
| Predictors Selection Scheme | Predictor Index |
|---|---|
| Scheme single-MLR | 3 15 70 34 74 53 16 50 48 60 39 64 37 27 25 |
| Scheme F-ratio | 3 39 15 16 10 76 27 26 1 50 31 18 4 55 48 |
| Scheme L1 | 3 37 15 76 4 26 25 70 39 1 75 21 50 19 18 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, L.; Wei, F.; Yan, Z.; Ma, J.; Xia, J. A Study of Objective Prediction for Summer Precipitation Patterns Over Eastern China Based on a Multinomial Logistic Regression Model. Atmosphere 2019, 10, 213. https://doi.org/10.3390/atmos10040213
Gao L, Wei F, Yan Z, Ma J, Xia J. A Study of Objective Prediction for Summer Precipitation Patterns Over Eastern China Based on a Multinomial Logistic Regression Model. Atmosphere. 2019; 10(4):213. https://doi.org/10.3390/atmos10040213
Chicago/Turabian StyleGao, Lihao, Fengying Wei, Zhongwei Yan, Jin Ma, and Jiangjiang Xia. 2019. "A Study of Objective Prediction for Summer Precipitation Patterns Over Eastern China Based on a Multinomial Logistic Regression Model" Atmosphere 10, no. 4: 213. https://doi.org/10.3390/atmos10040213
APA StyleGao, L., Wei, F., Yan, Z., Ma, J., & Xia, J. (2019). A Study of Objective Prediction for Summer Precipitation Patterns Over Eastern China Based on a Multinomial Logistic Regression Model. Atmosphere, 10(4), 213. https://doi.org/10.3390/atmos10040213





