Forecasting Particulate Matter Concentration Using Linear and Non-Linear Approaches for Air Quality Decision Support
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Acquisition
2.3. Imputation of Missing Values
2.4. Data Normalization
2.5. Multiple Linear Regression (MLR)
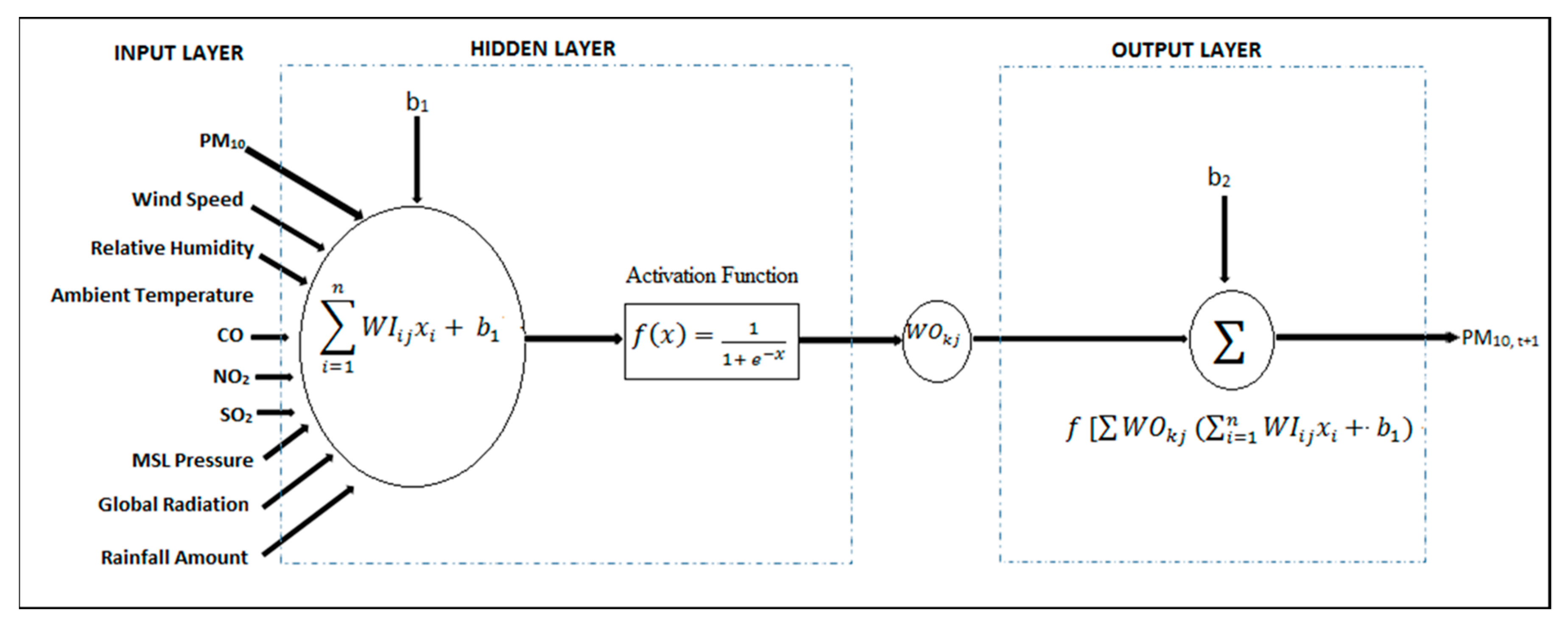
2.6. Multi-Layer Perceptron
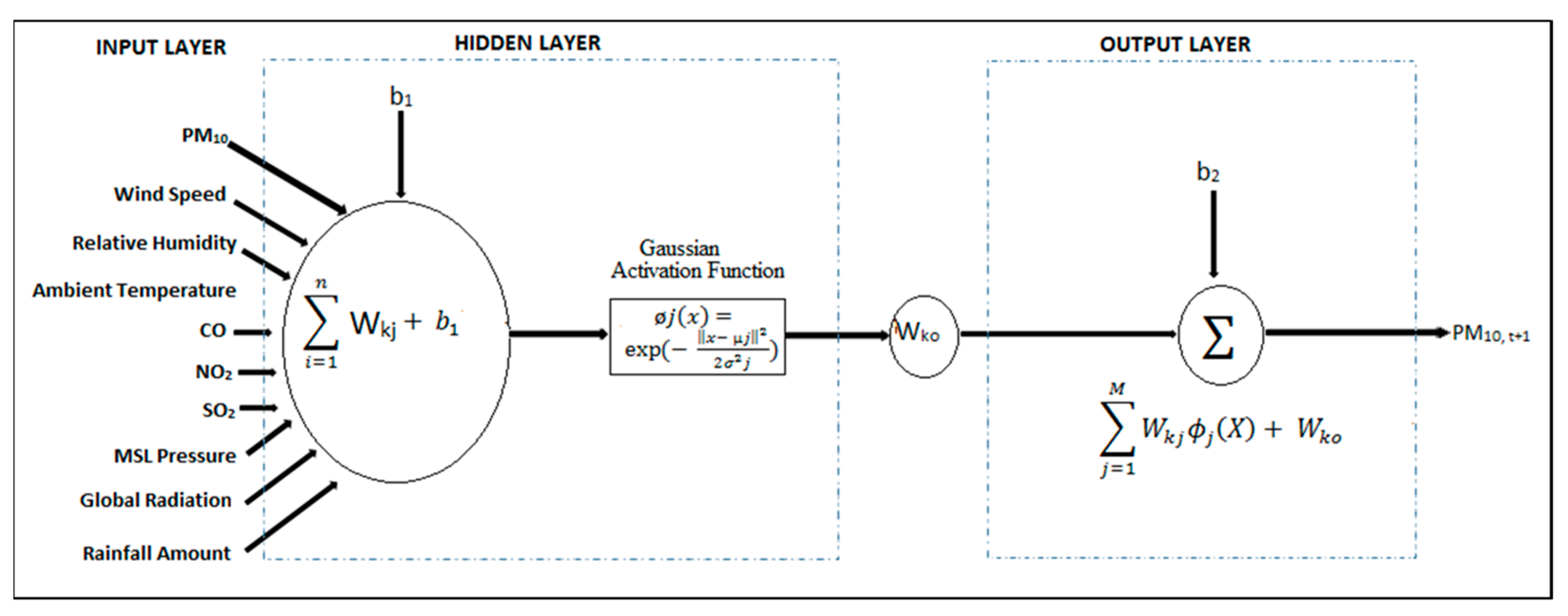
2.7. Radial Basis Function
2.8. Performance Indicators
- (a)
- Root Mean Square Error (RMSE):
- (b)
- Index of Agreement (IA):
- (c)
- Normalized Absolute Error (NAE):
- (d)
- Correlation Coefficient (R2):
- (e)
- Prediction Accuracy (PA):where = total number measurements at a particular site, = forecasted values, = observed values, = mean of forecasted values, = mean of observed values, Spred = standard deviation of forecasted values and Sobs = standard deviation of the observed values.
3. Results and Discussion
3.1. Descriptive Statistics
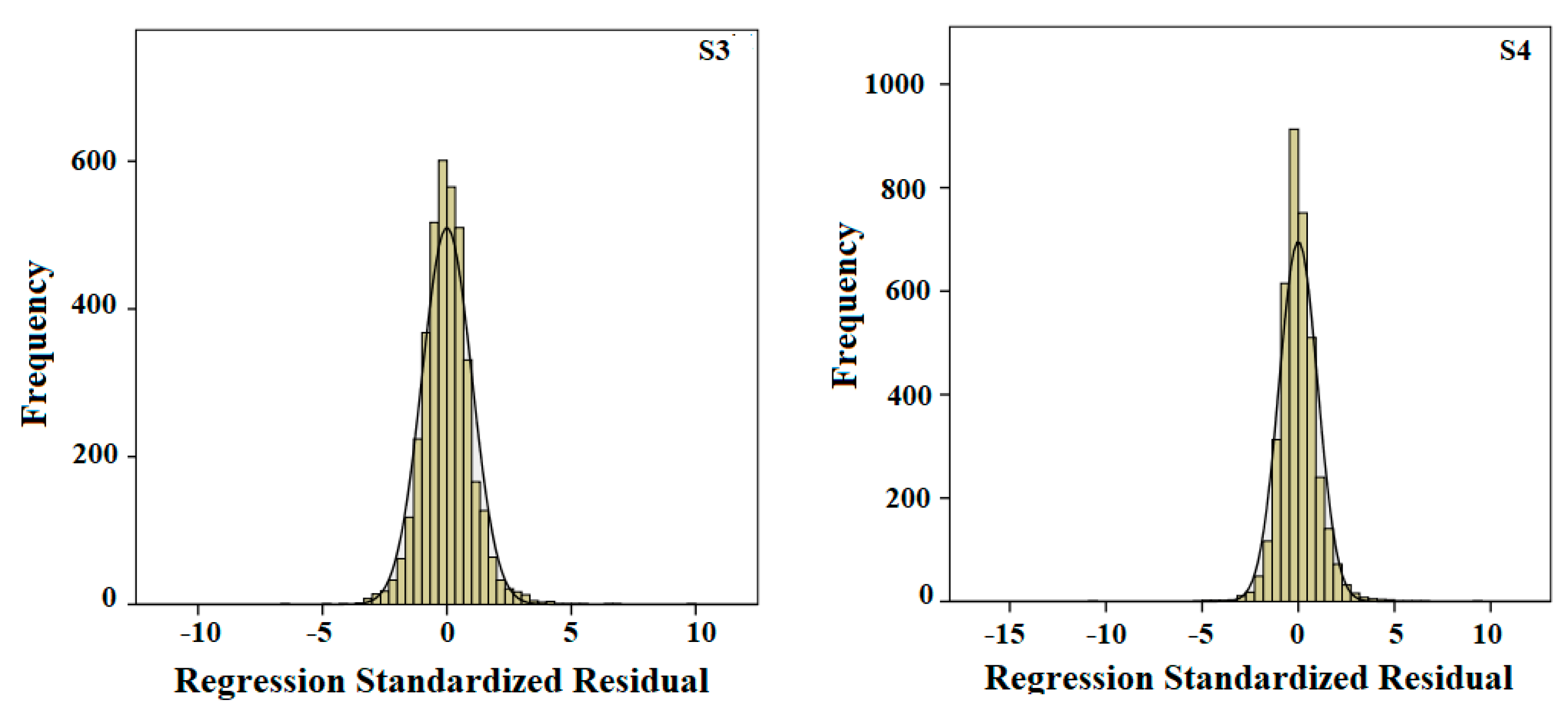
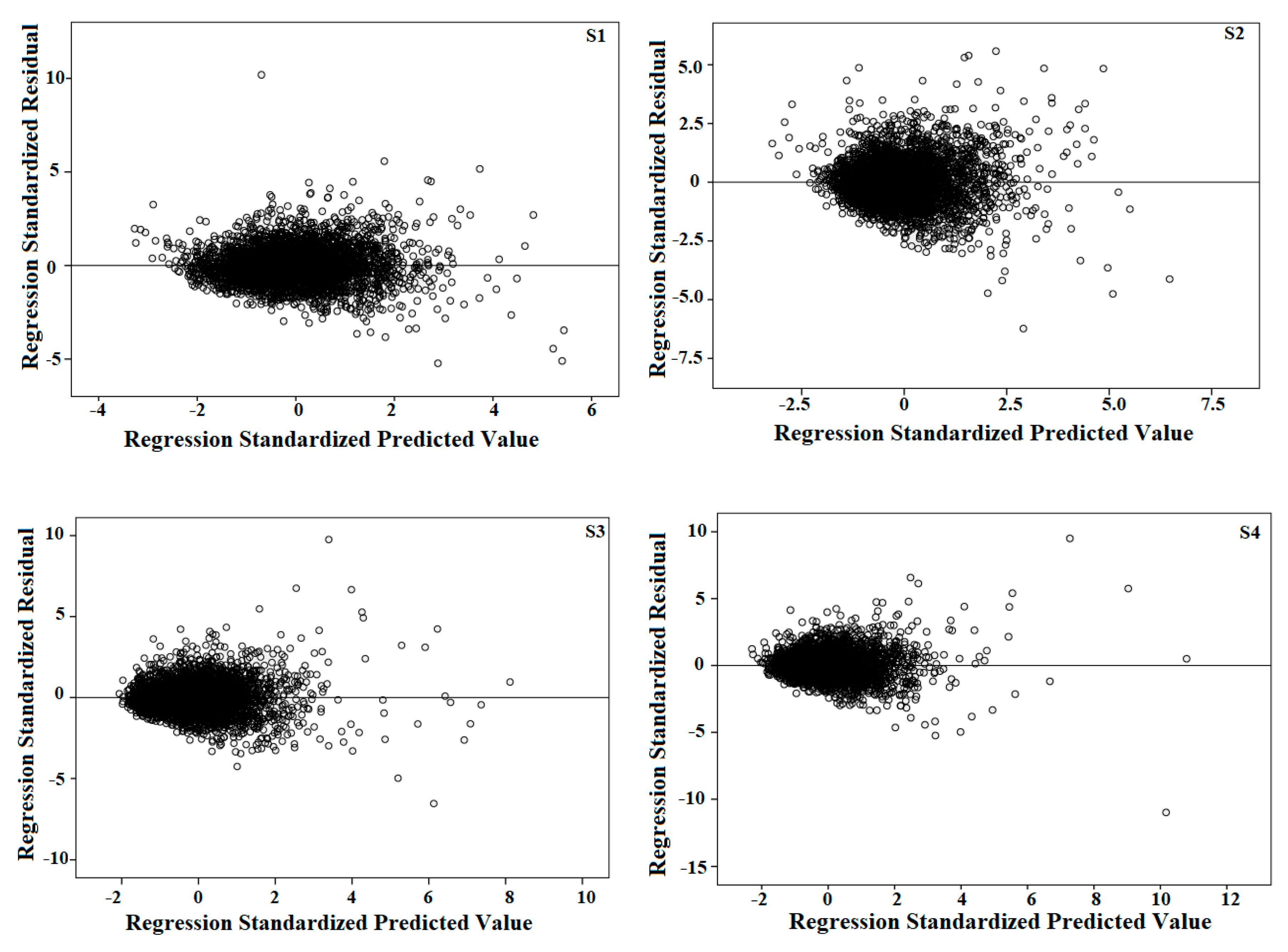
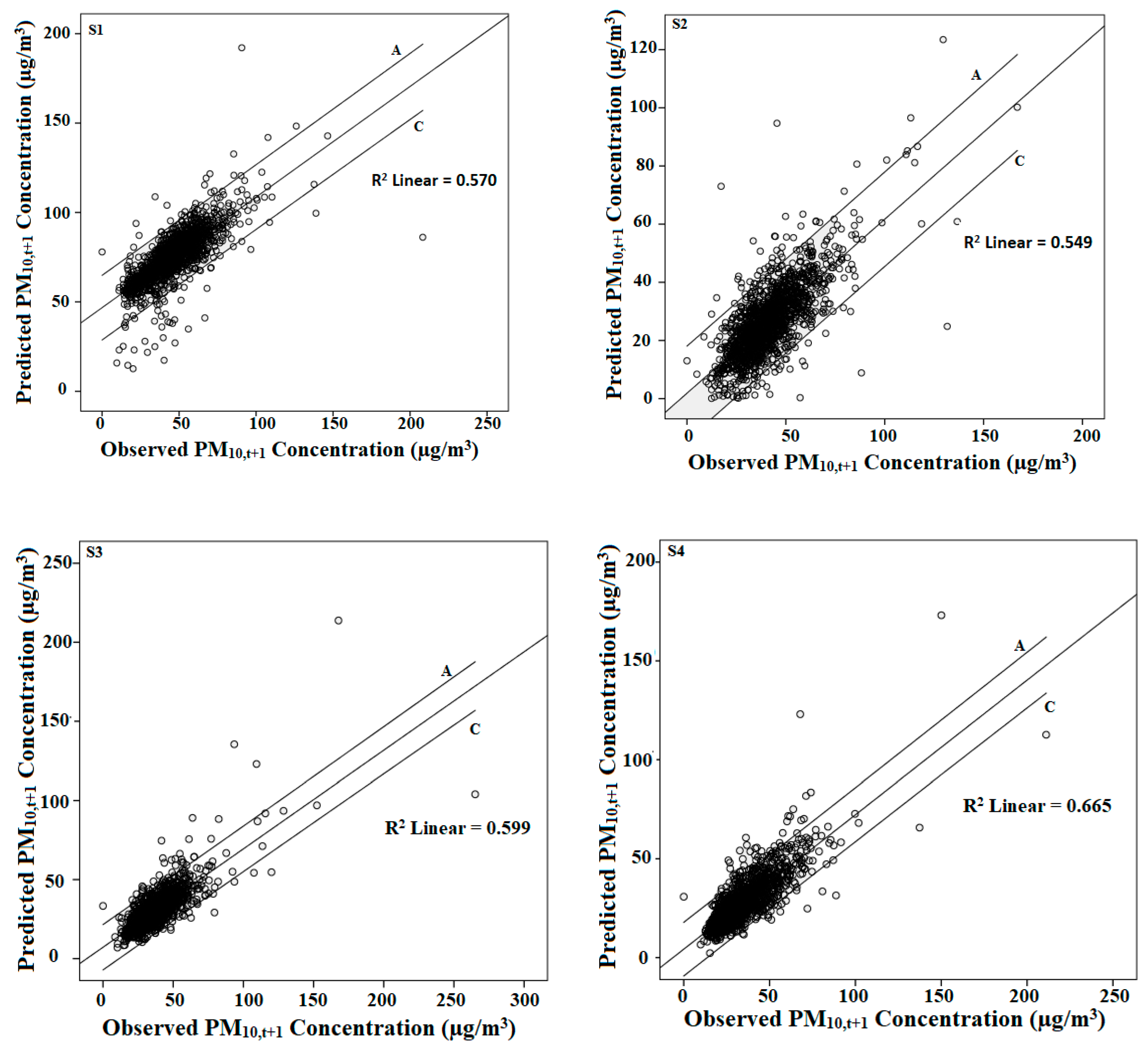
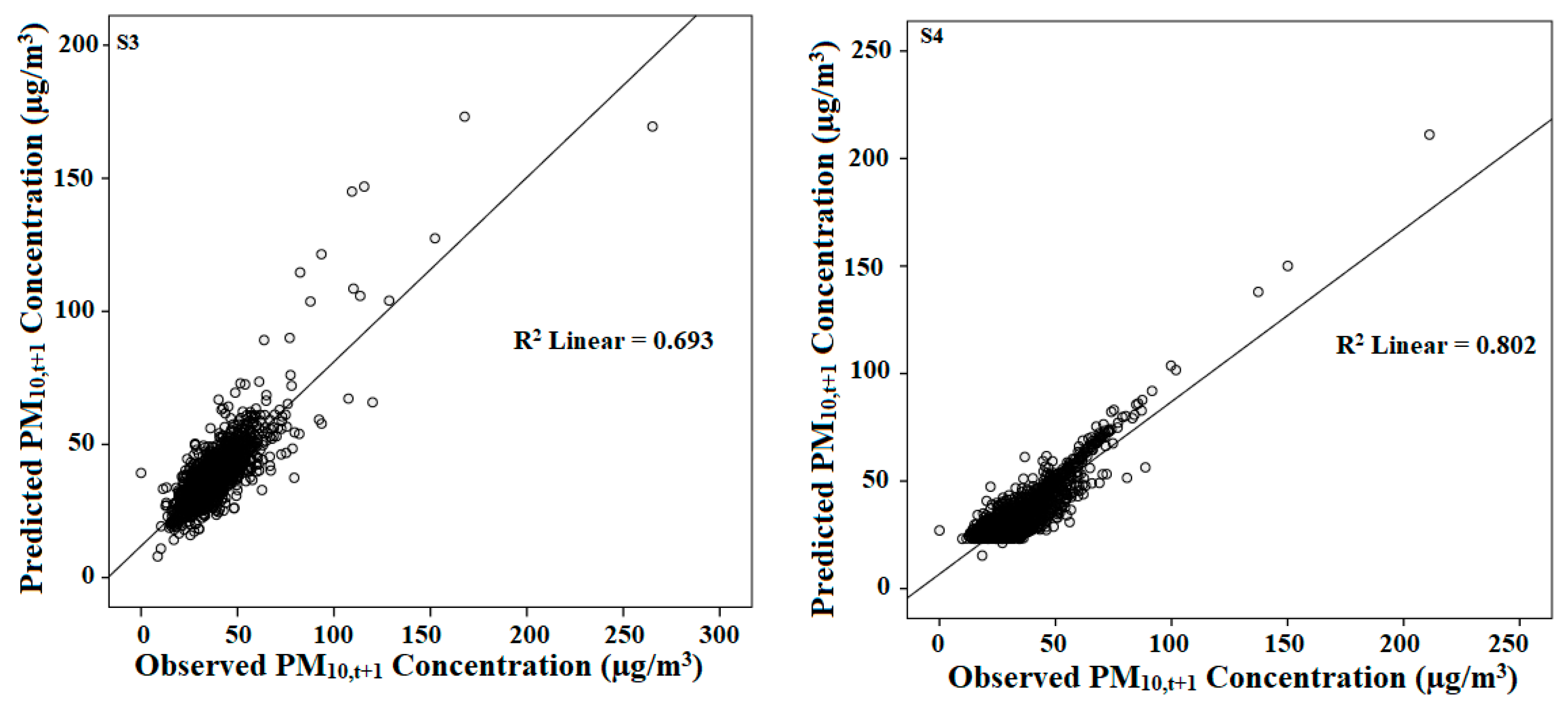
3.2. Multiple Linear Regression Model
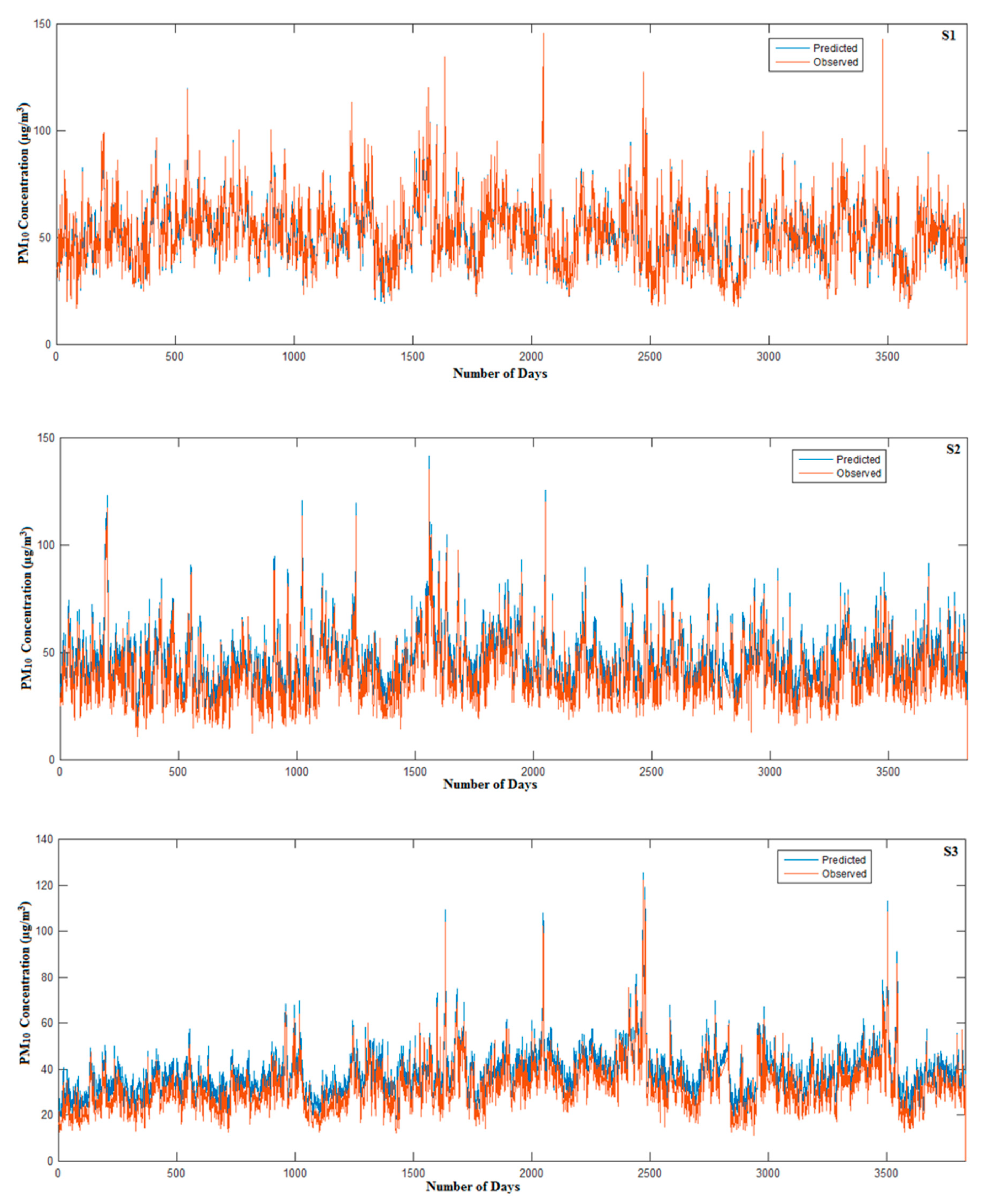
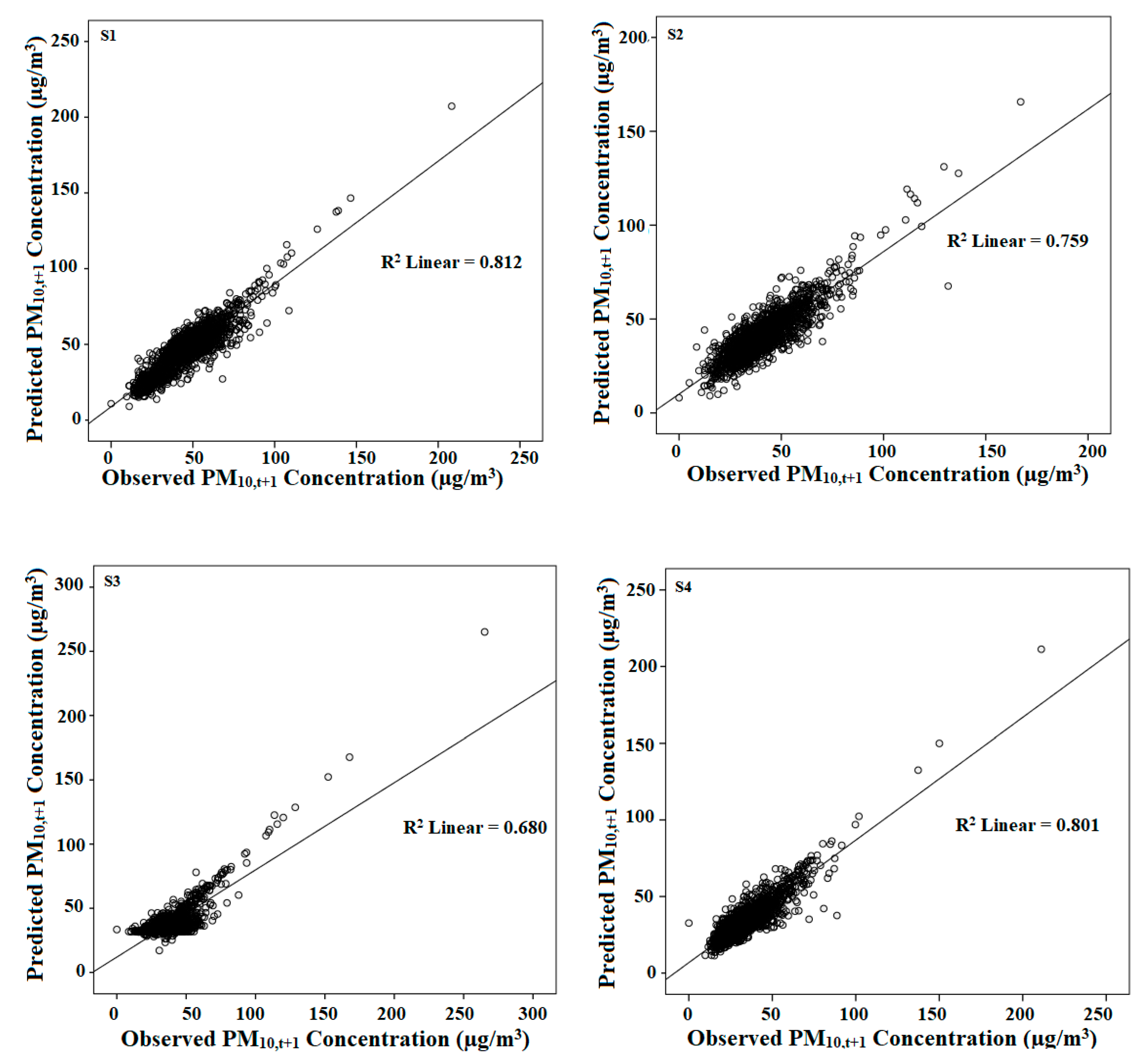
3.3. Multi-Layer Perceptron Model
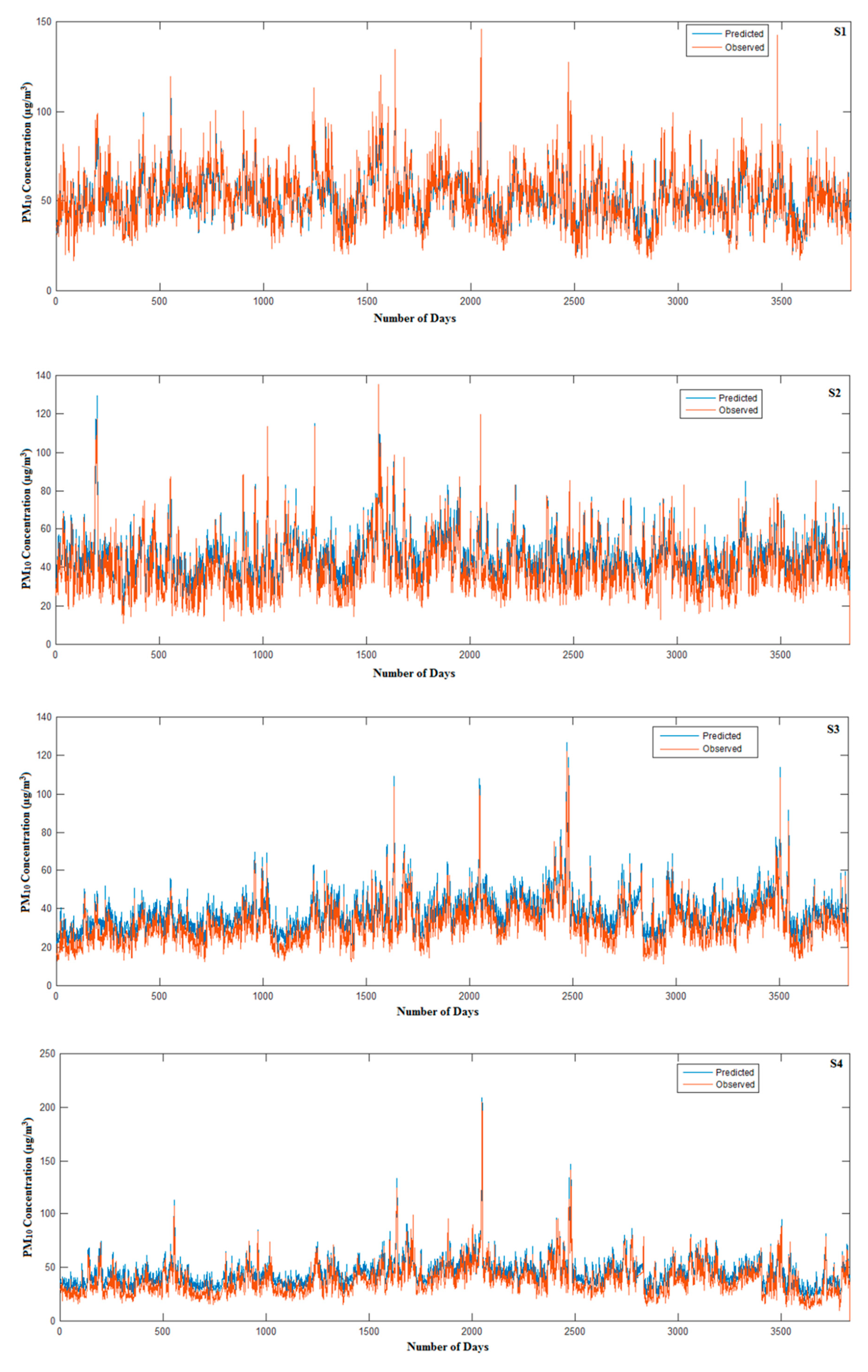
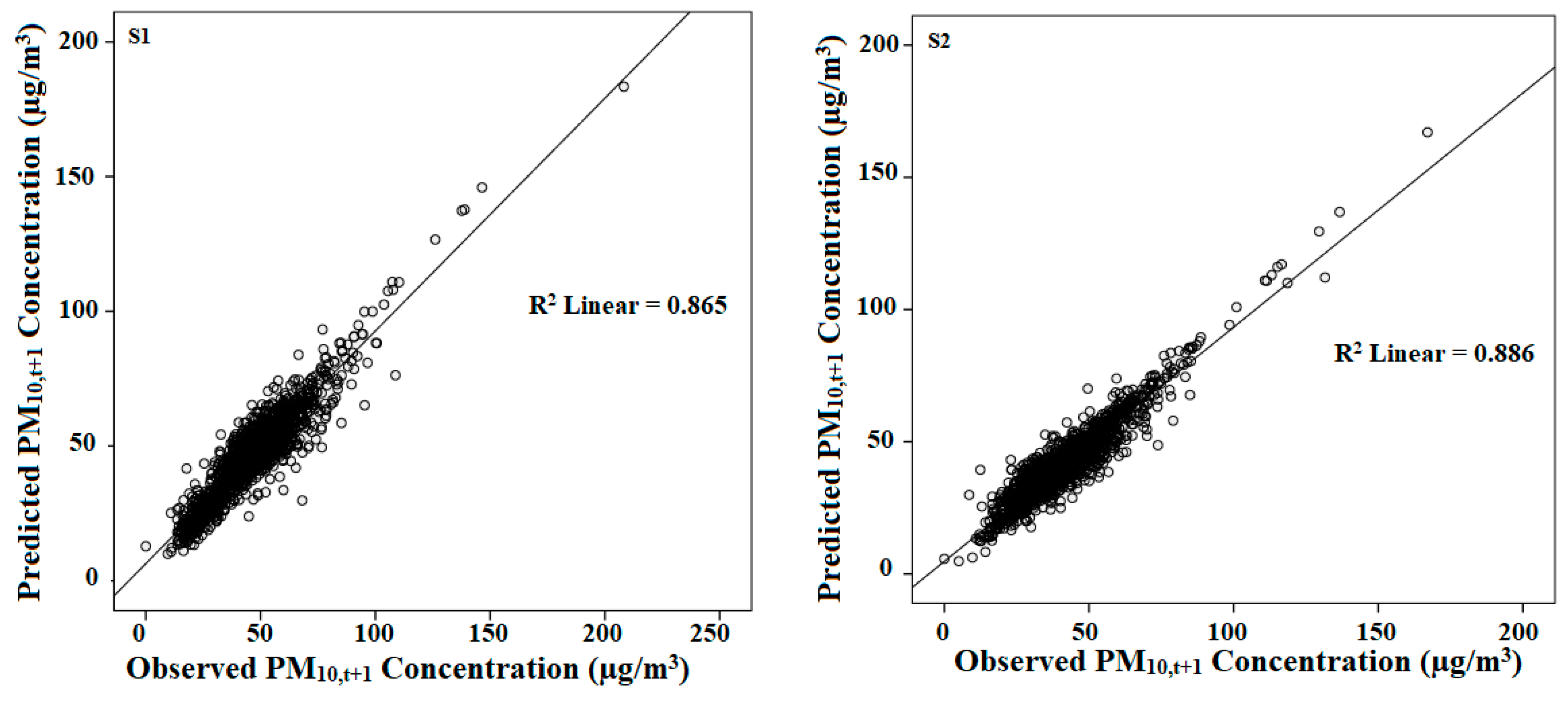
3.4. Radial Basis Function Models
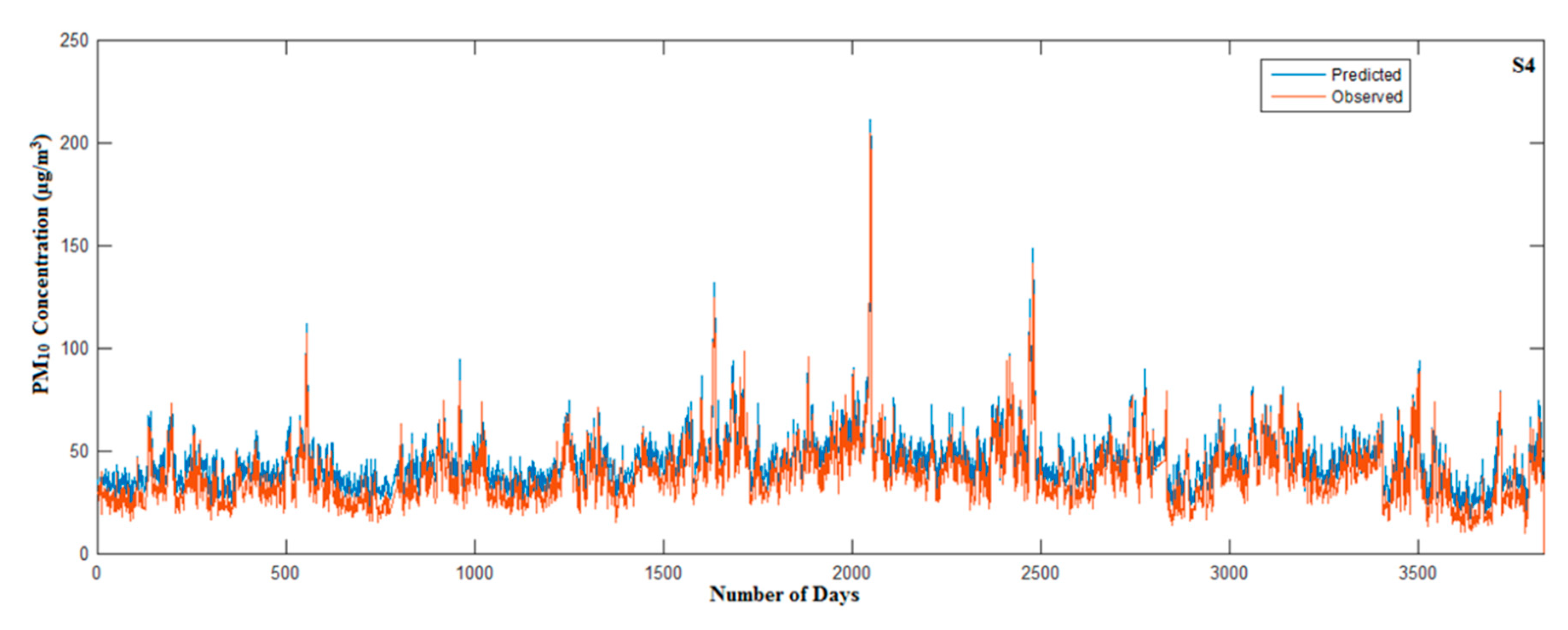
3.5. Models Evaluation and Selection
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Latif, M.T.; Azmi, S.Z.; Noor, A.D.M.; Ismail, A.S.; Johny, Z.; Idrus, S.; Mohamed, A.F.; Mokhtar, M. The impact of urban growth on regional air quality surrounding the Langat river basin. Environmentalist 2011, 31, 315–324. [Google Scholar] [CrossRef]
- Reddington, C.L.; Yoshioka, M.; Balasubramaniam, R.; Ridley, D.; Toh, Y.Y.; Arnold, S.R.; Spracklen, D.V. Contribution of vegetation and pea fires to particulate air pollution in Southeast Asia. Environ. Res. Lett. 2014, 9, 1–12. [Google Scholar] [CrossRef]
- Department of Environment, Malaysia. Malaysia Environmental Quality Report 2014. Available online: https://www.doe.gov.my/portalv1/en/ (accessed on 17 April 2019).
- Fong, S.Y.; Ismail, M.; Abdullah, S. Seasonal variation of criteria pollutant in an urban coastal environment: Kuala Terengganu. MATEC Web Conf. 2017, 87, 03011. [Google Scholar] [CrossRef]
- Ismail, M.; Yuen, F.S.; Abdullah, S. Particulate matter status and its relationship with meteorological factors in the East Coast of Peninsular Malaysia. J. Eng. Appl. Sci. 2016, 11, 2588–2593. [Google Scholar] [CrossRef]
- Razak, N.A.; Zubairi, Y.Z.; Yunus, R.M. Imputing missing values in modelling the PM10 concentrations. Sains Malays. 2014, 43, 1599–1607. [Google Scholar]
- Han, X.; Naeher, L.P. A review of traffic-related air pollution exposure assessment studies in the developing world. Env. Int. 2006, 32, 106–120. [Google Scholar] [CrossRef]
- Rai, P.K. Biomagnetic Monitoring of Particulate Matter. In Indo-Burma Hotspot Region, 1st ed.; Elsevier Science: Amsterdam, The Netherlands, 2016; pp. 75–109. [Google Scholar] [CrossRef]
- Utell, M.J.; Frampton, M.W. Acute health effects of ambient air pollution: The ultrafine particle hypothesis. J. Aerosol Med. 2000, 13, 355–359. [Google Scholar] [CrossRef]
- Perez, L.; Tobias, A.; Querol, X.; Kunzli, N.; Pey, J.; Alastuey, A.; Viana, M.; Valero, N.; Gonzalez-Cabre, M.; Sunyer, J. Coarse particles from Saharan dust and daily mortality. Epidemiology 2008, 19, 800–807. [Google Scholar] [CrossRef]
- World Health Organization. Guidelines for Air Quality; Department of Public Health, Environmental and Social Determinants of Health (PHE): Geneva, Switzerland, 2009. [Google Scholar]
- Carnevale, C.; Finzi, G.; Pederzoli, A.; Turini, E.; Volta, M. Lazy learning based surrogate models for air quality planning. Env. Model. Softw. 2016, 83, 47–57. [Google Scholar] [CrossRef]
- Fong, S.Y.; Abdullah, S.; Ismail, M. Forecasting of particulate matter (PM10) concentration based on gaseous pollutants and meteorological factors for different monsoon of urban coastal area in Terengganu. J. Sustain. Sci. Manag. 2018, 5, 3–17. [Google Scholar]
- Borrego, C.; Tchepel, O.; Costa, A.M.; Amorim, J.H.; Miranda, A.I. Emission and dispersion modelling of Lisbon air quality at local scale. Atmos. Environ. 2003, 35, 5197–5205. [Google Scholar] [CrossRef]
- Ha, Q.P.; Wahid, H.; Duc, H.; Azzi, M. Enhanced radial basis function neural networks for ozone level estimation. Neurocomputing 2015, 155, 62–70. [Google Scholar] [CrossRef]
- Zhang, Y.; Bocquet, M.; Mallet, V.; Seigneur, C.; Baklanov, A. Real-time air quality forecasting, part I: History, techniques and current status. Atmos. Env. 2012, 60, 632–655. [Google Scholar] [CrossRef]
- Diaz-Robles, L.A.; Ortega, J.C.; Fu, J.S.; Reed, G.D.; Chow, J.C.; Watson, J.G.; Moncada-Herrera, J.A. A hybrid ARIMA and artificial neural networks model to forecast particulate matter in urban areas: The case of Temuco, Chile. Atmos. Environ. 2008, 42, 8331–8340. [Google Scholar] [CrossRef]
- Karakitsios, S.P.; Papaloukas, C.L.; Kassomenos, P.A.; Pilidis, G.A. Assessment and forecasting of benzene concentrations in a street canyon using artificial neural networks and deterministic models: Their response to “what if” scenarios. Ecol. Model. 2006, 193, 253–270. [Google Scholar] [CrossRef]
- Ul-Saufie, A.Z.; Yahaya, A.S.; Ramli, N.A.; Hamid, H.A. Performance of multiple linear regression model for long-term PM10 concentration forecasting based on gaseous and meteorological parameters. J. Appl. Sci. 2012, 12, 1488–1494. [Google Scholar] [CrossRef]
- Abdullah, S.; Ismail, M.; Fong, S.Y. Multiple linear regression (MLR) models for long term PM10 concentration forecasting during different monsoon seasons. J. Sustain. Sci. Manag. 2017, 12, 60–69. [Google Scholar]
- Ismail, M.; Abdullah, S.; Jaafar, A.D.; Ibrahim, T.A.E.; Shukor, M.S.M. Statistical modeling approaches for PM10 forecasting at industrial areas of Malaysia. AIP Conf. Proc. 2018, 2020, 020044-1–020044-6. [Google Scholar] [CrossRef]
- Ul-Saufie, A.Z.; Yahya, A.S.; Ramli, N.A.; Hamid, H.A. Comparison between multiple linear regression and feed forward back propagation neural network models for predicting PM10 concentration level based on gaseous and meteorological parameters. Int. J. Appl. Sci. Technol. 2011, 1, 42–49. [Google Scholar]
- Jackson, L.S.; Carslaw, N.; Carslaw, D.C.; Emmerson, K.M. Modelling trends in OH radical concentrations using generalized additive models. Atmos. Chem. Phys. 2009, 9, 2021–2033. [Google Scholar] [CrossRef]
- O’brien, R.M. A caution regarding rules of thumb for variance inflation factors. Qual. Quant. 2007, 41, 673–690. [Google Scholar] [CrossRef]
- Zhang, G.P. Time series forecasting using a hybrid ARIMA and neural network model. Neurocomputing 2003, 50, 159–175. [Google Scholar] [CrossRef]
- Paschalidou, A.K.; Karakitsios, S.; Kleanthous, S.; Kassomenos, P.A. Forecasting hourly PM10 concentration in Cyprus through artificial neural networks and multiple regression models: Implications to local environmental management. Environ. Sci. Pollut. Res. 2011, 18, 316–327. [Google Scholar] [CrossRef] [PubMed]
- Al-Alawi, S.; Abdul-Wahab, S.; Bakheit, C. Combining principal component regression and artificial neural networks for more accurate forecasting of ground-level ozone. Environ. Model. Softw. 2008, 23, 396–403. [Google Scholar] [CrossRef]
- Abdullah, S.; Ismail, M.; Ahmed, A.N. Identification of air pollution potential sources through principal component analysis (PCA). Int. J. Civ. Eng. Technol. 2018, 9, 1435–1442. [Google Scholar]
- Domanska, D.; Wojtylak, M. Explorative forecasting of air pollution. Atmos. Environ. 2014, 93, 19–30. [Google Scholar] [CrossRef]
- Latif, M.T.; Dominick, D.; Ahamad, F.; Khan, M.F.; Juneng, L.; Hamzah, F.M.; Nazir, M.S.M. Long term assessment of air quality from a background station on the Malaysian Peninsula. Sci. Total. Environ. 2014, 482, 336–348. [Google Scholar] [CrossRef]
- Afroz, R.; Hassan, M.N.; Ibrahim, N.A. Review of air pollution and health in Malaysia. Environ. Res. 2003, 92, 71–77. [Google Scholar] [CrossRef]
- Kurt, A.; Oktay, A.B. Forecasting air pollutant indicator levels with geographic models 3 days in advance using neural network. Expert Syst. Appl. 2010, 37, 7986–7992. [Google Scholar] [CrossRef]
- Mohammed, N.I.; Ramli, N.A.; Yahya, A.S. Ozone phytotoxicity evaluation and forecasting of crops production in tropical regions. Atmos. Environ. 2013, 68, 343–349. [Google Scholar] [CrossRef]
- Wong, M.S.; Xiao, F.; Nichol, J.; Fung, J.; Kim, J.; Campbell, J.; Chan, P.W. A multi-scale hybrid neural network retrieval model for dust storm detection, a study in Asia. Atmos. Res. 2015, 158–159, 89–106. [Google Scholar] [CrossRef]
- Abdullah, S.; Ismail, M.; Samat, N.N.A.; Ahmed, A.N. Modelling particulate matter (PM10) concentration in industrialized area: A comparative study of linear and nonlinear algorithms. ARPN J. Eng. Appl. Sci. 2018, 13, 8226–8234. [Google Scholar]
- Alp, M.; Cigizoglu, K. Suspended sediment load simulation by two artificial neural network methods using hydrometeorological data. Environ. Model. Softw. 2007, 22, 2–13. [Google Scholar] [CrossRef]
- Fontes, T.; Silva, L.M.; Silva, M.P.; Barros, N.; Carvalho, A.C. Can artificial neural networks be used to predict the origin of ozone episodes? Sci. Total Environ. 2014, 488–489, 197–207. [Google Scholar] [CrossRef] [PubMed]
- De Mattos Neto, P.S.G.; Madeiro, F.; Ferreira, T.A.E.; Cavalcanti, G.D.C. Hybrid intelligent system for air quality forecasting using phase adjustment. Eng. Appl. Artif. Intel. 2014, 32, 185–191. [Google Scholar] [CrossRef]
- Efron, B.; Tibshirani, R. Improvements on cross-validation: The 623 + bootstrap method. J. Am. Stat. Assoc. 1997, 92, 548–560. [Google Scholar]
- Yu, R.; Liu, X.C.; Larson, T.; Wang, Y. Coherent approach for modeling and nowcasting hourly near-road Black Carbon concentrations in Seattle, Washington. Transp. Res. D 2015, 34, 104–115. [Google Scholar] [CrossRef]
- Abdullah, S.; Ismail, M.; Fong, S.Y.; Ahmed, A.N. Neural network fitting using Lavenberq Marquardt algorithm for PM10 concentration forecasting in Kuala Terengganu. J. Telecommun. Electron. Comput. Eng. 2016, 8, 27–31. [Google Scholar]
- Xia, C.; Wang, J.; McMenemy, K. Short, medium and long term load forecasting model and virtual load forecaster based on radial basis function neural networks. Int. J. Elec Power. 2010, 32, 743–750. [Google Scholar] [CrossRef]
- Feng, X.; Li, Q.; Zhu, Y.; Hou, J.; Jin, L.; Wang, J. Artificial neural networks forecasting of PM2.5 pollution using air mass trajectory based geographic model and wavelet transformation. Atmos. Environ. 2015, 107, 118–128. [Google Scholar] [CrossRef]
- Zhao, N.; Wen, X.; Yang, J.; Li, S.; Wang, Z. Modelling and forecasting of viscosity of water-based nanofluids by radial basis function neural networks. Powder Technol. 2015, 281, 173–183. [Google Scholar] [CrossRef]
- Juneng, L.; Latif, M.T.; Tangang, F. Factors influencing the variations of PM10 aerosol dust in Klang Valley, Malaysia during the summer. Atmos. Environ. 2011, 45, 4370–4378. [Google Scholar] [CrossRef]
- Abdullah, S.; Ismail, M.; Fong, S.Y.; Ahmed, A.N. Evaluation for long term PM10 forecasting using multi linear regression (MLR) and principal component regression (PCR) models. EnvironmentAsia 2016, 9, 101–110. [Google Scholar] [CrossRef]
- Kovac-Andric, E.; Brana, J.; Gvozdic, V. Impact of meteorological factors on ozone concentrations modelled by time series and multivariate statistical methods. Ecol. Inform. 2009, 4, 117–122. [Google Scholar] [CrossRef]
- Sarigiannis, D.A.; Karakitsios, S.P.; Kermenidou, M.; Nikolaki, S.; Zikopoulos, D.; Semelidis, S.; Papagiannakis, A.; Tzimou, R. Total exposure to airborne particulate matter in cities: The effect of biomass combustion. Sci. Total Environ. 2014, 493, 795–805. [Google Scholar] [CrossRef]
- Salazar-Ruiz, E.; Ordieres, J.B.; Vergara, E.P.; Capuz-Rizo, S.F. Development and comparative analysis of tropospheric ozone forecasting models using linear and artificial intelligence-based models in Mexicali, Baja California (Mexico) and Calexico, California (US). Environ. Model. Softw. 2008, 23, 1056–1069. [Google Scholar] [CrossRef]
- Biancofiore, F.; Verdecchia, M.; Carlo, P.D.; Tomassetti, B.; Aruffo, E.; Busilacchio, M.; Bianco, S.; Tommaso, S.D.; Colangeli, C. Analysis of surface ozone using a recurrent neural network. Sci. Total Environ. 2015, 514, 379–387. [Google Scholar] [CrossRef]
- Csepe, Z.; Makra, L.; Voukantsis, D.; Matyasovszky, I.; Tusnady, G.; Karatzas, K.; Thibaudon, M. Predicting daily ragweed pollen concentrations using computational intelligence techniques over two heavily polluted areas in Europe. Sci. Total Environ. 2014, 476–477, 542–552. [Google Scholar] [CrossRef]
- Arjun, K.S.; Aneesh, K. Modelling studies by application of artificial neural network using Matlab. J. Eng. Sci. Technol. 2015, 10, 1477–1486. [Google Scholar]
- Sun, G.; Hoff, S.J.; Zelle, B.C.; Nelson, M.A. Development and comparison backpropagation and generalized regression neural network models to predict diurnal and seasonal gas and PM10 concentrations and emissions from swine buildings. Am. Soc. Agric. Biol. Eng. 2008, 51, 685–694. [Google Scholar] [CrossRef]
- Fletcher, D.; Goss, E. Forecasting with neural networks: An application using bankruptcy data. Inf. Manag. 1993, 24, 159–167. [Google Scholar] [CrossRef]
- Voukantsis, D.; Karatzas, K.; Kukkonen, J.; Rasanen, T.; Karppinen, A.; Kolehmainen, M. Intercomparison of air quality data using principal component analysis, and forecasting of PM10 and PM2.5 concentrations using artificial neural networks, in Thessalloniki and Helsinki. Sci. Total Environ. 2011, 409, 1266–1276. [Google Scholar] [CrossRef] [PubMed]
- May, D.B.; Sivakumar, M. Prediction of urban storm water quality using artificial neural networks. Environ. Model. Softw. 2009, 24, 296–302. [Google Scholar] [CrossRef]
- Demirel, M.C.; Venancio, A.; Kahya, E. Flow forecast by SWAT model and ANN in Pracana basin, Portugal. Adv. Eng. Softw. 2009, 40, 467–473. [Google Scholar] [CrossRef]
- Ul-Saufie, A.Z.; Yahaya, A.S.; Ramli, N.A.; Rosaida, N.; Hamid, H.A. Future daily PM10 concentrations forecasting by combining regression models and feedforward backpropagation models with principal component analysis (PCA). Atmos. Environ. 2013, 77, 621–630. [Google Scholar] [CrossRef]
- Hossain, M.M.; Neaupane, K.; Tripathi, N.K.; Piantanakulchai, M. Forecasting of groundwater arsenic contamination using geographic information system and artificial neural network. EnvironmentAsia 2013, 6, 38–44. [Google Scholar]
- Singh, K.P.; Gupta, S.; Kumar, A.; Shukla, S.P. Linear and nonlinear modeling approaches for urban air quality forecasting. Sci. Total Environ. 2012, 426, 244–255. [Google Scholar] [CrossRef]
- Mathworks. MATLAB and Statistics Toolbox Release 2015b; The MathWorks, Inc.: Natick, MA, USA, 2015. [Google Scholar]
- Wang, W.; Xu, Z.; Lu, J.W. Three improved neural network models for air quality forecasting. Eng. Comput. 2003, 20, 192–210. [Google Scholar] [CrossRef]
- Broomhead, D.; Lowe, D. Multivariable functional interpolation and adaptive networks. Complex Syst. 1988, 2, 321–355. [Google Scholar]
- Daliakopouls, I.N.; Coulibaly, P.; Tsanis, I.K. Groundwater level forecasting using artificial neural networks. J. Hydrol. 2005, 309, 229–240. [Google Scholar] [CrossRef]
- Yu, L.; Lai, K.K.; Wang, S. Multistage RBF neural network ensemble learning for exchange rates forecasting. Neurocomputing 2008, 71, 3295–3302. [Google Scholar] [CrossRef]
- Turnbull, D.; Elkan, C. Fast recognition of musical genres using RBF networks. IEEE Trans. Knowl. Data Eng. 2005, 17, 580–584. [Google Scholar] [CrossRef]
- Abdullah, S.; Ismail, M.; Ghazali, N.A.; Ahmed, A.N. Forecasting particulate matter (PM10) concentration: A radial basis function neural network approach. AIP Conf. Proc. 2018, 2020, 020043-1–020043-6. [Google Scholar] [CrossRef]
- Foody, G.M. Supervised image classification by MLP and RBF neural networks with and without an exhaustively defined set of classes. Int. J. Remote Sens. 2004, 25, 3091–3104. [Google Scholar] [CrossRef]
- Ahmat, H.; Yahaya, A.S.; Ramli, N.A. The Malaysia PM10 analysis using extreme value. J. Eng. Sci. Technol. 2015, 10, 1560–1574. [Google Scholar]
- Ismail, M.; Abdullah, S.; Yuen, F.S. Study on environmental noise pollution at three different primary schools in Kuala Terengganu, Terengganu state. J. Sustain. Sci. Manag. 2015, 10, 103–111. [Google Scholar]
- Elabayoumi, M.; Ramli, N.A.; Yusof, N.F.F.M. Development and comparison of regression models and feedforward backpropagation neural network models to predict seasonal indoor PM2.5–10 and PM2.5 concentrations in naturally ventilated schools. Atmos. Pollut. Res. 2015, 6, 1013–1023. [Google Scholar] [CrossRef]
- Zhang, J.; Ding, W. Prediction of Air Pollutants Concentration Based on an Extreme Learning Machine: The Case of Hong Kong. Int J. Environ. Res. Public Health 2017, 14, 114. [Google Scholar] [CrossRef]
- Ceylan, Z.; Bulkan, S. Forecasting PM10 levels using ANN and MLR: A case study for Sakarya City. Glob. Nest J. 2018, 20, 281–290. [Google Scholar] [CrossRef]
- Ordieres, J.B.; Vergara, E.P.; Capuz, R.S.; Salazar, R.E. Neural network prediction model for fine particulate matter (PM2.5) on the US–Mexico border in El Paso (Texas) and Ciudad Juárez (Chihuahua). Environ. Model. Softw. 2005, 20, 547–559. [Google Scholar] [CrossRef]
- Chen, H.; Kim, A.S. Forecasting of permeate flux decline in cross flow membrane filtration of colloidal suspension: A radial basis function neural network approach. Desalination 2006, 192, 415–428. [Google Scholar] [CrossRef]
- Xing, J.J.; Luo, R.M.; Guo, H.L.; Li, Y.Q.; Fu, H.Y.; Yang, T.M.; Zhou, Y.P. Radial basis function network-based transformation for nonlinear partial least-squares as optimized by particle swarm optimization: Application to QSAR studies. Chemom. Intell. Lab. Syst. 2014, 130, 37–44. [Google Scholar] [CrossRef]
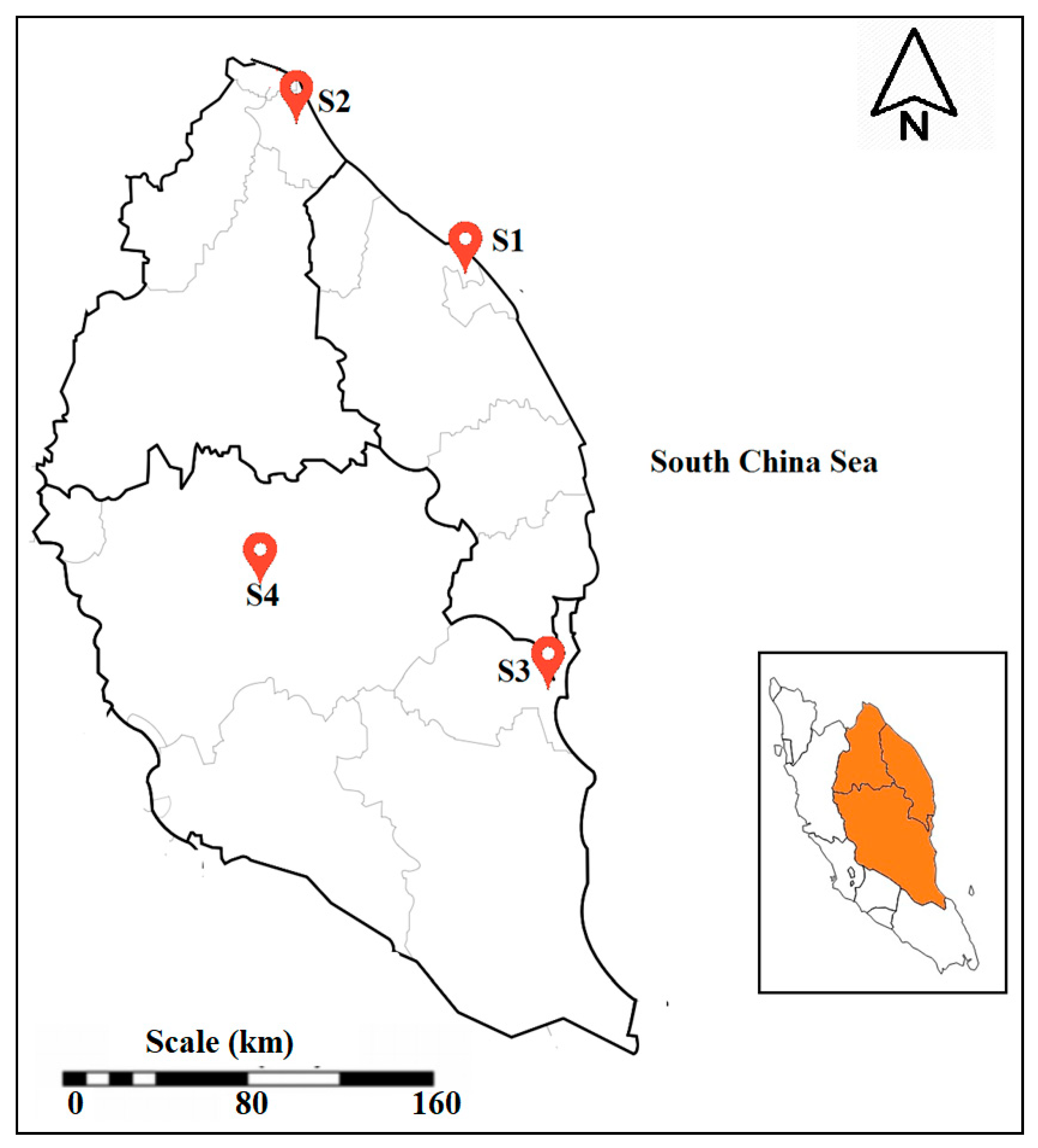
| Site | Station ID | Location | Classification | Latitude, Longitude |
|---|---|---|---|---|
| S1 | CA0034 | Chabang Tiga Primary School, Kuala Terengganu | Urban | 5°18.455′ N 103°07.213′ E |
| S2 | CA0022 | Tanjong Chat Secondary School, Kota Bharu, Kelantan | Urban | 6°08.443′ N 102°14.955′ E |
| S3 | CA0014 | Indera Mahkota Primary School, Kuantan, Pahang | Sub-Urban | 3°49.138′ N 103° 17.817′ E |
| S4 | CA0007 | Batu Embun Meteorological Station, Jerantut, Pahang | Rural | 3°58.238′ N 102°20.863′ E |
| Site | S1 | S2 | S3 | S4 |
|---|---|---|---|---|
| PM10 (µg/m3) | 51.72 ± 15.09 | 40.74 ± 14.32 | 34.08 ± 12.12 | 37.34 ± 14.79 |
| Wind Speed (m/s) | 1.50 ± 0.42 | 1.49 ± 0.47 | 1.81 ± 0.45 | 1.01 ± 0.19 |
| Temperature (°C) | 27.33 ± 1.45 | 27.00 ± 1.38 | 26.94 ± 1.51 | 26.45 ± 1.54 |
| Relative Humidity (%) | 81.14 ± 5.33 | 79.36 ± 5.68 | 83.94 ± 6.69 | 82.83 ± 5.16 |
| Rainfall Amount (mm) | 7.52 ± 21.23 | 7.48 ± 20.68 | 8.88 ± 23.72 | 5.93 ± 13.41 |
| Atmospheric Pressure (hPa) | 1010.18 ± 1.74 | 1010.01 ± 1.72 | 1009.86 ± 1.54 | 1009.97 ± 1.54 |
| CO (ppm) | 0.45 ± 0.15 | 0.65 ± 0.24 | 0.36 ± 0.14 | 0.30 ± 0.13 |
| SO2 (ppm) | 0.00093 ± 0.00075 | 0.00099 ± 0.0011 | 0.0013 ± 0.00076 | 0.00080 ± 0.00068 |
| NO2 (ppm) | 0.0055 ± 0.0016 | 0.0072 ± 0.0027 | 0.0059 ± 0.0020 | 0.0020 ± 0.00088 |
| Solar Radiation (MJ/m2) | Not Available | 18.37 ± 5.54 | 16.80 ± 4.86 | Not Available |
| Site | Model | R2 | Range of VIF | D-W Statistics |
|---|---|---|---|---|
| S1 | PM10,t+1 concentration = 0.037 + 0.709(PM10) − 0.231(Rainfall Amount) + 0.044(MSLP) + 0.101(NO2) + 0.039(Wind Speed) − 0.023(SO2) − 0.027(CO) | 0.594 | 1.077–1.921 | 2.007 |
| S2 | PM10,t+1 concentration = 0.116 + 0.763(PM10) − 0.148(Rainfall Amount) − 0.030(CO) + 0.034 (Ambient Temperature) − 0.040 (Relative Humidity) − 0.027(SO2) | 0.601 | 1.116–1.513 | 2.021 |
| S3 | PM10,t+1 concentration = 0.016 + 0.805(PM10) + 0.020 (Global radiation) + 0.032(NO2) | 0.680 | 1.054–1.205 | 2.131 |
| S4 | PM10,t+1 concentration = 0.044 + 0.820(PM10) − 0.086(Rainfall Amount) − 0.025(Wind Speed) − 0.009(SO2) − 0.024(CO) + 0.019(NO2) | 0.706 | 1.012–1.926 | 2.150 |
| Site | Number of Inputs | Range of Neurons |
|---|---|---|
| 1 | 9 | 1–19 |
| 2 | 10 | 1–21 |
| 3 | 10 | 1–21 |
| 4 | 9 | 1–19 |
| Activation Function for Hidden Layer | Activation Function for Output Layer | Optimum Number of Neurons in Hidden Layer | RMSE (µg/m3) | R2 |
|---|---|---|---|---|
| (a) Site 1 | ||||
| Logsig | Purelin | 18 | 8.49 | 0.691 |
| Logsig | Tansig | 17 | 8.58 | 0.684 |
| Tansig | Purelin | 17 | 8.54 | 0.687 |
| Tansig | Logsig | 18 | 8.57 | 0.685 |
| Logsig | Logsig | 17 | 8.60 | 0.683 |
| Tansig | Tansig | 19 | 8.51 | 0.690 |
| (b) Site 2 | ||||
| Logsig | Purelin | 20 | 9.44 | 0.722 |
| Logsig | Tansig | 21 | 9.45 | 0.720 |
| Tansig | Purelin | 21 | 9.48 | 0.718 |
| Tansig | Logsig | 20 | 9.49 | 0.716 |
| Logsig | Logsig | 19 | 9.50 | 0.715 |
| Tansig | Tansig | 20 | 9.45 | 0.720 |
| (c) Site 3 | ||||
| Logsig | Purelin | 19 | 7.60 | 0.766 |
| Logsig | Tansig | 21 | 7.63 | 0.761 |
| Tansig | Purelin | 17 | 7.59 | 0.767 |
| Tansig | Logsig | 21 | 7.62 | 0.761 |
| Logsig | Logsig | 17 | 7.64 | 0.760 |
| Tansig | Tansig | 20 | 7.60 | 0.765 |
| (d) Site 4 | ||||
| Logsig | Purelin | 18 | 9.57 | 0.794 |
| Logsig | Tansig | 15 | 9.59 | 0.792 |
| Tansig | Purelin | 19 | 9.59 | 0.792 |
| Tansig | Logsig | 19 | 9.65 | 0.786 |
| Logsig | Logsig | 18 | 9.61 | 0.790 |
| Tansig | Tansig | 17 | 9.62 | 0.790 |
| Spread Number | Number of Neurons | RMSE (µg/m3) | R2 |
|---|---|---|---|
| (a) Site 1 | |||
| 0.1 | 1736 | 4.08 | 0.928 |
| 0.2 | 2129 | 4.09 | 0.928 |
| 0.3 | 2336 | 4.09 | 0.928 |
| 0.4 | 2414 | 4.09 | 0.928 |
| 0.5 | 2447 | 4.09 | 0.928 |
| 0.6 | 2473 | 4.08 | 0.928 |
| 0.7 | 2519 | 4.09 | 0.928 |
| 0.8 | 2500 | 4.09 | 0.928 |
| 0.9 | 2695 | 4.09 | 0.928 |
| 1 | 3620 | 4.08 | 0.929 |
| (b) Site 2 | |||
| 0.1 | 1705 | 7.11 | 0.920 |
| 0.2 | 1745 | 7.11 | 0.920 |
| 0.3 | 2042 | 7.11 | 0.920 |
| 0.4 | 2171 | 7.11 | 0.920 |
| 0.5 | 2254 | 7.11 | 0.921 |
| 0.6 | 2264 | 7.11 | 0.920 |
| 0.7 | 2306 | 7.11 | 0.920 |
| 0.8 | 2331 | 7.11 | 0.920 |
| 0.9 | 2334 | 7.11 | 0.920 |
| 1 | 2332 | 7.11 | 0.920 |
| (c) Site 3 | |||
| 0.1 | 1181 | 6.56 | 0.893 |
| 0.2 | 1378 | 6.57 | 0.892 |
| 0.3 | 1587 | 6.57 | 0.892 |
| 0.4 | 1696 | 6.57 | 0.892 |
| 0.5 | 1753 | 6.57 | 0.892 |
| 0.6 | 1778 | 6.57 | 0.892 |
| 0.7 | 1826 | 6.57 | 0.892 |
| 0.8 | 1835 | 6.57 | 0.892 |
| 0.9 | 1857 | 6.57 | 0.892 |
| 1 | 1878 | 6.57 | 0.892 |
| (d) Site 4 | |||
| 0.1 | 730 | 9.19 | 0.827 |
| 0.2 | 458 | 9.19 | 0.826 |
| 0.3 | 545 | 9.19 | 0.826 |
| 0.4 | 619 | 9.19 | 0.826 |
| 0.5 | 684 | 9.19 | 0.826 |
| 0.6 | 715 | 9.19 | 0.826 |
| 0.7 | 723 | 9.19 | 0.826 |
| 0.8 | 754 | 9.19 | 0.826 |
| 0.9 | 772 | 9.19 | 0.826 |
| 1 | 764 | 9.19 | 0.826 |
| Site | Method | RMSE (µg/m3) | NAE | R2 | PA | IA |
|---|---|---|---|---|---|---|
| 1 | MLR | 28.0 | 0.499 | 0.569 | 0.546 | 0.543 |
| MLP | 7.42 | 0.120 | 0.811 | 0.810 | 0.946 | |
| RBF | 6.29 | 0.0981 | 0.864 | 0.863 | 0.963 | |
| 2 | MLR | 18.0 | 0.373 | 0.548 | 0.608 | 0.677 |
| MLP | 7.45 | 0.136 | 0.758 | 0.758 | 0.928 | |
| RBF | 5.12 | 0.0896 | 0.885 | 0.885 | 0.969 | |
| 3 | MLR | 11.4 | 0.225 | 0.598 | 0.878 | 0.807 |
| MLP | 8.11 | 0.170 | 0.679 | 0.680 | 0.898 | |
| RBF | 7.95 | 0.149 | 0.692 | 0.693 | 0.902 | |
| 4 | MLR | 10.6 | 0.235 | 0.665 | 0.912 | 0.838 |
| MLP | 6.39 | 0.135 | 0.800 | 0.799 | 0.942 | |
| RBF | 6.37 | 0.143 | 0.801 | 0.802 | 0.943 |
| Source | Country | Pollutants | R2 | Model Type |
|---|---|---|---|---|
| Elbayoumi et al., (2015) [71] | Malaysia | PM10 and PM2.5 | 0.44–0.57 (MLR) 0.65–0.78 (MLP) | MLR, ANN (MLP) |
| Zhang and Ding (2017) [72] | Hong Kong | PM2.5, NO2, NOx, SO2, O3 | 0.50–0.64 (MLR) 0.52–0.67 (ANN) | MLR, ANN (RBF, MLP, ELM) |
| Ceylan and Bulkan (2018) [73] | Turkey | PM10 | 0.32 (MLR) 0.84 (MLP) | MLR, ANN (MLP) |
| Abdullah et al., (2018) [35] | Malaysia | PM10 | 0.53 (MLR) 0.69 (MLP) | MLR, ANN (MLP) |
| Ul-Saufie et al., (2013) [58] | Malaysia | PM10 | 0.62 (MLR) 0.64 (MLP) | MLR, ANN (MLP), PCA |
| Ordieres et al., (2005) [74] | US-Mexico | PM2.5 | 0.40 (MLR) 0.38 (MLP) 0.37 (SMLP) 0.46 (RBF) | MLR, ANN (MLP, SMLP, RBF) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdullah, S.; Ismail, M.; Ahmed, A.N.; Abdullah, A.M. Forecasting Particulate Matter Concentration Using Linear and Non-Linear Approaches for Air Quality Decision Support. Atmosphere 2019, 10, 667. https://doi.org/10.3390/atmos10110667
Abdullah S, Ismail M, Ahmed AN, Abdullah AM. Forecasting Particulate Matter Concentration Using Linear and Non-Linear Approaches for Air Quality Decision Support. Atmosphere. 2019; 10(11):667. https://doi.org/10.3390/atmos10110667
Chicago/Turabian StyleAbdullah, Samsuri, Marzuki Ismail, Ali Najah Ahmed, and Ahmad Makmom Abdullah. 2019. "Forecasting Particulate Matter Concentration Using Linear and Non-Linear Approaches for Air Quality Decision Support" Atmosphere 10, no. 11: 667. https://doi.org/10.3390/atmos10110667
APA StyleAbdullah, S., Ismail, M., Ahmed, A. N., & Abdullah, A. M. (2019). Forecasting Particulate Matter Concentration Using Linear and Non-Linear Approaches for Air Quality Decision Support. Atmosphere, 10(11), 667. https://doi.org/10.3390/atmos10110667






