Automated Recognition of RNA Structure Motifs by Their SHAPE Data Signatures
Abstract
1. Introduction
2. Materials and Methods
2.1. Overview of Structure Profiling Experiments
2.2. Improvements to patteRNA’s Training Routine
2.2.1. Building the Training Set Using Kullback–Leibler Divergence
2.2.2. Determining an Optimal Number of Gaussian Components
2.2.3. Parameter Initialization
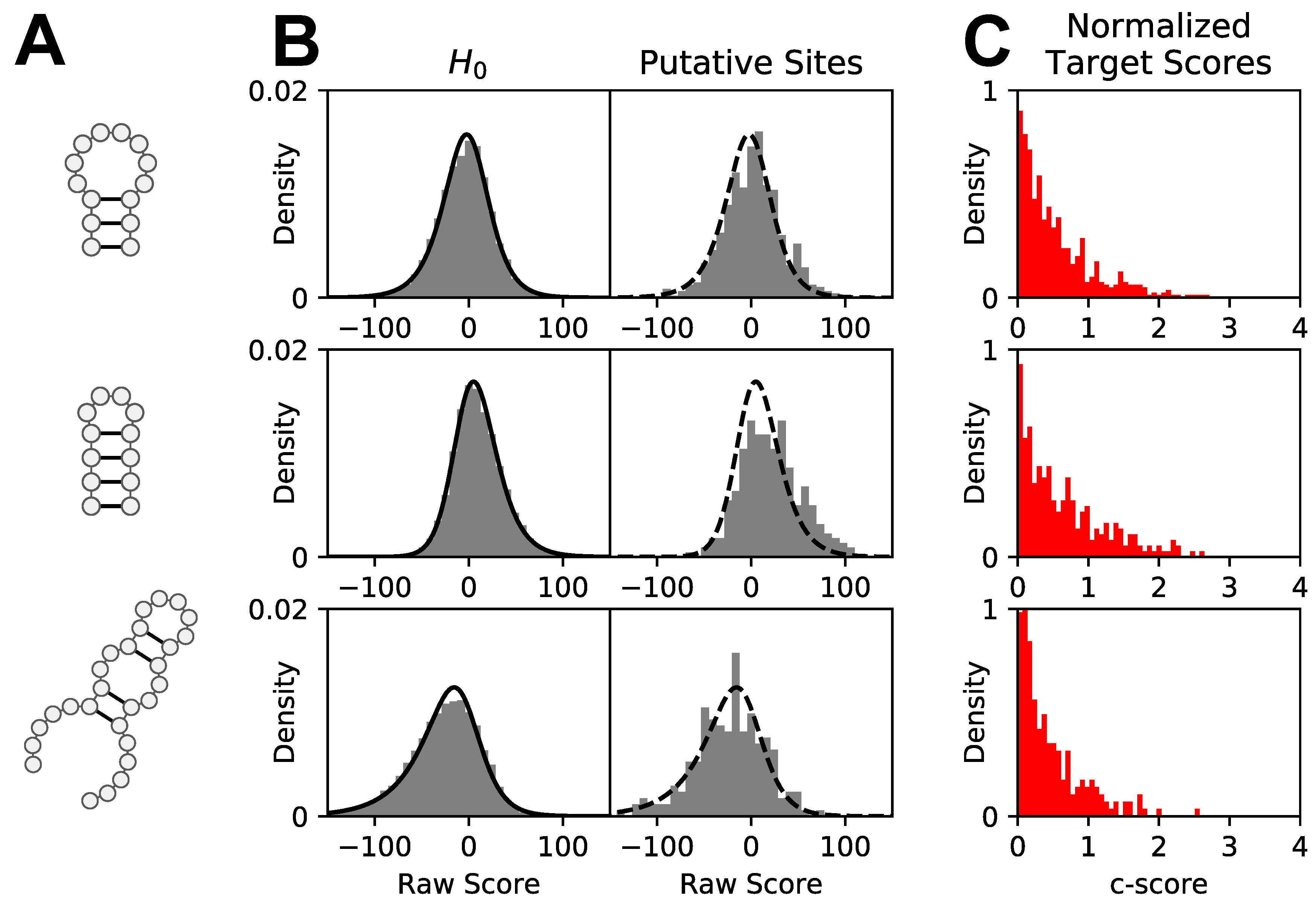
2.3. Computing Raw patteRNA Scores
2.4. Sequence-Based Constraints
2.5. Comparative Motif Scoring
2.6. Benchmarking patteRNA Scores
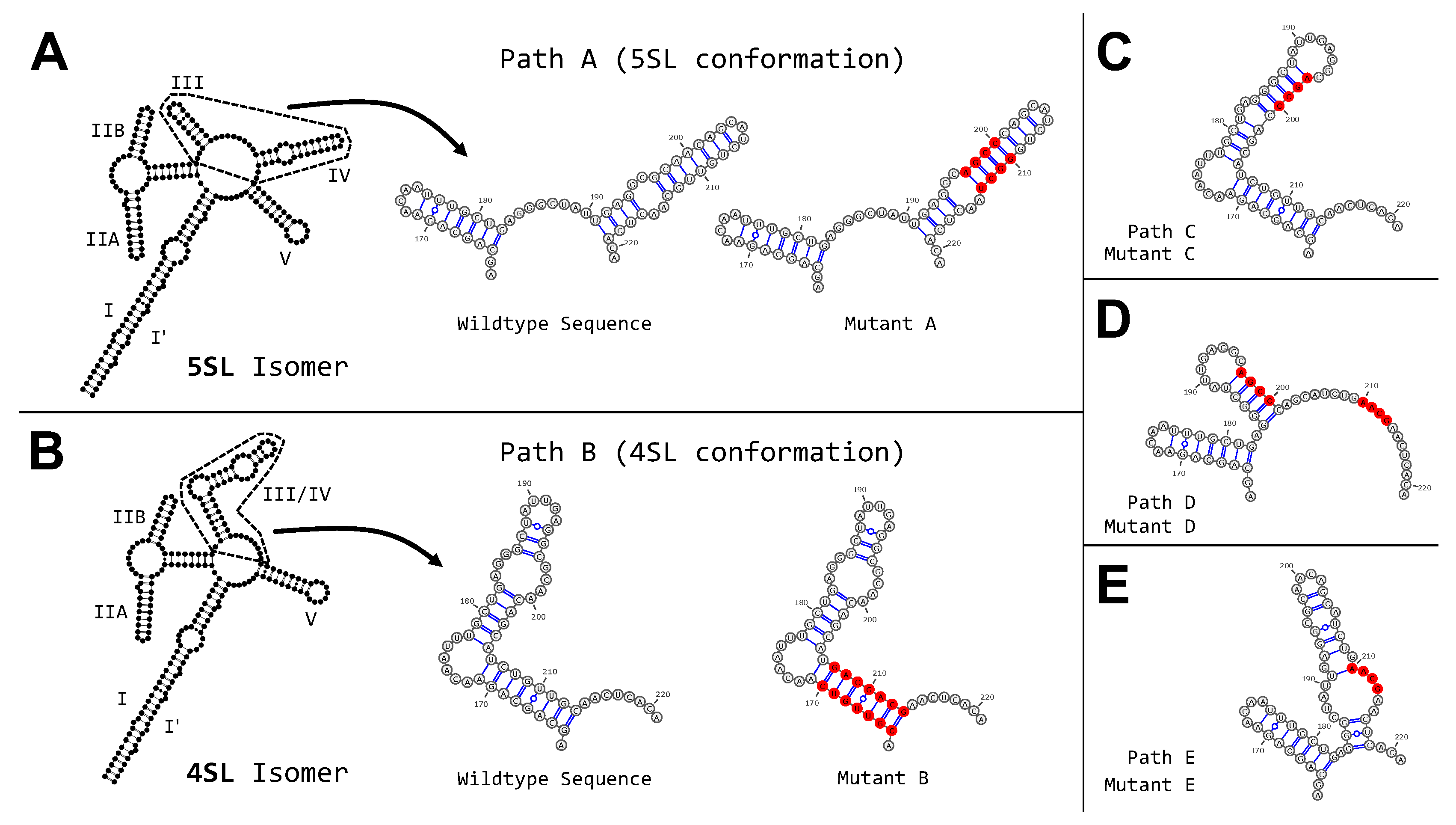
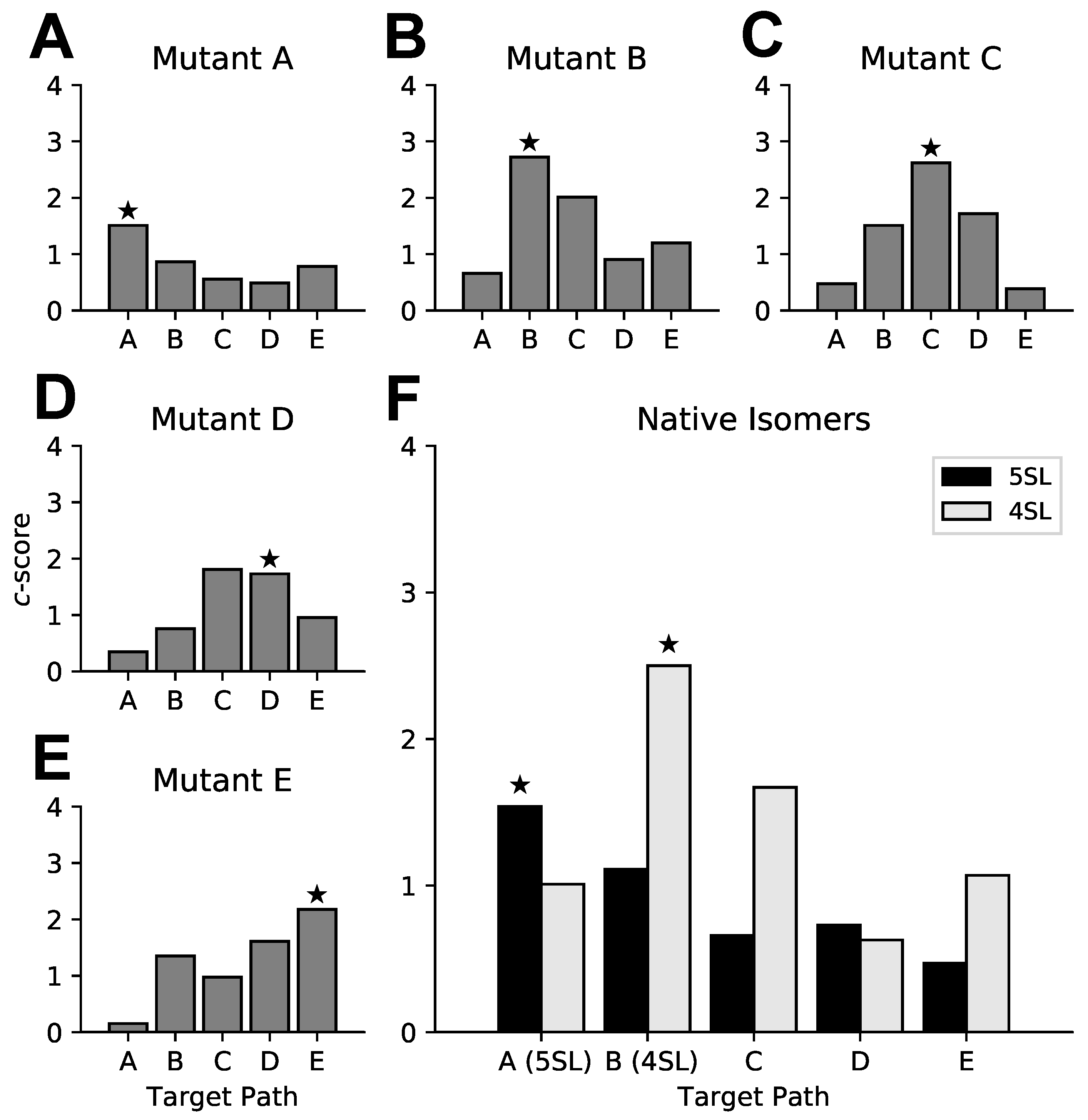
2.7. HIV Rev Response Element Mutant Analysis
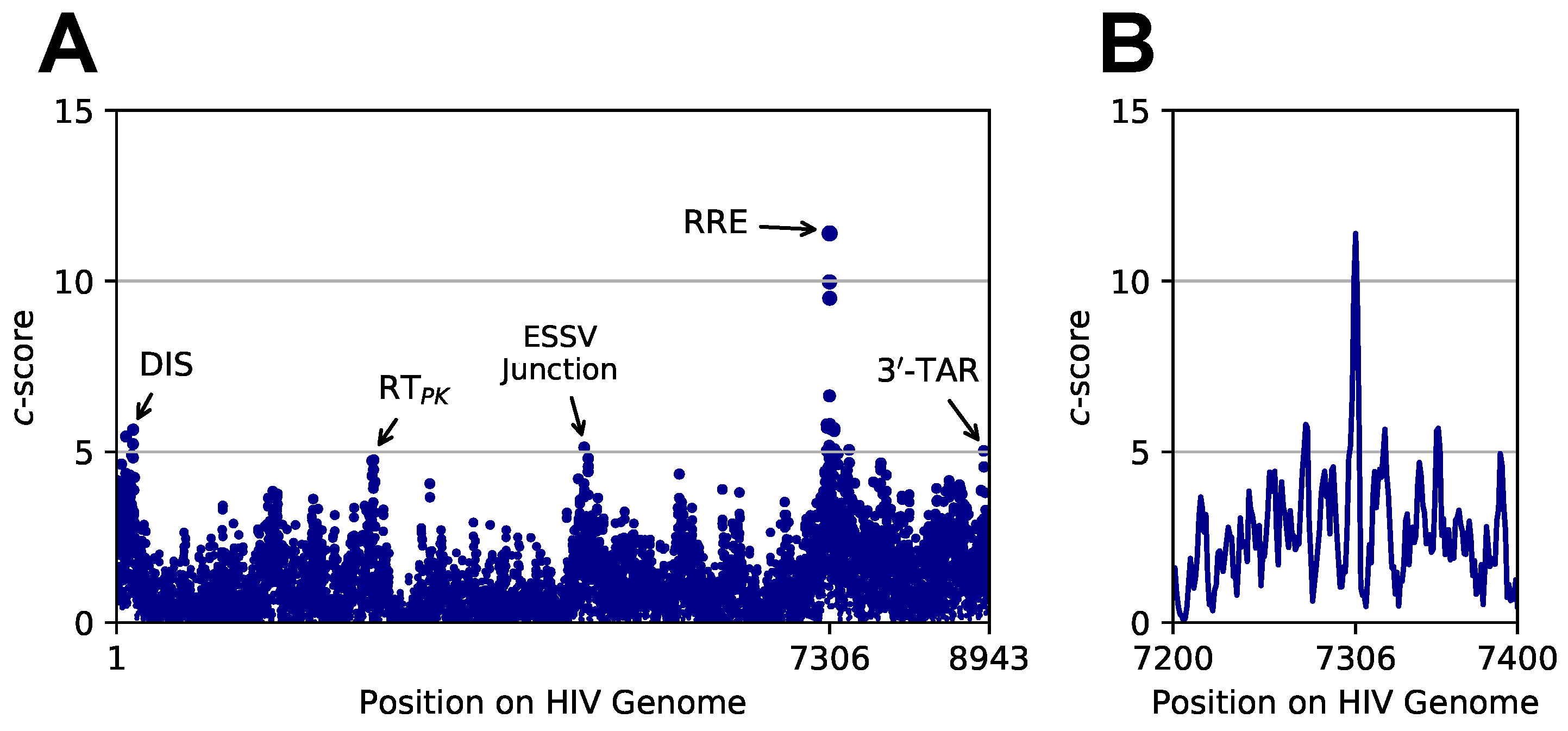
2.8. Searching the HIV Genome for Rev Response Element Motifs
2.9. In Silico SHAPE Mixtures of HIV-1 Structure Variants
3. Results
3.1. Overview of patteRNA Workflow
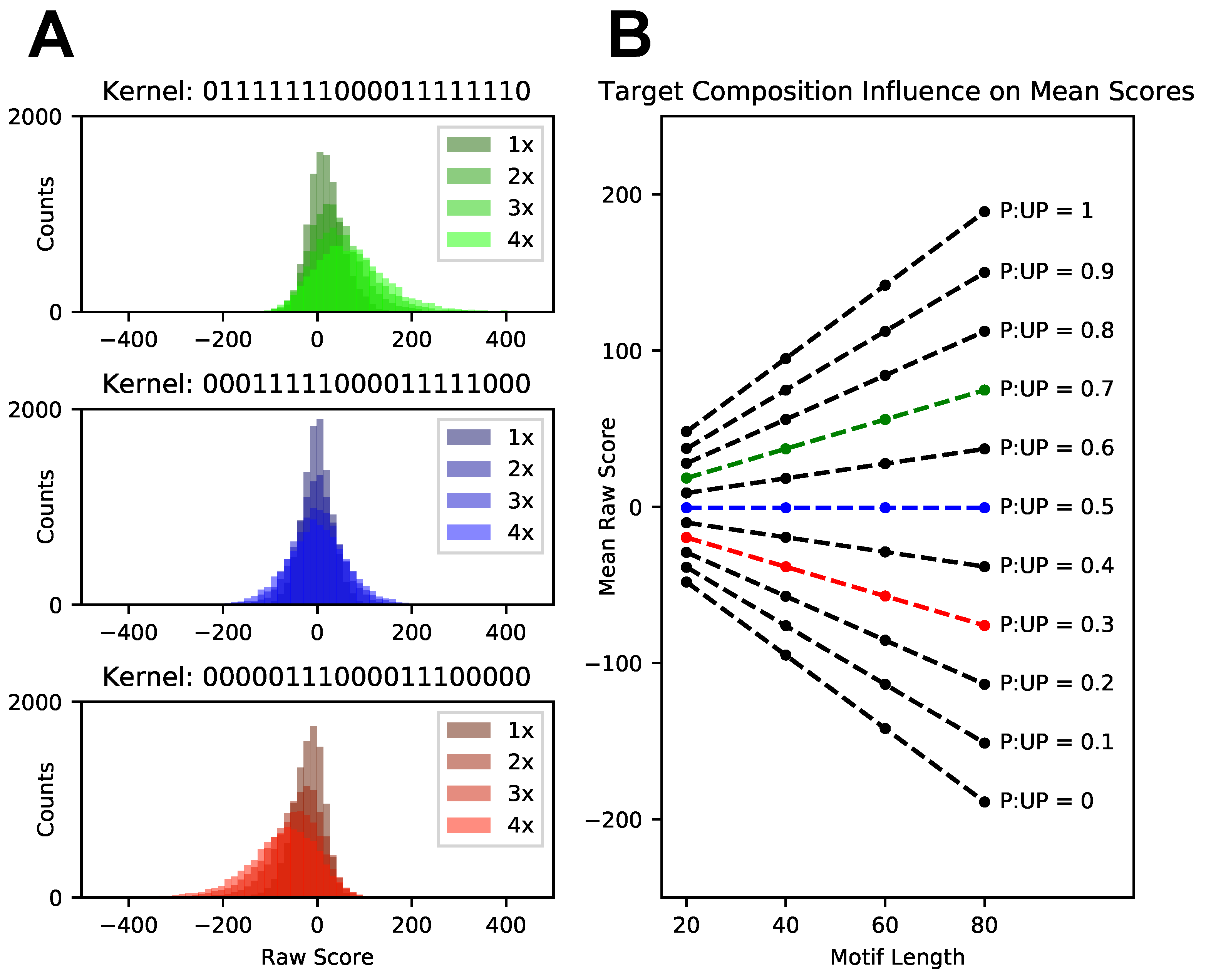
3.2. Score Normalization for Comparative and Integrative Analyses
3.3. Targeted Search of Alternative Motifs in HIV-1
3.4. Automating patteRNA’s Training Routine
4. Discussion
Supplementary Materials
Author Contributions
Acknowledgments
Conflicts of Interest
Appendix A
- Number of Gaussian components per pairing state (K): Auto-detected using Bayesian Information Criterion (BIC)
- Transition probabilities (derived from the Weeks set):
- Initial probability:
- Gaussian means: Based on data percentiles
- Gaussian variances: Equal to the variance of the data
- Gaussian weights:
References
- Eddy, S.R. Non-coding RNA genes and the modern RNA world. Nat. Rev. Genet. 2001, 2, 919–929. [Google Scholar] [CrossRef] [PubMed]
- Higgs, P.G.; Lehman, N. The RNA World: Molecular cooperation at the origins of life. Nat. Rev. Genet. 2015, 16, 7–17. [Google Scholar] [CrossRef] [PubMed]
- Forster, A.C.; Symons, R.H. Self-Cleavage of plus and minus RNAs of a Virusoid and a Structural Model for the Active Sites. Cell 1987, 49, 211–220. [Google Scholar] [CrossRef]
- Gamarnik, A.V.; Andino, R. Switch from translation to RNA replication in a positive-stranded RNA virus. Genes Dev. 1998, 12, 2293–2304. [Google Scholar] [CrossRef] [PubMed]
- Sharp, P.A. The centrality of RNA. Cell 2009, 136, 577–580. [Google Scholar] [CrossRef] [PubMed]
- Mortimer, S.A.; Kidwell, M.A.; Doudna, J.A. Insights into RNA structure and function from genome-wide studies. Nat. Rev. Genet. 2014, 15, 469–479. [Google Scholar] [CrossRef] [PubMed]
- Kwok, C.K. Dawn of the in vivo RNA structurome and interactome. Biochem. Soc. Trans. 2016, 44, 1395–1410. [Google Scholar] [CrossRef] [PubMed]
- Kubota, M.; Tran, C.; Spitale, R.C. Progress and challenges for chemical probing of RNA structure inside living cells. Nat. Chem. Biol. 2015, 11, 933–941. [Google Scholar] [CrossRef] [PubMed]
- Kutchko, K.M.; Laederach, A. Transcending the prediction paradigm: Novel applications of SHAPE to RNA function and evolution. Wiley Interdiscip. Rev. RNA 2016, 8, e1374. [Google Scholar] [CrossRef] [PubMed]
- Zubradt, M.; Gupta, P.; Persad, S.; Lambowitz, A.M.; Weissman, J.S.; Rouskin, S. DMS-MaPseq for genome-wide or targeted RNA structure probing in vivo. Nat. Methods 2017, 14, 75–82. [Google Scholar] [CrossRef] [PubMed]
- Chan, D.; Feng, C.; Spitale, R.C. Measuring RNA structure transcriptome-wide with icSHAPE. Methods 2017, 120, 85–90. [Google Scholar] [CrossRef] [PubMed]
- Choudhary, K.; Deng, F.; Aviran, S. Comparative and integrative analysis of RNA structural profiling data: Current practices and emerging questions. Quant. Biol. 2017, 5, 3–24. [Google Scholar] [CrossRef] [PubMed]
- Breaker, R.R. Riboswitches and the RNA World. Cold Spring Harb. Perspect. Biol. 2010, 4, a003566. [Google Scholar] [CrossRef] [PubMed]
- McCown, P.J.; Corbino, K.A.; Stav, S.; Sherlock, M.E.; Breaker, R.R. Riboswitch diversity and distribution. RNA 2017, 23, 995–1011. [Google Scholar] [CrossRef] [PubMed]
- Weinberg, Z.; Nelson, J.W.; Lünse, C.E.; Sherlock, M.E.; Breaker, R.R. Bioinformatic analysis of riboswitch structures uncovers variant classes with altered ligand specificity. Proc. Natl. Acad. Sci. USA 2017, 114, E2077–E2085. [Google Scholar] [CrossRef] [PubMed]
- Hallberg, Z.F.; Su, Y.; Kitto, R.Z.; Hammond, M.C. Engineering and in vivo applications of riboswitches. Ann. Rev. Biochem. 2017, 86, 515–539. [Google Scholar] [CrossRef] [PubMed]
- Zhao, B.; Guffy, S.L.; Williams, B.; Zhang, Q. An excited state underlies gene regulation of a transcriptional riboswitch. Nat. Chem. Biol. 2017, 13, 968–974. [Google Scholar] [CrossRef] [PubMed]
- Ignatova, Z.; Narberhaus, F. Systematic probing of the bacterial RNA structurome to reveal new functions. Curr. Opin. Microbiol. 2017, 36, 14–19. [Google Scholar] [CrossRef] [PubMed]
- Vasilyev, N.; Polonskaia, A.; Darnell, J.C.; Darnell, R.B.; Patel, D.J.; Serganov, A. Crystal structure reveals specific recognition of a G-quadruplex RNA by a β-turn in the RGG motif of FMRP. Proc. Natl. Acad. Sci. USA 2015, 112, E5391–E5400. [Google Scholar] [CrossRef] [PubMed]
- Kwok, C.K.; Marsico, G.; Sahakyan, A.B.; Chambers, V.S.; Balasubramanian, S. rG4-seq reveals widespread formation of G-quadruplex structures in the human transcriptome. Nat. Methods 2016, 13, 841–844. [Google Scholar] [CrossRef] [PubMed]
- Guo, J.U.; Bartel, D.P. RNA G-quadruplexes are globally unfolded in eukaryotic cells and depleted in bacteria. Science 2016, 353, aaf5371. [Google Scholar] [CrossRef] [PubMed]
- Ruggiero, E.; Richter, S.N. G-quadruplexes and G-quadruplex ligands: Targets and tools in antiviral therapy. Nucleic Acids Res. 2018, 46, 3270–3283. [Google Scholar] [CrossRef] [PubMed]
- Xue, Z.; Hennelly, S.; Doyle, B.; Gulati, A.A.; Novikova, I.V.; Sanbonmatsu, K.Y.; Boyer, L.A. A G-Rich motif in the lncRNA braveheart interacts with a zinc-finger transcription factor to specify the cardiovascular lineage. Mol. Cell 2016, 64, 37–50. [Google Scholar] [CrossRef] [PubMed]
- Weinberg, Z.; Lünse, C.E.; Corbino, K.A.; Ames, T.D.; Nelson, J.W.; Roth, A.; Perkins, K.R.; Sherlock, M.E.; Breaker, R.R. Detection of 224 candidate structured RNAs by comparative analysis of specific subsets of intergenic regions. Nucleic Acids Res. 2017. [Google Scholar] [CrossRef] [PubMed]
- Helm, M.; Motorin, Y. Detecting RNA modifications in the epitranscriptome: Predict and validate. Nat. Rev. Genet. 2017, 18, 275–291. [Google Scholar] [CrossRef] [PubMed]
- Lewis, C.J.; Pan, T.; Kalsotra, A. RNA modifications and structures cooperate to guide RNA-protein interactions. Nat. Rev. Mol. Cell Biol. 2017, 18, 202–210. [Google Scholar] [CrossRef] [PubMed]
- Sloma, M.F.; Mathews, D.H. Improving RNA Secondary Structure Prediction with Structure Mapping Data. In Methods in Enzymology; Chen, S.J., Burke-Aguero, D.H., Eds.; Elsevier: Waltham, MA, USA, 2015; Volume 553, pp. 91–114. [Google Scholar]
- Lorenz, R.; Wolfinger, M.T.; Tanzer, A.; Hofacker, I.L. Predicting RNA secondary structures from sequence and probing data. Methods 2016, 103, 86–98. [Google Scholar] [CrossRef] [PubMed]
- Markham, N.R.; Zuker, M. UNAFold. In Bioinformatics: Structure, Function and Applications; Keith, J.M., Ed.; Humana Press: Totowa, NJ, USA, 2008; pp. 3–31. [Google Scholar]
- Reuter, J.S.; Mathews, D.H. RNAstructure: Software for RNA secondary structure prediction and analysis. BMC Bioinform. 2010, 11, 129. [Google Scholar] [CrossRef] [PubMed]
- Lorenz, R.; Bernhart, S.H.; Höner Zu Siederdissen, C.; Tafer, H.; Flamm, C.; Stadler, P.F.; Hofacker, I.L. ViennaRNA Package 2.0. Algorithm. Mol. Biol. 2011, 6, 26. [Google Scholar] [CrossRef] [PubMed]
- Ledda, M.; Aviran, S. PATTERNA: Transcriptome-wide search for functional RNA elements via structural data signatures. Genome Biol. 2018, 19, 28. [Google Scholar] [CrossRef] [PubMed]
- Gardner, P.P.; Giegerich, R. A comprehensive comparison of comparative RNA structure prediction approaches. BMC Bioinform. 2004, 5, 140. [Google Scholar] [CrossRef] [PubMed]
- Rouskin, S.; Zubradt, M.; Washietl, S.; Kellis, M.; Weissman, J.S. Genome-wide probing of RNA structure reveals active unfolding of mRNA structures in vivo. Nature 2014, 505, 701–705. [Google Scholar] [CrossRef] [PubMed]
- Watters, K.E.; Strobel, E.J.; Yu, A.M.; Lis, J.T.; Lucks, J.B. Cotranscriptional folding of a riboswitch at nucleotide resolution. Nat. Struct. Mol. Biol. 2016, 23, 1124–1131. [Google Scholar] [CrossRef] [PubMed]
- Incarnato, D.; Morandi, E.; Anselmi, F.; Simon, L.M.; Basile, G.; Oliviero, S. In vivo probing of nascent RNA structures reveals principles of cotranscriptional folding. Nucleic Acids Res. 2017. [Google Scholar] [CrossRef] [PubMed]
- Wan, Y.; Qu, K.; Zhang, Q.C.; Flynn, R.A.; Manor, O.; Ouyang, Z.; Zhang, J.; Spitale, R.C.; Snyder, M.P.; Segal, E.; et al. Landscape and variation of RNA secondary structure across the human transcriptome. Nature 2014, 505, 706–709. [Google Scholar] [CrossRef] [PubMed]
- Eddy, S.R. Computational analysis of conserved RNA secondary structure in transcriptomes and genomes. Ann. Rev. Biophys. 2014, 43, 433–456. [Google Scholar] [CrossRef] [PubMed]
- Smola, M.J.; Christy, T.W.; Inoue, K.; Nicholson, C.O.; Friedersdorf, M.; Keene, J.D.; Lee, D.M.; Calabrese, J.M.; Weeks, K.M. SHAPE reveals transcript-wide interactions, complex structural domains, and protein interactions across the Xist lncRNA in living cells. Proc. Natl. Acad. Sci. USA 2016, 113, 10322–10327. [Google Scholar] [CrossRef] [PubMed]
- Sükösd, Z.; Swenson, M.S.; Kjems, J.; Heitsch, C.E. Evaluating the accuracy of SHAPE-directed RNA secondary structure predictions. Nucleic Acids Res. 2013, 41, 2807–2816. [Google Scholar] [CrossRef] [PubMed]
- Deng, F.; Ledda, M.; Vaziri, S.; Aviran, S. Data-directed RNA secondary structure prediction using probabilistic modeling. RNA 2016, 22, 1109–1119. [Google Scholar] [CrossRef] [PubMed]
- Rabiner, L. A tutorial on hidden Markov models and selected applications in speech recognition. Proc. IEEE 1989, 77, 257–286. [Google Scholar] [CrossRef]
- Weeks, K.M. Advances in RNA structure analysis by chemical probing. Curr. Opin. Struct. Biol. 2010, 20, 295–304. [Google Scholar] [CrossRef] [PubMed]
- Spitale, R.C.; Crisalli, P.; Flynn, R.A.; Torre, E.A.; Kool, E.T.; Chang, H.Y. RNA SHAPE analysis in living cells. Nat. Chem. Biol. 2013, 9, 18–20. [Google Scholar] [CrossRef] [PubMed]
- Aviran, S.; Trapnell, C.; Lucks, J.B.; Mortimer, S.A.; Luo, S.; Schroth, G.P.; Doudna, J.A.; Arkin, A.P.; Pachter, L. Modeling and automation of sequencing-based characterization of RNA structure. Proc. Natl. Acad. Sci. USA 2011, 108, 11069–11074. [Google Scholar] [CrossRef] [PubMed]
- Aviran, S.; Lucks, J.B.; Pachter, L. RNA structure characterization from chemical mapping experiments. In Proceedings of the 2011 49th Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 28–30 September 2011; pp. 1743–1750. [Google Scholar]
- Siegfried, N.A.; Busan, S.; Rice, G.M.; Nelson, J.A.E.; Weeks, K.M. RNA motif discovery by SHAPE and mutational profiling (SHAPE-MaP). Nat. Methods 2014, 11, 959–965. [Google Scholar] [CrossRef] [PubMed]
- Tang, Y.; Bouvier, E.; Kwok, C.K.; Ding, Y.; Nekrutenko, A.; Bevilacqua, P.C.; Assmann, S.M. StructureFold: Genome-wide RNA secondary structure mapping and reconstruction in vivo. Bioinformatics 2015, 31, 2668–2675. [Google Scholar] [CrossRef] [PubMed]
- Selega, A.; Sirocchi, C.; Iosub, I.; Granneman, S.; Sanguinetti, G. Robust statistical modeling improves sensitivity of high-throughput RNA structure probing experiments. Nat. Methods 2017, 14, 83–89. [Google Scholar] [CrossRef]
- Li, B.; Tambe, A.; Aviran, S.; Pachter, L. PROBer provides a general toolkit for analyzing sequencing-based toeprinting assays. Cell Syst. 2017, 4, 568–574. [Google Scholar] [CrossRef] [PubMed]
- Busan, S.; Weeks, K.M. Accurate detection of chemical modifications in RNA by mutational profiling (MaP) with ShapeMapper 2. RNA 2018, 24, 143–148. [Google Scholar] [CrossRef] [PubMed]
- Oliphant, T.E. Python for scientific computing. Comput. Sci. Eng. 2007, 9, 10–20. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On Information and Sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the Dimension of a Model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Sherpa, C.; Rausch, J.W.; Le Grice, S.F.; Hammarskjold, M.L.; Rekosh, D. The HIV-1 Rev response element (RRE) adopts alternative conformations that promote different rates of virus replication. Nucleic Acids Res. 2015, 43, 4676–4686. [Google Scholar] [CrossRef] [PubMed]
- Watts, J.M.; Dang, K.K.; Gorelick, R.J.; Leonard, C.W.; Bess, J.W., Jr.; Swanstrom, R.; Burch, C.L.; Weeks, K.M. Architecture and secondary structure of an entire HIV-1 RNA genome. Nature 2009, 460, 711. [Google Scholar] [CrossRef] [PubMed]
- Homan, P.J.; Favorov, O.V.; Lavender, C.A.; Kursun, O.; Ge, X.; Busan, S.; Dokholyan, N.V.; Weeks, K.M. Single-molecule correlated chemical probing of RNA. Proc. Natl. Acad. Sci. USA 2014, 111, 13858–13863. [Google Scholar] [CrossRef] [PubMed]
- Cordero, P.; Das, R. Rich RNA structure landscapes revealed by mutate-and-map analysis. PLoS Comput. Biol. 2015, 11, e1004473. [Google Scholar] [CrossRef] [PubMed]
- Spasic, A.; Assmann, S.M.; Bevilacqua, P.C.; Mathews, D.H. Modeling RNA secondary structure folding ensembles using SHAPE mapping data. Nucleic Acids Res. 2018, 46, 314–323. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Aviran, S. Statistical modeling of RNA structure profiling experiments enables parsimonious reconstruction of structure landscapes. Nat. Commun. 2018, 9, 606. [Google Scholar] [CrossRef] [PubMed]
- Deigan, K.E.; Li, T.W.; Mathews, D.H.; Weeks, K.M. Accurate SHAPE-directed RNA structure determination. Proc. Natl. Acad. Sci. USA 2008, 106, 97–102. [Google Scholar] [CrossRef] [PubMed]
- Hajdin, C.E.; Bellaousov, S.; Huggins, W.; Leonard, C.W.; Mathews, D.H.; Weeks, K.M. Accurate SHAPE-directed RNA secondary structure modeling, including pseudoknots. Proc. Natl. Acad. Sci. USA 2013, 110, 5498–5503. [Google Scholar] [CrossRef] [PubMed]
- Lavender, C.A.; Lorenz, R.; Zhang, G.; Tamayo, R.; Hofacker, I.L.; Weeks, K.M. Model-Free RNA sequence and structure alignment informed by SHAPE probing reveals a conserved alternate secondary structure for 16S rRNA. PLoS Comput. Biol. 2015, 11, e1004126. [Google Scholar] [CrossRef] [PubMed]
- McCarthy, M.I.; Abecasis, G.R.; Cardon, L.R.; Goldstein, D.B.; Little, J.; Ioannidis, J.P.A.; Hirschhorn, J.N. Genome-wide association studies for complex traits: Consensus, uncertainty and challenges. Nat. Rev. Genet. 2008, 9, 356–369. [Google Scholar] [CrossRef] [PubMed]
- Pollard, V.W.; Malim, M.H. The HIV-1 Rev protein. Ann. Rev. Microbiol. 1998, 52, 491–532. [Google Scholar] [CrossRef] [PubMed]
- Rausch, J.W.; Grice, S.F.J.L. HIV Rev Assembly on the Rev Response Element (RRE): A Structural Perspective. Viruses 2015, 7, 3053–3075. [Google Scholar] [CrossRef] [PubMed]
- DiMattia, M.A.; Watts, N.R.; Stahl, S.J.; Rader, C.; Wingfield, P.T.; Stuart, D.I.; Steven, A.C.; Grimes, J.M. Implications of the HIV-1 Rev dimer structure at 3.2 Å resolution for multimeric binding to the Rev response element. Proc. Natl. Acad. Sci. USA 2010, 107, 5810–5814. [Google Scholar] [CrossRef] [PubMed]
- Jayaraman, B.; Crosby, D.C.; Homer, C.; Ribeiro, I.; Mavor, D.; Frankel, A.D. RNA-directed remodeling of the HIV-1 protein Rev orchestrates assembly of the Rev–Rev response element complex. eLife 2014, 3, e04120. [Google Scholar] [CrossRef] [PubMed]
- Fang, X.; Wang, J.; O’Carroll, I.P.; Mitchell, M.; Zuo, X.; Wang, Y.; Yu, P.; Liu, Y.; Rausch, J.W.; Dyba, M.A.; et al. An unusual topological structure of the HIV-1 rev response element. Cell 2013, 155, 594–605. [Google Scholar] [CrossRef] [PubMed]
- Bai, Y.; Tambe, A.; Zhou, K.; Doudna, J.A. RNA-guided assembly of Rev-RRE nuclear export complexes. eLife 2014, 3, e03656. [Google Scholar] [CrossRef] [PubMed]
- Kjems, J.; Brown, M.; Chang, D.D.; Sharp, P.A. Structural analysis of the interaction between the human immunodeficiency virus Rev protein and the Rev response element. Proc. Natl. Acad. Sci. USA 1991, 88, 683–687. [Google Scholar] [CrossRef] [PubMed]
- Charpentier, B.; Stutz, F.; Rosbash, M. A dynamic in vivo view of the HIV-I Rev-RRE interaction. J. Mol. Biol. 1997, 266, 950–962. [Google Scholar] [CrossRef] [PubMed]
- Legiewicz, M.; Badorrek, C.S.; Turner, K.B.; Fabris, D.; Hamm, T.E.; Rekosh, D.; Hammarskjöld, M.L.; Le Grice, S.F.J. Resistance to RevM10 inhibition reflects a conformational switch in the HIV-1 Rev response element. Proc. Natl. Acad. Sci. USA 2008, 105, 14365–14370. [Google Scholar] [CrossRef] [PubMed]
- Dayton, E.; Powell, D.; Dayton, A. Functional analysis of CAR, the target sequence for the Rev protein of HIV-1. Science 1989, 246, 1625–1629. [Google Scholar] [CrossRef] [PubMed]
- Jayaraman, B.; Mavor, D.; Gross, J.D.; Frankel, A.D. Thermodynamics of Rev–RNA interactions in HIV-1 Rev–RRE assembly. Biochemistry 2015, 54, 6545–6554. [Google Scholar] [CrossRef] [PubMed]
- Mann, D.A.; Mikaélian, I.; Zemmel, R.W.; Green, S.M.; Lowe, A.D.; Kimura, T.; Singh, M.; Jonathan, P.; Butler, G.; Gait, M.J.; et al. A molecular rheostat: Co-operative Rev binding to stem I of the Rev-response element modulates human immunodeficiency virus type-1 late gene Expression. J. Mol. Biol. 1994, 241, 193–207. [Google Scholar] [CrossRef] [PubMed]
- Bilodeau, P.S.; Domsic, J.K.; Mayeda, A.; Krainer, A.R.; Stoltzfus, C.M. RNA Splicing at human immunodeficiency virus type 1 3′ splice site A2 is regulated by binding of hnRNP A/B proteins to an exonic splicing silencer element. J. Virol. 2001, 75, 8487–8497. [Google Scholar] [CrossRef] [PubMed]
- Karn, J.; Stoltzfus, C.M. Transcriptional and posttranscriptional regulation of HIV-1 gene expression. Cold Spring Harb. Perspect. Med. 2012, 2, a006916. [Google Scholar] [CrossRef] [PubMed]
- Choudhary, K.; Shih, N.P.; Deng, F.; Ledda, M.; Li, B.; Aviran, S. Metrics for rapid quality control in RNA structure probing experiments. Bioinformatics 2016, 32, 3575–3583. [Google Scholar] [CrossRef] [PubMed]
- Velagapudi, S.P.; Gallo, S.M.; Disney, M.D. Sequence-based design of bioactive small molecules that target precursor microRNAs. Nat. Chem. Biol. 2014, 10, 291–297. [Google Scholar] [CrossRef] [PubMed]
- Velagapudi, S.P.; Cameron, M.D.; Haga, C.L.; Rosenberg, L.H.; Lafitte, M.; Duckett, D.R.; Phinney, D.G.; Disney, M.D. Design of a small molecule against an oncogenic noncoding RNA. Proc. Natl. Acad. Sci. USA 2016, 113, 5898–5903. [Google Scholar] [CrossRef] [PubMed]
- Abdelsayed, M.M.; Ho, B.T.; Vu, M.M.K.; Polanco, J.; Spitale, R.C.; Lupták, A. Multiplex aptamer discovery through Apta-Seq and its application to ATP aptamers derived from human-genomic SELEX. ACS Chem. Biol. 2017, 12, 2149–2156. [Google Scholar] [CrossRef] [PubMed]
- Nawrocki, E.P.; Kolbe, D.L.; Eddy, S.R. Infernal 1.0: Inference of RNA alignments. Bioinformatics 2009, 25, 1335–1337. [Google Scholar] [CrossRef] [PubMed]
- Nawrocki, E.P.; Eddy, S.R. Infernal 1.1: 100-fold faster RNA homology searches. Bioinformatics 2013, 29, 2933–2935. [Google Scholar] [CrossRef] [PubMed]
- Kwok, C.K.; Ding, Y.; Tang, Y.; Assmann, S.M.; Bevilacqua, P.C. Determination of in vivo RNA structure in low-abundance transcripts. Nat. Commun. 2013, 4, 2971. [Google Scholar] [CrossRef] [PubMed]
- Long, D.; Lee, R.; Williams, P.; Chan, C.Y.; Ambros, V.; Ding, Y. Potent effect of target structure on microRNA function. Nat. Struct. Mol. Biol. 2007, 14, 287–294. [Google Scholar] [CrossRef] [PubMed]
- Watters, K.E.; Choudhary, K.; Aviran, S.; Lucks, J.B.; Perry, K.L.; Thompson, J.R. Probing of RNA structures in a positive sense RNA virus reveals selection pressures for structural elements. Nucleic Acids Res. 2018, 46, 2573–2584. [Google Scholar] [CrossRef] [PubMed]
- Kutchko, K.M.; Madden, E.A.; Morrison, C.; Plante, K.S.; Sanders, W.; Vincent, H.A.; Cruz Cisneros, M.C.; Long, K.M.; Moorman, N.J.; Heise, M.T.; et al. Structural divergence creates new functional features in alphavirus genomes. Nucleic Acids Res. 2018, 46, 3657–3670. [Google Scholar] [CrossRef] [PubMed]
- Radecki, P.; Ledda, M.; Aviran, S. Automated recognition of RNA structure motifs by their SHAPE data signatures [Data set]. Zenodo 2018. [Google Scholar] [CrossRef]
| Dataset | Reagent | Search Target | Top c-Score |
|---|---|---|---|
| Path A (5SL) | 10.6 | ||
| Path B (4SL) | 11.4 | ||
| NMIA | Path C | 11.0 | |
| Path D | 10.6 | ||
| Path E | 11.4 | ||
| Path A (5SL) | 12.2 | ||
| Path B (4SL) | 12.4 | ||
| Siegfried Set | 1M6 | Path C | 11.5 |
| Path D | 12.4 | ||
| Path E | 12.4 | ||
| Path A (5SL) | 11.5 | ||
| Path B (4SL) | 13.0 | ||
| 1M7 | Path C | 12.2 | |
| Path D | 11.8 | ||
| Path E | 11.9 | ||
| Path A (5SL) | 12.9 | ||
| Path B (4SL) | 13.2 | ||
| Watts Set | 1M7 | Path C | 12.7 |
| Path D | 11.9 | ||
| Path E | 12.6 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Radecki, P.; Ledda, M.; Aviran, S. Automated Recognition of RNA Structure Motifs by Their SHAPE Data Signatures. Genes 2018, 9, 300. https://doi.org/10.3390/genes9060300
Radecki P, Ledda M, Aviran S. Automated Recognition of RNA Structure Motifs by Their SHAPE Data Signatures. Genes. 2018; 9(6):300. https://doi.org/10.3390/genes9060300
Chicago/Turabian StyleRadecki, Pierce, Mirko Ledda, and Sharon Aviran. 2018. "Automated Recognition of RNA Structure Motifs by Their SHAPE Data Signatures" Genes 9, no. 6: 300. https://doi.org/10.3390/genes9060300
APA StyleRadecki, P., Ledda, M., & Aviran, S. (2018). Automated Recognition of RNA Structure Motifs by Their SHAPE Data Signatures. Genes, 9(6), 300. https://doi.org/10.3390/genes9060300





