Transitions from Single- to Multi-Locus Processes during Speciation with Gene Flow
Abstract
1. Introduction
2. Materials and Methods
2.1. Simulations
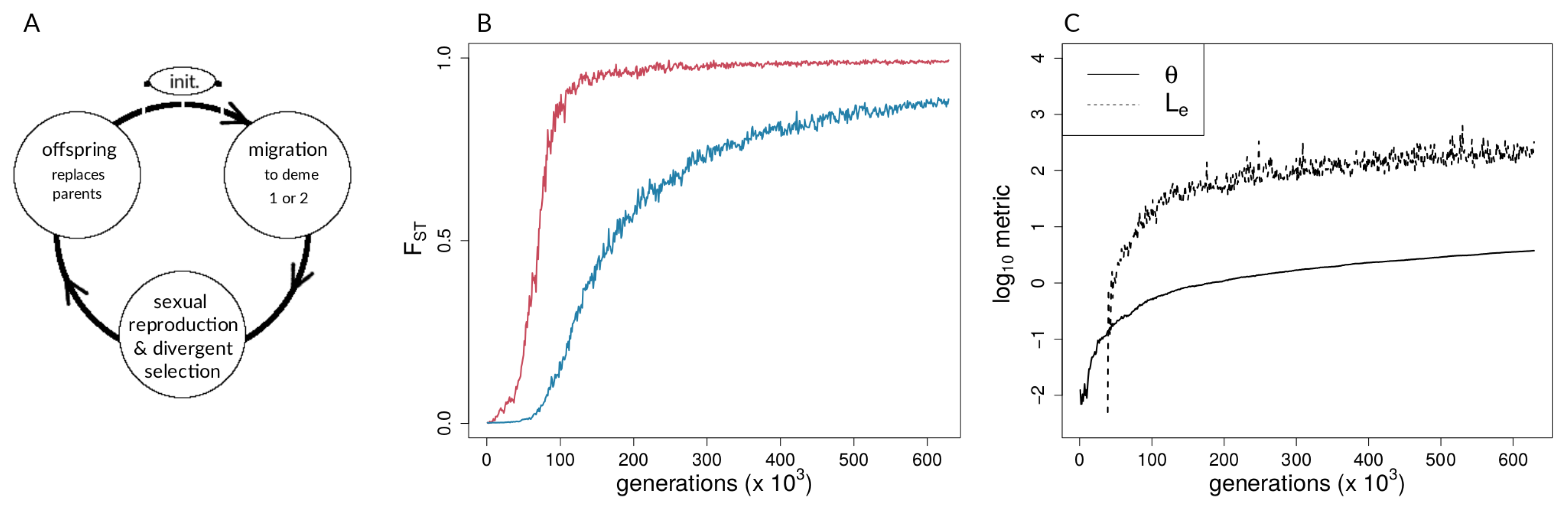
2.1.1. Model Overview and Life Cycle
2.1.2. Migration
2.1.3. Selection, Fitness, and Reproduction
2.1.4. Recombination
2.1.5. Mutation
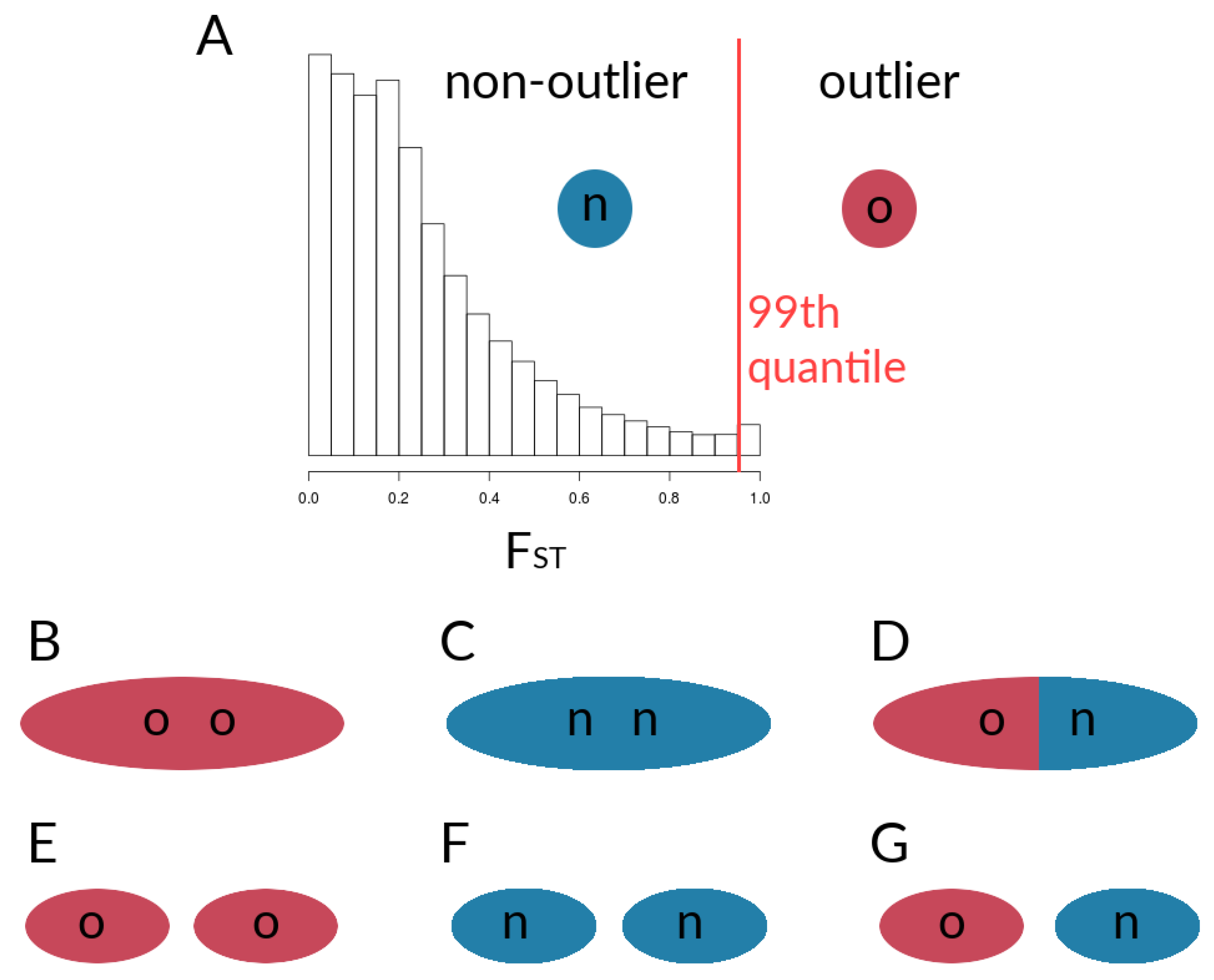
2.1.6. Data Derived from Simulations and Metrics Computed from Simulation Data
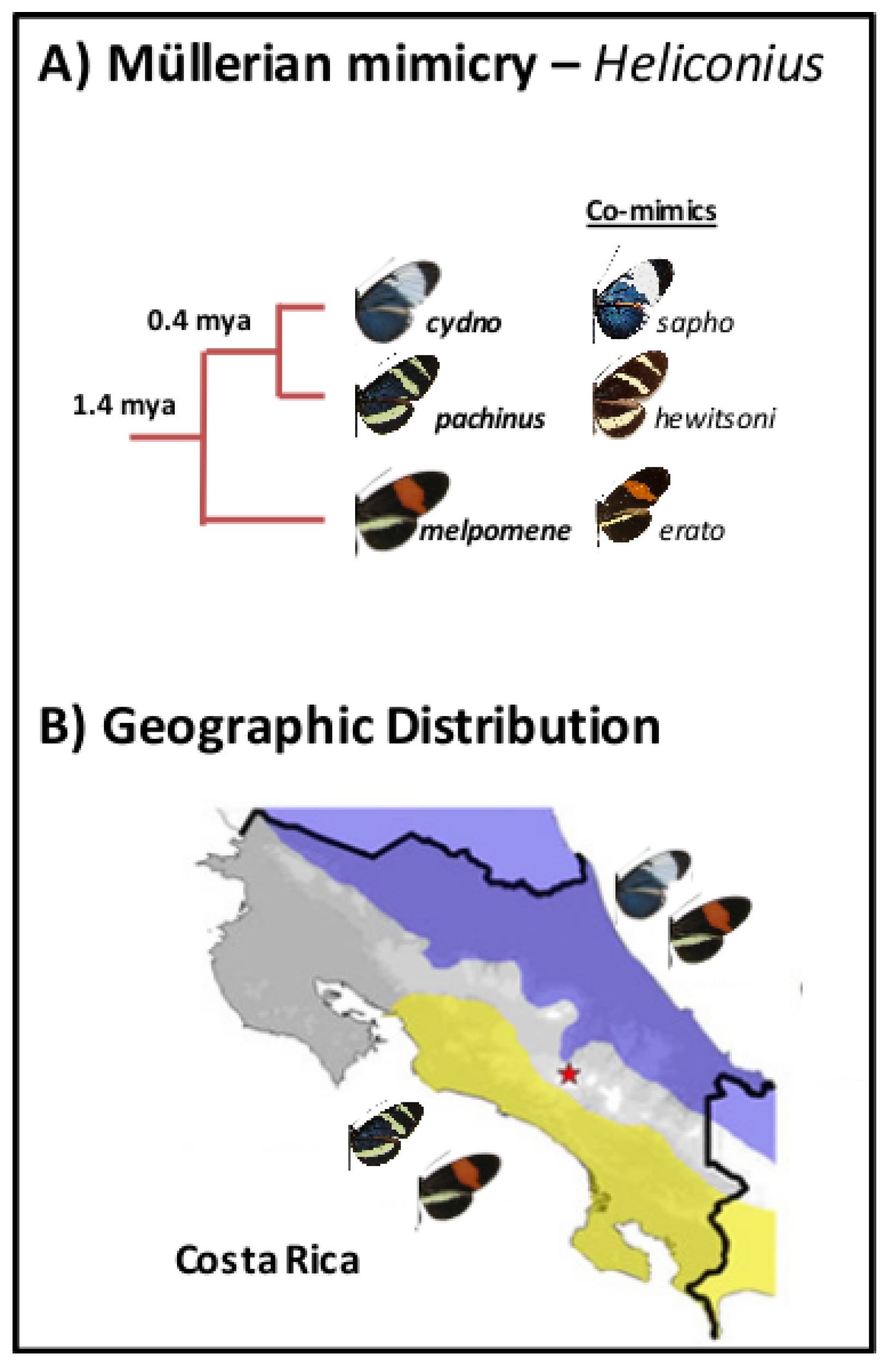
2.2. Empirical Data and Analyses
2.2.1. Genotyping and Descriptive Population Genetic Statistics
2.2.2. Within-Species LD between Heliconius Loci
3. Results
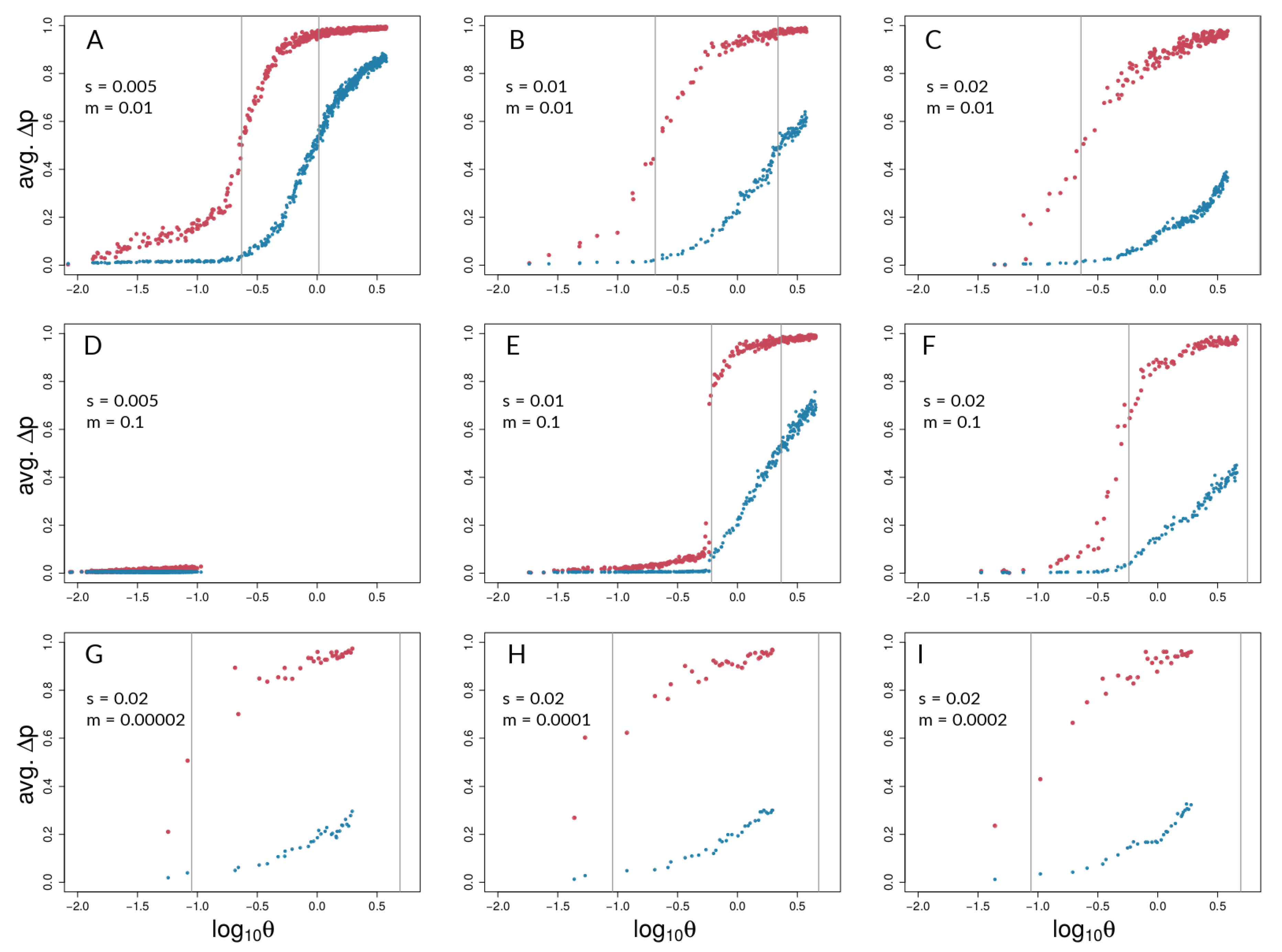
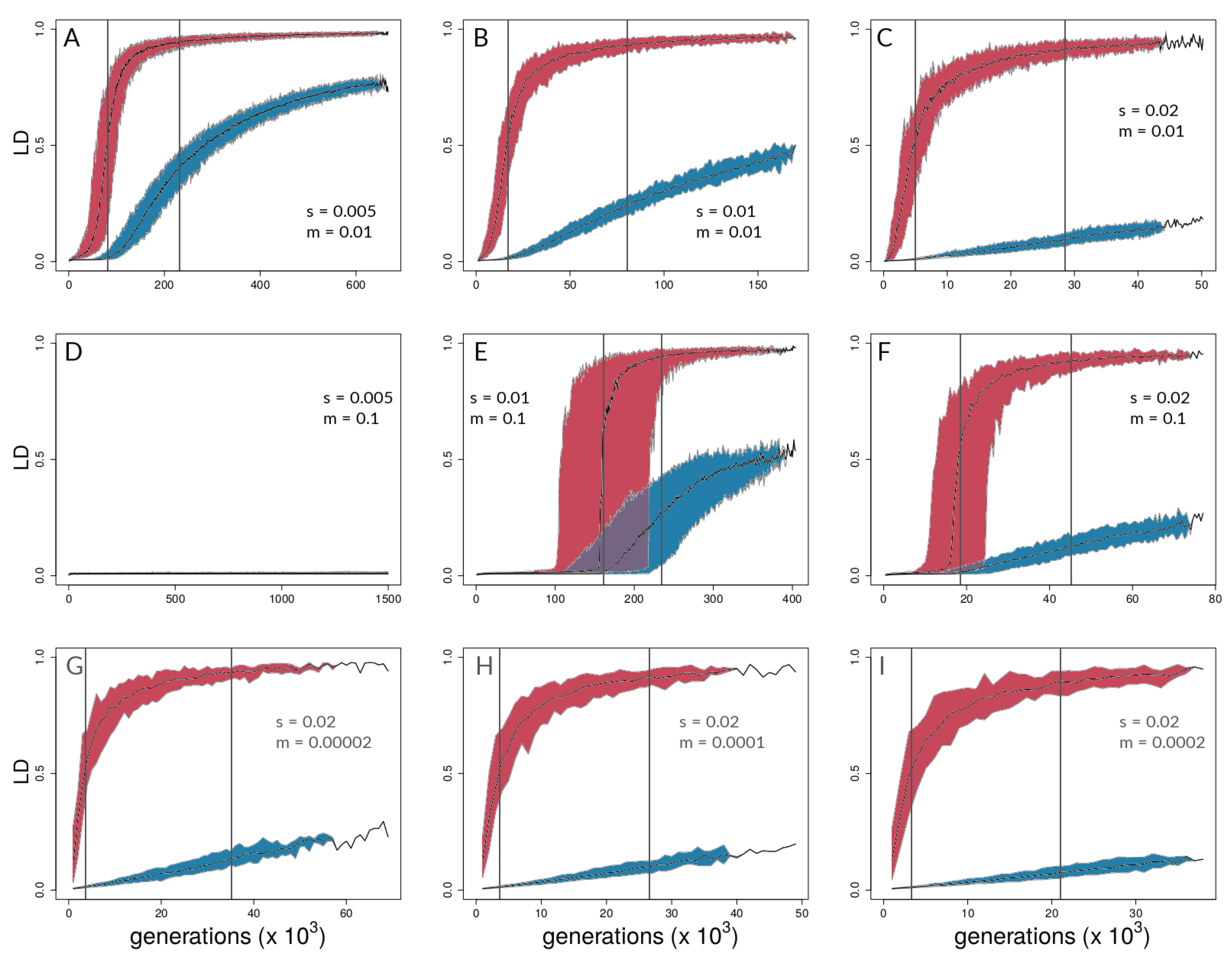
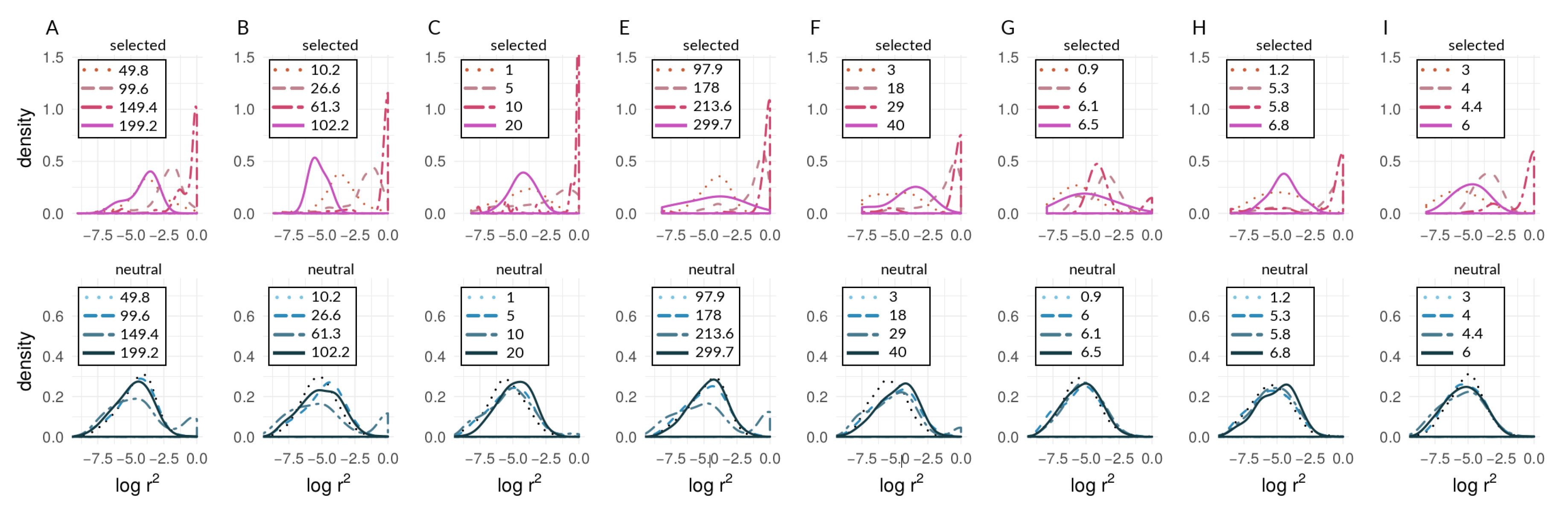
3.1. Investigating Coupling and Its Effects on Selected Versus Neutral Sites Using Simulations
3.2. Empirical Data and Analyses
3.2.1. Genotyping and Descriptive Population Genetic Statistics
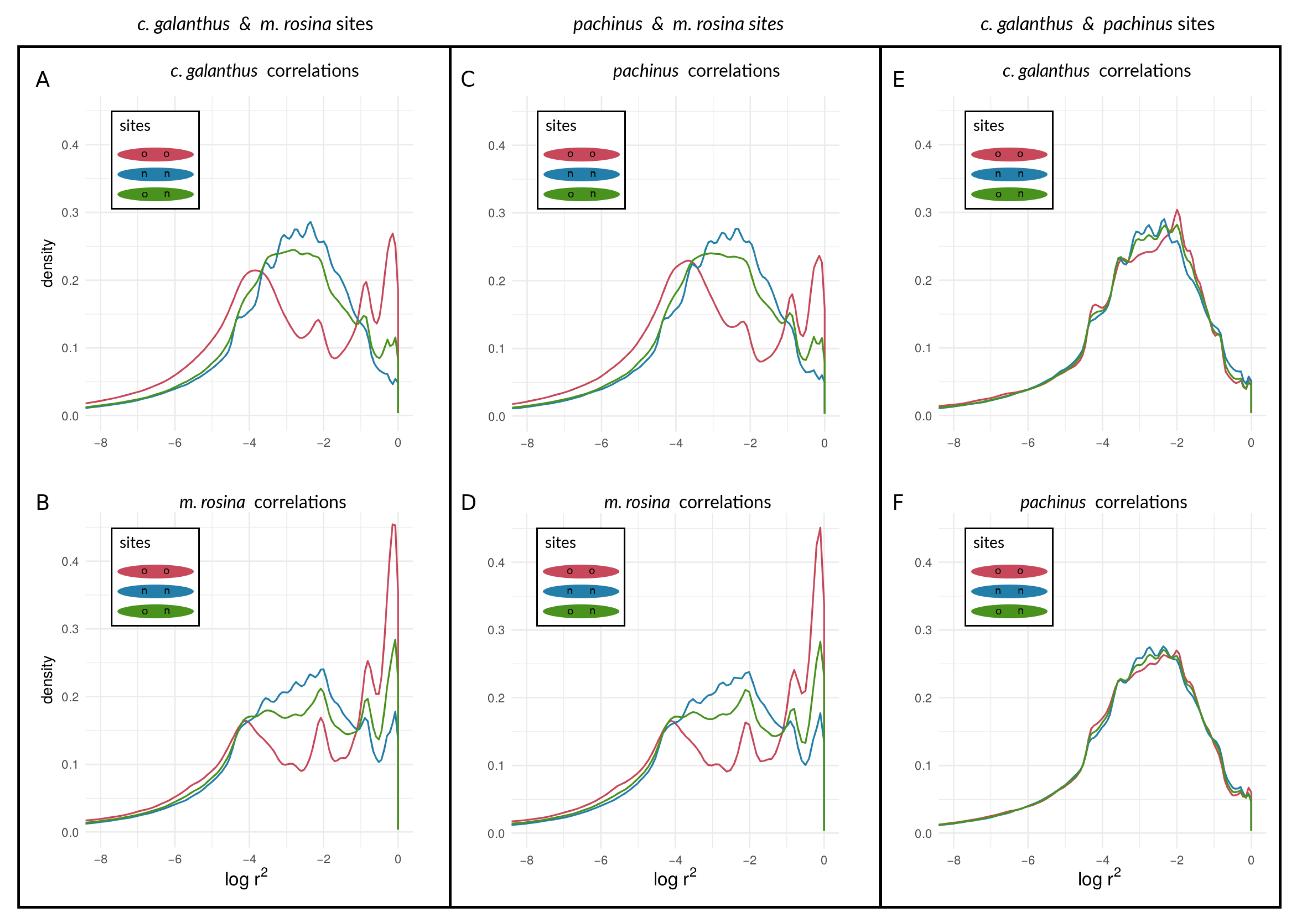
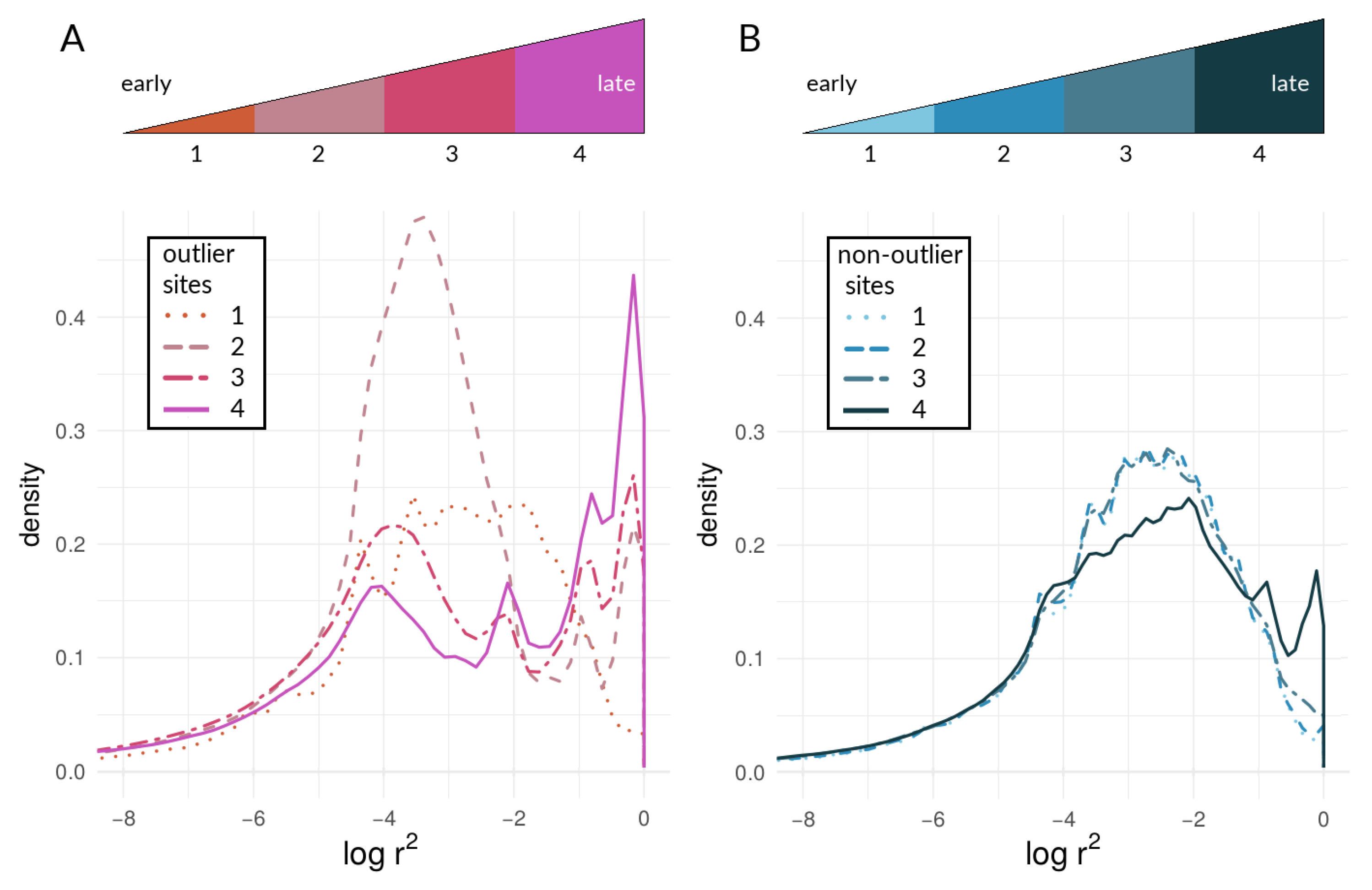
3.2.2. Within-Species LD between Heliconius Loci
4. Discussion
4.1. Simulations
4.2. Examining the Speciation Continuum in Heliconius by Using LD as a Proxy for Coupling
5. Conclusions
Supplementary Materials
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Seehausen, O.; Butlin, R.K.; Keller, I.; Wagner, C.E.; Boughman, J.W.; Hohenlohe, P.A.; Peichel, C.L.; Saetre, G.P.; Bank, C.; Brännström, A.; et al. Genomics and the origin of species. Nat. Rev. Genet. 2014, 15, 176–192. [Google Scholar] [CrossRef] [PubMed]
- Harrison, R.G.; Larson, E.L. Hybridization, introgression, and the nature of species boundaries. J. Hered. 2014, 105, 795–809. [Google Scholar] [CrossRef] [PubMed]
- Butlin, R.K.; Smadja, C.M. Coupling, reinforcement, and speciation. Am. Nat. 2018, 191. [Google Scholar] [CrossRef] [PubMed]
- Barton, N.H. Multilocus clines. Evolution 1983, 37, 454–471. [Google Scholar] [CrossRef] [PubMed]
- Felsenstein, J. Skepticism towards Santa Rosalia, or why are there so few kinds of animals? Evolution 1981, 35, 124–138. [Google Scholar] [CrossRef] [PubMed]
- Abbott, R.; Albach, D.; Ansell, S.; Arntzen, J.W.; Baird, S.J.E.; Bierne, N.; Boughman, J.; Brelsford, A.; Buerkle, C.A.; Buggs, R.; et al. Hybridization and speciation. J. Evol. Biol. 2013, 26, 229–246. [Google Scholar] [CrossRef] [PubMed]
- Barton, N.H.; Bengtsson, B.O. The barrier to genetic exchange between hybridising populations. Heredity 1986, 56, 357–376. [Google Scholar] [CrossRef]
- Baird, S.J.E. A simulation study of multilocus clines. Evolution 1995, 49, 1038–1045. [Google Scholar] [CrossRef] [PubMed]
- Kruuk, L.E.B.; Baird, S.J.E.; Gale, K.S.; Barton, N.H. A comparison of multilocus clines maintained by environmental adaptation or by selection against hybrids. Genetics 1999, 153, 1959–1971. [Google Scholar] [PubMed]
- Barton, N.H.; De Cara, M.A.R. The evolution of strong reproductive isolation. Evolution 2009, 63, 1171–1190. [Google Scholar] [CrossRef] [PubMed]
- Yeaman, S.; Otto, S.P. Establishment and maintenance of adaptive genetic divergence under migration, selection, and drift. Evolution 2011, 65, 2123–2129. [Google Scholar] [CrossRef] [PubMed]
- Feder, J.L.; Nosil, P. The efficacy of divergence hitchhiking in generating genomic islands during ecological speciation. Evolution 2010, 64, 1729–1747. [Google Scholar] [CrossRef] [PubMed]
- Feder, J.L.; Gejji, R.; Yeaman, S.; Nosil, P. Establishment of new mutations under divergence and genome hitchhiking. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2012, 367, 461–474. [Google Scholar] [CrossRef] [PubMed]
- Via, S. Divergence hitchhiking and the spread of genomic isolation during ecological speciation-with-gene-flow. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2012, 367, 451–460. [Google Scholar] [CrossRef] [PubMed]
- Flaxman, S.M.; Feder, J.L.; Nosil, P. Genetic hitchhiking and the dynamic buildup of genomic divergence during speciation with gene flow. Evolution 2013, 67, 2577–2591. [Google Scholar] [CrossRef] [PubMed]
- Yeaman, S.; Whitlock, M.C. The genetic architecture of adaptation under migration–selection balance. Evolution 2011, 65, 1897–1911. [Google Scholar] [CrossRef] [PubMed]
- Yeaman, S. Genomic rearrangements and the evolution of clusters of locally adaptive loci. Proc. Natl. Acad. Sci. USA 2013, 110, E1743–E1751. [Google Scholar] [CrossRef] [PubMed]
- Flaxman, S.M.; Wacholder, A.C.; Feder, J.L.; Nosil, P. Theoretical models of the influence of genomic architecture on the dynamics of speciation. Mol. Ecol. 2014, 23, 4074–4088. [Google Scholar] [CrossRef] [PubMed]
- Bierne, N.; Welch, J.; Loire, E.; Bonhomme, F.; David, P. The coupling hypothesis: Why genome scans may fail to map local adaptation genes. Mol. Ecol. 2011, 20, 2044–2072. [Google Scholar] [CrossRef] [PubMed]
- Feder, J.L.; Nosil, P.; Wacholder, A.C.; Egan, S.P.; Berlocher, S.H.; Flaxman, S.M. Genome-wide congealing and rapid transitions across the speciation continuum during speciation with gene flow. J. Hered. 2014, 105, 810–820. [Google Scholar] [CrossRef] [PubMed]
- Nosil, P.; Gompert, Z.; Farkas, T.E.; Comeault, A.A.; Feder, J.L.; Buerkle, C.A.; Parchman, T.L. Genomic consequences of multiple speciation processes in a stick insect. Proc. R. Soc. Lond. Biol. 2012, 5058–5065. [Google Scholar] [CrossRef] [PubMed]
- Nosil, P.; Feder, J.L. Genomic divergence during speciation: Causes and consequences. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2012, 367, 332–342. [Google Scholar] [CrossRef] [PubMed]
- Nosil, P.; Feder, J.L.; Flaxman, S.M.; Gompert, Z. Tipping points in the dynamics of speciation. Nat. Ecol. Evol. 2017, 1. [Google Scholar] [CrossRef] [PubMed]
- Bürger, R.; Akerman, A. The effects of linkage and gene flow on local adaptation: A two-locus continent—Island model. Theor. Popul. Biol. 2011, 80, 272–288. [Google Scholar] [CrossRef] [PubMed]
- Akerman, A.; Bürger, R. The consequences of gene flow for local adaptation and differentiation: A two-locus two-deme model. J. Math. Biol. 2014, 68, 1135–1198. [Google Scholar] [CrossRef] [PubMed]
- Aeschbacher, S.; Bürger, R. The effect of linkage on establishment and survival of locally beneficial mutations. Genetics 2014, 197, 317–336. [Google Scholar] [CrossRef] [PubMed]
- Barton, N. Gene flow past a cline. Heredity 1979, 43, 333. [Google Scholar] [CrossRef]
- Bengtsson, B. The flow of genes through a genetic barrier. In Evolution—Essays in Honour of John Maynard Smith; Greenwood, P.J., Harvey, P.S.M., Eds.; Cambridge University Press: New York, NY, USA, 1985; Chapter 3; Volume 1, pp. 31–42. [Google Scholar]
- Charlesworth, B.; Nordborg, M.; Charlesworth, D. The effects of local selection, balanced polymorphism and background selection on equilibrium patterns of genetic diversity in subdivided populations. Genet. Res. 1997, 70, 155–174. [Google Scholar] [CrossRef] [PubMed]
- Southcott, L.; Kronforst, M.R. A neutral view of the evolving genomic architecture of speciation. Ecol. Evol. 2017, 7, 6358–6366. [Google Scholar] [CrossRef] [PubMed]
- Kronforst, M.R.; Hansen, M.E.B.; Crawford, N.G.; Gallant, J.R.; Zhang, W.; Kulathinal, R.J.; Kapan, D.D.; Mullen, S.P. Hybridization reveals the evolving genomic architecture of speciation. Cell Rep. 2013, 5, 666–677. [Google Scholar] [CrossRef] [PubMed]
- Beltrán, M.; Jiggins, C.D.; Bull, V.; Linares, M.; Mallet, J.; McMillan, W.O.; Bermingham, E. Phylogenetic discordance at the species boundary: Comparative gene genealogies among rapidly radiating Heliconius butterflies. Mol. Biol. Evol. 2000, 19, 2176–2190. [Google Scholar] [CrossRef] [PubMed]
- Bull, V.; Beltrán, M.; Jiggins, C.D.; McMillan, W.O.; Bermingham, E.; Mallet, J. Polyphyly and gene flow between non-sibling Heliconius species. BMC Biol. 2006, 4, 11. [Google Scholar] [CrossRef] [PubMed]
- Kronforst, M.R.; Young, L.G.; Blume, L.M.; Gilbert, L.E. Multilocus analyses of admixture and introgression among hybridizing Heliconius butterflies. Evolution 2006, 60, 1254–1268. [Google Scholar] [CrossRef] [PubMed]
- Kronforst, M.R.; Gilbert, L.E. The population genetics of mimetic diversity in Heliconius butterflies. Proc. R. Soc. Lond. Biol. 2008, 275, 493–500. [Google Scholar] [CrossRef] [PubMed]
- Martin, S.H.; Dasmahapatra, K.K.; Nadeau, N.J.; Salazar, C.; Walters, J.R.; Simpson, F.; Blaxter, M.; Manica, A.; Mallet, J.; Jiggins, C.D. Genome-wide evidence for speciation with gene flow in Heliconius butterflies. Genome Res. 2013, 23, 1817–1828. [Google Scholar] [CrossRef] [PubMed]
- Jiggins, C.D.; Naisbit, R.E.; Coe, R.L.; Mallet, J. Reproductive isolation caused by colour pattern mimicry. Nature 2001, 411, 302. [Google Scholar] [CrossRef] [PubMed]
- Jiggins, C.D.; Salazar, C.; Linares, M.; Mavarez, J. Hybrid trait speciation and Heliconius butterflies. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2008, 363, 3047–3054. [Google Scholar] [CrossRef] [PubMed]
- Kronforst, M.R.; Kapan, D.D.; Gilbert, L.E. Parallel genetic architecture of parallel adaptive radiations in mimetic Heliconius butterflies. Genetics 2006, 174, 535–539. [Google Scholar] [CrossRef] [PubMed]
- Chamberlain, N.L.; Hill, R.I.; Kapan, D.D.; Gilbert, L.E.; Kronforst, M.R. Polymorphic butterfly reveals the missing link in ecological speciation. Science 2009, 326, 847–850. [Google Scholar] [CrossRef] [PubMed]
- Benson, W.W. Resource partitioning in passion vine butterflies. Evolution 1978, 32, 493–518. [Google Scholar] [CrossRef] [PubMed]
- Estrada, C.; Jiggins, C.D. Patterns of pollen feeding and habitat preference among Heliconius species. Ecol. Entomol. 2002, 27, 448–456. [Google Scholar] [CrossRef]
- Mallet, J.; Gilbert, L.E., Jr. Why are there so many mimicry rings? Correlations between habitat, behaviour and mimicry in Heliconius butterflies. Biol. J. Linnean Soc. 1995, 55, 159–180. [Google Scholar] [CrossRef]
- Smiley, J. Plant chemistry and the evolution of host specificity: New evidence from Heliconius and Passiflora. Science 1978, 201, 745–747. [Google Scholar] [CrossRef] [PubMed]
- Merrill, R.M.; Wallbank, R.W.; Bull, V.; Salazar, P.C.; Mallet, J.; Stevens, M.; Jiggins, C.D. Disruptive ecological selection on a mating cue. Proc. R. Soc. Lond. Biol. 2012, 279, 4907–4913. [Google Scholar] [CrossRef] [PubMed]
- Kronforst, M.R.; Papa, R. The functional basis of wing patterning in Heliconius butterflies: The molecules behind mimicry. Genetics 2015, 200, 1–19. [Google Scholar] [CrossRef] [PubMed]
- Flaxman, S.M. bu2s 2014. Available online: https://github.com/flaxmans/bu2s (accessed on 14 February 2018).
- Barton, N. Does hybridization influence speciation? J. Evol. Biol. 2013, 26, 267–269. [Google Scholar] [CrossRef] [PubMed]
- Nei, M. Analysis of gene diversity in subdivided populations. Proc. Natl. Acad. Sci. USA 1973, 70, 3321–3323. [Google Scholar] [CrossRef] [PubMed]
- Vuilleumier, S.; Goudet, J.; Perrin, N. Evolution in heterogeneous populations: From migration models to fixation probabilities. Theor. Popul. Biol. 2010, 78, 250–258. [Google Scholar] [CrossRef] [PubMed]
- Nosil, P.; Feder, J.L.; Flaxman, S.M.; Gompert, Z. Supplementary Methods to Tipping Points in the Dynamics of Speciation 2017. Available online: https://media.nature.com/original/nature-assets/natecolevol/2017/s41559-016-0001/extref/s41559-016-0001-s1.pdf (accessed on 14 February 2018).
- Nosil, P.; Feder, J.L.; Flaxman, S.M.; Gompert, Z. Migration-Selection Balance Notebook 2017. Available online: https://raw.githubusercontent.com/flaxmans/NatureEE2017/master/figures-and-scripts/MigrationSelectionBalance.nb (accessed on 14 February 2018).
- R Development Core Team. R: A Language and Environment for Statistical Computing; The R Foundation for Statistical Computing: Vienna, Austria, 2017. [Google Scholar]
- Fischer, B.; Pau, G.; Smith, M. rhdf5: HDF5 Interface to R, R Package Version 2.22.0. 2017.
- Schilling, M.P. Code to Accompany Schilling et al. (2018) Genes. Transitions from Single to Multi-Locus Processes during Speciaion with Gene Flow. Available online: https://github.com/schimar/schilling2018genes (accessed on 14 February 2018).
- Lepbase: The Lepidopteran Genome Database 2017. Available online: http://download.lepbase.org/v4/sequence/HeliconiusmelpomenemelpomeneHmel2.5.scaffolds.fa.gz (accessed on 14 February 2018).
- Li, H.; Durbin, R. Fast and accurate short read alignment with Burrows-Wheeler transform. Bioinformatics 2009, 25, 1754–1760. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Vinckenbosch, N.; Tian, G.; Huerta-Sanchez, E.; Jiang, T.; Jiang, H.; Albrechtsen, A.; Andersen, G.; Cao, H.; Korneliussen, T.; et al. Resequencing of 200 human exomes identifies an excess of low-frequency non-synonymous coding variants. Nat. Genet. 2010, 42, 969–972. [Google Scholar] [CrossRef] [PubMed]
- McKenna, A.; Hanna, M.; Banks, E.; Sivachenko, A.; Cibulskis, K.; Kernytsky, A.; Garimella, K.; Altshuler, D.; Gabriel, S.; Daly, M.; et al. The Genome Analysis Toolkit: A MapReduce framework for analyzing next-generation DNA sequencing data. Genome Res. 2010, 20, 1297–1303. [Google Scholar] [CrossRef] [PubMed]
- Danecek, P.; Auton, A.; Abecasis, G.; Albers, C.A.; Banks, E.; DePristo, M.A.; Handsaker, R.E.; Lunter, G.; Marth, G.T.; Sherry, S.T.; et al. The variant call format and VCFtools. Bioinformatics 2011, 27, 2156–2158. [Google Scholar] [CrossRef] [PubMed]
- Weir, B.S.; Cockerham, C.C. Estimating F-Statistics for the analysis of population structure. Evolution 1984, 38, 1358–1370. [Google Scholar] [PubMed]
- Li, H. A statistical framework for SNP calling, mutation discovery, association mapping and population genetical parameter estimation from sequencing data. Bioinformatics 2011, 27, 2987–2993. [Google Scholar] [CrossRef] [PubMed]
- Wright, S. Variability within and among natural populations. In Evolution and the Genetics of Populations; University of Chicago Press: Chicago, IL, USA, 1978. [Google Scholar]
- Wickham, H. ggplot2: Elegant Graphics for Data Analysis; Springer: New York, NY, USA, 2009. [Google Scholar]
- Feder, J.; Nosil, P.; Gompert, Z.; Flaxman, S.; Schilling, M. Barnacles, barrier loci and the systematic building of species. J. Evol. Biol. 2017, 30, 1494–1497. [Google Scholar] [CrossRef] [PubMed]
- Jiggins, C.; Martin, S. Glittering gold and the quest for Isla de Muerta. J. Evol. Biol. 2017, 30, 1509–1511. [Google Scholar] [CrossRef] [PubMed]
- Lindtke, D.; Yeaman, S. Identifying the loci of speciation: The challenge beyond genome scans. J. Evol. Biol. 2017, 30, 1478–1481. [Google Scholar] [CrossRef] [PubMed]
- Szymura, J.M.; Barton, N.H. Genetic analysis of a hybrid zone between the fire-bellied toads, Bombina bombina and B. variegata near Cracow in Southern Poland. Evolution 1986, 40, 1141–1159. [Google Scholar] [PubMed]
- Mallet, J.; Barton, N.; Lamas, G.; Santisteban, J.; Muedas, M.; Eeley, H. Estimates of selection and gene flow from measures of cline width and linkage disequilibrium in Heliconius hybrid zones. Genetics 1990, 124, 921–936. [Google Scholar] [PubMed]
- Turner, J.; Johnson, M.S.; Eanes, W.F. Contrasted modes of evolution in the same genome: Allozymes and adaptive change in Heliconius. Proc. Natl. Acad. Sci. USA 1979, 76, 1924–1928. [Google Scholar] [CrossRef] [PubMed]
- Jiggins, C.; McMillan, W.; King, P.; Mallet, J. The maintenance of species differences across a Heliconius hybrid zone. Heredity 1997, 79, 495. [Google Scholar] [CrossRef]
- Jiggins, C.D.; Davies, N. Genetic evidence for a sibling species of Heliconius charithonia (Lepidoptera; Nymphalidae). Biol. J. Linnean Soc. 1998, 64, 57–67. [Google Scholar] [CrossRef]
- Mallet, J.; McMillan, W.O.; Jiggins, C.D. Mimicry and warning color at the boundary between races and species. In Endless Forms: Species and Speciation; Oxford University Press: Oxford, UK, 1998; pp. 390–403. [Google Scholar]
- Butlin, R.K. Recombination and speciation. Mol. Ecol. 2005, 14, 2621–2635. [Google Scholar] [CrossRef] [PubMed]
- Kirkpatrick, M.; Barton, N. Chromosome inversions, local adaptation and speciation. Genetics 2006, 173, 419–434. [Google Scholar] [CrossRef] [PubMed]
- Feder, J.L.; Nosil, P. Chromosomal inversions and species differences: When are genes affecting adaptive divergence and reproductive isolation expected to reside within inversions? Evolution 2009, 63, 3061–3075. [Google Scholar] [CrossRef] [PubMed]
- Ortiz-Barrientos, D.; Engelstädter, J.; Rieseberg, L.H. Recombination rate evolution and the origin of species. Trends Ecol. Evol. 2016, 31, 226–236. [Google Scholar] [CrossRef] [PubMed]

| Parameter | Notation (If Applicable) | Value(s) Used (and Units if Applicable) |
|---|---|---|
| Mean selection coefficient for divergently selected mutations (mean of exponential distribution from which new mutations’ coefficients were drawn) | s | 0.005, 0.01, 0.02 |
| Migration rate | m | 0.00002, 0.0001, 0.0002, 0.01, 0.1 (probability per individual per generation) |
| Total population size | N | 5000 individuals |
| Mutations per generation (population mutation rate) | 10 per generation | |
| Number of chromosomes in a genome (haploid number) | c | 4 |
| Recombination length of each individual chromosome | l | 50 centiMorgan (cM) |
| Ratio of neutral:selected mutations | 10:1 |
| s | 0.005 | 0.01 | 0.02 | |
|---|---|---|---|---|
| m | ||||
| 0.01 | A | B | C | |
| 0.1 | D | E | F | |
| 0.00002 | G | - | - | |
| 0.0001 | H | - | - | |
| 0.0002 | I | - | - | |
| Genotype at Locus i | Fitness Contribution of Locus in Deme 1 | Fitness Contribution of Locus in Deme 2 |
|---|---|---|
| 1 | ||
| 1 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schilling, M.P.; Mullen, S.P.; Kronforst, M.; Safran, R.J.; Nosil, P.; Feder, J.L.; Gompert, Z.; Flaxman, S.M. Transitions from Single- to Multi-Locus Processes during Speciation with Gene Flow. Genes 2018, 9, 274. https://doi.org/10.3390/genes9060274
Schilling MP, Mullen SP, Kronforst M, Safran RJ, Nosil P, Feder JL, Gompert Z, Flaxman SM. Transitions from Single- to Multi-Locus Processes during Speciation with Gene Flow. Genes. 2018; 9(6):274. https://doi.org/10.3390/genes9060274
Chicago/Turabian StyleSchilling, Martin P., Sean P. Mullen, Marcus Kronforst, Rebecca J. Safran, Patrik Nosil, Jeffrey L. Feder, Zachariah Gompert, and Samuel M. Flaxman. 2018. "Transitions from Single- to Multi-Locus Processes during Speciation with Gene Flow" Genes 9, no. 6: 274. https://doi.org/10.3390/genes9060274
APA StyleSchilling, M. P., Mullen, S. P., Kronforst, M., Safran, R. J., Nosil, P., Feder, J. L., Gompert, Z., & Flaxman, S. M. (2018). Transitions from Single- to Multi-Locus Processes during Speciation with Gene Flow. Genes, 9(6), 274. https://doi.org/10.3390/genes9060274






