The Cross-Entropy Based Multi-Filter Ensemble Method for Gene Selection
Abstract
1. Introduction
2. Materials and Methods
2.1. Datasets
2.2. Filtering Process
2.2.1. Signal-to-Noise Ratio
2.2.2. t-Statistic
2.2.3. Pearson Correlation Coefficient
2.2.4. Combination of Filtered Genes
- (1)
- Suppose , and ;
- (2)
- Use the filter to calculate the statistical scores and rank them, where ;
- (3)
- Select the genes with the top ranking score in each list, add into , and delete the genes from ;
- (4)
- Take the union of the filtered lists, which consolidates the overlapping genes and reduces the size of the combined list of the filtered genes;
- (5)
- Repeat steps (2)–(4) until all of the top genes are added to and there are no duplication genes.
2.3. Cross-Entropy Method
2.4. Calculation of Redundancy
- (1)
- Set the threshold of independence be , and ;
- (2)
- Use to calculate the cross-entropy between two genes, where ;
- (3)
- If , then , , and go to step (4);
- (4)
- If , then , and go to step (4).
- (5)
- Repeat (2)–(3), until .
2.5. Selection of Optimal Subset
- (1)
- Initialization ;
- (2)
- For each , calculate the classification accuracy for classifier M;
- (3)
- Select a subset of the genes with the highest accuracy , ;
- (4)
- For each , calculate the classification of , which is referred to as ;
- (5)
- If , then , ;
- (6)
- Repeat (4)–(5), until the accuracy is 100 or is null.
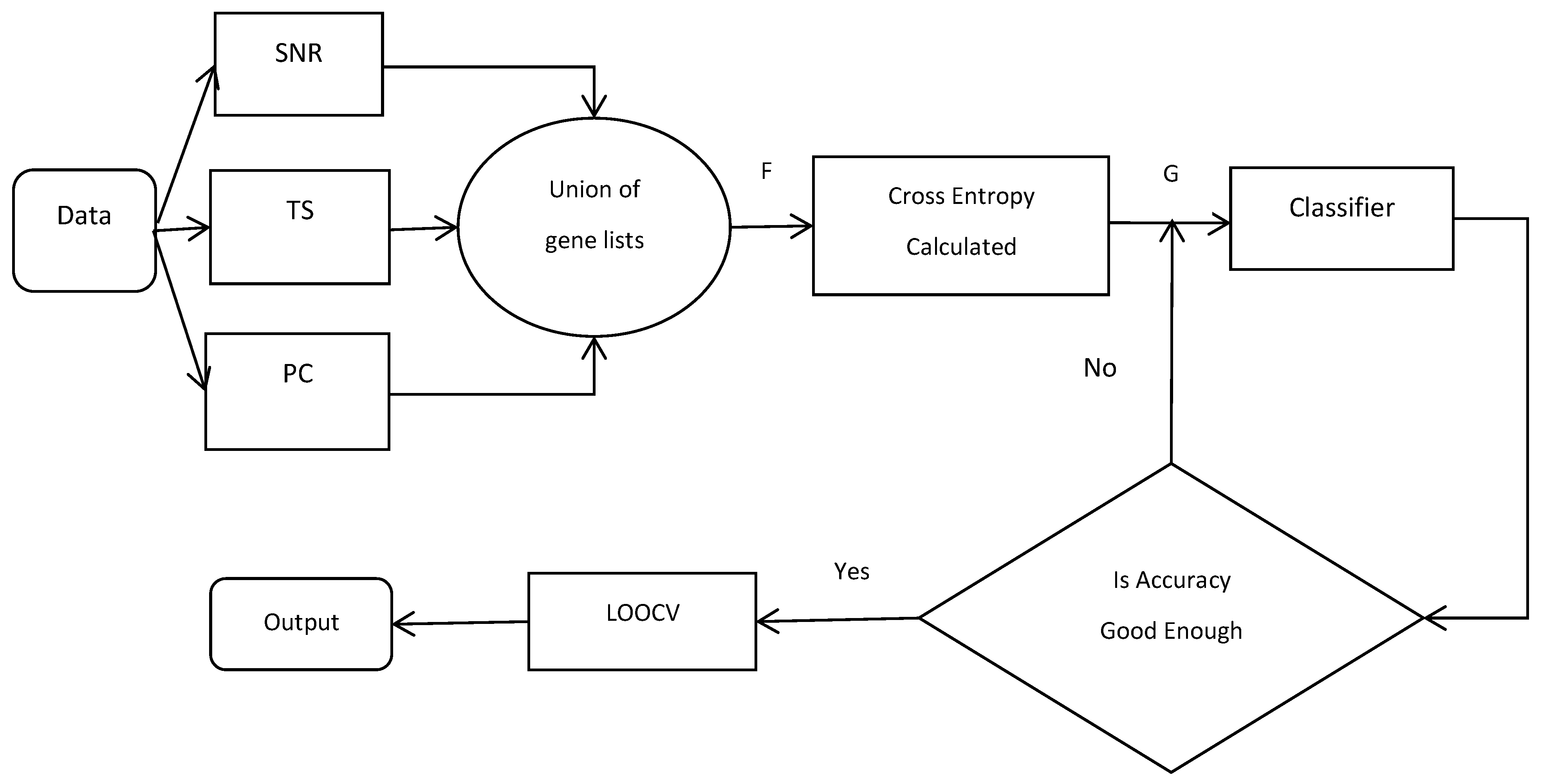
2.6. Flowchart of CEMFE Method
| Our proposed algorithm can be described as follows: |
| Input: data set , number of filter , number of union filtered gene , number of genes subset () , classifier Output: optimal feature subset R For to do = use the filter calculate the statistical scores and rank it = select genes with top ranking score in each list End of For F /*the union of the list of genes*/ Initialization: For to do Calculate /*For all */ If , , End of For Return G Initialization: /*optimal feature subset*/ , For to do = calculate classification accuracy of If , End of For Return , |
3. Results and Discussion
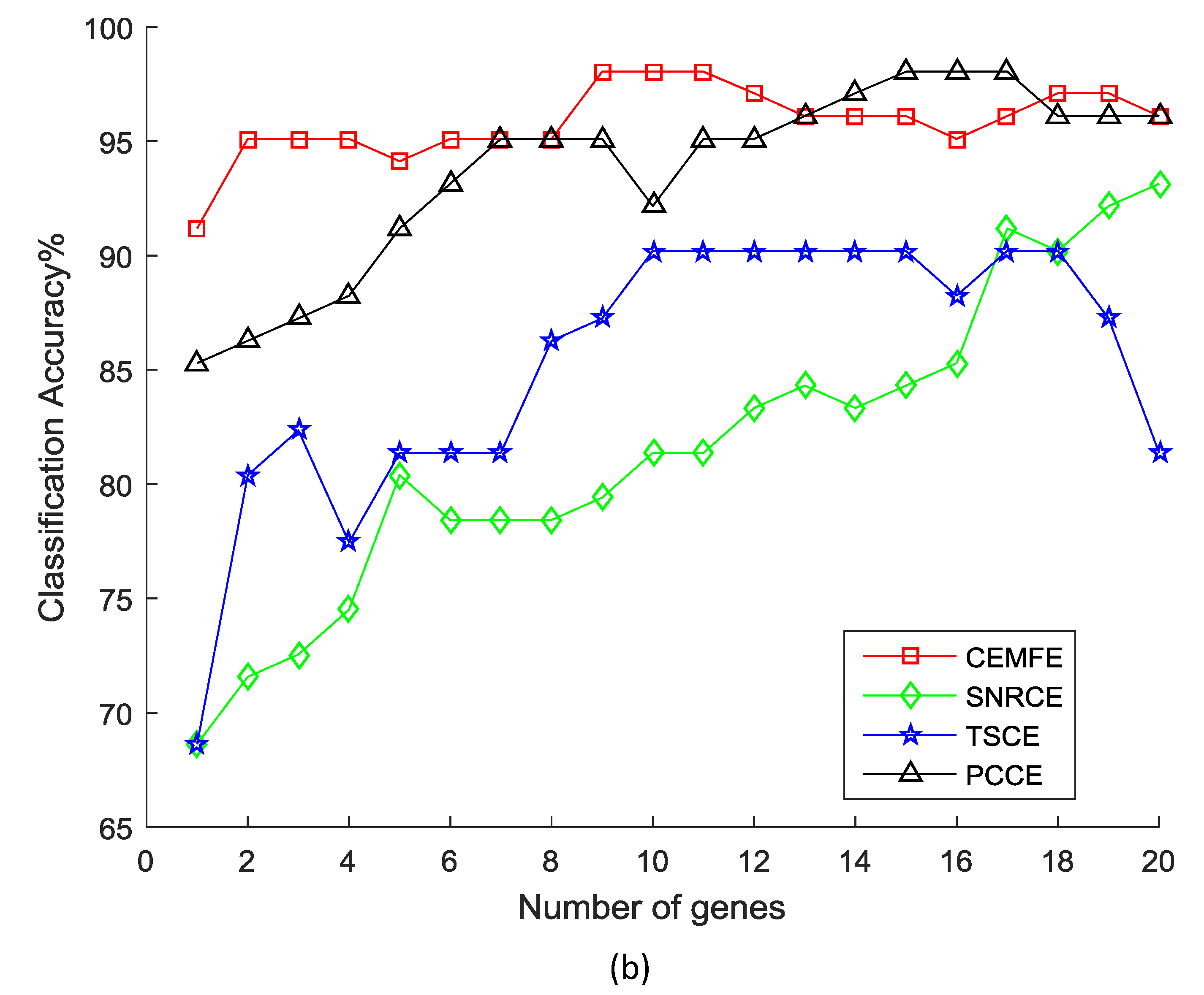
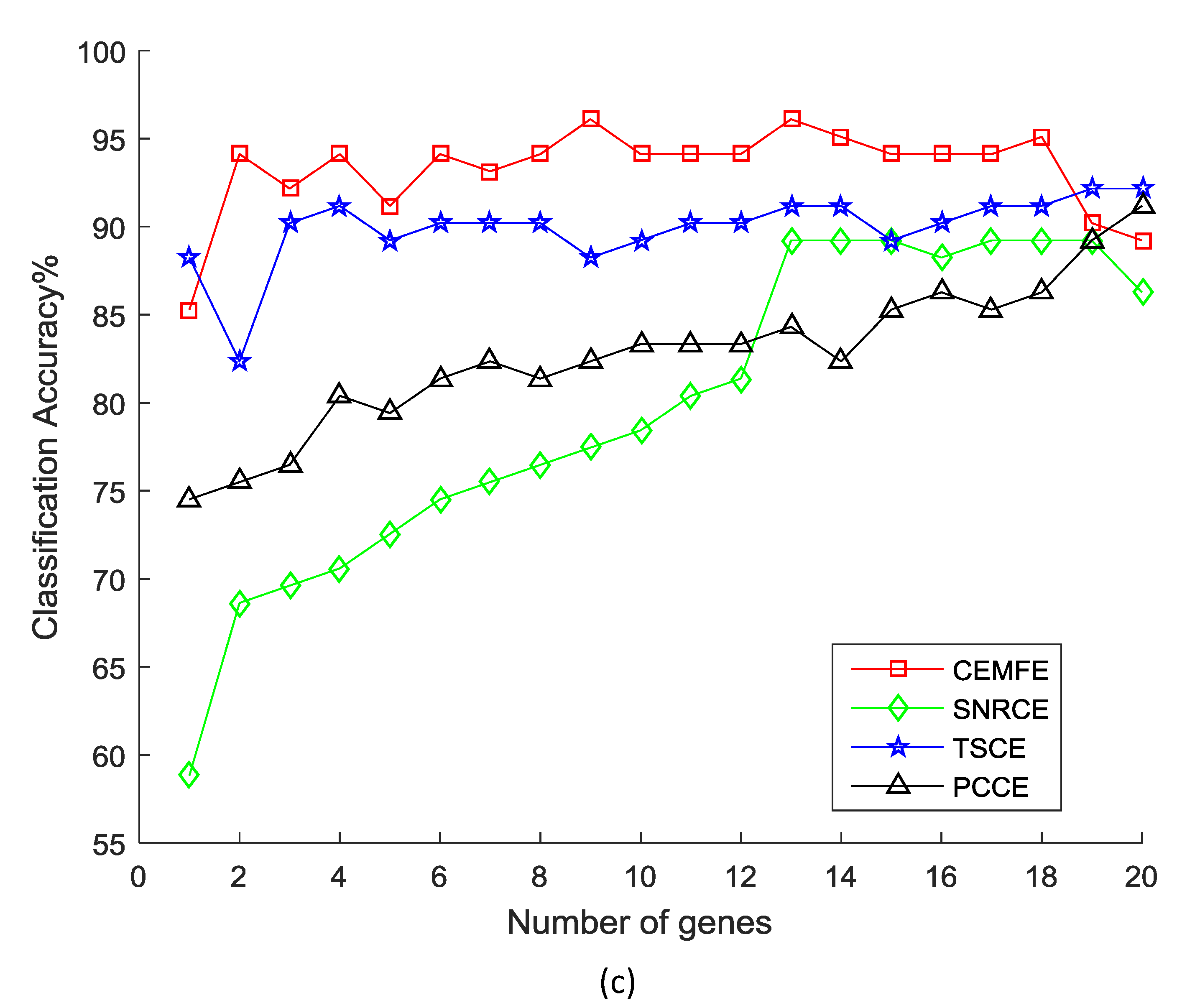
3.1. Results on Microarray Data
3.2. Discussion
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Rakkeitwinai, S.; Lursinsap, C.; Aporntewan, C.; Mutirangura, A. New feature selection for gene expression classification based on degree of class overlap in principle dimensions. Comput. Biol. Med. 2015, 64, 292–298. [Google Scholar] [CrossRef] [PubMed]
- Zhou, W.; Dickerson, J.A. A novel class dependent feature selection method for cancer biomarker discovery. Comput. Biol. Med. 2014, 47, 66–75. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Song, Q.; Wang, G.; Zhang, K.; He, L.; Jia, X. A dissimilarity-based imbalance data classification algorithm. Appl. Intell. 2015, 42, 544–565. [Google Scholar] [CrossRef]
- Xiong, H.; Zhang, Y.; Chen, X.W.; Yu, J. Cross-platform microarray data integration using the normalized linear transform. Int. J. Data Min. Bioinform. 2010, 4, 142–157. [Google Scholar] [CrossRef] [PubMed]
- Kabir, M.M.; Shahjahan, M.; Murase, K. A new local search based hybrid genetic algorithm for feature selection. Neurocomputing 2011, 74, 2914–2928. [Google Scholar] [CrossRef]
- Pugalendhi, G.; Vijayakumar, A.; Kim, K.J. A new data-driven method for microarray data classification. Inter. J. Data Min. Bioinform. 2016, 15, 101–124. [Google Scholar] [CrossRef]
- Marafino, B.J.; John Boscardin, W.; Dudley, R.A. Efficient and sparse feature selection for biomedical text classification via the elastic net: Application to ICU risk stratification from nursing notes. J. Biomed. Inform. 2015, 54, 114–120. [Google Scholar] [CrossRef] [PubMed]
- You, W.; Yang, Z.; Yuan, M.; Ji, G. TotalPLS: local dimension reduction for multicategory microarray data. IEEE Trans. Hum. Mach. Syst. 2014, 44, 125–138. [Google Scholar]
- Magendiran, N.; Selvarajan, S. Substantial Gene Selection in Disease Prediction based on Cluster Centre Initialization Algorithm. Indian J. 2016, 6, 258. [Google Scholar] [CrossRef]
- Saeys, Y.; Inza, I.; Larrañaga, P. A review of feature selection techniques in bioinformatics. Bioinformatics 2007, 23, 2507–2517. [Google Scholar] [CrossRef] [PubMed]
- Kohavi, R.; John, G.H. Wrappers for Feature Subset Selection; Elsevier Science Publishers Ltd.: New York, NY, USA, 1997. [Google Scholar]
- Kamkar, I.; Gupta, S.K.; Phung, D.; Venkatesh, S. Stable feature selection for clinical prediction: Exploiting ICD tree structure using Tree-Lasso. J. Biomed. Inform. 2015, 53, 277. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Zhang, D. Feature selection with effective distance. Neurocomputing 2016, 215, 100–109. [Google Scholar] [CrossRef]
- Xu, J.; Li, T.; Sun, L.; Li, Y. Feature selection method based on signal-to-noise ratio and neighborhood rough set. Data Acquis. Process. 2015, 30, 973–981. [Google Scholar]
- Bolón-Canedo, V.; Sánchez-Maroño, N.; Alonso-Betanzos, A. Data classification using an ensemble of filters. Neurocomputing 2014, 135, 13–20. [Google Scholar] [CrossRef]
- Leung, Y.; Hung, Y. A Multiple-filter-multiple-wrapper approach to gene selection and microarray data classification. IEEE/ACM Trans. Comput. Biol. Bioinform. 2010, 7, 108–117. [Google Scholar] [CrossRef] [PubMed]
- Meyer, P.E.; Schretter, C.; Bontempi, G. Information-theoretic feature selection in microarray data using variable complementarity. IEEE J. Sel. Top. Signal Proc. 2008, 2, 261–274. [Google Scholar] [CrossRef]
- Golub, T.R.; Slonim, D.K.; Tamayo, P.; Huard, C.; Gaasenbeek, M.; Mesirov, J.P.; Coller, H.; Loh, M.L.; Downing, J.R.; Caligiuri, M.A.; et al. Molecular classification of cancer: class discovery and class prediction by gene expression monitoring. Science 1999, 286, 205–214. [Google Scholar] [CrossRef]
- Speed, T. Statistical Analysis of Gene Expression Microarray Data; Chapman & Hall/CRC: Boca Raton, FL, USA, 2003. [Google Scholar]
- Ding, C.; Peng, H. Minimum redundancy feature selection from microarray gene expression data. In Proceedings of the IEEE Bioinformatics Conference, Stanford, CA, USA, 11–14 August 2003; pp. 523–528. [Google Scholar]
- Leung, Y.Y.; Chang, C.Q.; Hung, Y.S.; Fung, P.C.W. Gene selection for brain cancer classification. In Proceedings of the International Conference of the IEEE Engineering in Medicine and Biology Society Embs ’06, New York, NY, USA, 30 August–3 September 2006; pp. 5846–5849. [Google Scholar]
- Hall, M.A. Correlation-Based Feature Selection for Machine Learning; University of Waikato: Hamilton, New Zealand, 1999; p. 19. [Google Scholar]
- Peng, H.; Long, F.; Ding, C. Feature selection based on mutual information: criteria of max-dependency, max-relevance, and min-redundancy. IEEE Comput. Soc. 2005, 8, 1226–1238. [Google Scholar]
- Yu, L.; Liu, H. Feature selection for high-dimensional data: A fast correlation-based filter solution. In Proceedings of the Twentieth International Conference on International Conference on Machine Learning, Washington, DC, USA, 21–24 August 2003; pp. 856–863. [Google Scholar]
- Liu, J.; Zhou, H.B. Tumor classification based on gene microarray data and hybrid learning method. In Proceedings of the International Conference on Machine Learning and Cybernetics, Xi’an, China, 5 November 2003; Volume 4, pp. 2275–2280. [Google Scholar]
- Shreem, S.S.; Abdullah, S.; Nazri, M.Z.A.; Alzaqebah, M. Hybridizing relief, mRMR filters and GA wrapper approaches for gene selection. J. Theor. Appl. Inform. Technol. 2013, 46, 1034–1039. [Google Scholar]
- Brahim, A.B.; Limam, M. Robust ensemble feature selection for high dimensional data sets. In Proceedings of the International Conference on High Performance Computing and Simulation, Helsinki, Finland, 1–5 July 2013; pp. 151–157. [Google Scholar]
- Inza, I.; Larrañaga, P.; Blanco, R.; Cerrolaza, A.J. Filter versus wrapper gene selection approaches in DNA microarray domains. Artif. Intell. Med. 2004, 31, 91–103. [Google Scholar] [CrossRef] [PubMed]
- Tabakhi, S.; Moradi, P.; Akhlaghian, F. An unsupervised feature selection algorithm based on ant colony optimization. Eng. Appl. Artif. Intell. 2014, 32, 112–123. [Google Scholar] [CrossRef]
- Choe, Y. Information criterion for minimum cross-entropy model selection. arXiv, 2017; arXiv:1704.04315. [Google Scholar]
- Rubinstein, R.Y.; Kroese, D.P. The Cross-Entropy Method: A unified Approach to Combinatiorial Optimization, Monte-Carlo Simulation and Machine Learning; Springer: New York, NY, USA, 2004; pp. 92–94. [Google Scholar]
- Botev, Z.I.; Kroese, D.P.; Rubinstein, R.Y.; L’Ecuyer, P. The cross-entropy method for optimization. Handb. Stat. 2013, 31, 35–59. [Google Scholar]
- Benham, T.; Duan, Q.; Kroese, D.P.; Liquet, B. CEoptim: cross-entropy R package for optimization. arXiv, 2015; arXiv:1503.01842. [Google Scholar]
- Su, Y.; Li, Y.; Zhang, Z.; Pan, L. Feature identification for phenotypic classification based on genes and gene pairs. Curr. Bioinform. 2017, 12. [Google Scholar] [CrossRef]
- Lin, S.; Ding, J. Integration of ranked lists via cross entropy Monte Carlo with applications to mRNA and microRNA Studies. Biometrics 2009, 65, 9. [Google Scholar] [CrossRef] [PubMed]
- Bala, R.; Agrawal, R.K. Mutual information and cross entropy framework to determine relevant gene subset for cancer classification. Informatica 2011, 35, 375–382. [Google Scholar]
- Li, X.; Lu, H.; Wang, M. A hybrid gene selection method for multi-category tumor classification using microarray data. Int. J. Bioautomation 2013, 17, 249–258. [Google Scholar]
- Utkin, L.V.; Zhuk, Y.A.; Chekh, A.I. An ensemble-based feature selection algorithm using combination of support vector machine and filter methods for solving classification problems. Eur. J. Technol. Des. 2013, 1, 70–76. [Google Scholar] [CrossRef]
- Duan, K.B.; Rajapakse, J.C.; Wang, H.; Azuaje, F. Multiple SVM-RFE for gene selection in cancer classification with expression data. IEEE Trans. Nanobiosci. 2005, 4, 228–234. [Google Scholar] [CrossRef]
- Abeel, T.; Helleputte, T.; van de Peer, Y.; Dupont, P.; Saeys, Y. Robust biomarker identification for cancer diagnosis with ensemble feature selection methods. Bioinformatics 2010, 26, 392–398. [Google Scholar] [CrossRef] [PubMed]
- Microarray Datasets. Available online: http://csse.szu.edu.cn/staff/zhuzx/Datasets.html (accessed on 11 July 2017).
- Hengpraprohm, S. GA-Based Classifier with SNR weighted features for cancer microarray data classification. Int. J. Signal Proc. Syst. 2013, 1, 29–33. [Google Scholar] [CrossRef][Green Version]
- Li, X.; Peng, S.; Chen, J.; Lü, B.; Zhang, H.; Lai, M. SVM-T-RFE: A novel gene selection algorithm for identifying metastasis-related genes in colorectal cancer using gene expression profiles. Biochem. Biophys. Res. Commun. 2012, 419, 148–153. [Google Scholar] [CrossRef] [PubMed]
- Benesty, J.; Chen, J.; Huang, Y. On the importance of the Pearson correlation coefficient in noise reduction. IEEE Trans. Audio Speech Lang. Proc. 2008, 16, 757–765. [Google Scholar] [CrossRef]
- Hui, K.P.; Bean, N.; Kraetzl, M.; Kroese, D.P. The Cross-Entropy method for network reliability estimation. Ann. Oper. Res. 2005, 134, 101. [Google Scholar] [CrossRef]
- Rubinstein, R. The Cross-Entropy Method for Combinatorial and Continuous Optimization. Methodol. Comput. Appl. Probab. 1999, 1, 127–190. [Google Scholar] [CrossRef]
- Chan, J.C.; Eisenstat, E. Marginal likelihood estimation with the cross-entropy method. Econom. Rev. 2015, 34, 256–285. [Google Scholar] [CrossRef]
- Qi, X.; Liang, C.; Zhang, J. Generalized cross-entropy based group decision making with unknown expert and attribute weights under interval-valued intuitionistic fuzzy environment. Comput. Ind. Eng. 2015, 79, 52–64. [Google Scholar] [CrossRef]
- Li, X.; Peng, S. Identification of metastasis-associated genes in colorectal cancer through an integrated genomic and transcriptomic analysis. Chin. J. Cancer Res. 2013, 25, 623–636. [Google Scholar] [PubMed]
- Kapur, J.N.; Kesavan, H.K. Entropy optimization principles and Their Applications. Water Sci. Technol. Libr. 1992, 9, 3–20. [Google Scholar]
- Hall, M.; Frank, E.; Holmes, G.; Pfahringer, B.; Reutemann, P.; Witten, I. The WEKA data mining software: An update. ACM SIGKDD Explor. Newsl. 2009, 11, 10–18. [Google Scholar] [CrossRef]
- Li, X.; Gong, X.; Peng, X.; Peng, S. SSiCP: a new SVM based Recursive Feature Elimination Algorithm for Multiclass Cancer Classification. Int. J. Multimed. Ubiquituos Eng. 2014, 9, 347–360. [Google Scholar] [CrossRef]

| Dataset | Samples | Number of Samples | Classes | |
|---|---|---|---|---|
| Class 1 | Class 2 | |||
| Colon | 2000 | 40 (T) | 22 (N) | 2 |
| Prostate | 12,600 | 52 (T) | 50 (N) | 2 |
| Leukemia | 7129 | 25 (AML) | 47 (ALL) | 2 |
| Lymphoma | 7129 | 58 (DLBCL) | 19 (FL) | 2 |
| Lung | 12600 | 31 (MPM) | 150 (ADCA) | 2 |
| Dataset | Classifier | CEMFE | SNRCE | TSCE | PCCE |
|---|---|---|---|---|---|
| Colon | SVM | 93.55 (23) | 90.32 (7) | 90.32 (18) | 93.55 (33) |
| KNN | 96.77 (14) | 88.71 (17) | 83.87 (13) | 90.32 (7) | |
| NB | 96.77 (9) | 88.71 (17) | 85.48 (6) | 91.91 (21) | |
| Prostate | SVM | 97.10 (17) | 88.24 (11) | 97.10 (22) | 91.18 (7) |
| KNN | 98.04 (9) | 94.12 (26) | 90.20 (10) | 98.04 (15) | |
| NB | 96.10 (9) | 89.22 (13) | 93.14 (22) | 92.16 (27) | |
| Leukemia | SVM | 97.22 (6) | 95.83 (17) | 90.28 (17) | 95.83 (35) |
| KNN | 98.61 (7) | 89.06 (28) | 88.89 (23) | 93.06 (8) | |
| NB | 100 (12) | 83.33 (26) | 96.88 (19) | 94.44 (33) | |
| Lymphoma | SVM | 100 (26) | 88.31 (34) | 96.10 (66) | 84.42 (36) |
| KNN | 98.70 (16) | 93.51 (7) | 79.22 (14) | 97.40 (41) | |
| NB | 98.70 (18) | 94.81 (9) | 96.10 (14) | 80.52 (22) | |
| Lung | SVM | 100 (4) | 98.34 (24) | 100 (36) | 99.45 (33) |
| KNN | 100 (3) | 100 (21) | 100 (40) | 100 (18) | |
| NB | 98.90 (9) | 96.13 (17) | 98.90 (23) | 98.90 (41) |
| Dataset | NB | KNN | ||||
|---|---|---|---|---|---|---|
| FCBF | mRMR | CEMFE | FCBF | mRMR | CEMFE | |
| Colon | 91.94 | 88.79 | 96.77 | 88.71 | 77.42 | 96.77 |
| Prostate | 97.06 | 98.04 | 96.08 | 97.06 | 97.06 | 98.04 |
| Leukemia | 100 | 100 | 100 | 100 | 100 | 98.61 |
| Lymphoma | 93.51 | 94.81 | 98.70 | 93.51 | 97.40 | 98.70 |
| Lung | 86.67 | 99.13 | 100 | 83.33 | 96.13 | 98.90 |
| Average | 93.84 | 96.15 | 98.31 | 92.52 | 93.60 | 98.20 |
| N/Data Set | Colon | Prostate | Leukemia | Lymphoma | Lung | |
|---|---|---|---|---|---|---|
| 50 | Avg. no. of genes | 15.3 | 12.3 | 8.3 | 20 | 5.3 |
| Avg. performance | 95.70 | 97.08 | 98.61 | 99.13 | 99.63 | |
| 100 | Avg. no. of genes | 10.6 | 12.3 | 11.6 | 20 | 5.3 |
| Avg. performance | 93.55 | 95.93 | 93.06 | 100 | 99.63 | |
| 200 | Avg. no. of genes | 10.6 | 12.3 | 13.3 | 22.3 | 3.6 |
| Avg. performance | 91.94 | 95.93 | 90.28 | 98.70 | 98.90 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.; Lu, C.; Li, X. The Cross-Entropy Based Multi-Filter Ensemble Method for Gene Selection. Genes 2018, 9, 258. https://doi.org/10.3390/genes9050258
Sun Y, Lu C, Li X. The Cross-Entropy Based Multi-Filter Ensemble Method for Gene Selection. Genes. 2018; 9(5):258. https://doi.org/10.3390/genes9050258
Chicago/Turabian StyleSun, Yingqiang, Chengbo Lu, and Xiaobo Li. 2018. "The Cross-Entropy Based Multi-Filter Ensemble Method for Gene Selection" Genes 9, no. 5: 258. https://doi.org/10.3390/genes9050258
APA StyleSun, Y., Lu, C., & Li, X. (2018). The Cross-Entropy Based Multi-Filter Ensemble Method for Gene Selection. Genes, 9(5), 258. https://doi.org/10.3390/genes9050258




