FST-Based Marker Prioritization Within Quantitative Trait Loci Regions and Its Impact on Genomic Selection Accuracy: Insights from a Simulation Study with High-Density Marker Panels for Bovines
Abstract
1. Introduction
2. Materials and Methods
2.1. Simulation: Population Structure
2.2. Genome Structure
2.3. SNP Prioritization Method: FST Approach
- (1)
- Global FST scores are calculated for all 600K SNPs in the panel using Equation (1) and the 25% quantile of FST score distribution is determined as the global threshold point. To justify this specific threshold, a preliminary grid search across a range of FST quantile values was conducted. This analysis revealed that using the 25% quantile allowed for the identification of genomic windows encompassing approximately 99% of the simulated QTL, which collectively accounted for 98% and 93% of the total genetic variance in the simulation for the 500 and 2000 simulated QTL scenarios, respectively.
- (2)
- The average FST scores for each window and QTL position is calculated (e.g., 50 SNP up and down stream of the QTL). This window-based averaging helped identify broader genomic regions under selection rather than relying on individual SNP scores.
- (3)
- QTL regions with average window’s FST scores exceeding a defined threshold (e.g., average scores based on all 600K SNP markers) are qualified and retained. This step further refines the selection to focus on regions exhibiting strong signals of genomic differentiation.
- (4)
- Within a window surrounding each retained QTL region, a small number of SNPs are randomly prioritized. The goal is to retain 1% (6000 SNPs) of the total SNPs in the panel for subsequent analyses.
2.4. Statistical Model and Data Analysis
3. Results
3.1. Detected QTL and Their Contribution to the Total Genetic Variance
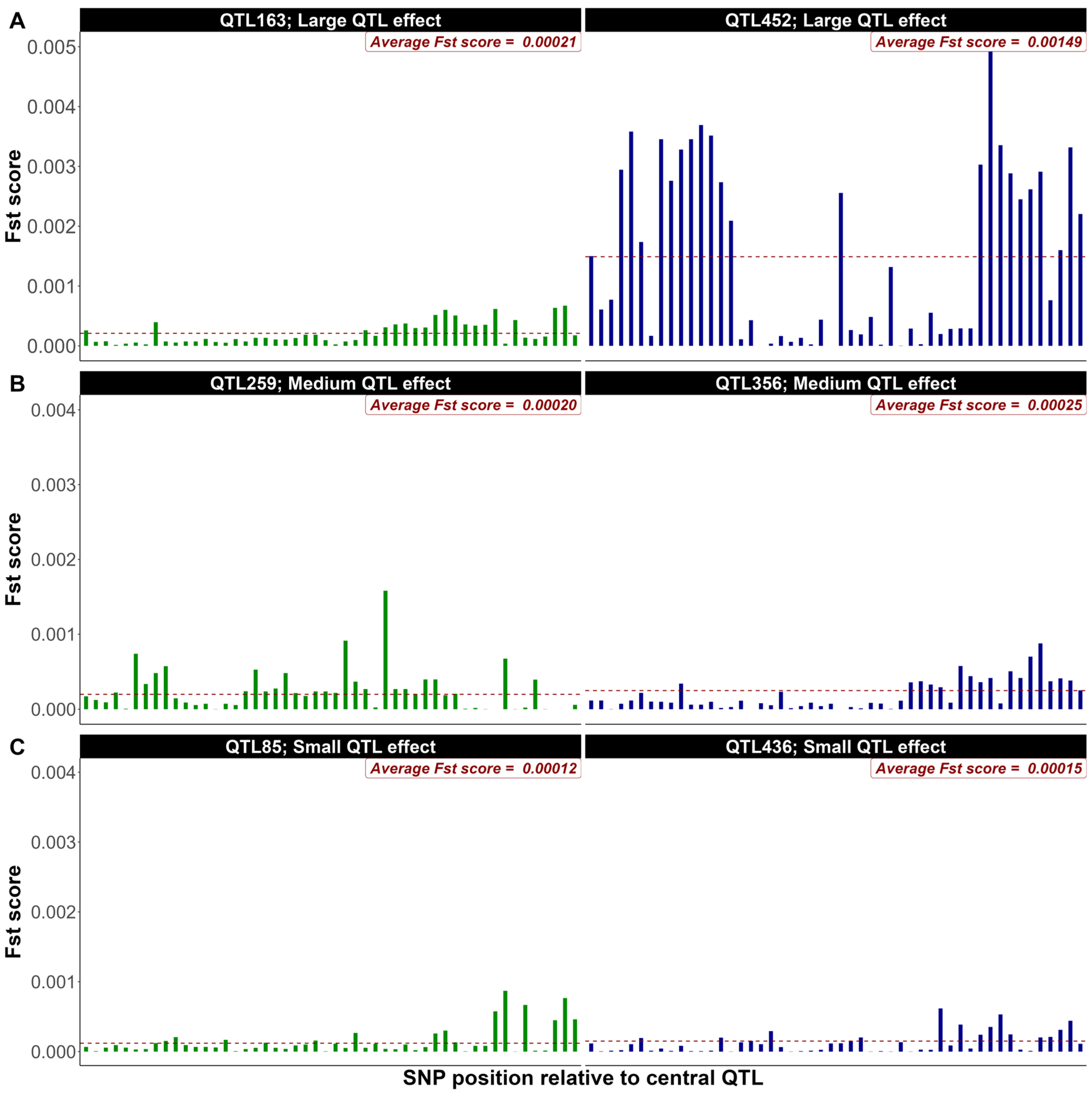
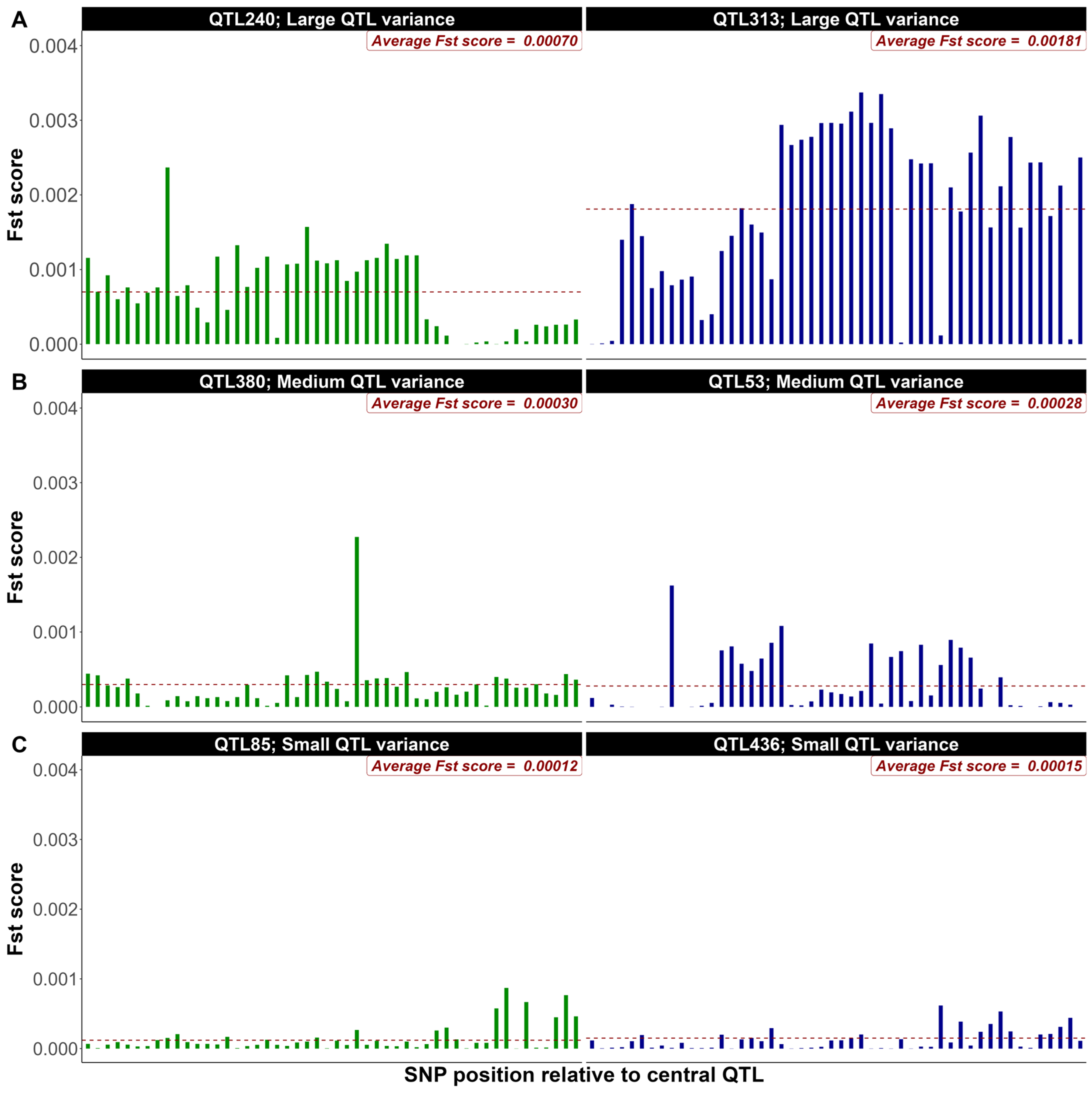
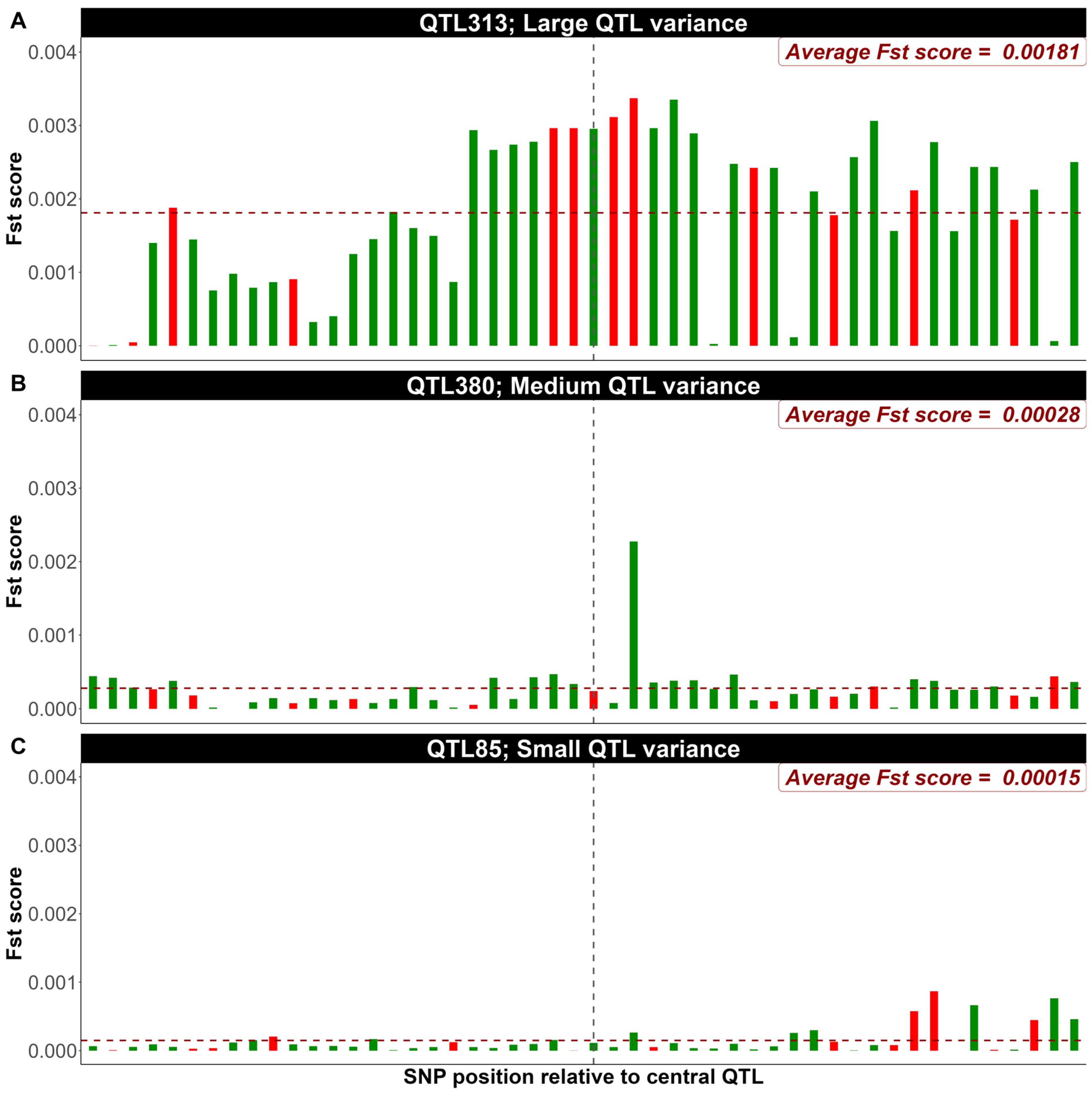
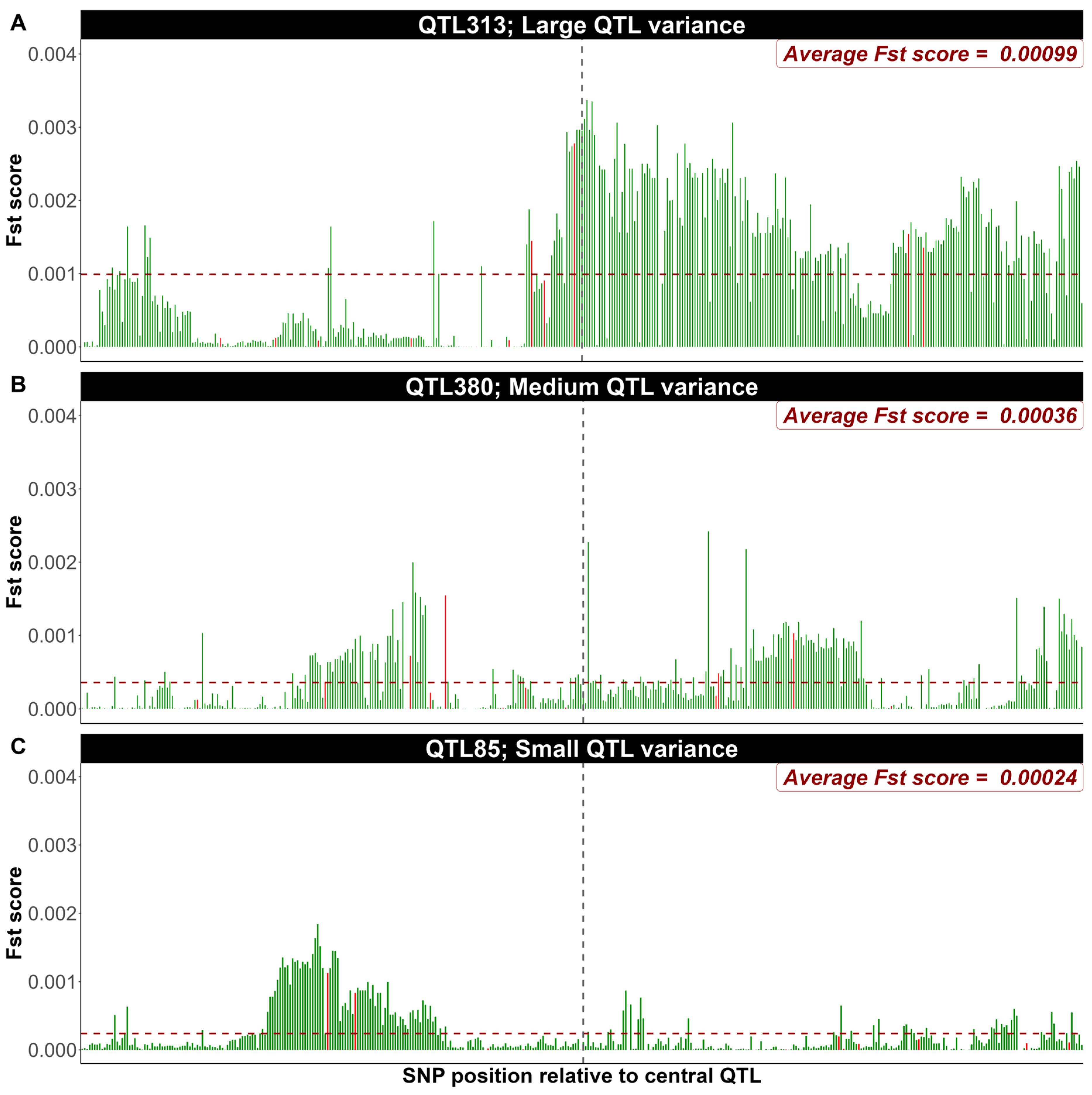
3.2. Exploring FST Score Patterns Across QTL Effect Classes
3.3. Genomic Predictions Across the Different Simulation Scenarios
4. Discussion
4.1. Detected QTL and Their Contribution to the Total Genetic Variance
4.2. Exploring FST Score Patterns Across QTL Effect Classes
4.3. Genomic Predictions Across the Different Simulation Scenarios
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schefers, J.M.; Weigel, K.A. Genomic Selection in Dairy Cattle: Integration of DNA Testing into Breeding Programs. Anim. Front. 2012, 2, 4–9. [Google Scholar] [CrossRef]
- VanRaden, P.; Van Tassell, C.; Wiggans, G.; Sonstegard, T.; Schnabel, R.; Taylor, J.; Schenkel, F. Invited Review: Reliability of Genomic Predictions for North American Holstein Bulls. J. Dairy Sci. 2009, 92, 16–24. [Google Scholar] [CrossRef]
- Su, G.; Guldbrandtsen, B.; Gregersen, V.; Lund, M. Preliminary Investigation on Reliability of Genomic Estimated Breeding Values in the Danish Holstein Population. J. Dairy Sci. 2010, 93, 1175–1183. [Google Scholar] [CrossRef]
- Su, G.; Brøndum, R.F.; Ma, P.; Guldbrandtsen, B.; Aamand, G.P.; Lund, M.S. Comparison of Genomic Predictions Using Medium-Density (∼54,000) and High-Density (∼777,000) Single Nucleotide Polymorphism Marker Panels in Nordic Holstein and Red Dairy Cattle Populations. J. Dairy Sci. 2012, 95, 4657–4665. [Google Scholar] [CrossRef]
- Meuwissen, T.; Hayes, B.; Goddard, M. Genomic Selection: A Paradigm Shift in Animal Breeding. Anim. Front. 2016, 6, 6–14. [Google Scholar] [CrossRef]
- Zhao, C.; Teng, J.; Zhang, X.; Wang, D.; Zhang, X.; Li, S.; Jiang, X.; Li, H.; Ning, C.; Zhang, Q. Towards a Cost-Effective Implementation of Genomic Prediction Based on Low Coverage Whole Genome Sequencing in Dezhou Donkey. Front. Genet. 2021, 12, 728764. [Google Scholar] [CrossRef]
- Hickey, J.M. Sequencing Millions of Animals for Genomic Selection 2.0. J. Anim. Breed. Genet. 2013, 130, 331–332. [Google Scholar] [CrossRef]
- Georges, M. Towards Sequence-Based Genomic Selection of Cattle. Nat. Genet. 2014, 46, 807–809. [Google Scholar] [CrossRef] [PubMed]
- Daetwyler, H.D.; Capitan, A.; Pausch, H.; Stothard, P.; van Binsbergen, R.; Brøndum, R.F.; Liao, X.; Djari, A.; Rodriguez, S.C.; Grohs, C.; et al. Whole-Genome Sequencing of 234 Bulls Facilitates Mapping of Monogenic and Complex Traits in Cattle. Nat. Genet. 2014, 46, 858–865. [Google Scholar] [CrossRef]
- Solberg, T.R.; Sonesson, A.K.; Woolliams, J.A.; Meuwissen, T.H.E. Genomic Selection Using Different Marker Types and Densities. J. Anim. Sci. 2008, 86, 2447–2454. [Google Scholar] [CrossRef]
- Harris, B.; Johnson, D. The Impact of High Density SNP Chips on Genomic Evaluation in Dairy Cattle. Interbull Bull. 2010, 42, 40–43. [Google Scholar]
- VanRaden, P.M.; Null, D.J.; Sargolzaei, M.; Wiggans, G.R.; Tooker, M.E.; Cole, J.B.; Sonstegard, T.S.; Connor, E.E.; Winters, M.; Kaam, J.B.C.H.M.; et al. Genomic Imputation and Evaluation Using High-Density Holstein Genotypes. J. Dairy Sci. 2013, 96, 668–678. [Google Scholar] [CrossRef] [PubMed]
- Toghiani, S.; Chang, L.-Y.; Ling, A.; Aggrey, S.E.; Rekaya, R. Genomic Differentiation as a Tool for Single Nucleotide Polymorphism Prioritization for Genome Wide Association and Phenotype Prediction in Livestock. Livest. Sci. 2017, 205, 24–30. [Google Scholar] [CrossRef]
- Chang, L.-Y.; Toghiani, S.; Aggrey, S.E.; Rekaya, R. Increasing Accuracy of Genomic Selection in Presence of High Density Marker Panels through the Prioritization of Relevant Polymorphisms. BMC Genet. 2019, 20, 21. [Google Scholar] [CrossRef]
- Chang, L.-Y.; Toghiani, S.; Hay, E.H.; Aggrey, S.E.; Rekaya, R. A Weighted Genomic Relationship Matrix Based on Fixation Index (FST) Prioritized SNPs for Genomic Selection. Genes 2019, 10, 922. [Google Scholar] [CrossRef] [PubMed]
- Meuwissen, T.H.; Hayes, B.J.; Goddard, M.E. Prediction of Total Genetic Value Using Genome-Wide Dense Marker Maps. Genetics 2001, 157, 1819–1829. [Google Scholar] [CrossRef]
- Erbe, M.; Hayes, B.J.; Matukumalli, L.K.; Goswami, S.; Bowman, P.J.; Reich, C.M.; Mason, B.A.; Goddard, M.E. Improving Accuracy of Genomic Predictions within and between Dairy Cattle Breeds with Imputed High-Density Single Nucleotide Polymorphism Panels. J. Dairy Sci. 2012, 95, 4114–4129. [Google Scholar] [CrossRef]
- Chang, L.-Y.; Toghiani, S.; Ling, A.; Aggrey, S.E.; Rekaya, R. High Density Marker Panels, SNPs Prioritizing and Accuracy of Genomic Selection. BMC Genet. 2018, 19, 4. [Google Scholar] [CrossRef]
- Aggrey, S.; Toghiani, S.; Chang, L.-Y.; Rekaya, R. Improving Accuracy of Genomic Prediction Using a Selected Small Set of Prioritized SNP Markers. In Proceedings of the 68th Annual Poultry Breeders’ Round Table Conference, St. Louis, MO, USA, 2 January 2020; p. 10. [Google Scholar]
- Sargolzaei, M.; Schenkel, F.S. QMSim: A Large-Scale Genome Simulator for Livestock. Bioinformatics 2009, 25, 680–681. [Google Scholar] [CrossRef]
- Wright, S. The Genetical Structure of Populations. Ann. Eugen. 1951, 15, 323–354. [Google Scholar] [CrossRef]
- Nei, M. Analysis of Gene Diversity in Subdivided Populations. Proc. Natl. Acad. Sci. USA 1973, 70, 3321–3323. [Google Scholar] [CrossRef] [PubMed]
- Misztal, I.; Tsuruta, S.; Lourenco, D.; Masuda, Y.; Aguilar, I.; Legarra, A.; Vitezica, Z.G. BLUPF90 Family of Programs. 2022. Available online: http://nce.ads.uga.edu/software/ (accessed on 22 March 2025).
- Wang, S.; Xie, F.; Xu, S. Estimating Genetic Variance Contributed by a Quantitative Trait Locus: A Random Model Approach. PLoS Comput. Biol. 2022, 18, e1009923. [Google Scholar] [CrossRef] [PubMed]
- Ribeiro, A.; Golicz, A.; Hackett, C.A.; Milne, I.; Stephen, G.; Marshall, D.; Flavell, A.J.; Bayer, M. An Investigation of Causes of False Positive Single Nucleotide Polymorphisms Using Simulated Reads from a Small Eukaryote Genome. BMC Bioinform. 2015, 16, 382. [Google Scholar] [CrossRef] [PubMed]
- Farrer, R.A.; Henk, D.A.; MacLean, D.; Studholme, D.J.; Fisher, M.C. Using False Discovery Rates to Benchmark SNP-Callers in next-Generation Sequencing Projects. Sci. Rep. 2013, 3, 1512. [Google Scholar] [CrossRef]
- Muir, W.M. Comparison of Genomic and Traditional BLUP-Estimated Breeding Value Accuracy and Selection Response under Alternative Trait and Genomic Parameters. J. Anim. Breed. Genet. 2007, 124, 342–355. [Google Scholar] [CrossRef]
- Habier, D.; Fernando, R.L.; Dekkers, J.C.M. The Impact of Genetic Relationship Information on Genome-Assisted Breeding Values. Genetics 2007, 177, 2389–2397. [Google Scholar] [CrossRef]
- Calus, M.P.L.; Meuwissen, T.H.E.; de Roos, A.P.W.; Veerkamp, R.F. Accuracy of Genomic Selection Using Different Methods to Define Haplotypes. Genetics 2008, 178, 553–561. [Google Scholar] [CrossRef]
| Population Structure | |
|---|---|
| Step 1: Historical generations (HG) | |
| Size of HG [number of generations] | 5000[0] 400[1000] 50,000[1300] |
| Step 2: Recent generations | |
| Founder male selected from HG | 100 |
| Founder female selected from HG | 15,000 |
| Number of offspring per dam | 1 |
| Mating design | random |
| Selection design | EBV |
| EBV estimation method | BLUP animal model |
| Sex ratio | 0.50 |
| Sire replacement rate | 0.50 |
| Dam replacement rate | 0.30 |
| Number of generations | 10 |
| Genotyped generations | 9, 10 |
| Heritability of trait | 0.40, 0.10 |
| Phenotypic variance | 1 |
| Genomic structure | |
| Number of Chromosomes | 29 |
| Total Chromosome length | 2319 cM |
| Number of SNP markers | 600K SNP |
| Marker distribution | Evenly spaced |
| Number of QTL | 500, 2000 |
| QTL distribution | Random |
| MAF threshold for markers and QTL | 0.05 |
| QTL allele effects | Normal distribution |
| Marker and QTL recurrent mutation | 2.5 × 10−5 |
| QTL Group 1 | # Simulated QTL | # Selected QTL | Allele Substitution | Variance Explained (%) | ||
|---|---|---|---|---|---|---|
| Mean | SD | Mean | SD | |||
| Top 5% | 500 | 25 | 0.1056 | 0.0163 | 1.063 | 0.338 |
| 2000 | 100 | 0.0515 | 0.0076 | 0.283 | 0.116 | |
| Q25_Q75 | 500 | 250 | 0.0315 | 0.0107 | 0.103 | 0.065 |
| 2000 | 1000 | 0.0156 | 0.0052 | 0.024 | 0.016 | |
| Bottom 5% | 500 | 25 | 0.0013 | 0.0007 | 0.00017 | 0.00015 |
| 2000 | 100 | 0.0008 | 0.0005 | 0.00006 | 0.00006 | |
| Scenarios 1 | Large QTL | Medium QTL | Small QTL | |||
|---|---|---|---|---|---|---|
| 95% Quantile 2 | 25–75% Quantiles | 5% Quantile | ||||
| Mean | SD | Mean | SD | Mean | SD | |
| W1Q1 | 0.00056 | 0.00043 | 0.00037 | 0.00031 | 0.00038 | 0.00034 |
| W2Q1 | 0.00052 | 0.00048 | 0.00037 | 0.00036 | 0.00041 | 0.00037 |
| W3Q1 | 0.00045 | 0.00046 | 0.00037 | 0.00041 | 0.00040 | 0.00043 |
| W4Q1 | 0.00038 | 0.00044 | 0.00037 | 0.00045 | 0.00038 | 0.00046 |
| W1Q2 | 0.00050 | 0.00040 | 0.00042 | 0.00035 | 0.00041 | 0.00037 |
| W2Q2 | 0.00049 | 0.00046 | 0.00041 | 0.00041 | 0.00040 | 0.00039 |
| W3Q2 | 0.00045 | 0.00049 | 0.00041 | 0.00046 | 0.00041 | 0.00045 |
| W4Q2 | 0.00045 | 0.00053 | 0.00042 | 0.00051 | 0.00042 | 0.00049 |
| Scenarios 1 | #QTL | # SNPs | %GV | VG | VE | h2 | Accuracy |
|---|---|---|---|---|---|---|---|
| FULL600K | 500 | 600K | 96.86 | 0.35 | 0.61 | 0.37 (0.005) | 0.77 (0.006) |
| Top1%FST | - | 6000 | - | 0.27 | 0.76 | 0.26 (0.014) | 0.60 (0.020) |
| W1Q1P2 | 496 | 5906 | 95.91 | 0.32 | 0.62 | 0.34 (0.004) | 0.88 (0.004) |
| W2Q1P2 | 498 | 5949 | 96.48 | 0.32 | 0.62 | 0.34 (0.005) | 0.85 (0.002) |
| W3Q1P2 | 499 | 5964 | 96.45 | 0.32 | 0.63 | 0.34 (0.005) | 0.82 (0.004) |
| W4Q1P2 | 498 | 5950 | 96.36 | 0.31 | 0.65 | 0.32 (0.002) | 0.78 (0.006) |
| Scenarios 1 | #QTL | # SNPs | %GV | VG | VE | h2 | Accuracy |
|---|---|---|---|---|---|---|---|
| FULL600K | 500 | 600K | 96.87 | 0.10 | 0.90 | 0.10 (0.004) | 0.66 (0.007) |
| Top1%FST | - | 6000 | - | 0.06 | 0.94 | 0.06 (0.002) | 0.48 (0.013) |
| W1Q1P2 | 493 | 5887 | 95.47 | 0.09 | 0.90 | 0.09 (0.002) | 0.78 (0.007) |
| W2Q1P2 | 498 | 5944 | 96.47 | 0.09 | 0.90 | 0.09 (0.002) | 0.75 (0.007) |
| W3Q1P2 | 499 | 5957 | 96.65 | 0.09 | 0.91 | 0.09 (0.002) | 0.71 (0.007) |
| W4Q1P2 | 498 | 5950 | 96.63 | 0.09 | 0.91 | 0.09 (0.002) | 0.68 (0.009) |
| Scenarios 1 | #QTL | # SNPs | %GV | VG | VE | h2 | Accuracy |
|---|---|---|---|---|---|---|---|
| FULL600K | 2000 | 600K | 96.69 | 0.36 | 0.60 | 0.37 (0.01) | 0.78 (0.01) |
| Top1%FST | - | 6000 | - | 0.25 | 0.76 | 0.25 (0.007) | 0.56 (0.02) |
| W1Q2P1 | 1976 | 5901 | 95.25 | 0.32 | 0.63 | 0.34 (0.004) | 0.83 (0.01) |
| W2Q2P1 | 1995 | 5954 | 96.22 | 0.31 | 0.65 | 0.32 (0.004) | 0.80 (0.01) |
| W3Q2P1 | 1997 | 5948 | 96.41 | 0.31 | 0.65 | 0.32 (0.003) | 0.76 (0.01) |
| W4Q2P1 | 1991 | 5929 | 96.17 | 0.29 | 0.66 | 0.30 (0.003) | 0.75 (0.01) |
| Scenarios 1 | #QTL | # SNPs | %GV | VG | VE | h2 | Accuracy |
|---|---|---|---|---|---|---|---|
| FULL600K | 2000 | 600K | 94.42 | 0.09 | 0.90 | 0.09 (0.004) | 0.64 (0.004) |
| Top1%FST | - | 6000 | - | 0.05 | 0.95 | 0.05 (0.004) | 0.43 (0.014) |
| W1Q2P1 | 1975 | 5888 | 93.17 | 0.08 | 0.91 | 0.08 (0.004) | 0.67 (0.004) |
| W2Q2P1 | 1995 | 5955 | 94.12 | 0.08 | 0.91 | 0.08 (0.003) | 0.65 (0.005) |
| W3Q2P1 | 1996 | 5957 | 94.28 | 0.08 | 0.91 | 0.08 (0.003) | 0.63 (0.005) |
| W4Q2P1 | 1992 | 5943 | 94.07 | 0.08 | 0.92 | 0.08 (0.004) | 0.62 (0.008) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Toghiani, S.; Aggrey, S.E.; Rekaya, R. FST-Based Marker Prioritization Within Quantitative Trait Loci Regions and Its Impact on Genomic Selection Accuracy: Insights from a Simulation Study with High-Density Marker Panels for Bovines. Genes 2025, 16, 563. https://doi.org/10.3390/genes16050563
Toghiani S, Aggrey SE, Rekaya R. FST-Based Marker Prioritization Within Quantitative Trait Loci Regions and Its Impact on Genomic Selection Accuracy: Insights from a Simulation Study with High-Density Marker Panels for Bovines. Genes. 2025; 16(5):563. https://doi.org/10.3390/genes16050563
Chicago/Turabian StyleToghiani, Sajjad, Samuel E. Aggrey, and Romdhane Rekaya. 2025. "FST-Based Marker Prioritization Within Quantitative Trait Loci Regions and Its Impact on Genomic Selection Accuracy: Insights from a Simulation Study with High-Density Marker Panels for Bovines" Genes 16, no. 5: 563. https://doi.org/10.3390/genes16050563
APA StyleToghiani, S., Aggrey, S. E., & Rekaya, R. (2025). FST-Based Marker Prioritization Within Quantitative Trait Loci Regions and Its Impact on Genomic Selection Accuracy: Insights from a Simulation Study with High-Density Marker Panels for Bovines. Genes, 16(5), 563. https://doi.org/10.3390/genes16050563






