Optimizing Model Performance and Interpretability: Application to Biological Data Classification
Abstract
1. Introduction
- We propose a novel framework that integrates interpretable feature selection and robust model selection by incorporating adversarial samples, thereby enhancing both predictive performance and biological interpretability.
- We introduce a domain-specific feature selection strategy based on target-related pathways in transcriptomic data, which outperforms conventional general-purpose methods.
- We develop a stacking meta-classifier that demonstrates superior performance in both binary and ternary classification problems, underscoring its potential for broad applications in omics data analysis.
2. Materials and Methods
2.1. Datasets
2.2. Basic Machine Learning Models
2.3. Feature Selection for Transcriptomic-Data-Based Classification
2.4. Model Selection for a Given Classification Problem
2.5. Constructing an Integrative Pipeline
2.6. Comparative Evaluation of Predictive Performance, Interpretability, and Robustness of Models
3. Results
3.1. Feature Gene Selection
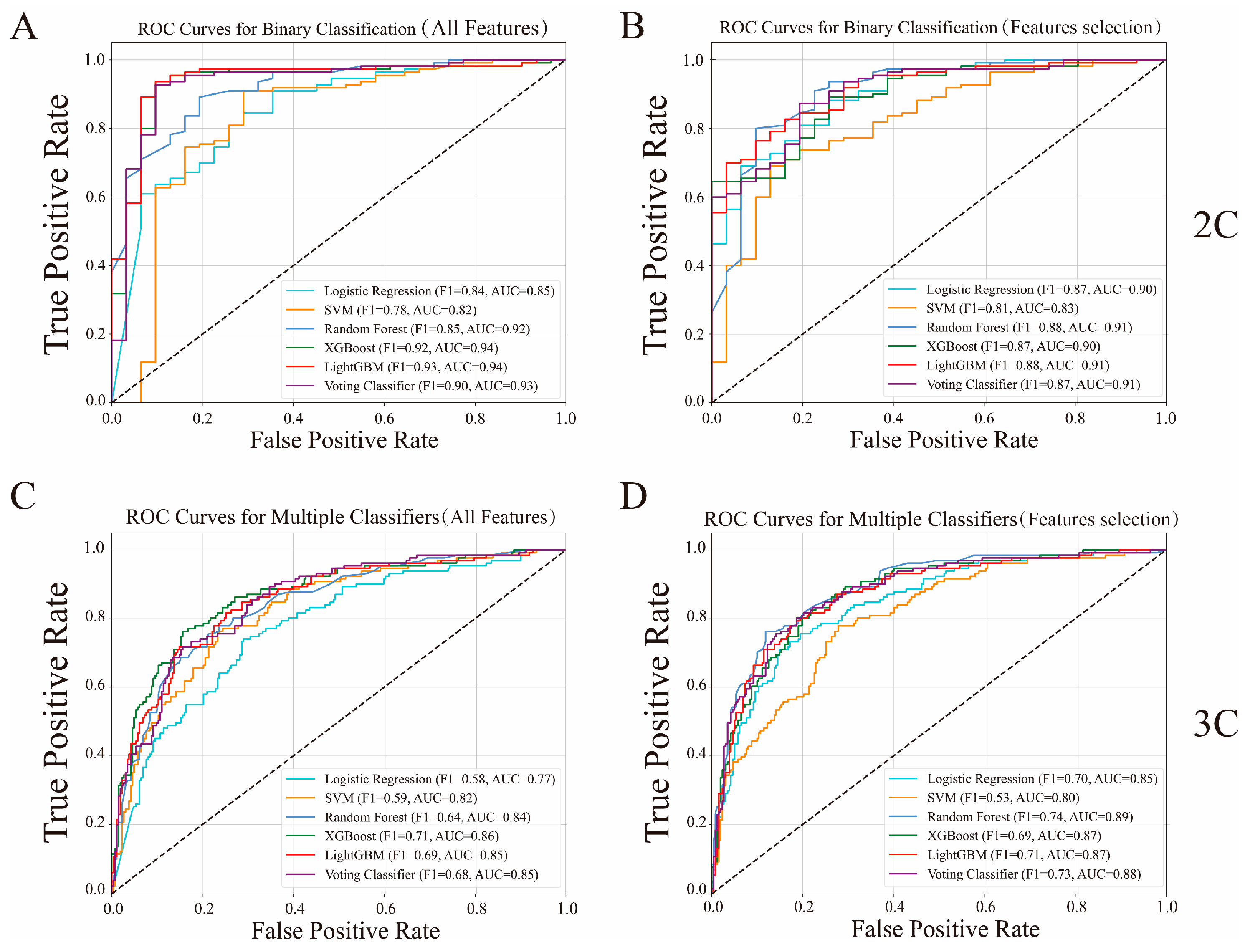
3.2. Model Assessment
3.3. Performance Analysis of a Stacking-Based Voting Meta-Classifier
3.4. Comparison Between General-Purpose Feature Selection and Our Feature Selection
3.5. Comparison of Model Interpretability
3.5.1. Comparison with the White-Box Models
3.5.2. Comparison with SHAP Models
3.5.3. Comparison with Neural Network Models
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Valous, N.A.; Popp, F.; Zörnig, I.; Jäger, D.; Charoentong, P. Graph machine learning for integrated multi-omics analysis. Br. J. Cancer 2024, 131, 205–211. [Google Scholar] [CrossRef] [PubMed]
- Shen, C. Fast and Scalable Multi-Kernel Encoder Classifier. In Proceedings of the Future Technologies Conference 2024, London, UK, 14–15 November 2024; Volume 1156, pp. 161–177. [Google Scholar] [CrossRef]
- Tolles, J.; Meurer, W.J. Logistic Regression: Relating Patient Characteristics to Outcomes. JAMA 2016, 316, 533–534. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. LightGBM: A Highly Efficient Gradient Boosting Decision Tree. In Advances in Neural Information Processing Systems; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates, Inc.: New York, NY, USA, 2017; Available online: https://proceedings.neurips.cc/paper_files/paper/2017/file/6449f44a102fde848669bdd9eb6b76fa-Paper.pdf (accessed on 4 December 2017).
- Wolpert, D.H. What is important about the No Free Lunch theorems? arXiv 2020, arXiv:2007.10928. [Google Scholar] [CrossRef]
- Doshi-Velez, F.; Kim, B. Towards A Rigorous Science of Interpretable Machine Learning. arXiv 2017, arXiv:1702.08608. [Google Scholar] [CrossRef]
- Rudin, C. Stop explaining black box machine learning models for high stakes decisions and use interpretable models instead. Nat. Mach. Intell. 2019, 1, 206–215. [Google Scholar] [CrossRef]
- Caruana, R.; Lou, Y.; Gehrke, J.; Koch, P.; Sturm, M.; Elhadad, N. Intelligible Models for HealthCare: Predicting Pneumonia Risk and Hospital 30-day Readmission. In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, in KDD ’15, Sydney, Australia, 10–13 August 2015; Association for Computing Machinery: New York, NY, USA, 2015; pp. 1721–1730. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.-I. A unified approach to interpreting model predictions. In Proceedings of the 31st International Conference on Neural Information Processing Systems, in NIPS’17, Long Beach, CA, USA, 4–9 December 2017; Curran Associates Inc.: Red Hook, NY, USA, 2017; pp. 4768–4777. [Google Scholar]
- Rudin, C.; Chen, C.; Chen, Z.; Huang, H.; Semenova, L.; Zhong, C. Interpretable Machine Learning: Fundamental Principles and 10 Grand Challenges. arXiv 2021, arXiv:2103.11251. [Google Scholar] [CrossRef]
- Cedergreen, N.; Pedersen, K.E.; Fredensborg, B.L. Quantifying synergistic interactions: A meta-analysis of joint effects of chemical and parasitic stressors. Sci. Rep. 2023, 13, 13641. [Google Scholar] [CrossRef]
- Guo, Y.; Hu, H.; Chen, W.; Yin, H.; Wu, J.; Hsieh, C.-Y.; He, Q.; Cao, J. SynergyX: A multi-modality mutual attention network for interpretable drug synergy prediction. Brief. Bioinform. 2024, 25, bbae015. [Google Scholar] [CrossRef] [PubMed]
- He, S.; Chen, H.; Zhu, Z.; Ward, D.G.; Cooper, H.J.; Viant, M.R.; Heath, J.K.; Yao, X. Robust twin boosting for feature selection from high-dimensional omics data with label noise. Inf. Sci. 2015, 291, 1–18. [Google Scholar] [CrossRef]
- Xiao, G.; Guan, R.; Cao, Y.; Huang, Z.; Xu, Y. KISL: Knowledge-injected semi-supervised learning for biological co-expression network modules. Front. Genet. 2023, 14, 1151962. [Google Scholar] [CrossRef] [PubMed]
- Kurakin, A.; Goodfellow, I.; Bengio, S. Adversarial examples in the physical world. arXiv 2017, arXiv:1607.02533. [Google Scholar] [CrossRef]
- Sheng, J.; Lam, S.; Zhang, J.; Zhang, Y.; Cai, J. Multi-omics fusion with soft labeling for enhanced prediction of distant metastasis in nasopharyngeal carcinoma patients after radiotherapy. Comput. Biol. Med. 2024, 168, 107684. [Google Scholar] [CrossRef] [PubMed]
- Pérez-González, A.P.; García-Kroepfly, A.L.; Pérez-Fuentes, K.A.; García-Reyes, R.I.; Solis-Roldan, F.F.; Alba-González, J.A.; Hernández-Lemus, E.; de Anda-Jáuregui, G. The ROSMAP project: Aging and neurodegenerative diseases through omic sciences. Front. Neuroinform. 2024, 18, 1443865. [Google Scholar] [CrossRef] [PubMed]
- Huang, Z.; Chen, Q.; Mu, X.; An, Z.; Xu, Y. Elucidating the Functional Roles of Long Non-Coding RNAs in Alzheimer’s Disease. Int. J. Mol. Sci. 2024, 25, 9211. [Google Scholar] [CrossRef]
- Mounir, M.; Lucchetta, M.; Silva, T.C.; Olsen, C.; Bontempi, G.; Chen, X.; Noushmehr, H.; Colaprico, A.; Papaleo, E. New functionalities in the TCGAbiolinks package for the study and integration of cancer data from GDC and GTEx. PLoS Comput. Biol. 2019, 15, e1006701. [Google Scholar] [CrossRef] [PubMed]
- Tomczak, K.; Czerwińska, P.; Wiznerowicz, M. The Cancer Genome Atlas (TCGA): An immeasurable source of knowledge. Contemp. Oncol. 2015, 19, A68–A77. [Google Scholar] [CrossRef]
- Zhan, P.L.; Canavan, M.E.; Ermer, T.; Pichert, M.D.; Li, A.X.; Maduka, R.C.; Kaminski, M.F.; Boffa, D.J. Nonregional Lymph Nodes as the Only Metastatic Site in Stage IV Esophageal Cancer. JTO Clin. Res. Rep. 2022, 3, 100426. [Google Scholar] [CrossRef] [PubMed]
- Park, S.-Y.; Nam, J.-S. The force awakens: Metastatic dormant cancer cells. Exp. Mol. Med. 2020, 52, 569–581. [Google Scholar] [CrossRef] [PubMed]
- Harrow, J.; Frankish, A.; Gonzalez, J.M.; Tapanari, E.; Diekhans, M.; Kokocinski, F.; Aken, B.L.; Barrell, D.; Zadissa, A.; Searle, S.; et al. GENCODE: The reference human genome annotation for The ENCODE Project. Genome Res. 2012, 22, 1760–1774. [Google Scholar] [CrossRef]
- Trupp, M.; Altman, T.; Fulcher, C.A.; Caspi, R.; Krummenacker, M.; Paley, S.; Karp, P.D. Beyond the genome (BTG) is a (PGDB) pathway genome database: HumanCyc. Genome Biol. 2010, 11 (Suppl. S1), O12. [Google Scholar] [CrossRef]
- Crammer, K.; Singer, Y. On the algorithmic implementation of multiclass kernel-based vector machines. J. Mach. Learn. Res. 2002, 2, 265–292. [Google Scholar]
- Ganaie, M.A.; Tanveer, M.; Suganthan, P.N.; Snasel, V. Oblique and rotation double random forest. Neural Netw. 2022, 153, 496–517. [Google Scholar] [CrossRef]
- Qahtan, A. Machine Learning—Evaluation (Cross-validation, Metrics, Importance Scores...). In Clinical Applications of Artificial Intelligence in Real-World Data; Asselbergs, F.W., Denaxas, S., Oberski, D.L., Moore, J.H., Eds.; Springer International Publishing: Cham, Switzerland, 2023; pp. 175–187. [Google Scholar] [CrossRef]
- Riyahi, S.; Dev, H.; Behzadi, A.; Kim, J.; Attari, H.; Raza, S.I.; Margolis, D.J.; Jonisch, A.; Megahed, A.; Bamashmos, A.; et al. Pulmonary Embolism in Hospitalized Patients with COVID-19: A Multicenter Study. Radiology 2021, 301, E426. [Google Scholar] [CrossRef]
- Yu, T. AIME: Autoencoder-based integrative multi-omics data embedding that allows for confounder adjustments. PLoS Comput. Biol. 2022, 18, e1009826. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Altmann, A.; Toloşi, L.; Sander, O.; Lengauer, T. Permutation importance: A corrected feature importance measure. Bioinformatics 2010, 26, 1340–1347. [Google Scholar] [CrossRef] [PubMed]
- Love, M.I.; Huber, W.; Anders, S. Moderated estimation of fold change and dispersion for RNA-seq data with DESeq2. Genome Biol. 2014, 15, 550. [Google Scholar] [CrossRef] [PubMed]
- Wu, T.; Hu, E.; Xu, S.; Chen, M.; Guo, P.; Dai, Z.; Feng, T.; Zhou, L.; Tang, W.; Zhan, L.; et al. clusterProfiler 4.0: A universal enrichment tool for interpreting omics data. Innovation 2021, 2, 100141. [Google Scholar] [CrossRef] [PubMed]
- Hanel, R.; Corominas-Murtra, B.; Liu, B.; Thurner, S. Fitting Power-laws in empirical data with estimators that work for all exponents. PLoS ONE 2017, 12, e0170920. [Google Scholar] [CrossRef]
- Xie, K.; Hou, Y.; Zhou, X. Deep centroid: A general deep cascade classifier for biomedical omics data classification. Bioinformatics 2024, 40, btae039. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Chow, K.-H.; Wei, W.; Liu, L. Exploring Model Learning Heterogeneity for Boosting Ensemble Robustness. arXiv 2023, arXiv:2310.02237. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, L.; Wang, B.; Li, F.; Zhang, Z. Feature clustering based support vector machine recursive feature elimination for gene selection. Appl. Intell. 2018, 48, 594–607. [Google Scholar] [CrossRef]
- Islam, M.R.; Matin, A. Detection of COVID 19 from CT Image by The Novel LeNet-5 CNN Architecture. In Proceedings of the 2020 23rd International Conference on Computer and Information Technology (ICCIT), Dhaka, Bangladesh, 19–21 December 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Hu, Q.; Guo, Y.; Xie, X.; Cordy, M.; Ma, L.; Papadakis, M.; Le Traon, Y. Test Optimization in DNN Testing: A Survey. ACM Trans. Softw. Eng. Methodol. 2024, 33, 1–42. [Google Scholar] [CrossRef]
- Hassija, V.; Chamola, V.; Mahapatra, A.; Singal, A.; Goel, D.; Huang, K.; Scardapane, S.; Spinelli, I.; Mahmud, M.; Hussain, A. Interpreting Black-Box Models: A Review on Explainable Artificial Intelligence. Cogn. Comput. 2024, 16, 45–74. [Google Scholar] [CrossRef]
- Biswas, A.; Liu, S.; Garg, S.; Morshed, M.G.; Vakili, H.; Ghosh, A.W.; Balachandran, P.V. Integrating adaptive learning with post hoc model explanation and symbolic regression to build interpretable surrogate models. MRS Commun. 2024, 14, 983–989. [Google Scholar] [CrossRef]
- Knezevic, N.N.; Manchikanti, L.; Hirsch, J.A. Principles of Evidence-Based Medicine. In Essentials of Interventional Techniques in Managing Chronic Pain; Singh, V., Falco, F.J.E., Kaye, A.D., Soin, A., Hirsch, J.A., Eds.; Springer International Publishing: Cham, Switzerland, 2024; pp. 101–118. [Google Scholar] [CrossRef]
- Yang, Z.; Zhang, A.; Sudjianto, A. GAMI-Net: An explainable neural network based on generalized additive models with structured interactions. Pattern Recognit. 2021, 120, 108192. [Google Scholar] [CrossRef]
- Marcílio, W.E.; Eler, D.M. From explanations to feature selection: Assessing SHAP values as feature selection mechanism. In Proceedings of the 2020 33rd SIBGRAPI Conference on Graphics, Patterns and Images (SIBGRAPI), Porto de Galinhas, Brazil, 7–10 November 2020; pp. 340–347. [Google Scholar] [CrossRef]
- van der Knaap, J.A.; Verrijzer, C.P. Undercover: Gene control by metabolites and metabolic enzymes. Genes Dev. 2016, 30, 2345–2369. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Yao, L.; Yang, J.; Wang, Z.; Du, G. PI3K/Akt and HIF-1 signaling pathway in hypoxia-ischemia. Mol. Med. Rep. 2018, 18, 3547–3554. [Google Scholar] [CrossRef]
- Song, Y.-S.; Annalora, A.J.; Marcus, C.B.; Jefcoate, C.R.; Sorenson, C.M.; Sheibani, N. Cytochrome P450 1B1: A Key Regulator of Ocular Iron Homeostasis and Oxidative Stress. Cells 2022, 11, 2930. [Google Scholar] [CrossRef]
- Miki, Y.; Kidoguchi, Y.; Sato, M.; Taketomi, Y.; Taya, C.; Muramatsu, K.; Gelb, M.H.; Yamamoto, K.; Murakami, M. Dual Roles of Group IID Phospholipase A2 in Inflammation and Cancer. J. Biol. Chem. 2016, 291, 15588–15601. [Google Scholar] [CrossRef] [PubMed]
- Tan, R.; Zhou, Y.; An, Z.; Xu, Y. Cancer Is a Survival Process under Persistent Microenvironmental and Cellular Stresses. Genom. Proteom. Bioinform. 2022, 21, 1260–1265. [Google Scholar] [CrossRef] [PubMed]
- Sun, H.; Zhang, C.; Cao, S.; Sheng, T.; Dong, N.; Xu, Y. Fenton reactions drive nucleotide and ATP syntheses in cancer. J. Mol. Cell Biol. 2018, 10, 448–459. [Google Scholar] [CrossRef]
- Röhrig, F.; Schulze, A. The multifaceted roles of fatty acid synthesis in cancer. Nat. Rev. Cancer 2016, 16, 732–749. [Google Scholar] [CrossRef]
- Li, J.; Lim, J.Y.S.; Eu, J.Q.; Chan, A.K.M.H.; Goh, B.C.; Wang, L.; Wong, A.L.-A. Reactive Oxygen Species Modulation in the Current Landscape of Anticancer Therapies. Antioxid. Redox Signal. 2024, 41, 322–341. [Google Scholar] [CrossRef] [PubMed]
- Sun, H.; Zhou, Y.; Skaro, M.F.; Wu, Y.; Qu, Z.; Mao, F.; Zhao, S.; Xu, Y. Metabolic Reprogramming in Cancer Is Induced to Increase Proton Production. Cancer Res. 2020, 80, 1143–1155. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Chang, W.; Lu, X.; Wang, J.; Zhang, C.; Xu, Y. Acid–base Homeostasis and Implications to the Phenotypic Behaviors of Cancer. Genom. Proteom. Bioinform. 2023, 21, 1133–1148. [Google Scholar] [CrossRef] [PubMed]
- Górska, A.; Mazur, A.J. Integrin-linked kinase (ILK): The known vs. the unknown and perspectives. Cell. Mol. Life Sci. 2022, 79, 100. [Google Scholar] [CrossRef] [PubMed]
- Feng, S.; Zhou, M.; Huang, Z.; Xiao, X.; Zhong, B. A colorectal liver metastasis prediction model based on the combination of lipoprotein-associated phospholipase A2 and serum biomarker levels. Clin. Chim. Acta 2025, 568, 120143. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Liu, F.; Wang, C.; Wang, C.; Tang, Y.; Jiang, Z. Glutathione S-transferase A1 mediates nicotine-induced lung cancer cell metastasis by promoting epithelial-mesenchymal transition. Exp. Ther. Med. 2017, 14, 1783–1788. [Google Scholar] [CrossRef] [PubMed]
- He, W.; Cao, X.; Rong, K.; Chen, X.; Han, S.; Qin, A. Combination of AZD3463 and DZNep Prevents Bone Metastasis of Breast Cancer by Suppressing Akt Signaling. Front. Pharmacol. 2021, 12, 652071. [Google Scholar] [CrossRef] [PubMed]
- Xia, W.; Wang, H.; Zhou, X.; Wang, Y.; Xue, L.; Cao, B.; Song, J. The role of cholesterol metabolism in tumor therapy, from bench to bed. Front. Pharmacol. 2023, 14, 928821. [Google Scholar] [CrossRef]
- Liu, W.; Chakraborty, B.; Safi, R.; Kazmin, D.; Chang, C.; McDonnell, D.P. Dysregulated cholesterol homeostasis results in resistance to ferroptosis increasing tumorigenicity and metastasis in cancer. Nat. Commun. 2021, 12, 5103. [Google Scholar] [CrossRef]
- Giacomini, I.; Gianfanti, F.; Desbats, M.A.; Orso, G.; Berretta, M.; Prayer-Galetti, T.; Ragazzi, E.; Cocetta, V. Cholesterol Metabolic Reprogramming in Cancer and Its Pharmacological Modulation as Therapeutic Strategy. Front. Oncol. 2021, 11, 682911. [Google Scholar] [CrossRef] [PubMed]
- Loyola-González, O. Black-Box vs. White-Box: Understanding Their Advantages and Weaknesses from a Practical Point of View. IEEE Access 2019, 7, 154096–154113. [Google Scholar] [CrossRef]
- Lee, Y.-G.; Oh, J.-Y.; Kim, D.; Kim, G. SHAP Value-Based Feature Importance Analysis for Short-Term Load Forecasting. J. Electr. Eng. Technol. 2023, 18, 579–588. [Google Scholar] [CrossRef]
- Bull, C.; Byrne, R.M.; Fisher, N.C.; Corry, S.M.; Amirkhah, R.; Edwards, J.; Hillson, L.V.S.; Lawler, M.; Ryan, A.E.; Lamrock, F.; et al. Dual gene set enrichment analysis (dualGSEA); an R function that enables more robust biological discovery and pre-clinical model alignment from transcriptomics data. Sci. Rep. 2024, 14, 30202. [Google Scholar] [CrossRef] [PubMed]
- Verdasco, M.P.; García-Cuesta, E. An Interpretable Rule Creation Method for Black-Box Models based on Surrogate Trees—Srules. arXiv 2024, arXiv:2407.20070. [Google Scholar] [CrossRef]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. “Why Should I Trust You? In ”: Explaining the Predictions of Any Classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, in KDD ’16, San Francisco, CA, USA, 13–17 August 2016; Association for Computing Machinery: New York, NY, USA, 2016; pp. 1135–1144. [Google Scholar]
- Crawford, J.; Greene, C.S. Incorporating biological structure into machine learning models in biomedicine. Curr. Opin. Biotechnol. 2020, 63, 126–134. [Google Scholar] [CrossRef]
- Szegedy, C.; Zaremba, W.; Sutskever, I.; Bruna, J.; Erhan, D.; Goodfellow, I.; Fergus, R. Intriguing properties of neural networks. arXiv 2014, arXiv:1312.6199. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Murphy, K.P. Machine Learning: A Probabilistic Perspective; The MIT Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Sauber-Cole, R.; Khoshgoftaar, T.M. The use of generative adversarial networks to alleviate class imbalance in tabular data: A survey. J. Big Data 2022, 9, 98. [Google Scholar] [CrossRef]





| Model | Labels | Score | CS | CR | Final Score |
|---|---|---|---|---|---|
| LR | 2C | 0.7492 | 0.2073 | −0.3200 | 1.2591 |
| SVM | 2C | 0.6739 | 0.1327 | 2.1650 | 1.4316 |
| RF | 2C | 0.8221 | 0.1710 | 0.9150 | 1.5647 |
| XGB | 2C | 0.7892 | 0.1869 | −0.1950 | 1.3720 |
| LGBM | 2C | 0.7791 | 0.1969 | −0.6000 | 1.3013 |
| Stacking | 2C | 0.8097 | 0.1904 | 0.2700 | 1.4560 |
| LR | 3C | 0.5262 | 0.1325 | 0.1067 | 0.9306 |
| SVM | 3C | 0.4641 | 0.0948 | 1.0167 | 0.9351 |
| RF | 3C | 0.5692 | 0.1617 | −0.4167 | 0.9350 |
| XGB | 3C | 0.5452 | 0.1786 | −0.8800 | 0.8238 |
| LGBM | 3C | 0.5412 | 0.1928 | −1.2100 | 0.7686 |
| Stacking | 3C | 0.6659 | 0.1902 | −1.0600 | 1.0356 |
| Method | Labels | F1_Score | CS | CR | Final Score |
|---|---|---|---|---|---|
| Stacking | 2C | 0.8097 | 0.1904 | 0.2700 | 1.4560 |
| EBM | 2C | 0.6869 | 0.18017 | 0.8699 | 1.2806 |
| RuleFit | 2C | 0.6414 | 0.2215 | −2.555 | 0.8058 |
| LeNet | 2C | 0.6286 | 0.1145 | 2.633 | 1.4060 |
| DNN | 2C | 0.6684 | −0.0018 | 2.246 | 1.5632 |
| Stacking | 3C | 0.6659 | 0.1902 | −1.0600 | 1.0356 |
| EBM | 3C | 0.5366 | 0.16255 | −0.32 | 0.8787 |
| RuleFit | 3C | 0.5470 | 0.16258 | −0.4633 | 0.8671 |
| LeNet | 3C | 0.2344 | 0.00061 | 1.9013 | 0.6583 |
| DNN | 3C | 0.2653 | −0.0006 | 1.914 | 0.7226 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Z.; Mu, X.; Cao, Y.; Chen, Q.; Qiao, S.; Shi, B.; Xiao, G.; Wang, Y.; Xu, Y. Optimizing Model Performance and Interpretability: Application to Biological Data Classification. Genes 2025, 16, 297. https://doi.org/10.3390/genes16030297
Huang Z, Mu X, Cao Y, Chen Q, Qiao S, Shi B, Xiao G, Wang Y, Xu Y. Optimizing Model Performance and Interpretability: Application to Biological Data Classification. Genes. 2025; 16(3):297. https://doi.org/10.3390/genes16030297
Chicago/Turabian StyleHuang, Zhenyu, Xuechen Mu, Yangkun Cao, Qiufen Chen, Siyu Qiao, Bocheng Shi, Gangyi Xiao, Yan Wang, and Ying Xu. 2025. "Optimizing Model Performance and Interpretability: Application to Biological Data Classification" Genes 16, no. 3: 297. https://doi.org/10.3390/genes16030297
APA StyleHuang, Z., Mu, X., Cao, Y., Chen, Q., Qiao, S., Shi, B., Xiao, G., Wang, Y., & Xu, Y. (2025). Optimizing Model Performance and Interpretability: Application to Biological Data Classification. Genes, 16(3), 297. https://doi.org/10.3390/genes16030297






