Male Pedigree Toolbox: A Versatile Software for Y-STR Data Analyses
Abstract
1. Introduction
2. Materials and Methods
2.1. Automatic Pairwise Distance Calculation from TGF Files
2.2. Recognizing Pairwise Mutations
2.3. Estimating Y-STR Mutation Rates from Pedigrees
2.4. Drawing Dendrograms
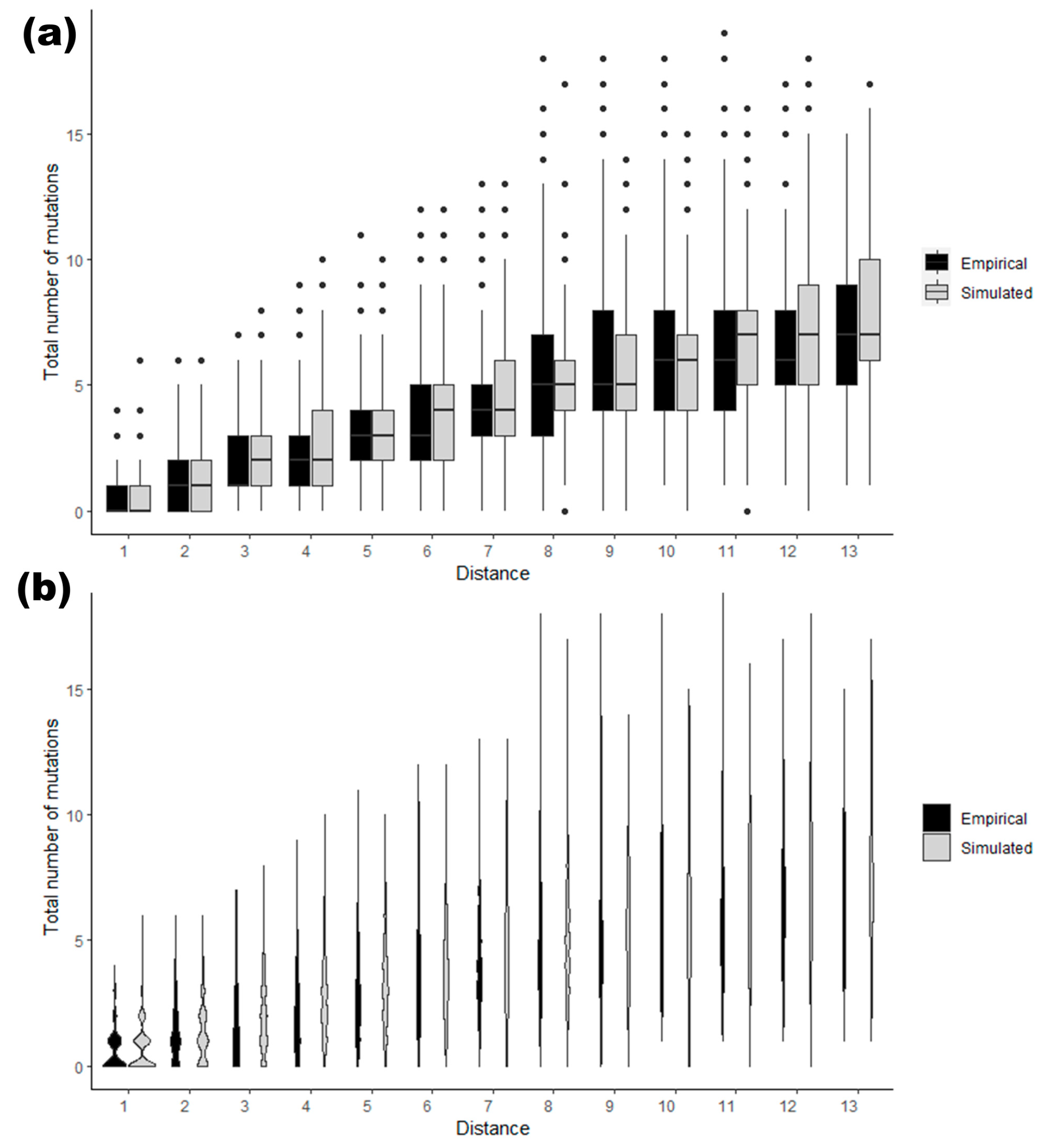
2.5. Simulating Relative Pairs
2.6. Building New Models with Machine Learning
2.7. Running the Prediction Models
3. Discussion and Examples
3.1. Examples for Dendrograms from Pedigree and Population Data
3.2. Example for Mutation Analysis
3.3. Simulating Pedigrees and Predicting the Level of Relatedness
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Module Name | Input File(s) | Output File(s) | Purpose |
|---|---|---|---|
| 1. Pairwise distance | - TGF file(s) in a folder | distances.csv | Calculating the number of separating meioses between all individuals with genotypic data in the pedigree |
| 2. Pairwise mutation | - Allele file (csv) - (distances.csv) | - Summary_out.csv - Full_out.csv - (Differentiation_out.csv) - (Prediction_out.csv) | Comparing the genotypes of all typed individuals in the pedigree and calculating the number of mutational steps between each individual. Calculating the differentiation rate and making a prediction file are optional. |
| 3. Pedigree mutation | - Allele file (csv) - TGF file(s) in a folder | Per pedigree: - Pedigree drawings of all markers and markers with mutation individually (pdf) - all_marker_edge_info.csv - mutation rate within pedigree (csv) Overall pedigrees: - Total_mutations.csv | Performing a mutational analysis, taking the provided pedigree structure into account. Visualizations are an easy way to view genetic variation within the pedigree. When typing multiple pedigrees, the overall mutation rate can be automatically estimated using this module. |
| 4. Dendrograms | - Full_out.csv - (Mutation rate file (csv)) | Per pedigree: - A dendrogram (png) | Generating dendrograms that can be used to create visualizations of genetic similarities when the pedigree structure is (partially) unknown. By providing a file with the mutation rates, the distances will be weighted where markers with a higher mutation rate have less influence. |
| 5. Simulate (command line only) | - Mutation rate file (2stepmodel (csv)) | - Simulation_output (csv) | Based on the provided mutation rates, a user-defined number of simulations will be performed on a user-defined number of separating meioses. These data can be used as input for prediction models but can also provide insight about the expected mutational behavior of a given set of Y-STRs. |
| 6. Model builder (command line only) | - Simulation output (csv) | - Model output (csv) | Here, users can build their own custom models; this may be required, for example, when using a non-standard Y-STR kit, or when the mutation rate in the population of interest deviates strongly from the mean rates. |
| 7. Running Prediction | - Prediction file - Model file - (Model training file) | - Prediction table - (Prediction plots) | If the user wants to validate their prediction model using empirical data, this module allows for a large number of predictions to be conducted using a pre-computed or a custom prediction model. |
Appendix B

References
- Ralf, A.; Lubach, D.; Kousouri, N.; Winkler, C.; Schulz, I.; Roewer, L.; Purps, J.; Lessig, R.; Krajewski, P.; Ploski, R.; et al. Identification and characterization of novel rapidly mutating Y-chromosomal short tandem repeat markers. Hum. Mutat. 2020, 41, 1680–1696. [Google Scholar] [CrossRef]
- Ralf, A.; Montiel González, D.; Zandstra, D.; van Wersch, B.; Kousouri, N.; de Knijff, P.; Adnan, A.; Claerhout, S.; Ghanbari, M.; Larmuseau, M.H.D. Large-scale pedigree analysis highlights rapidly mutating Y-chromosomal short tandem repeats for differentiating patrilineal relatives and predicting their degrees of consanguinity. Hum. Genet. 2023, 142, 145–160. [Google Scholar] [CrossRef]
- Turrina, S.; Caratti, S.; Ferrian, M.; De Leo, D. Are rapidly mutating Y-short tandem repeats useful to resolve a lineage? Expanding mutability data on distant male relationships. Transfusion 2016, 56, 533–538. [Google Scholar] [CrossRef] [PubMed]
- Claerhout, S.; Roelens, J.; Van der Haegen, M.; Verstraete, P.; Larmuseau, M.H.D.; Decorte, R. Ysurnames? The patrilineal Y-chromosome and surname correlation for DNA kinship research. Forensic Sci. Int. Genet. 2020, 44, 102204. [Google Scholar] [CrossRef] [PubMed]
- Claerhout, S.; Van der Haegen, M.; Vangeel, L.; Larmuseau, M.H.D.; Decorte, R. A game of hide and seq: Identification of parallel Y-STR evolution in deep-rooting pedigrees. Eur. J. Hum. Genet. 2019, 27, 637–646. [Google Scholar] [CrossRef] [PubMed]
- Kasu, M.; Cloete, K.W.; Pitere, R.; Tsiana, K.J.; D’Amato, M.E. The genetic landscape of South African males: A Y-STR perspective. Forensic Sci. Int. Genet. 2022, 58, 102677. [Google Scholar] [CrossRef] [PubMed]
- Della Rocca, C.; Trombetta, B.; Barni, F.; D’Atanasio, E.; Hajiesmaeil, M.; Berti, A.; Hadi, S.; Cruciani, F. Improving discrimination capacity through rapidly mutating Y-STRs in structured populations from the African continent. Forensic Sci. Int. Genet. 2022, 61, 102755. [Google Scholar] [CrossRef] [PubMed]
- Lin, H.; Ye, Q.; Tang, P.; Mo, T.; Yu, X.; Tang, J. Analyzing genetic polymorphism and mutation of 44 Y-STRs in a Chinese Han population of Southern China. Leg. Med. 2020, 42, 101643. [Google Scholar] [CrossRef] [PubMed]
- Wei, W.; Ayub, Q.; Xue, Y.; Tyler-Smith, C. A comparison of Y-chromosomal lineage dating using either resequencing or Y-SNP plus Y-STR genotyping. Forensic Sci. Int. Genet. 2013, 7, 568–572. [Google Scholar] [CrossRef]
- Larmuseau, M.H.D.; Vanderheyden, N.; Van Geystelen, A.; van Oven, M.; de Knijff, P.; Decorte, R. Recent radiation within Y-chromosomal haplogroup R-M269 resulted in high Y-STR haplotype resemblance. Ann. Hum. Genet. 2014, 78, 92–103. [Google Scholar] [CrossRef]
- Otagiri, T.; Sato, N.; Asamura, H.; Parvanova, E.; Kayser, M.; Ralf, A. RMplex reveals population differences in RM Y-STR mutation rates and provides improved father-son differentiation in Japanese. Forensic Sci. Int. Genet. 2022, 61, 102766. [Google Scholar] [CrossRef]
- Neuhuber, F.; Dunkelmann, B.; Grießner, I.; Helm, K.; Kayser, M.; Ralf, A. Improving the differentiation of closely related males by RMplex analysis of 30 Y-STRs with high mutation rates. Forensic Sci. Int. Genet. 2022, 58, 102682. [Google Scholar] [CrossRef]
- Wang, F.; Song, F.; Wang, X.; Song, M.; Zhou, Y.; Liu, J.; Wang, Z.; Hou, Y. Mutation analysis for newly suggested 30 Y-STR loci with high mutation rates in Chinese father-son pairs. Sci. Rep. 2022, 12, 15680. [Google Scholar] [CrossRef]
- Lee, D.G.; Kim, S.J.; Cho, W.-C.; Cho, Y.; Park, J.H.; Lee, J.; Jung, J.Y. Analysis of mutation rates and haplotypes of 23 Y-chromosomal STRs in Korean father–son pairs. Forensic Sci. Int. Genet. 2023, 65, 102875. [Google Scholar] [CrossRef] [PubMed]
- Fan, H.; Zeng, Y.; Wu, W.; Liu, H.; Xu, Q.; Du, W.; Hao, H.; Liu, C.; Ren, W.; Wu, W. The Y-STR landscape of coastal southeastern Han: Forensic characteristics, haplotype analyses, mutation rates, and population genetics. Electrophoresis 2021, 42, 1578–1593. [Google Scholar] [CrossRef]
- Nazir, S.; Adnan, A.; Rehman, R.A.; Al-Qahtani, W.S.; Alsaleh, A.B.; Al-Harthi, H.S.; Safhi, F.A.; Almheiri, R.; Lootah, R.; Alreyami, A. Mutation rate analysis of RM Y-STRs in deep-rooted multi-generational Punjabi Pedigrees from Pakistan. Genes 2022, 13, 1403. [Google Scholar] [CrossRef]
- Boattini, A.; Sarno, S.; Mazzarisi, A.M.; Viroli, C.; De Fanti, S.; Bini, C.; Larmuseau, M.H.D.; Pelotti, S.; Luiselli, D. Estimating Y-Str mutation rates and Tmrca through deep-rooting Italian pedigrees. Sci. Rep. 2019, 9, 9032. [Google Scholar] [CrossRef] [PubMed]
- Čokić, V.P.; Kecmanović, M.; Bosić, D.Z.; Jakovski, Z.; Veljković, A.; Katić, S.; Marković, M.K.; Keckarević, D. A comprehensive mutation study in wide deep-rooted R1b Serbian pedigree: Mutation rates and male relative differentiation capacity of 36 Y-STR markers. Forensic Sci. Int. Genet. 2019, 41, 137–144. [Google Scholar] [CrossRef]
- Kayser, M. Forensic use of Y-chromosome DNA: A general overview. Hum. Genet. 2017, 136, 621–635. [Google Scholar] [CrossRef] [PubMed]
- Harris, C.R.; Millman, K.J.; Van Der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef]
- McKinney, W. Data structures for statistical computing in python. In Proceedings of the 9th Python in Science Conference, Austin, TX, USA, 28 June–3 July 2010; pp. 51–56. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J. SciPy 1.0: Fundamental algorithms for scientific computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef]
- Hunter, J.D. Matplotlib: A 2D graphics environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- da Costa-Luis, C.O. tqdm: A fast, extensible progress meter for python and cli. J. Open Source Softw. 2019, 4, 1277. [Google Scholar] [CrossRef]
- Ballantyne, K.N.; Goedbloed, M.; Fang, R.; Schaap, O.; Lao, O.; Wollstein, A.; Choi, Y.; van Duijn, K.; Vermeulen, M.; Brauer, S. Mutability of Y-chromosomal microsatellites: Rates, characteristics, molecular bases, and forensic implications. Am. J. Hum. Genet. 2010, 87, 341–353. [Google Scholar] [CrossRef]
- Ellson, J.; Gansner, E.; Koutsofios, L.; North, S.C.; Woodhull, G. Graphviz—Open source graph drawing tools. In Proceedings of the Graph Drawing: 9th International Symposium, GD 2001, Vienna, Austria, 23–26 September 2001; pp. 483–484. [Google Scholar]
- Wang, F.; Song, F.; Song, M.; Li, J.; Xie, M.; Hou, Y. Genetic reconstruction and phylogenetic analysis by 193 Y-SNPs and 27 Y-STRs in a Chinese Yi ethnic group. Electrophoresis 2021, 42, 1480–1487. [Google Scholar] [CrossRef] [PubMed]
- Bandelt, H.-J.; Forster, P.; Röhl, A. Median-joining networks for inferring intraspecific phylogenies. Mol. Biol. Evol. 1999, 16, 37–48. [Google Scholar] [CrossRef] [PubMed]
- Kruijver, M.; Taylor, D.; Buckleton, J. Extending the discrete Laplace method: Incorporating multi-copy loci, partial repeats and null alleles. Forensic Sci. Int. Genet. 2023, 65, 102876. [Google Scholar] [CrossRef] [PubMed]
- Caliebe, A.; Jochens, A.; Willuweit, S.; Roewer, L.; Krawczak, M. No shortcut solution to the problem of Y-STR match probability calculation. Forensic Sci. Int. Genet. 2015, 15, 69–75. [Google Scholar] [CrossRef]
- Andersen, M.M.; Eriksen, P.S.; Morling, N. Weight of evidence of Y-STR matches computed with the discrete Laplace method: Impact of adding a suspect’s profile to a reference database. Forensic Sci. Int. Genet. 2023, 64, 102839. [Google Scholar] [CrossRef]
- Walsh, B. Estimating the time to the most recent common ancestor for the Y chromosome or mitochondrial DNA for a pair of individuals. Genetics 2001, 158, 897–912. [Google Scholar] [CrossRef] [PubMed]
- Claerhout, S.; Vanpaemel, S.; Gill, M.S.; Antiga, L.G.; Baele, G.; Decorte, R. YMrCA: Improving Y-chromosomal ancestor time estimation for DNA kinship research. Hum. Mutat. 2021, 42, 1307–1320. [Google Scholar] [CrossRef] [PubMed]
- Puch-Solis, R.; Pope, S.; Tully, G. Considerations on the application of a mutation model for Y-STR interpretation. Sci. Justice 2024, 64, 180–192. [Google Scholar] [CrossRef]
- Antão-Sousa, S.; Pinto, N.; Rende, P.; Amorim, A.; Gusmão, L. The sequence of the repetitive motif influences the frequency of multistep mutations in Short Tandem Repeats. Sci. Rep. 2023, 13, 10251. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ralf, A.; van Wersch, B.; Montiel González, D.; Kayser, M. Male Pedigree Toolbox: A Versatile Software for Y-STR Data Analyses. Genes 2024, 15, 227. https://doi.org/10.3390/genes15020227
Ralf A, van Wersch B, Montiel González D, Kayser M. Male Pedigree Toolbox: A Versatile Software for Y-STR Data Analyses. Genes. 2024; 15(2):227. https://doi.org/10.3390/genes15020227
Chicago/Turabian StyleRalf, Arwin, Bram van Wersch, Diego Montiel González, and Manfred Kayser. 2024. "Male Pedigree Toolbox: A Versatile Software for Y-STR Data Analyses" Genes 15, no. 2: 227. https://doi.org/10.3390/genes15020227
APA StyleRalf, A., van Wersch, B., Montiel González, D., & Kayser, M. (2024). Male Pedigree Toolbox: A Versatile Software for Y-STR Data Analyses. Genes, 15(2), 227. https://doi.org/10.3390/genes15020227






