LBF-MI: Limited Boolean Functions and Mutual Information to Infer a Gene Regulatory Network from Time-Series Gene Expression Data
Abstract
1. Introduction
2. Materials and Methods
2.1. Boolean Network Inference Problem
2.2. Structural Performance Matrices
2.3. A Random Boolean Network
2.4. Generation of Random Boolean Networks
- Minimum two nodes are required for connectivity;
- It is essential for each node to possess at least one incoming edge and at least one outgoing edge.
2.5. Generation of Time-Series Gene Expression Dataset or Boolean Trajectories from Random Boolean Networks
- Consider a random initial state in which each value represents the state of a gene.
- Then, formulate a random update function, which considers any of the two Boolean functions: AND or OR while updating each gene.
- Calculate the next state.
- Repeat step 3 until a steady state is found.
2.6. Multivariate Mutual Informational
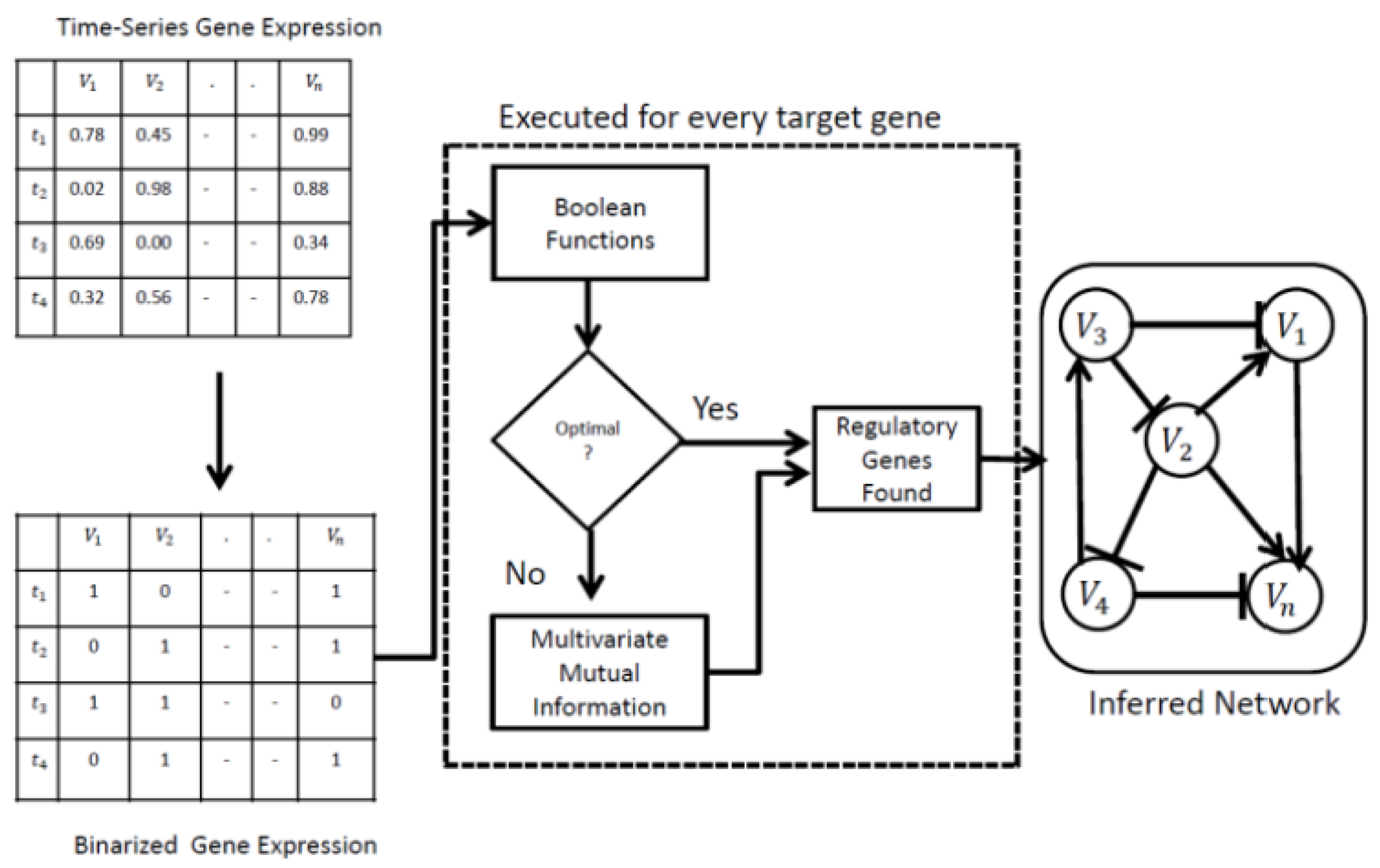
2.7. Workflow of the Proposed Method
3. Proposed Method
- (a)
- In the first phase, LBF-MI is employed to find the optimum solutions for a target gene. Optimum solutions are simply the regulatory genes for a target gene, achieved when the gene-wise dynamics between the target gene and the regulatory gene reach 1 (see Materials and Methods section for more details). Consider a target gene, and a regulatory gene, In this study, a one-time gap is used between a target gene and a regulatory gene. For a given target gene, initially, an exhaustive search was conducted for its regulatory interactions, considering two Boolean functions: and and the optimal fitting function was identified that approximates the gene-wise dynamics consistency to 1. Gene-wise dynamics consistency is the similarity between the predicted Boolean time-series data and the observed data The optimal fitting function refers to one of the two Boolean functions mentioned above that maximizes gene-wise dynamics consistency. If there is no difference between the Boolean time-series data and , an optimal regulatory gene is obtained. Otherwise, step 2 is executed.
- (b)
- In the second phase, this research conducts an exhaustive search for regulatory gene tuples using multivariate mutual information. The multivariate mutual information measures how much information is shared among the target gene and regulatory genes by considering both their entropies and their joint entropy (see Materials and Methods section). First, a value of equal to 1 is selected, specifying the computation of mutual information between a target gene and a regulatory gene. Subsequently, the value of is incremented by 1 iteratively until reaches the limit of Finally, the best tuple with the highest mutual information score was selected. It is worth mentioning that step 1 and step 2 are executed independently for every target gene. All results are combined to build a final random Boolean network.
4. Results
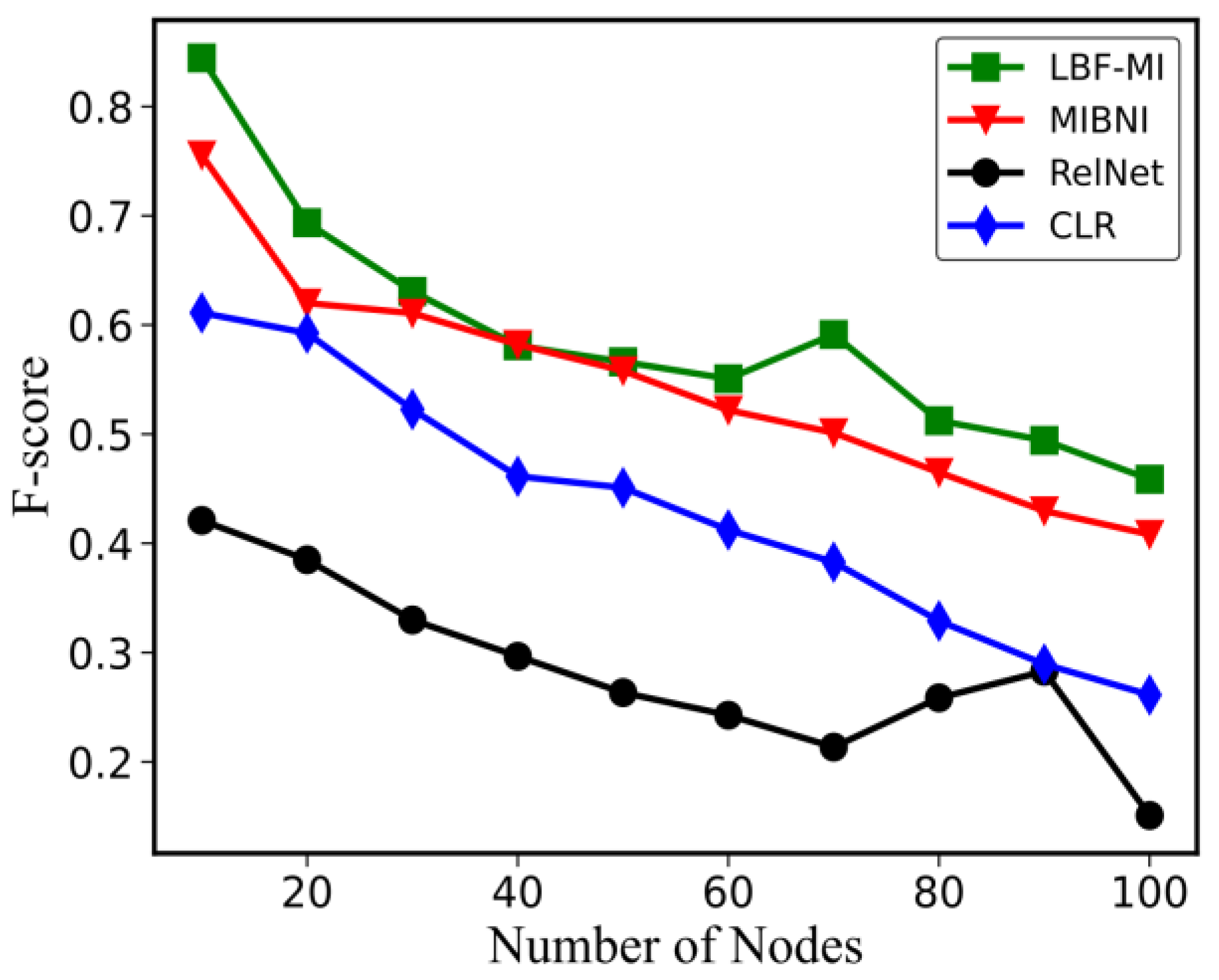
4.1. Performance on Artificial Gene Expression Dataset
4.2. Performance on the Real Gene Expression Dataset
4.2.1. Case Study 1: E. coli Gene Regulatory Network
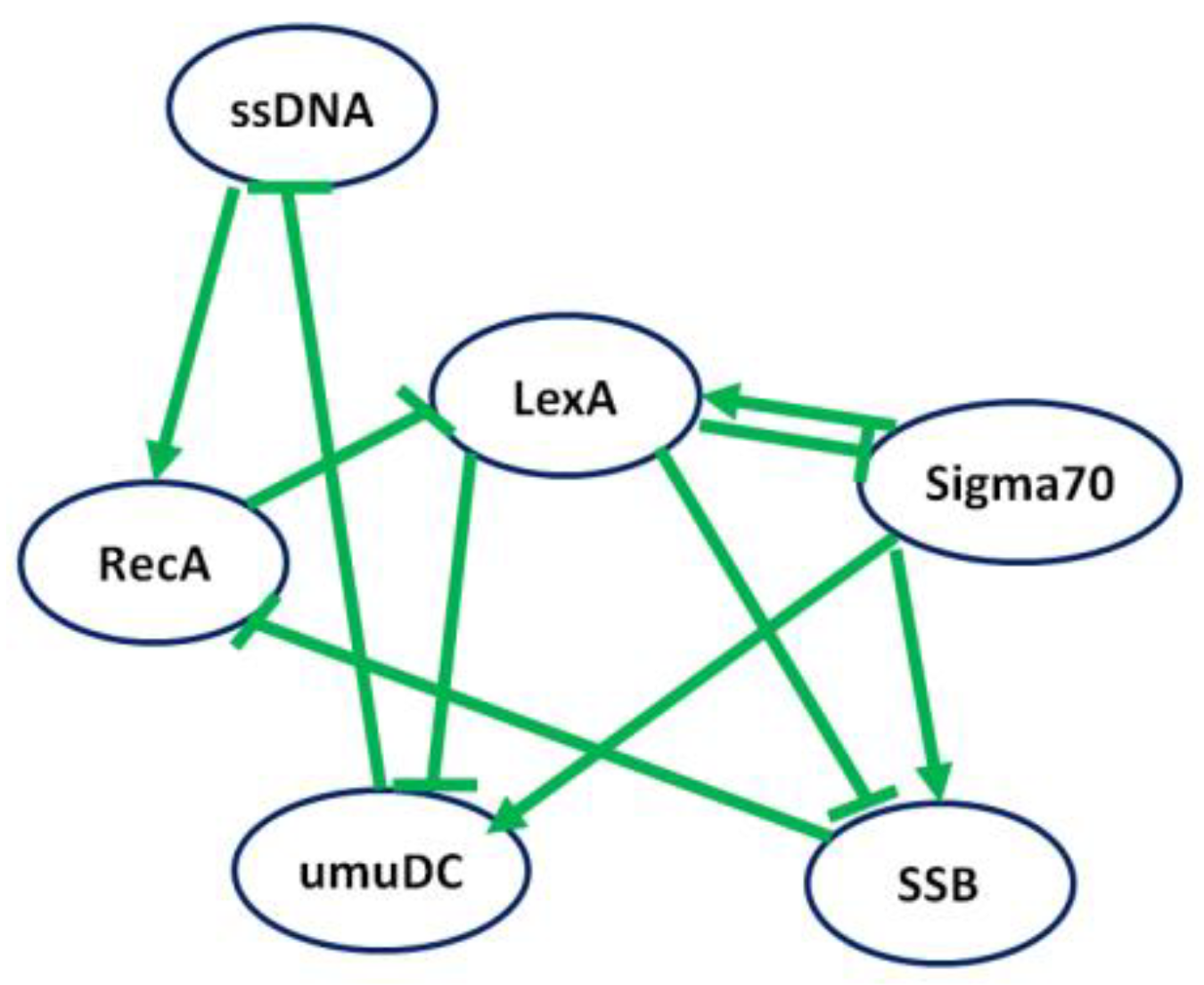
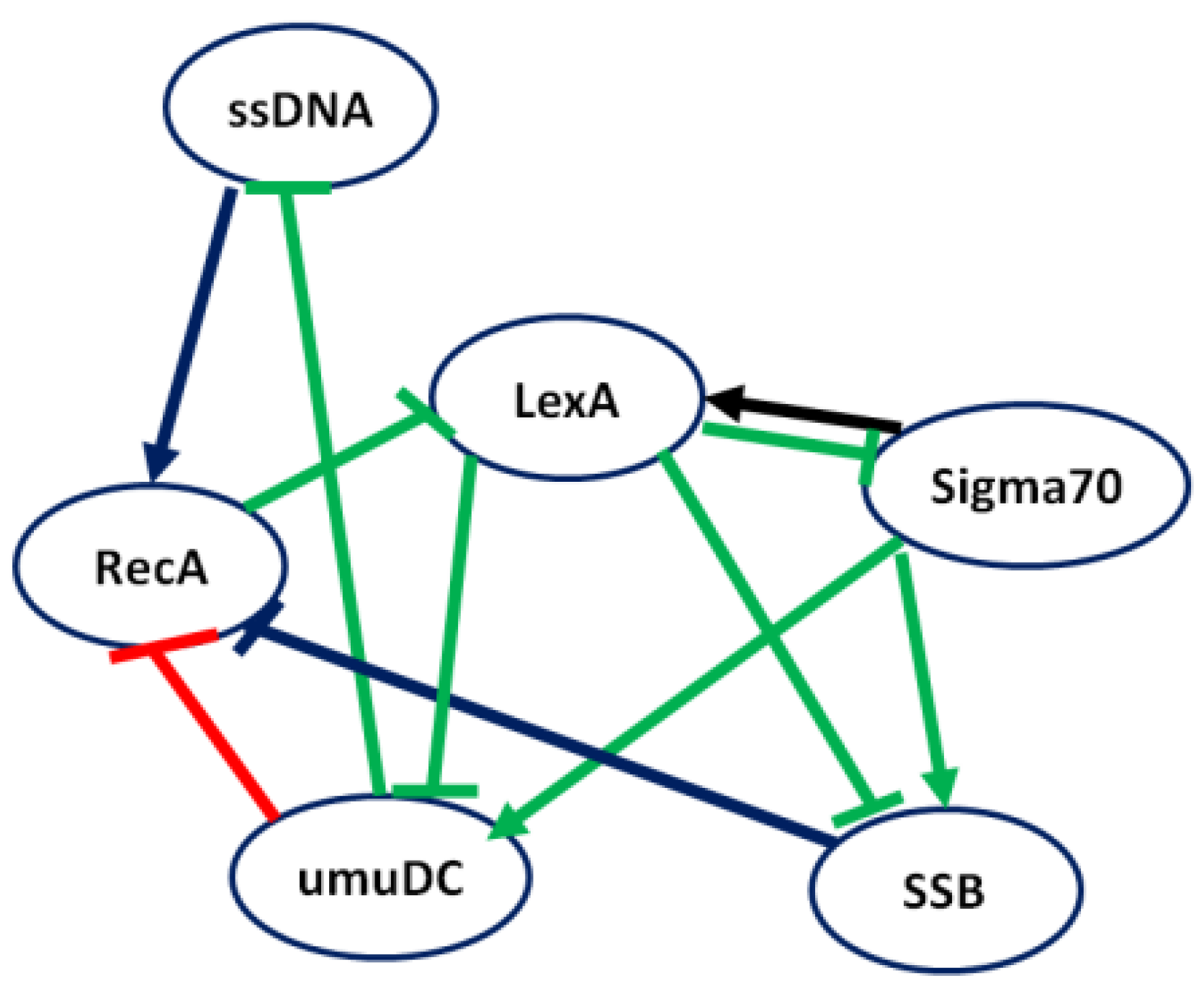
4.2.2. Case Study 2: Regulatory Network of the SOS Response of E. coli
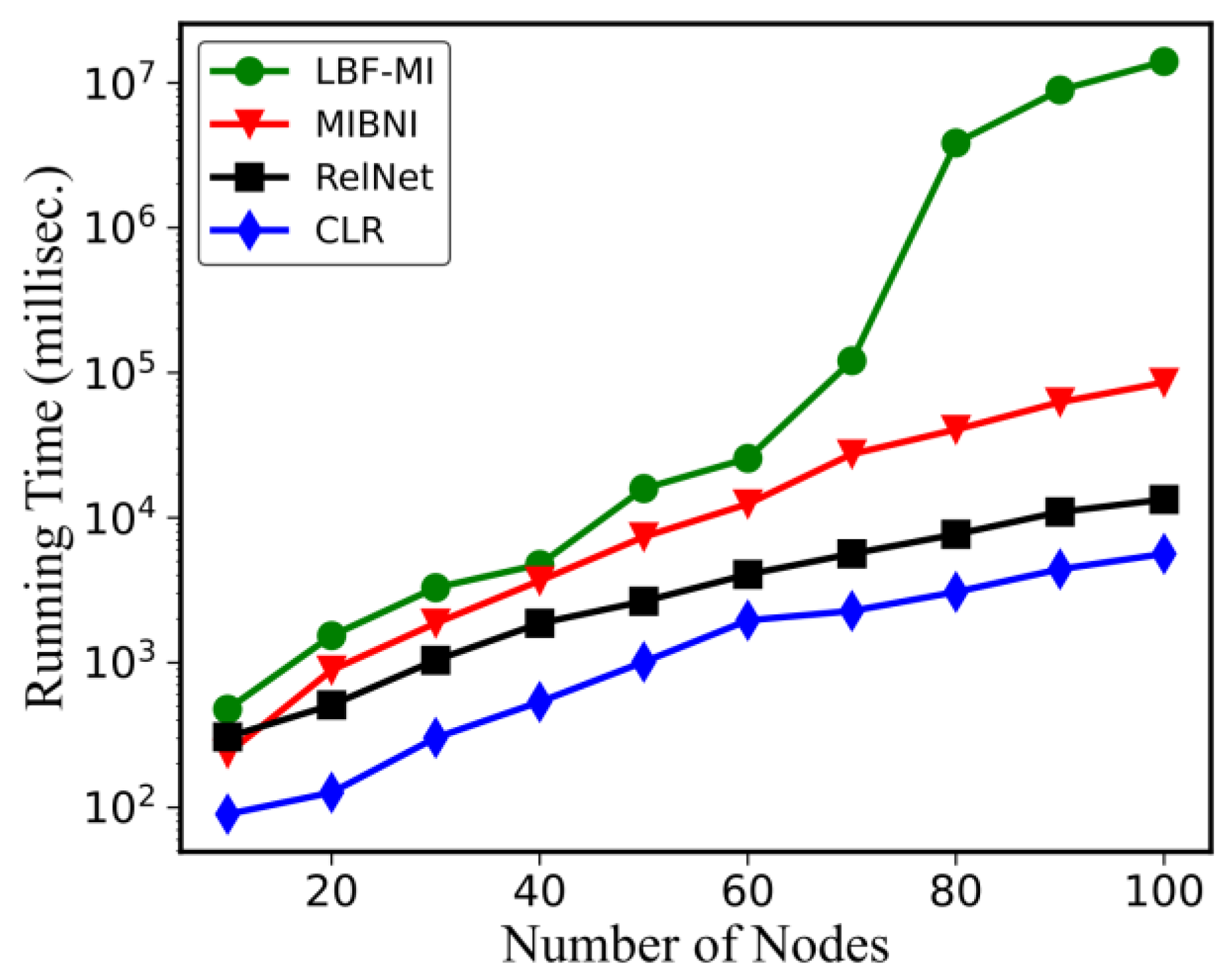
4.3. Computation Time Comparisons
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gkmen, A.; Frank, E.-S. Inferring the conservative causal core of gene regulatory networks. BMC Syst. Biol. 2010, 4, 132. [Google Scholar] [CrossRef]
- Lv, Y.; Bao, E. Apoptosis induced in chicken embryo fibroblasts in vitro by a polyinosinic: Polycytidylic acid copolymer. Toxicol. Vitr. 2009, 23, 1360–1364. [Google Scholar] [CrossRef] [PubMed]
- Stefan, R.M.; Piyush, B.M.; Melissa, J.D.; Mark, A.R. Supervised, semi-supervised and unsupervised inference of gene regulatory networks. Brief. Bioinform. 2013, 15, 195–211. [Google Scholar] [CrossRef]
- Seiya, I.; Takao, G.; Satoru, M. Estimation of Genetic Networks and Functional Structures between Genes by Using Bayesian Networks and Nonparametric Regression. Pac. Symp. Biocomput. 2002, 7, 175–186. [Google Scholar] [CrossRef]
- Ting, C.; Hongyu, L.H.; George, M.C. Modeling Gene Expression with Differential Equations. Pac. Symp. Biocomput. 1999, 4, 29–40. [Google Scholar]
- Stuart, A.K. Metabolic stability and epigenesis in randomly constructed genetic nets. J. Theor. Biol. 1969, 22, 437–467. [Google Scholar]
- Barman, S.; Kwon, Y.K. A novel mutual information-based Boolean network inference method from time-series gene expression data. PLoS ONE 2017, 12, e0171097. [Google Scholar] [CrossRef]
- Barman, S.; Kwon, Y.K. A Boolean network inference from time-series gene expression data using a genetic algorithm. Bioinformatics 2018, 34, i927–i933. [Google Scholar] [CrossRef] [PubMed]
- Barman, S.; Kwon, Y.K. A neuro-evolution approach to infer a Boolean network from time-series gene expressions. Bioinformatics 2020, 36, i762–i769. [Google Scholar] [CrossRef] [PubMed]
- Zhang, D.; Gao, S.; Liu, Z.P.; Gao, R. LogicGep: Boolean networks inference using symbolic regression from time-series transcriptomic profiling data. Brief. Bioinform. 2024, 25, bbae286. [Google Scholar] [CrossRef]
- Liang, S.; Fuhrman, S.; Somogyi, R. Reveal, a general reverse engineering algorithm for inference of genetic network architectures. Pac. Symp. Biocomput. 1998, 3, 18–29. [Google Scholar]
- Harri, L.; Ilya, S.; Olli, Y.-H. On Learning Gene Regulatory Networks Under the Boolean Network Model. Mach. Learn. 2003, 52, 147–167. [Google Scholar] [CrossRef]
- Shengtong, H.; Raymond, K.W.W.; Thomas, C.M.L.; Linghao, S.; Shuo-Yen, R.L.; Xiaodan, F. A Full Bayesian Approach for Boolean Genetic Network Inference. PLoS ONE 2014, 9, e115806. [Google Scholar] [CrossRef]
- Atul, J.B.; Isaac, S.K. Mutual information relevance networks: Functional genomic clustering using pairwise entropy measurements. Pac. Symp. Biocomput. 2000, 5, 418–429. [Google Scholar] [CrossRef]
- Jeremiah, J.F.; Boris, H.; Joshua, T.T.; Ilaria, M.; Jamey, W.; Guillaume, C.; Simon, K.; James, J.C.; Timothy, S.G. Large-Scale Mapping and Validation of Escherichia coli Transcriptional Regulation from a Compendium of Expression Profiles. PLoS Biol. 2007, 5, e8. [Google Scholar] [CrossRef]
- Adam, A.M.; Ilya, N.; Katia, B.; Chris, W.; Gustavo, S.; Riccardo Dalla, F.; Andrea, C. ARACNE: An Algorithm for the Reconstruction of Gene Regulatory Networks in a Mammalian Cellular Context. BMC Bioinform. 2006, 7 (Suppl. S1), S7. [Google Scholar] [CrossRef]
- Albert-László, B.; Réka, A. Emergence of Scaling in Random Networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef]
- James, M. Some methods for classification and analysis of multivariate observations. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, Volume 1: Statistics; University of California Press: Berkeley, CA, USA, 1967; pp. 281–297. [Google Scholar]
- Thomas, S.; Daniel, M.; Dario, F. GeneNetWeaver: In silico benchmark generation and performance profiling of network inference methods. Bioinformatics 2011, 27, 2263–2270. [Google Scholar] [CrossRef]
- Bin, S.; Xiang, L.; Dongliang, Z.; Jiayi, W.; Qi, O. From Boolean Network Model to Continuous Model Helps in Design of Functional Circuits. PLoS ONE 2015, 10, e0128630. [Google Scholar] [CrossRef]



| k | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| F-Score | 0.6600 | 0.7972 | 0.8047 | 0.8190 | 0.7291 | 0.7291 | 0.6810 | 0.6810 | 0.6810 |
| Methods | F-Score | Precision | Recall |
|---|---|---|---|
| LBF-MI | 0.6000 | 0.4285 | 1 |
| MIBNI | 0.2424 | 0.1666 | 0.4444 |
| RelNet | 0.1999 | 0.1888 | 0.2222 |
| CLR | 0.1904 | 0.1666 | 0.2222 |
| Time | ssDNA | RecA | LexA | Sigma 70 | UmuD C | SSB |
|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 1 | 0 | 0 | 0 |
| 2 | 1 | 1 | 1 | 0 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 | 0 |
| 4 | 1 | 1 | 0 | 1 | 0 | 0 |
| 5 | 1 | 1 | 0 | 1 | 1 | 1 |
| 6 | 0 | 0 | 0 | 1 | 1 | 1 |
| 7 | 0 | 0 | 1 | 1 | 1 | 1 |
| 8 | 0 | 0 | 1 | 0 | 0 | 0 |
| Methods | F-Score | Precision | Recall |
|---|---|---|---|
| LBF-MI | 0.7000 | 0.8750 | 0.7000 |
| MIBNI | 0.3414 | 0.2916 | 0.4117 |
| RelNet | 0.6666 | 0.7500 | 0.6000 |
| CLR | 0.5263 | 0.5555 | 0.5000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barman, S.; Farid, F.A.; Gope, H.L.; Hafiz, M.F.B.; Khan, N.A.; Ahmad, S.; Mansor, S. LBF-MI: Limited Boolean Functions and Mutual Information to Infer a Gene Regulatory Network from Time-Series Gene Expression Data. Genes 2024, 15, 1530. https://doi.org/10.3390/genes15121530
Barman S, Farid FA, Gope HL, Hafiz MFB, Khan NA, Ahmad S, Mansor S. LBF-MI: Limited Boolean Functions and Mutual Information to Infer a Gene Regulatory Network from Time-Series Gene Expression Data. Genes. 2024; 15(12):1530. https://doi.org/10.3390/genes15121530
Chicago/Turabian StyleBarman, Shohag, Fahmid Al Farid, Hira Lal Gope, Md. Ferdous Bin Hafiz, Niaz Ashraf Khan, Sabbir Ahmad, and Sarina Mansor. 2024. "LBF-MI: Limited Boolean Functions and Mutual Information to Infer a Gene Regulatory Network from Time-Series Gene Expression Data" Genes 15, no. 12: 1530. https://doi.org/10.3390/genes15121530
APA StyleBarman, S., Farid, F. A., Gope, H. L., Hafiz, M. F. B., Khan, N. A., Ahmad, S., & Mansor, S. (2024). LBF-MI: Limited Boolean Functions and Mutual Information to Infer a Gene Regulatory Network from Time-Series Gene Expression Data. Genes, 15(12), 1530. https://doi.org/10.3390/genes15121530






