Evaluating DNA Mixtures with Contributors from Different Populations Using Probabilistic Genotyping
Abstract
1. Introduction
2. Methods
2.1. Likelihood Ratio Framework
2.2. Likelihood Ratio for Comparison of a POI to a Single Sample
2.2.1. Simple Stratification
2.2.2. Full Stratification
2.2.3. Example Calculations
2.3. Simulation Study
2.4. Contributors from the Same Population
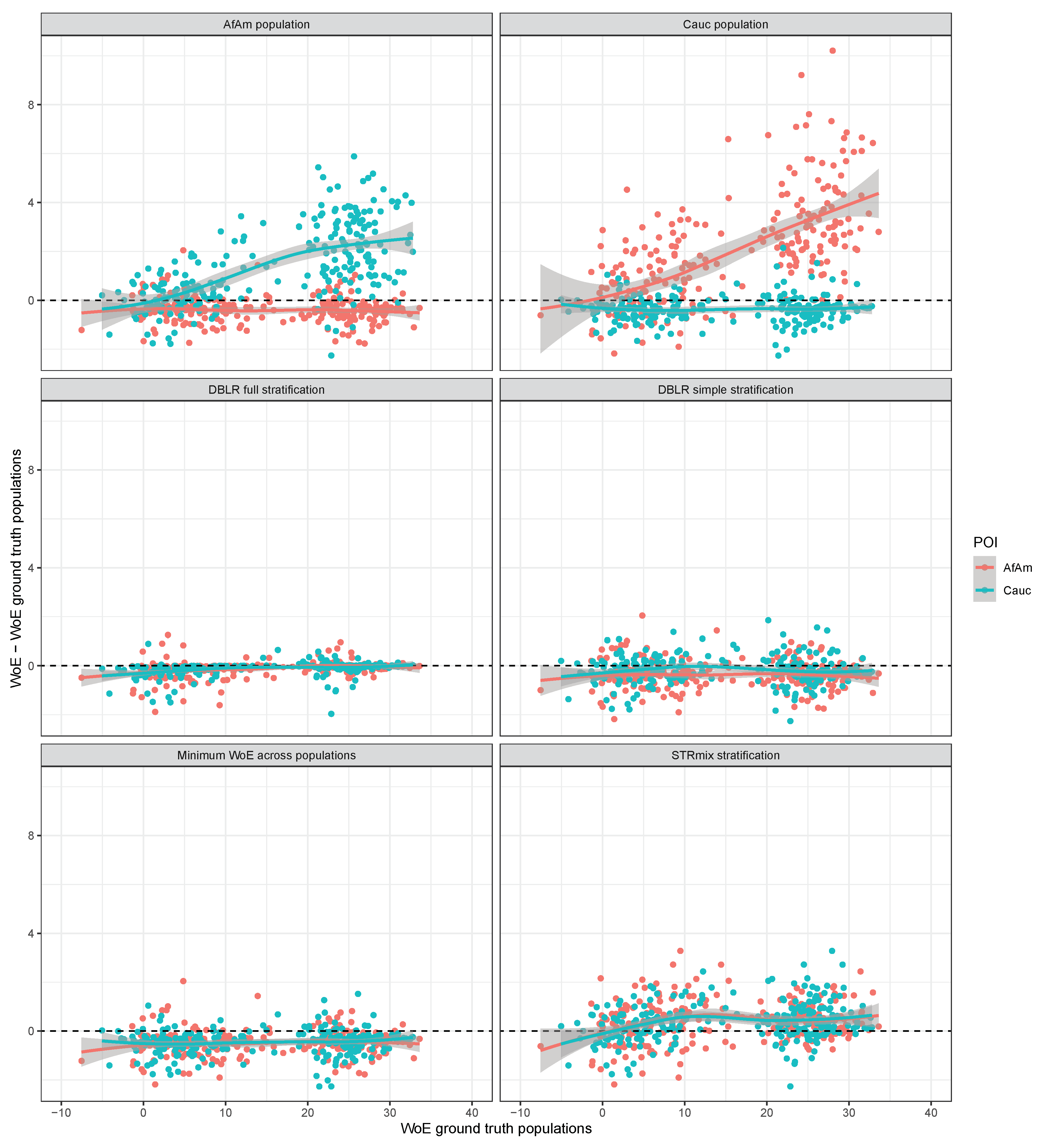
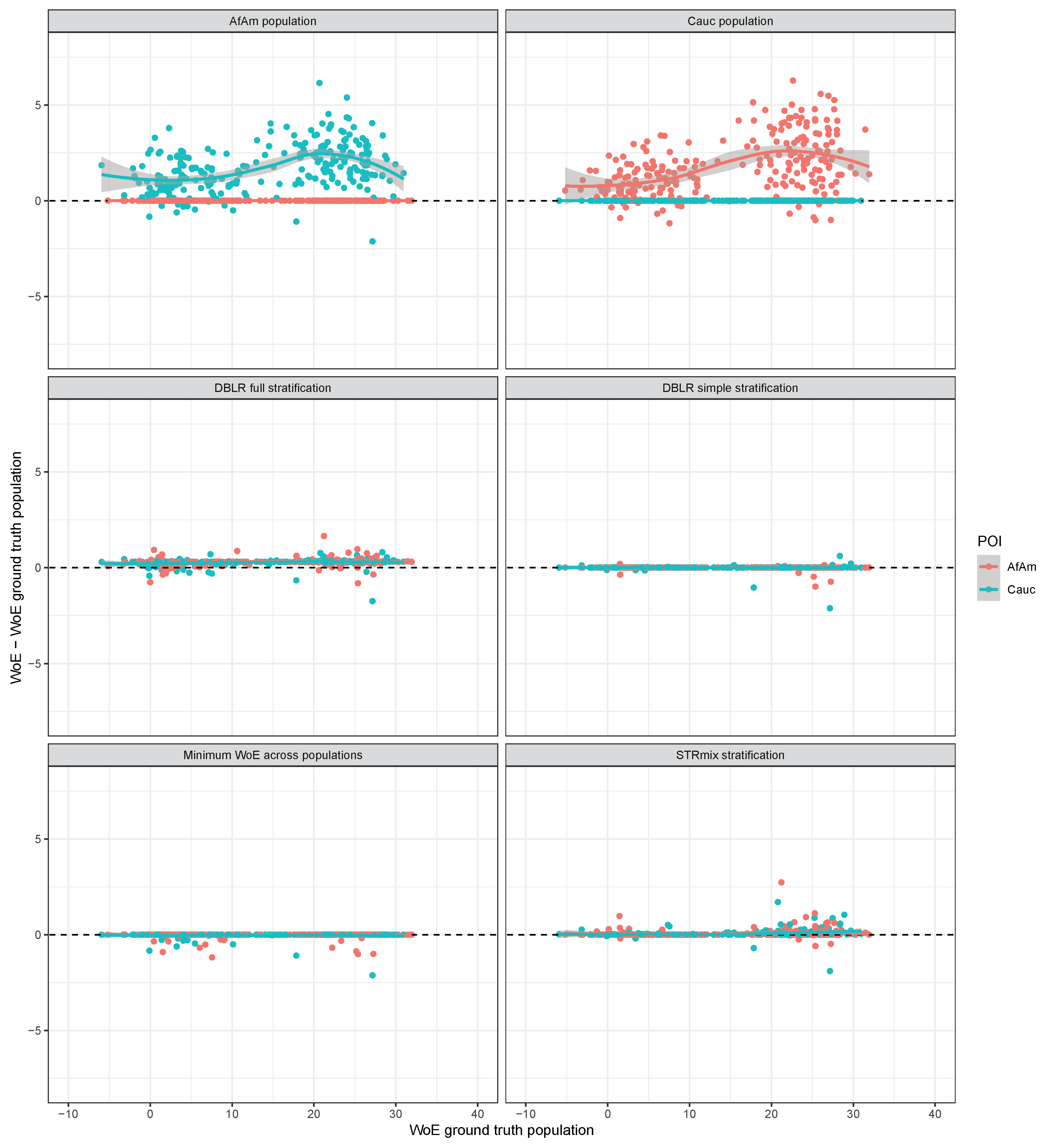
3. Results
3.1. The Case of
3.2. The Case of
3.3. Contributors from the Same Population
4. Discussion
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Meester, R.; Slooten, K. Probability and Forensic Evidence: Theory, Philosophy, and Applications; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar]
- Buckleton, J.S.; Bright, J.A.; Taylor, D. Forensic DNA Evidence Interpretation; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Balding, D.J.; Steele, C.D. Weight-of-Evidence for Forensic DNA Profiles; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Balding, D.J.; Nichols, R.A. DNA profile match probability calculation: How to allow for population stratification, relatedness, database selection and single bands. Forensic Sci. Int. 1994, 64, 125–140. [Google Scholar] [CrossRef] [PubMed]
- Balding, D.J.; Bishop, M.; Cannings, C. Handbook of Statistical Genetics; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- National Research Council. The Evaluation of Forensic DNA Evidence; National Research Council: Washington, DC, USA, 1996. [Google Scholar]
- Gill, P.; Haned, H.; Bleka, O.; Hansson, O.; Dørum, G.; Egeland, T. Genotyping and interpretation of STR-DNA: Low-template, mixtures and database matches—Twenty years of research and development. Forensic Sci. Int. Genet. 2015, 18, 100–117. [Google Scholar] [CrossRef] [PubMed]
- Butler, J.M. The future of forensic DNA analysis. Philos. Trans. R. Soc. B Biol. Sci. 2015, 370, 20140252. [Google Scholar] [CrossRef] [PubMed]
- Devesse, L. Characterisation and Differentiation of five UK Populations Using Massively Parallel Sequencing of Forensic STRs. Ph.D. Thesis, King’s College London, London, UK, 2022. [Google Scholar]
- Steffen, C.R.; Coble, M.D.; Gettings, K.B.; Vallone, P.M. Corrigendum to ‘US population data for 29 autosomal STR loci’[Forensic Sci. Int. Genet. 7 (2013) e82–e83]. Forensic Sci. Int. Genet. 2017, 31, e36–e40. [Google Scholar] [CrossRef] [PubMed]
- Budowle, B.; Moretti, T.R.; Baumstark, A.L.; Defenbaugh, D.A.; Keys, K.M. Population data on the thirteen CODIS core short tandem repeat loci in African Americans, US Caucasians, Hispanics, Bahamians, Jamaicans, and Trinidadians. J. Forensic Sci. 1999, 44, 1277–1286, Erratum in J. Forensic Sci. 2015, 60, 1114–1116. [Google Scholar] [CrossRef]
- SWGDAM Ad Hoc Working Group on Genotyping Results Reported as Likelihood Ratios. Recommendations of the SWGDAM Ad Hoc Working Group on Genotyping Results Reported as Likelihood Ratios. 2018. Available online: https://www.swgdam.org/_files/ugd/4344b0_dd5221694d1448588dcd0937738c9e46.pdf (accessed on 12 October 2022).
- Ge, J.; Budowle, B. Kinship index variations among populations and thresholds for familial searching. PLoS ONE 2012, 7, e37474. [Google Scholar] [CrossRef] [PubMed]
- Gill, P.; Hicks, T.; Butler, J.M.; Connolly, E.; Gusmão, L.; Kokshoorn, B.; Morling, N.; van Oorschot, R.A.; Parson, W.; Prinz, M.; et al. DNA commission of the International society for forensic genetics: Assessing the value of forensic biological evidence-Guidelines highlighting the importance of propositions: Part I: Evaluation of DNA profiling comparisons given (sub-) source propositions. Forensic Sci. Int. Genet. 2018, 36, 189–202. [Google Scholar] [CrossRef] [PubMed]
- Triggs, C.; Harbison, S.; Buckleton, J. The calculation of DNA match probabilities in mixed race populations. Sci. Justice J. Forensic Sci. Soc. 2000, 40, 33–38. [Google Scholar] [CrossRef] [PubMed]
- Kelly, H.; Kerr, Z.; Cheng, K.; Kruijver, M.; Bright, J.A. Developmental validation of a software implementation of a flexible framework for the assignment of likelihood ratios for forensic investigations. Forensic Sci. Int. Rep. 2021, 4, 100231. [Google Scholar] [CrossRef]
- Kruijver, M.; Taylor, D.; Bright, J.A. Evaluating DNA evidence possibly involving multiple (mixed) samples, common donors and related contributors. Forensic Sci. Int. Genet. 2021, 54, 102532. [Google Scholar] [CrossRef]
- Kruijver, M. simDNAmixtures: Simulate Forensic DNA Mixtures. R Package Version 0.2. 2022. Available online: https://linkinghub.elsevier.com/retrieve/pii/S1872497321000703 (accessed on 12 November 2022).
- Kruijver, M.; Bright, J.A. A tool for simulating single source and mixed DNA profiles. Forensic Sci. Int. Genet. 2022, 60, 102746. [Google Scholar] [CrossRef]
- Toscanini, U.; Salas, A.; García-Magariños, M.; Gusmão, L.; Raimondi, E. Population stratification in Argentina strongly influences likelihood ratio estimates in paternity testing as revealed by a simulation-based approach. Int. J. Leg. Med. 2010, 124, 63–69. [Google Scholar] [CrossRef]
- Laurent, F.X.; Fischer, A.; Oldt, R.F.; Kanthaswamy, S.; Buckleton, J.S.; Hitchin, S. Streamlining the decision-making process for international DNA kinship matching using Worldwide allele frequencies and tailored cutoff log10LR thresholds. Forensic Sci. Int. Genet. 2022, 57, 102634. [Google Scholar] [CrossRef] [PubMed]
- Oldt, R.F.; Kanthaswamy, S. Expanded CODIS STR allele frequencies–Evidence for the irrelevance of race-based DNA databases. Leg. Med. 2020, 42, 101642. [Google Scholar] [CrossRef] [PubMed]


| Genotype Combination (s) | Weight () |
|---|---|
| (13/14, 11/11) | 0.3 |
| (11/14, 11/13) | 0.27 |
| (11/13, 11/14) | 0.23 |
| (11/11, 13/14) | 0.2 |
| Frequency in | Frequency in | |
|---|---|---|
| Allele (a) | Population A () | Population B () |
| 11 | 0.6 | 0.5 |
| 13 | 0.3 | 0.3 |
| 14 | 0.1 | 0.2 |
| Population | Implementation | |
|---|---|---|
| African American only | DBLRTM, STRmixTM | 0, |
| Caucausian only | DBLRTM, STRmixTM | 0, |
| Simple stratified | DBLRTM | 0, |
| Fully stratified | DBLRTM | 0, |
| STRmixTM stratified | STRmixTM | 0, |
| Ground truth (mixed) | DBLRTM | 0, |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kruijver, M.; Kelly, H.; Bright, J.-A.; Buckleton, J. Evaluating DNA Mixtures with Contributors from Different Populations Using Probabilistic Genotyping. Genes 2023, 14, 40. https://doi.org/10.3390/genes14010040
Kruijver M, Kelly H, Bright J-A, Buckleton J. Evaluating DNA Mixtures with Contributors from Different Populations Using Probabilistic Genotyping. Genes. 2023; 14(1):40. https://doi.org/10.3390/genes14010040
Chicago/Turabian StyleKruijver, Maarten, Hannah Kelly, Jo-Anne Bright, and John Buckleton. 2023. "Evaluating DNA Mixtures with Contributors from Different Populations Using Probabilistic Genotyping" Genes 14, no. 1: 40. https://doi.org/10.3390/genes14010040
APA StyleKruijver, M., Kelly, H., Bright, J.-A., & Buckleton, J. (2023). Evaluating DNA Mixtures with Contributors from Different Populations Using Probabilistic Genotyping. Genes, 14(1), 40. https://doi.org/10.3390/genes14010040





