PromoterLCNN: A Light CNN-Based Promoter Prediction and Classification Model
Abstract
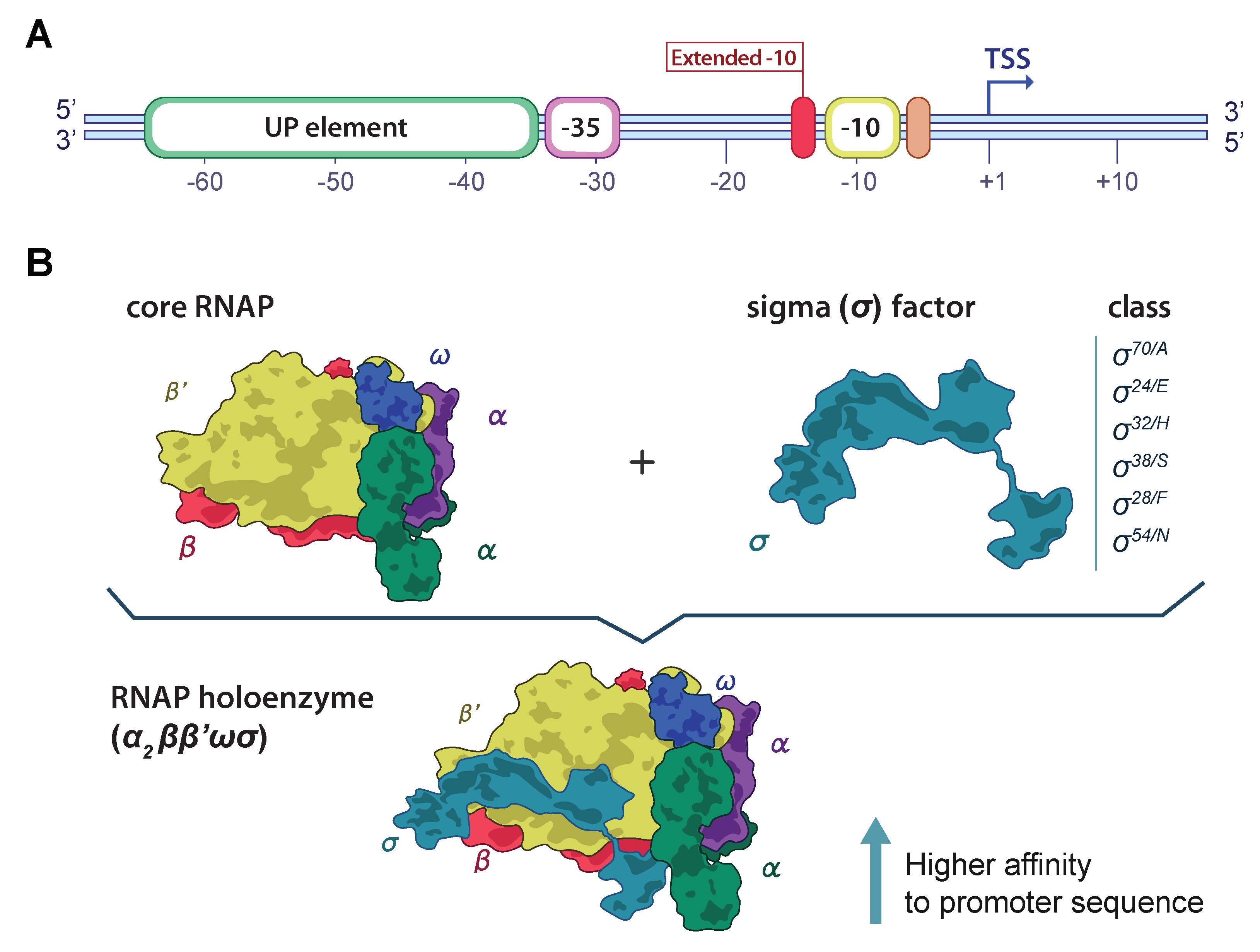
:1. Introduction
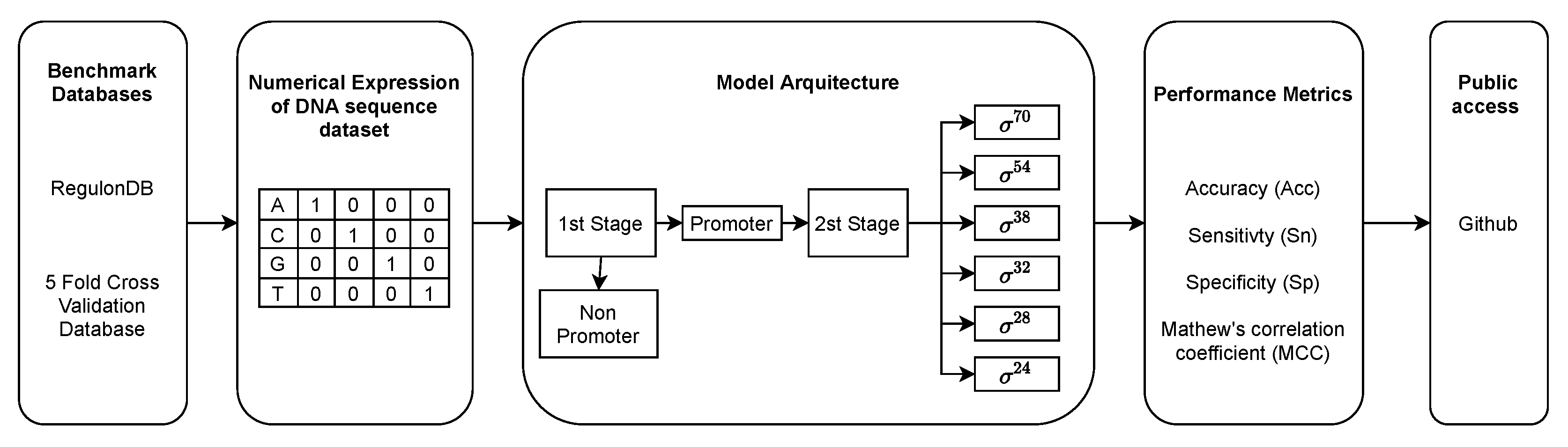
2. Inputs and Methods
2.1. Benchmark and Test Datasets
2.2. Mathematical Formulation of DNA Sequence
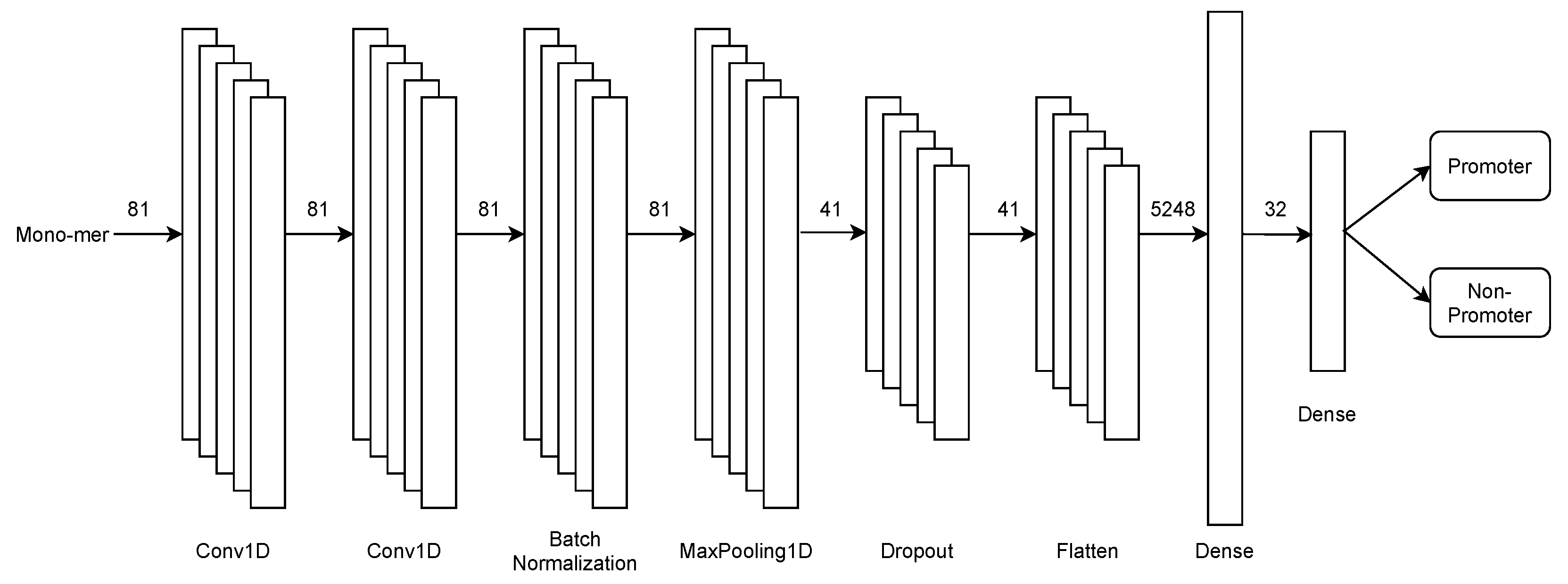
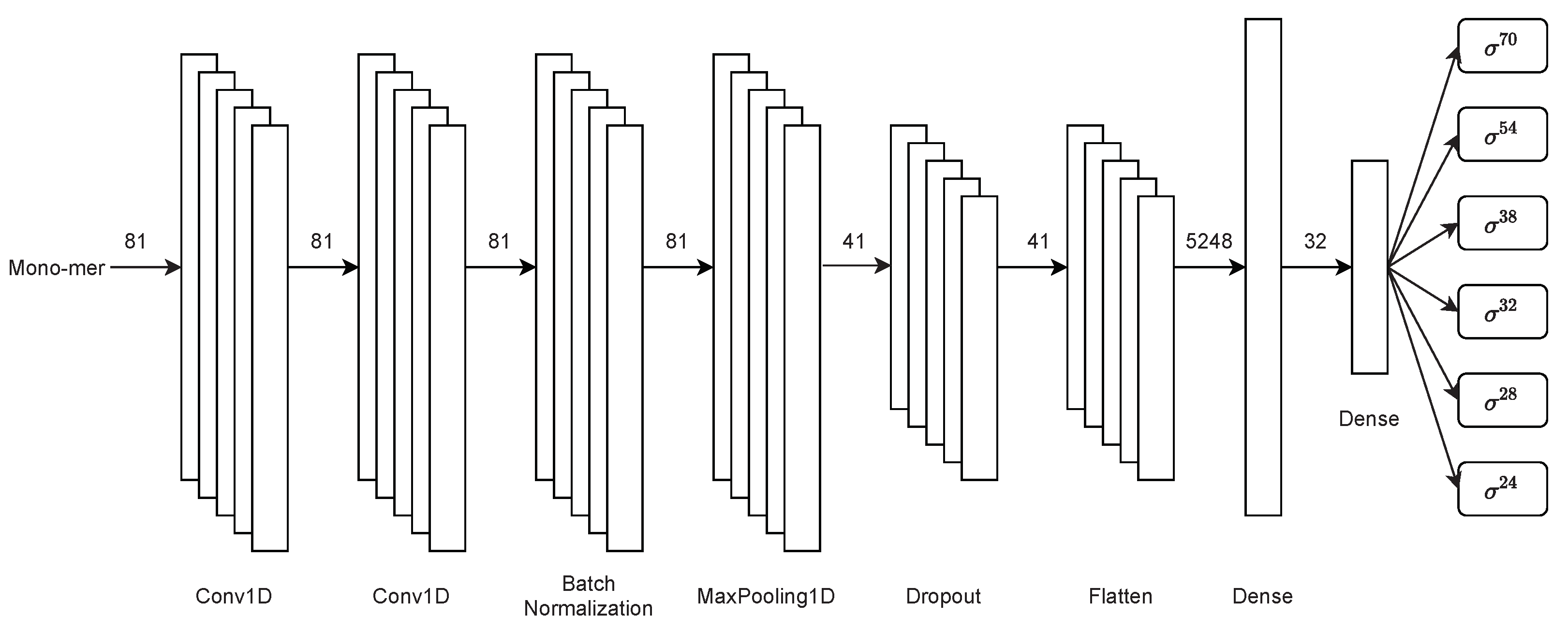
2.3. Model Architecture
2.3.1. First Stage
2.3.2. Second Stage
2.3.3. Hyperparameter Tuning
2.4. Performance Metrics
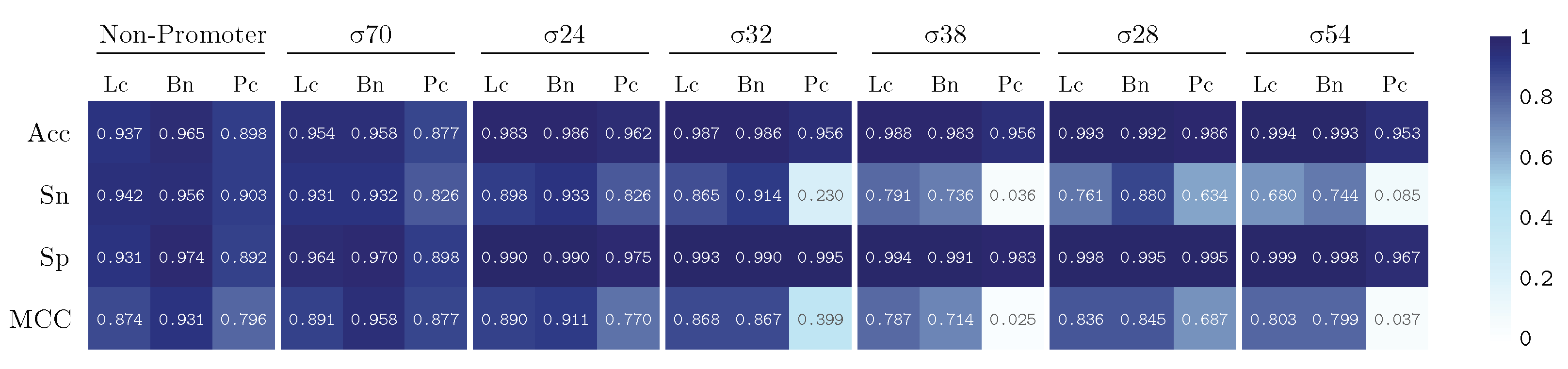
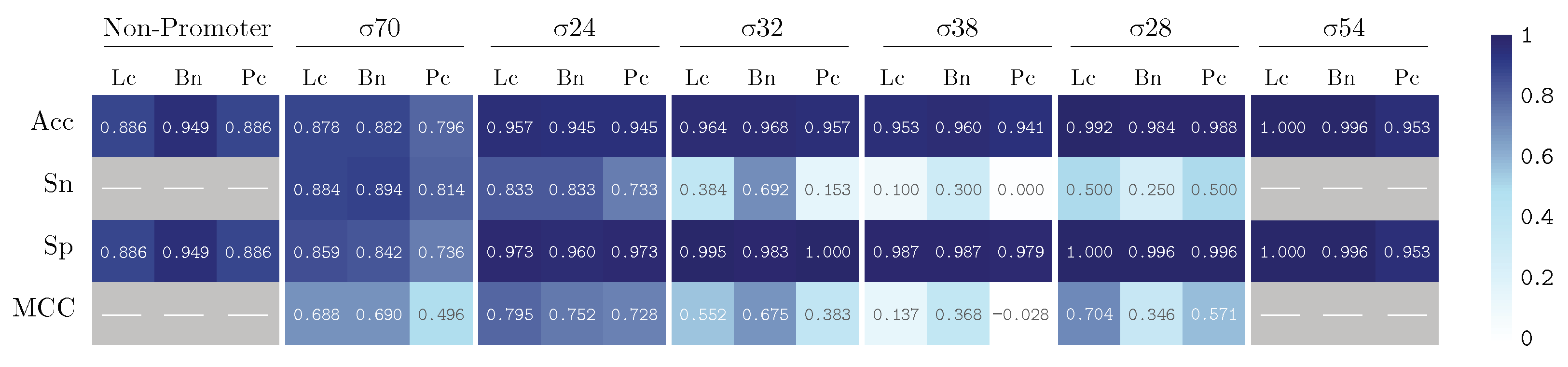
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Helmann, J.D. Where to begin? Sigma factors and the selectivity of transcription initiation in bacteria. Mol. Microbiol. 2019, 112, 335–347. [Google Scholar] [CrossRef] [Green Version]
- Bervoets, I.; Van Brempt, M.; Van Nerom, K.; Van Hove, B.; Maertens, J.; De Mey, M.; Charlier, D. A sigma factor toolbox for orthogonal gene expression in Escherichia coli. Nucleic Acids Res. 2018, 46, 2133–2144. [Google Scholar] [CrossRef] [Green Version]
- Mitchell, J.E.; Zheng, D.; Busby, S.J.W.; Minchin, S.D. Identification and analysis of ‘extended -10’ promoters in Escherichia coli. Nucleic Acids Res. 2003, 31, 4689–4695. [Google Scholar] [CrossRef] [Green Version]
- Typas, A.; Hengge, R. Differential ability of sigma(s) and sigma70 of Escherichia coli to utilize promoters containing half or full UP-element sites. Mol. Microbiol. 2005, 55, 250–260. [Google Scholar] [CrossRef]
- Abril, A.G.; Rama, J.L.R.; Sánchez-Pérez, A.; Villa, T.G. Prokaryotic sigma factors and their transcriptional counterparts in Archaea and Eukarya. Appl. Microbiol. Biotechnol. 2020, 104, 4289–4302. [Google Scholar] [CrossRef]
- Cassiano, M.H.A.; Silva-Rocha, R. Benchmarking bacterial promoter prediction tools: Potentialities and limitations. mSystems 2020, 5, 439. [Google Scholar] [CrossRef]
- Oubounyt, M.; Louadi, Z.; Tayara, H.; Chong, K.T. DeePromoter: Robust Promoter Predictor Using Deep Learning. Front. Genet. 2019, 10, 286. [Google Scholar] [CrossRef] [Green Version]
- Di Salvo, M.; Pinatel, E.; Talà, A.; Fondi, M.; Peano, C.; Alifano, P. G4PromFinder: An algorithm for predicting transcription promoters in GC-rich bacterial genomes based on AT-rich elements and G-quadruplex motifs. BMC Bioinform. 2018, 19, 36. [Google Scholar] [CrossRef] [Green Version]
- Ishihama, A.; Shimada, T.; Yamazaki, Y. Transcription profile of Escherichia coli: Genomic SELEX search for regulatory targets of transcription factors. Nucleic Acids Res. 2016, 44, 2058–2074. [Google Scholar] [CrossRef] [Green Version]
- Dahl, J.; Collas, P. A rapid micro chromatin immunoprecipitation assay (ChIP). Nat. Protoc. 2008, 3, 1032–1045. [Google Scholar] [CrossRef]
- Matsumine, H.; Yamamura, Y.; Hattori, N.; Kobayashi, T.; Kitada, T.; Yoritaka, A.; Mizuno, Y. A Microdeletion of D6S305 in a Family of Autosomal Recessive Juvenile Parkinsonism (PARK2). Genomics 1998, 49, 143–146. [Google Scholar] [CrossRef]
- Behjati, S.; Tarpey, P.S. What is next generation sequencing? Arch. Dis. Child. Educ. Pract. 2013, 98, 236–238. [Google Scholar] [CrossRef]
- Zhang, J.; Chiodini, R.; Badr, A.; Zhang, G. The impact of next-generation sequencing on genomics. J. Genet. Genom. 2011, 38, 95–109. [Google Scholar] [CrossRef] [Green Version]
- Solovyev, V.; Salamov, A. Automatic annotation of microbial genomes and metagenomic sequences. In Metagenomics and Its Applications in Agriculture, Biomedicine and Environmental Studies; Li, R.W., Ed.; Nova Science Publishers, Inc.: Hauppauge, NY, USA, 2011; pp. 61–78. [Google Scholar]
- Wang, J.; Hannenhalli, S. A mammalian promoter model links cis elements to genetic networks. Biochem. Biophys. Res. Commun. 2006, 347, 166–177. [Google Scholar] [CrossRef]
- Münch, R.; Hiller, K.; Grote, A.; Scheer, M.; Klein, J.; Schobert, M.; Jahn, D. Virtual Footprint and PRODORIC: An integrative framework for regulon prediction in prokaryotes. Bioinformatics 2005, 21, 4187–4189. [Google Scholar] [CrossRef] [Green Version]
- He, W.; Jia, C.; Duan, Y.; Zou, Q. 70ProPred: A predictor for discovering sigma70 promoters based on combining multiple features. BMC Syst. Biol. 2018, 12, 44. [Google Scholar] [CrossRef]
- Amin, R.; Rahman, C.R.; Ahmed, S.; Sifat, M.H.R.; Liton, M.N.K.; Rahman, M.M.; Khan, M.Z.H.; Shatabda, S. iPromoter-BnCNN: A novel branched CNN-based predictor for identifying and classifying sigma promoters. Bioinformatics 2020, 36, 4869–4875. [Google Scholar] [CrossRef]
- Qian, Y.; Zhang, Y.; Guo, B.; Ye, S.; Wu, Y.; Zhang, J. An Improved Promoter Recognition Model Using Convolutional Neural Network. In Proceedings of the 2018 IEEE 42nd Annual Computer Software and Applications Conference (COMPSAC), Tokyo, Japan, 23–27 July 2018; Volume 1, pp. 471–476. [Google Scholar] [CrossRef]
- Umarov, R.K.; Solovyev, V.V. Recognition of prokaryotic and eukaryotic promoters using convolutional deep learning neural networks. PLoS ONE 2017, 12, e0171410. [Google Scholar] [CrossRef]
- Rahman, M.S.; Aktar, U.; Jani, M.R.; Shatabda, S. iPro70-FMWin: Identifying Sigma70 promoters using multiple windowing and minimal features. Mol. Genet. Genom. 2019, 294, 69–84. [Google Scholar] [CrossRef]
- Shujaat, M.; Wahab, A.; Tayara, H.; Chong, K.T. pcPromoter-CNN: A CNN-Based Prediction and Classification of Promoters. Genes 2020, 11, 1529. [Google Scholar] [CrossRef]
- Zhang, M.; Li, F.; Marquez-Lago, T.T.; Leier, A.; Fan, C.; Kwoh, C.K.; Chou, K.C.; Song, J.; Jia, C. MULTiPly: A novel multi-layer predictor for discovering general and specific types of promoters. Bioinformatics 2019, 35, 2957–2965. [Google Scholar] [CrossRef]
- Feng, P.; Ding, H.; Yang, H.; Chen, W.; Lin, H.; Chou, K.C. iRNA-PseColl: Identifying the occurrence sites of different RNA modifications by incorporating collective effects of nucleotides into PseKNC. Mol. Ther.-Nucleic Acids 2017, 7, 155–163. [Google Scholar] [CrossRef] [Green Version]
- Chou, K.C. Some remarks on protein attribute prediction and pseudo amino acid composition. J. Theory Biol. 2011, 273, 236–247. [Google Scholar] [CrossRef]
- Gama-Castro, S.; Salgado, H.; Santos-Zavaleta, A.; Ledezma-Tejeida, D.; Muñiz-Rascado, L.; García-Sotelo, J.S.; Alquicira-Hernández, K.; Martínez-Flores, I.; Pannier, L.; Castro-Mondragón, J.A.; et al. RegulonDB version 9.0: High-level integration of gene regulation, coexpression, motif clustering and beyond. Nucleic Acids Res. 2016, 44, D133–D143. [Google Scholar] [CrossRef] [Green Version]
- Santos-Zavaleta, A.; Salgado, H.; Gama-Castro, S.; Sánchez-Pérez, M.; Gómez-Romero, L.; Ledezma-Tejeida, D.; García-Sotelo, J.S.; Alquicira-Hernández, K.; Muñiz-Rascado, L.J.; Peña-Loredo, P.; et al. RegulonDB v 10.5: Tackling challenges to unify classic and high throughput knowledge of gene regulation in E. coli K-12. Nucleic Acids Res. 2019, 47, D212–D220. [Google Scholar] [CrossRef] [Green Version]
| Classes | Training Dataset | Test Dataset |
|---|---|---|
| Promoter () | 2860 | 256 |
| Non-Promoter () | 2860 | 0 |
| -Promoter | 1694 | 199 |
| -Promoter | 484 | 30 |
| -Promoter | 291 | 13 |
| -Promoter | 163 | 10 |
| -Promoter | 134 | 4 |
| -Promoter | 94 | 0 |
| Hyper Parameter | Candidate Values |
|---|---|
| Number of Convolution Filters | 16, 32, 64, 128 |
| Convolution Kernel Size | 3, 5, 7, 9 |
| Kernel Regularizers (L2) | 1× 10, 1 × 10, 1 × 10, 1 × 10 |
| Dropout Rate | 0.15, 0.20, …, 0.50 |
| Dense Layer Neurons | 8, 16, …, 64 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hernández, D.; Jara, N.; Araya, M.; Durán, R.E.; Buil-Aranda, C. PromoterLCNN: A Light CNN-Based Promoter Prediction and Classification Model. Genes 2022, 13, 1126. https://doi.org/10.3390/genes13071126
Hernández D, Jara N, Araya M, Durán RE, Buil-Aranda C. PromoterLCNN: A Light CNN-Based Promoter Prediction and Classification Model. Genes. 2022; 13(7):1126. https://doi.org/10.3390/genes13071126
Chicago/Turabian StyleHernández, Daryl, Nicolás Jara, Mauricio Araya, Roberto E. Durán, and Carlos Buil-Aranda. 2022. "PromoterLCNN: A Light CNN-Based Promoter Prediction and Classification Model" Genes 13, no. 7: 1126. https://doi.org/10.3390/genes13071126
APA StyleHernández, D., Jara, N., Araya, M., Durán, R. E., & Buil-Aranda, C. (2022). PromoterLCNN: A Light CNN-Based Promoter Prediction and Classification Model. Genes, 13(7), 1126. https://doi.org/10.3390/genes13071126






