Gene-Based Methods for Estimating the Degree of the Skewness of X Chromosome Inactivation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Notations
2.2. Point Estimate and CI of by Fieller’s Method
2.3. Penalized Point Estimate and CI of by PF Method
2.4. Point Estimate and Credible Interval of by Bayesian Method
3. Results
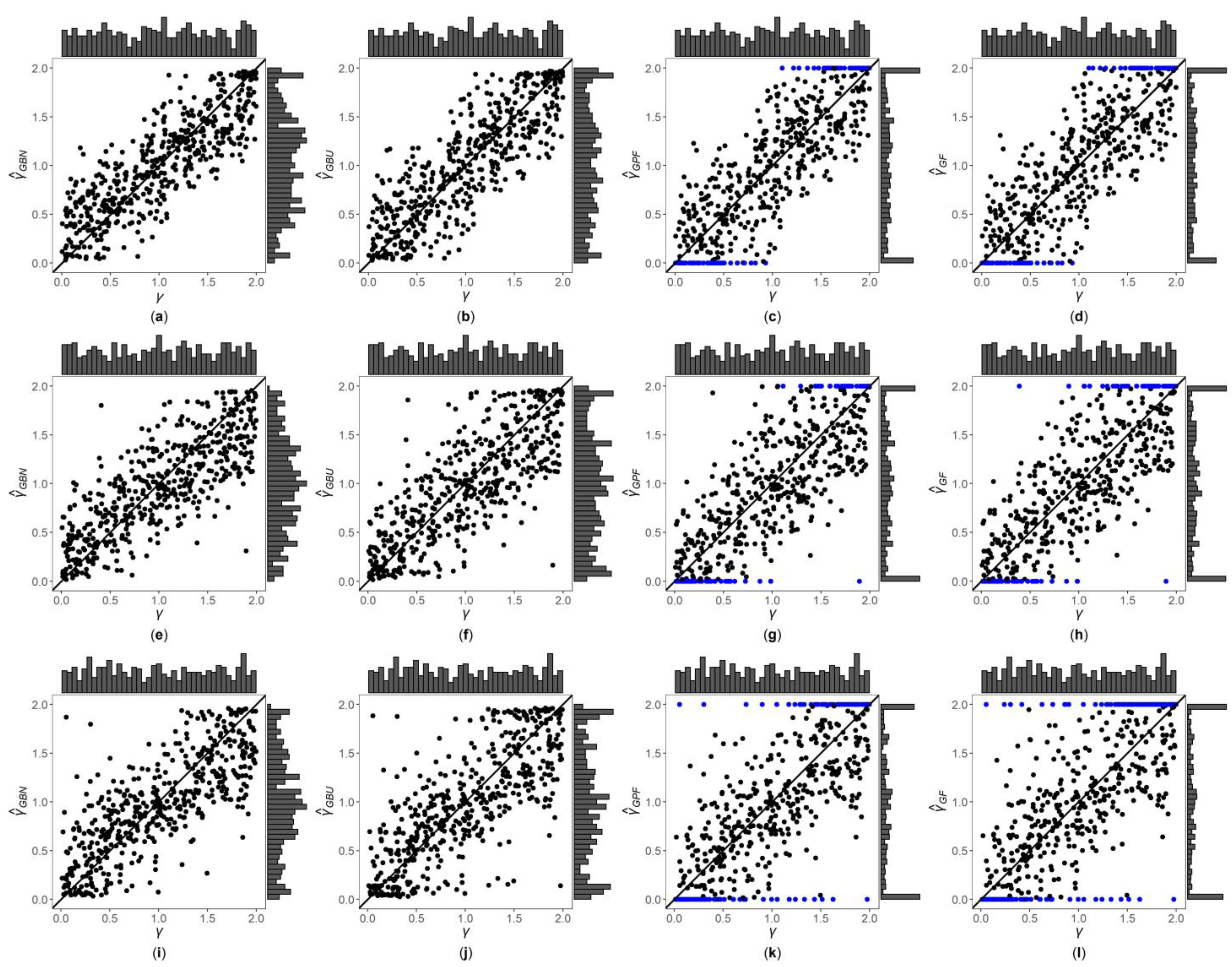
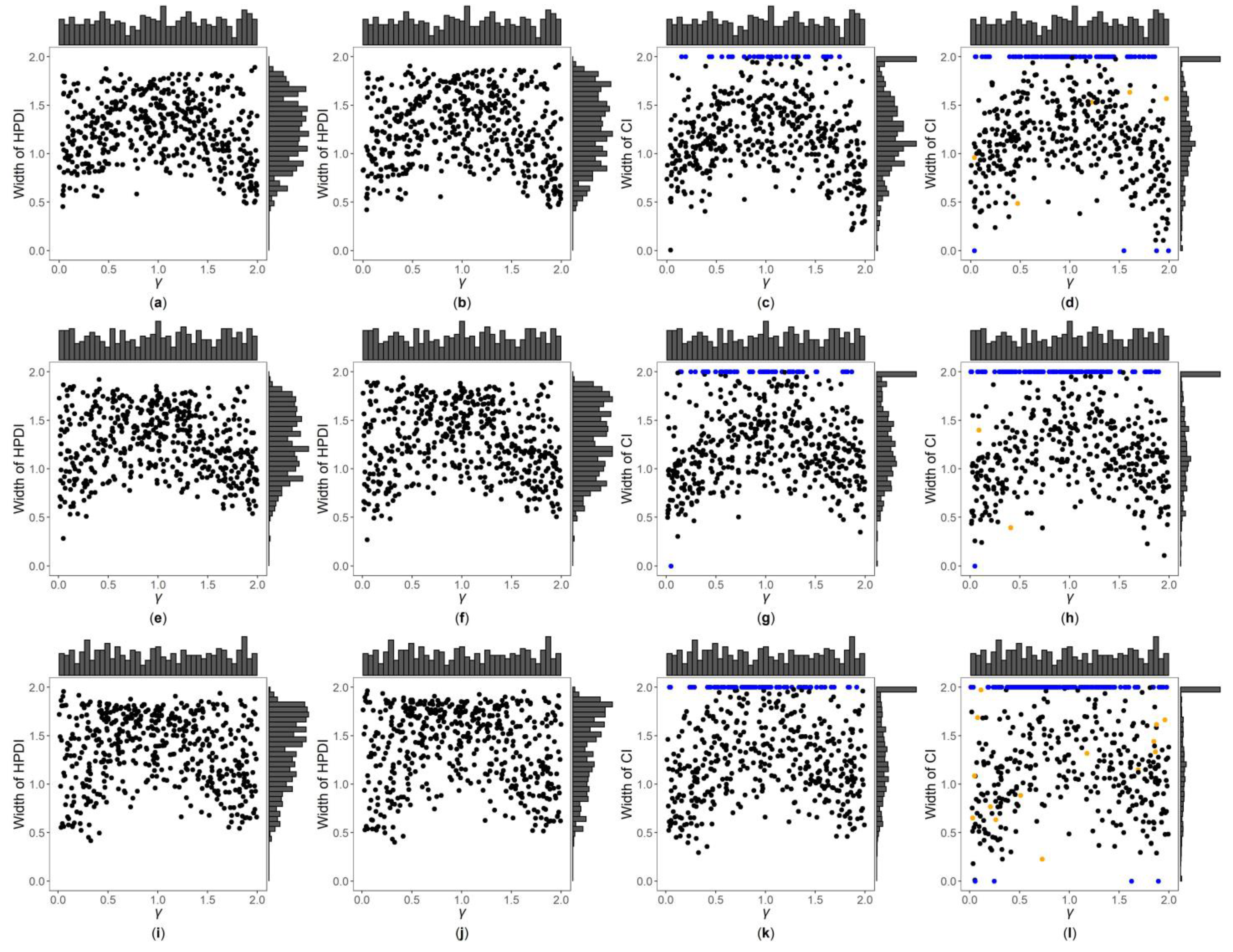
3.1. Simulation Settings
3.2. Simulation Results
3.3. Application to MCTFR Data
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Lyon, M.F. Gene action in the X-chromosome of the mouse (Mus musculus L.). Nature 1961, 190, 372–373. [Google Scholar] [CrossRef] [PubMed]
- Amos-Landgraf, J.M.; Cottle, A.; Plenge, R.M.; Friez, M.; Schwartz, C.E.; Longshore, J.; Willard, H.F. X chromosome-inactivation patterns of 1,005 phenotypically unaffected females. Am. J. Hum. Genet. 2006, 79, 493–499. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Plenge, R.M.; Stevenson, R.A.; Lubs, H.A.; Schwartz, C.E.; Willard, H.F. Skewed X-chromosome inactivation is a common feature of X-linked mental retardation disorders. Am. J. Hum. Genet. 2002, 71, 168–173. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shvetsova, E.; Sofronova, A.; Monajemi, R.; Gagalova, K.; Draisma, H.; White, S.J.; Santen, G.; Chuva de Sousa Lopes, S.M.; Heijmans, B.T.; van Meurs, J.; et al. Skewed X-inactivation is common in the general female population. Eur. J. Hum. Genet. 2019, 27, 455–465. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Medema, R.H.; Burgering, B.M. The X factor: Skewing X inactivation towards cancer. Cell 2007, 129, 1253–1254. [Google Scholar] [CrossRef] [Green Version]
- Deng, X.; Berletch, J.B.; Nguyen, D.K.; Disteche, C.M. X chromosome regulation: Diverse patterns in development, tissues and disease. Nat. Rev. Genet. 2014, 15, 367–378. [Google Scholar] [CrossRef]
- Posynick, B.J.; Brown, C.J. Escape from X-chromosome inactivation: An evolutionary perspective. Front. Cell Dev. Biol. 2019, 7, 241. [Google Scholar] [CrossRef]
- Peeters, S.B.; Cotton, A.M.; Brown, C.J. Variable escape from X-chromosome inactivation: Identifying factors that tip the scales towards expression. Bioessays 2014, 36, 746–756. [Google Scholar] [CrossRef]
- Minks, J.; Robinson, W.P.; Brown, C.J. A skewed view of X chromosome inactivation. J. Clin. Invest. 2008, 118, 20–23. [Google Scholar] [CrossRef]
- Chabchoub, G.; Uz, E.; Maalej, A.; Mustafa, C.A.; Rebai, A.; Mnif, M.; Bahloul, Z.; Farid, N.R.; Ozcelik, T.; Ayadi, H. Analysis of skewed X-chromosome inactivation in females with rheumatoid arthritis and autoimmune thyroid diseases. Arthritis Res. Ther. 2009, 11, R106. [Google Scholar] [CrossRef] [Green Version]
- Sun, Z.; Fan, J.; Wang, Y. X-chromosome inactivation and related diseases. Genet. Res. 2022, 2022, 1391807. [Google Scholar] [CrossRef] [PubMed]
- Okumura, K.; Fujimori, Y.; Takagi, A.; Murate, T.; Ozeki, M.; Yamamoto, K.; Katsumi, A.; Matsushita, T.; Naoe, T.; Kojima, T. Skewed X chromosome inactivation in fraternal female twins results in moderately severe and mild haemophilia B. Haemophilia 2008, 14, 1088–1093. [Google Scholar] [CrossRef] [PubMed]
- Garagiola, I.; Mortarino, M.; Siboni, S.M.; Boscarino, M.; Mancuso, M.E.; Biganzoli, M.; Santagostino, E.; Peyvandi, F. X chromosome inactivation: A modifier of factor VIII and IX plasma levels and bleeding phenotype in Haemophilia carriers. Eur. J. Hum. Genet. 2021, 29, 241–249. [Google Scholar] [CrossRef]
- Zuo, T.; Wang, L.; Morrison, C.; Chang, X.; Zhang, H.; Li, W.; Liu, Y.; Wang, Y.; Liu, X.; Chan, M.; et al. FOXP3 is an X-linked breast cancer suppressor gene and an important repressor of the HER-2/ErbB2 oncogene. Cell 2007, 129, 1275–1286. [Google Scholar] [CrossRef] [Green Version]
- Li, G.; Jin, T.; Liang, H.; Tu, Y.; Zhang, W.; Gong, L.; Su, Q.; Gao, G. Skewed X-chromosome inactivation in patients with esophageal carcinoma. Diagn. Pathol. 2013, 8, 55. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Simmonds, M.J.; Kavvoura, F.K.; Brand, O.J.; Newby, P.R.; Jackson, L.E.; Hargreaves, C.E.; Franklyn, J.A.; Gough, S.C. Skewed X chromosome inactivation and female preponderance in autoimmune thyroid disease: An association study and meta-analysis. J. Clin. Endocrinol. Metab. 2014, 99, E127–E131. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Giliberto, F.; Radic, C.P.; Luce, L.; Ferreiro, V.; de Brasi, C.; Szijan, I. Symptomatic female carriers of Duchenne muscular dystro-phy (DMD): Genetic and clinical characterization. J. Neurol. Sci. 2014, 336, 36–41. [Google Scholar] [CrossRef] [Green Version]
- Sangha, K.K.; Stephenson, M.D.; Brown, C.J.; Robinson, W.P. Extremely skewed X-chromosome inactivation is increased in women with recurrent spontaneous abortion. Am. J. Hum. Genet. 1999, 65, 913–917. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, Y.; Xu, S.Q.; Liu, W.; Fung, W.K.; Zhou, J.Y. A robust test for X-chromosome genetic association accounting for X-chromosome inactivation and imprinting. Genet. Res. 2020, 102, e2. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Martin, E.R.; Morris, R.W.; Li, Y.J. Association test for X-linked QTL in family-based designs. Am. J. Hum. Genet. 2009, 84, 431–444. [Google Scholar] [CrossRef] [Green Version]
- Zheng, G.; Joo, J.; Zhang, C.; Geller, N.L. Testing association for markers on the X chromosome. Genet. Epidemiol. 2007, 31, 834–843. [Google Scholar] [CrossRef] [PubMed]
- Clayton, D. Testing for association on the X chromosome. Biostatistics 2008, 9, 593–600. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Yu, R.; Shete, S. X-chromosome genetic association test accounting for X-inactivation, skewed X-inactivation, and escape from X-inactivation. Genet. Epidemiol. 2014, 38, 483–493. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Wang, B.Q.; Liu-Fu, G.; Fung, W.K.; Zhou, J.Y. X-chromosome genetic association test incorporating X-chromosome inactivation and imprinting effects. J. Genet. 2019, 98, 99. [Google Scholar] [CrossRef] [PubMed]
- Ma, L.; Hoffman, G.; Keinan, A. X-inactivation informs variance-based testing for X-linked association of a quantitative trait. BMC Genomics 2015, 16, 241. [Google Scholar] [CrossRef] [Green Version]
- Gao, F.; Chang, D.; Biddanda, A.; Ma, L.; Guo, Y.; Zhou, Z.; Keinan, A. XWAS: A software toolset for genetic data analysis and association studies of the X chromosome. J. Hered. 2015, 106, 666–671. [Google Scholar] [CrossRef] [Green Version]
- Madsen, B.E.; Browning, S.R. A groupwise association test for rare mutations using a weighted sum statistic. PLoS Genet. 2009, 5, e1000384. [Google Scholar] [CrossRef] [Green Version]
- Li, B.; Leal, S.M. Methods for detecting associations with rare variants for common diseases: Application to analysis of sequence data. Am. J. Hum. Genet. 2008, 83, 311–321. [Google Scholar] [CrossRef] [Green Version]
- Schork, N.J.; Murray, S.S.; Frazer, K.A.; Topol, E.J. Common vs. rare allele hypotheses for complex diseases. Curr. Opin. Genet. Dev. 2009, 19, 212–219. [Google Scholar] [CrossRef] [Green Version]
- Han, F.; Pan, W. A data-adaptive sum test for disease association with multiple common or rare variants. Hum. Hered. 2010, 70, 42–54. [Google Scholar] [CrossRef] [Green Version]
- Ionita-Laza, I.; Buxbaum, J.D.; Laird, N.M.; Lange, C. A new testing strategy to identify rare variants with either risk or protective effect on disease. PLoS Genet. 2011, 7, e1001289. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Price, A.L.; Kryukov, G.V.; de Bakker, P.I.; Purcell, S.M.; Staples, J.; Wei, L.J.; Sunyaev, S.R. Pooled association tests for rare variants in exon-resequencing studies. Am. J. Hum. Genet. 2010, 86, 832–838. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, M.C.; Lee, S.; Cai, T.; Li, Y.; Boehnke, M.; Lin, X. Rare-variant association testing for sequencing data with the sequence kernel association test. Am. J. Hum. Genet. 2011, 89, 82–93. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, S.; Emond, M.J.; Bamshad, M.J.; Barnes, K.C.; Rieder, M.J.; Nickerson, D.A.; NHLBI GO Exome Sequencing Project—ESP Lung Project Team; Christiani, D.C.; Wurfel, M.M.; Lin, X. Optimal unified approach for rare-variant association testing with application to small-sample case-control whole-exome sequencing studies. Am. J. Hum. Genet. 2012, 91, 224–237. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ionita-Laza, I.; Lee, S.; Makarov, V.; Buxbaum, J.D.; Lin, X. Sequence kernel association tests for the combined effect of rare and common variants. Am. J. Hum. Genet. 2013, 92, 841–853. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ma, C.; Boehnke, M.; Lee, S.; GoT2D Investigators. Evaluating the calibration and power of three gene-based association tests of rare variants for the X chromosome. Genet. Epidemiol. 2015, 39, 499–508. [Google Scholar] [CrossRef] [PubMed]
- Turkmen, A.S.; Lin, S. Detecting X-linked common and rare variant effects in family-based sequencing studies. Genet. Epidemiol. 2021, 45, 36–45. [Google Scholar] [CrossRef]
- Xu, S.Q.; Zhang, Y.; Wang, P.; Liu, W.; Wu, X.B.; Zhou, J.Y. A statistical measure for the skewness of X chromosome inactivation based on family trios. BMC Genet. 2018, 19, 109. [Google Scholar] [CrossRef]
- Wang, P.; Zhang, Y.; Wang, B.Q.; Li, J.L.; Wang, Y.X.; Pan, D.; Wu, X.B.; Fung, W.K.; Zhoui, J.Y. A statistical measure for the skewness of X chromosome inactivation based on case-control design. BMC Bioinformatics 2019, 20, 11. [Google Scholar] [CrossRef]
- Li, B.H.; Yu, W.Y.; Zhou, J.Y. A statistical measure for the skewness of X chromosome inactivation for quantitative traits and its application to the MCTFR data. BMC Genom. Data 2021, 22, 24. [Google Scholar] [CrossRef]
- Wang, P.; Xu, S.; Wang, Y.X.; Wu, B.; Fung, W.K.; Gao, G.; Liang, Z.; Liu, N. Penalized Fieller’s confidence interval for the ratio of bivariate normal means. Biometrics 2021, 77, 1355–1368. [Google Scholar] [CrossRef] [PubMed]
- Stephens, M.; Balding, D.J. Bayesian statistical methods for genetic association studies. Nat. Rev. Genet. 2009, 10, 681–690. [Google Scholar] [CrossRef] [PubMed]
- Annis, J.; Miller, B.J.; Palmeri, T.J. Bayesian inference with Stan: A tutorial on adding custom distributions. Behav. Res. Methods 2017, 49, 863–886. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kruschke J., K. Bayesian data analysis. Wiley Interdiscip. Rev. Cogn. Sci. 2010, 1, 658–676. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Deng, S.; Sun, L.; Li, L.; Hu, Y.Q. A nonparametric test for association with multiple loci in the retrospective case-control study. Stat. Methods Med. Res. 2020, 29, 589–602. [Google Scholar] [CrossRef]
- Basu, S.; Pan, W. Comparison of statistical tests for disease association with rare variants. Genet. Epidemiol. 2011, 35, 606–619. [Google Scholar] [CrossRef] [PubMed]
- Turkmen, A.S.; Yan, Z.; Hu, Y.Q.; Lin, S. Kullback-Leibler distance methods for detecting disease association with rare variants from sequencing data. Ann. Hum. Genet. 2015, 79, 199–208. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- McGue, M.; Zhang, Y.; Miller, M.B.; Basu, S.; Vrieze, S.; Hicks, B.; Malone, S.; Oetting, W.S.; Iacono, W.G. A genome-wide association study of behavioral disinhibition. Behav. Genet. 2013, 43, 363–373. [Google Scholar] [CrossRef] [Green Version]
- Asadollahi, H.; Vaez Torshizi, R.; Ehsani, A.; Masoudi, A.A. An association of CEP78, MEF2C, VPS13A and ARRDC3 genes with survivability to heat stress in an F2 chicken population. J. Anim. Breed. Genet. 2022. [Google Scholar] [CrossRef]
- McCaw, Z.R.; Lane, J.M.; Saxena, R.; Redline, S.; Lin, X. Operating characteristics of the rank-based inverse normal transformation for quantitative trait analysis in genome-wide association studies. Biometrics 2020, 76, 1262–1272. [Google Scholar] [CrossRef]
- Ng, K.T.; Yeung, O.W.; Liu, J.; Li, C.X.; Liu, H.; Liu, X.B.; Qi, X.; Ma, Y.Y.; Lam, Y.F.; Lau, M.Y.; et al. Clinical significance and functional role of transmembrane protein 47 (TMEM47) in chemoresistance of hepatocellular carcinoma. Int. J. Oncol. 2020, 57, 956–966. [Google Scholar] [CrossRef]
- Men, X.; Su, M.; Ma, J.; Mou, Y.; Dai, P.; Chen, C.; Cheng, X.A. Overexpression of TMEM47 induces tamoxifen resistance in human breast cancer cells. Technol. Cancer Res. Treat. 2021, 20, 15330338211004916. [Google Scholar] [CrossRef]

| Trait | a | b | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 2 | Total | 0 | 2 | Total | ||||
| Quantitative | 500 | 0 | 0.6 | 8.6 | 10.6 | 19.2 | 8.6 | 11.8 | 20.4 |
| 500 | 0 | 1 | 7.6 | 19.2 | 26.8 | 7.6 | 21.4 | 29.0 | |
| 500 | 0.4 | 0.6 | 9.6 | 8.2 | 17.8 | 9.6 | 10.6 | 20.2 | |
| 500 | 0.4 | 1 | 11.2 | 16.0 | 27.2 | 11.2 | 21.2 | 32.4 | |
| 500 | 1 | 0.6 | 13.4 | 11.8 | 25.2 | 13.4 | 15.0 | 28.4 | |
| 500 | 1 | 1 | 9.0 | 9.0 | 18.0 | 9.0 | 15.8 | 24.8 | |
| 2000 | 0 | 0.6 | 5.2 | 6.0 | 11.2 | 5.2 | 6.2 | 11.4 | |
| 2000 | 0 | 1 | 5.0 | 9.4 | 14.4 | 5.0 | 9.6 | 14.6 | |
| 2000 | 0.4 | 0.6 | 5.6 | 4.6 | 10.2 | 5.6 | 5.0 | 10.6 | |
| 2000 | 0.4 | 1 | 6.4 | 10.8 | 17.2 | 6.4 | 11.2 | 17.6 | |
| 2000 | 1 | 0.6 | 9.8 | 7.0 | 16.8 | 9.8 | 7.2 | 17.0 | |
| 2000 | 1 | 1 | 1.4 | 12.2 | 13.6 | 1.4 | 13.8 | 15.2 | |
| Qualitative | 500 | 0 | 0.6 | 19.6 | 12.8 | 32.4 | 19.6 | 20.0 | 39.6 |
| 500 | 0 | 1 | 23.8 | 17.0 | 40.8 | 23.8 | 20.4 | 44.2 | |
| 500 | 0.4 | 0.6 | 18.8 | 12.8 | 31.6 | 18.8 | 22.0 | 40.8 | |
| 500 | 0.4 | 1 | 29.2 | 10.0 | 39.2 | 29.2 | 19.2 | 48.4 | |
| 500 | 1 | 0.6 | 22.0 | 9.0 | 31.0 | 22.0 | 19.2 | 41.2 | |
| 500 | 1 | 1 | 27.8 | 0.6 | 28.4 | 27.8 | 7.8 | 35.6 | |
| 2000 | 0 | 0.6 | 9.4 | 12.8 | 22.2 | 9.4 | 14.6 | 24.0 | |
| 2000 | 0 | 1 | 8.0 | 19.4 | 27.4 | 8.0 | 21.4 | 29.4 | |
| 2000 | 0.4 | 0.6 | 14.6 | 10.8 | 25.4 | 14.6 | 13.2 | 27.8 | |
| 2000 | 0.4 | 1 | 13.4 | 16.4 | 29.8 | 13.4 | 20.0 | 33.4 | |
| 2000 | 1 | 0.6 | 11.8 | 10.4 | 22.2 | 11.8 | 15.4 | 27.2 | |
| 2000 | 1 | 1 | 16.2 | 5.0 | 21.2 | 16.2 | 13.0 | 29.2 | |
| Trait | a | b | |||||
|---|---|---|---|---|---|---|---|
| Quantitative | 500 | 0 | 0.6 | 0.0976 | 0.1022 | 0.1236 | 0.1287 |
| 500 | 0 | 1 | 0.1409 | 0.1601 | 0.2344 | 0.2549 | |
| 500 | 0.4 | 0.6 | 0.1335 | 0.1395 | 0.1579 | 0.1633 | |
| 500 | 0.4 | 1 | 0.1953 | 0.2248 | 0.3008 | 0.3601 | |
| 500 | 1 | 0.6 | 0.1414 | 0.1592 | 0.2079 | 0.2363 | |
| 500 | 1 | 1 | 0.1623 | 0.1703 | 0.2690 | 0.3475 | |
| 2000 | 0 | 0.6 | 0.0359 | 0.0379 | 0.0403 | 0.0405 | |
| 2000 | 0 | 1 | 0.0541 | 0.0642 | 0.0793 | 0.0805 | |
| 2000 | 0.4 | 0.6 | 0.0480 | 0.0512 | 0.0555 | 0.0558 | |
| 2000 | 0.4 | 1 | 0.0755 | 0.0773 | 0.0922 | 0.0959 | |
| 2000 | 1 | 0.6 | 0.0481 | 0.0509 | 0.0578 | 0.0591 | |
| 2000 | 1 | 1 | 0.0687 | 0.0727 | 0.0962 | 0.1160 | |
| Qualitative | 500 | 0 | 0.6 | 0.2765 | 0.3382 | 0.4849 | 0.5503 |
| 500 | 0 | 1 | 0.3100 | 0.4038 | 0.5286 | 0.5788 | |
| 500 | 0.4 | 0.6 | 0.3320 | 0.4087 | 0.5785 | 0.6344 | |
| 500 | 0.4 | 1 | 0.3826 | 0.4700 | 0.6416 | 0.7254 | |
| 500 | 1 | 0.6 | 0.3405 | 0.4329 | 0.5915 | 0.6369 | |
| 500 | 1 | 1 | 0.7519 | 0.7673 | 1.0190 | 1.0193 | |
| 2000 | 0 | 0.6 | 0.1207 | 0.1367 | 0.1595 | 0.1668 | |
| 2000 | 0 | 1 | 0.1362 | 0.1503 | 0.2133 | 0.2306 | |
| 2000 | 0.4 | 0.6 | 0.1320 | 0.1492 | 0.1937 | 0.2090 | |
| 2000 | 0.4 | 1 | 0.2168 | 0.2460 | 0.3347 | 0.3647 | |
| 2000 | 1 | 0.6 | 0.1431 | 0.1615 | 0.2144 | 0.2364 | |
| 2000 | 1 | 1 | 0.3163 | 0.3263 | 0.4684 | 0.5145 |
| Trait | a | b | PF | Fieller | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| EP | NP | DP | EP | NP | DP | |||||
| Quantitative | 500 | 0 | 0.6 | 0.0 | 7.2 | 0.0 | 0.8 | 16.6 | 1.0 | |
| 500 | 0 | 1 | 0.0 | 19.0 | 0.0 | 0.2 | 21.8 | 0.0 | ||
| 500 | 0.4 | 0.6 | 0.2 | 10.2 | 0.0 | 0.2 | 22.2 | 0.4 | ||
| 500 | 0.4 | 1 | 1.4 | 27.2 | 0.0 | 0.4 | 33.8 | 0.0 | ||
| 500 | 1 | 0.6 | 0.0 | 14.8 | 0.0 | 0.8 | 31.2 | 2.8 | ||
| 500 | 1 | 1 | 6.8 | 3.6 | 0.0 | 1.0 | 3.6 | 0.0 | ||
| 2000 | 0 | 0.6 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ||
| 2000 | 0 | 1 | 0.6 | 0.0 | 0.0 | 0.6 | 0.2 | 0.0 | ||
| 2000 | 0.4 | 0.6 | 0.0 | 0.0 | 0.0 | 0.2 | 0.0 | 0.0 | ||
| 2000 | 0.4 | 1 | 0.0 | 2.4 | 0.0 | 0.4 | 4.2 | 0.0 | ||
| 2000 | 1 | 0.6 | 0.0 | 0.2 | 0.0 | 0.0 | 2.2 | 0.0 | ||
| 2000 | 1 | 1 | 0.2 | 0.2 | 0.0 | 0.2 | 0.6 | 0.0 | ||
| Qualitative | 500 | 0 | 0.6 | 0.0 | 43.4 | 0.0 | 0.6 | 65.0 | 2.8 | |
| 500 | 0 | 1 | 1.4 | 58.2 | 0.0 | 1.4 | 64.4 | 0.0 | ||
| 500 | 0.4 | 0.6 | 0.0 | 45.4 | 0.0 | 0.0 | 68.2 | 4.0 | ||
| 500 | 0.4 | 1 | 1.8 | 55.2 | 0.0 | 1.2 | 64.0 | 1.0 | ||
| 500 | 1 | 0.6 | 0.0 | 44.0 | 0.0 | 0.4 | 75.0 | 3.6 | ||
| 500 | 1 | 1 | 10.4 | 53.4 | 0.0 | 0.0 | 54.2 | 0.0 | ||
| 2000 | 0 | 0.6 | 0.0 | 10.8 | 0.0 | 0.4 | 19.8 | 0.6 | ||
| 2000 | 0 | 1 | 0.4 | 20.8 | 0.0 | 0.6 | 25.2 | 0.0 | ||
| 2000 | 0.4 | 0.6 | 0.0 | 14.4 | 0.0 | 0.2 | 27.0 | 1.4 | ||
| 2000 | 0.4 | 1 | 1.2 | 26.2 | 0.0 | 0.6 | 31.0 | 0.2 | ||
| 2000 | 1 | 0.6 | 0.0 | 19.0 | 0.0 | 0.2 | 36.6 | 2.2 | ||
| 2000 | 1 | 1 | 12.4 | 4.8 | 0.0 | 0.2 | 16.0 | 0.0 | ||
| Trait | a | b | CP | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| GBN | GBU | PF | Fieller | GBN | GBU | PF | Fieller | GBN | GBU | PF | Fieller | ||||
| Quantitative | 500 | 0 | 0.6 | 96.2 | 95.8 | 95.8 | 95.2 | 1.2357 | 1.2524 | 1.2338 | 1.2674 | 1.2439 | 1.2571 | 1.2072 | 1.2328 |
| 500 | 0 | 1 | 96.2 | 97.0 | 97.8 | 95.8 | 1.3536 | 1.3695 | 1.4593 | 1.4375 | 1.3959 | 1.4152 | 1.4749 | 1.5010 | |
| 500 | 0.4 | 0.6 | 95.0 | 95.6 | 95.6 | 96.2 | 1.2663 | 1.2862 | 1.2815 | 1.3305 | 1.2662 | 1.2973 | 1.2449 | 1.2682 | |
| 500 | 0.4 | 1 | 95.6 | 96.6 | 94.2 | 95.6 | 1.4718 | 1.4977 | 1.5555 | 1.5887 | 1.5158 | 1.5571 | 1.6734 | 1.6888 | |
| 500 | 1 | 0.6 | 96.2 | 96.6 | 95.4 | 94.2 | 1.3457 | 1.3689 | 1.3363 | 1.3767 | 1.4001 | 1.4490 | 1.2991 | 1.3461 | |
| 500 | 1 | 1 | 94.6 | 95.4 | 87.8 | 93.8 | 1.2841 | 1.2983 | 1.2918 | 1.3827 | 1.3135 | 1.3316 | 1.4814 | 1.4465 | |
| 2000 | 0 | 0.6 | 94.6 | 94.2 | 94.8 | 94.6 | 0.7216 | 0.7258 | 0.7377 | 0.7413 | 0.7149 | 0.7230 | 0.7406 | 0.7425 | |
| 2000 | 0 | 1 | 95.8 | 96.0 | 95.8 | 94.2 | 0.8934 | 0.8946 | 0.9184 | 0.9249 | 0.9068 | 0.9035 | 0.9396 | 0.9469 | |
| 2000 | 0.4 | 0.6 | 94.0 | 95.4 | 94.4 | 94.6 | 0.7895 | 0.7958 | 0.8067 | 0.8152 | 0.7770 | 0.7850 | 0.8087 | 0.8124 | |
| 2000 | 0.4 | 1 | 95.6 | 96.2 | 97.4 | 96.2 | 1.0439 | 1.0505 | 1.0800 | 1.0950 | 1.0415 | 1.0420 | 1.0857 | 1.0828 | |
| 2000 | 1 | 0.6 | 95.8 | 96.6 | 96.2 | 96.2 | 0.8284 | 0.8325 | 0.8406 | 0.8539 | 0.7933 | 0.7974 | 0.8211 | 0.8190 | |
| 2000 | 1 | 1 | 95.4 | 95.6 | 96.6 | 95.0 | 0.9483 | 0.9560 | 0.9750 | 1.0066 | 0.9988 | 0.9982 | 1.0294 | 1.0527 | |
| Qualitative | 500 | 0 | 0.6 | 92.6 | 94.2 | 95.4 | 95.0 | 1.6289 | 1.6667 | 1.6720 | 1.7236 | 1.7202 | 1.7749 | 1.8354 | 2.0000 |
| 500 | 0 | 1 | 94.0 | 96.0 | 90.0 | 94.8 | 1.6575 | 1.6934 | 1.7053 | 1.7578 | 1.7387 | 1.7848 | 2.0000 | 2.0000 | |
| 500 | 0.4 | 0.6 | 93.0 | 94.6 | 93.6 | 96.0 | 1.6782 | 1.7193 | 1.6986 | 1.7668 | 1.7516 | 1.8033 | 1.8721 | 2.0000 | |
| 500 | 0.4 | 1 | 93.0 | 94.8 | 84.6 | 94.0 | 1.6775 | 1.7154 | 1.6108 | 1.7788 | 1.7360 | 1.7830 | 2.0000 | 2.0000 | |
| 500 | 1 | 0.6 | 92.6 | 94.8 | 93.0 | 96.0 | 1.7318 | 1.7742 | 1.6981 | 1.7965 | 1.7837 | 1.8283 | 1.8659 | 2.0000 | |
| 500 | 1 | 1 | 77.0 | 74.4 | 74.2 | 99.4 | 1.3896 | 1.3523 | 1.4088 | 1.8704 | 1.4854 | 1.4788 | 2.0000 | 2.0000 | |
| 2000 | 0 | 0.6 | 94.6 | 95.8 | 96.6 | 95.0 | 1.2519 | 1.2686 | 1.2531 | 1.2774 | 1.2388 | 1.2710 | 1.1933 | 1.2177 | |
| 2000 | 0 | 1 | 97.0 | 96.8 | 97.2 | 95.6 | 1.3832 | 1.4010 | 1.4869 | 1.4734 | 1.4162 | 1.4502 | 1.5404 | 1.5295 | |
| 2000 | 0.4 | 0.6 | 96.2 | 96.6 | 96.8 | 95.2 | 1.3468 | 1.3682 | 1.3443 | 1.3908 | 1.4163 | 1.4514 | 1.3443 | 1.3965 | |
| 2000 | 0.4 | 1 | 95.0 | 95.8 | 93.6 | 95.4 | 1.4765 | 1.5029 | 1.5565 | 1.5781 | 1.5153 | 1.5623 | 1.6985 | 1.6909 | |
| 2000 | 1 | 0.6 | 96.4 | 96.8 | 94.2 | 95.0 | 1.4216 | 1.4488 | 1.3842 | 1.4516 | 1.5241 | 1.5772 | 1.3174 | 1.4640 | |
| 2000 | 1 | 1 | 89.8 | 89.6 | 84.6 | 98.6 | 1.3833 | 1.3967 | 1.3764 | 1.6143 | 1.4576 | 1.4936 | 1.7096 | 1.6751 | |
| Trait | a | b | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| GBN | GBU | PF | Fieller | GBN | GBU | PF | Fieller | ||||
| Quantitative | 500 | 0 | 0.6 | 0.3309 | 0.3619 | 0.4066 | 0.4851 | 0.5036 | 0.5697 | 0.5403 | 0.6862 |
| 500 | 0 | 1 | 0.3020 | 0.3364 | 0.4429 | 0.4948 | 0.4613 | 0.5274 | 0.6959 | 0.7625 | |
| 500 | 0.4 | 0.6 | 0.3312 | 0.3624 | 0.4198 | 0.4868 | 0.5334 | 0.5910 | 0.5862 | 0.8516 | |
| 500 | 0.4 | 1 | 0.2631 | 0.2917 | 0.4881 | 0.4498 | 0.3741 | 0.4244 | 0.6279 | 0.6390 | |
| 500 | 1 | 0.6 | 0.3585 | 0.3890 | 0.4492 | 0.5487 | 0.5765 | 0.6382 | 0.7346 | 1.0386 | |
| 500 | 1 | 1 | 0.2563 | 0.2891 | 0.6080 | 0.4568 | 0.3086 | 0.3487 | 0.7633 | 0.5616 | |
| 2000 | 0 | 0.6 | 0.1961 | 0.2118 | 0.2251 | 0.2350 | 0.2369 | 0.2684 | 0.2520 | 0.2564 | |
| 2000 | 0 | 1 | 0.2623 | 0.2874 | 0.3381 | 0.3514 | 0.3609 | 0.4000 | 0.4281 | 0.4336 | |
| 2000 | 0.4 | 0.6 | 0.2214 | 0.2419 | 0.2500 | 0.2723 | 0.2874 | 0.3203 | 0.2952 | 0.3094 | |
| 2000 | 0.4 | 1 | 0.3084 | 0.3386 | 0.4154 | 0.4447 | 0.3816 | 0.4537 | 0.5550 | 0.5927 | |
| 2000 | 1 | 0.6 | 0.2720 | 0.2941 | 0.3049 | 0.3455 | 0.3455 | 0.3840 | 0.3589 | 0.3830 | |
| 2000 | 1 | 1 | 0.3184 | 0.3442 | 0.4515 | 0.4661 | 0.3969 | 0.4519 | 0.6674 | 0.6647 | |
| Qualitative | 500 | 0 | 0.6 | 0.2535 | 0.2727 | 0.3893 | 0.4565 | 0.2800 | 0.2841 | 0.5975 | 0.4816 |
| 500 | 0 | 1 | 0.2005 | 0.2194 | 0.5012 | 0.4440 | 0.2140 | 0.2336 | 0.4291 | 0.3656 | |
| 500 | 0.4 | 0.6 | 0.1998 | 0.2129 | 0.3599 | 0.4105 | 0.2059 | 0.1966 | 0.5632 | 0.3726 | |
| 500 | 0.4 | 1 | 0.1611 | 0.1782 | 0.6086 | 0.4317 | 0.1748 | 0.1658 | 0.6470 | 0.2657 | |
| 500 | 1 | 0.6 | 0.1553 | 0.1632 | 0.3705 | 0.4144 | 0.1162 | 0.1055 | 0.5430 | 0.0354 | |
| 500 | 1 | 1 | 0.2933 | 0.3707 | 0.8749 | 0.2417 | 0.3847 | 0.5508 | 1.9212 | 0.1898 | |
| 2000 | 0 | 0.6 | 0.3501 | 0.3824 | 0.4415 | 0.5142 | 0.5624 | 0.6511 | 0.6639 | 0.8792 | |
| 2000 | 0 | 1 | 0.2936 | 0.3261 | 0.4417 | 0.4911 | 0.4447 | 0.5120 | 0.7372 | 0.8589 | |
| 2000 | 0.4 | 0.6 | 0.3518 | 0.3824 | 0.4411 | 0.5098 | 0.5682 | 0.6366 | 0.6747 | 1.0159 | |
| 2000 | 0.4 | 1 | 0.2487 | 0.2780 | 0.4936 | 0.4545 | 0.3529 | 0.3963 | 0.6457 | 0.6883 | |
| 2000 | 1 | 0.6 | 0.3456 | 0.3758 | 0.4350 | 0.5209 | 0.5482 | 0.6068 | 0.7529 | 0.9691 | |
| 2000 | 1 | 1 | 0.2762 | 0.3174 | 0.7095 | 0.3578 | 0.2032 | 0.2535 | 0.7992 | 0.3615 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, M.-K.; Yuan, Y.-X.; Zhu, B.; Wang, K.-W.; Fung, W.K.; Zhou, J.-Y. Gene-Based Methods for Estimating the Degree of the Skewness of X Chromosome Inactivation. Genes 2022, 13, 827. https://doi.org/10.3390/genes13050827
Li M-K, Yuan Y-X, Zhu B, Wang K-W, Fung WK, Zhou J-Y. Gene-Based Methods for Estimating the Degree of the Skewness of X Chromosome Inactivation. Genes. 2022; 13(5):827. https://doi.org/10.3390/genes13050827
Chicago/Turabian StyleLi, Meng-Kai, Yu-Xin Yuan, Bin Zhu, Kai-Wen Wang, Wing Kam Fung, and Ji-Yuan Zhou. 2022. "Gene-Based Methods for Estimating the Degree of the Skewness of X Chromosome Inactivation" Genes 13, no. 5: 827. https://doi.org/10.3390/genes13050827
APA StyleLi, M.-K., Yuan, Y.-X., Zhu, B., Wang, K.-W., Fung, W. K., & Zhou, J.-Y. (2022). Gene-Based Methods for Estimating the Degree of the Skewness of X Chromosome Inactivation. Genes, 13(5), 827. https://doi.org/10.3390/genes13050827











