A Deep-Learning Sequence-Based Method to Predict Protein Stability Changes Upon Genetic Variations
Abstract
1. Introduction
2. Materials and Methods
2.1. Datasets and Cross-Validation
2.2. Sequence Profiles
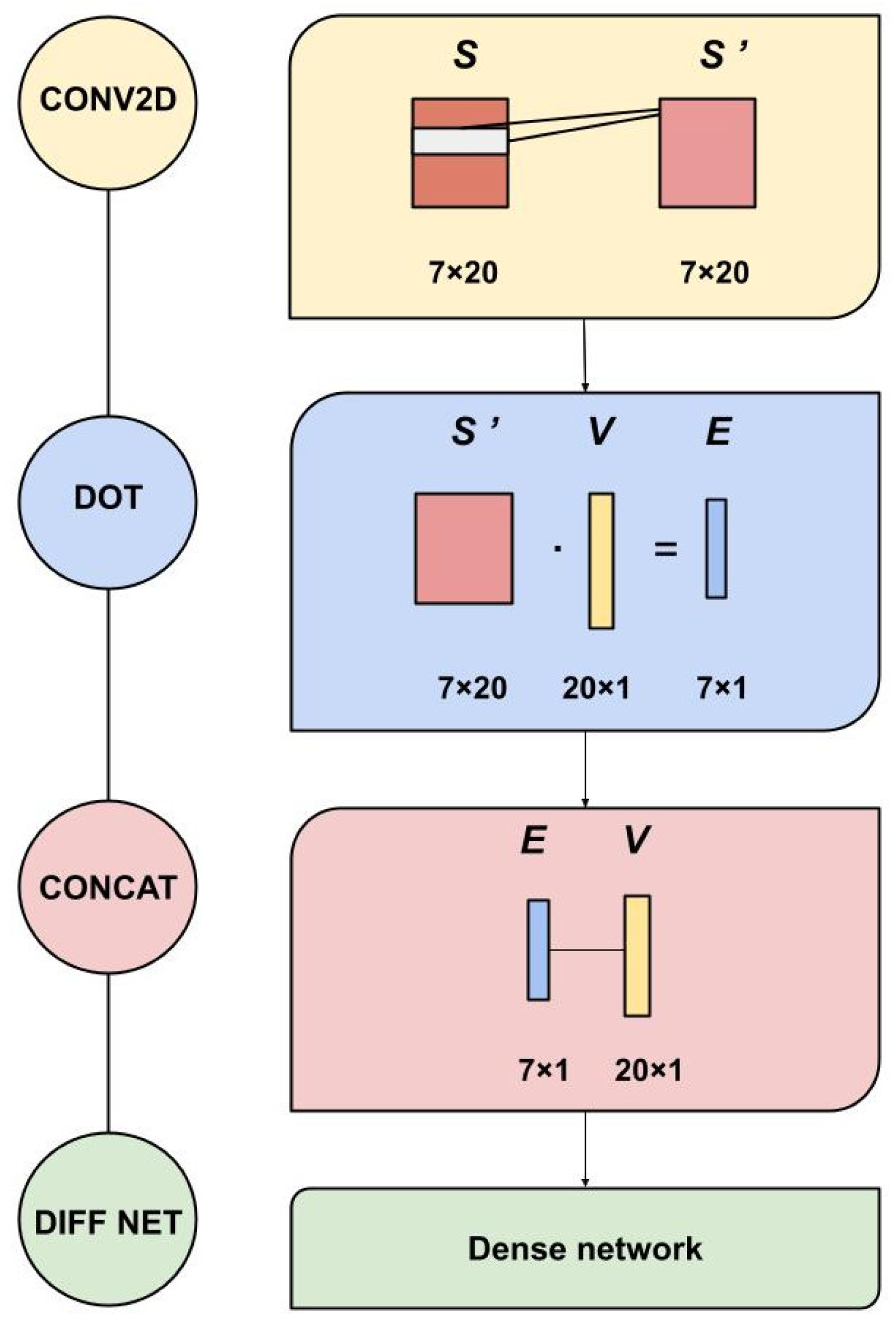
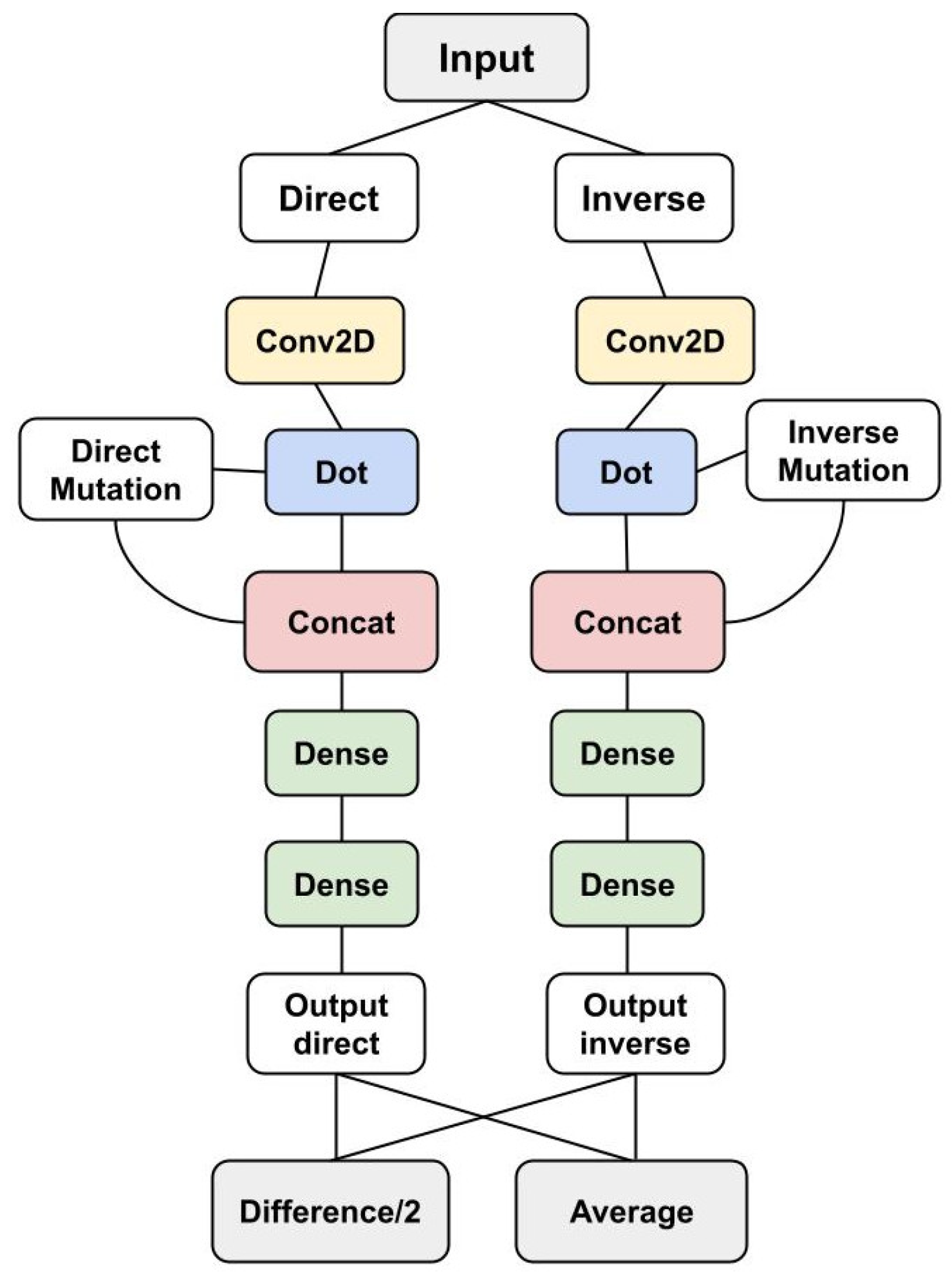
2.3. ACDC-NN-Seq Architecture
- Variation (V): 20 features (one for each amino acid) coding for the variation by setting all the entries to 0 with the exception of the wild-type and the variant residue positions set to and 1, respectively. This input corresponds to a one-dimensional matrix ;
- Sequence (S or 1D-input): 140 features representing protein profile information of the variation neighbourhood. Considering i as the variant position in the sequence, we used a window of 3 residues, i.e., , so to obtain elements, with the profile information of these 7 positions. This input then corresponds to a sequence of 7 vectors taken from the protein profile.
2.4. Pre-Training Phase
2.5. Transfer Learning on Experimental Data
2.6. Performance Evaluation
3. Results
3.1. Learning 3D Properties on Artificial Data
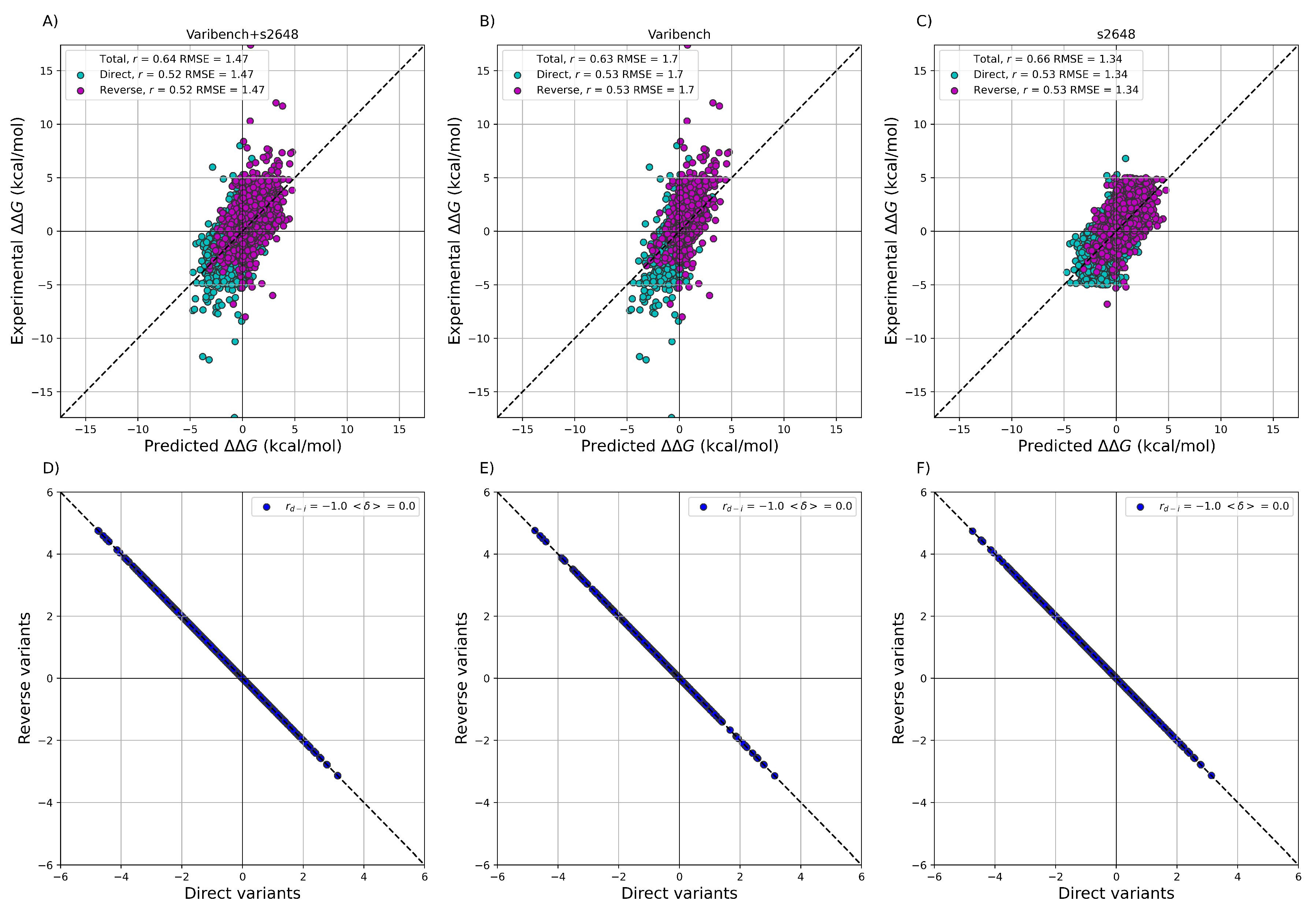
3.2. Prediction of the Experimental Values
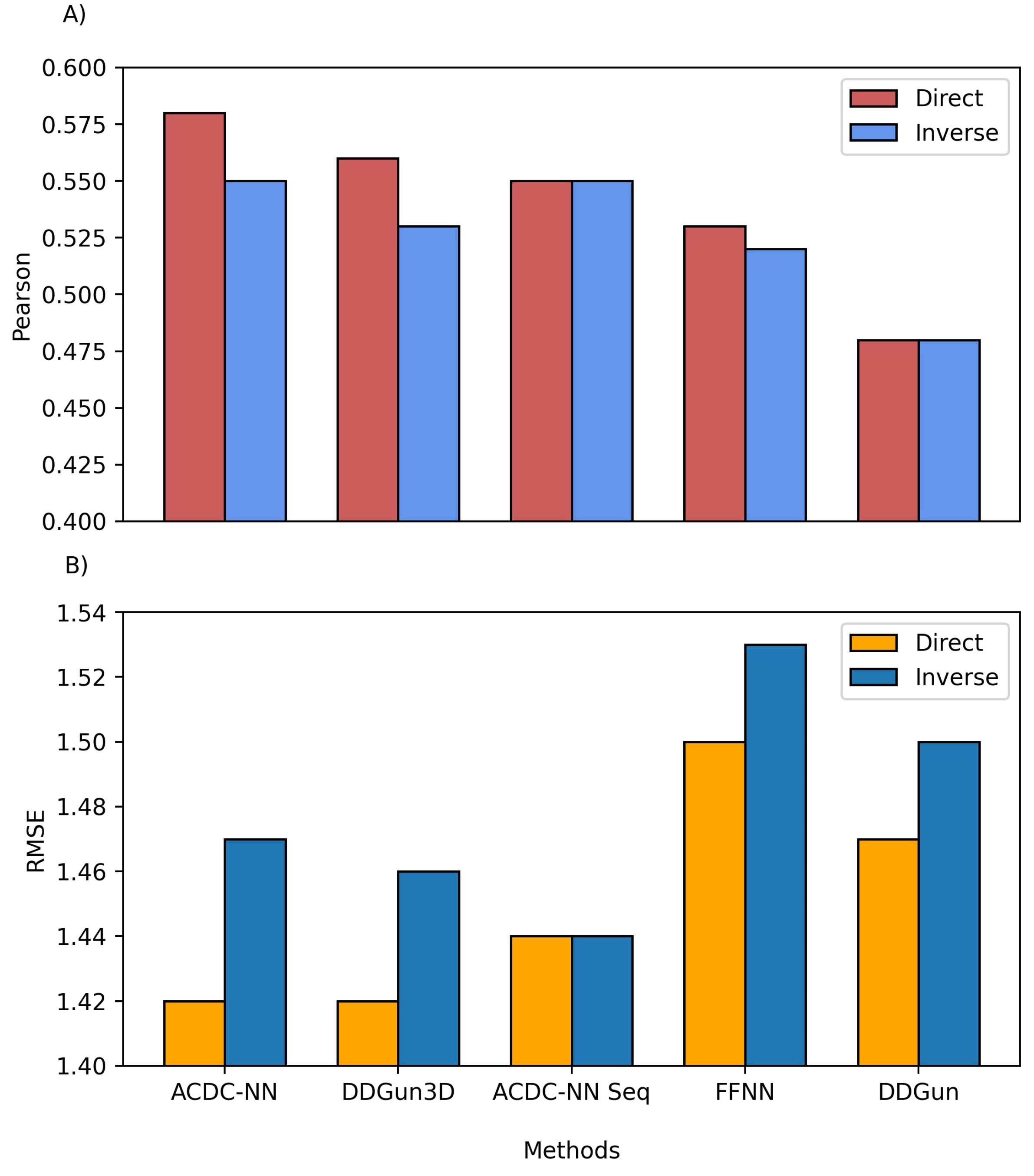
3.3. Comparison with Other Sequence-Based Machine-Learning Methods
3.4. Frataxin CAGI 5 Challenge
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ACDC-NN | Antisymmetric Convolutional Differential Concatenated - Neural Network |
| NGS | Next Generation Sequencing |
References
- Hartl, F.U. Protein misfolding diseases. Annu. Rev. Biochem. 2017, 86, 21–26. [Google Scholar] [CrossRef]
- Martelli, P.L.; Fariselli, P.; Savojardo, C.; Babbi, G.; Aggazio, F.; Casadio, R. Large scale analysis of protein stability in OMIM disease related human protein variants. BMC Genom. 2016, 17, 239–247. [Google Scholar] [CrossRef]
- Cheng, T.M.; Lu, Y.E.; Vendruscolo, M.; Blundell, T.L. Prediction by graph theoretic measures of structural effects in proteins arising from non-synonymous single nucleotide polymorphisms. PLoS Comput. Biol. 2008, 4, e1000135. [Google Scholar] [CrossRef]
- Compiani, M.; Capriotti, E. Computational and theoretical methods for protein folding. Biochemistry 2013, 52, 8601–8624. [Google Scholar] [CrossRef]
- Casadio, R.; Vassura, M.; Tiwari, S.; Fariselli, P.; Luigi Martelli, P. Correlating disease-related mutations to their effect on protein stability: A large-scale analysis of the human proteome. Hum. Mutat. 2011, 32, 1161–1170. [Google Scholar] [CrossRef]
- Birolo, G.; Benevenuta, S.; Fariselli, P.; Capriotti, E.; Giorgio, E.; Sanavia, T. Protein Stability Perturbation Contributes to the Loss of Function in Haploinsufficient Genes. Front. Mol. Biosci. 2021, 8, 10. [Google Scholar] [CrossRef]
- Schymkowitz, J.; Borg, J.; Stricher, F.; Nys, R.; Rousseau, F.; Serrano, L. The FoldX web server: An online force field. Nucleic Acids Res. 2005, 33, W382–W388. [Google Scholar] [CrossRef]
- Wainreb, G.; Wolf, L.; Ashkenazy, H.; Dehouck, Y.; Ben-Tal, N. Protein stability: A single recorded mutation aids in predicting the effects of other mutations in the same amino acid site. Bioinformatics 2011, 27, 3286–3292. [Google Scholar] [CrossRef] [PubMed]
- Parthiban, V.; Gromiha, M.M.; Schomburg, D. CUPSAT: Prediction of protein stability upon point mutations. Nucleic Acids Res. 2006, 34, W239–W242. [Google Scholar] [CrossRef] [PubMed]
- Pucci, F.; Bernaerts, K.V.; Kwasigroch, J.M.; Rooman, M. Quantification of biases in predictions of protein stability changes upon mutations. Bioinformatics 2018, 34, 3659–3665. [Google Scholar] [CrossRef]
- Li, B.; Yang, Y.T.; Capra, J.A.; Gerstein, M.B. Predicting changes in protein thermodynamic stability upon point mutation with deep 3D convolutional neural networks. PLOS Comput. Biol. 2020, 16, e1008291. [Google Scholar] [CrossRef]
- Kellogg, E.H.; Leaver-Fay, A.; Baker, D. Role of conformational sampling in computing mutation-induced changes in protein structure and stability. Proteins Struct. Funct. Bioinform. 2011, 79, 830–838. [Google Scholar] [CrossRef]
- Fariselli, P.; Martelli, P.L.; Savojardo, C.; Casadio, R. INPS: Predicting the impact of non-synonymous variations on protein stability from sequence. Bioinformatics 2015, 31, 2816–2821. [Google Scholar] [CrossRef] [PubMed]
- Montanucci, L.; Capriotti, E.; Frank, Y.; Ben-Tal, N.; Fariselli, P. DDGun: An untrained method for the prediction of protein stability changes upon single and multiple point variations. BMC Bioinform. 2019, 20, 335. [Google Scholar] [CrossRef]
- Li, G.; Panday, S.K.; Alexov, E. SAAFEC-SEQ: A Sequence-Based Method for Predicting the Effect of Single Point Mutations on Protein Thermodynamic Stability. Int. J. Mol. Sci. 2021, 22, 606. [Google Scholar] [CrossRef]
- Capriotti, E.; Fariselli, P.; Casadio, R. I-Mutant2. 0: Predicting stability changes upon mutation from the protein sequence or structure. Nucleic Acids Res. 2005, 33, W306–W310. [Google Scholar] [CrossRef]
- Cheng, J.; Randall, A.; Baldi, P. Prediction of protein stability changes for single-site mutations using support vector machines. Proteins Struct. Funct. Bioinform. 2006, 62, 1125–1132. [Google Scholar] [CrossRef]
- Sanavia, T.; Birolo, G.; Montanucci, L.; Turina, P.; Capriotti, E.; Fariselli, P. Limitations and challenges in protein stability prediction upon genome variations: Towards future applications in precision medicine. Comput. Struct. Biotechnol. J. 2020. [Google Scholar] [CrossRef]
- Savojardo, C.; Fariselli, P.; Martelli, P.L.; Casadio, R. INPS-MD: A web server to predict stability of protein variants from sequence and structure. Bioinformatics 2016, 32, 2542–2544. [Google Scholar] [CrossRef]
- Fang, J. A critical review of five machine learning-based algorithms for predicting protein stability changes upon mutation. Brief. Bioinform. 2020, 21, 1285–1292. [Google Scholar] [CrossRef]
- Usmanova, D.R.; Bogatyreva, N.S.; Ariño Bernad, J.; Eremina, A.A.; Gorshkova, A.A.; Kanevskiy, G.M.; Lonishin, L.R.; Meister, A.V.; Yakupova, A.G.; Kondrashov, F.A.; et al. Self-consistency test reveals systematic bias in programs for prediction change of stability upon mutation. Bioinformatics 2018, 34, 3653–3658. [Google Scholar] [CrossRef] [PubMed]
- Montanucci, L.; Savojardo, C.; Martelli, P.L.; Casadio, R.; Fariselli, P. On the biases in predictions of protein stability changes upon variations: The INPS test case. Bioinformatics 2019, 35, 2525–2527. [Google Scholar] [CrossRef] [PubMed]
- Capriotti, E.; Fariselli, P.; Rossi, I.; Casadio, R. A three-state prediction of single point mutations on protein stability changes. BMC Bioinform. 2008, 9, 1–9. [Google Scholar] [CrossRef]
- Benevenuta, S.; Pancotti, C.; Fariselli, P.; Birolo, G.; Sanavia, T. An antisymmetric neural network to predict free energy changes in protein variants. J. Phys. D Appl. Phys. 2021, 54, 245403. [Google Scholar] [CrossRef]
- Kumar, M.D.; Bava, K.A.; Gromiha, M.M.; Prabakaran, P.; Kitajima, K.; Uedaira, H.; Sarai, A. ProTherm and ProNIT: Thermodynamic databases for proteins and protein-nucleic acid interactions. Nucleic Acids Res. 2006, 34, D204–D206. [Google Scholar] [CrossRef]
- Dehouck, Y.; Kwasigroch, J.M.; Gilis, D.; Rooman, M. PoPMuSiC 2.1: A web server for the estimation of protein stability changes upon mutation and sequence optimality. BMC Bioinform. 2011, 12, 1–12. [Google Scholar] [CrossRef]
- Nair, P.S.; Vihinen, M. V ari B ench: A benchmark database for variations. Hum. Mutat. 2013, 34, 42–49. [Google Scholar] [CrossRef]
- Pires, D.E.; Ascher, D.B.; Blundell, T.L. mCSM: Predicting the effects of mutations in proteins using graph-based signatures. Bioinformatics 2014, 30, 335–342. [Google Scholar] [CrossRef] [PubMed]
- Kepp, K.P. Towards a “Golden Standard” for computing globin stability: Stability and structure sensitivity of myoglobin mutants. Biochim. Biophys. Acta 2015, 1854, 1239–1248. [Google Scholar] [CrossRef] [PubMed]
- Andreoletti, G.; Pal, L.R.; Moult, J.; Brenner, S.E. Reports from the fifth edition of CAGI: The Critical Assessment of Genome Interpretation. Hum. Mutat. 2019, 40, 1197–1201. [Google Scholar] [CrossRef] [PubMed]
- Aggarwal, A. BlastClust. 2013. Available online: http://ftp.gen-info.osaka-u.ac.jp/biosoft/blast/executables/release/2.2.14/ (accessed on 10 June 2021).
- Zimmermann, L.; Stephens, A.; Nam, S.Z.; Rau, D.; Kübler, J.; Lozajic, M.; Gabler, F.; Söding, J.; Lupas, A.N.; Alva, V. A Completely Reimplemented MPI Bioinformatics Toolkit with a New HHpred Server at its Core. J. Mol. Biol. 2018, 430, 2237–2243. [Google Scholar] [CrossRef]
- Bromley, J.; Guyon, I.; LeCun, Y.; Säckinger, E.; Shah, R. Signature verification using a “siamese” time delay neural network. Adv. Neural Inf. Process. Syst. 1993, 6, 737–744. [Google Scholar] [CrossRef]
- Chopra, S.; Hadsell, R.; LeCun, Y. Learning a similarity metric discriminatively, with application to face verification. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; Volume 1, pp. 539–546. [Google Scholar]
- Chollet, F. Keras. 2015. Available online: https://keras.io (accessed on 10 June 2021).
- Montanucci, L.; Martelli, P.L.; Ben-Tal, N.; Fariselli, P. A natural upper bound to the accuracy of predicting protein stability changes upon mutations. Bioinformatics 2019, 35, 1513–1517. [Google Scholar] [CrossRef] [PubMed]
- Benevenuta, S.; Fariselli, P. On the Upper Bounds of the Real-Valued Predictions. Bioinform. Biol. Insights 2019, 13, 1177932219871263. [Google Scholar] [CrossRef] [PubMed]
- Savojardo, C.; Martelli, P.L.; Casadio, R.; Fariselli, P. On the critical review of five machine learning-based algorithms for predicting protein stability changes upon mutation. Brief. Bioinform. 2019, 21, 1285–1292. [Google Scholar] [CrossRef] [PubMed]
- Petrosino, M.; Pasquo, A.; Novak, L.; Toto, A.; Gianni, S.; Mantuano, E.; Veneziano, L.; Minicozzi, V.; Pastore, A.; Puglisi, R.; et al. Characterization of human frataxin missense variants in cancer tissues. Hum. Mutat. 2019, 40, 1400–1413. [Google Scholar] [CrossRef]
- Savojardo, C.; Petrosino, M.; Babbi, G.; Bovo, S.; Corbi-Verge, C.; Casadio, R.; Fariselli, P.; Folkman, L.; Garg, A.; Karimi, M.; et al. Evaluating the predictions of the protein stability change upon single amino acid substitutions for the FXN CAGI5 challenge. Hum. Mutat. 2019, 40, 1392–1399. [Google Scholar] [CrossRef] [PubMed]
| Dataset | Number of Variants | Usage | Experimental |
|---|---|---|---|
| IvankovDDGun | 600,000 | Pre-Training | No |
| Ivankov2000 | 2000 | Transfer Learning | No |
| S2648 | 2648 | Transfer Learning | Yes |
| Varibench | 1420 | Transfer Learning | Yes |
| Ssym | 684 | Test | Yes |
| Myoglobin | 134 | Test | Yes |
| p53 | 42 | Test | Yes |
| Frataxin-CAGI | 8 | Test | Yes |
| NN Parameters | Before Transfer-Learning | After Transfer-Learning |
|---|---|---|
| Hidden units | 12,864 | 12,864 |
| Dropout | 0.05 | 0.35 |
| Epochs | 45 | 30 |
| Batch-size | 500 | 150 |
| Optimizer | Adam | Adam |
| Loss | logcosh + abs | logcosh + abs |
| Dataset | Pearson/RMSE | Antisymmetry | ||
|---|---|---|---|---|
| Direct | Reverse | |||
| IvankovDDGun (Test) | 0.97/0.06 | 0.97/0.06 | −1.0 | 0.0 |
| Method | Pearson/RMSE | Antisymmetry | ||
|---|---|---|---|---|
| Direct | Reverse | |||
| ACDC-NN-Seq | 0.55/1.44 | 0.55/1.44 | −0.99 | −0.01 |
| INPS-NoSeqId [22] | 0.48/1.42 | 0.47/1.45 | −0.99 | −0.06 |
| INPS [13] | 0.51/1.42 | 0.50/1.44 | −0.99 | −0.04 |
| SAAFEC-SEQ [15] | 0.71/1.09 | −0.39/2.71 | 0.58 | −1.84 |
| I-Mutant2.0 [16] | 0.7/1.12 | 0.05/2.54 | −0.17 | −1.01 |
| MUpro [17] | 0.79/0.94 | 0.07/2.51 | −0.02 | −0.97 |
| Method | Pearson/RMSE | Antisymmetry | ||
|---|---|---|---|---|
| Direct | Reverse | |||
| ACDC-NN-Seq | 0.56/0.97 | 0.56/0.97 | −1.00 | 0.00 |
| INPS | 0.60/0.99 | 0.61/0.98 | −1.00 | 0.01 |
| SAAFEC-SEQ | 0.63/0.89 | 0.30/1.63 | −0.21 | −1.50 |
| I-Mutant2.0 | 0.56/1.12 | 0.39/1.71 | −0.45 | −0.88 |
| MUpro | 0.51/0.99 | 0.35/1.75 | −0.17 | −0.79 |
| Method | Pearson/RMSE | Antisymmetry | ||
|---|---|---|---|---|
| Direct | Reverse | |||
| ACDC-NN-Seq | 0.62/1.62 | 0.62/1.62 | −1.00 | 0.00 |
| INPS | 0.72/1.49 | 0.70/1.54 | −0.99 | −0.01 |
| SAAFEC-SEQ | 0.52/1.64 | −0.18/2.97 | 0.06 | −1.79 |
| I-Mutant2.0 | 0.35/1.75 | 0.22/2.81 | −0.24 | −1.02 |
| MUpro | 0.23/1.78 | 0.04/2.87 | 0.12 | −0.98 |
| Method | Pearson/RMSE | Antisymmetry | ||
|---|---|---|---|---|
| Direct | Reverse | |||
| ACDC-NN-Seq | 0.88/2.83 | 0.88/2.83 | −1.00 | 0.00 |
| INPS | 0.65/3.29 | 0.57/3.38 | −0.99 | −0.01 |
| SAAFEC-SEQ | 0.67/3.3 | 0.1/4.85 | 0.2 | −1.94 |
| I-Mutant2.0 | 0.84/2.82 | 0.53/5.08 | −0.74 | −1.22 |
| MUpro | 0.33/3.6 | 0.13/4.97 | −0.23 | −0.45 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pancotti, C.; Benevenuta, S.; Repetto, V.; Birolo, G.; Capriotti, E.; Sanavia, T.; Fariselli, P. A Deep-Learning Sequence-Based Method to Predict Protein Stability Changes Upon Genetic Variations. Genes 2021, 12, 911. https://doi.org/10.3390/genes12060911
Pancotti C, Benevenuta S, Repetto V, Birolo G, Capriotti E, Sanavia T, Fariselli P. A Deep-Learning Sequence-Based Method to Predict Protein Stability Changes Upon Genetic Variations. Genes. 2021; 12(6):911. https://doi.org/10.3390/genes12060911
Chicago/Turabian StylePancotti, Corrado, Silvia Benevenuta, Valeria Repetto, Giovanni Birolo, Emidio Capriotti, Tiziana Sanavia, and Piero Fariselli. 2021. "A Deep-Learning Sequence-Based Method to Predict Protein Stability Changes Upon Genetic Variations" Genes 12, no. 6: 911. https://doi.org/10.3390/genes12060911
APA StylePancotti, C., Benevenuta, S., Repetto, V., Birolo, G., Capriotti, E., Sanavia, T., & Fariselli, P. (2021). A Deep-Learning Sequence-Based Method to Predict Protein Stability Changes Upon Genetic Variations. Genes, 12(6), 911. https://doi.org/10.3390/genes12060911








