A Continuous Statistical Phasing Framework for the Analysis of Forensic Mitochondrial DNA Mixtures
Abstract
1. Introduction
- How does the algorithm perform with rare (i.e., low frequency) variants?
- What kind of effects do increases of the size (thereby population haplotype frequency information) and quality (presence of similar haplotypes) of the panel have on phasing accuracy?
- Which statistical phasing strategies can be employed to better handle mixture ratios that have been traditionally harder to deconvolve (e.g., 1:1 and 50:1)?
2. Materials and Methods
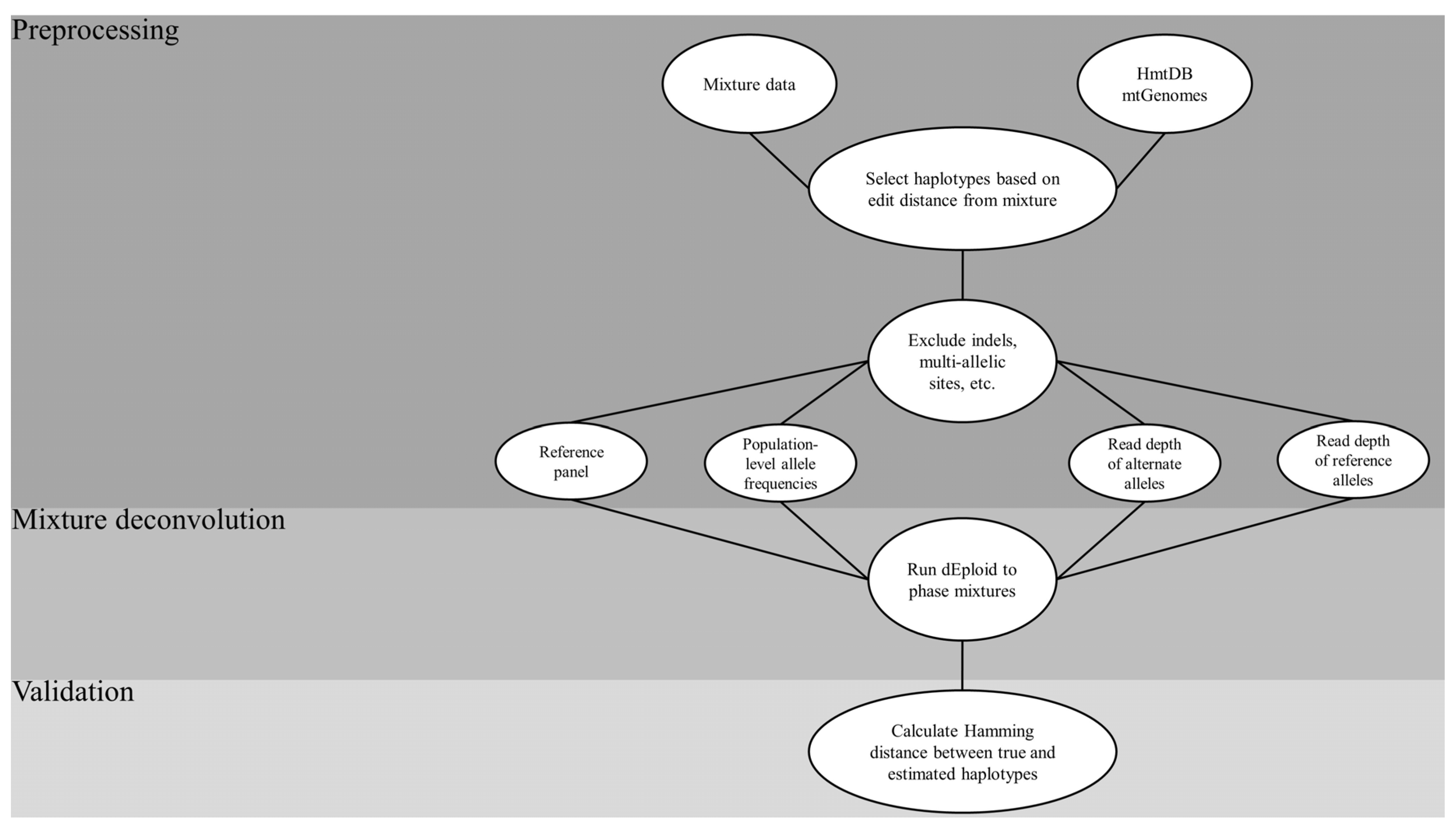
2.1. Simulations with In Silico Mixtures
2.1.1. Outline of Data and Bioinformatic Approach
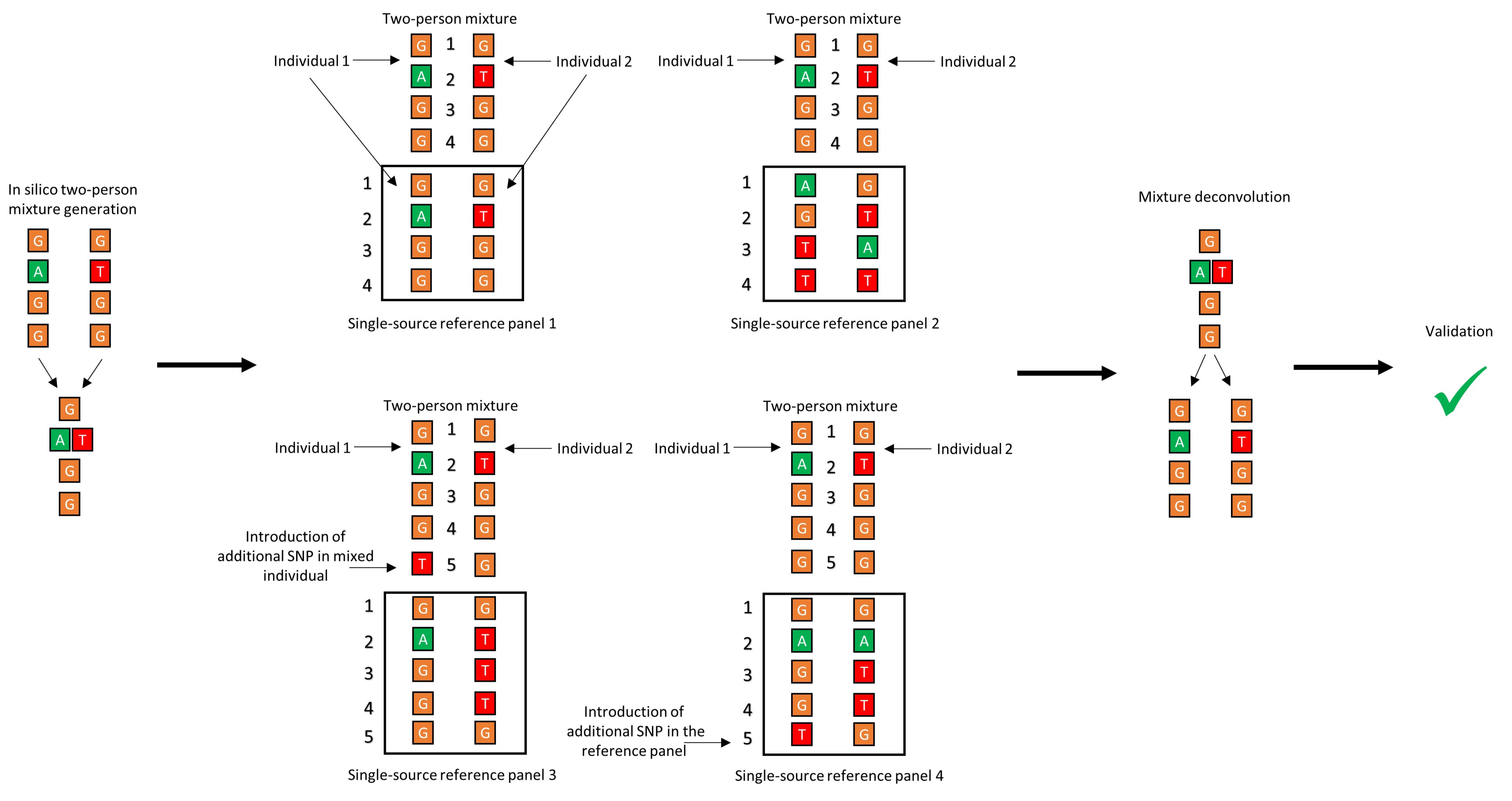
2.1.2. Investigating the Effect of Panel Composition on Phasing Accuracy
- Panel 1: Replicating an idealized scenario, this panel included both of the single-source haplotypes included in the mixture.
- Panel 2: Using a hold-out cross validation (CV) approach [67,68], namely the hold-two-out CV, this panel was made by leaving out the two haplotypes that were used to create the mixture during each round of deconvolution. The hold-out CV allows validation of the performance of the core algorithm, as well as mimicking of real-world forensic data, whereby haplotype information for both donors is unlikely to be included in the reference database.
- Panel 3: Reproduction of the presence of a closely related haplotype within the reference data, which was done by creating “ancestral” and “derived” haplotypes that differed from one another by one SNP. This difference was introduced in one of the haplotypes in the mixture while keeping the original sequence in the panel file. The other haplotype was excluded from the panel.
- Panel 4: Same as above for panel 3 except this time one SNP was introduced in one of the haplotypes in the panel, while retaining the original sequence of the same haplotype to make the in silico mixture. The other haplotype was excluded from the panel.
2.1.3. Optimized Reference Panel and Phasing Parameters
- Sourcing of the HmtDB for complete mtGenomes;
- Creating in silico mixtures from a sample dataset;
- Selecting haplotypes from the sourced genomes that are a pre-defined edit distance from the haplotypes in the mixtures to create a reference panel;
- Running the core DEploid algorithm to deconvolve the mixtures, using the panel as a prior while tweaking key parameter combinations;
- Assessing the accuracy of the estimated haplotypes that resulted from each combination using the Hamming distance between them.
- The coercion of a He site into an HoR or HoA site;
- The coercion of an HoR or HoA site into a He site;
- Point-switching of alleles between the two haplotypes (e.g., two switches within three consecutive heterozygous sites [42]).
2.2. Validation with In Vitro Mitochondrial Mixtures
3. Results
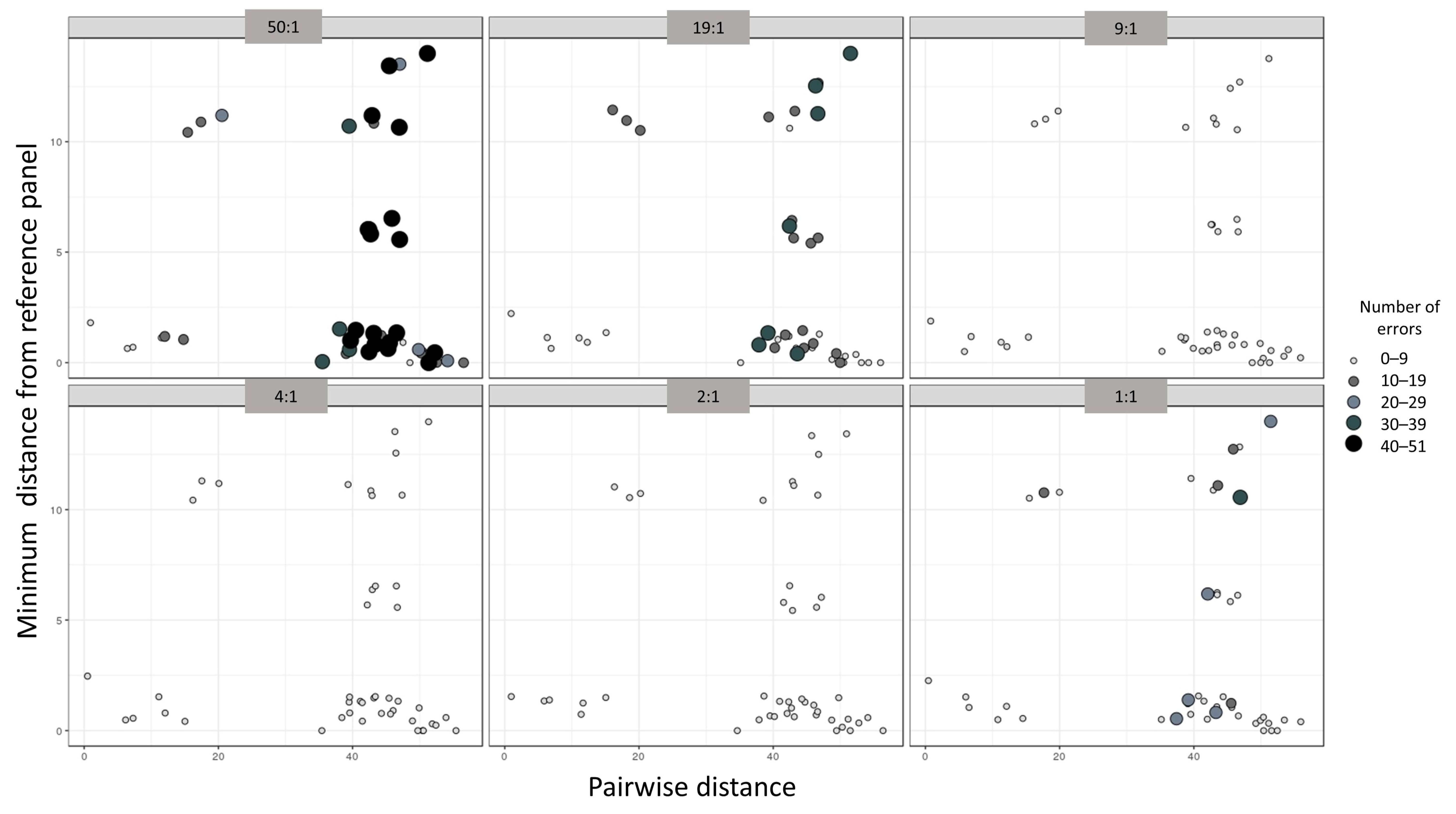
3.1. Differentially Modified Reference Panels
3.2. Enhanced Reference Panel with Fine-Tuned Parameters
3.3. Performance with In Vitro Mixtures
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Weir, B.S.; Triggs, C.M.; Starling, L.; Stowell, L.I.; Walsh, K.A.J.; Buckleton, J. Interpreting DNA Mixtures. J. Forensic Sci. 1997, 42, 14100J. [Google Scholar] [CrossRef]
- Cowell, R.G.; Graversen, T.; Lauritzen, S.; Mortera, J. Analysis of forensic DNA mixtures with artefacts. J. R. Stat. Soc. Ser. C (Appl. Stat.) 2015, 64, 1–48. [Google Scholar] [CrossRef]
- Cihlar, J.C.; Stoljarova, M.; King, J.; Budowle, B. Massively parallel sequencing-enabled mixture analysis of mitochondrial DNA samples. Int. J. Leg. Med. 2018, 132, 1263–1272. [Google Scholar] [CrossRef]
- Holland, M.M.; McQuillan, M.R.; O’Hanlon, K.A. Second generation sequencing allows for mtDNA mixture deconvolution and high resolution detection of heteroplasmy. Croat. Med. J. 2011, 52, 299–313. [Google Scholar] [CrossRef]
- Luo, S.; Valencia, C.A.; Zhang, J.; Lee, N.C.; Slone, J.; Gui, B.; Wang, X.; Li, Z.; Dell, S.; Brown, J.; et al. Biparental Inheritance of Mitochondrial DNA in Humans. Proc. Natl. Acad. Sci. USA 2018, 115, 13039–13044. [Google Scholar] [CrossRef]
- Schwartz, M.; Vissing, J. Paternal Inheritance of Mitochondrial DNA. N. Engl. J. Med. 2002, 347, 576–580. [Google Scholar] [CrossRef]
- Comas, D.; Paabo, S.; Bertranpetit, J. Heteroplasmy in the control region of human mitochondrial DNA. Genome Res. 1995, 5, 89–90. [Google Scholar] [CrossRef]
- Budowle, B.; Allard, M.W.; Wilson, M.R.; Chakraborty, R. Forensics andmitochondrialdna: Applications, Debates, and Foundations. Annu. Rev. Genom. Hum. Genet. 2003, 4, 119–141. [Google Scholar] [CrossRef]
- Clayton, T.; Whitaker, J.; Sparkes, R.; Gill, P. Analysis and interpretation of mixed forensic stains using DNA STR profiling. Forensic Sci. Int. 1998, 91, 55–70. [Google Scholar] [CrossRef]
- Vohr, S.H.; Gordon, R.; Eizenga, J.M.; Erlich, H.A.; Calloway, C.D.; Green, R.E. A Phylogenetic Approach for Haplotype Analysis of Sequence Data from Complex Mitochondrial Mixtures. Forensic Sci. Int. Genet. 2017, 30, 93–105. [Google Scholar] [CrossRef]
- Evett, I.W.; Buffery, C.; Willott, G.; Stoney, D. A guide to interpreting single locus profiles of DNA mixtures in forensic cases. J. Forensic Sci. Soc. 1991, 31, 41–47. [Google Scholar] [CrossRef]
- Andreasson, H.; Nilsson, M.; Budowle, B.; Frisk, S.; Allen, M. Quantification of mtDNA mixtures in forensic evidence material using pyrosequencing. Int. J. Leg. Med. 2006, 120, 383–390. [Google Scholar] [CrossRef] [PubMed]
- Wilson, M.R.; Dizinno, J.A.; Polanskey, D.; Replogle, J.; Budowle, B. Validation of mitochondrial DNA sequencing for forensic casework analysis. Int. J. Leg. Med. 1995, 108, 68–74. [Google Scholar] [CrossRef] [PubMed]
- Butler, J.M. Forensic DNA Typing: Biology, Technology, and Genetics of STR Markers; Elsevier: Amsterdam, The Netherlands, 2005; ISBN 978-0-08-047061-0. [Google Scholar]
- Butler, J.M.; Levin, B.C. Forensic applications of mitochondrial DNA. Trends Biotechnol. 1998, 16, 158–162. [Google Scholar] [CrossRef]
- Robin, E.D.; Wong, R. Mitochondrial DNA molecules and virtual number of mitochondria per cell in mammalian cells. J. Cell. Physiol. 1988, 136, 507–513. [Google Scholar] [CrossRef] [PubMed]
- Budowle, B.; Wilson, M.R.; Dizinno, J.A.; Stauffer, C.; Fasano, M.A.; Holland, M.M.; Monson, K.L. Mitochondrial DNA regions HVI and HVII population data. Forensic Sci. Int. 1999, 103, 23–35. [Google Scholar] [CrossRef]
- King, J.L.; LaRue, B.L.; Novroski, N.M.; Stoljarova, M.; Seo, S.B.; Zeng, X.; Warshauer, D.H.; Davis, C.P.; Parson, W.; Sajantila, A.; et al. High-quality and high-throughput massively parallel sequencing of the human mitochondrial genome using the Illumina MiSeq. Forensic Sci. Int. Genet. 2014, 12, 128–135. [Google Scholar] [CrossRef]
- Just, R.S.; Scheible, M.K.; Fast, S.A.; Sturk-Andreaggi, K.; Röck, A.W.; Bush, J.M.; Higginbotham, J.L.; Peck, M.A.; Ring, J.D.; Huber, G.E.; et al. Full mtGenome reference data: Development and characterization of 588 forensic-quality haplotypes representing three U.S. populations. Forensic Sci. Int. Genet. 2015, 14, 141–155. [Google Scholar] [CrossRef]
- Kim, H.; Erlich, H.A.; Calloway, C.D. Analysis of mixtures using next generation sequencing of mitochondrial DNA hypervariable regions. Croat. Med. J. 2015, 56, 208–217. [Google Scholar] [CrossRef]
- Strobl, C.; Cihlar, J.C.; Lagacé, R.; Wootton, S.; Roth, C.; Huber, N.; Schnaller, L.; Zimmermann, B.; Huber, G.; Hong, S.L.; et al. Evaluation of mitogenome sequence concordance, heteroplasmy detection, and haplogrouping in a worldwide lineage study using the Precision ID mtDNA Whole Genome Panel. Forensic Sci. Int. Genet. 2019, 42, 244–251. [Google Scholar] [CrossRef]
- Brandhagen, M.D.; Just, R.S.; Irwin, J.A. Validation of NGS for mitochondrial DNA casework at the FBI Laboratory. Forensic Sci. Int. Genet. 2020, 44, 102151. [Google Scholar] [CrossRef] [PubMed]
- Irwin, J.A.; Just, R.S.; Parson, W. Heredity In Civil; Criminal Investigation Massively Parallel Mitochondrial DNA Sequencing in Forensic Genetics: Principles and Opportunities. Handb. Forensic Genet. Biodivers. Hered. Civil Crim. Investig. 2016, 2, 293. [Google Scholar]
- Churchill, J.D.; Peters, D.; Capt, C.; Strobl, C.; Parson, W.; Budowle, B. Working towards implementation of whole genome mitochondrial DNA sequencing into routine casework. Forensic Sci. Int. Genet. Suppl. Ser. 2017, 6, e388–e389. [Google Scholar] [CrossRef]
- Li, M.; Schönberg, A.; Schaefer, M.; Schroeder, R.; Nasidze, I.; Stoneking, M. Detecting Heteroplasmy from High-Throughput Sequencing of Complete Human Mitochondrial DNA Genomes. Am. J. Hum. Genet. 2010, 87, 237–249. [Google Scholar] [CrossRef] [PubMed]
- AlAmoudi, E.; Mehmood, R.; Albeshri, A.; Gojobori, T. DNA Profiling Methods and Tools: A Review. In Lecture Notes of the Institute for Computer Sciences, Social Informatics and Telecommunications Engineering; Mehmood, R., Bhaduri, B., Katib, I., Chlamtac, I., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 216–231. [Google Scholar]
- Bleka, Ø.; Storvik, G.O.; Gill, P. EuroForMix: An open source software based on a continuous model to evaluate STR DNA profiles from a mixture of contributors with artefacts. Forensic Sci. Int. Genet. 2016, 21, 35–44. [Google Scholar] [CrossRef] [PubMed]
- Coble, M.D.; Bright, J.-A. Probabilistic genotyping software: An overview. Forensic Sci. Int. Genet. 2019, 38, 219–224. [Google Scholar] [CrossRef] [PubMed]
- Hu, N.; Cong, B.; Li, S.; Ma, C.; Fu, L.; Zhang, X. Current developments in forensic interpretation of mixed DNA samples (Review). Biomed. Rep. 2014, 2, 309–316. [Google Scholar] [CrossRef]
- Russell, D.; Christensen, W.; Lindsey, T. A simple unconstrained semi-continuous model for calculating likelihood ratios for complex DNA mixtures. Forensic Sci. Int. Genet. Suppl. Ser. 2015, 5, e37–e38. [Google Scholar] [CrossRef]
- Bright, J.-A.; Taylor, D.; McGovern, C.; Cooper, S.; Russell, L.; Abarno, D.; Buckleton, J.S. Developmental validation of STRmix™, expert software for the interpretation of forensic DNA profiles. Forensic Sci. Int. Genet. 2016, 23, 226–239. [Google Scholar] [CrossRef]
- Ge, J.; Budowle, B.; Chakraborty, R. Interpreting Y chromosome STR haplotype mixture. Leg. Med. 2010, 12, 137–143. [Google Scholar] [CrossRef]
- Curran, J.M.; Gill, P.; Bill, M. Interpretation of repeat measurement DNA evidence allowing for multiple contributors and population substructure. Forensic Sci. Int. 2005, 148, 47–53. [Google Scholar] [CrossRef] [PubMed]
- Van Oven, M. PhyloTree Build 17: Growing the human mitochondrial DNA tree. Forensic Sci. Int. Genet. Suppl. Ser. 2015, 5, e392–e394. [Google Scholar] [CrossRef]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum Likelihood from Incomplete Data Via the EMAlgorithm. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 1977, 39, 1–22. [Google Scholar] [CrossRef]
- Bandelt, H.-J.; Salas, A. Current Next Generation Sequencing technology may not meet forensic standards. Forensic Sci. Int. Genet. 2012, 6, 143–145. [Google Scholar] [CrossRef] [PubMed]
- Woerner, A.E.; Cihlar, J.C.; Smart, U.; Budowle, B. Numt identification and removal with RtN! Bioinformatics 2020, 36, 5115–5116. [Google Scholar] [CrossRef]
- Lopez, J.V.; Yuhki, N.; Masuda, R.; Modi, W.; O’Brien, S.J. Numt, a recent transfer and tandem amplification of mitochondrial DNA to the nuclear genome of the domestic cat. J. Mol. Evol. 1994, 39, 174–190. [Google Scholar]
- Browning, S.R.; Browning, B.L. Haplotype phasing: Existing methods and new developments. Nat. Rev. Genet. 2011, 12, 703–714. [Google Scholar] [CrossRef]
- Browning, S.R.; Browning, B.L. Rapid and Accurate Haplotype Phasing and Missing-Data Inference for Whole-Genome Association Studies By Use of Localized Haplotype Clustering. Am. J. Hum. Genet. 2007, 81, 1084–1097. [Google Scholar] [CrossRef]
- Stephens, M.; Smith, N.J.; Donnelly, P. A New Statistical Method for Haplotype Reconstruction from Population Data. Am. J. Hum. Genet. 2001, 68, 978–989. [Google Scholar] [CrossRef]
- Choi, Y.; Chan, A.P.; Kirkness, E.; Telenti, A.; Schork, N.J. Comparison of phasing strategies for whole human genomes. PLoS Genet. 2018, 14, e1007308. [Google Scholar] [CrossRef]
- Williams, A.L.; Patterson, N.; Glessner, J.; Hakonarson, H.; Reich, D. Phasing of Many Thousands of Genotyped Samples. Am. J. Hum. Genet. 2012, 91, 238–251. [Google Scholar] [CrossRef] [PubMed]
- Delaneau, O.; Coulonges, C.; Zagury, J.-F. Shape-IT: New rapid and accurate algorithm for haplotype inference. BMC Bioinform. 2008, 9, 540. [Google Scholar] [CrossRef] [PubMed]
- Howie, B.N.; Donnelly, P.; Marchini, J. A Flexible and Accurate Genotype Imputation Method for the Next Generation of Genome-Wide Association Studies. PLoS Genet. 2009, 5, e1000529. [Google Scholar] [CrossRef] [PubMed]
- Weale, M.E. A survey of current software for haplotype phase inference. Hum. Genom. 2004, 1, 141–144. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Miar, Y.; Sargolzaei, M.; Schenkel, F.S. A comparison of different algorithms for phasing haplotypes using Holstein cattle genotypes and pedigree data. J. Dairy Sci. 2017, 100, 2837–2849. [Google Scholar] [CrossRef] [PubMed]
- Zhu, S.J.; Almagro-Garcia, J.; McVean, G. Deconvolution of multiple infections in Plasmodium falciparum from high throughput sequencing data. Bioinformatics 2018, 34, 9–15. [Google Scholar] [CrossRef]
- Chang, H.-H.; Worby, C.J.; Yeka, A.; Nankabirwa, J.; Kamya, M.R.; Staedke, S.G.; Dorsey, G.; Murphy, M.; Neafsey, D.E.; Jeffreys, A.E.; et al. THE REAL McCOIL: A method for the concurrent estimation of the complexity of infection and SNP allele frequency for malaria parasites. PLoS Comput. Biol. 2017, 13, e1005348. [Google Scholar] [CrossRef]
- Galinsky, K.J.; Valim, C.; Salmier, A.; De Thoisy, B.; Musset, L.; Legrand, E.; Faust, A.; Baniecki, M.L.; Ndiaye, D.; Daniels, R.F.; et al. COIL: A methodology for evaluating malarial complexity of infection using likelihood from single nucleotide polymorphism data. Malar. J. 2015, 14, 1–9. [Google Scholar] [CrossRef]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of State Calculations by Fast Computing Machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Hastings, W.K. Monte Carlo Sampling Methods Using Markov Chains and Their Applications. Biometrika 1970, 57, 97–109. [Google Scholar] [CrossRef]
- Li, N.; Stephens, M. Modeling Linkage Disequilibrium and Identifying Recombination Hotspots Using Single-Nucleotide Polymorphism Data. Genetics 2003, 165, 2213–2233. [Google Scholar] [PubMed]
- Stephens, M.; Donnelly, P. A Comparison of Bayesian Methods for Haplotype Reconstruction from Population Genotype Data. Am. J. Hum. Genet. 2003, 73, 1162–1169. [Google Scholar] [CrossRef] [PubMed]
- Geman, S.; Geman, D. Stochastic Relaxation, Gibbs Distributions, and the Bayesian Restoration of Images. IEEE Trans. Pattern Anal. Mach. Intell. 1984, 6, 721–741. [Google Scholar] [CrossRef] [PubMed]
- Lin, S.; Cutler, D.J.; Zwick, M.E.; Chakravarti, A. Haplotype Inference in Random Population Samples. Am. J. Hum. Genet. 2002, 71, 1129–1137. [Google Scholar] [CrossRef] [PubMed]
- Pompanon, F.; Bonin, A.; Bellemain, E.; Taberlet, P. Genotyping errors: Causes, consequences and solutions. Nat. Rev. Genet. 2005, 6, 847–859. [Google Scholar] [CrossRef] [PubMed]
- R Core Team, R. R: A Language and Environment for Statistical Computing. In R Foundation for Statistical Computing; R Core Team: Vienna, Austria, 2013. [Google Scholar]
- Andrews, R.M.; Kubacka, I.; Chinnery, P.F.; Chrzanowska-Lightowlers, Z.M.; Turnbull, D.M.; Howell, N. Reanalysis and revision of the Cambridge reference sequence for human mitochondrial DNA. Nat. Genet. 1999, 23, 147. [Google Scholar] [CrossRef]
- Parson, W.; Dür, A. EMPOP—A forensic mtDNA database. Forensic Sci. Int. Genet. 2007, 1, 88–92. [Google Scholar] [CrossRef]
- Kimura, M. The number of heterozygous nucleotide sites maintained in a finite population due to steady flux of mutations. Genetics 1969, 61, 893–903. [Google Scholar] [CrossRef]
- Attimonelli, M.; Accetturo, M.; Santamaria, M.; Lascaro, D.; Scioscia, G.; Pappadà, G.; Russo, L.; Zanchetta, L.; Tommaseo-Ponzetta, M. HmtDB, a Human Mitochondrial Genomic Resource Based on Variability Studies Supporting Population Genetics and Biomedical Research. BMC Bioinform. 2005, 6, S4. [Google Scholar] [CrossRef]
- Clima, R.; Preste, R.; Calabrese, C.; Diroma, M.A.; Santorsola, M.; Scioscia, G.; Simone, D.; Shen, L.; Gasparre, G.; Attimonelli, M. HmtDB 2016: Data update, a better performing query system and human mitochondrial DNA haplogroup predictor. Nucleic Acids Res. 2017, 45, D698–D706. [Google Scholar] [CrossRef]
- Hamming, R.W. Error Detecting and Error Correcting Codes. Bell Syst. Tech. J. 1950, 29, 147–160. [Google Scholar] [CrossRef]
- Browning, B.L.; Browning, S.R. A Unified Approach to Genotype Imputation and Haplotype-Phase Inference for Large Data Sets of Trios and Unrelated Individuals. Am. J. Hum. Genet. 2009, 84, 210–223. [Google Scholar] [CrossRef] [PubMed]
- Loh, P.-R.; Danecek, P.; Palamara, P.F.; Fuchsberger, C.; Reshef, Y.A.; Finucane, H.K.; Schoenherr, S.; Forer, S.S.L.; McCarthy, S.; Abecasis, C.F.G.R.; et al. Reference-based phasing using the Haplotype Reference Consortium panel. Nat. Genet. 2016, 48, 1443–1448. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.-H. Estimating classification error rate: Repeated cross-validation, repeated hold-out and bootstrap. Comput. Stat. Data Anal. 2009, 53, 3735–3745. [Google Scholar] [CrossRef]
- Stone, M. Cross-Validatory Choice and Assessment of Statistical Predictions (with Discussion). J. R. Stat. Soc. Ser. B (Methodol.) 1976, 38, 102. [Google Scholar] [CrossRef]
- Lunn, D.J.; Best, N.; Thomas, A.; Wakefield, J.; Spiegelhalter, D. Bayesian Analysis of Population PK/PD Models: General Concepts and Software. J. Pharmacokinet. Pharmacodyn. 2002, 29, 271–307. [Google Scholar] [CrossRef] [PubMed]
- Rambaut, A.; Drummond, A.J.; Xie, D.; Baele, G.; Suchard, M.A. Posterior Summarization in Bayesian Phylogenetics Using Tracer 1.7. Syst. Biol. 2018, 67, 901–904. [Google Scholar] [CrossRef]
- Bansal, V. OUP accepted manuscript. Bioinformatics 2019, 35, i242–i248. [Google Scholar] [CrossRef]
- Delaneau, O.; Zagury, J.-F.; Robinson, M.R.; Marchini, J.L.; Dermitzakis, E.T. Accurate, scalable and integrative haplotype estimation. Nat. Commun. 2019, 10, 1–10. [Google Scholar] [CrossRef]
- Roth, C.; Parson, W.; Strobl, C.; Lagacé, R.; Short, M. MVC: An integrated mitochondrial variant caller for forensics. Aust. J. Forensic Sci. 2019, 51, S52–S55. [Google Scholar] [CrossRef]
- Alqahtani, F.; Măndoiu, I.I. Mitochondrial Haplogroup Assignment for High-Throughput Sequencing Data from Single Individual and Mixed DNA Samples. In Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2020; pp. 1–12. [Google Scholar]
- Kang, H.; Qin, Z.S.; Niu, T.; Liu, J.S. Incorporating Genotyping Uncertainty in Haplotype Inference for Single-Nucleotide Polymorphisms. Am. J. Hum. Genet. 2004, 74, 495–510. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Handsaker, B.; Wysoker, A.; Fennell, T.; Ruan, J.; Homer, N.; Marth, G.; Abecasis, G.; Durbin, R. The sequence alignment/map format and SAMtools. Bioinformatics 2009, 25, 2078–2079. [Google Scholar] [CrossRef] [PubMed]
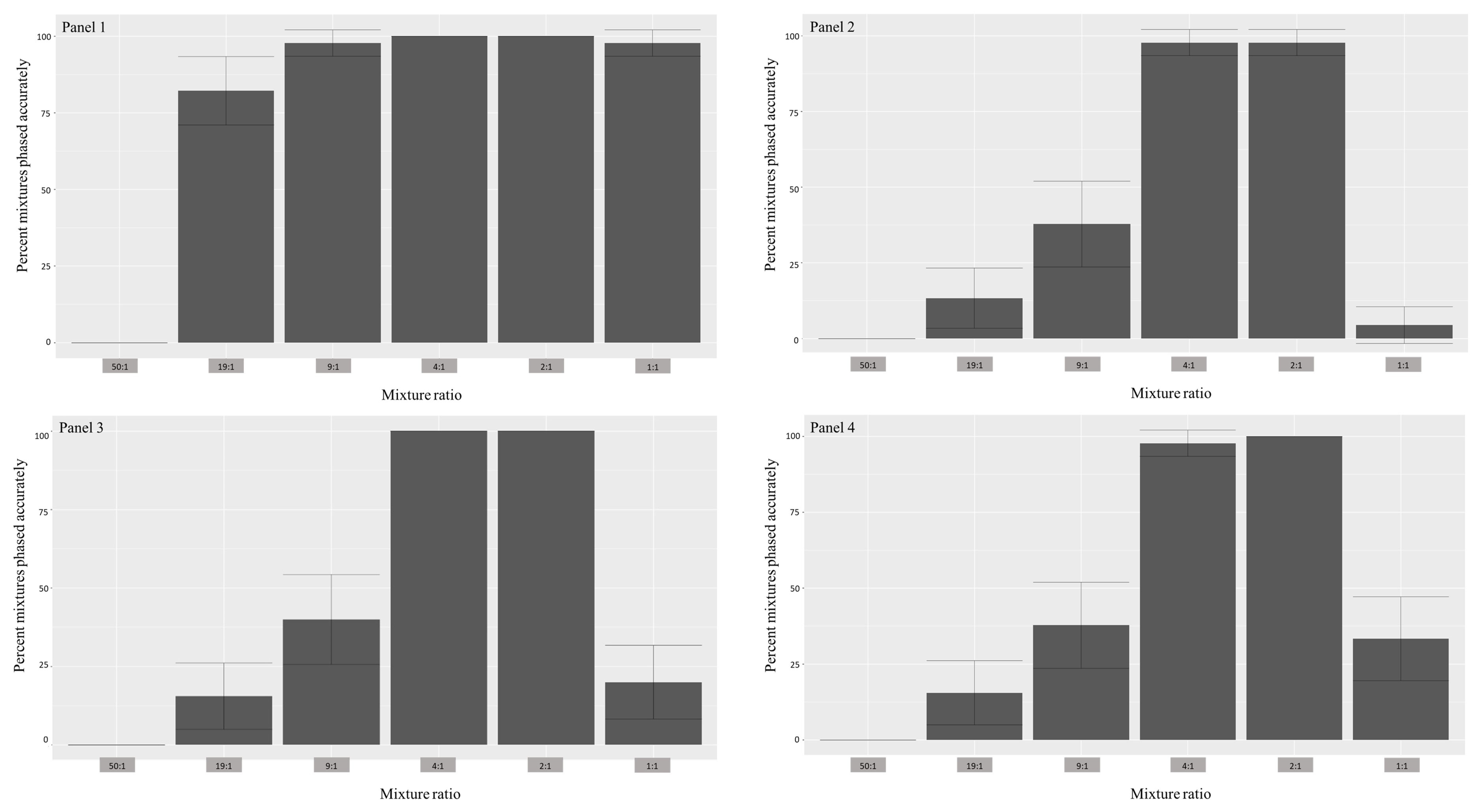
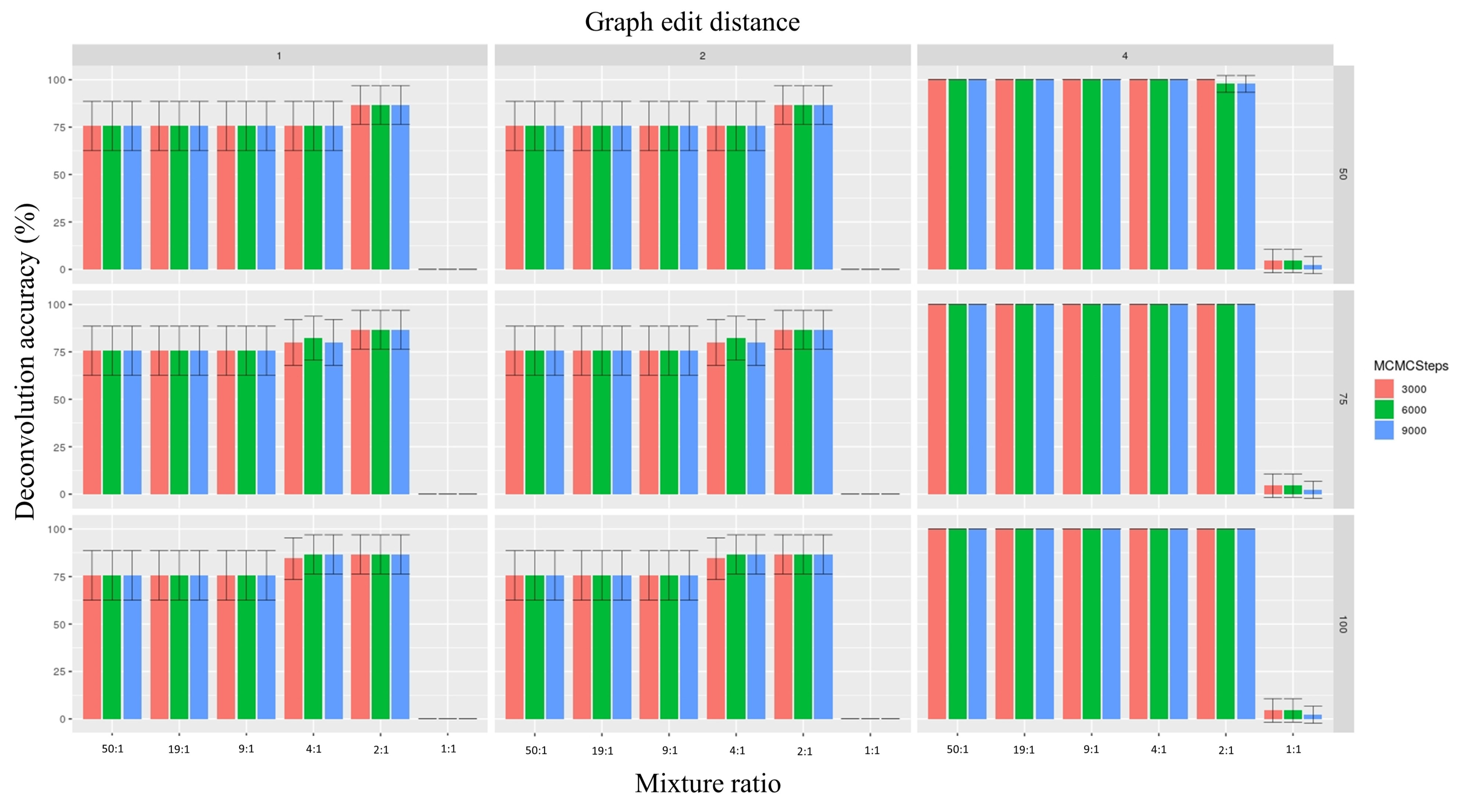

| Reference Panel 1 | Reference Panel 2 | Reference Panel 3 | Reference Panel 4 | |||||
|---|---|---|---|---|---|---|---|---|
| Proportions | Major | Minor | Major | Minor | Major | Minor | Major | Minor |
| 50:1 | 100% | 0% | 100% | 0% | 100% | 0% | 100% | 2.2% (4.3%) |
| 19:1 | 100% | 82.2% (11.8%) | 100% | 13.3% (9.9%) | 100% | 15.5% (10.6%) | 100% | 20% (11.7%) |
| 9:1 | 100% | 97.8% (4.3%) | 100% | 37.8% (14.1%) | 100% | 40% (14.3%) | 100% | 35.5% (14%) |
| 4:1 | 100% | 100% | 100% | 97.8% (4.3%) | 100% | 100% | 100% | 97.8% (4.3%) |
| 2:1 | 100% | 100% | 100% | 97.8% (4.3%) | 100% | 100% | 100% | 100% |
| 1:1 | 97.8% (4.3%) | 97.8% (4.3%) | 6.6% (7.3%) | 4.4% (6%) | 20% (11.7%) | 20% (11.7) | 40.9% (14.36%) | 38.6% (14.2%) |
| Major (Panel 3) | Major (Panel 4) | Minor (Panel 3) | Minor (Panel 4) | Major (Panel 3) | Major (Panel 1) | Minor (Panel 3) | Minor (Panel 1) | Major (Panel 3) | Major (Panel 2) | Minor (Panel 3) | Minor (Panel 2) | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Number of successes | 19 | 9 | 18 | 9 | 19 | 44 | 18 | 44 | 19 | 3 | 18 | 3 |
| 95% confidence interval | 0.014–0.430 | 0.007–0.407 | 0.383–0.728 | 0.406–0.749 | 0.172–0.539 | 0.178–0.533 | ||||||
| p-value | 0.04 | 0.06 | 3.38 × 10−8 | 1.254 × 10−8 | 0.0002 | 0.0001 | ||||||
| Estimate | Standard Error | t-Value | p-Value for t-Test | |
|---|---|---|---|---|
| Minimum Distance from Panel | −2.2381 | 0.6497 | −3.445 | 0.000664 |
| Pairwise Distance | −0.1939 | 0.2082 | 0.931 | 0.352452 |
| Read Count | MCMC Steps | Graph Edit Distance | |||
|---|---|---|---|---|---|
| 50 | R2 = 0.74 | 3000 | R2 = 0.74 | 1 | R2 = 0.66 |
| 75 | R2 = 0.74 | 6000 | R2 = 0.74 | 2 | R2 = 0.66 |
| 100 | R2 = 0.73 | 9000 | R2 = 0.74 | 4 | R2 = 0.99 |
| Graph Edit Distance | 1 vs. 2 | 1 vs. 4 | 2 vs. 4 |
|---|---|---|---|
| 95% confidence interval | 0.924–1.083 | 1.039–1.218 | 1.039–1.218 |
| p-value | 1.0 | 0.003 | 0.003 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Smart, U.; Cihlar, J.C.; Mandape, S.N.; Muenzler, M.; King, J.L.; Budowle, B.; Woerner, A.E. A Continuous Statistical Phasing Framework for the Analysis of Forensic Mitochondrial DNA Mixtures. Genes 2021, 12, 128. https://doi.org/10.3390/genes12020128
Smart U, Cihlar JC, Mandape SN, Muenzler M, King JL, Budowle B, Woerner AE. A Continuous Statistical Phasing Framework for the Analysis of Forensic Mitochondrial DNA Mixtures. Genes. 2021; 12(2):128. https://doi.org/10.3390/genes12020128
Chicago/Turabian StyleSmart, Utpal, Jennifer Churchill Cihlar, Sammed N. Mandape, Melissa Muenzler, Jonathan L. King, Bruce Budowle, and August E. Woerner. 2021. "A Continuous Statistical Phasing Framework for the Analysis of Forensic Mitochondrial DNA Mixtures" Genes 12, no. 2: 128. https://doi.org/10.3390/genes12020128
APA StyleSmart, U., Cihlar, J. C., Mandape, S. N., Muenzler, M., King, J. L., Budowle, B., & Woerner, A. E. (2021). A Continuous Statistical Phasing Framework for the Analysis of Forensic Mitochondrial DNA Mixtures. Genes, 12(2), 128. https://doi.org/10.3390/genes12020128









