1. Introduction
Cancer is one of the leading causes of death worldwide and has been posing extensive public concerns. In cancer studies, prognosis modeling is a critical step that greatly contributes to understanding cancer etiology, developing effective therapeutic methods, and improving life quality. Significant effort has been devoted to searching for prognostic factors, among which omics markers have important implications. For example,
EGFR has been suggested as a strong prognostic indicator in multiple cancers, such as ovarian, cervical, and bladder cancers. Nicholson, et al. [
1] reviewed over 200 studies and reported that relapse-free-interval or survival data are directly in relation to the increased EGFR levels in breast, gastric, colorectal, and many other cancers. Petitjean, et al. [
2] found that the mutation of
TP53 has an impact on the prognosis of breast and several other cancers. Gao, et al. [
3] used a Cox model to find that a high level of MMP-14 mRNA expression leads to a significantly shorter overall survival for breast cancer. Chiu, et al. [
4] characterized prognostic alteration for melanoma with a panel of five genes, including
CSMD2, CNTNAP5, NRDE2, ADAM6, and
TRPM2. Despite considerable successes, our understanding of cancer prognosis is still limited. The limited progress in cancer analytics may be attributable to small sample sizes, high dimensionality and low signal-to-noise ratios of omics data, as well as the underlying molecular complexity of cancers.
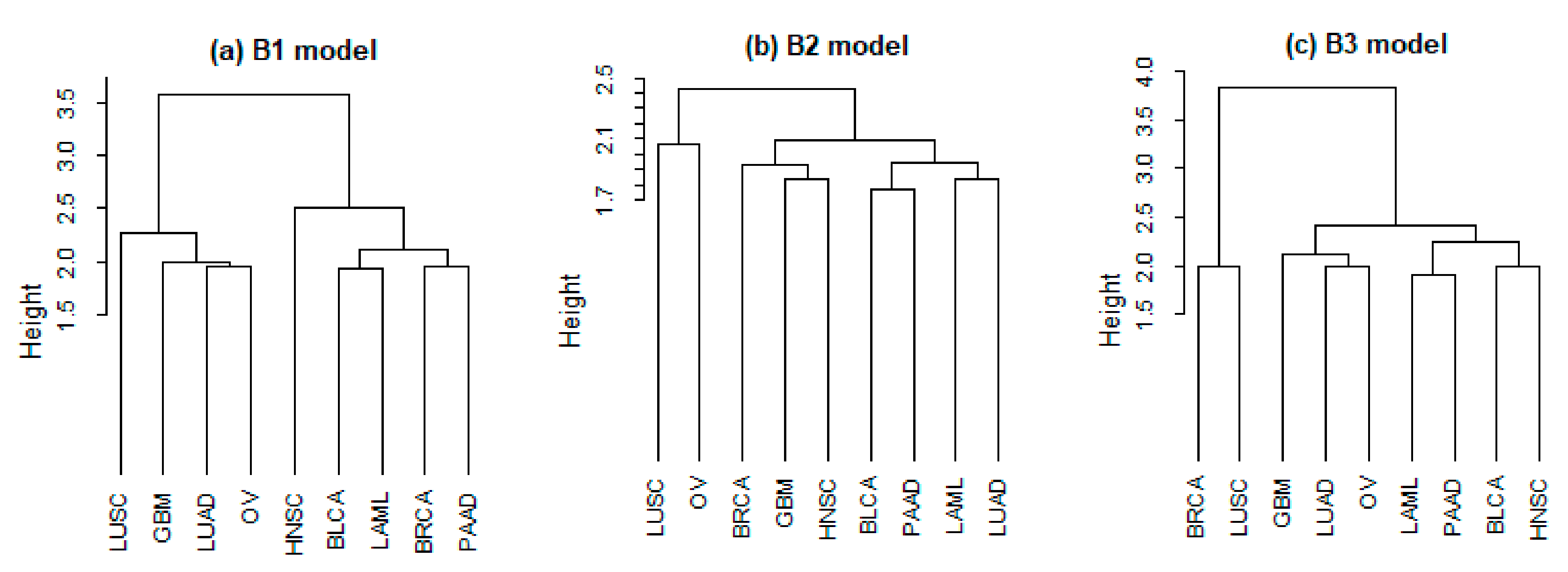
Most of the existing studies, including the aforementioned, focus on a single type of cancer, and analysis often suffers from a lack of sufficient information. Cancer types have been typically classified according to organ- and tissue histology-based pathology criteria. This is especially true in “old” studies. More recently, with the development of high-throughput profiling, increasing attention has been paid to the molecular basis of cancers, providing a novel perspective on cancer types. A representative recent work is Hoadley, et al. [
5], which conducted the molecular clustering of 33 different types of tumors in The Cancer Genome Atlas (TCGA) with data on aneuploidy, DNA methylation, mRNA, and miRNA. Their results show that some cancers, which were treated as completely different diseases according to traditional organ- and tissue histology-based pathology criteria, are closely related according to their molecular characteristics. For example, squamous cell carcinoma can occur in lung, bladder, cervix, head, and neck, and different histopathological types are often observed. However, in Hoadley, et al. [
5], these cancer types have been found to have similar molecular characteristics.
Molecular similarity across cancers has been well established in the literature. Prognosis of many different cancer types is mediated by some common mechanisms associated with certain common pathways. For example, the p53 pathway inhibits cell growth and stimulates cell death, which plays an important role in a large fraction of cancers. In addition, there are other genes/pathways that have important roles in many cancer types, such as apoptosis, hypoxia-inducible transcription factor (HIF)-1, mitogen activated protein kinase (MAPK) phosphoinositide3-kinase (PI3K), and receptor tyrosine kinases (RTKs) [
6]. Published studies have found that different cancer types may share common oncogenes, tumor-suppressor genes and stability genes, the alternations of which are responsible for the genesis and prognosis of cancers. For example,
BRCA1 gene mutation is often found in both breast and ovarian cancers [
7]. These two cancer types are perhaps the most common cancers in female and often occur together [
7]. Another example is lung adenocarcinoma and lung squamous cell carcinoma which are two major lung cancer subtypes. Many genes have been reported to be associated with both cancer subtypes, including
EGFR [
8],
TP53 [
8],
AKT1,
DDR2 [
9],
FGFR1 [
10],
KRAS [
8],
PTEN, and others. With molecular similarity, one cancer may contain information useful for the analysis of other cancers. Overall, it is of interest and also reasonable to conduct the integrative analysis of molecular profiles of multiple cancer types to increase information and more accurately describe the underlying prognosis.
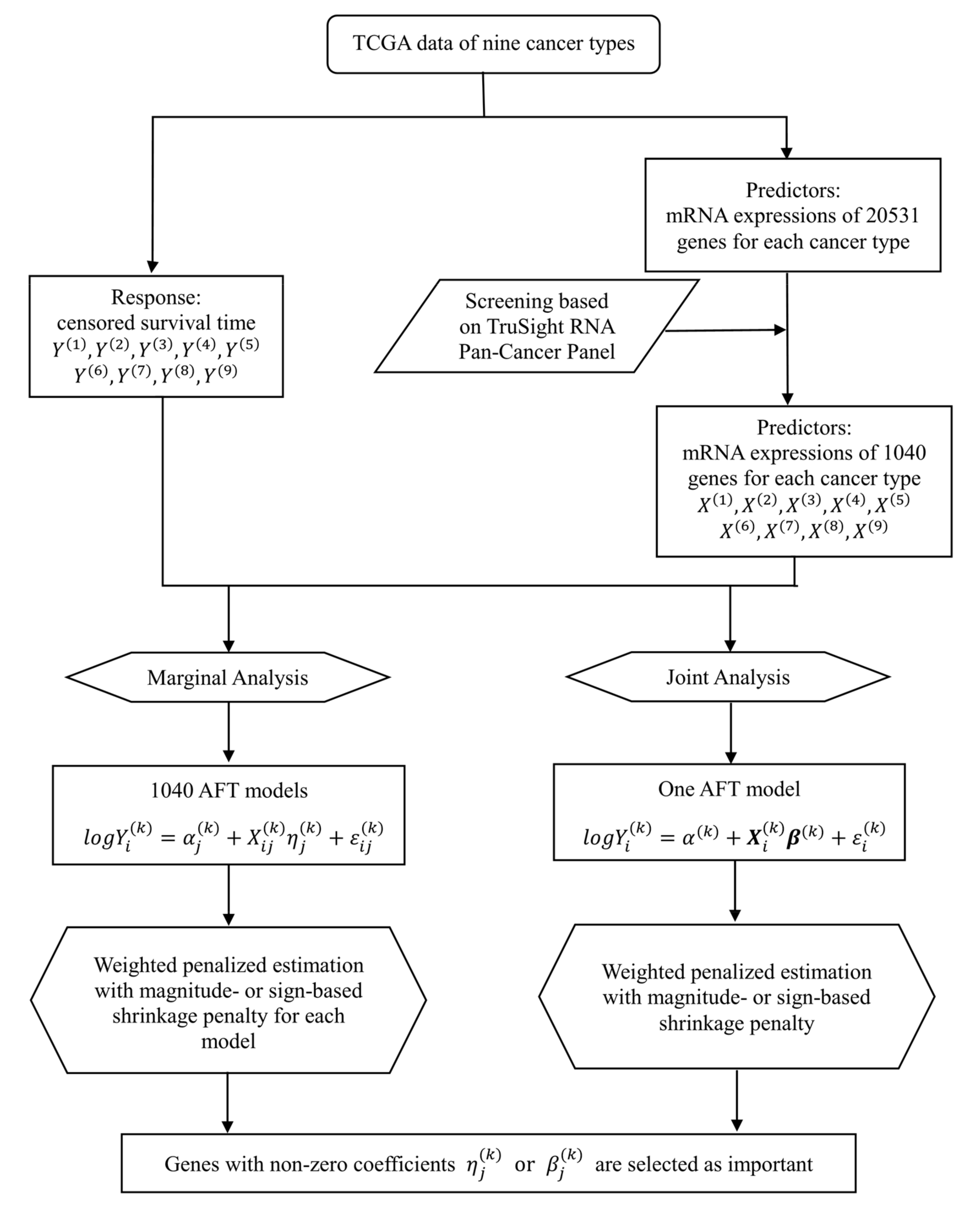
More recently, much effort has been devoted to collecting omics profiles of tumor samples with different cancer types under a unified protocol. A representative example is TCGA organized by The National Cancer Institute (NCI) which has generated a large amount of cross-platform genomic data for exploring the complex landscapes of human cancers. Specifically, it has collected multi-omics data from over 20,000 primary cancer and matched normal samples spanning 33 cancer types, including breast cancer, lung squamous cell carcinoma, lung adenocarcinoma, and others. Other examples include the International Cancer Genome Consortium (ICGC), Therapeutically Applicable Research to Generate Effective Treatments (TARGET), and others. With the clinical and omics data on multiple cancer types, these databases provide a good opportunity to conduct cancer modeling through data integration.
In the literature, there are a few related studies, which can be generally classified into two families. The first family adopts a meta-analysis strategy, which first analyzes different cancer types separately and then compares results across cancer types to search for overlapping findings. An example is Cava, et al. [
11], which first analyzed gene expression data on 16 cancer types separately and then identified 895 de-regulated genes with a central role in pathways. Yu, et al. [
12] systematically analyzed gene expressions across diverse cancers during the inflammatory timeline. After comparing the differentially expressed genes among cancers, they found three novel pan-cancer gene expression patterns, in which the gene expressions are regulated differently in the early and late phases of inflammation. Using a cohort of 3899 samples with 10 cancer types, Sharma, et al. [
13] adopted a bottom-up approach to quantify the effects of gene expression variations and identified novel recurrent regulatory mutations influencing known cancer genes, such as
GRIN2D and
NKX2-1, in multiple cancer types. The second family of approaches stacks data from multiple cancer types together to create a “mega” dataset, and then conducts analysis as if there is in fact just a single dataset. An example is Martinez-Ledesma, et al. [
14], which used a network-based exploration approach to identify gene expression biomarkers that are predictive of clinical outcomes in 12 cancer types. Using TCGA data on 3281 samples with 12 cancer types, Leiserson, et al. [
15] performed a pan-cancer analysis of mutated networks with a new algorithm, HotNet2, and found some significantly mutated subnetworks as well as those with less characterized roles in cancers. Beyond studies on cancer omics data, similar strategies have also been considered in other fields of biomedical research to collectively analyze multiple datasets. For example, Xing, et al. [
16] proposed two variations of a stacking algorithm to simultaneously predict the resistance of multiple drugs using mutation information, leading to improvement in prediction performance. As another example of drug analysis, Matlock, et al. [
17] developed stacking models built on multiple cell lines, multiple tested drugs, as well as genomic information for drug sensitivity prediction in cancer cell lines. Medical imaging data integration has also been conducted. For example, a meta-analysis based support vector machine was introduced in [
18] to collectively analyze multiple types of images, such as fluorodeoxyglucose positron emission tomography (FDG-PET) and magnetic resonance imaging (MRI), for identifying susceptible brain regions and predicting the incidence of Alzheimer’s disease.
Despite considerable successes, both families have limitations. The former neglects integration in the discovery process. Data on each cancer type still suffers from a lack of sufficient information resulting from a small sample size, high noises, and other reasons. As such, the “delay” in integration may make the analysis less effective. For the latter one, although sample size increases by stacking, subjects with different cancer types are treated as if they were from the same population. It cannot effectively accommodate the heterogeneity across cancer types. In addition, in some of the existing studies, “classic” statistical techniques have been adopted, and there is a lack of utilizing state-of-the-art techniques.
Motivated by the limitations of single cancer type analysis and recent successes of integrative analysis in other contexts, in this study our goal is to conduct more effective integrative analysis of multiple cancer types with high dimensional omics data. By contrast with the single cancer type analysis, omics data from multiple cancer types are jointly analyzed to effectively borrow information across cancer types and generate more reliable findings. By contrast with the existing meta-analysis- and stacking-based approaches, the proposed analysis integrates data on multiple cancer types in the discovery process and effectively accommodate the heterogeneity across cancer types. By contrast with the analysis on categorical and continuous outcomes, the more challenging prognosis analysis is conducted. The proposed analysis is based on the penalization technique which has a solid statistical ground and satisfactory performance in published studies. TCGA mRNA expression data on nine cancer types are analyzed to demonstrate the proposed integrative analysis approach. Overall, this study provides a practically useful new venue for cancer prognosis modeling with multiple cancer types.