Mathematical Modeling Unveils a New Role for Transient Mitochondrial Permeability Transition in ROS Damage Prevention
Abstract
1. Introduction
2. Materials and Methods
2.1. General Model
2.2. MPT
2.3. Bifurcation Analysis
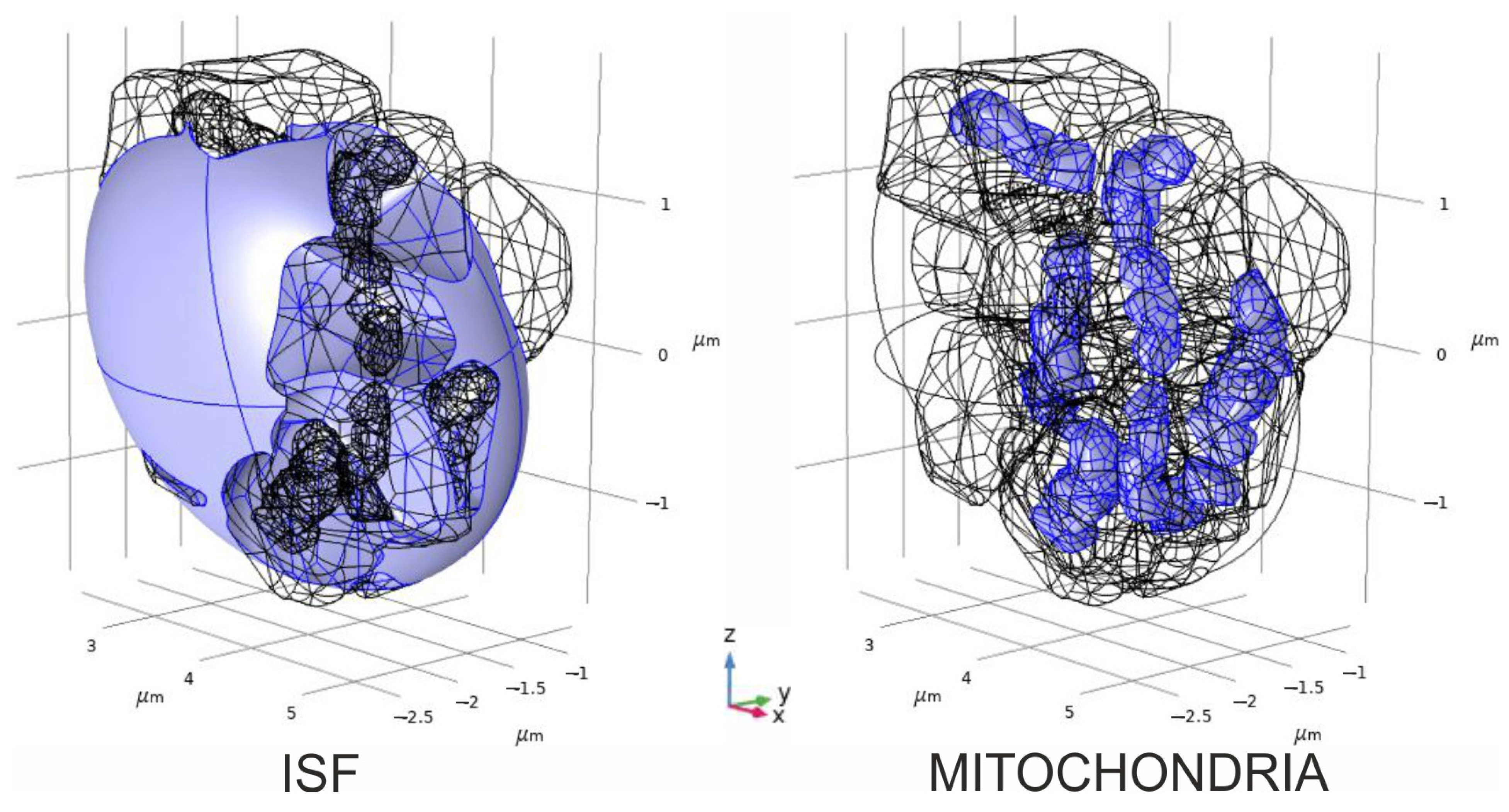
2.4. Convectional Reaction–Diffusion of Glutamate and Hydrogen Peroxide
| Value | Value | Literature Source and Comments |
|---|---|---|
| 1.29 × 10−6 cm2/s | [25] | |
| 1 μM | [26,27] | |
| 5 × 10−7 m/s | [28] 1 | |
| 1.25 × 10−8 mol/m2 | [29] | |
| 1.25 × 10−9 mol/m2 | [29] | |
| 41 s−1 | [30] | |
| 12 μM | [30] | |
| 1.83 × 10−9 m2/s | [31] | |
| 10 nM | [32] | |
| 0.3 | Assumed in the modeling | |
| 1 | [32] | |
| 0.5 | [33] | |
| 5.05 μmol/l/min | [23] | |
| 106 μmol/l/min | [23] |
3. Results
3.1. Bistability of Respiration
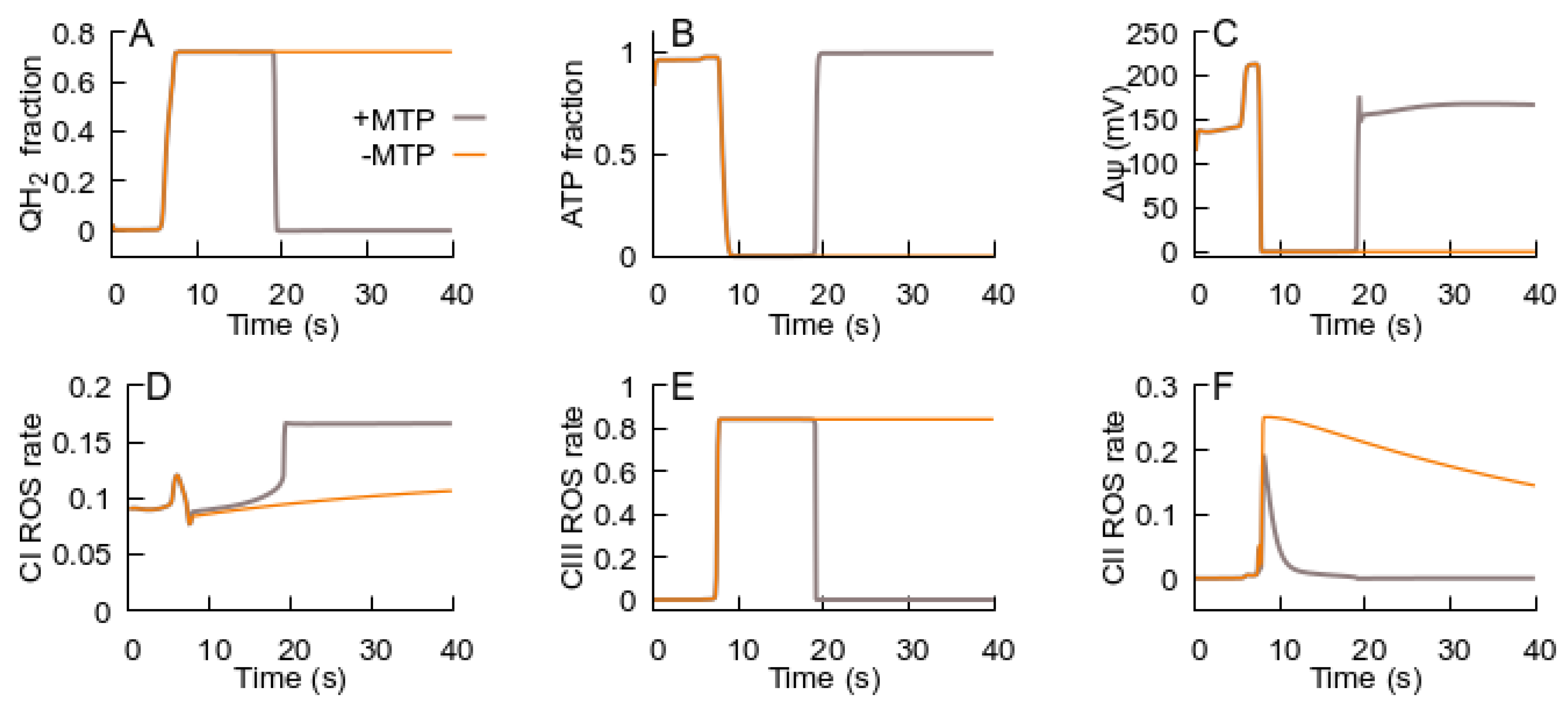
3.2. MPT Returns the RC to an ATP-Producing State
3.3. H+ as a Modifier of RC Bifurcation Characteristics
3.4. Ca2+ as a Modifier of RC Bifurcation Characteristics
3.5. Bifurcation Analysis of the Reduced RC Part of the Model
3.6. Spatial–Temporal Switching Between the ATP-Producing States and the ROS-Producing Ones of Neuronal Mitochondria
4. Discussion
5. Conclusions
- An ROS burst is generated due to the RC transition from an ATP-producing to an ROS-producing state, which is caused by H+ deficiency or free ubiquinone pool reduction and a respective deficiency of the oxidized form.
- Glutamate, as an activator of respiratory complex II, can induce ubiquinone reduction and the transition to an ROS-producing state.
- Once glutamate induces the RC switch to an ROS-producing state, a subsequent decrease in glutamate levels cannot cause a transition back to an ATP-producing state if the MPT does not occur.
- ROS generated in an ROS-producing state can induce the MPT.
- The MPT, in turn, is an adaptive response to the RC transition from an ATP-producing to an ROS-producing state. It promotes the RC to return to an ATP-producing state, and the decrease in ROS generation in the latter state terminates the MPT.
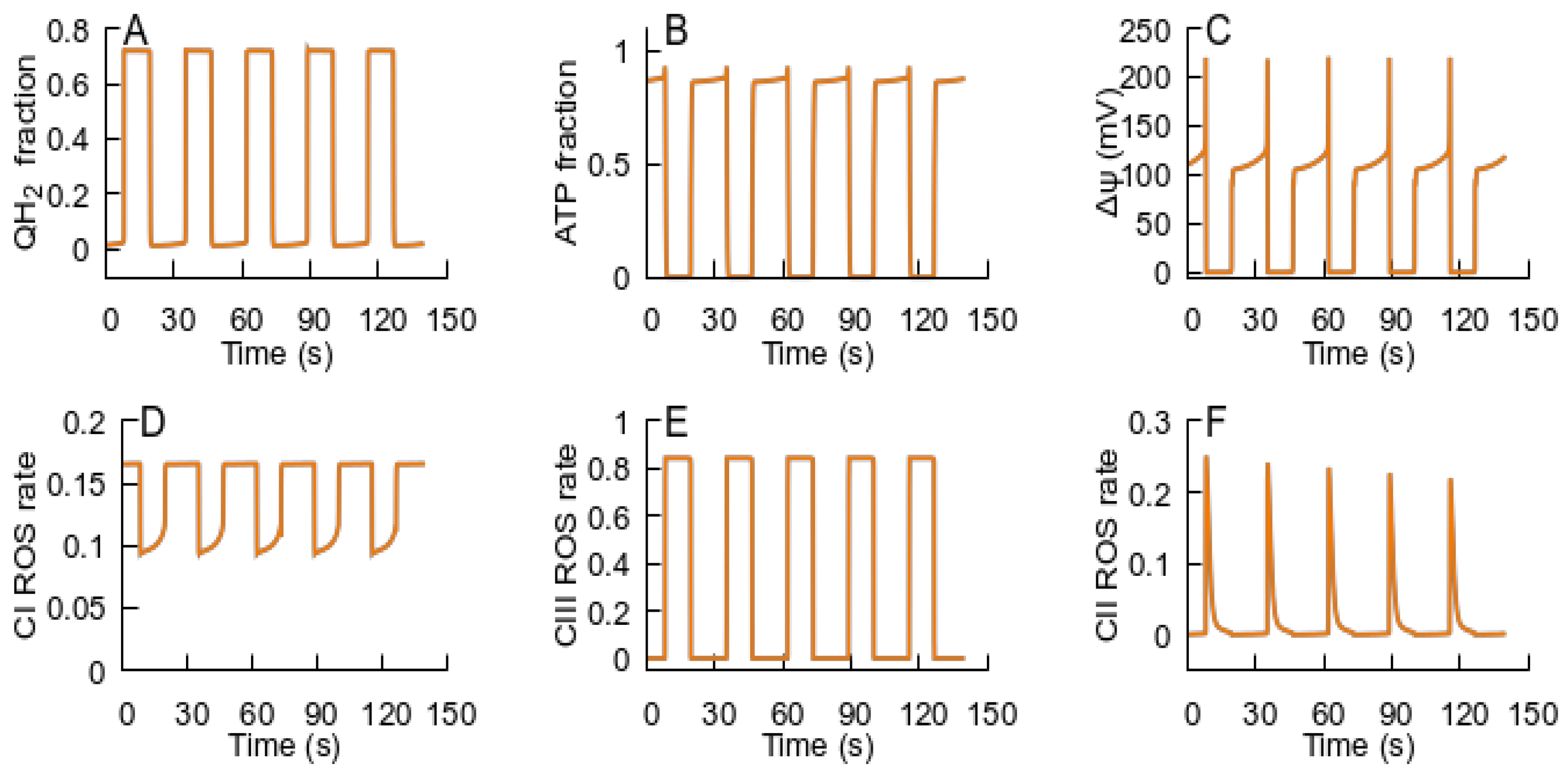
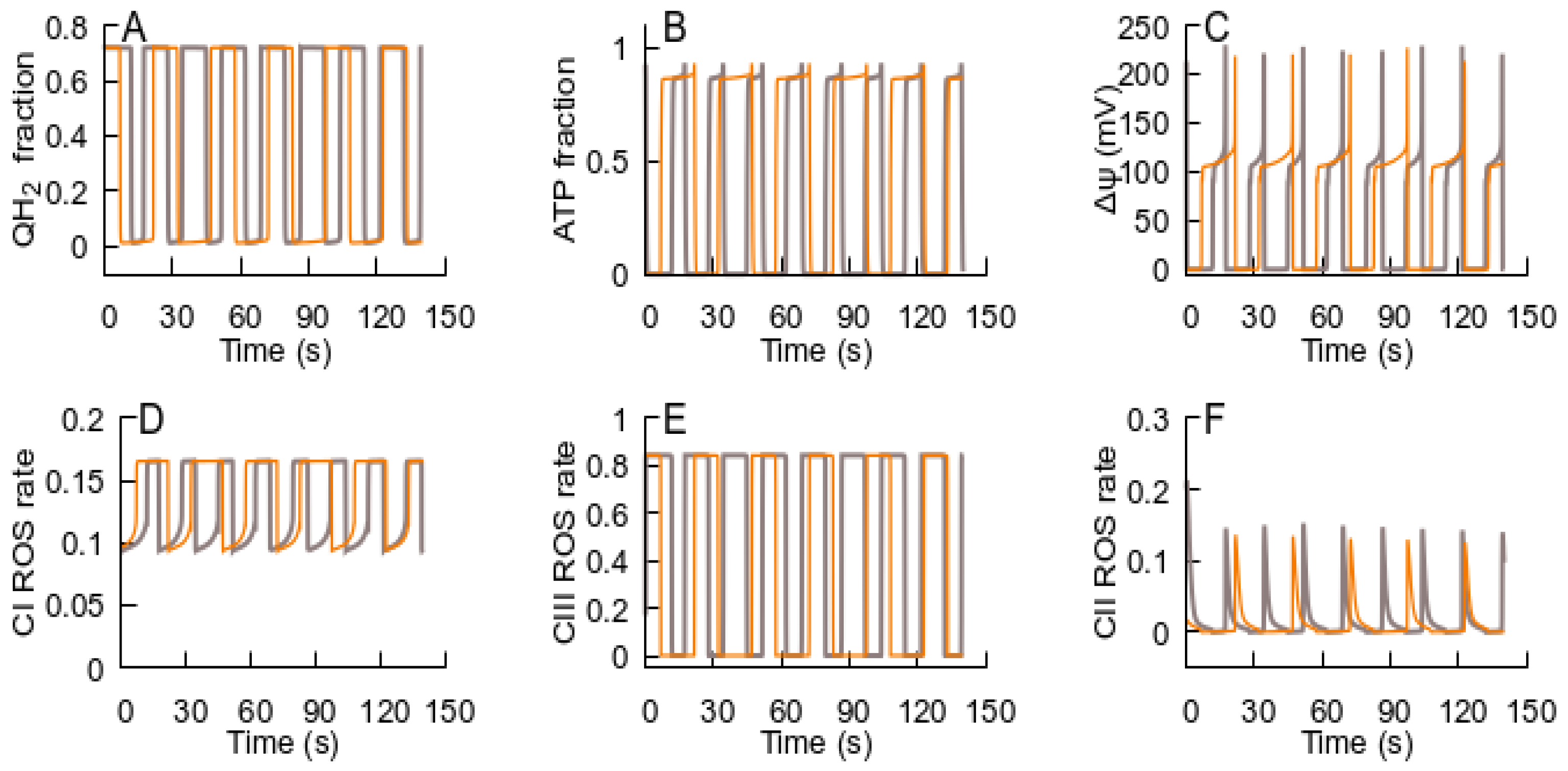
- After the RC returns to an ATP-producing state, the metabolic conditions may provoke repeated transition to an ROS-producing state, and the oscillations of the RC and MPT can be observed. If the new conditions after the cycle are consistent with an ATP-producing state, the system remains in this state. Such an oscillation can explain the metabolic oscillation observed under various conditions [35,58].
- If the MPT is unable to restore the RC ATP-producing state, it remains in an ROS-producing state and the MPT becomes irreversible.
- The spatial–temporal patterns of glutamate concentrations and H2O2 production fluxes were evaluated in a 3D digital phantom of nervous parenchyma. The effect of glutamate on the RC transitions, ROS burst, and the MPT depends on the spatial arrangement of organelles in relation to the locations of synapses.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, C.; Jackson, R.M. Reactive species mechanisms of cellular hypoxia-reoxygenation injury. Am. J. Physiol. Cell Physiol. 2002, 282, C227–C241. [Google Scholar] [CrossRef] [PubMed]
- Selivanov, V.A.; Zagubnaya, O.A.; Nartsissov, Y.R.; Cascante, M. Unveiling a key role of oxaloacetate-glutamate interaction in regulation of respiration and ROS generation in nonsynaptic brain mitochondria using a kinetic model. PLoS ONE 2021, 16, e0255164. [Google Scholar] [CrossRef]
- Selivanov, V.A.; Votyakova, T.V.; Zeak, J.A.; Trucco, M.; Roca, J.; Cascante, M. Bistability of mitochondrial respiration underlies paradoxical reactive oxygen species generation induced by anoxia. PLoS Comput. Biol. 2009, 5, e1000619. [Google Scholar] [CrossRef] [PubMed]
- Haworth, R.A.; Hunter, D.R. The Ca2+-induced membrane transition in mitochondria. II. Nature of the Ca2+ trigger site. Arch. Biochem. Biophys. 1979, 195, 460–467. [Google Scholar] [CrossRef]
- Hunter, D.R.; Haworth, R.A. The Ca2+-induced membrane transition in mitochondria. I. The protective mechanisms. Arch. Biochem. Biophys. 1979, 195, 453–459. [Google Scholar] [CrossRef] [PubMed]
- Hunter, D.R.; Haworth, R.A. The Ca2+-induced membrane transition in mitochondria. III. Transitional Ca2+ release. Arch. Biochem. Biophys. 1979, 195, 468–477. [Google Scholar] [CrossRef] [PubMed]
- Briston, T.; Selwood, D.L.; Szabadkai, G.; Duchen, M.R. Mitochondrial Permeability Transition: A Molecular Lesion with Multiple Drug Targets. Trends Pharmacol. Sci. 2019, 40, 50–70. [Google Scholar] [CrossRef]
- Morciano, G.; Giorgi, C.; Bonora, M.; Punzetti, S.; Pavasini, R.; Wieckowski, M.R.; Campo, G.; Pinton, P. Molecular identity of the mitochondrial permeability transition pore and its role in ischemia-reperfusion injury. J. Mol. Cell. Cardiol. 2015, 78, 142–153. [Google Scholar] [CrossRef]
- Zorov, D.B.; Juhaszova, M.; Sollott, S.J. Mitochondrial reactive oxygen species (ROS) and ROS-induced ROS release. Physiol. Rev. 2014, 94, 909–950. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Zhai, D.; Huang, Y. Study on the relationship between calcium-induced calcium release from mitochondria and PTP opening. Mol. Cell. Biochem. 2000, 213, 29–35. [Google Scholar] [CrossRef]
- Bernardi, P.; Vassanelli, S.; Veronese, P.; Colonna, R.; Szabó, I.; Zoratti, M. Modulation of the mitochondrial permeability transition pore: Effect of protons and divalent cations. J. Biol. Chem. 1992, 267, 2934–2939. [Google Scholar] [CrossRef] [PubMed]
- Zorov, D.B.; Filburn, C.R.; Klotz, L.O.; Zweier, J.L.; Sollott, S.J. Reactive oxygen species (ROS)-induced ROS release: A new phenomenon accompanying induction of the mitochondrial permeability transition in cardiac myocytes. J. Exp. Med. 2000, 192, 1001–1014. [Google Scholar] [CrossRef] [PubMed]
- Dynnik, V.V.; Grishina, E.V.; Fedotcheva, N.I. The mitochondrial NO-synthase/guanylate cyclase/protein kinase G signaling system underpins the dual effects of nitric oxide on mitochondrial respiration and opening of the permeability transition pore. FEBS J. 2020, 287, 1525–1536. [Google Scholar] [CrossRef] [PubMed]
- Selivanov, V.A.; Zagubnaya, O.A.; Foguet, C.; Nartsissov, Y.R.; Cascante, M. MITODYN: An Open Source Software for Quantitative Modeling of Mitochondrial and Cellular Energy Metabolic Flux Dynamics in Health and Disease. Methods Mol. Biol. 2022, 2399, 123–149. [Google Scholar] [CrossRef] [PubMed]
- Goldman, D.E. Potential, impedance, and rectification in membranes. J. Gen. Physiol. 1943, 27, 37–60. [Google Scholar] [CrossRef]
- Hodgkin, A.L.; Katz, B. The effect of sodium ions on the electrical activity of the giant axon of the squid. J. Physiol. 1949, 108, 37–77. [Google Scholar] [CrossRef]
- Bindel, D.; Friedman, M.; Govaerts, W.; Hughes, J.; Kuznetsov, Y.A. Numerical computation of bifurcations in large equilibrium systems in matlab. J. Comput. Appl. Math. 2014, 261, 232–248. [Google Scholar] [CrossRef]
- Bindel, D.; Govaerts, W.; Hughes, J.; Kuznetsov, Y.A.; Pekker, M.; Veldman, D. CL_MATCONTL 2015p0: Continuation Toolbox in MATLAB. 2015. Available online: https://uahedu/faculty/pekker (accessed on 6 May 2025).
- Nartsissov, Y.R. A novel algorithm of the digital nervous tissue phantom creation based on 3D Voronoi diagram application. J. Phys. Conf. Ser. 2021, 2090, 012009. [Google Scholar] [CrossRef]
- Nartsissov, Y.R.; Ivontsin, L.A. Mathematical Modelling of Physiological Effects Caused by a Glycine Receptors Post-Synaptic Density Spatial Polymorphism. Mathematics 2023, 11, 2499. [Google Scholar] [CrossRef]
- Zagubnaya, O.A.; Nartsissov, Y.R. An Algorithm for Creating a Synaptic Cleft Digital Phantom Suitable for Further Numerical Modeling. Algorithms 2024, 17, 451. [Google Scholar] [CrossRef]
- Alcaide, D.; Cacheux, J.; Bancaud, A.; Muramatsu, R.; Matsunaga, Y. Solute transport in the brain tissue: What are the key biophysical parameters tying in vivo and in vitro studies together? Biomater. Sci. 2023, 11, 3450–3460. [Google Scholar] [CrossRef] [PubMed]
- Lobysheva, N.V.; Selin, A.A.; Vangeli, I.M.; Byvshev, I.M.; Yaguzhinsky, L.S.; Nartsissov, Y.R. Glutamate induces H2O2 synthesis in nonsynaptic brain mitochondria. Free. Radic. Biol. Med. 2013, 65, 428–435. [Google Scholar] [CrossRef]
- Nartsissov, Y.R. A spatial classification applied to convectional reaction-diffusion boundary problems basing on a geometrical polymorphism of biological objects. J. Phys. Conf. Ser. 2024, 2701, 012084. [Google Scholar] [CrossRef]
- Rǎdulescu, A.R.; Todd, G.C.; Williams, C.L.; Bennink, B.A.; Lemus, A.A.; Chesbro, H.E.; Bourgeois, J.R.; Kopec, A.M.; Zuloaga, D.G.; Scimemi, A. Estimating the glutamate transporter surface density in distinct sub-cellular compartments of mouse hippocampal astrocytes. PLoS Comput. Biol. 2022, 18, e1009845. [Google Scholar] [CrossRef] [PubMed]
- Featherstone, D.E.; Shippy, S.A. Regulation of synaptic transmission by ambient extracellular glutamate. Neuroscientist 2008, 14, 171–181. [Google Scholar] [CrossRef] [PubMed]
- Hayashi, M.K. Structure-function relationship of transporters in the glutamate–glutamine cycle of the central nervous system. Int. J. Mol. Sci. 2018, 19, 1177. [Google Scholar] [CrossRef]
- Zhan, W.; Arifin, D.Y.; Lee, T.K.; Wang, C.H. Mathematical Modelling of Convection Enhanced Delivery of Carmustine and Paclitaxel for Brain Tumour Therapy. Pharm. Res. 2017, 34, 860–873. [Google Scholar] [CrossRef]
- Furness, D.N.; Dehnes, Y.; Akhtar, A.Q.; Rossi, D.J.; Hamann, M.; Grutle, N.J.; Gundersen, V.; Holmseth, S.; Lehre, K.P.; Ullensvang, K.; et al. A quantitative assessment of glutamate uptake into hippocampal synaptic terminals and astrocytes: New insights into a neuronal role for excitatory amino acid transporter 2 (EAAT2). Neuroscience 2008, 157, 80–94. [Google Scholar] [CrossRef] [PubMed]
- Mim, C.; Balani, P.; Rauen, T.; Grewer, C. The glutamate transporter subtypes EAAT4 and EAATs 1-3 transport glutamate with dramatically different kinetics and voltage dependence but share a common uptake mechanism. J. Gen. Physiol. 2005, 126, 571–589. [Google Scholar] [CrossRef]
- van Stroe-Biezen, S.A.M.; Everaerts, F.M.; Janssen, L.J.J.; Tacken, R.A. Diffusion coefficients of oxygen, hydrogen peroxide and glucose in a hydrogel. Anal. Chim. Acta 1993, 273, 553–560. [Google Scholar] [CrossRef]
- Sies, H.; Berndt, C.; Jones, D.P. Oxidative Stress. Annu. Rev. Biochem. 2017, 86, 715–748. [Google Scholar] [CrossRef] [PubMed]
- Starkov, A.A.; Andreyev, A.Y.; Zhang, S.F.; Starkova, N.N.; Korneeva, M.; Syromyatnikov, M.; Popov, V.N. Scavenging of H2O2 by mouse brain mitochondria. J. Bioenerg. Biomembr. 2014, 46, 471–477. [Google Scholar] [CrossRef]
- Mitchell, P. Possible molecular mechanisms of the protonmotive function of cytochrome systems. J. Theor. Biol. 1976, 62, 327–367. [Google Scholar] [CrossRef]
- Aklima, J.; Onojima, T.; Kimura, S.; Umiuchi, K.; Shibata, T.; Kuraoka, Y.; Oie, Y.; Suganuma, Y.; Ohta, Y. Effects of Matrix pH on Spontaneous Transient Depolarization and Reactive Oxygen Species Production in Mitochondria. Front. Cell Dev. Biol. 2021, 9, 692776. [Google Scholar] [CrossRef] [PubMed]
- Jasielec, J.J.; Filipek, R.; Dołowy, K.; Lewenstam, A. Precipitation of inorganic salts in mitochondrial matrix. Membranes 2020, 10, 81. [Google Scholar] [CrossRef]
- Belosludtsev, K.N.; Dubinin, M.V.; Belosludtseva, N.V.; Mironova, G.D. Mitochondrial Ca2+ Transport: Mechanisms, Molecular Structures, and Role in Cells. Biochemistry 2019, 84, 593–607. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Danbolt, N.C. Glutamate as a neurotransmitter in the healthy brain. J. Neural Transm. 2014, 121, 799–817. [Google Scholar] [CrossRef] [PubMed]
- Olivares-Bañuelos, T.N.; Chí-Castañeda, D.; Ortega, A. Glutamate transporters: Gene expression regulation and signaling properties. Neuropharmacology 2019, 161, 107550. [Google Scholar] [CrossRef]
- Massucci, F.A.; DiNuzzo, M.; Giove, F.; Maraviglia, B.; Castillo, I.P.; Marinari, E.; Martino, A.D. Energy metabolism and glutamate-glutamine cycle in the brain: A stoichiometric modeling perspective. BMC Syst. Biol. 2013, 7, 103. [Google Scholar] [CrossRef]
- Belov Kirdajova, D.; Kriska, J.; Tureckova, J.; Anderova, M. Ischemia-Triggered Glutamate Excitotoxicity From the Perspective of Glial Cells. Front. Cell. Neurosci. 2020, 14, 51. [Google Scholar] [CrossRef]
- Magi, S.; Piccirillo, S.; Amoroso, S.; Lariccia, V. Excitatory amino acid transporters (Eaats): Glutamate transport and beyond. Int. J. Mol. Sci. 2019, 20, 5674. [Google Scholar] [CrossRef] [PubMed]
- Mazat, J.P.; Ransac, S. The fate of glutamine in human metabolism. The interplay with glucose in proliferating cells. Metabolites 2019, 9, 81. [Google Scholar] [CrossRef] [PubMed]
- Bernardi, P.; Di Lisa, F.; Fogolari, F.; Lippe, G. From ATP to PTP and back: A dual function for The mitochondrial ATP synthase. Circ. Res. 2015, 116, 1850–1862. [Google Scholar] [CrossRef] [PubMed]
- Carafoli, E.; Gamble, R.L.; Lehninger, A.L. K+-dependent rebounds and oscillations in respiration-linked movements of Ca++ and H+ in rat liver mitochondria. Biochem. Biophys. Res. Commun. 1965, 21, 488–493. [Google Scholar] [CrossRef]
- Skvortsova, V.I.; Nartsissov, Y.R.; Bodykhov, M.K.; Kichuck, I.V.; Pryanikova, N.A.; Gudkova, Y.V.; Soldatenkova, T.D.; Kondrashova, T.T.; Kalinina, E.V.; Novichkova, M.D.; et al. Oxidative stress and oxygen status in ischemic stroke. Zhurnal Nevrol. i Psihiatr. Im. S.S. Korsakova 2007, 107, 30–36. [Google Scholar]
- Malik, A.R.; Willnow, T.E. Excitatory amino acid transporters in physiology and disorders of the central nervous system. Int. J. Mol. Sci. 2019, 20, 5671. [Google Scholar] [CrossRef]
- Valtcheva, S.; Venance, L. Control of long-term plasticity by glutamate transporters. Front. Synaptic Neurosci. 2019, 11, 10. [Google Scholar] [CrossRef]
- Zuo, L.; Wijegunawardana, D. Redox Role of ROS and Inflammation in Pulmonary Diseases. Adv. Exp. Med. Biol. 2021, 1304, 187–204. [Google Scholar] [CrossRef]
- Wu, Y.; Chen, M.; Jiang, J. Mitochondrial dysfunction in neurodegenerative diseases and drug targets via apoptotic signaling. Mitochondrion 2019, 49, 35–45. [Google Scholar] [CrossRef]
- de las Heras, N.; Giménez, V.M.M.; Ferder, L.; Manucha, W.; Lahera, V. Implications of oxidative stress and potential role of mitochondrial dysfunction in COVID-19: Therapeutic effects of vitamin D. Antioxidants 2020, 9, 897. [Google Scholar] [CrossRef]
- Singh, S.P.; Amar, S.; Gehlot, P.; Patra, S.K.; Kanwar, N.; Kanwal, A. Mitochondrial modulations, autophagy pathways shifts in viral infections: Consequences of COVID-19. Int. J. Mol. Sci. 2021, 22, 8180. [Google Scholar] [CrossRef] [PubMed]
- Hirst, J. Towards the molecular mechanism of respiratory complex I. Biochem. J. 2010, 425, 327–339. [Google Scholar] [CrossRef]
- Horsefield, R.; Iwata, S.; Byrne, B. Complex II from a structural perspective. Curr. Protein Pept. Sci. 2004, 5, 107–118. [Google Scholar] [CrossRef]
- Trumpower, B.L. A concerted, alternating sites mechanism of ubiquinol oxidation by the dimeric cytochrome bc1 complex. Biochim. et Biophys. Acta-Bioenerg. 2002, 1555, 166–173. [Google Scholar] [CrossRef] [PubMed]
- Guzy, R.D.; Hoyos, B.; Robin, E.; Chen, H.; Liu, L.; Mansfield, K.D.; Simon, M.C.; Hammerling, U.; Schumacker, P.T. Mitochondrial complex III is required for hypoxia-induced ROS production and cellular oxygen sensing. Cell Metab. 2005, 1, 401–408. [Google Scholar] [CrossRef]
- Dlasková, A.; Špaček, T.; Škobisová, E.; Šantorová, J.; Ježek, P. Certain aspects of uncoupling due to mitochondrial uncoupling proteins in vitro and in vivo. Biochim. et Biophys. Acta-Bioenerg. 2006, 1757, 467–473. [Google Scholar] [CrossRef]
- Kuba, K. Ca2+-induced Ca2+ Release in Neurones. Jpn. J. Physiol. 1994, 44, 613–650. [Google Scholar] [CrossRef] [PubMed]
- Andersen, J.V.; Markussen, K.H.; Jakobsen, E.; Schousboe, A.; Waagepetersen, H.S.; Rosenberg, P.A.; Aldana, B.I. Glutamate metabolism and recycling at the excitatory synapse in health and neurodegeneration. Neuropharmacology 2021, 196, 108719. [Google Scholar] [CrossRef]
- Chiu, D.N.; Jahr, C.E. Extracellular Glutamate in the Nucleus Accumbens Is Nanomolar in Both Synaptic and Non-synaptic Compartments. Cell Rep. 2017, 18, 2576–2583. [Google Scholar] [CrossRef]
- Danbolt, N.C. Glutamate uptake. Prog. Neurobiol. 2001, 65, 1–105. [Google Scholar] [CrossRef]
- Grewer, C.; Rauen, T. Electrogenic glutamate transporters in the CNS: Molecular mechanism, pre-steady-state kinetics, and their impact on synaptic signaling. J. Membr. Biol. 2005, 203, 1–20. [Google Scholar] [CrossRef] [PubMed]
- McKenna, M.C.; Stridh, M.H.; McNair, L.F.; Sonnewald, U.; Waagepetersen, H.S.; Schousboe, A. Glutamate oxidation in astrocytes: Roles of glutamate dehydrogenase and aminotransferases. J. Neurosci. Res. 2016, 94, 1561–1571. [Google Scholar] [CrossRef]
- Selivanov, V.A.; Zeak, J.A.; Roca, J.; Cascante, M.; Trucco, M.; Votyakova, T.V. The role of external and matrix pH in mitochondrial reactive oxygen species generation. J. Biol. Chem. 2008, 283, 29292–29300. [Google Scholar] [CrossRef] [PubMed]
- Todd, A.C.; Hardingham, G.E. The regulation of astrocytic glutamate transporters in health and neurodegenerative diseases. Int. J. Mol. Sci. 2020, 21, 9607. [Google Scholar] [CrossRef]
- Torres-Salazar, D.; Gonzalez-Suarez, A.D.M.; Amara, S.G. Transport and channel functions in EAATs: The missing link. Channels 2016, 10, 86–87. [Google Scholar] [CrossRef]
- Verdon, G.; Boudker, O. Crystal structure of an asymmetric trimer of a bacterial glutamate transporter homolog. Nat. Struct. Mol. Biol. 2012, 19, 355–357. [Google Scholar] [CrossRef] [PubMed]





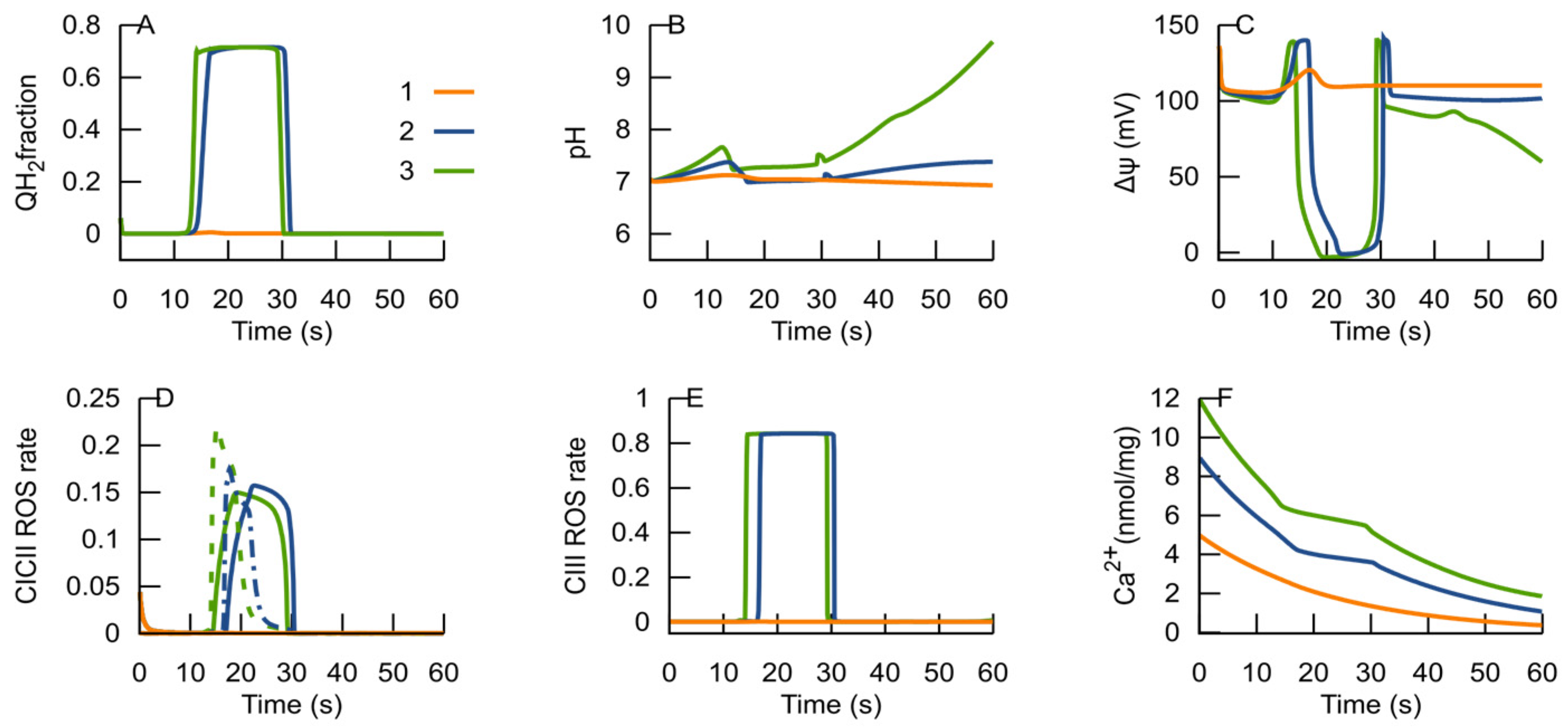
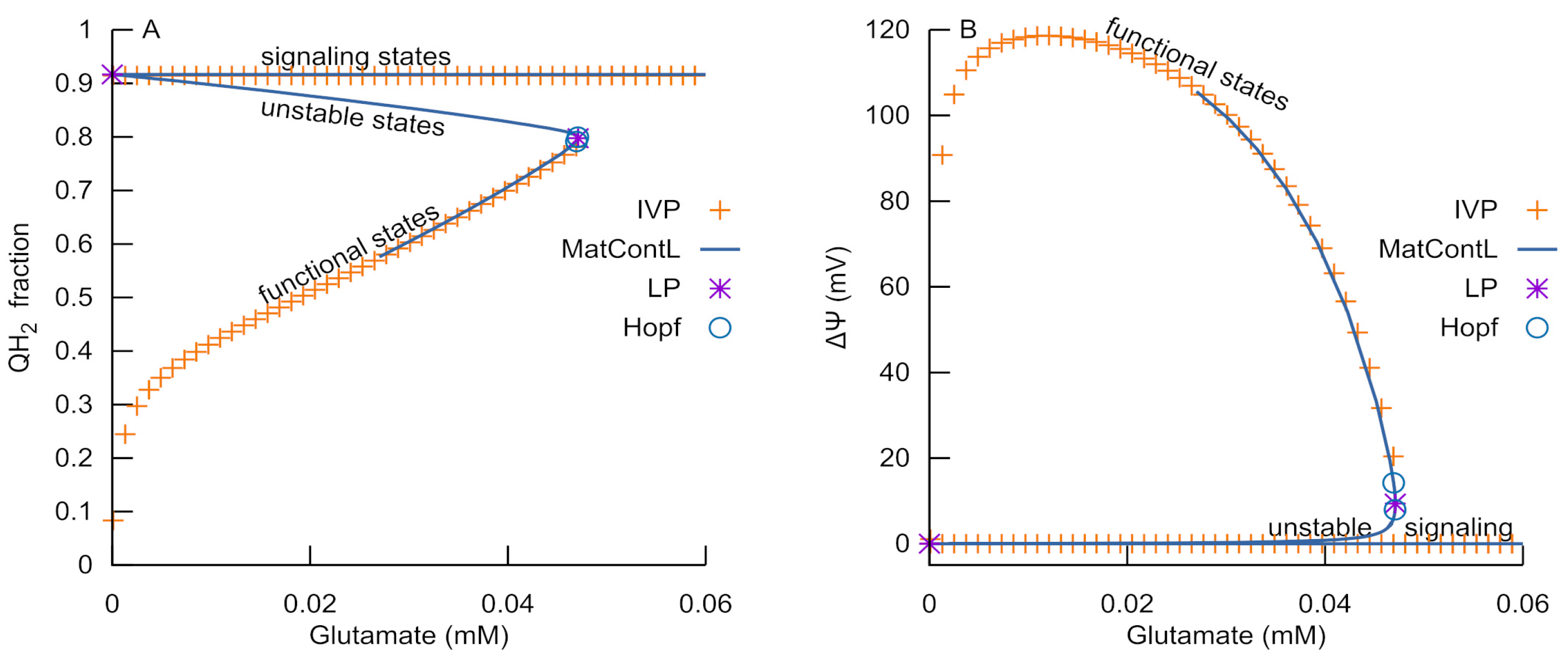

| MPT | ROS-Producing State of the RC |
|---|---|
| Induced by high ROS concentration | Generate ROS at a high rate |
| Facilitated at high pH values | Facilitated at high pH |
| Induced by Ca2+ | Induced by Ca2+ |
| Δψ peak precedes MPT | Δψ peak precedes the transition to ROS-producing states |
| Respiration is inhibited | Respiration is inhibited |
| Can be triggered periodically | Can be triggered periodically |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zagubnaya, O.A.; Selivanov, V.A.; Pekker, M.; Jonkhout, C.J.H.; Nartsissov, Y.R.; Cascante, M. Mathematical Modeling Unveils a New Role for Transient Mitochondrial Permeability Transition in ROS Damage Prevention. Cells 2025, 14, 1006. https://doi.org/10.3390/cells14131006
Zagubnaya OA, Selivanov VA, Pekker M, Jonkhout CJH, Nartsissov YR, Cascante M. Mathematical Modeling Unveils a New Role for Transient Mitochondrial Permeability Transition in ROS Damage Prevention. Cells. 2025; 14(13):1006. https://doi.org/10.3390/cells14131006
Chicago/Turabian StyleZagubnaya, Olga A., Vitaly A. Selivanov, Mark Pekker, Carel J. H. Jonkhout, Yaroslav R. Nartsissov, and Marta Cascante. 2025. "Mathematical Modeling Unveils a New Role for Transient Mitochondrial Permeability Transition in ROS Damage Prevention" Cells 14, no. 13: 1006. https://doi.org/10.3390/cells14131006
APA StyleZagubnaya, O. A., Selivanov, V. A., Pekker, M., Jonkhout, C. J. H., Nartsissov, Y. R., & Cascante, M. (2025). Mathematical Modeling Unveils a New Role for Transient Mitochondrial Permeability Transition in ROS Damage Prevention. Cells, 14(13), 1006. https://doi.org/10.3390/cells14131006









