Dynamic Carbohydrate Supply and Demand Model of Vegetative Growth: Response to Temperature, Light, Carbon Dioxide, and Day Length
Abstract
:1. Introduction
1.1. Supply and Demand
1.2. Carbon Starvation
1.3. Photosynthesis Inhibition
1.4. Starch-Less Mutants
1.5. Seedlings Compared to Larger Plants
1.6. Objectives
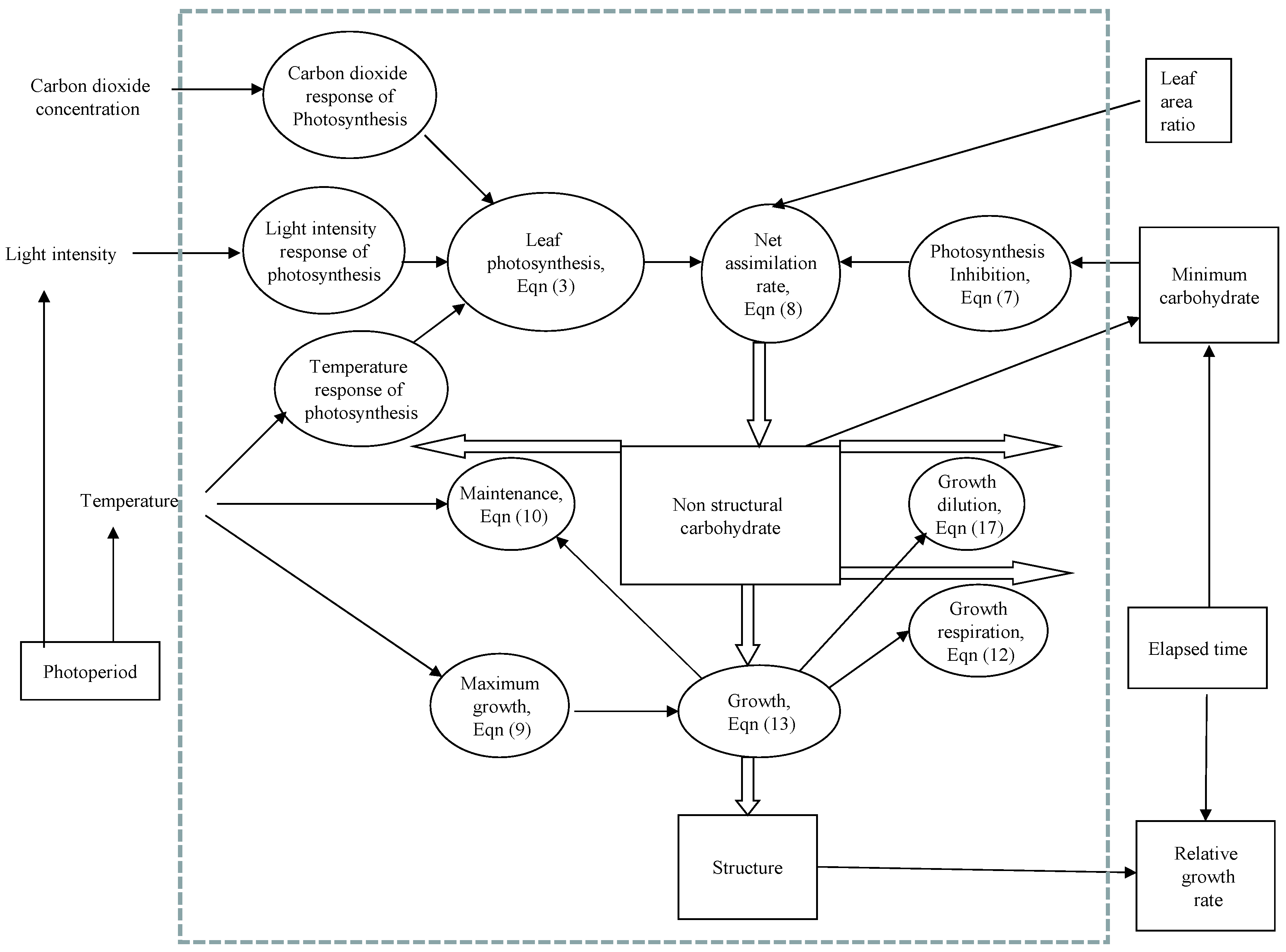
2. Model Development
3. Parameter Estimation
4. Results
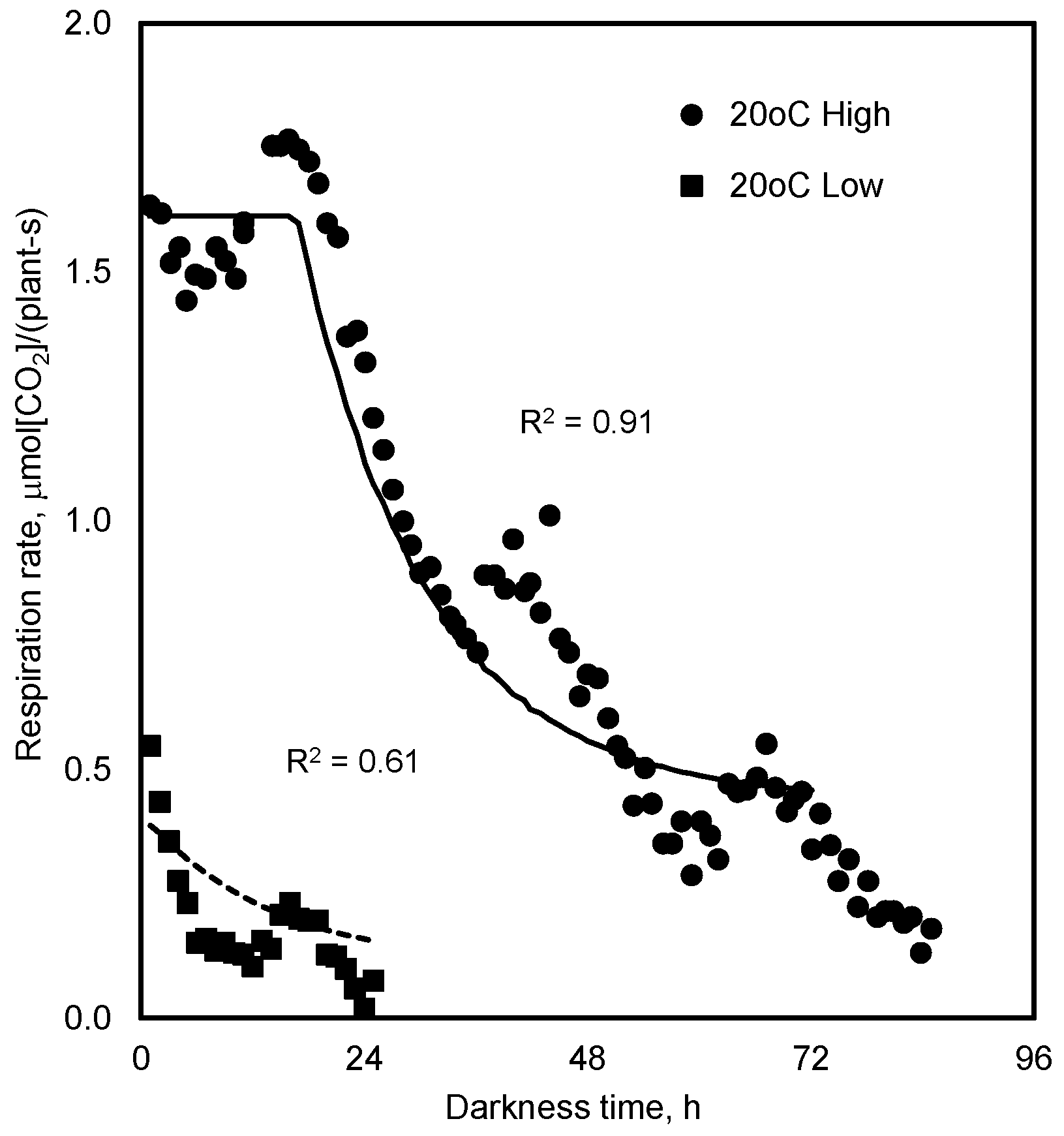
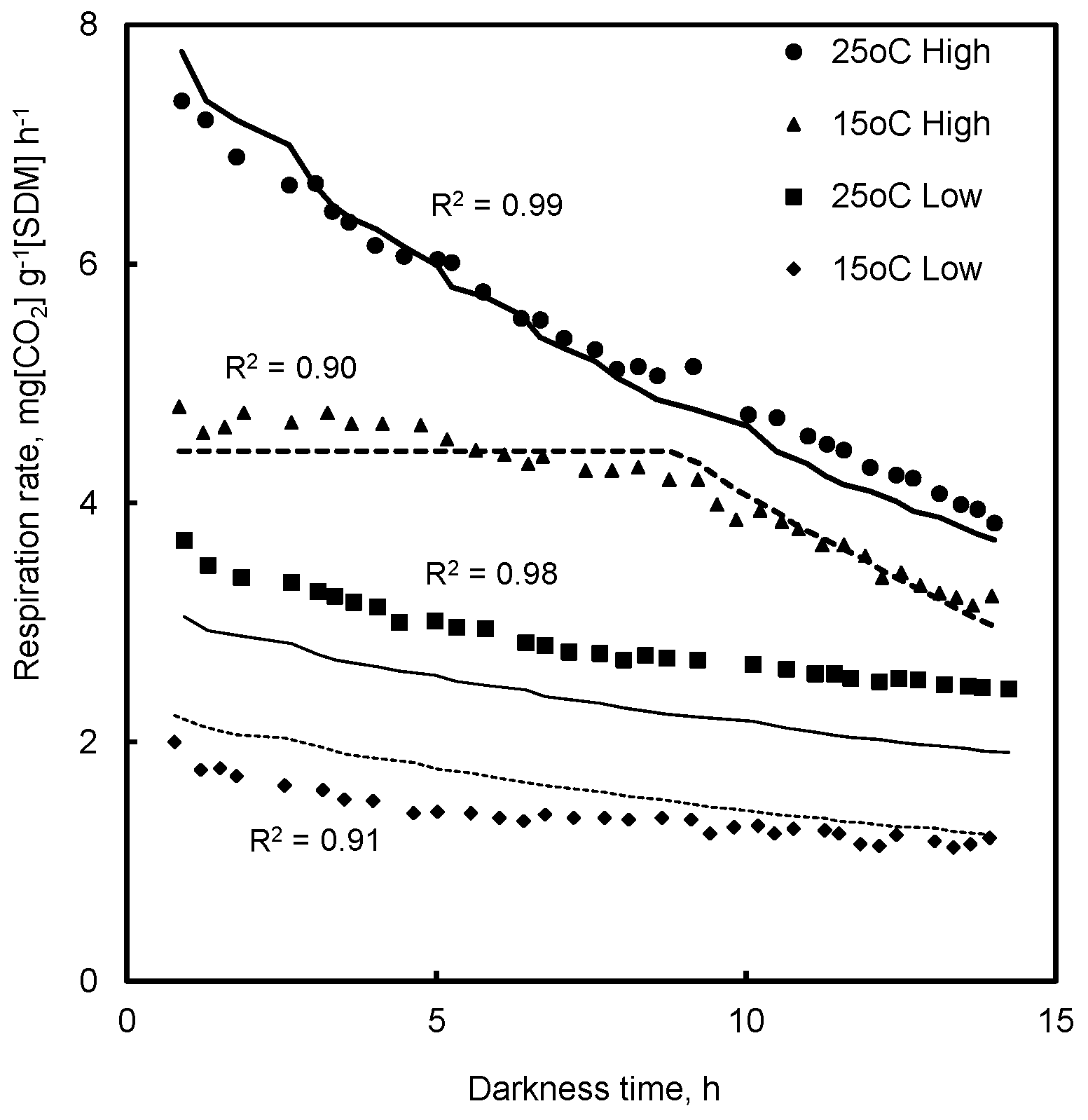
4.1. Respiration in Prolonged Darkness
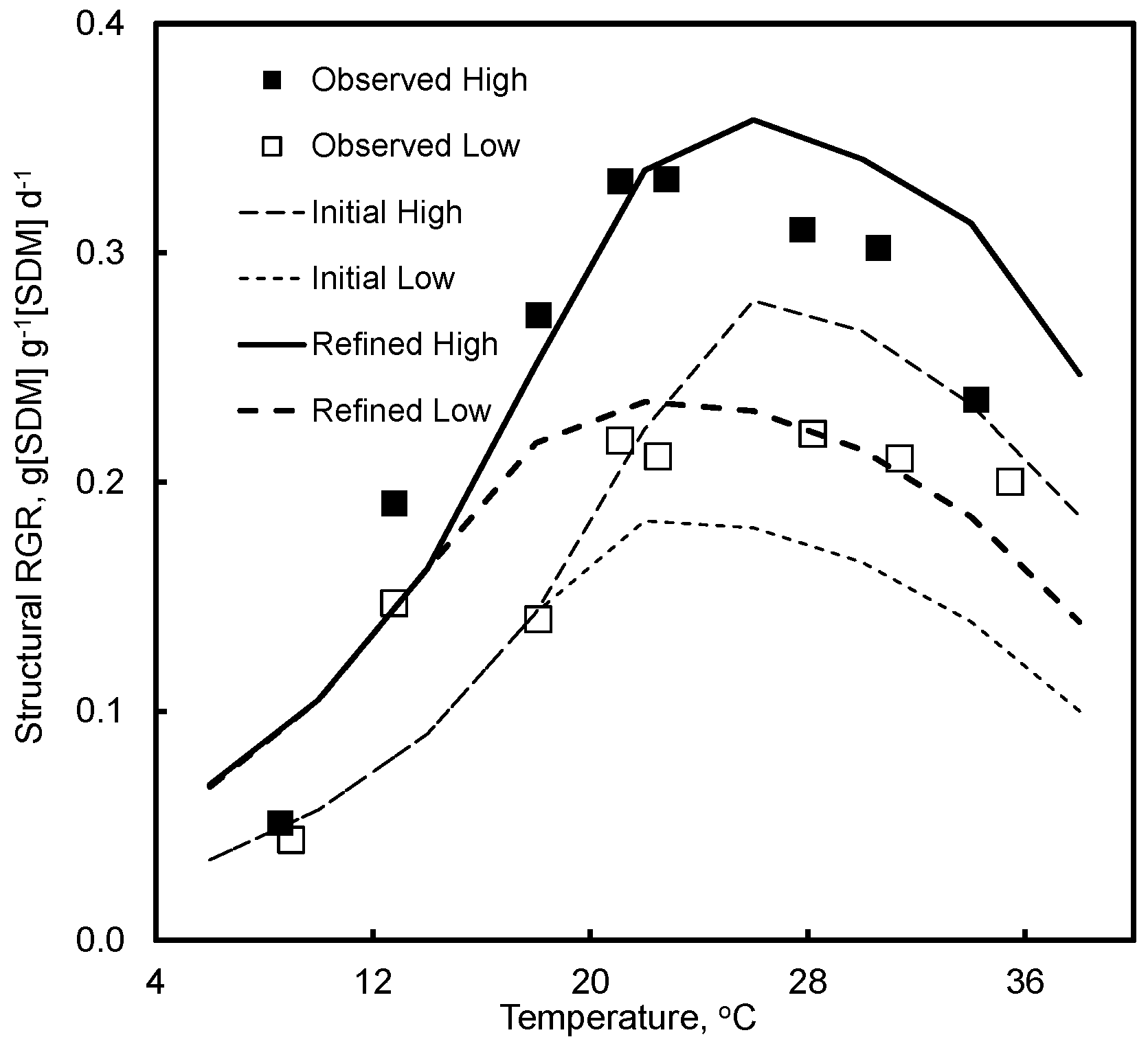
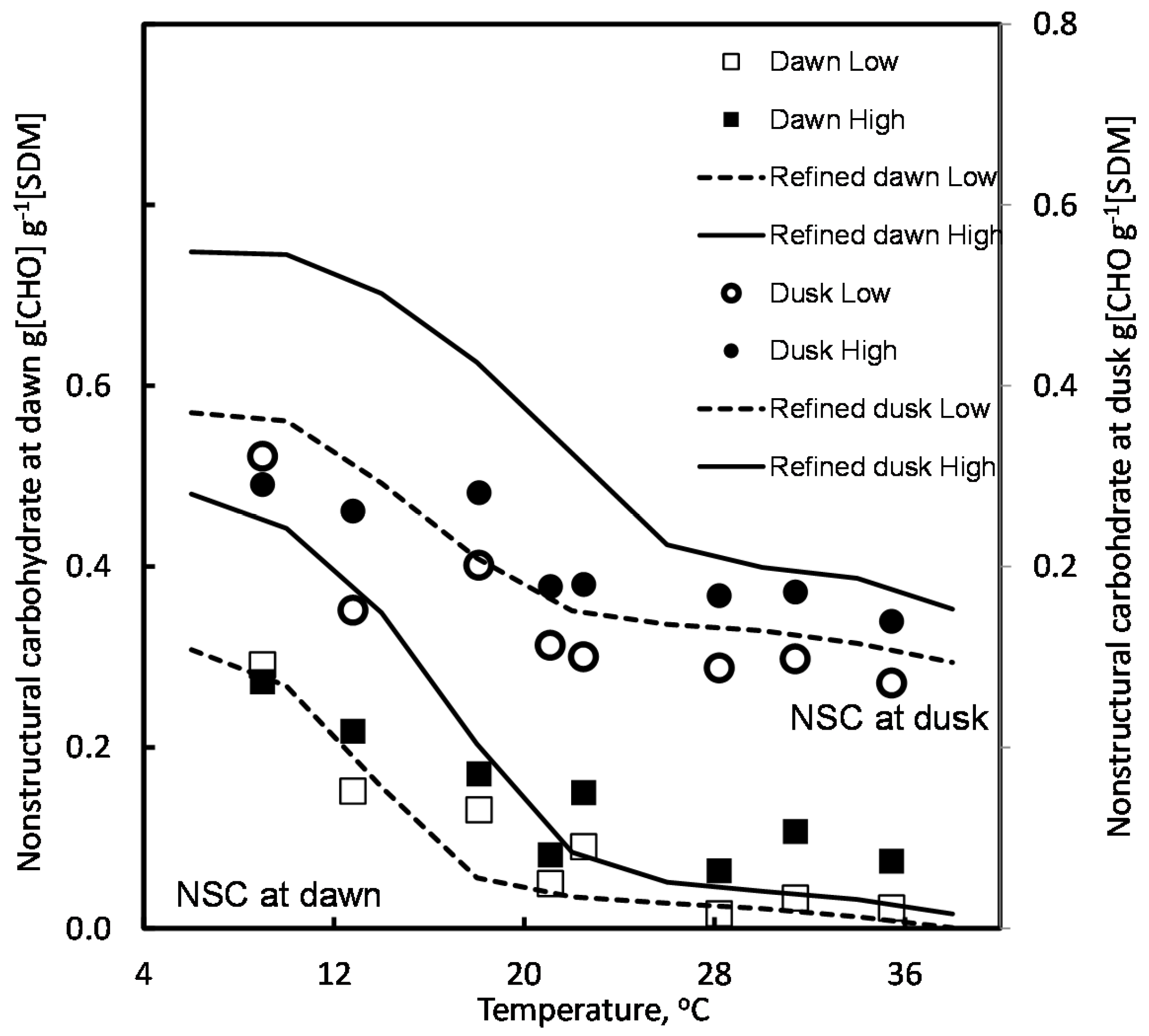
4.2. Effect of Temperature and Light
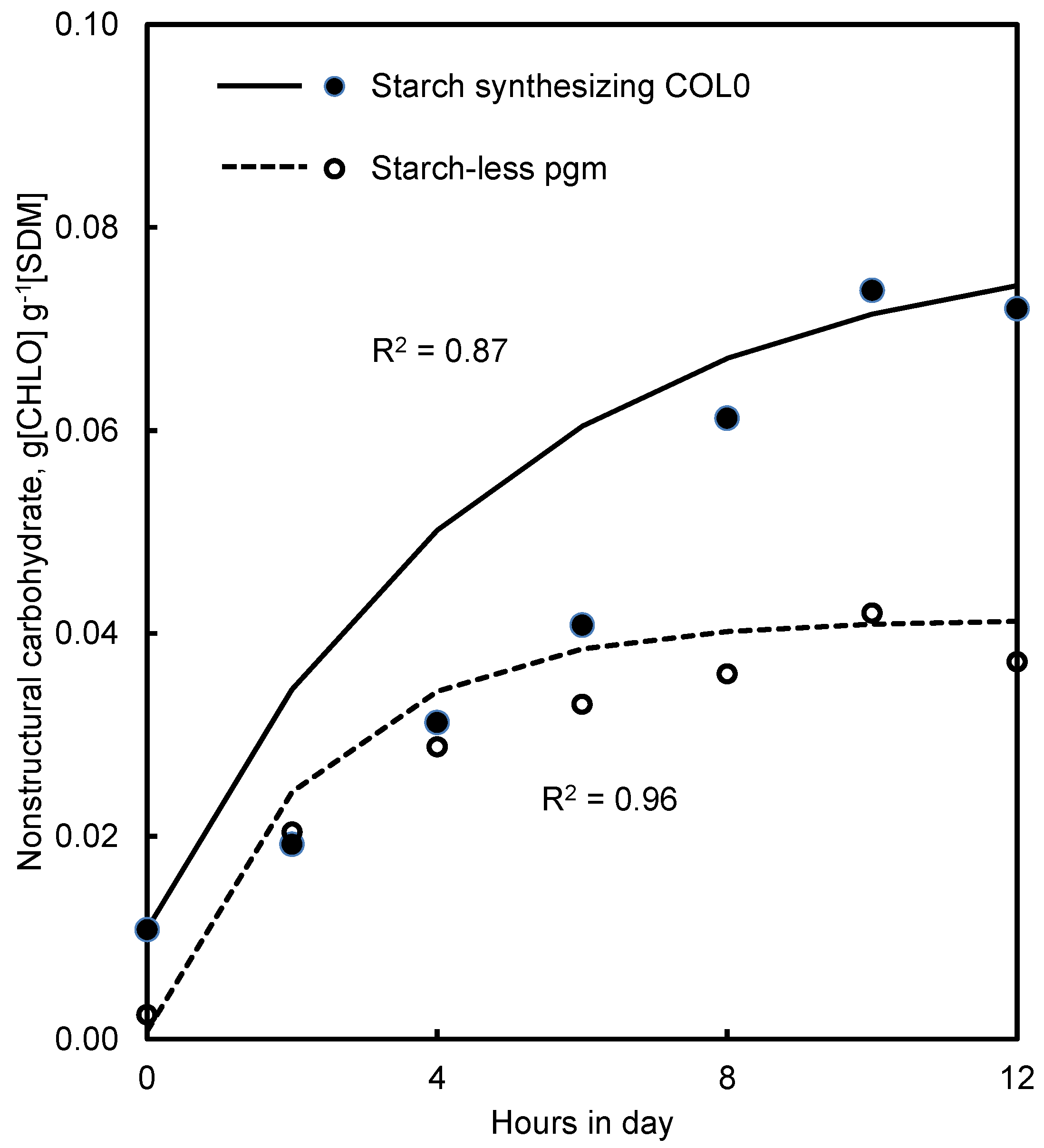
4.3. Starch and Starch-Less Mutants of Arabidopsis
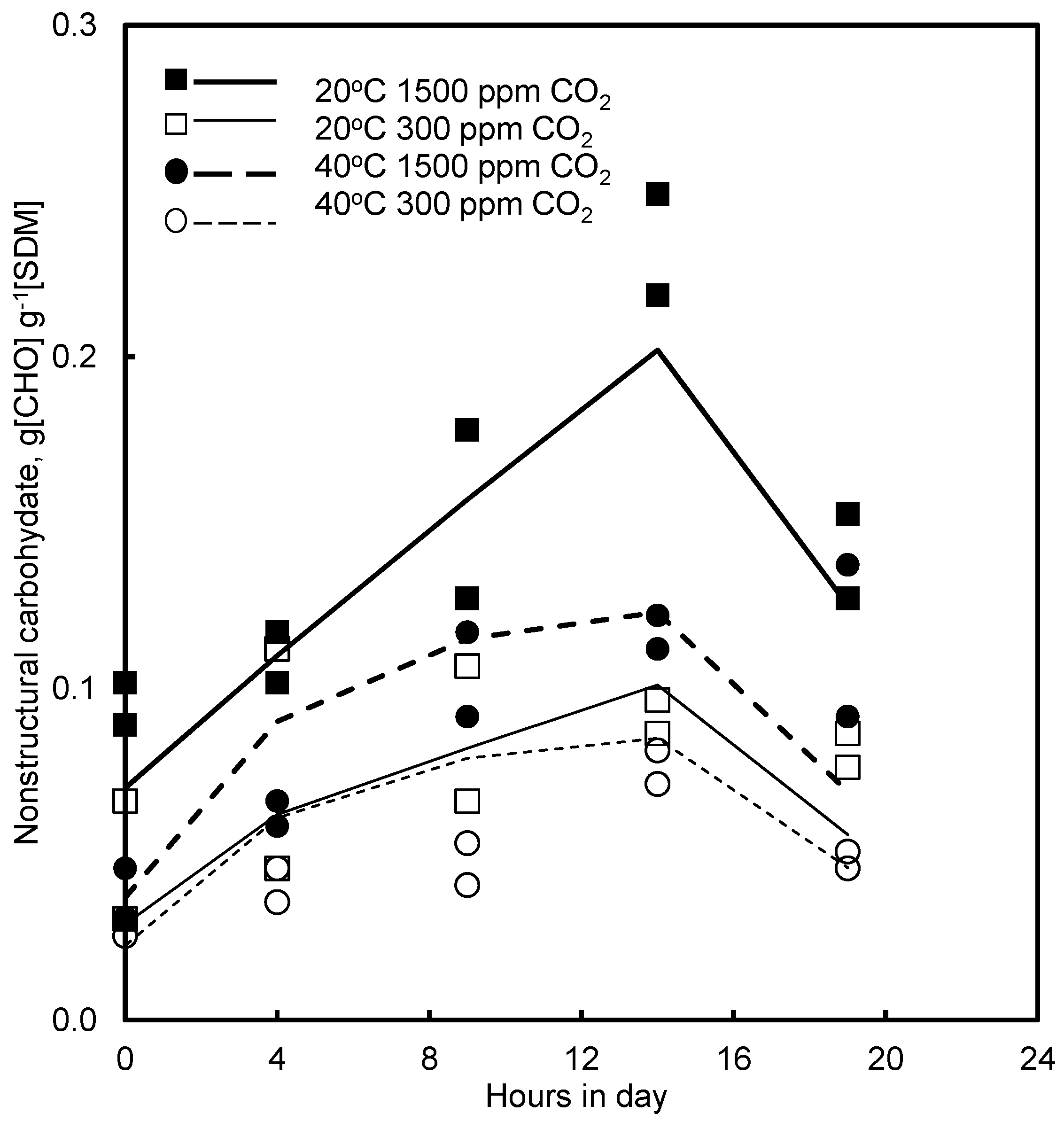
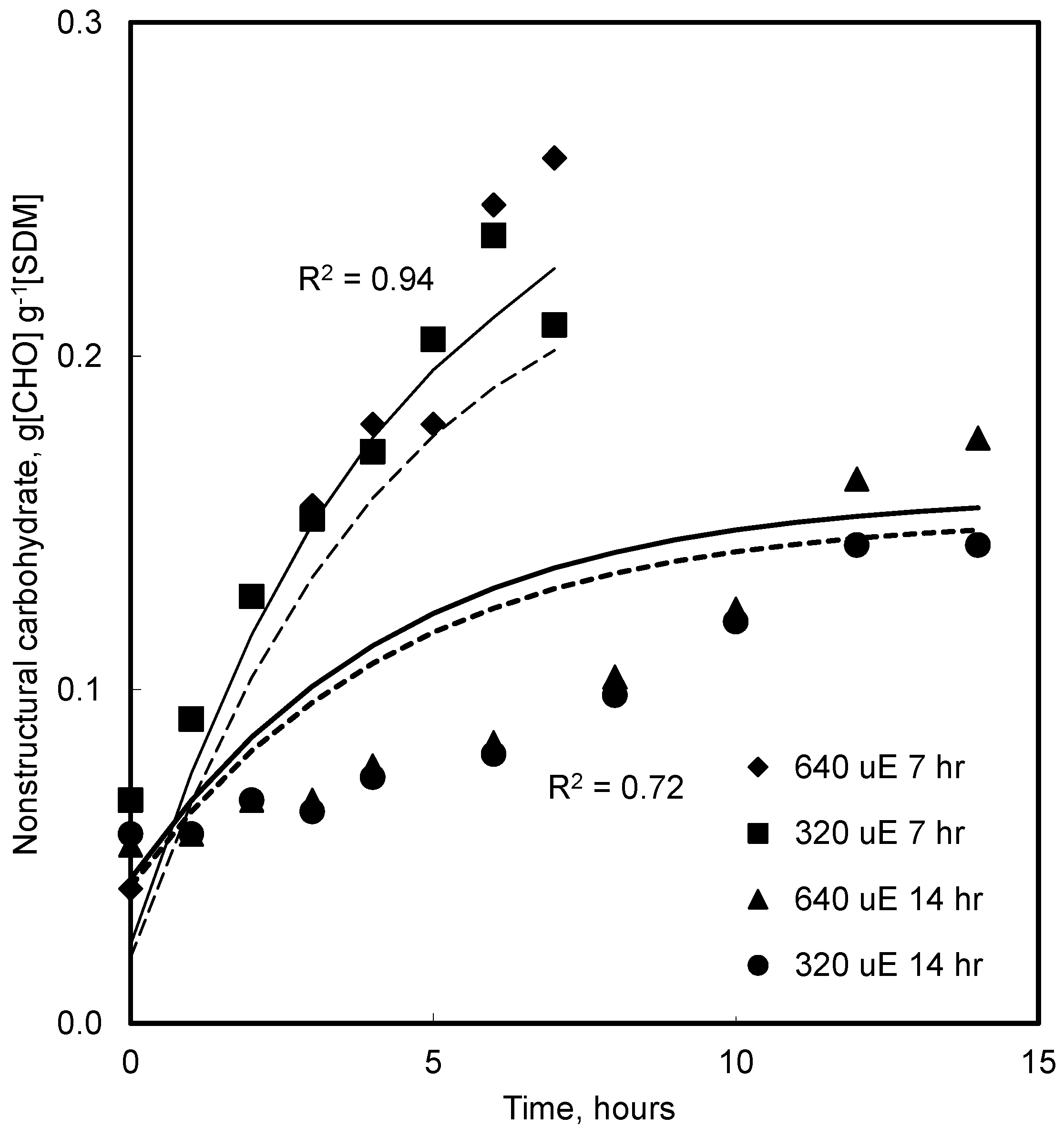
4.4. Effect of CO2 and Photoperiod
5. Discussion
5.1. Temperature Effects on Respiration
5.2. Dependence of Photosynthesis
5.3. Values for n0
5.4. Starch and Starch-Less Plants
5.5. CO2 and Growth
5.6. NSC and Growth
6. Summary
7. Experimental Methods
7.1. Respiration in Prolonged Darkness
7.2. Effect of Temperature and Light
7.3. Starch and Starch-Less Mutants of Arabidopsis
7.4. Effect of CO2 and Photoperiod
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| C | NSC content | g[CHO] m−2[ground], g[CHO] g−1[SDM] |
| Rate of change of | g[CHO] m−2[ground] h−1, g[CHO] g−1[SDM] h−1 | |
| Ca | Carbon dioxide concentration | μmol[CO2] mol−1[air] |
| Cd | Minimum NSC content | g[CHO] g−1[SDM] |
| Response of photosynthesis to light | − | |
| Growth respiration rate | g[CHO] m−2[ground] h−1, g[CHO] g−1[SDM] h−1 | |
| Response of photosynthesis to temperature | − | |
| Photosynthesis inhibition rate | g[CHO] m−2[ground] h−1, g[CHO] g−1[SDM] h−1 | |
| Response of photosynthesis to carbon dioxide concentration | − | |
| Light flux | μmol[PAR] m−2[leaf] s−1 | |
| Maintenance respiration rate | g[CHO] m−2[ground] h−1, g[CHO] g−1[SDM] h−1 | |
| Maintenance respiration at 0 °C | g[CHO] m−2[ground] h−1, g[CHO] g−1[SDM] h−1 | |
| Maximum rate of metabolism | g[CHO] m−2[ground] h−1, g[CHO] g−1[SDM] h−1 | |
| Rate of metabolism at 0 °C | g[CHO] m−2[ground] h−1, g[CHO] g−1[SDM] h−1 | |
| Maximum rate of photosynthesis | g[CHO] m−2[leaf] h−1 | |
| Specific photosynthesis rate | g[CHO] m−2[leaf] h−1 | |
| Potential gross photosynthesis rate | g[CHO] m−2[ground] h−1, g[CHO] g−1[SDM] h−1 | |
| Temperature quotient: ratio of reaction rates at 10 °C difference | − | |
| Structural dry matter content | g[SDM] m−2[ground] | |
| Structural growth rate | g[SDM] m−2[ground] h−1, g[SDM] h−1 | |
| Temperature | °C | |
| Time | h | |
| αD | Response of growth to NSC in the dark | h−1 |
| αL | Response of growth to NSC in the light | h−1 |
| β | Factor relating photosynthesis inhibition to NSC | g[SDM] g−1[CHO] |
| γ | Light intensity at half maximum photosynthesis | μmol[PAR] m−2[leaf] s−1 |
| δ | CO2 concentration at half maximum photosynthesis | μmol[CO2] mol−1[air] |
| ε | Growth conversion efficiency | – |
| ζ | Exponential temperature coefficient for maximum metabolism | °C−1 |
| κ | Sensitivity of photosynthesis to temperature | °C−2 |
| τ | Threshold temperature for photosynthesis | °C |
| Λ | Total leaf area index | m2[leaf] m−2[ground] |
| λ | Ratio of leaf area to structural dry matter | m2[leaf] kg−1[SDM] |
| θ | Exponential temperature coefficient for maintenance respiration | °C−1 |
References
- Alagarswamy, G.; Boote, K.J.; Allen, L.H.; Jones, J.W. Evaluating the CROPGRO-Soybean model ability to simulate photosynthesis response to carbon dioxide levels. Agron. J. 2006, 98, 34–42. [Google Scholar] [CrossRef]
- Kim, S.-H.; Yang, Y.; Timlin, D.L.; Fleischer, D.H.; Dathe, A.; Reddy, R.R.; Staver, K. Modeling temperature responses and biomass in Maize with MAIZSIM. Agron. J. 2012, 104, 1523–1537. [Google Scholar] [CrossRef]
- Timlin, D.; Rahman, S.M.L.; Baker, J.; Reddy, V.R.; Fleisher, D.; Quebedeaux, B. Whole plant photosynthesis, development, and carbon partitioning in potato as a function of temperature. Agron. J. 2006, 98, 1195–1203. [Google Scholar] [CrossRef]
- Verdoodt, A.; van Ranst, E.; Ye, L. Daily simulation of potential dry matter production of annual field crops in tropical environments. Agron. J. 2004, 96, 1739–1753. [Google Scholar] [CrossRef]
- Scaife, M.A. The early relative growth rates of six lettuce cultivars as affected by temperature. Ann. Appl. Biol. 1973, 74, 119–128. [Google Scholar] [CrossRef]
- Kemp, D.R.; Blacklow, W.M. Diurnal extension rates of wheat leaves in relation to temperatures and carbohydrate concentrations of the extension zone. J. Exp. Bot. 1980, 31, 821–828. [Google Scholar] [CrossRef]
- Yamori, W.; Noguchi, K.; Hikosaka, K.; Terashima, I. Phenotypic plasticity in photosynthetic temperature acclimation among crop species with different cold tolerances. Plant Physiol. 2010, 152, 388–399. [Google Scholar] [CrossRef] [PubMed]
- Farquhar, G.D.; von Caemmerer, S.; Berry, J.A. A biochemical model of photosynthetic CO2 assimilation in leaves of C3 species. Planta 1980, 149, 78–90. [Google Scholar] [CrossRef] [PubMed]
- Gent, M.P.N.; Seginer, I. A carbohydrate supply and demand model of vegetative growth: Response to temperature and light. Plant Cell Environ. 2012, 35, 1274–1286. [Google Scholar] [CrossRef] [PubMed]
- Seginer, I.; Gent, M.P.N. Short and long term vegetative growth response to temperature, interpreted by the dynamics of a carbohydrate storage. Sci. Hort. 2014, 171, 14–26. [Google Scholar] [CrossRef]
- Breeze, V.; Elston, J. Some effects of temperature and substrate content upon respiration and the carbon balance of field beans (Vicia faba L.). Ann. Bot. 1978, 42, 863–876. [Google Scholar] [CrossRef]
- Baysdorfer, C.; Warmbrodt, R.D.; VanDerWoude, W.J. Mechanisms of starvation tolerance in pearl millet. Plant Physiol. 1988, 88, 1381–1385. [Google Scholar] [CrossRef] [PubMed]
- Brouquisse, R.; Gaudillère, J.P.; Raymond, P. Induction of a carbon-starvation-related proteolysis in whole maize plants submitted to light/dark cycles and to extended darkness. Plant Physiol. 1998, 117, 1281–1291. [Google Scholar] [CrossRef] [PubMed]
- Gary, C.; Baldet, P.; Bertin, N.; Devaux, C.; Tchamitchian, M. Time-course of tomato whole-plant respiration and fruit and stem growth during prolonged darkness in relation to carbohydrate reserves. Ann. Bot. 2003, 91, 1–10. [Google Scholar] [CrossRef]
- Devaux, C.; Baldet, P.; Joubes, J.; Dieuaide-Noubhani, M.; Just, D.; Chevalier, C.; Raymond, P. Physiological, biochemical and molecular analysis of sugar-starvation responses in tomato roots. J. Exp. Bot. 2003, 54, 1143–1151. [Google Scholar] [CrossRef] [PubMed]
- Moser, L.E.; Volenec, J.J.; Nelson, C.J. Respiration, carbohydrate content, and leaf growth of tall fescue. Crop Sci. 1982, 22, 781–786. [Google Scholar] [CrossRef]
- Hendershot, K.L.; Volenec, J.J. Shoot growth, dark respiration, and nonstructural carbohydrates of contrasting alfalfa genotypes. Crop Sci. 1989, 29, 1271–1275. [Google Scholar] [CrossRef]
- Acock, B.; Acock, M.C.; Pasternak, D. Interactions of CO2 enrichment and temperature on carbohydrate production and accumulation in muskmelon leaves. J. Am. Soc. Hort. Sci. 1990, 115, 525–529. [Google Scholar]
- Fondy, B.R.; Geiger, D.R.; Servaites, J.C. Photosynthesis, carbohydrate metabolism, and export in Beta vulgaris L. and Phaseolus vulgaris L. during square and sinusoidal light regimes. Plant Physiol. 1989, 89, 396–402. [Google Scholar] [CrossRef] [PubMed]
- Krapp, A.; Stitt, M. An evaluation of direct and indirect mechanisms for the “sink-regulation” of photosynthesis in spinach: Changes in gas exchange, carbohydrates, metabolites, enzyme activities and steady-state transcript levels after cold-girdling source leaves. Planta 1995, 195, 313–323. [Google Scholar] [CrossRef]
- Ayari, O.; Dorais, M.; Gosselin, A. Daily variations in photosynthetic efficiency of greenhouse tomato plants during winter and spring. J. Am. Soc. Hort. Sci. 2000, 125, 235–241. [Google Scholar]
- Geiger, D.R.; Servaites, J.C. Diurnal regulation of photosynthetic carbon metabolism in C3 plants. Annu. Rev. Plant Biol. 1994, 45, 235–256. [Google Scholar] [CrossRef]
- Geiger, D.R.; Servaites, J.C.; Fuchs, M.A. Role of starch in carbon translocation and partitioning at the plant level. Aust. J. Plant Physiol. 2000, 27, 571–582. [Google Scholar] [CrossRef]
- Gerhardt, R.; Stitt, M.; Heldt, H.W. Subcellular metabolite levels in spinach leaves: Regulation of sucrose synthesis during diurnal alterations in photosynthetic partitioning. Plant Physiol. 1987, 83, 399–407. [Google Scholar] [CrossRef] [PubMed]
- Matt, P.; Schurr, U.; Krapp, A.; Stitt, M. Growth of tobacco in short day conditions leads to high starch, low sugars, altered diurnal changes of the Nia transcript and low nitrate reductase activity, and an inhibition of amino acid synthesis. Planta 1998, 207, 27–41. [Google Scholar] [CrossRef] [PubMed]
- Zeeman, S.C.; Northrop, F.; Smith, A.M.; Rees, T. A starch-accumulating mutant of Arabidopsis thaliana deficient in a chloroplastic starch-hydrolysing enzyme. Plant J. 1998, 153, 357–365. [Google Scholar] [CrossRef]
- Chatterton, N.J.; Silvius, J.E. Photosynthate partitioning into starch in soybean leaves: Irradiance level and daily photosynthetic period duration effects. Plant Physiol. 1981, 67, 257–260. [Google Scholar] [CrossRef] [PubMed]
- Caspar, T.; Huber, S.C.; Somerville, C.R. Alterations in growth, photosynthesis and respiration in a starch deficient mutant of Arabidopsis thaliana (L.) Heynh deficient in chloroplast phosphoglucomutase. Plant Physiol. 1985, 79, 11–17. [Google Scholar] [CrossRef] [PubMed]
- Lin, T.P.; Caspar, T.; Somerville, C.R.; Preiss, J. A starch deficient mutant of Arabidopsis thaliana with low ADP glucose pyrophosphorylase activity lacks one of the 2 subunits of the enzyme. Plant Physiol. 1988, 88, 1175–1181. [Google Scholar] [CrossRef] [PubMed]
- Gent, M.P.N. Carbohydrate level and growth of tomato plants. II. The effect of irradiance and temperature. Plant Physiol. 1986, 81, 1075–1079. [Google Scholar] [CrossRef] [PubMed]
- Gibon, Y.; Blasing, O.E.; Palacios-Rios, N.; Pankovic, D.; Hendriks, J.H.M.; Fisahn, H.; Hohne, M.; Genther, M.; Stitt, M. Adjustment of diurnal starch turnover to short days: Depletion of sugar during the night leads to a temporary inhibition of carbohydrate utilization, accumulation of sugars and post-translational activation of ADP-glucose pyrophosphorylase in the following light period. Plant J. 2004, 39, 847–862. [Google Scholar] [PubMed]
- Penning de Vries, F.W.T.; Witlage, J.M.; Kremer, D. Rates of respiration and structural growth in young wheat, ryegrass, and maize plants in relation to temperature, water stress, and sugar concentration. Ann. Bot. 1979, 44, 595–609. [Google Scholar] [CrossRef]
- Gent, M.P.N. Composition of hydroponic lettuce: Effect of time of day, plant size, and season. J. Sci. Food Agric. 2012, 92, 542–550. [Google Scholar] [CrossRef] [PubMed]
- Van Iersel, M.W. Carbon use efficiency depends on growth respiration, maintenance respiration, and relative growth rate. A case study with lettuce. Plant Cell Environ. 2003, 26, 1441–1449. [Google Scholar] [CrossRef]
- Thimm, O.; Blaesing, O.E.; Gibon, Y.; Nagel, A.; Meyer, S.; Krueger, P.; Selbig, J.; Mueller, L.A.; Rhee, S.Y.; Stitt, M. Mapman: A user-driven tool to display genomics data sets onto diagrams of metabolic pathways and other biological processes. Plant J. 2004, 37, 914–939. [Google Scholar] [CrossRef] [PubMed]
| Reference | [14] | [11] | [9] | [30] | [31] | [18] | [27] | ||
|---|---|---|---|---|---|---|---|---|---|
| Parameter | Units | Symbol | Tomato | Bean | Seedling Tomato | Seedling Tomato | Arabidopsis | Melon | Soybean |
| Maximum photosynthesis | µmol CO2 m−2 s−1 | Pmax | 36 | 45 | 45 | 45 | 45 | ||
| Half maximum light | µmol[PAR] m−2 s−1 | γ | 309 | 309 | 309 | 309 | 309 | ||
| Half maximum CO2 | µmol mol−1 | δ | 225 | 225 | 225 | 225 | 225 | ||
| Temperature optimum for PS | °C | τ | 24 | 24 | 24 | 27 | 27 | ||
| Decrease per °C from τ | °C−2 | κ | 0.0013 | 0.0013 | 0.0013 | 0.0013 | 0.0013 | ||
| PS inhibition factor | g[SDM] g−1 [CHO] | β | 0.9 | 1.25 | 1.25 | 1.25 | 1.25 | ||
| Total respiration at 0 °C | mg[CHO] g−1 [SDM] h−1 | n0 | 0.025 | 0.05 | 0.03 | 0.035 | 0.035 | 0.025 | 0.035 |
| Exponential response of total | °C−1 | ζ | 0.11 | 0.11 | 0.11 | 0.11 | 0.11 | 0.11 | 0.11 |
| Maintenance respiration at 0 °C | mg[CHO] g−1 [SDM] h−1 | m0 | 0.007 | 0.007 | 0.007 | 0.007 | 0.007 | 0.007 | 0.007 |
| Exponential response of maintenance | °C−1 | θ | 0.0693 | 0.0693 | 0.0693 | 0.0693 | 0.0693 | 0.0693 | 0.0693 |
| Conversion efficiency | dmnl | ε | 0.75 | 0.75 | 0.75 | 0.75 | 0.75 | 0.75 | 0.75 |
| Growth in dark | h−1 | αD | 0.07 | 0.07 | 0.07 | 0.07 | 0.07 | 0.07 | 0.07 |
| Growth in light | h−1 | αL | 0.07 | 0.14 | 0.14 * 0.28 | 0.14 | 0.14 |
| Non-Structural Carbohydrate | Relative Growth Rate | ||||
|---|---|---|---|---|---|
| Observed | Predicted | Predicted | |||
| Photoperiod | Dawn | Dusk | Dawn | Dusk | |
| h | g[CHO] g−1[SDM] | g[CHO] g−1[SDM] | g g−1 d−1 | ||
| Starch type | COL0 | ||||
| 6 | 0.007 | 0.046 | 0.0 | 0.058 | 0.048 |
| 9 | 0.009 | 0.062 | 0.003 | 0.069 | 0.087 |
| 12 | 0.006 | 0.073 | 0.011 | 0.074 | 0.122 |
| 16 | 0.021 | 0.095 | 0.025 | 0.076 | 0.166 |
| 20 | 0.051 | 0.079 | 0.045 | 0.075 | 0.206 |
| R2 | 0.90 | 0.84 | |||
| Starch-less | pgm | ||||
| 6 | 0.002 | 0.058 | 0.0 | 0.038 | 0.047 |
| 9 | 0.002 | 0.047 | 0.0 | 0.041 | 0.086 |
| 12 | 0.003 | 0.041 | 0.001 | 0.041 | 0.126 |
| 16 | 0.004 | 0.024 | 0.009 | 0.041 | 0.175 |
| 20 | 0.002 | 0.012 | 0.022 | 0.040 | 0.220 |
| R2 | 0.03 | 0.22 | |||
| Parameter | [30] | [31] | [18] | [27] | ||
|---|---|---|---|---|---|---|
| Units | Symbol | Tomato | Arabidopsis | Melon | Soybean | |
| Light | µmol[PAR] m−2 s−1 | L | 87–134 325–409 | 140 | 208 | 320 640 |
| Temperature | °C | T | 9–36 | 25 | 20, 40 | 27 |
| Carbon dioxide concentration | µmol[CO2] mol−1 | Ca | 450 | 380 | 300 1500 | 330 |
| Day length | h | 12 | 6–20 | 14 | 7, 14 | |
| Leaf area ratio | m2 kg−1 [SDM] | λ | 32.3–47.9 25.5–38.5 | 18.5 | 21, 30 19, 27 | 18, 20 36, 40 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gent, M.P.N. Dynamic Carbohydrate Supply and Demand Model of Vegetative Growth: Response to Temperature, Light, Carbon Dioxide, and Day Length. Agronomy 2018, 8, 21. https://doi.org/10.3390/agronomy8020021
Gent MPN. Dynamic Carbohydrate Supply and Demand Model of Vegetative Growth: Response to Temperature, Light, Carbon Dioxide, and Day Length. Agronomy. 2018; 8(2):21. https://doi.org/10.3390/agronomy8020021
Chicago/Turabian StyleGent, Martin P. N. 2018. "Dynamic Carbohydrate Supply and Demand Model of Vegetative Growth: Response to Temperature, Light, Carbon Dioxide, and Day Length" Agronomy 8, no. 2: 21. https://doi.org/10.3390/agronomy8020021
APA StyleGent, M. P. N. (2018). Dynamic Carbohydrate Supply and Demand Model of Vegetative Growth: Response to Temperature, Light, Carbon Dioxide, and Day Length. Agronomy, 8(2), 21. https://doi.org/10.3390/agronomy8020021




