Process Importance Identification for the SPAC System Under Different Water Conditions: A Case Study of Winter Wheat
Abstract
1. Introduction
2. Materials and Methods
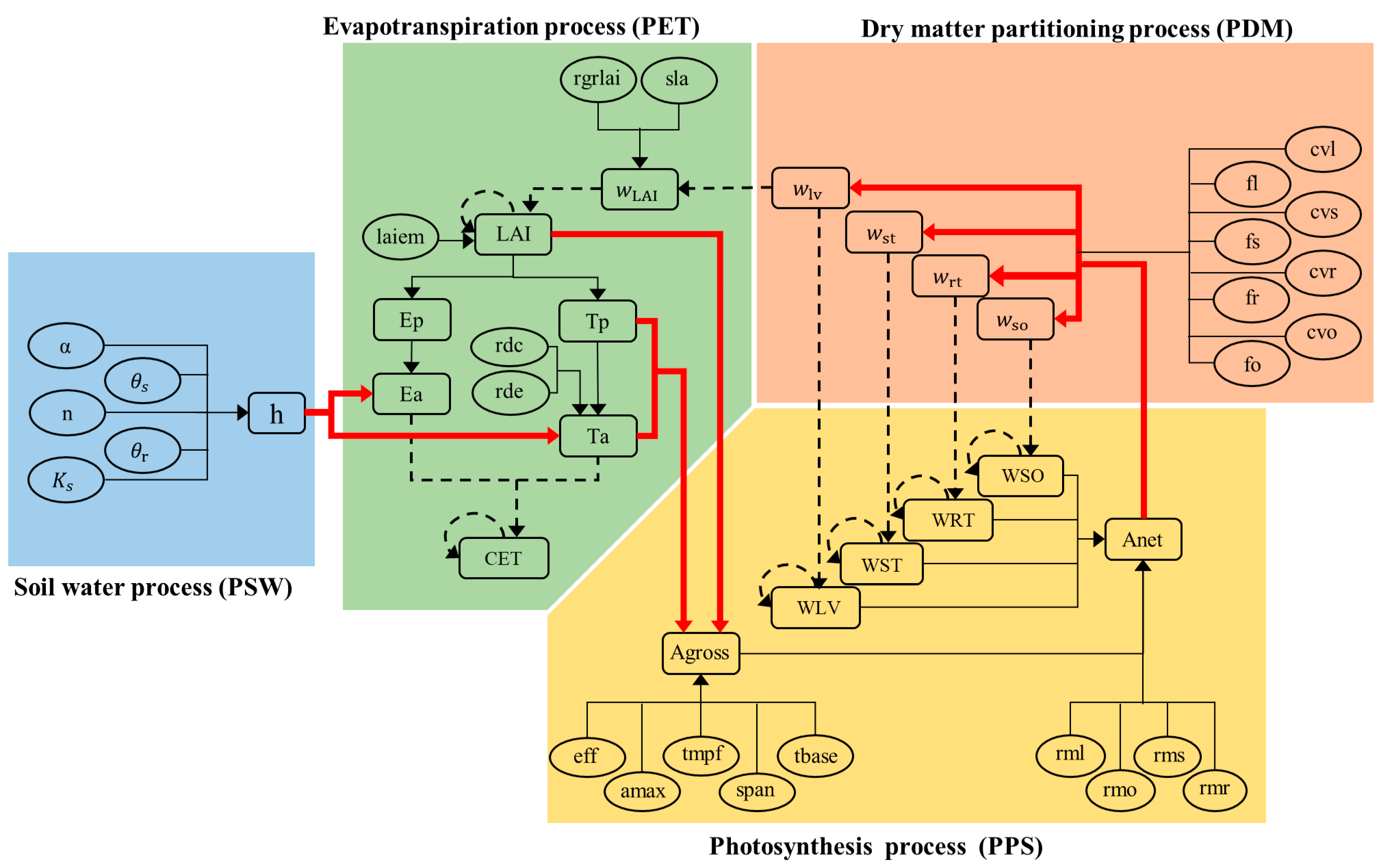
2.1. Description of the SWAP Model Simulation for the SPAC System
2.2. Subprocess Sensitivity Analysis Based on BN
2.2.1. Variance Decomposition for Subprocesses
2.2.2. Numerical Estimation for Subprocess Sensitivities
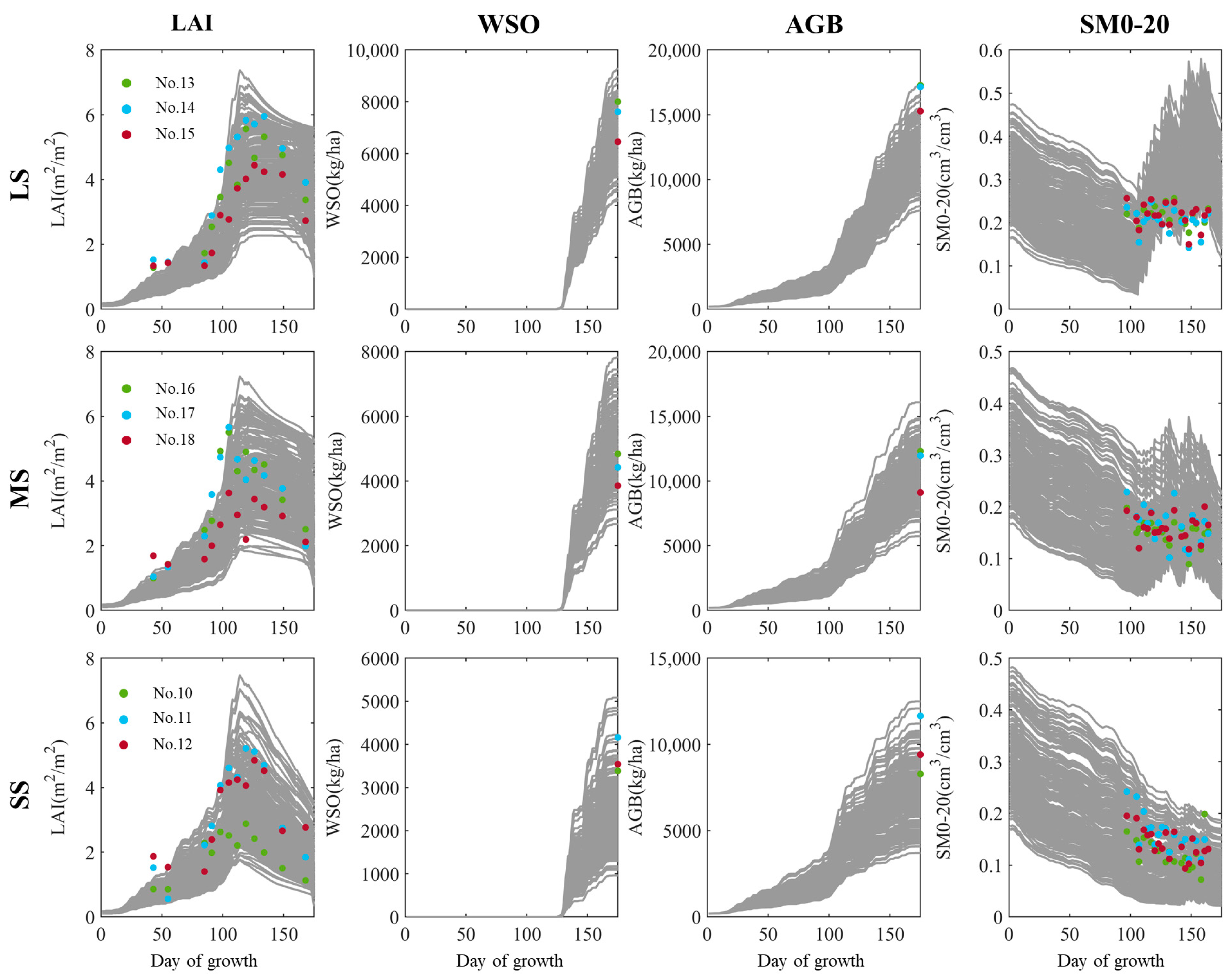
2.3. Site and Data Descriptions
2.4. Implementations
3. Results and Discussion
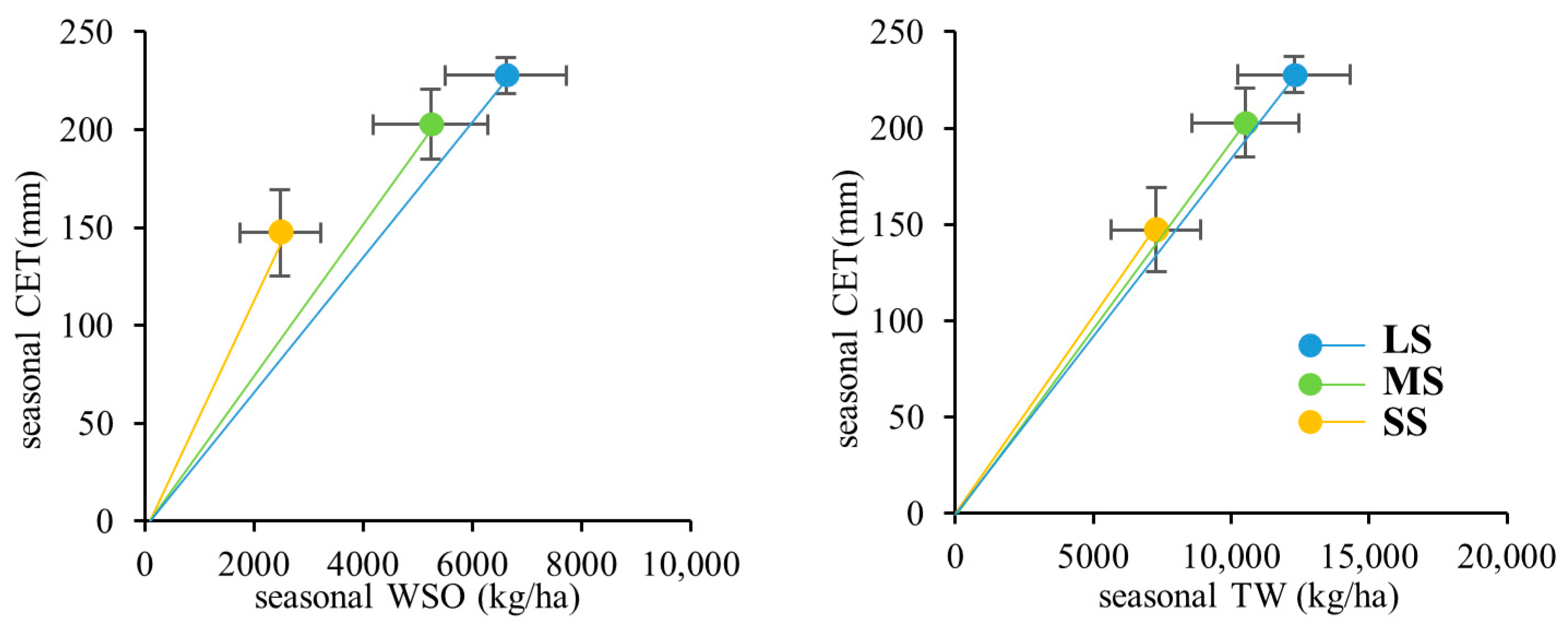
3.1. Examination of the Investigated Simulation Uncertainty
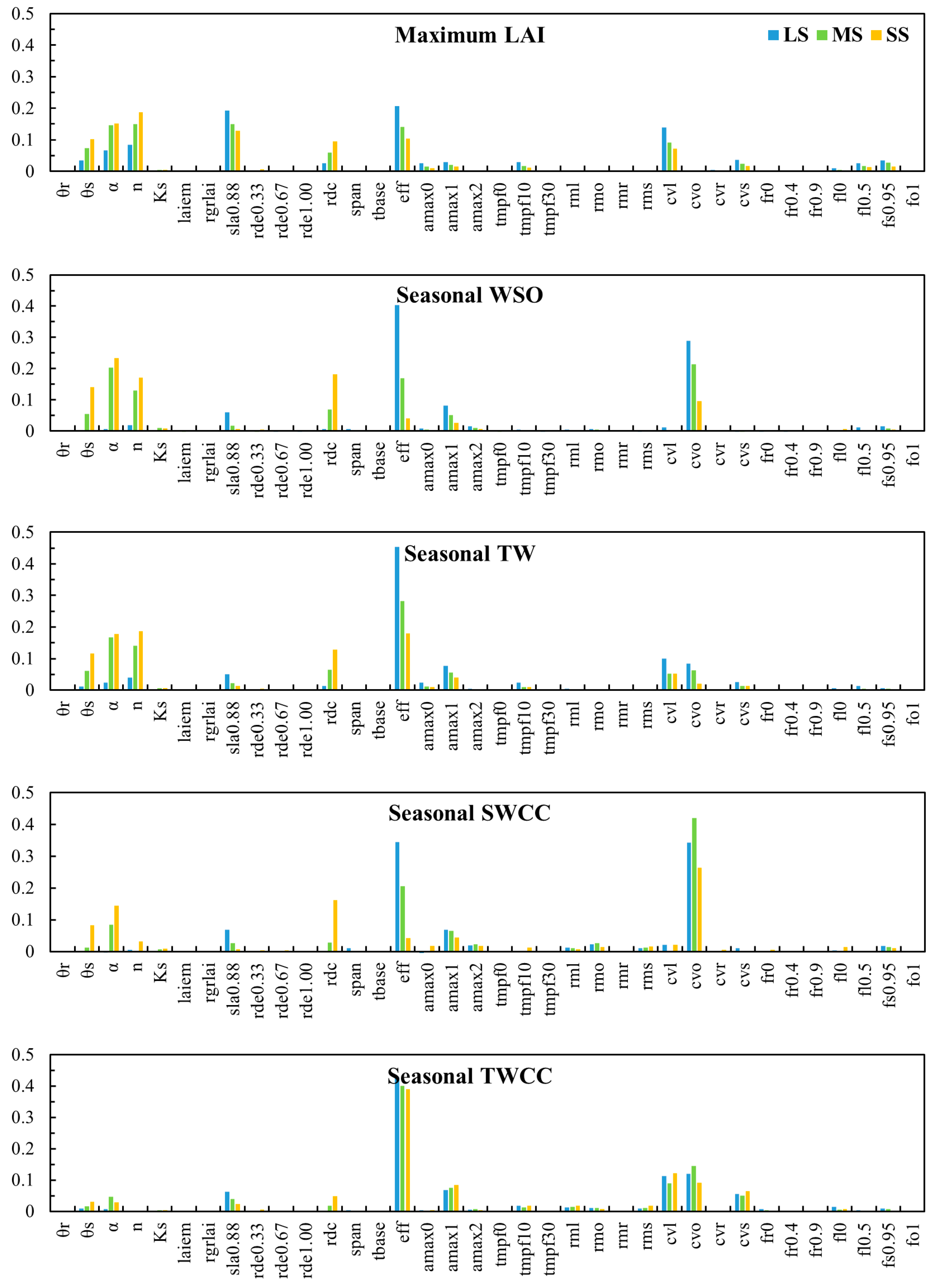
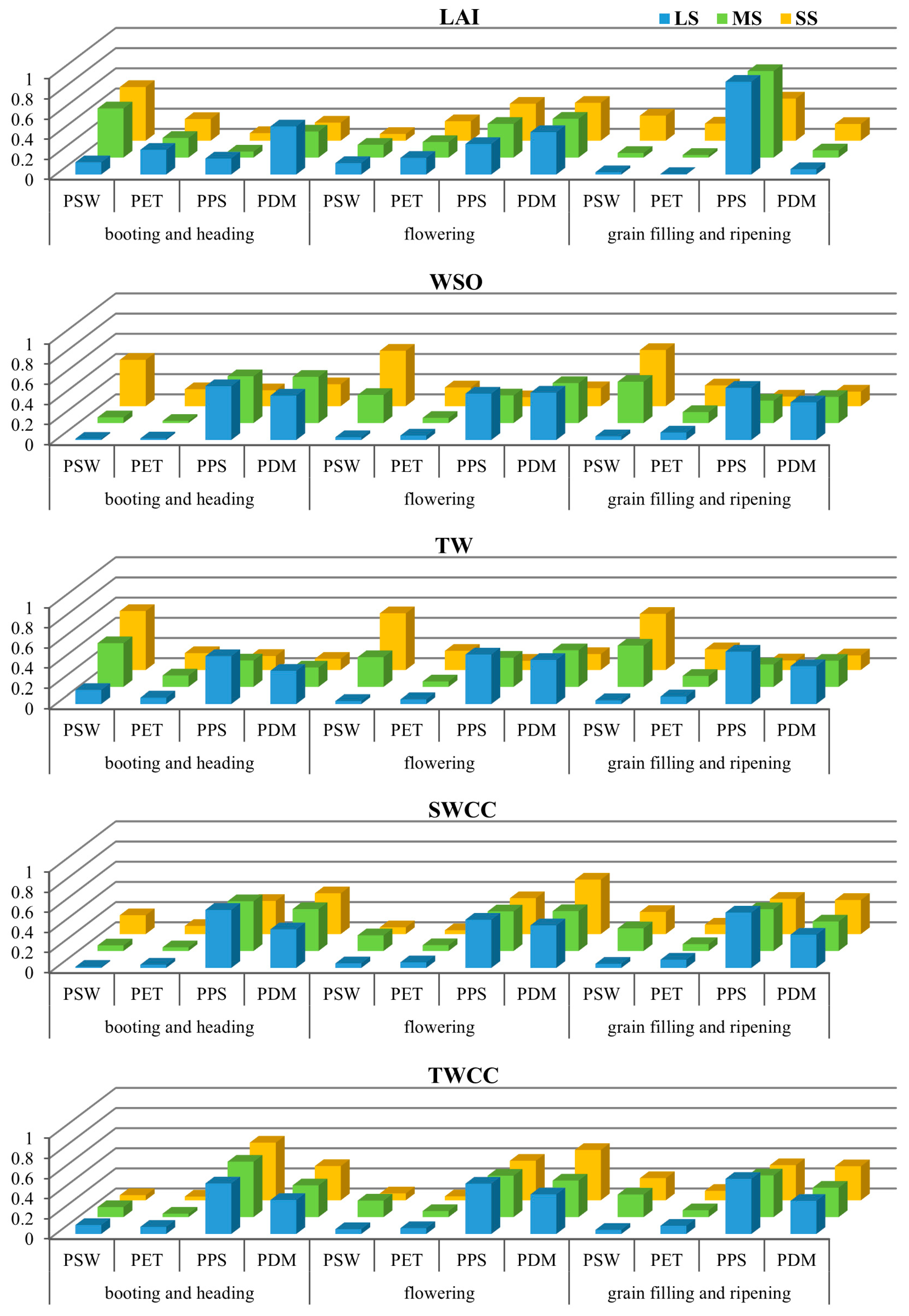
3.2. Impact of Water Stress on Subprocess Importance for Different Seasonal Indicators
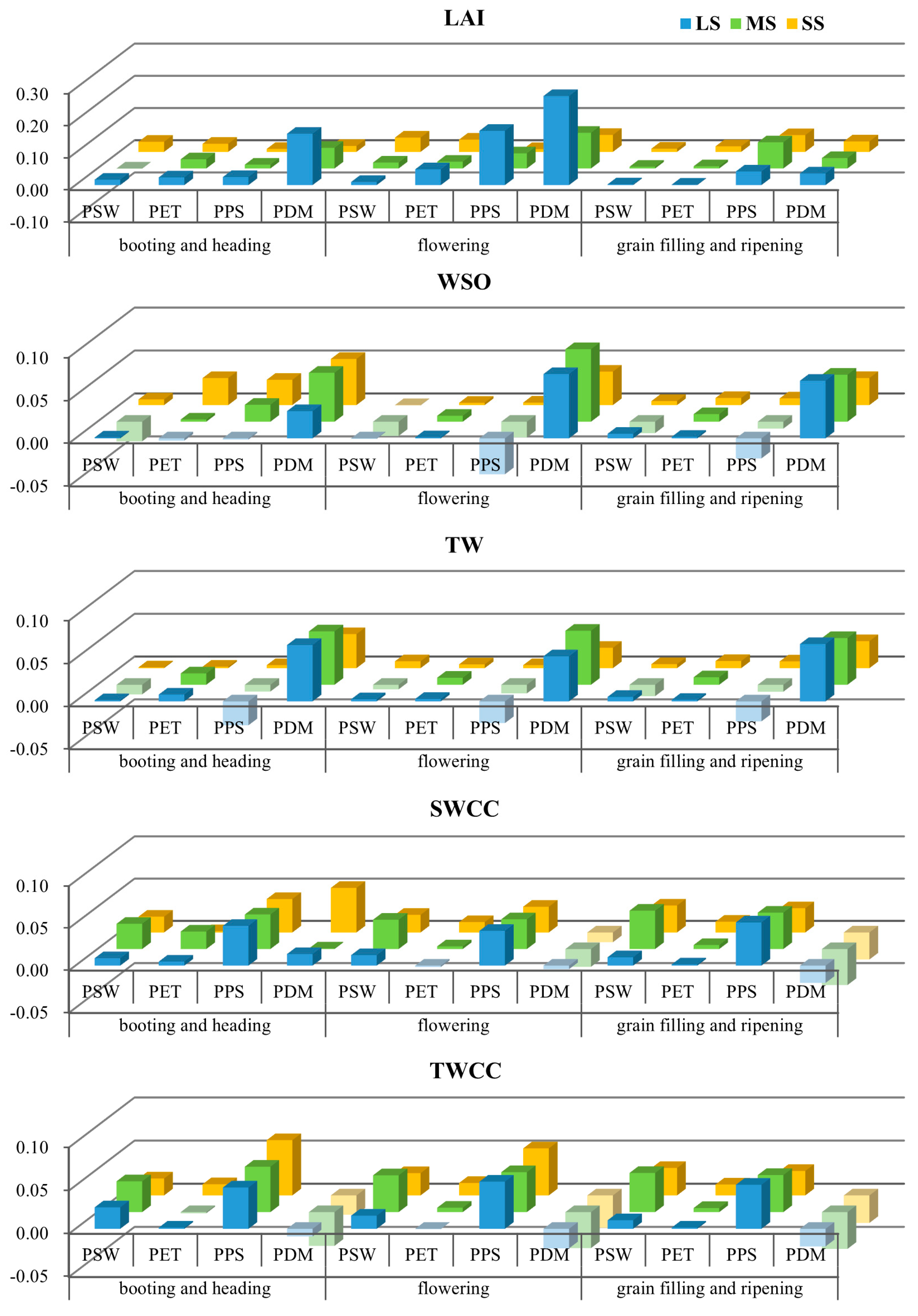
3.3. Impact of Water Stress on Subprocess Importance at Different Growth Stages
3.4. The Influence of Parameter Interactions on Subprocess Importance Identification
3.5. Limitations and Outlook
4. Conclusions
- (1)
- Under minimal water stress, the subprocesses of photosynthesis and dry matter partitioning (PPS and PDM) play the major roles in determining the agricultural outputs and water use efficiency. In this case, uncertainties in modeling the subprocesses of soil water movement and plant water uptake (PSM and PET) have a limited impact. As water becomes increasingly undersupplied, the importance of PSM and PET increases, with PSM becoming the predominant subprocess under sever water stress. This suggests that the water and carbon processes alternately act as limiting factors under variable water conditions.
- (2)
- The response of the subprocess importance to water stress is modulated by the crop phenology and has different patterns for different SPAC system states. For canopy development (LAI), the water supply has a significant impact during the booting and heading stage and the grain filling and ripening stage, but not during flowering. For the yield (WSO), the water stress threshold required to reverse the dominance of subprocesses decreases as yield formation progresses. For the total biomass (TW), even moderate water stress can lead to significant changes in subprocess importance throughout all growth stages.
- (3)
- Compared to conventional parameter sensitivity analysis, the proposed subprocess sensitivity analysis offers several advantages: it accounts for the counteracting or overlapping effects of parameter uncertainty, synthesizes the divergent responses of the parameter importance to varying water conditions, and identifies important subprocesses even in the absence of highly sensitive parameters.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| SPAC | Soil–plant–atmosphere continuum |
| SWAP | Soil–water–atmosphere–plant model |
| BN | Bayesian network |
| LAI | Leaf area index |
| WSO | Dry weight of storage organs |
| TW | Total dry weight of all organs |
| SWCC | Water consumption coefficient of storage organs |
| TWCC | Water consumption coefficient of total dry weight |
| CET | Cumulative evapotranspiration from the beginning of the crop season |
| AGB | Aboveground biomass |
| PSW | Subprocess of soil water movement |
| PET | Subprocess of evapotranspiration |
| PPS | Subprocess of photosynthesis |
| PDM | Subprocess of dry matter partitioning |
| LS | Least water stress |
| MS | Moderate water stress |
| SS | Severe water stress |
Appendix A
Appendix A.1

References
- Abrahamsen, P.; Hansen, S. Daisy: An Open Soil-Crop-Atmosphere System Model. Environ. Model. Softw. 2000, 15, 313–330. [Google Scholar] [CrossRef]
- de Wit, A.; Boogaard, H.; Fumagalli, D.; Janssen, S.; Knapen, R.; van Kraalingen, D.; Supit, I.; van der Wijngaart, R.; van Diepen, K. 25 Years of the WOFOST Cropping Systems Model. Agric. Syst. 2019, 168, 154–167. [Google Scholar] [CrossRef]
- Bouman, B.; Kropff, M.; Tuong, T.; Wopereis, M.; ten Berge, H.; van Laar, H.H. ORYZA2000: Modeling Lowland Rice; IRRI: Los Baños, Philippines, 2001; ISBN 978-971-22-0171-4. [Google Scholar]
- Sławiński, C.; Sobczuk, H. Soil–Plant–Atmosphere Continuum. In Encyclopedia of Agrophysics; Gliński, J., Horabik, J., Lipiec, J., Eds.; Springer: Dordrecht, The Netherlands, 2011; pp. 805–810. ISBN 978-90-481-3585-1. [Google Scholar]
- Makowski, D.; Naud, C.; Jeuffroy, M.H.; Barbottin, A.; Monod, H. Global Sensitivity Analysis for Calculating the Contribution of Genetic Parameters to the Variance of Crop Model Prediction. Reliab. Eng. Syst. Saf. 2006, 91, 1142–1147. [Google Scholar] [CrossRef]
- Varella, H.; Buis, S.; Launay, M.; Guérif, M. Global Sensitivity Analysis for Choosing the Main Soil Parameters of a Crop Model to Be Determined. Agric. Sci. 2012, 03, 949–961. [Google Scholar] [CrossRef]
- Sheikholeslami, R.; Razavi, S.; Haghnegahdar, A. What Should We Do When a Model Crashes? Recommendations for Global Sensitivity Analysis of Earth and Environmental Systems Models. Geosci. Model. Dev. 2019, 12, 4275–4296. [Google Scholar] [CrossRef]
- Razavi, S.; Jakeman, A.; Saltelli, A.; Prieur, C.; Iooss, B.; Borgonovo, E.; Plischke, E.; Lo Piano, S.; Iwanaga, T.; Becker, W.; et al. The Future of Sensitivity Analysis: An Essential Discipline for Systems Modeling and Policy Support. Environ. Model. Softw. 2021, 137, 104954. [Google Scholar] [CrossRef]
- Zheng, J.; Zhang, S. Decomposing the Total Uncertainty in Wheat Modeling: An Analysis of Model Structure, Parameters, Weather Data Inputs, and Squared Bias Contributions. Agric. Syst. 2025, 224, 104215. [Google Scholar] [CrossRef]
- Li, X.; Tan, J.; Li, H.; Wang, L.; Niu, G.; Wang, X. Sensitivity Analysis of the WOFOST Crop Model Parameters Using the EFAST Method and Verification of Its Adaptability in the Yellow River Irrigation Area, Northwest China. Agronomy 2023, 13, 2294. [Google Scholar] [CrossRef]
- Liang, H.; Xu, J.; Chen, L.; Li, B.; Hu, K. Bayesian Calibration and Uncertainty Analysis of an Agroecosystem Model under Different N Management Practices. Eur. J. Agron. 2022, 133, 126429. [Google Scholar] [CrossRef]
- Jin, X.; Li, Z.; Nie, C.; Xu, X.; Feng, H.; Guo, W.; Wang, J. Parameter Sensitivity Analysis of the AquaCrop Model Based on Extended Fourier Amplitude Sensitivity under Different Agro-Meteorological Conditions and Application. Field Crops Res. 2018, 226, 1–15. [Google Scholar] [CrossRef]
- Xu, T.; Valocchi, A.J. A Bayesian Approach to Improved Calibration and Prediction of Groundwater Models with Structural Error. Water Resour. Res. 2015, 51, 9290–9311. [Google Scholar] [CrossRef]
- Gupta, H.V.; Clark, M.P.; Vrugt, J.A.; Abramowitz, G.; Ye, M. Towards a Comprehensive Assessment of Model Structural Adequacy. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Alderman, P.D.; Stanfill, B. Quantifying Model-Structure- and Parameter-Driven Uncertainties in Spring Wheat Phenology Prediction with Bayesian Analysis. Eur. J. Agron. 2017, 88, 1–9. [Google Scholar] [CrossRef]
- Zhang, S.; Tao, F.; Zhang, Z. Uncertainty from Model Structure Is Larger than That from Model Parameters in Simulating Rice Phenology in China. Eur. J. Agron. 2017, 87, 30–39. [Google Scholar] [CrossRef]
- Silva, L.C.R.; Lambers, H. Soil-Plant-Atmosphere Interactions: Structure, Function, and Predictive Scaling for Climate Change Mitigation. Plant Soil 2021, 461, 5–27. [Google Scholar] [CrossRef]
- Kannenberg, S.A.; Barnes, M.L.; Bowling, D.R.; Driscoll, A.W.; Guo, J.S.; Anderegg, W.R.L. Quantifying the Drivers of Ecosystem Fluxes and Water Potential across the Soil-Plant-Atmosphere Continuum in an Arid Woodland. Agric. For. Meteorol. 2023, 329, 109269. [Google Scholar] [CrossRef]
- Mai, J.; Craig, J.R.; Tolson, B.A. Simultaneously Determining Global Sensitivities of Model Parameters and Model Structure. Hydrol. Earth Syst. Sci. 2020, 24, 5835–5858. [Google Scholar] [CrossRef]
- Günther, D.; Marke, T.; Essery, R.; Strasser, U. Uncertainties in Snowpack Simulations—Assessing the Impact of Model Structure, Parameter Choice, and Forcing Data Error on Point-Scale Energy Balance Snow Model Performance. Water Resour. Res. 2019, 55, 2779–2800. [Google Scholar] [CrossRef]
- Baroni, G.; Tarantola, S. A General Probabilistic Framework for Uncertainty and Global Sensitivity Analysis of Deterministic Models: A Hydrological Case Study. Environ. Model. Softw. 2014, 51, 26–34. [Google Scholar] [CrossRef]
- Sobol, I.M. Global Sensitivity Indices for Nonlinear Mathematical Models and Their Monte Carlo Estimates. Math. Comput. Simul. 2001, 55, 271–280. [Google Scholar] [CrossRef]
- Darwiche, A. Modeling and Reasoning with Bayesian Networks; Cambridge University Press: Cambridge, UK, 2009; ISBN 978-1-139-47890-8. [Google Scholar]
- Dai, H.; Chen, X.; Ye, M.; Song, X.; Hammond, G.; Hu, B.; Zachara, J.M. Using Bayesian Networks for Sensitivity Analysis of Complex Biogeochemical Models. Water Resour. Res. 2019, 55, 3541–3555. [Google Scholar] [CrossRef]
- Kroes, J.G.; Van Dam, J.C.; Groenendijk, P.; Hendriks, R.F.A.; Jacobs, C.M.J. SWAP Version 3.2. Theory Description and User Manual; Alterra: Wageningen, The Netherlands, 2009. [Google Scholar]
- Heinen, M.; Mulder, M.; van Dam, J.; Bartholomeus, R.; de Jong van Lier, Q.; de Wit, J.; de Wit, A.; Hack-Ten Broeke, M. SWAP 50 Years: Advances in Modelling Soil-Water-Atmosphere-Plant Interactions. Agric. Water Manag. 2024, 298, 108883. [Google Scholar] [CrossRef]
- Richards, L.A. Capillary Conduction of Liquids Through Porous Mediums. Physics 1931, 1, 318–333. [Google Scholar] [CrossRef]
- van Genuchten, M.T. A Closed-Form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Saltelli, A.; Annoni, P.; Azzini, I.; Campolongo, F.; Ratto, M.; Tarantola, S. Variance Based Sensitivity Analysis of Model Output. Design and Estimator for the Total Sensitivity Index. Comput. Phys. Commun. 2010, 181, 259–270. [Google Scholar] [CrossRef]
- Draper, D.; Pereira, A.; Prado, P.; Saltelli, A.; Cheal, R.; Eguilior, S.; Mendes, B.; Tarantola, S. Scenario and Parametric Uncertainty in GESAMAC: A methodological study in nuclear waste disposal risk assessment. Comput. Phys. Commun. 1999, 117, 142–155. [Google Scholar] [CrossRef]
- Saltelli, A. Making Best Use of Model Evaluations to Compute Sensitivity Indices. Comput. Phys. Commun. 2002, 145, 280–297. [Google Scholar] [CrossRef]
- Li, F.; Wei, C.; Zhang, F.; Zhang, J.; Nong, M.; Kang, S. Water-Use Efficiency and Physiological Responses of Maize under Partial Root-Zone Irrigation. Agric. Water Manag. 2010, 97, 1156–1164. [Google Scholar] [CrossRef]
- Kang, S.; Shi, W.; Zhang, J. An Improved Water-Use Efficiency for Maize Grown under Regulated Deficit Irrigation. Field Crops Res. 2000, 67, 207–214. [Google Scholar] [CrossRef]
- Cheng, M.; Wang, H.; Fan, J.; Zhang, F.; Wang, X. Effects of Soil Water Deficit at Different Growth Stages on Maize Growth, Yield, and Water Use Efficiency under Alternate Partial Root-Zone Irrigation. Water 2021, 13, 148. [Google Scholar] [CrossRef]
- Bleiholder, H.; Weber, E.; Lancashire, P.; Feller, C.; Buhr, L.; Hess, M.; Wicke, H.; Hack, H.; Meier, U.; Klose, R. Growth Stages of Mono-and Dicotyledonous Plants. In BBCH Monograph; Federal Biological Research Centre for Agriculture and Forestry: Brunswick, Germany, 2001. [Google Scholar]
- Wang, J.; Li, X.; Lu, L.; Fang, F. Parameter Sensitivity Analysis of Crop Growth Models Based on the Extended Fourier Amplitude Sensitivity Test Method. Environ. Model. Softw. 2013, 48, 171–182. [Google Scholar] [CrossRef]
- de Almeida Pereira, R.A.; dos Santos Vianna, M.; Nassif, D.S.P.; dos Santos Carvalho, K.; Marin, F.R. Global Sensitivity and Uncertainty Analysis of a Sugarcane Model Considering the Trash Blanket Effect. Eur. J. Agron. 2021, 130, 126371. [Google Scholar] [CrossRef]
- Lu, Y.; Chibarabada, T.P.; McCabe, M.F.; De Lannoy, G.J.M.; Sheffield, J. Global Sensitivity Analysis of Crop Yield and Transpiration from the FAO-AquaCrop Model for Dryland Environments. Field Crops Res. 2021, 269, 108182. [Google Scholar] [CrossRef]
- Hillel, D.; Guron, Y. Relation between Evapotranspiration Rate and Maize Yield. Water Resour. Res. 1973, 9, 743–748. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, S.; Sun, H.; Shao, L.; Wang, Y. Changes in Evapotranspiration over Irrigated Winter Wheat and Maize in North China Plain over Three Decades. Agric. Water Manag. 2011, 98, 1097–1104. [Google Scholar] [CrossRef]
- Zhang, Y.; Kendy, E.; Qiang, Y.; Changming, L.; Yanjun, S.; Hongyong, S. Effect of Soil Water Deficit on Evapotranspiration, Crop Yield, and Water Use Efficiency in the North China Plain. Agric. Water Manag. 2004, 64, 107–122. [Google Scholar] [CrossRef]
- Zhao, F.-H.; Yu, G.-R.; Li, S.-G.; Ren, C.-Y.; Sun, X.-M.; Mi, N.; Li, J.; Ouyang, Z. Canopy Water Use Efficiency of Winter Wheat in the North China Plain. Agric. Water Manag. 2007, 93, 99–108. [Google Scholar] [CrossRef]
- Ercoli, L.; Lulli, L.; Mariotti, M.; Masoni, A.; Arduini, I. Post-Anthesis Dry Matter and Nitrogen Dynamics in Durum Wheat as Affected by Nitrogen Supply and Soil Water Availability. Eur. J. Agron. 2008, 28, 138–147. [Google Scholar] [CrossRef]
- Saltelli, A.; Tarantola, S. On the Relative Importance of Input Factors in Mathematical Models: Safety Assessment for Nuclear Waste Disposal. J. Am. Stat. Assoc. 2002, 97, 702–709. [Google Scholar] [CrossRef]
- Chapagain, R.; Remenyi, T.A.; Harris, R.M.B.; Mohammed, C.L.; Huth, N.; Wallach, D.; Rezaei, E.E.; Ojeda, J.J. Decomposing Crop Model Uncertainty: A Systematic Review. Field Crops Res. 2022, 279, 108448. [Google Scholar] [CrossRef]
- Wallach, D.; Thorburn, P.J. Estimating Uncertainty in Crop Model Predictions: Current Situation and Future Prospects. Eur. J. Agron. 2017, 88, A1–A7. [Google Scholar] [CrossRef]

| Parameter | Description | Unit | Variation Range |
|---|---|---|---|
| Residual water content | cm3/cm3 | 0.017–0.026 | |
| Saturated water content | cm3/cm3 | 0.450–0.674 | |
| Shape parameter of main drying curve | 1/cm | 0.0393–0.0590 | |
| n | Shape parameter | - | 1.219–1.828 |
| Saturated vertical hydraulic conductivity | cm/d | 17.03–25.55 | |
| laiem | Leaf area index at emergence | m2/m2 | 0.2918–0.4376 |
| rgrlai | Maximum relative increase in LAI | m2/m2/d | 0.00877–0.01316 |
| sla0.88 | Specific leaf area at Dvs = 0.88 | ha/kg | 0.00120–0.00180 |
| rde0.33 | Relative root density when relative rooting depth is 0.33 | - | 0.31469–0.47203 |
| rde0.67 | Relative root density when relative rooting depth is 0.67 | - | 0.05000–0.07500 |
| rde1.00 | Relative root density when relative rooting depth is 1.00 | - | 0.01248–0.01872 |
| rdc | Maximum rooting depth of crop | cm | 65.32–97.97 |
| span | Life span of leaves under optimum conditions | d | 27.29–40.93 |
| tbase | Lower threshold temperature for aging of leaves | °C | 1.45–2.17 |
| eff | Light use efficiency of leaves | kg CO2/J | 0.474–0.711 |
| amax0 | Max CO2 assimilation rate at Dvs = 0 | kg/ha/h | 32.000–48.000 |
| amax1 | Max CO2 assimilation rate at Dvs = 1 | kg/ha/h | 29.906–44.860 |
| amax2 | Max CO2 assimilation rate at Dvs = 2 | kg/ha/h | 16.000–24.000 |
| tmpf0 | Reduction factor of amax when average day temperature is 0 °C | - | 0.008–0.012 |
| tmpf10 | Reduction factor of amax when average day temperature is 10 °C | - | 0.493–0.740 |
| tmpf30 | Reduction factor of amax when average day temperature is 30 °C | - | 0.400–0.600 |
| rml | Relative maintenance respiration rate of leaves | kgCH2O/kg/d | 0.01480–0.02220 |
| rms | Relative maintenance respiration rate of storage organs | kgCH2O/kg/d | 0.01564–0.02346 |
| rmr | Relative maintenance respiration rate of roots | kgCH2O/kg/d | 0.01200–0.01800 |
| rmo | Relative maintenance respiration rate of stems | kgCH2O/kg/d | 0.01879–0.02819 |
| cvl | Efficiency of carbohydrate conversion into leaves | kg/kg | 0.5601–0.8402 |
| cvs | Efficiency of carbohydrate conversion into storage organs | kg/kg | 0.5845–0.8768 |
| cvr | Efficiency of carbohydrate conversion into roots | kg/kg | 0.5552–0.8328 |
| cvo | Efficiency of carbohydrate conversion into stems | kg/kg | 0.5517–0.8275 |
| fr0 | Fraction of total dry matter increase partitioned to roots at Dvs = 0 | kg/kg | 0.320–0.480 |
| fr0.4 | Fraction of total dry matter increase partitioned to roots at Dvs = 0.4 | kg/kg | 0.120–0.180 |
| fr0.9 | Fraction of total dry matter increase partitioned to roots at Dvs = 0.9 | kg/kg | 0.008–0.012 |
| fl0 | Fraction of total dry matter increase partitioned to leaves at Dvs = 0 | kg/kg | 0.480–0.720 |
| fl0.5 | Fraction of total dry matter increase partitioned to leaves at Dvs = 0.5 | kg/kg | 0.5967–0.8951 |
| fs0.95 | Fraction of total dry matter increase partitioned to stems at Dvs = 0.95 | kg/kg | 0.7024–1.0000 |
| fo1 | Fraction of total dry matter increase partitioned to storage organs at Dvs = 1 | kg/kg | 0.6472–0.9708 |
| LS | MS | SS | |
|---|---|---|---|
| Irrigation Amount (mm) | 192.73 | 72.12 | 12.50 |
| SM0-20 (cm3/cm3) | |||
| Grain Yield (kg/ha) | |||
| Lysimeter No. | 13, 14, 15 | 16, 17, 18 | 10, 11, 12 |
| Growth Stage Duration (days) | emergence: 32; tillering: 58; stem elongation: 15; booting and heading: 24; flowering: 6; grain filling and ripening: 40 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Shi, L.; Li, J. Process Importance Identification for the SPAC System Under Different Water Conditions: A Case Study of Winter Wheat. Agronomy 2025, 15, 753. https://doi.org/10.3390/agronomy15030753
Wang L, Shi L, Li J. Process Importance Identification for the SPAC System Under Different Water Conditions: A Case Study of Winter Wheat. Agronomy. 2025; 15(3):753. https://doi.org/10.3390/agronomy15030753
Chicago/Turabian StyleWang, Lijun, Liangsheng Shi, and Jinmin Li. 2025. "Process Importance Identification for the SPAC System Under Different Water Conditions: A Case Study of Winter Wheat" Agronomy 15, no. 3: 753. https://doi.org/10.3390/agronomy15030753
APA StyleWang, L., Shi, L., & Li, J. (2025). Process Importance Identification for the SPAC System Under Different Water Conditions: A Case Study of Winter Wheat. Agronomy, 15(3), 753. https://doi.org/10.3390/agronomy15030753






