Comparing Regression and Classification Models to Estimate Leaf Spot Disease in Peanut (Arachis hypogaea L.) for Implementation in Breeding Selection
Abstract
1. Introduction
2. Materials and Methods
2.1. Genetic Material
2.2. Site Description
2.3. Experimental Set Up
2.4. Data Collection
2.4.1. Visual Ground Rating
2.4.2. Normalized Difference Vegetation Index (NDVI)
2.4.3. Red–Green–Blue (RGB) Imaging
2.5. Data Analysis
3. Results
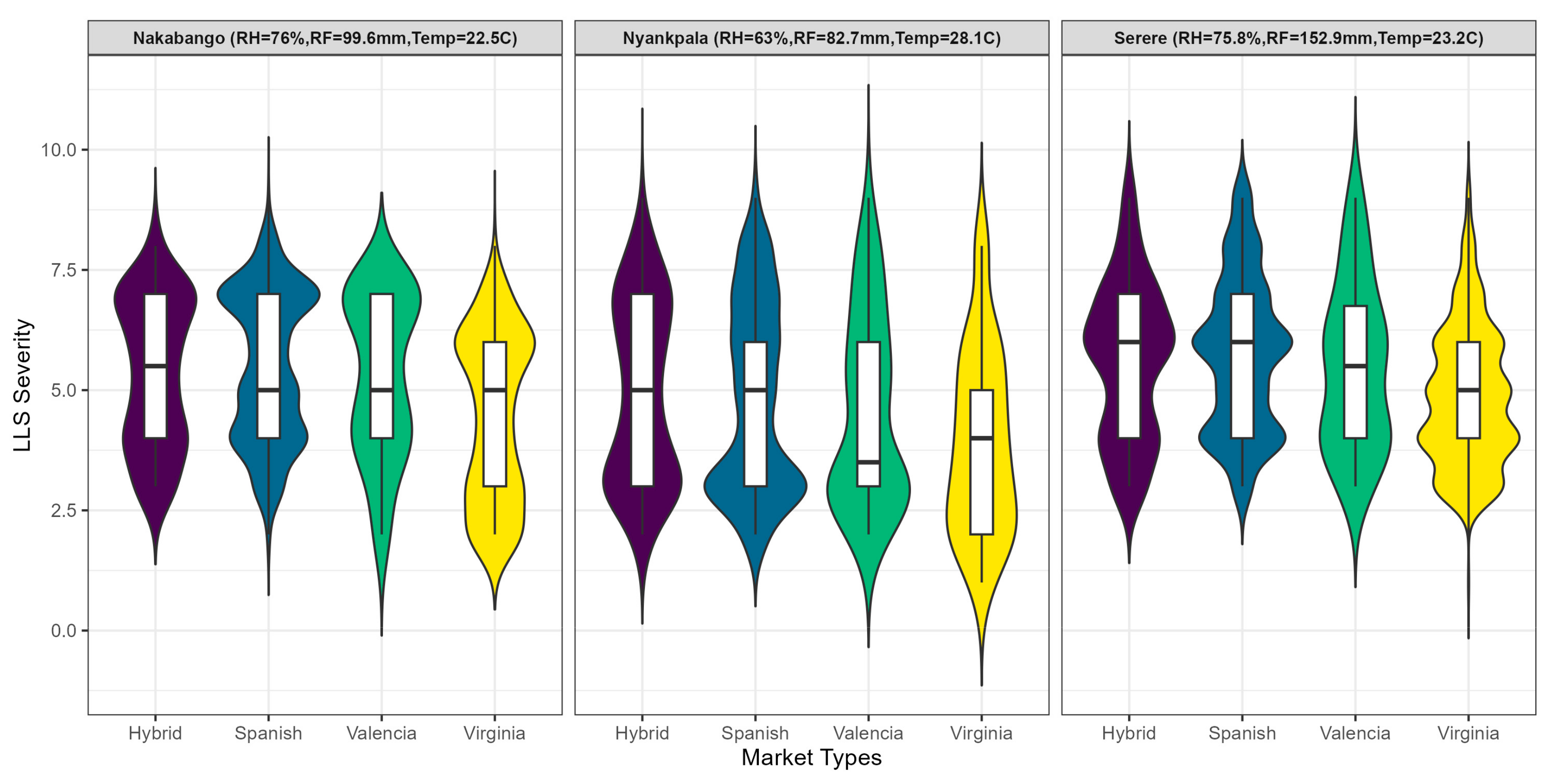
3.1. Disease Distribution across the Three Locations
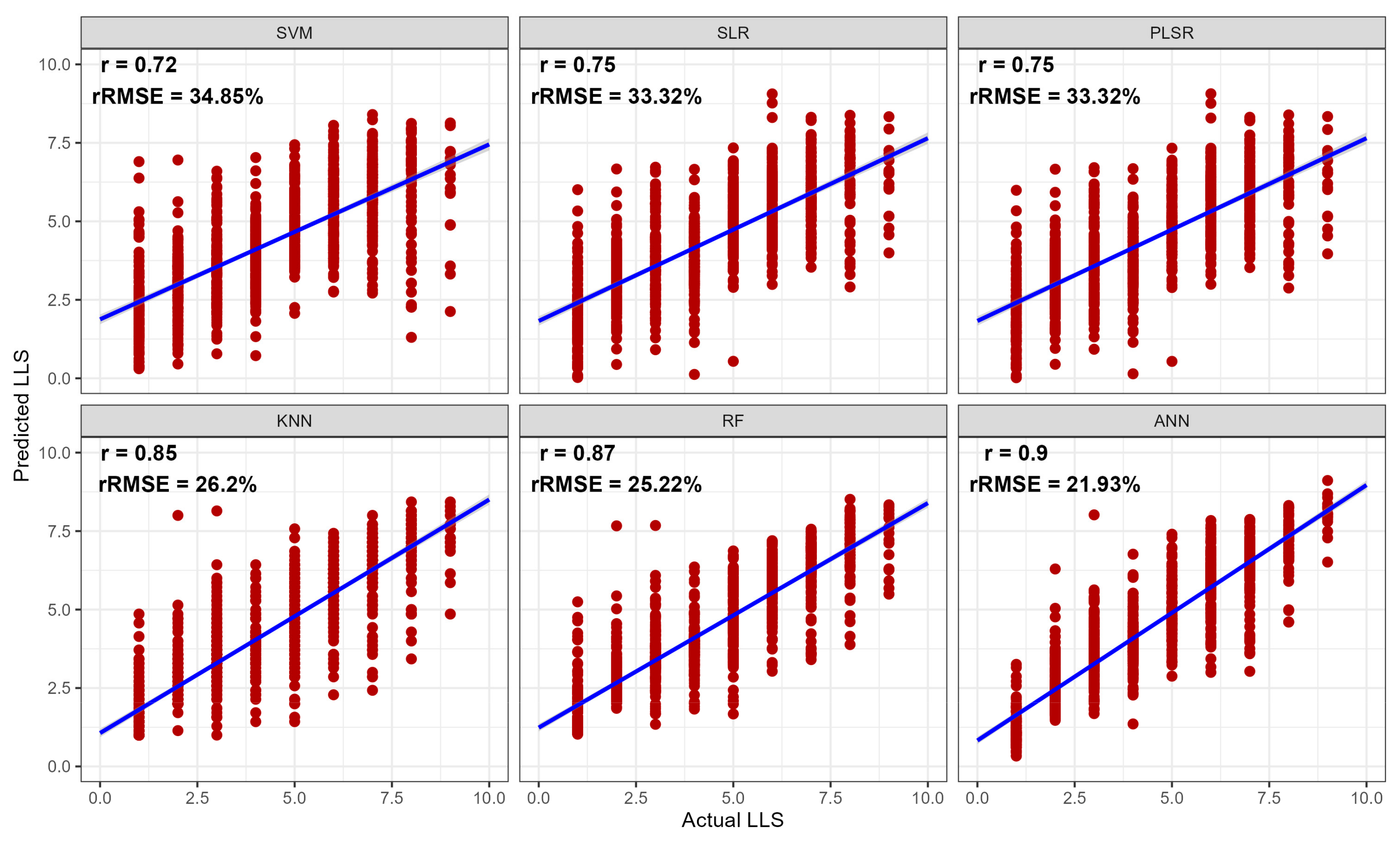
3.2. Late Leaf Spot Estimation Using Machine Learning
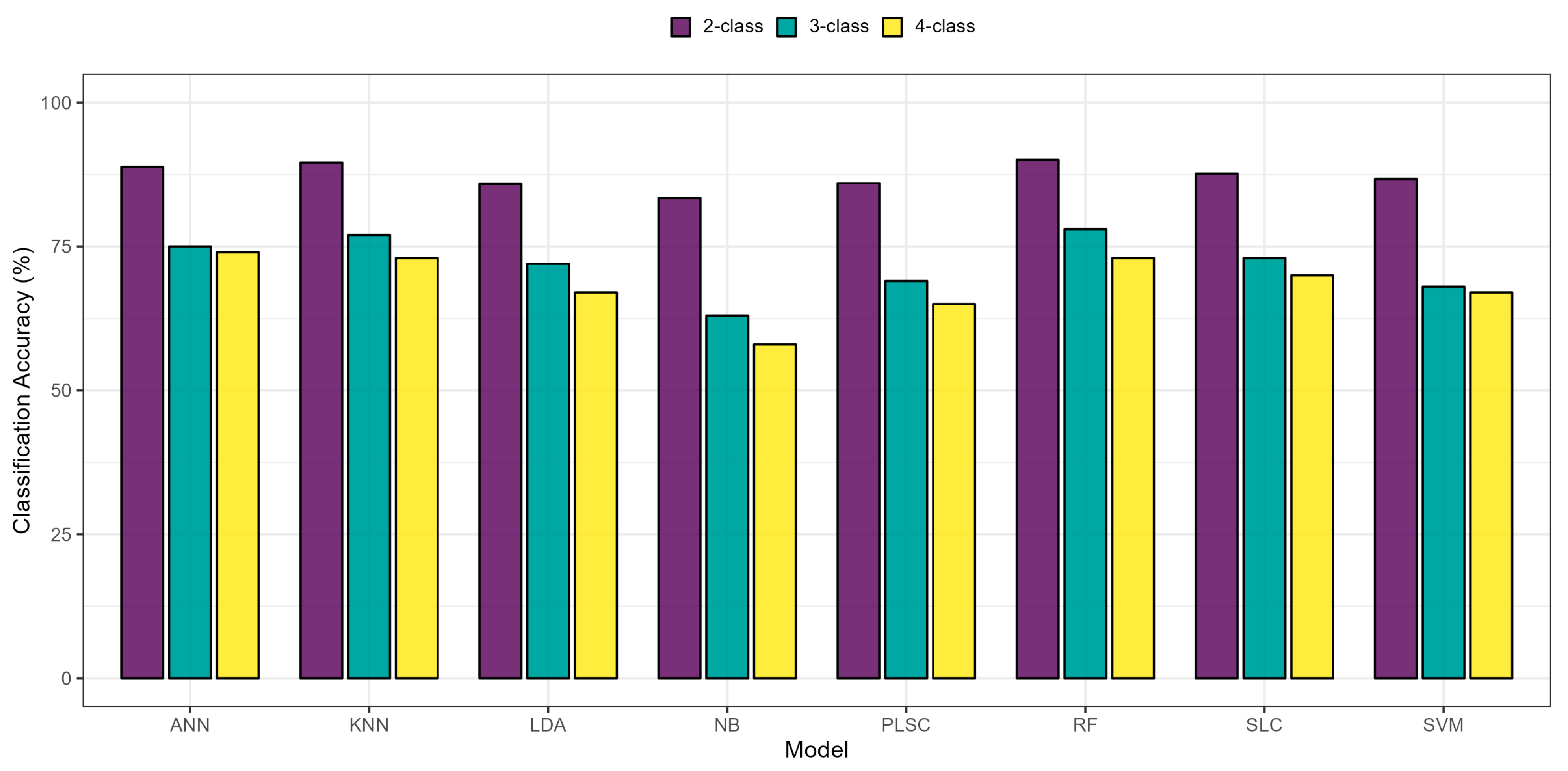
3.3. LLS Severity Classification Using Machine Learning
3.3.1. Binary Classification Models
3.3.2. Multiclass Resistance Classification
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Okello, D.K.; Biruma, M.; Deom, C.M. Overview of groundnuts research in Uganda: Past, present and future. Afr. J. Biotechnol. 2010, 9, 6448–6459. [Google Scholar]
- FAOSTAT. Food and Agriculture Organization of the United Nations; FAOSTAT Statistical Database: Rome, Italy, 2023; Available online: https://www.fao.org/faostat/en/#data/QCL (accessed on 22 March 2024).
- Deom, C.M.; Okello, D.K. Developing Improved Varieties of Groundnut; Sivasankar, S., Ed.; Burleigh Dodds Science Publishing: Cambridge, UK, 2018; pp. 145–176. [Google Scholar]
- Oteng-Frimpong, R.; Konlan, S.P.; Denwar, N.N. Evaluation of Selected Groundnut (Arachis hypogaea L.) Lines for Yield and Haulm Nutritive Quality Traits. Int. J. Agron. 2017, 2017, 7479309. [Google Scholar] [CrossRef]
- Abady, S.; Shimelis, H.; Janila, P.; Mashilo, J. Groundnut (Arachis hypogaea L.) improvement in sub-Saharan Africa: A review. Acta Agric. Scand. Sect. B-Soil Plant Sci. 2019, 69, 528–545. [Google Scholar] [CrossRef]
- Waliyar, F.; Kumar, P.L.; Ntare, B.R.; Monyo, E.; Nigam, S.N.; Reddy, A.S.; Osiru, M.; Diallo, A.T. A Century of Research on Groundnut Rosette Disease and Its Management; Information Bulletin No. 75; International Crops Research Institute for the Semi-Arid Tropics: Patancheru, India, 2007. [Google Scholar]
- Singh, M.P.; Erickson, J.E.; Boote, K.J.; Tillman, B.L.; van Bruggen, A.H.C.; Jones, J.W. Photosynthetic consequences of late leaf spot differ between two peanut cultivars with variable levels of resistance. Crop Sci. 2011, 51, 2741–2748. [Google Scholar] [CrossRef]
- Culbreath, A.K.; Stevenson, K.L.; Brenneman, T.B. Management of Late Leaf Spot of Peanut with Benomyl and Chlorothalonil: A Study in Preserving Fungicide Utility. Plant Dis. 2002, 86, 349–355. [Google Scholar] [CrossRef] [PubMed]
- Shokes, F.; Gorbert, D.W.; Jackson, L.F. Control of Early and Late Leafspot on two peanut cultivars. Peanut Sci. 1983, 10, 17–21. [Google Scholar] [CrossRef]
- Lamon, S.; Chu, Y.; Guimaraes, L.A.; Bertioli, D.J.; Leal-bertioli, S.C.M.; Santos, J.F.; Godoy, I.J.; Culbreath, A.K.; Holbrook, C.C.; Ozias-akins, P. Characterization of peanut lines with interspecific introgressions conferring late leaf spot resistance. Crop Sci. 2021, 61, 1724–1738. [Google Scholar] [CrossRef]
- Kalule Okello, D.; Monyo, E.; Michael, D.C.; Jane, I.; Herbert Kefa, O. Groundnut Production Guide for Uganda: Recommended Practices for Farmers; National Agricultural Research Organisation: Entebbe, Uganda, 2013. [Google Scholar]
- Natsugah, S.K.; Abudulai, M.; Oti-Boateng, C.; Brandenburg, R.; Jordan, D. Management of Leaf Spot Diseases of Peanut with Fungicides and Local Detergents in Ghana. Plant Pathol. J. 2007, 6, 248–253. [Google Scholar]
- Araus, J.L.; Cairns, J.E. Field high-throughput phenotyping: The new crop breeding frontier. Trends Plant Sci. 2014, 19, 52–61. [Google Scholar] [CrossRef]
- Foster, D.J.; Wynne, J.C.; Beute, M.K. Evaluation of detached leaf culture for screening peanuts for leafspot resistance. Peanut Sci. 1980, 7, 98–100. [Google Scholar] [CrossRef]
- Subrahmanyam, P.; McDonald, D.; Waliayar, F.; Reddy, L.J.; Nigam, S.N.; Gibbons, R.W.; Rao, V.R.; Singh, A.K.; Pande, S.; Reddy, P.M.; et al. Screening Methods and Sources of Resistance to Rust and Late Leaf Spot of Groundnut; Information Bulletin No. 47; International Crops Research Institute for the Semi-Arid Tropics: Patancheruvu, India, 1995; p. 21. [Google Scholar]
- Chiteka, Z.A.; Gorbet, D.W.; Shokes, F.M.; Kucharek, T.A.; The, F. Components of Resistance to Late Leafspot in Peanut. I. Levels and Variability—Implications for Selection. Peanut Sci. 1988, 15, 25–30. [Google Scholar] [CrossRef]
- Milberg, P.; Bergstedt, J.; Fridman, J.; Odell, G.; Westerberg, L. Observer bias and random variation in vegetation monitoring data. J. Veg. Sci. 2008, 19, 633–644. [Google Scholar] [CrossRef]
- Rutkoski, J.; Poland, J.; Mondal, S.; Autrique, E.; Pérez, L.G.; Crossa, J.; Reynolds, M.; Singh, R. Canopy Temperature and Vegetation Indices from High-Throughput Phenotyping Improve Accuracy of Pedigree and Genomic Selection for Grain Yield in Wheat. G3 Genes Genomes Genet. 2016, 6, 2799–2808. [Google Scholar] [CrossRef] [PubMed]
- Araus, J.L.; Kefauver, S.C.; Zaman-allah, M.; Olsen, M.S.; Cairns, J.E. Translating High-Throughput Phenotyping into Genetic Gain. Trends Plant Sci. 2018, 23, 451–466. [Google Scholar] [CrossRef] [PubMed]
- Schweiger, A.K.; Cavender-Bares, J.; Townsend, P.A.; Hobbie, S.E.; Madritch, M.D.; Wang, R.; Tilman, D.; Gamon, J.A. Plant spectral diversity integrates functional and phylogenetic components of biodiversity and predicts ecosystem function. Nat. Ecol. Evol. 2018, 2, 976–982. [Google Scholar] [CrossRef] [PubMed]
- Behmann, J.; Mahlein, A.; Rumpf, T.; Ro, C.; Plu, L. A review of advanced machine learning methods for the detection of biotic stress in precision crop protection. Precis. Agric. 2014, 16, 239–260. [Google Scholar] [CrossRef]
- Watt, M.; Fiorani, F.; Usadel, B.; Rascher, U.; Muller, O.; Schurr, U. Phenotyping: New Windows into the Plant for Breeders. Annu. Rev. Plant Biol. 2020, 71, 689–712. [Google Scholar] [CrossRef] [PubMed]
- White, J.W.; Andrade-Sanchez, P.; Gore, M.A.; Bronson, K.F.; Coffelt, T.A.; Conley, M.M.; Feldmann, K.A.; French, A.N.; Heun, J.T.; Hunsaker, D.J.; et al. Field-based phenomics for plant genetics research. Field Crops Res. 2012, 133, 101–112. [Google Scholar] [CrossRef]
- Vapnik, V.N. The Nature of Statistical Learning Theory. In Statistics for Engineering and Information Science, 2nd ed.; Springer: New York, NY, USA, 2000. [Google Scholar]
- Breiman, L. Statistics; Department University of California: Berkeley, CA, USA, 2001. [Google Scholar]
- Pal, S.K.; Member, S.; Mitra, S.; Member, S. Multilayer Perceptron, Fuzzy Sets, and Classification. IEEE Trans. Neural Netw. 1992, 3, 683–697. [Google Scholar] [CrossRef]
- Maxwell, A.E.; Warner, T.A.; Fang, F. Implementation of machine-learning classification in remote sensing: An applied review. Int. J. Remote Sens. 2018, 39, 2784–2817. [Google Scholar] [CrossRef]
- Singh, A.; Ganapathysubramanian, B.; Singh, A.K.; Sarkar, S. Machine Learning for High-Throughput Stress Phenotyping in Plants. Trends Plant Sci. 2016, 21, 110–124. [Google Scholar] [CrossRef] [PubMed]
- Raza, S.; Prince, G.; Clarkson, J.P.; Rajpoot, N.M. Automatic Detection of Diseased Tomato Plants Using Thermal and Stereo Visible Light Images. PLoS ONE 2015, 10, e0123262. [Google Scholar] [CrossRef] [PubMed]
- Wiesner-Hanks, T.; Wu, H.; Stewart, E.; DeChant, C.; Kaczmar, N.; Lipson, H.; Gore, M.A.; Nelson, R.J. Millimeter-Level Plant Disease Detection From Aerial Photographs via Deep Learning and Crowdsourced Data. Front. Plant Sci. 2019, 10, 1550. [Google Scholar] [CrossRef] [PubMed]
- Dang, L.M.; Ibrahim Hassan, S.; Suhyeon, I.; Kumar Sangaiah, A.; Mehmood, I.; Rho, S.; Seo, S.; Moon, H. UAV based wilt detection system via convolutional neural networks. Sustain. Comput. Inform. Syst. 2020, 28, 100250. [Google Scholar] [CrossRef]
- Rumpf, T.; Mahlein, A.K.; Steiner, U.; Oerke, E.C.; Dehne, H.W.; Plümer, L. Early detection and classification of plant diseases with Support Vector Machines based on hyperspectral reflectance. Comput. Electron. Agric. 2010, 74, 91–99. [Google Scholar] [CrossRef]
- Sarkar, S.; Thomason, W.; Cazenave, A.; Abbot, L.; Balota, M.; Oakes, J.; Mccall, D. High-throughput measurement of peanut canopy height using digital surface models. Plant Phenome J. 2020, 3, e20003. [Google Scholar] [CrossRef]
- Sarkar, S.; Cazenave, A.B.; Oakes, J.; McCall, D.; Thomason, W.; Abbott, L.; Balota, M. Aerial high-throughput phenotyping of peanut leaf area index and lateral growth. Sci. Rep. 2021, 11, 21661. [Google Scholar] [CrossRef] [PubMed]
- Brunno, J.; Souza, C.; Luns, S.; De Almeida, H.; De Oliveira, M.F. Integrating Satellite and UAV Data to Predict Peanut Maturity upon Artificial Neural Networks. Agronomy 2022, 12, 1512. [Google Scholar] [CrossRef]
- Chapu, I.; Okello, D.K.; Okello, R.C.O.; Odong, T.L.; Sarkar, S.; Balota, M. Exploration of alternative approaches to phenotyping of late leaf spot and groundnut rosette virus disease for groundnut breeding. Front. Plant Sci. 2022, 13, 912332. [Google Scholar] [CrossRef]
- Sie, E.K.; Oteng-Frimpong, R.; Kassim, Y.B.; Puozaa, D.K.; Adjebeng-Danquah, J.; Masawudu, A.R.; Ofori, K.; Danquah, A.; Cazenave, A.B.; Hoisington, D.; et al. RGB-image method enables indirect selection for leaf spot resistance and yield estimation in a groundnut breeding program in Western Africa. Front. Plant Sci. 2022, 13, 957061. [Google Scholar] [CrossRef]
- Achola, E.; Wasswa, P.; Fonceka, D.; Paul, J.; Prasad, C.; Ozias, P.; Jean, A.; Rami, F.; Michael, C.; David, D.; et al. Genome-wide association studies reveal novel loci for resistance to groundnut rosette disease in the African core groundnut collection. Theor. Appl. Genet. 2023, 136, 35. [Google Scholar] [CrossRef] [PubMed]
- Conde, S.; Rami, J.-F.; Okello, D.K.; Sambou, A.; Muitia, A.; Oteng-Frimpong, R.; Makweti, L.; Sako, D.; Faye, I.; Chintu, J.; et al. The groundnut improvement network for Africa (GINA) germplasm collection: A unique genetic resource for breeding and gene discovery. G3 Genes Genomes Genet. 2024, 14, jkad244. [Google Scholar] [CrossRef] [PubMed]
- Kefauver, S.C.; Romero, A.G.; Buchaillot, M.L.; Vergara-Diaz, O.; Fernandez-Gallego, J.A.; El-Haddad, G.; Akl, A.; Araus, J.L. Open-Source Software for Crop Physiological Assessments Using High Resolution RGB Images. In Proceedings of the IGARSS 2020-2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 4359–4362. [Google Scholar] [CrossRef]
- Rueden, C.T.; Schindelin, J.; Hiner, M.C.; DeZonia, B.E.; Walter, A.E.; Arena, E.T.; Eliceiri, K.W. ImageJ2: ImageJ for the next generation of scientific image data. BMC Bioinform. 2017, 18, 1–26. [Google Scholar] [CrossRef] [PubMed]
- Schindelin, J.; Arganda-Carreras, I.; Frise, E.; Kaynig, V.; Longair, M.; Pietzsch, T.; Preibisch, S.; Rueden, C.; Saalfeld, S.; Schmid, B.; et al. Fiji: An open-source platform for biological-image analysis. Nat. Methods 2012, 9, 676–682. [Google Scholar] [CrossRef] [PubMed]
- Cheng, H.D.; Jiang, X.H.; Sun, Y.; Wang, J. Color image segmentation: Advances and prospects. Pattern Recognit. 2001, 34, 2259–2281. [Google Scholar] [CrossRef]
- Casadesus, J.; Kaya, Y.; Bort, J.; Nachit, M.M.; Araus, J.L.; Amor, S.; Ferrazzano, G.; Maalouf, F. Using vegetation indices derived from conventional digital cameras as selection criteria for wheat breeding in water-limited environments. Ann. Appl. Biol. 2007, 150, 227–236. [Google Scholar] [CrossRef]
- Zaman-Allah, M.; Vergara, O.; Araus, J.L.; Tarekegne, A.; Magorokosho, C.; Tejada, P.J.Z.; Hornero, A. Unmanned aerial platform-based multi-spectral imaging for field phenotyping of maize. Plant Methods 2015, 11, 35. [Google Scholar] [CrossRef] [PubMed]
- Sarkar, S.; Oakes, J.; Cazenave, A.-B.; Burow, M.D.; Bennett, R.S.; Chamberlin, K.D.; Wang, N.; White, M.; Payton, P.; Mahan, J.; et al. Evaluation of the US peanut germplasm mini-core collection in the Virginia-Carolina region using traditional and new high-throughput methods. Agronomy 2022, 12, 1945. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2023. [Google Scholar]
- Max, A.; Wing, J.; Weston, S.; Williams, A.; Keefer, C.; Engelhardt, A.; Cooper, T.; Mayer, Z.; Ziem, A.; Scrucca, L.; et al. Package ‘caret’ R Topics Documented. 2021. Available online: https://cran.r-project.org/web/packages/caret/caret.pdf (accessed on 22 March 2024).
- Taunk, K.; De, S.; Verma, S.; Swetapadma, A. A brief review of nearest neighbor algorithm for learning and classification. In Proceedings of the 2019 International Conference on Intelligent Computing and Control Systems (ICCS), Madurai, India, 15–17 May 2019; pp. 1255–1260. [Google Scholar]
- Chen, S.; Webb, G.I.; Liu, L.; Ma, X. A novel selective naïve Bayes algorithm. Knowl.-Based Syst. 2020, 192, 105361. [Google Scholar] [CrossRef]
- Xanthopoulos, P.; Pardalos, P.M.; Trafalis, T.B.; Xanthopoulos, P.; Pardalos, P.M.; Trafalis, T.B. Linear discriminant analysis. In Robust Data Mining; Springer: Berlin/Heidelberg, Germany, 2013; pp. 27–33. [Google Scholar] [CrossRef]
- Jeppesen, J.H.; Jacobsen, R.H.; Inceoglu, F.; Toftegaard, T.S. A cloud detection algorithm for satellite imagery based on deep learning. Remote Sens. Environ. 2019, 229, 247–259. [Google Scholar] [CrossRef]
- Butler, D. Weather Requirements for Infection by Late Leaf Spot in Groundnut. International Crops Research Institute for the Semi-Arid Tropics: Patancheruvu, India, 1990. [Google Scholar]
- Wadia, K.; Butler, D. Relationship between temperature and latent periods of rust and leaf-spot diseases of groundnut. Plant Pathol. 1994, 43, 121–129. [Google Scholar] [CrossRef]
- Okello, D.K.; Deom, C.M.; Puppala, N.; Monyo, E.; Bravo-Ureta, B. Registration of ‘Serenut 5R’ Groundnut. J. Plant Regist. 2016, 10, 115–118. [Google Scholar] [CrossRef]
- Okello, D.K.; Deom, C.M.; Puppala, N. Registration of ‘Naronut 1R’ groundnut. J. Plant Regist. 2023, 17, 40–46. [Google Scholar] [CrossRef]
- Amare, K.; Seltene, A.; Daniel, E.; Jemal, A.; Addisu, G.; Aliyi, R.; Yohanese, P. East African Journal of Sciences (2017) Registration of ‘Babile-1’, ‘Babile-2’, and ‘Babile-3’ Groundnut Varieties 2. Agronomic and Morphological. East Afr. J. Sci. 2017, 11, 59–64. [Google Scholar]
- Kavzoglu, T. Environmental Modelling & Software Increasing the accuracy of neural network classification using refined training data. Environ. Model. Softw. 2009, 24, 850–858. [Google Scholar] [CrossRef]
- Ghorbani, M.A.; Khatibi, R.; Hosseini, B.; Bilgili, M. Relative importance of parameters affecting wind speed prediction using artificial neural networks. Theor. Appl. Climatol. 2013, 114, 107–114. [Google Scholar] [CrossRef]
- Yoosefzadeh-najafabadi, M.; Earl, H.J.; Tulpan, D.; Sulik, J.; Eskandari, M. Application of Machine Learning Algorithms in Plant Breeding: Predicting Yield from Hyperspectral Reflectance in Soybean. Front. Plant Sci. 2021, 11, 624273. [Google Scholar] [CrossRef] [PubMed]
- Hesami, M.; Condori-apfata, J.A.; Valencia, M.V.; Mohammadi, M. Application of Artificial Neural Network for Modeling and Studying In Vitro Genotype-Independent Shoot Regeneration in Wheat. Appl. Sci. 2020, 10, 5370. [Google Scholar] [CrossRef]
- Etminan, A.; Pour-Aboughadareh, A.; Mohammadi, R.; Shooshtari, L.; Yousefiazarkhanian, M.; Moradkhani, H. Determining the best drought tolerance indices using artificial neural network (ANN): Insight into application of intelligent agriculture in agronomy and plant breeding. Cereal Res. Commun. 2019, 47, 170–181. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, M.; Zhu, J.; Geng, S. Spectral prediction of Phytophthora infestans infection on tomatoes using artificial neural network (ANN). Int. J. Remote Sens. 2008, 29, 1693–1706. [Google Scholar] [CrossRef]
- Wu, D.; Feng, L.; Zhang, C.; He, Y. Early detection of Botrytis cinerea on eggplant leaves based on visible and near-infrared spectroscopy. Trans. ASABE 2008, 51, 1133–1139. [Google Scholar] [CrossRef]
- Huang, K.Y. Application of artificial neural network for detecting Phalaenopsis seedling diseases using color and texture features. Comput. Electron. Agric. 2007, 57, 3–11. [Google Scholar] [CrossRef]
- Cabrera-Bosquet, L.; Crossa, J.; Von Zitzewitz, J.; Serret, M.D.; Araus, L. High-throughput Phenotyping and Genomic Selection: The Frontiers of Crop Breeding Converge Genomic Selection: A Step Forward from. J. Integr. Plant Biol. 2012, 54, 312–320. [Google Scholar] [CrossRef] [PubMed]
- Gann, D.; Richards, J. Scaling of classification systems—Effects of class precision on detection accuracy from medium resolution multispectral data. Landsc. Ecol. 2023, 38, 659–687. [Google Scholar] [CrossRef]
- Dwivedi, S.L.; Goldman, I.; Ceccarelli, S.; Ortiz, R. Advanced Analytics, Phenomics and Biotechnology Approaches to Enhance Genetic Gains in Plant Breeding, 1st ed.; Elsevier Inc.: Amsterdam, The Netherlands, 2020; Volume 162. [Google Scholar]
- Baranowski, P.; Jedryczka, M.; Mazurek, W.; Babula-Skowronska, D.; Siedliska, A.; Kaczmarek, J. Hyperspectral and thermal imaging of oilseed rape (Brassica napus) response to fungal species of the genus Alternaria. PLoS ONE 2015, 10, e0122913. [Google Scholar] [CrossRef]
- Govardhan, M.; Veena, M.B. Diagnosis of Tomato Plant Diseases using Random Forest. In Proceedings of the 2019 Global Conference for Advancement in Technology (GCAT), Bangaluru, India, 18–20 October 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Wójtowicz, A.; Piekarczyk, J.; Czernecki, B.; Ratajkiewicz, H. A random forest model for the classification of wheat and rye leaf rust symptoms based on pure spectra at leaf scale. J. Photochem. Photobiol. B Biol. 2021, 223, 112278. [Google Scholar] [CrossRef] [PubMed]
- Caelen, O. A Bayesian interpretation of the confusion matrix. Ann. Math. Artif. Intell. 2017, 81, 429–450. [Google Scholar] [CrossRef]
- Oteng-Frimpong, R.; Karikari, B.; Sie, E.K.; Kassim, Y.B.; Puozaa, D.K.; Rasheed, M.A.; Fonceka, D.; Okello, D.K.; Balota, M.; Burow, M.; et al. Multi-locus genome-wide association studies reveal genomic regions and putative candidate genes associated with leaf spot diseases in African groundnut (Arachis hypogaea L.) germplasm. Front. Plant Sci. 2023, 13, 1076744. [Google Scholar] [CrossRef]
- Liu, H.Q.; Huete, A. Feedback based modification of the NDVI to minimize canopy background and atmospheric noise. IEEE Trans. Geosci. Remote Sens. 1995, 33, 457–465. [Google Scholar] [CrossRef]
- Kassim, Y.B.; Oteng-Frimpong, R.; Puozaa, D.K.; Sie, E.K.; Abdul Rasheed, M.; Abdul Rashid, I.; Danquah, A.; Akogo, D.A.; Rhoads, J.; Hoisington, D.; et al. High-Throughput Plant Phenotyping (HTPP) in Resource-Constrained Research Programs: A Working Example in Ghana. Agronomy 2022, 12, 2733. [Google Scholar] [CrossRef]
- Crain, J.L.; Wei, Y.; Barker, J.; Thompson, S.M.; Alderman, P.D.; Reynolds, M.; Zhang, N.; Poland, J. Development and Deployment of a Portable Field Phenotyping Platform. Crop Sci. 2016, 56, 965. [Google Scholar] [CrossRef]
- Andrade-Sanchez, P.; Gore, M.A.; Heun, J.T.; Thorp, K.R.; Carmo-Silva, A.E.; French, A.N.; Salvucci, M.E.; White, J.W. Development and evaluation of a field-based high-throughput phenotyping platform. Funct. Plant Biol. 2014, 41, 68–79. [Google Scholar] [CrossRef] [PubMed]
- Lane, H.M.; Murray, S.C. High throughput can produce better decisions than high accuracy when phenotyping plant populations. Crop Sci. 2021, 61, 3301–3313. [Google Scholar] [CrossRef]
- Bali, N.; Singla, A. Emerging Trends in Machine Learning to Predict Crop Yield and Study Its Influential Factors: A Survey. Arch. Comput. Methods Eng. 2022, 29, 95–112. [Google Scholar] [CrossRef]
- Zhou, Z.-H. Ensemble Learning BT—Encyclopedia of Biometrics; Li, S.Z., Jain, A., Eds.; Springer: Boston, MA, USA, 2009; pp. 270–273. [Google Scholar]
- Feng, L.; Zhang, Z.; Ma, Y.; Du, Q.; Williams, P.; Drewry, J.; Luck, B. Alfalfa yield prediction using UAV-based hyperspectral imagery and ensemble learning. Remote Sens. 2020, 12, 2028. [Google Scholar] [CrossRef]
- Vasilakos, C.; Kavroudakis, D.; Georganta, A. Machine Learning Classification Ensemble of Multitemporal Sentinel-2 Images: The Case of a Mixed Mediterranean Ecosystem. Remote Sens. 2020, 12, 2005. [Google Scholar] [CrossRef]

| Market Types | |||||
|---|---|---|---|---|---|
| Country of Origin | Hybrid | Spanish | Valencia | Virginia | Total |
| Ghana | 3 | 16 | 2 | 15 | 36 |
| Malawi | 9 | 9 | 1 | 8 | 27 |
| Mali | 1 | 17 | - | 3 | 21 |
| Mozambique | - | 13 | 1 | 4 | 18 |
| Niger | 9 | 24 | 1 | - | 34 |
| Senegal | 1 | 7 | - | 9 | 17 |
| Togo | 2 | 6 | 2 | 4 | 14 |
| Uganda | 3 | 15 | 4 | 20 | 42 |
| Zambia | 4 | 3 | 7 | 14 | |
| Total | 32 | 110 | 11 | 70 | 223 |
| Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Weather Parameters | Serere, 2020 | |||||||||||
| Av. Temperature (°C) | 24.3 | 25.1 | 24.6 | 23.9 | 22.8 | 21.5 | 21 | 22.2 | 23.1 | 22.8 | 23.4 | 23.8 |
| Relative humidity (%) | 67.9 | 64.9 | 75.1 | 76.7 | 82.8 | 83.8 | 82.1 | 79.4 | 77.6 | 80.4 | 75.1 | 63.2 |
| Wind speed (m/s) | 1.9 | 2.1 | 1.5 | 1.5 | 1.3 | 1.6 | 1.6 | 1.2 | 1.3 | 1.2 | 1.8 | 2.1 |
| Precipitation (mm) | 63.3 | 73.8 | 189.8 | 242.6 | 195.1 | 142.4 | 152.9 | 116 | 342.8 | 189.8 | 94.9 | 31.6 |
| Nakabango, 2021 | ||||||||||||
| Av. Temperature (°C) | 22.6 | 22.9 | 23.4 | 22 | 21.9 | 21.5 | 21.4 | 22.8 | 22.4 | 23.4 | 22.8 | 23.4 |
| Relative humidity (%) | 73.6 | 74 | 74.4 | 83.7 | 83 | 79.5 | 73.8 | 71.2 | 75.4 | 73.6 | 77.1 | 72.9 |
| Wind speed (m/s) | 1.5 | 1.6 | 1.7 | 1.5 | 1.4 | 2.0 | 2.4 | 1.7 | 1.5 | 1.4 | 1.4 | 1.5 |
| Precipitation (mm) | 163.5 | 42.2 | 100.2 | 227.1 | 98.8 | 23.5 | 12.4 | 25 | 96.5 | 119.3 | 186.9 | 100.2 |
| Nyankapala, 2021 | ||||||||||||
| Av. Temperature (°C) | 27.6 | 29.3 | 30.6 | 31.3 | 29.8 | 28.4 | 26.8 | 26 | 26.4 | 27.3 | 27.8 | 26.1 |
| Relative humidity (%) | 35.7 | 29.4 | 52.6 | 55.9 | 67.6 | 71.7 | 78.8 | 83.4 | 82.7 | 80.1 | 68.9 | 49.3 |
| Wind speed (m/s) | 2.7 | 2.6 | 2.4 | 2.6 | 2.2 | 2.0 | 2.1 | 1.6 | 1.3 | 1.3 | 1.3 | 2.4 |
| Precipitation (mm) | 0 | 0 | 15.8 | 55.3 | 101 | 83.3 | 161.9 | 261 | 173.1 | 126.9 | 14.3 | 0.1 |
| RGB Indices | Basis of Derivation | Reference |
|---|---|---|
| Hue | Color description in form of angles [0–360° (0°—red; 60°—yellow; 120°—green; 240°—blue)] | [43] |
| a* | Green (−a*)–red (+a*) component in CIE-Lab color space | [43] |
| b* | Blue (−b*)–yellow (+b*) component in CIE-Lab color space | [43] |
| u* | Green (−u*)–red (+u*) component in CIE-Luv color space | [43] |
| v* | Blue (−v*)–yellow (+v*) component in CIE-Luv color space | [43] |
| Green Area (GA) | Percentage of Pixels from 60–120° of the hue angle | [44] |
| Greener Area (GGA) | Percentage of Pixels from 80–120° of the hue angle | [44] |
| Crop Senescence Index (CSI) | [45] | |
| Greenness index (GI) | [46] | |
| Greenness Product Index (GPI) | [46] | |
| Normalized Greenness Product Index (NGPI) | [46] |
| Metric (%) | ANN | KNN | LDA | PLSC | NB | RF | SLC | SVM |
|---|---|---|---|---|---|---|---|---|
| Accuracy | 88.85 | 89.59 | 85.90 | 85.99 | 83.41 | 90.05 | 87.65 | 86.73 |
| Kappa | 64.09 | 63.75 | 47.06 | 44.37 | 50.57 | 66.25 | 56.75 | 52.56 |
| Sensitivity | 92.2 | 94.92 | 94.69 | 96.16 | 86.44 | 94.46 | 93.90 | 93.90 |
| Precision | 94.01 | 92.51 | 88.77 | 87.82 | 92.73 | 93.41 | 91.22 | 90.23 |
| Recall | 92.2 | 94.92 | 94.69 | 96.16 | 86.44 | 94.46 | 93.90 | 93.90 |
| F1 | 93.1 | 93.70 | 91.63 | 91.80 | 89.47 | 93.93 | 92.54 | 92.03 |
| Specificity | 74.00 | 66.00 | 47.00 | 41.00 | 70.00 | 71.00 | 60.00 | 55.00 |
| 3 Classes | 4 Classes | |||
|---|---|---|---|---|
| Model | Accuracy | Kappa | Accuracy | Kappa |
| ANN | 76.10 | 62.22 | 74.45 | 65.89 |
| KNN | 77.42 | 64.25 | 73.36 | 64.19 |
| LDA | 72.07 | 55.25 | 67.10 | 55.56 |
| NB | 62.86 | 42.21 | 57.51 | 43.01 |
| PLSC | 68.66 | 49.57 | 65.90 | 54.04 |
| RF | 77.60 | 64.75 | 72.81 | 63.51 |
| SLC | 72.72 | 56.85 | 69.86 | 59.54 |
| SVM | 68.20 | 49.43 | 63.04 | 50.27 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chapu, I.; Chandel, A.; Sie, E.K.; Okello, D.K.; Oteng-Frimpong, R.; Okello, R.C.O.; Hoisington, D.; Balota, M. Comparing Regression and Classification Models to Estimate Leaf Spot Disease in Peanut (Arachis hypogaea L.) for Implementation in Breeding Selection. Agronomy 2024, 14, 947. https://doi.org/10.3390/agronomy14050947
Chapu I, Chandel A, Sie EK, Okello DK, Oteng-Frimpong R, Okello RCO, Hoisington D, Balota M. Comparing Regression and Classification Models to Estimate Leaf Spot Disease in Peanut (Arachis hypogaea L.) for Implementation in Breeding Selection. Agronomy. 2024; 14(5):947. https://doi.org/10.3390/agronomy14050947
Chicago/Turabian StyleChapu, Ivan, Abhilash Chandel, Emmanuel Kofi Sie, David Kalule Okello, Richard Oteng-Frimpong, Robert Cyrus Ongom Okello, David Hoisington, and Maria Balota. 2024. "Comparing Regression and Classification Models to Estimate Leaf Spot Disease in Peanut (Arachis hypogaea L.) for Implementation in Breeding Selection" Agronomy 14, no. 5: 947. https://doi.org/10.3390/agronomy14050947
APA StyleChapu, I., Chandel, A., Sie, E. K., Okello, D. K., Oteng-Frimpong, R., Okello, R. C. O., Hoisington, D., & Balota, M. (2024). Comparing Regression and Classification Models to Estimate Leaf Spot Disease in Peanut (Arachis hypogaea L.) for Implementation in Breeding Selection. Agronomy, 14(5), 947. https://doi.org/10.3390/agronomy14050947







