Non-Destructive Classification of Maize Seeds Based on RGB and Hyperspectral Data with Improved Grey Wolf Optimization Algorithms
Abstract
1. Introduction
| Sorting Technology | Data Type | Model | Number of Varieties and Categories | Accuracy | Ref. |
|---|---|---|---|---|---|
| Machine learning | NIRS | DT, SVM, RF, MLP, NB | 7 types of pine nuts | Each model achieved 80% | Huang [27] |
| Hyperspectral | ELM | 5 types of wheat | 86.26% | Bao [28] | |
| RGB | MLP, LDA, SVM etc. | 5 types of maize | Each model achieved 93% | Xu [29] | |
| Deep learning | RGB | MF Swin-Transformer | 19 types of maize | 96.47% | Bi [30] |
| Hyperspectral image | CNN-LSTM | 5 types of maize | 95.26% | Wang [31] | |
| NIRS | CNN, RNN, LSTM, etc. | 4 years of cotton seeds | Each model achieved 93.5% | Duan [32] | |
| RGB+NIRS | 2Branch-CNN | 10 types of rice | 98% | Ye [33] | |
| RGB+NIRS | BP Neural Network | 10 types of maize | 97.7 | Yang [34] |
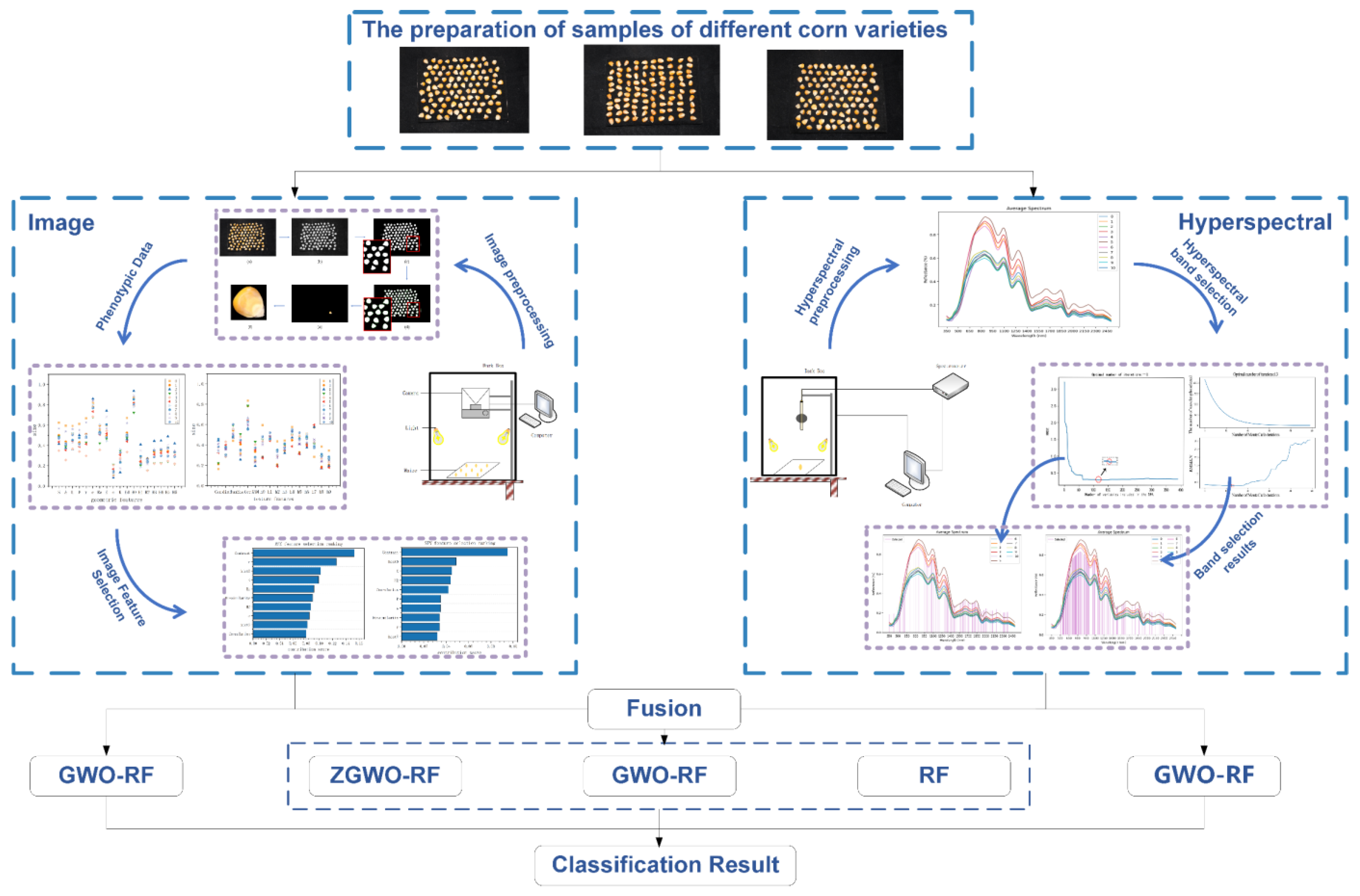
2. Materials and Methods
2.1. Data Acquisition
2.1.1. Image Data Acquisition
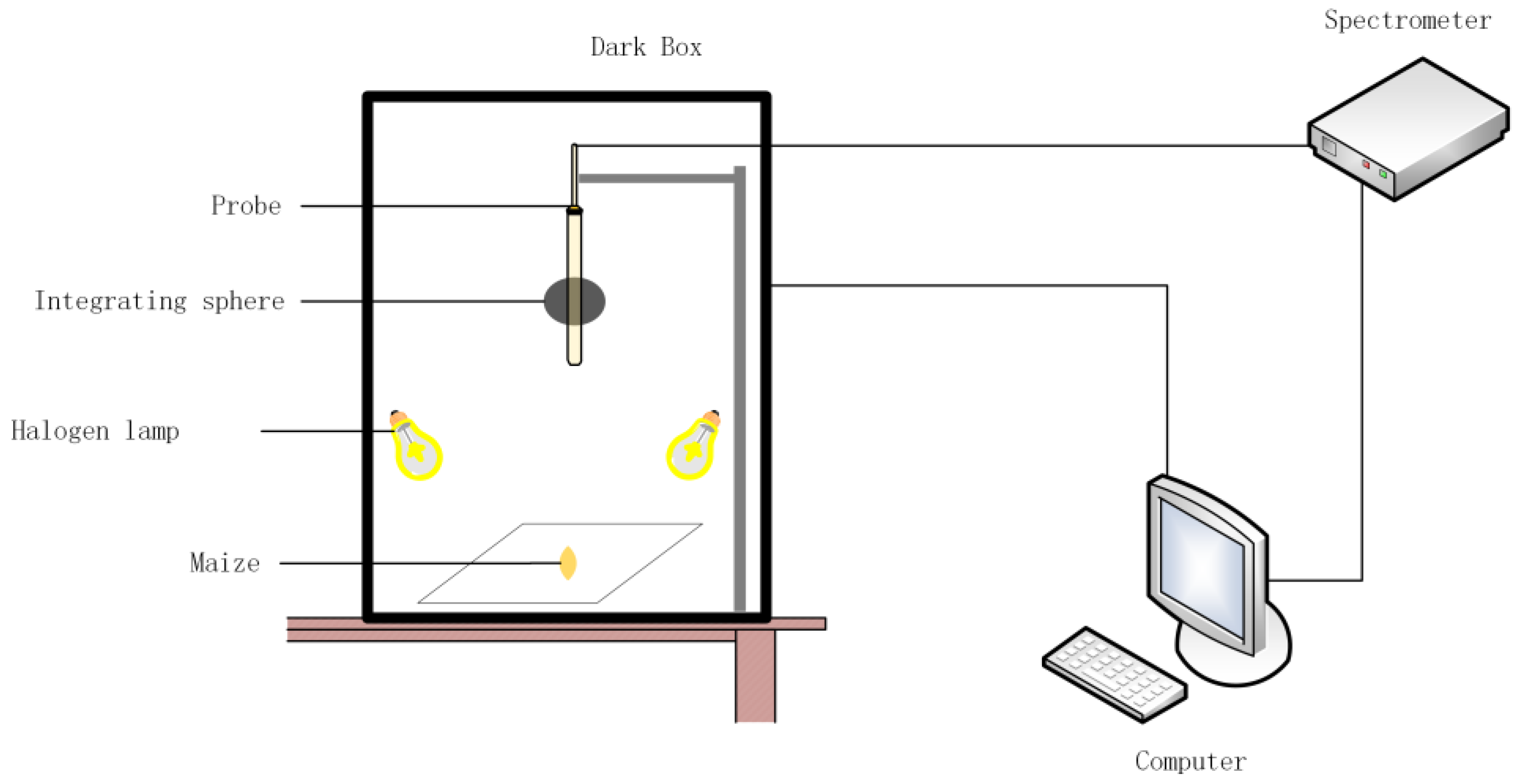
2.1.2. Hyperspectral Data Acquisition
2.2. Experimental Procedure
2.3. Data Preprocessing
2.3.1. Image Data Preprocessing
2.3.2. Hyperspectral Data Preprocessing
2.4. Maize Seed Classification odel
2.4.1. Random Forest Classification Model
2.4.2. Grey Wolf Optimization Algorithm and Its Improvements
2.4.3. Classification Model Based on ZGWO-RF
- (1)
- Create new populations by utilizing reverse learning to establish wolves based on a hierarchy and initialize packs of wolves.
- (2)
- Determine the fitness of every single wolf pack and use the RF model to rank them from smallest to largest.
- (3)
- Determine the fitness and make public the version of (4) for the head wolf.
- (4)
- Relocate every wolf in the pack to their new location.
- (5)
- Sort, recalculate the fitness value, and feed back to the RF model.
- (6)
- Check to see if the maximum number of iterations has been reached and output if it has; if not, go back to steps (3)–(5).
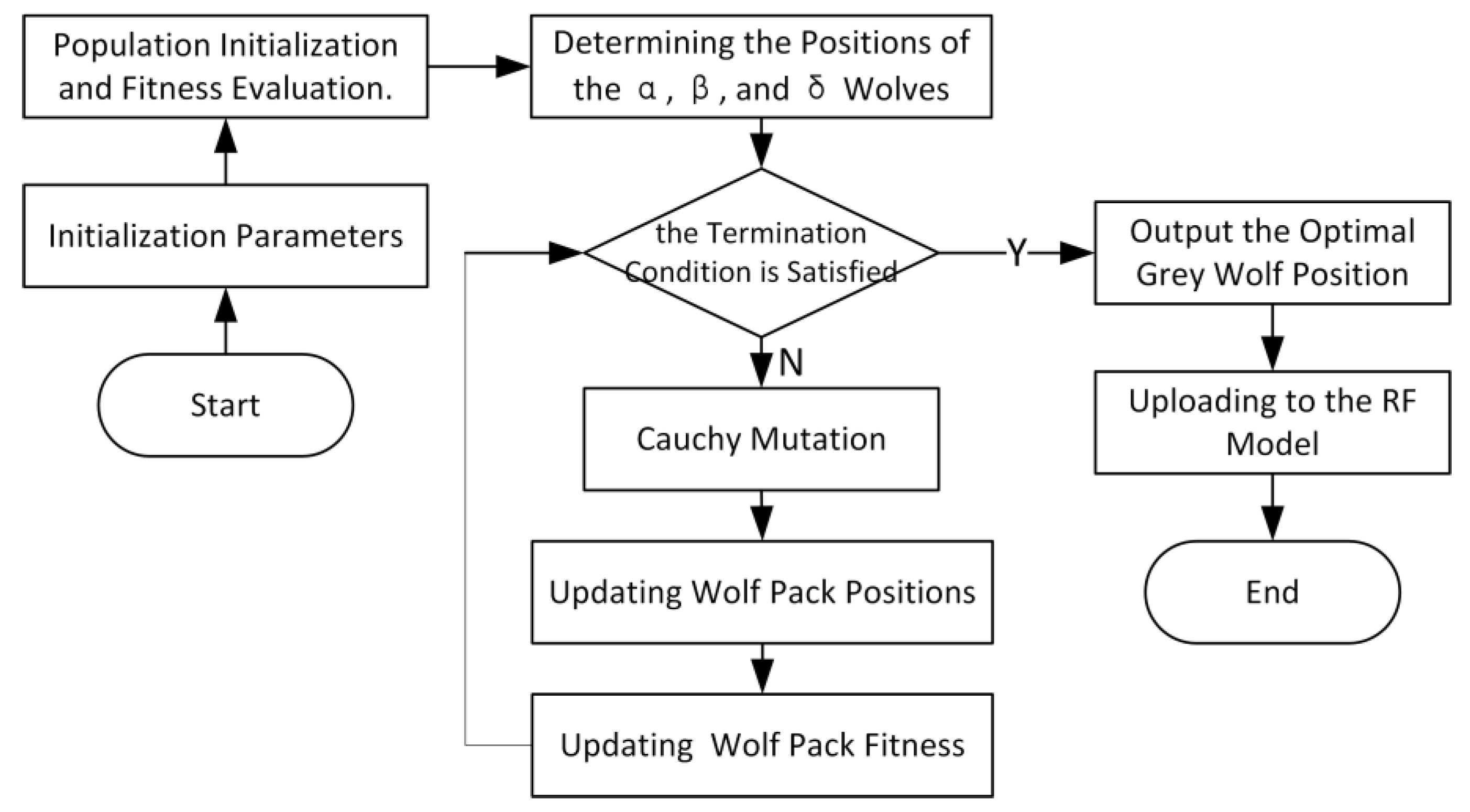
2.5. Classification Model Evaluation Indicators
3. Results and Discussion
3.1. Construction of a Classification Model for Morphological Traits of Maize Seeds
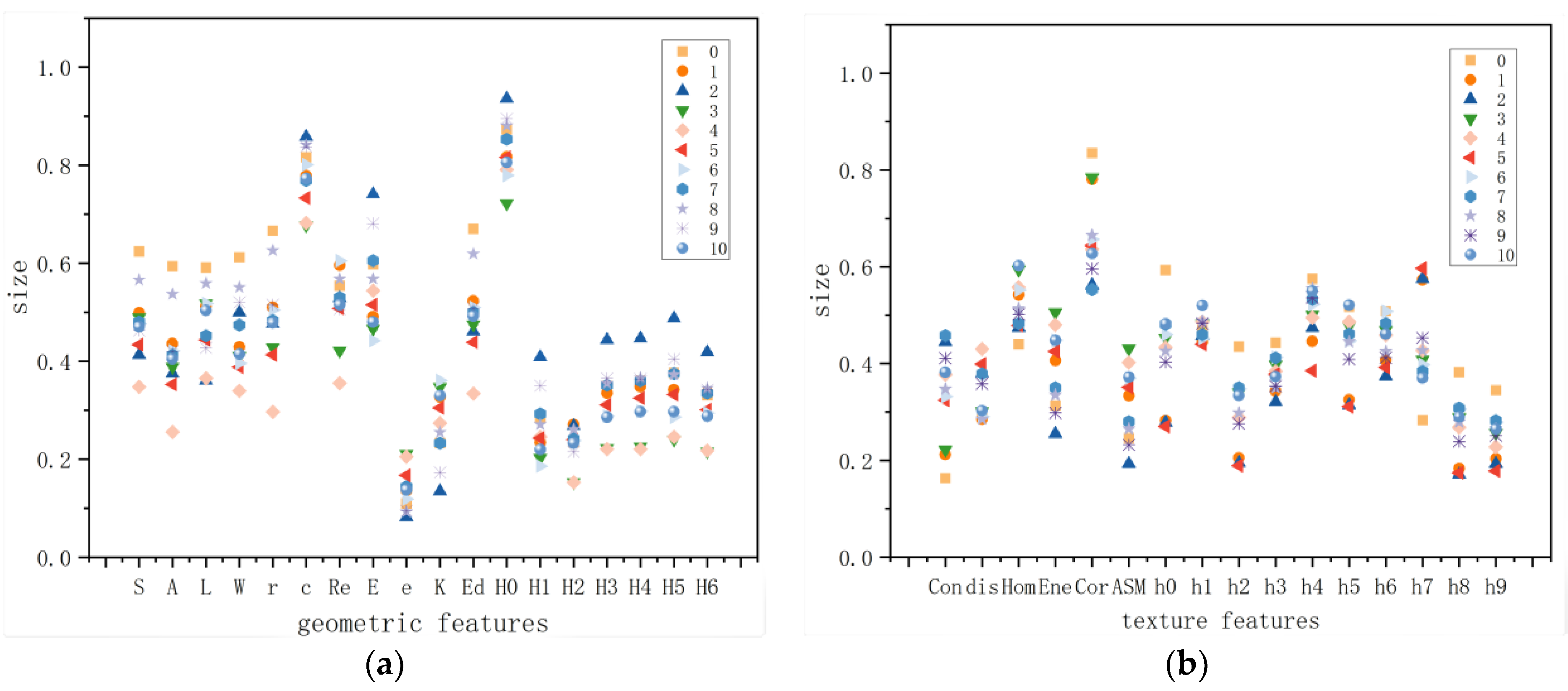
3.1.1. Parameter Analysis Based on Morphological Feature Averages
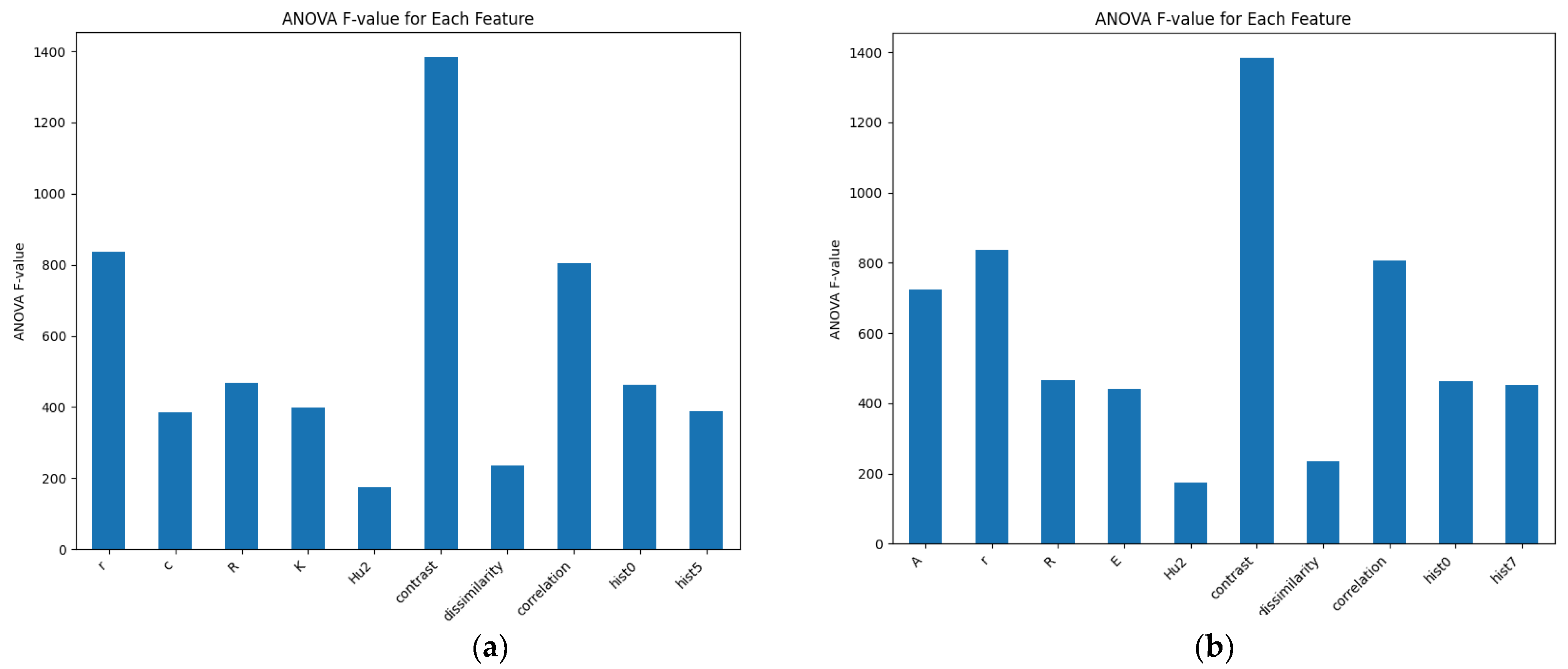
3.1.2. Morphological Feature Selection Using RFE and SFM
- (1)
- RFE
- (2)
- SFM
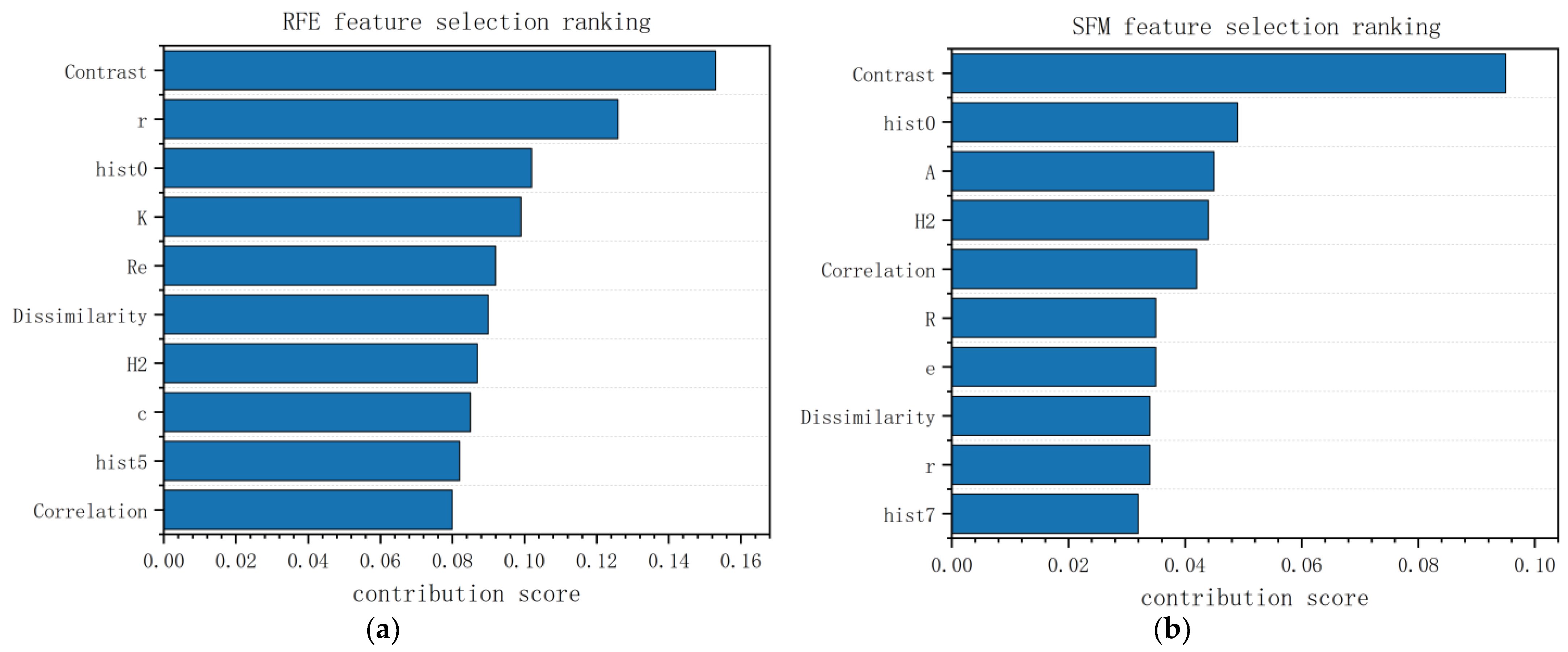
3.1.3. Maize Seed Morphological Feature Classification Model Based on GWO-RF
3.2. Construction of a Classification Model for Hyperspectral Data of Maize Seeds
3.2.1. Spectral Curve Analysis
3.2.2. Selection of Hyperspectral Feature Bands Using SPA and CARS
- (1)
- SPA
- (2)
- CARS
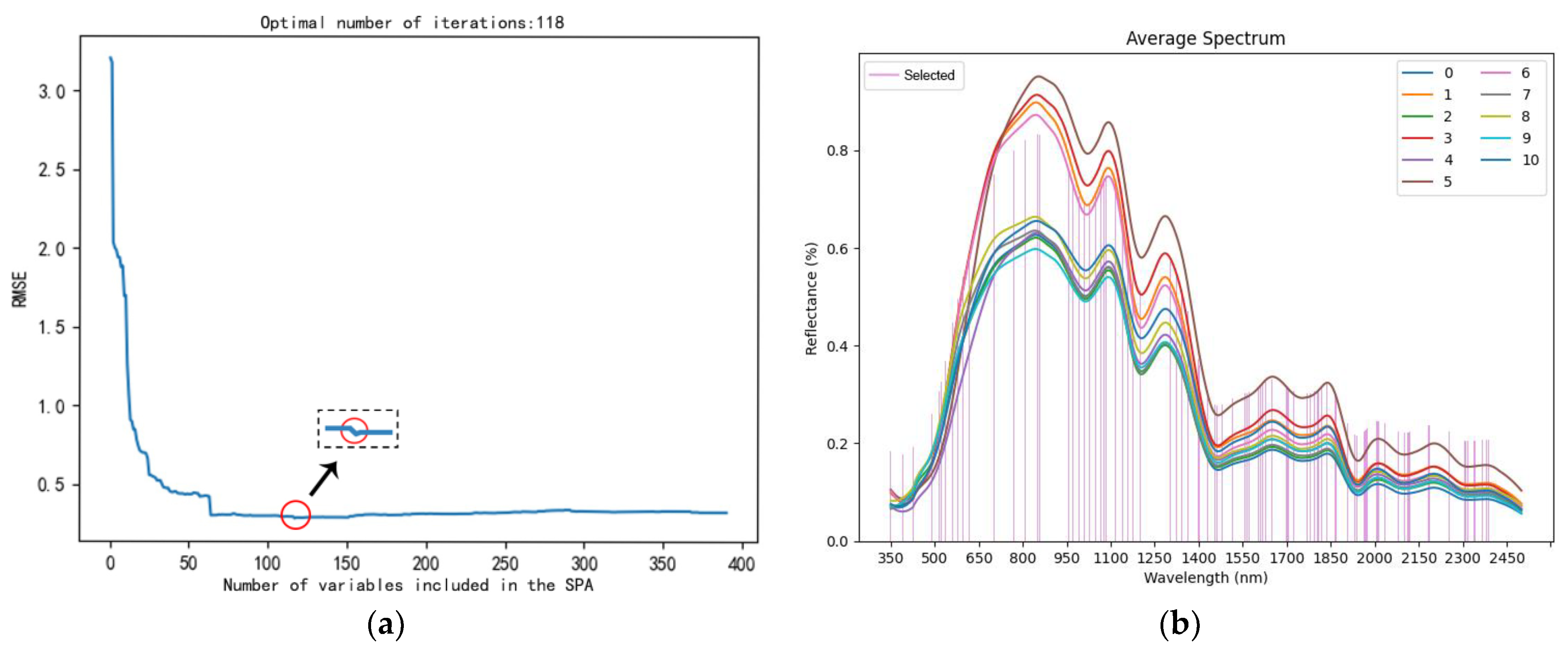

3.2.3. Maize Seed Hyperspectral Data Classification Model Based on GWO-RF
3.3. Construction of a Maize Seed Classification Model Based on GWO-RF Feature Fusion
3.4. Classification Model of Maize Seeds Based on Improved Grey Wolf Optimization Algorithm
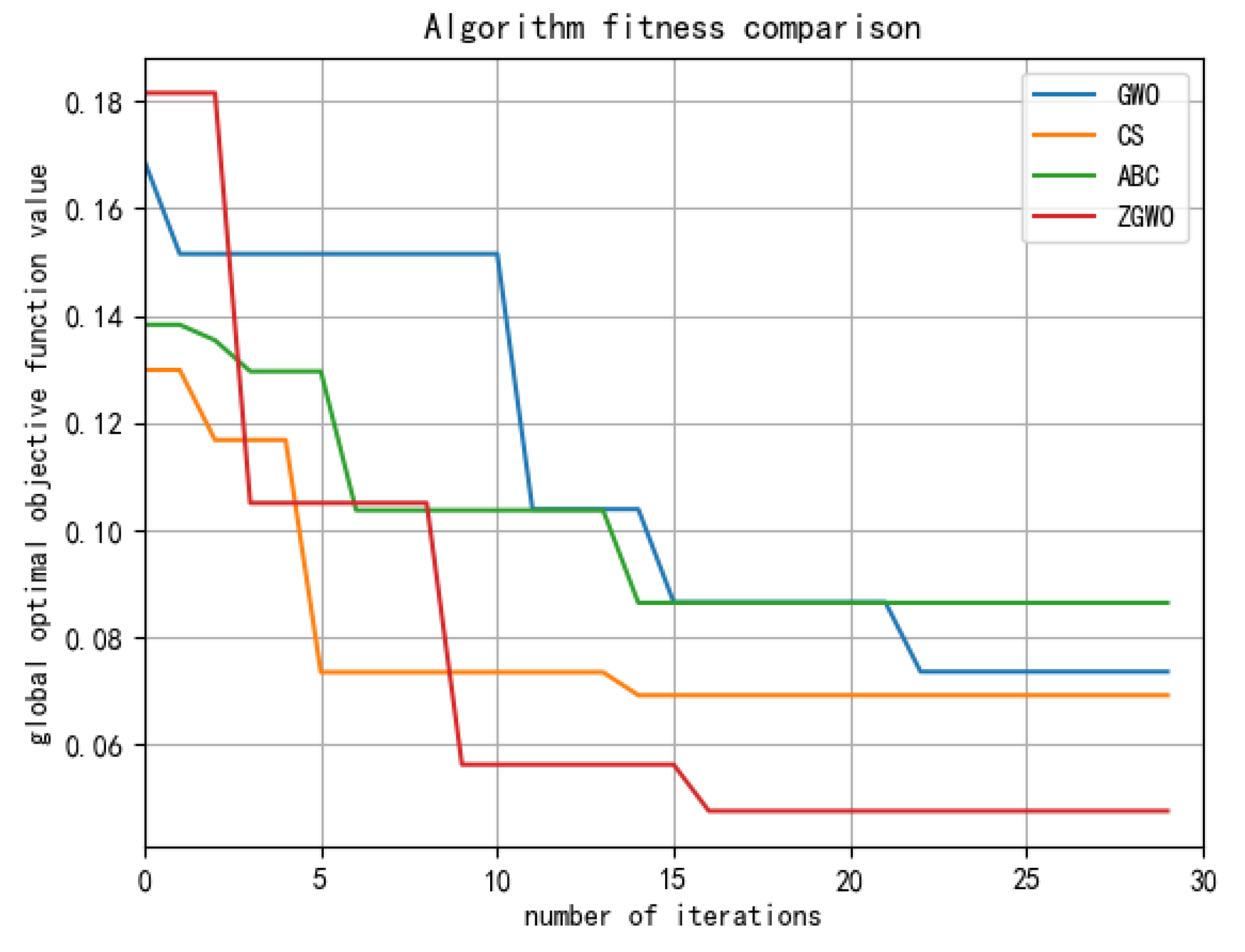
3.4.1. The Comparative Experimental Analysis
3.4.2. Analysis of Classification Results
3.4.3. Confusion Matrix
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kumar, C.; Mubvumba, P.; Huang, Y.; Dhillon, J.; Reddy, K. Multi-Stage Corn Yield Prediction Using High-Resolution UAV Multispectral Data and Machine Learning Models. Agronomy 2023, 13, 1277. [Google Scholar] [CrossRef]
- Wang, S.; Liu, C.; Han, L.; Li, T.; Yang, G.; Chen, T. Corn Grain or Corn Silage: Effects of the Grain-to-Fodder Crop Conversion Program on Farmers’ Income in China. Agriculture 2022, 12, 976. [Google Scholar] [CrossRef]
- Shah, A.N.; Tanveer, M.; Abbas, A.; Yildirim, M.; Shah, A.A.; Ahmad, M.I.; Wang, Z.W.; Sun, W.W.; Song, Y.H. Combating Dual Challenges in Maize Under High Planting Density: Stem Lodging and Kernel Abortion. Front. Plant Sci. 2021, 12, 699085. [Google Scholar] [CrossRef]
- Cui, Y.J.; Xu, L.J.; An, D.; Liu, Z.; Gu, J.C.; Li, S.M.; Zhang, X.D.; Zhu, D.H. Identification of maize seed varieties based on near infrared reflectance spectroscopy and chemometrics. Int. J. Agric. Biol. Eng. 2018, 11, 177–183. [Google Scholar] [CrossRef]
- Yang, S.; Zhu, Q.B.; Huang, M.; Qin, J.W. Hyperspectral Image-Based Variety Discrimination of Maize Seeds by Using a Multi-Model Strategy Coupled with Unsupervised Joint Skewness-Based Wavelength Selection Algorithm. Food Anal. Methods 2017, 10, 424–433. [Google Scholar] [CrossRef]
- Wang, H.; Wang, K.; Wu, J.Z.; Han, P. Progress in Research on Rapid and Non-Destructive Detection of Seed Quality Based on Spectroscopy and Imaging Technology. Spectrosc. Spectr. Anal. 2021, 41, 52–59. [Google Scholar]
- Ali, A.; Qadri, S.; Mashwani, W.K.; Belhaouari, S.B.; Naeem, S.; Rafique, S.; Jamal, F.; Chesneau, C.; Anam, S. Machine learning approach for the classification of corn seed using hybrid features. Int. J. Food Prop. 2020, 23, 1110–1124. [Google Scholar] [CrossRef]
- Zhu, D.Z.; Wang, C.; Pang, B.S.; Shan, F.H.; Wu, Q.; Zhao, C.J. Identification of Wheat Cultivars Based on the Hyperspectral Image of Single Seed. J. Nanoelectron. Optoelectron. 2012, 7, 167–172. [Google Scholar] [CrossRef]
- Lesiak, A.D.; Cody, R.B.; Dane, A.J.; Musah, R.A. Plant Seed Species Identification from Chemical Fingerprints: A High-Throughput Application of Direct Analysis in Real Time Mass Spectrometry. Anal. Chem. 2015, 87, 8748–8757. [Google Scholar] [CrossRef]
- Setimela, P.S.; Warburton, M.L.; Erasmus, T. DNA fingerprinting of open-pollinated maize seed lots to establish genetic purity using simple sequence repeat markers. S. Afr. J. Plant Soil 2016, 33, 141–148. [Google Scholar] [CrossRef]
- Liu, S.X.; Zhang, H.J.; Wang, Z.; Zhang, C.Q.; Li, Y.; Wang, J.X. Determination of maize seed purity based on multi-step clustering. Appl. Eng. Agric. 2018, 34, 659–665. [Google Scholar] [CrossRef]
- Xu, P.; Tan, Q.; Zhang, Y.P.; Zha, X.T.; Yang, S.M.; Yang, R.B. Research on Maize Seed Classification and Recognition Based on Machine Vision and Deep Learning. Agriculture 2022, 12, 232. [Google Scholar] [CrossRef]
- Wang, L.X.; Liu, L.H.; Zhang, F.T.; Li, H.B.; Pang, B.S.; Zhao, C.P. Detecting seed purity of wheat varieties using microsatellite markers based on eliminating the influence of non-homozygous loci. Seed Sci. Technol. 2014, 42, 393–413. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, D.; Liu, J.C.; An, D. Vis-NIR hyperspectral imaging combined with incremental learning for open world maize seed varieties identification. Comput. Electron. Agric. 2022, 199, 107153. [Google Scholar] [CrossRef]
- Huang, S.; Fan, X.F.; Sun, L.; Shen, Y.L.; Suo, X.S. Research on Classification Method of Maize Seed Defect Based on Machine Vision. J. Sens. 2019, 2019, 2716975. [Google Scholar] [CrossRef]
- Yasmin, J.; Lohumi, S.; Ahmed, M.R.; Kandpal, L.M.; Faqeerzada, M.A.; Kim, M.S.; Cho, B.K. Improvement in Purity of Healthy Tomato Seeds Using an Image-Based One-Class Classification Method. Sensors 2020, 20, 2690. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.L.; Hong, H.M.; You, Z.H.; Cheng, F. Spectral and Image Integrated Analysis of Hyperspectral Data for Waxy Corn Seed Variety Classification. Sensors 2015, 15, 15578–15594. [Google Scholar] [CrossRef] [PubMed]
- ElMasry, G.; Mandour, N.; Wagner, M.H.; Demilly, D.; Verdier, J.; Belin, E.; Rousseau, D. Utilization of computer vision and multispectral imaging techniques for classification of cowpea (Vigna unguiculata) seeds. Plant Methods 2019, 15, 24. [Google Scholar] [CrossRef]
- Ma, R.; Wang, J.; Zhao, W.; Guo, H.J.; Dai, D.N.; Yun, Y.L.; Li, L.; Hao, F.Q.; Bai, J.Q.; Ma, D.X. Identification of Maize Seed Varieties Using MobileNetV2 with Improved Attention Mechanism CBAM. Agriculture 2023, 13, 11. [Google Scholar] [CrossRef]
- Bodor, Z.; Majadi, M.; Benedek, C.; Zaukuu, J.L.Z.; Bálint, M.V.; Csobod, E.C.; Kovacs, Z. Detection of Low-Level Adulteration of Hungarian Honey Using near Infrared Spectroscopy. Chemosensors 2023, 11, 89. [Google Scholar] [CrossRef]
- Barreto, L.C.; Martinez-Arias, R.; Schechert, A. Field Detection of Rhizoctonia Root Rot in Sugar Beet by Near Infrared Spectrometry. Sensors 2021, 21, 8068. [Google Scholar] [CrossRef] [PubMed]
- Stejskal, V.; Vendl, T.; Li, Z.H.; Aulicky, R. Efficacy of visual evaluation of insect-damaged kernels of malting barley by Sitophilus granaries from various observation perspectives. J. Stored Prod. Res. 2020, 89, 101711. [Google Scholar] [CrossRef]
- Cui, Y.J.; Ge, W.Z.; Li, J.; Zhang, J.W.; An, D.; Wei, Y.G. Screening of maize haploid kernels based on near infrared spectroscopy quantitative analysis. Comput. Electron. Agric. 2019, 158, 358–368. [Google Scholar] [CrossRef]
- Ambrose, A.; Kandpal, L.M.; Kim, M.S.; Lee, W.H.; Cho, B.K. High speed measurement of corn seed viability using hyperspectral imaging. Infrared Phys. Technol. 2016, 75, 173–179. [Google Scholar] [CrossRef]
- Dong, G.; Guo, J.; Wang, C.; Chen, Z.L.; Zheng, L.; Zhu, D.Z. The Classification of Wheat Varieties Based on Near Infrared Hyperspectral Imaging and Information Fusion. Spectrosc. Spectr. Anal. 2015, 35, 3369–3374. [Google Scholar]
- Jin, S.L.; Zhang, W.D.; Yang, P.F.; Zheng, Y.; An, J.L.; Zhang, Z.Y.; Qu, P.X.; Pan, X.P. Spatial-spectral feature extraction of hyperspectral images for wheat seed identification. Comput. Electr. Eng. 2022, 101, 108077. [Google Scholar] [CrossRef]
- Huang, B.A.S.; Liu, J.; Jiao, J.Y.; Lu, J.; Lv, D.J.; Mao, J.W.; Zhao, Y.J.; Zhang, Y. Applications of machine learning in pine nuts classification. Sci. Rep. 2022, 12, 8799. [Google Scholar] [CrossRef]
- Bao, Y.D.; Mi, C.X.; Wu, N.; Liu, F.; He, Y. Rapid Classification of Wheat Grain Varieties Using Hyperspectral Imaging and Chemometrics. Appl. Sci. 2019, 9, 4119. [Google Scholar] [CrossRef]
- Xu, P.; Yang, R.B.; Zeng, T.W.; Zhang, J.; Zhang, Y.P.; Tan, Q. Varietal classification of maize seeds using computer vision and machine learning techniques. J. Food Process Eng. 2021, 44, e13846. [Google Scholar] [CrossRef]
- Bi, C.G.; Hu, N.; Zou, Y.Q.; Zhang, S.; Xu, S.Z.; Yu, H.L. Development of Deep Learning Methodology for Maize Seed Variety Recognition Based on Improved Swin Transformer. Agronomy 2022, 12, 1843. [Google Scholar] [CrossRef]
- Wang, Y.; Song, S.R. Variety identification of sweet maize seeds based on hyperspectral imaging combined with deep learning. Infrared Phys. Technol. 2023, 130, 104611. [Google Scholar] [CrossRef]
- Duan, L.; Yan, T.Y.; Wang, J.L.; Ye, W.X.; Chen, W.; Gao, P.; Lü, X. Combine Hyperspectral Imaging and Machine Learning to Identify the Age of Cotton Seeds. Spectrosc. Spectr. Anal. 2021, 41, 3857–3863. [Google Scholar]
- Ye, W.C.; Luo, S.Y.; Li, J.H.; Li, Z.R.; Fan, Z.W.; Xu, H.T.; Zhao, J.; Lan, Y.B.; Deng, H.D.; Long, Y.B. Research on Classification Method of Hybrid Rice Seeds Based on the Fusion of Near-Infrared Spectra and Images. Spectrosc. Spectr. Anal. 2023, 43, 2935–2941. [Google Scholar]
- Yang, D.F.; Hu, J. Accurate Identification of Maize Varieties Based on Feature Fusion of Near Infrared Spectrum and Image. Spectrosc. Spectr. Anal. 2023, 43, 2588–2595. [Google Scholar]
- Owoyele, O.; Pal, P.; Torreira, A.V.; Probst, D.; Shaxted, M.; Wilde, M.; Senecal, P.K. Application of an automated machine learning-genetic algorithm (AutoML-GA) coupled with computational fluid dynamics simulations for rapid engine design optimization. Int. J. Engine Res. 2022, 23, 1586–1601. [Google Scholar] [CrossRef]
- Franco, M.A.; Krasnogor, N.; Bacardit, J. Automatic Tuning of Rule-Based Evolutionary Machine Learning via Problem Structure Identification. IEEE Comput. Intell. Mag. 2020, 15, 28–46. [Google Scholar] [CrossRef]
- Yang, L.; Shami, A. On hyperparameter optimization of machine learning algorithms: Theory and practice. Neurocomputing 2020, 415, 295–316. [Google Scholar] [CrossRef]
- Dong, G.R.; Liu, C.Y.; Liu, D.Z.; Mao, X.A. Adaptive Multi-Level Search for Global Optimization: An Integrated Swarm Intelligence-Metamodelling Technique. Appl. Sci. 2021, 11, 2277. [Google Scholar] [CrossRef]
- Mashwani, W.K.; Hamdi, A.; Jan, M.A.; Göktas, A.; Khan, F. Large-scale global optimization based on hybrid swarm intelligence algorithm. J. Intell. Fuzzy Syst. 2020, 39, 1257–1275. [Google Scholar] [CrossRef]
- Tang, J.; Liu, G.; Pan, Q.T. A Review on Representative Swarm Intelligence Algorithms for Solving Optimization Problems: Applications and Trends. IEEE/CAA J. Autom. Sin. 2021, 8, 1627–1643. [Google Scholar] [CrossRef]
- Yildirim, S.; Kaya, Y.; Kiliç, F. A modified feature selection method based on metaheuristic algorithms for speech emotion recognition. Appl. Acoust. 2021, 173, 107721. [Google Scholar] [CrossRef]
- Xie, X.J.; Xia, F.; Wu, Y.F.; Liu, S.Y.; Yan, K.; Xu, H.L.; Ji, Z.W. A Novel Feature Selection Strategy Based on Salp Swarm Algorithm for Plant Disease Detection. Plant Phenomics 2023, 2023, 39. [Google Scholar] [CrossRef]
- Belge, E.; Altan, A.; Hacioglu, R. Metaheuristic Optimization-Based Path Planning and Tracking of Quadcopter for Payload Hold-Release Mission. Electronics 2022, 11, 1208. [Google Scholar] [CrossRef]
- Hamdi, M.; Hilali-Jaghdam, I.; Khayyat, M.M.; Elnaim, B.M.E.; Abdel-Khalek, S.; Mansour, R.F. Chicken Swarm-Based Feature Subset Selection with Optimal Machine Learning Enabled Data Mining Approach. Appl. Sci. 2022, 12, 6787. [Google Scholar] [CrossRef]
- Shao, C.X.; Cheng, F.X.; Mao, S.; Hu, J. Vehicle Intelligent Classification Based on Big Multimodal Data Analysis and Sparrow Search Optimization. Big Data 2022, 10, 547–558. [Google Scholar] [CrossRef] [PubMed]
- Bedolla-Ibarra, M.G.; Cabrera-Hernandez, M.D.; Aceves-Fernández, M.A.; Tovar-Arriaga, S. Classification of attention levels using a Random Forest algorithm optimized with Particle Swarm Optimization. Evol. Syst. 2022, 13, 687–702. [Google Scholar] [CrossRef]
- Dogan, M.; Taspinar, Y.S.; Cinar, I.; Kursun, R.; Ozkan, I.A.; Koklu, M. Dry bean cultivars classification using deep cnn features and salp swarm algorithm based extreme learning machine. Comput. Electron. Agric. 2023, 204, 107575. [Google Scholar] [CrossRef]
- Colmer, J.; O’Neill, C.M.; Wells, R.; Bostrom, A.; Reynolds, D.; Websdale, D.; Shiralagi, G.; Lu, W.; Lou, Q.J.; Le Cornu, T.; et al. SeedGerm: A cost-effective phenotyping platform for automated seed imaging and machine-learning based phenotypic analysis of crop seed germination. New Phytol. 2020, 228, 778–793. [Google Scholar] [CrossRef]
- Carles, S.; Lamhamedi, M.S.; Beaulieu, J.; Stowe, D.C.; Colas, F.; Margolis, H.A. Genetic Variation in Seed Size and Germination Patterns and their Effect on White Spruce Seedling Characteristics. Silvae Genet. 2009, 58, 152–161. [Google Scholar] [CrossRef]
- Neuweiler, J.E.; Maurer, H.P.; Würschum, T. Long-term trends and genetic architecture of seed characteristics, grain yield and correlated agronomic traits in triticale (×Triticosecale Wittmack). Plant Breed. 2020, 139, 717–729. [Google Scholar] [CrossRef]
- Bhargava, A.; Bansal, A. Fruits and vegetables quality evaluation using computer vision: A review. J. King Saud Univ.-Comput. Inf. Sci. 2021, 33, 243–257. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Probst, P.; Wright, M.N.; Boulesteix, A.L. Hyperparameters and tuning strategies for random forest. Wiley Interdiscip. Rev.-Data Min. Knowl. Discov. 2019, 9, e1301. [Google Scholar] [CrossRef]



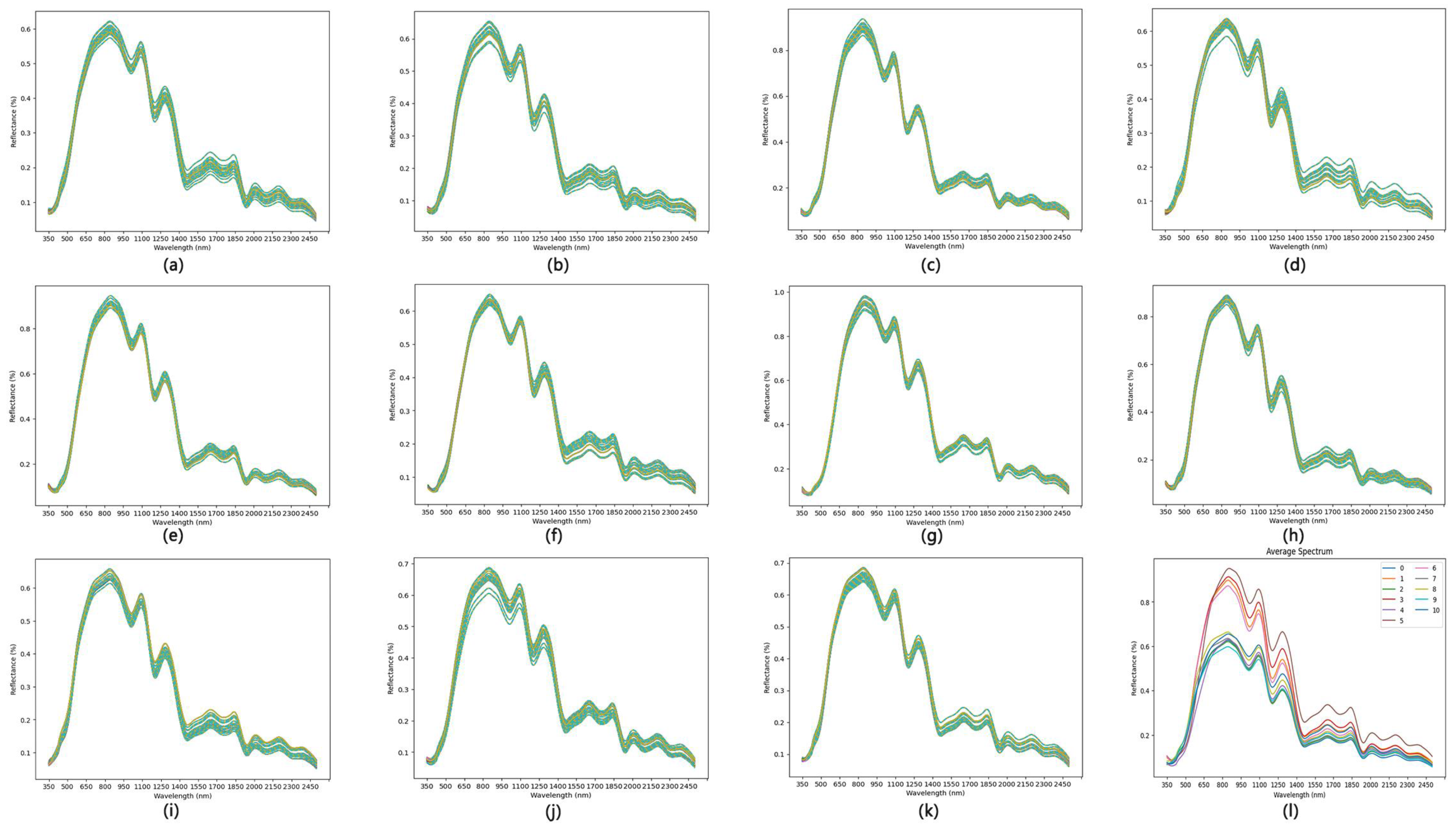

| Selection Algorithm | Training Set | Test Set | ||||
|---|---|---|---|---|---|---|
| A | P | R | A | P | R | |
| None | 0.491 | 0.485 | 0.487 | 0.475 | 0.468 | 0.463 |
| RFE | 0.499 | 0.519 | 0.490 | 0.497 | 0.492 | 0.486 |
| SFM | 0.485 | 0.489 | 0.481 | 0.489 | 0.491 | 0.478 |
| Selection Algorithm | Training Set | Test Set | ||||
|---|---|---|---|---|---|---|
| A | P | R | A | P | R | |
| None | 0.876 | 0.796 | 0.871 | 0.837 | 0.774 | 0.852 |
| SPA | 0.880 | 0.901 | 0.878 | 0.882 | 0.888 | 0.884 |
| CARS | 0.876 | 0.795 | 0.871 | 0.826 | 0.767 | 0.842 |
| Selection Algorithm | Training Set | Test Set | ||||
|---|---|---|---|---|---|---|
| A | P | R | A | P | R | |
| RFE-SPA | 0.926 | 0.915 | 0.927 | 0.933 | 0.941 | 0.937 |
| RFE-CARS | 0.896 | 0.887 | 0.889 | 0.915 | 0.924 | 0.919 |
| SFM-SPA | 0.896 | 0.895 | 0.892 | 0.907 | 0.915 | 0.911 |
| SFM-CARS | 0.857 | 0.901 | 0.876 | 0.905 | 0.940 | 0.910 |
| None | 0.887 | 0.885 | 0.888 | 0.858 | 0.879 | 0.866 |
| Model | Training Set | Test Set | ||||
|---|---|---|---|---|---|---|
| A | P | R | A | P | R | |
| ZGWO-RF | 0.952 | 0.943 | 0.951 | 0.959 | 0.962 | 0.961 |
| GWO-RF | 0.926 | 0.915 | 0.927 | 0.933 | 0.941 | 0.937 |
| ABC-RF | 0.913 | 0.865 | 0.859 | 0.87 | 0.887 | 875 |
| CS-RF | 0.931 | 0.923 | 0.931 | 0.943 | 0.953 | 0.945 |
| RF | 0.737 | 0.815 | 0.760 | 0.751 | 0.821 | 0.741 |
| Model | Training Set | Test Set | ||||
|---|---|---|---|---|---|---|
| A | P | R | A | P | R | |
| ZGWO-RF | 0.852 | 0.909 | 0.869 | 0.897 | 0.939 | 0.902 |
| GWO-RF | 0.887 | 0.885 | 0.888 | 0.858 | 0.877 | 0.866 |
| ABC-RF | 0.876 | 0.771 | 0.846 | 0.828 | 0.774 | 0.84 |
| CS-RF | 0.883 | 0.877 | 0.884 | 0.858 | 0.874 | 0.866 |
| RF | 0.729 | 0.819 | 0.718 | 0.701 | 0.811 | 0.726 |
| Models with Different Features | Result | ||
|---|---|---|---|
| A | P | R | |
| Img-GWO-RF | 0.497 | 0.492 | 0.486 |
| Hyperspectral-GWO-RF | 0.882 | 0.888 | 0.884 |
| Fusion-GWO-RF | 0.933 | 0.941 | 0.937 |
| Fusion-ZGWO-RF | 0.959 | 0.962 | 0.961 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bi, C.; Zhang, S.; Chen, H.; Bi, X.; Liu, J.; Xie, H.; Yu, H.; Song, S.; Shi, L. Non-Destructive Classification of Maize Seeds Based on RGB and Hyperspectral Data with Improved Grey Wolf Optimization Algorithms. Agronomy 2024, 14, 645. https://doi.org/10.3390/agronomy14040645
Bi C, Zhang S, Chen H, Bi X, Liu J, Xie H, Yu H, Song S, Shi L. Non-Destructive Classification of Maize Seeds Based on RGB and Hyperspectral Data with Improved Grey Wolf Optimization Algorithms. Agronomy. 2024; 14(4):645. https://doi.org/10.3390/agronomy14040645
Chicago/Turabian StyleBi, Chunguang, Shuo Zhang, He Chen, Xinhua Bi, Jinjing Liu, Hao Xie, Helong Yu, Shaozhong Song, and Lei Shi. 2024. "Non-Destructive Classification of Maize Seeds Based on RGB and Hyperspectral Data with Improved Grey Wolf Optimization Algorithms" Agronomy 14, no. 4: 645. https://doi.org/10.3390/agronomy14040645
APA StyleBi, C., Zhang, S., Chen, H., Bi, X., Liu, J., Xie, H., Yu, H., Song, S., & Shi, L. (2024). Non-Destructive Classification of Maize Seeds Based on RGB and Hyperspectral Data with Improved Grey Wolf Optimization Algorithms. Agronomy, 14(4), 645. https://doi.org/10.3390/agronomy14040645







