Design of an Autonomous Orchard Navigation System Based on Multi-Sensor Fusion

Abstract

To address the limitations of traditional GNSS-based navigation systems in orchard environments, we propose a multi-sensor fusion-based autonomous navigation method for orchards. A crawler-type agricultural platform was used as a test vehicle, and an autonomous orchard navigation system was constructed using a 2D LiDAR, a dynamic electronic compass, and an encoder. The proposed system first filters LiDAR point cloud data and uses the DBSCAN–ratio–threshold method to process data and identify clusters of tree trunks. By matching the center coordinates of trunk clusters with a fruit tree distribution map, the platform’s positional measurements are determined. An extended Kalman filter fusion algorithm is then employed to obtain a posterior estimate of the platform’s position and pose. Experimental results demonstrate that in localization accuracy tests and navigation tests, the proposed system provides high navigation accuracy and robustness, making it suitable for autonomous walking operations in orchard environments.

1. Introduction

With its orchard planting area reaching 12.808 million hectares, China currently leads the world in both fruit cultivation acreage and production volume [1]. To reduce costs, orchards are shifting toward large-scale and standardized development. Orchard construction is increasingly focusing on the integration of agronomy and agricultural machinery, providing favorable conditions for the promotion and application of intelligent equipment in orchard operations. Orchard production involves multiple stages and a high demand for labor. Taking apple orchards as an example, labor costs account for more than 60% of the total production cost [1]. Therefore, it is urgent to develop simple, lightweight, and intelligent orchard machinery to replace manual labor. Autonomous navigation is not only a common support technology for orchard platforms performing tasks such as spraying, fertilizing, and harvesting but also a core technology for the intelligent operation of such equipment.

The localization of operation platforms is a prerequisite for achieving autonomous navigation, which relies on the efficient acquisition of position and pose information by the navigation system. To achieve position and pose acquisition for operation platforms, the primary technologies currently used include 2D LiDAR [2,3], 3D LiDAR [4], cameras [5], and GNSS [6,7,8]. Compared with LiDAR and cameras, GNSS is a relatively mature technology for localization and navigation. Real-time kinematic positioning (RTK)-GNSS can achieve centimeter-level localization accuracy in open environments. However, in orchard environments, when tree canopies or other objects heavily obstruct signals, RTK-GNSS may experience reduced localization accuracy or even localization failure [9]. Both cameras and LiDAR can capture rich environmental information; however, cameras are strongly affected by lighting conditions, whereas LiDAR offers all-weather environmental data acquisition. Many domestic and foreign scholars have studied LiDAR-based orchard navigation methods. To achieve the localization of operating platforms, the conventional approach is to obtain environmental information within the operation area using LiDAR, establish a prior map for autonomous navigation based on this information, and then match the environmental information sensed by the operating platform with the prior map. Navigation systems based on 3D LiDAR require extensive storage space and high computational power to construct prior maps due to the large amount of point cloud data generated, leading to higher equipment costs. In contrast, 2D LiDAR offers advantages such as compact size, easier integration, and lower computational demands.

Autonomous navigation in orchards with 2D LiDAR relies significantly on the navigation line extraction. For autonomous navigation line extraction, Higuti et al. [10] employed the least squares method to extract navigation lines from filtered 2D LiDAR point cloud data. The system achieved total travel distances of 1115 m, 1022 m, and 660 m in two cornfields and one sorghum field, indicating the promising prospects of LiDAR-based navigation methods in outdoor environments. However, the autonomous navigation approach utilized in their study had limitations at headland owing to insufficient orchard information, resulting in challenges in executing turning, and limiting its practical applications in real-world scenarios. Malavazi et al. [11] developed an autonomous navigation method that does not rely on prior crop information using an improved PEARL algorithm to extract navigation lines. However, the autonomous navigation method used in this work also had limitations in the turning function. Jiang et al. [12] used density-based spatial clustering of applications with noise (DBSCAN) and K-means to classify 2D LiDAR point cloud data and then employed the random sample consensus (RANSAC) method to extract navigation lines and adjusted the steering angle of the vehicle based on the distance between LiDAR and the tree trunk in the turning stage to realize the turning function. Andersen et al. [13] used the least square method to extract the navigation line from the LiDAR returned data and judged that the LiDAR point cloud data density in the fruit tree line was higher than that in the headland to determine whether it was in the fruit tree row or the headland. In this work, they used the GPS results as the ground truth to evaluate the navigation effect. The navigation system built by Bergerman et al. [14] used the least square method to extract navigation lines and the extended Kalman filter to solve the pose estimation problem. The system was tested for 350 km, and the test results showed that a vehicle with an autonomous navigation function can effectively improve production efficiency. Libby et al. [15] used the Hough transform [16,17] to extract navigation lines from LiDAR data. The test of more than 20 km showed that the system they constructed had a good navigation effect, but reflective bands were needed for auxiliary navigation when it was in the headland. Barawid et al. [18] used the Hough transform as an algorithm to identify tree rows. In this work, they considered that the output of the Hough transform contained noise, which would make the steering control unstable. Therefore, they used the linear time series general auto-regression method to process the output of the Hough transform to obtain the minimum lateral error. In the visual navigation method designed for unmanned ground vehicles (UGV), Zhou et al. [19] proposed a method combining the Hough matrix and RANSAC [20] to extract the navigation path, considering that the traditional Hough transform and least square method are difficult to apply in visual outdoor navigation. The experimental results showed that the accuracy of the method in path acquisition was 90.36–96.81%, but the method is not good in real-time, and the time reserved for program running needs to be controlled above 0.55 s. Guyonneau et al. [21] used the PEARL/Ruby algorithm [22] as the navigation line search algorithm. In the offline simulation, this method showed good anti-interference to weeds, uneven tree rows, and other conditions. The final navigation effect of this method was not clear. Additional research has focused on recognizing trees and obstacles [23,24], the motion control of operation platforms [25,26], and the establishment of a 2D LiDAR rangefinder model [27,28]. In most of the above studies, autonomous navigation depended on the accurate identification and extraction of crop row features. However, a key limitation is that a platform can only acquire distance information relative to the crop rows on either side, resulting in low localization accuracy. Shalal et al. [29] constructed a fruit tree distribution map of an operation area using 2D LiDAR and camera sensors and combined 2D LiDAR, cameras, and IMU data to localize their platform and achieve autonomous navigation. This method only requires a single mapping process for the fruit tree distribution, which can then be used for navigation. Regardless, the inclusion of visual information in the navigation system introduces redundancy, leading to wasted system resources. Additionally, the use of an IMU leads to cumulative errors in azimuth measurements, which increase the system’s azimuth error. In contrast, a dynamic electronic compass does not suffer from cumulative error during azimuth measurement. Such a compass can provide long-term stable azimuth measurements and improve the accuracy and performance of autonomous navigation systems.

To address the redundancy in multi-sensor fusion navigation systems involving 2D LiDAR and achieve high navigation accuracy, we propose an autonomous navigation method that integrates 2D LiDAR and electronic compass data. The proposed method uses RTK-GNSS to construct a fruit tree distribution map of the operation area, filters LiDAR point cloud data using a pass-through filter, and applies the DBSCAN–ratio–threshold method to identify tree trunk clusters. The platform’s position is determined by matching the center coordinates of the trunk clusters with the fruit tree distribution map. An extended Kalman filter fusion algorithm is employed to obtain a posterior estimate of the platform’s position and pose. Finally, fuzzy control is used to achieve motion control and enable the platform’s autonomous navigation.

2. Materials and Methods

2.1. System Hardware Components

The hardware architecture of the proposed autonomous orchard navigation system is presented in Figure 1, and the actual setup is depicted in Figure 2. The main hardware components included a dynamic electronic compass, 2D LiDAR, an industrial control computer, and a crawler-type mobile platform. The system functions as follows: The sensor system, which consists of the electronic compass, 2D LiDAR, and encoder, transmits measurement data to the industrial control computer for state estimation. The computed motion control quantities for the motor driver are then sent to the motor driver to execute the platform’s motion control. The dynamic electronic compass used in this system is the DFEC900 [30] model manufactured by Dfwee Co., Ltd., Wuhan, China. It has a data output frequency of 50 Hz, an azimuth accuracy of ≤0.5°, and an angular resolution of 0.01°. The compass supports USART communication and allows for both hard and soft iron calibration. The 2D LiDAR is the LMS111 [31] model from SICK AG, Waldkirch, Germany, which has a scanning radius of 20 m, scanning range of −45° to 225°, scanning frequency of 25 Hz, and scanning angular resolution of 0.25°. The industrial control computer is produced by Shanghai Senke Electronic Technology Co., Ltd. (Shanghai, China) and has a main frequency of 2.0 GHz. It operates on the Windows 10 platform and is mounted on the upper support frame of the crawler chassis. The crawler chassis is manufactured by Shandong Qingke Intelligent Technology Co., Ltd., Jinan, China, and has dimensions of 100 cm in length and 80 cm in width, with a maximum driving speed of 4 km/h.

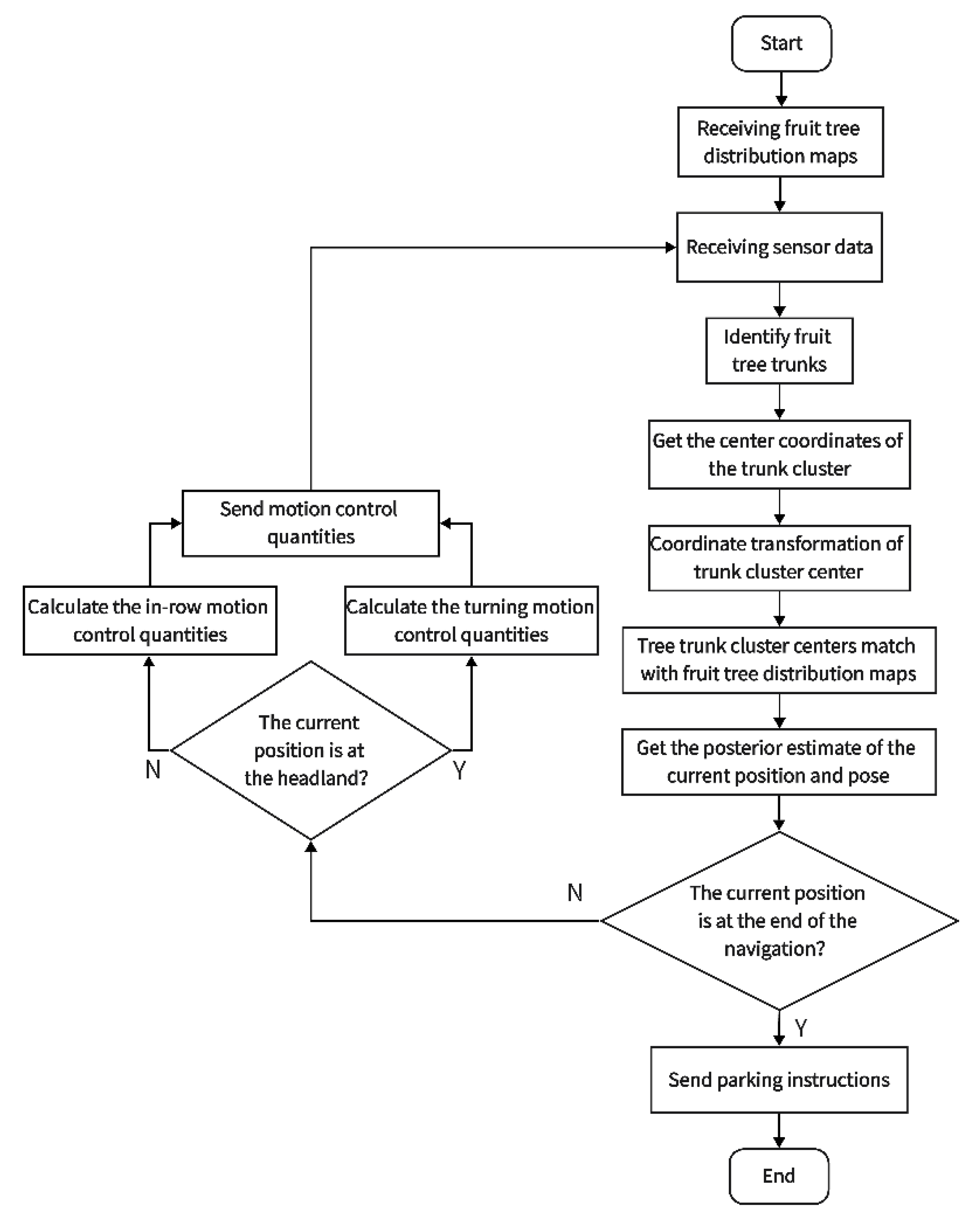
2.2. System Software Implementation

The software implementation and architecture of the proposed autonomous navigation method are illustrated in Figure 3. The main steps are as follows: (1) Collect sensor data and the fruit tree distribution map of the orchard; (2) Extract the center coordinates of trunk clusters from the LiDAR data; (3) Perform a coordinate transformation of the extracted trunk cluster center coordinates into the orchard’s local coordinate system; (4) Match the transformed trunk cluster center coordinates with the fruit tree distribution map to obtain the positional measurements of the platform at the current moment; (5) Apply the extended Kalman filter to obtain a posterior estimate of the platform’s current position and pose; (6) Complete the motion control of the platform using a fuzzy control method. The system’s state estimation and motion control programs run on Windows 10 using MATLAB R2019a and are executed as MATLAB scripts.

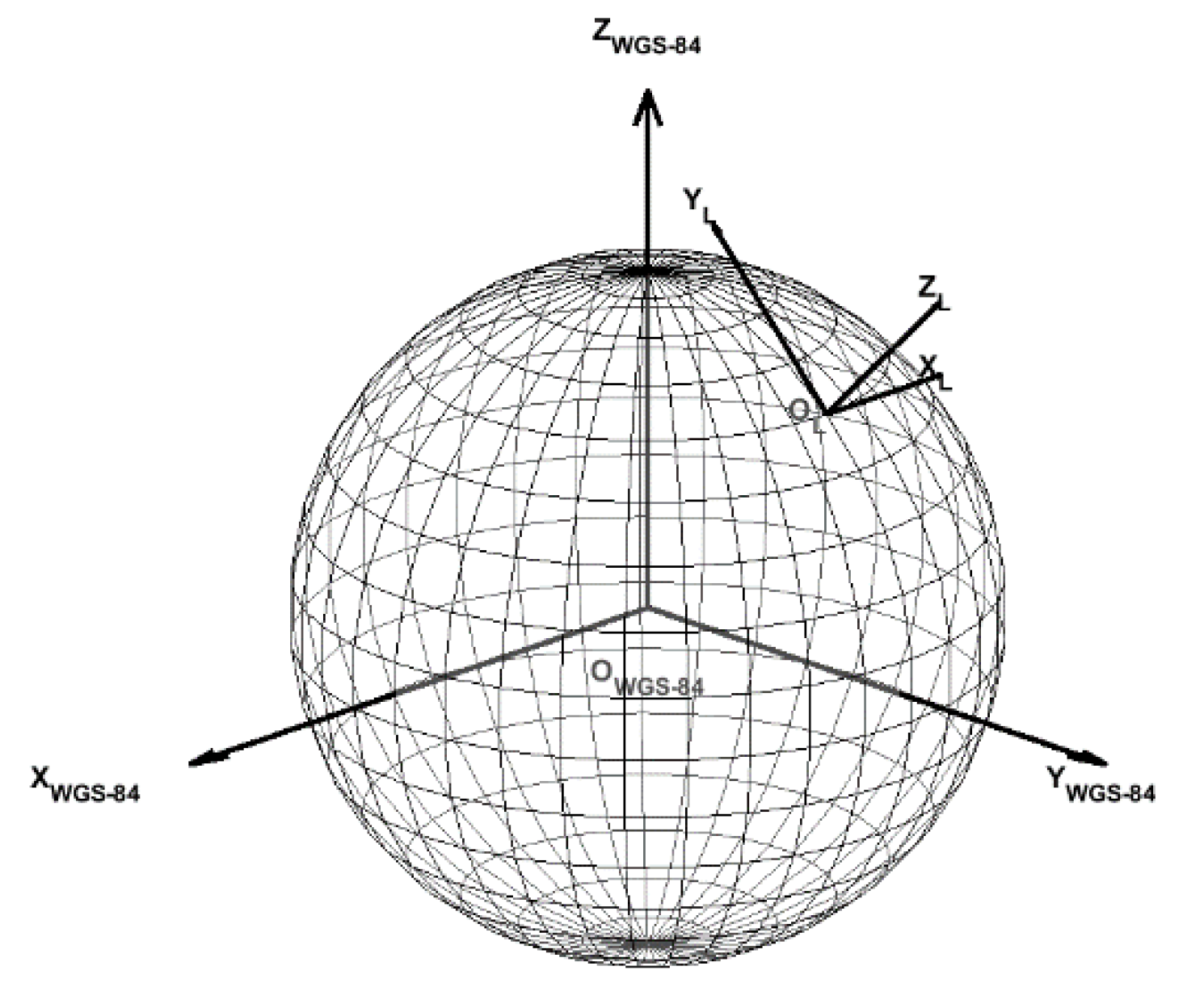
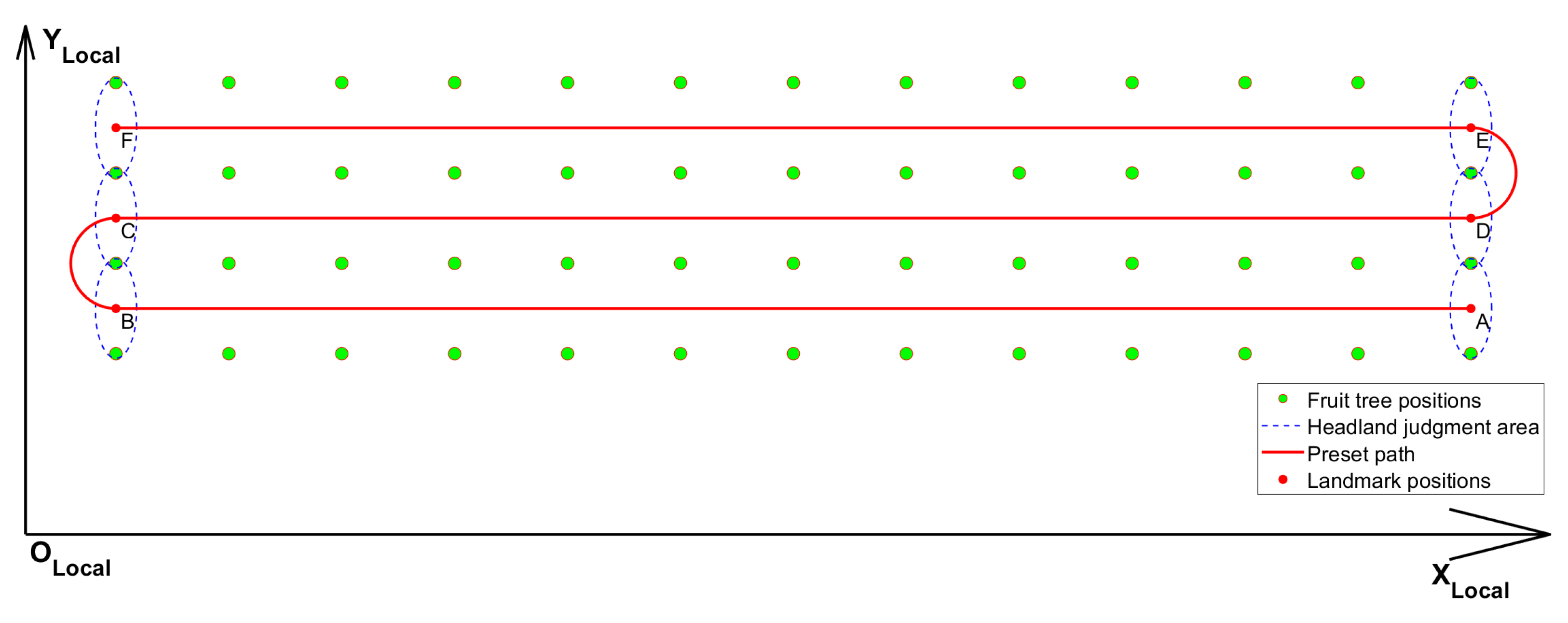
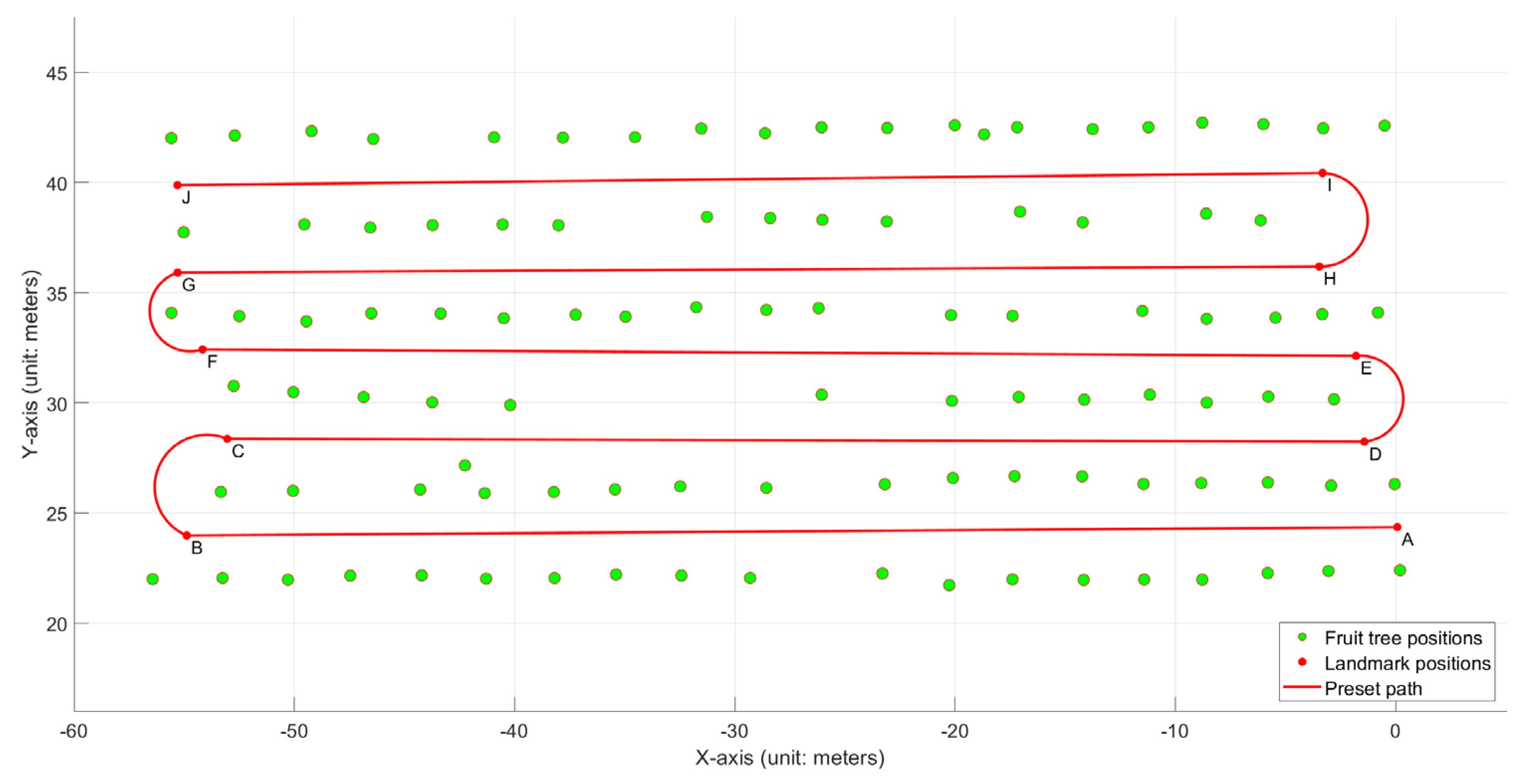
2.2.1. Establishment of the Orchard’s Local Coordinate System and Fruit Tree Distribution Map

Prior to beginning navigation, the positional information of the fruit trees must be acquired to construct the orchard’s fruit tree distribution map. The positional information of the fruit trees can be obtained by measuring their spherical coordinates in the WGS-84 coordinate system. All navigation calculations were performed in the local coordinate system, which required the establishment of a local coordinate system and the definition of a transformation relationship between WGS-84 and local coordinates.

The local coordinate system was defined as a horizontal coordinate system with the origin $O_L$ located at a point on the local reference ellipsoid’s surface. The $X_L$ axis points eastward along the reference ellipsoid’s prime vertical, $Y_L$ axis points toward the geographic north pole along the reference ellipsoid’s principal vertical, and $Z_L$ axis points outward along the outer normal direction of the ellipsoid’s surface toward the zenith, as shown in Figure 4. The transformation between WGS-84 spherical coordinates and WGS-84 Cartesian coordinates is defined by Equation (1).

$$\left[\begin{array}{l}{x}_{\mathrm{e}}\hfill \\ y_{\mathrm{e}}\hfill \\ z_{\mathrm{e}}\hfill \end{array}\right]=\left[\begin{array}{l}\left(R_{\mathrm{N}}+h\right)\cos (\lambda )\cos (\phi )\hfill \\ \left(R_{\mathrm{N}}+h\right)\sin (\lambda )\cos (\phi )\hfill \\ \left(R_{\mathrm{N}}\left(1-e^2\right)+h\right)\sin (\phi )\hfill \end{array}\right]$$

(1)

Here, $\left(X_{\mathrm{e}},Y_{\mathrm{e}},Z_{\mathrm{e}}\right)$ are the WGS-84 Cartesian coordinates of any point on the Earth’s surface; $\lambda$, $\phi$, and $h$ are the geographical latitude, longitude, and altitude, respectively, of that point; $R_N$ is the radius of curvature in the prime vertical; and $e$ is the first eccentricity of the ellipsoid. The transformation between WGS-84 Cartesian coordinates and the local coordinate system is defined by Equation (2).

$$\left[\begin{array}{l}{X}_{\mathrm{e}}\hfill \\ Y_{\mathrm{e}}\hfill \\ Z_{\mathrm{e}}\hfill \end{array}\right]=\left[\begin{array}{ccc}-\sin (\lambda )& -\cos (\lambda )\sin (\phi )& \cos (\lambda )\cos (\phi )\\ \cos (\lambda )& -\sin (\lambda )\sin (\phi )& \sin (\lambda )\cos (\phi )\\ 0& \cos (\phi )& \sin (\phi )\end{array}\right]\left[\begin{array}{l}{X}_{\mathrm{L}}\hfill \\ Y_{\mathrm{L}}\hfill \\ Z_{\mathrm{L}}\hfill \end{array}\right]+\left[\begin{array}{l}{X}_{\mathrm{oc}}\hfill \\ Y_{\mathrm{oc}}\hfill \\ Z_{\mathrm{oe}}\hfill \end{array}\right]$$

(2)

Here, $\left(X_L,Y_L,Z_L\right)$ and $\left(X_{\mathrm{e}},Y_{\mathrm{e}},Z_{\mathrm{e}}\right)$ are the horizontal and WGS-84 Cartesian coordinates of a point, respectively; $\left(X_{\mathrm{oe}},Y_{\mathrm{oe}},Z_{\mathrm{oe}}\right)$ are the WGS-84 Cartesian coordinates of the origin of the local horizontal coordinate system at this point; and $\lambda$ and $\phi$ are the geographical latitude and longitude of the point, respectively. The signs of $\lambda$ and $\phi$ are adjusted based on the hemisphere in which the point is located.

By defining a point as the origin of the horizontal coordinate system, a local coordinate system can be established with this point as its origin. Once the WGS-84 spherical coordinates of any other point are obtained, they can be converted into WGS-84 Cartesian coordinates. By using the transformation relationship between the WGS-84 Cartesian coordinates and horizontal coordinates, the horizontal coordinates of the point in the defined local coordinate system can be determined, thereby enabling the conversion of WGS-84 spherical coordinates into local coordinates.

Before implementing navigation functionality, any point within the orchard can be selected as the origin of the local coordinate system to establish a local coordinate system. By acquiring the spherical coordinates of the fruit tree trunks in the WGS-84 coordinate system, the local coordinates of the fruit tree trunks in the established local coordinate system can be obtained based on the transformation relationship between the WGS-84 spherical coordinates and local coordinates. This process enables the construction of a fruit tree distribution map for the orchard.

2.2.2. Identification of Fruit Tree Trunks and Acquisition of Trunk Cluster Center Coordinates

When performing state estimation of the platform’s position and pose through multi-source sensor fusion, the first step was to identify and extract fruit tree trunk information from the LiDAR scan results. This process involved determining the distance from the center of each fruit tree trunk to the LiDAR scanning center, as well as the azimuth of the trunk centers in the LiDAR coordinate system.

As the measurement distance increased, the measurement error of the LiDAR also increased, and interference in the scan results became more prominent. Therefore, prior to processing the LiDAR scan results, a pass-through filter was applied, and data outside the filtered region were discarded. After applying the pass-through filter, the DBSCAN algorithm was used to remove noise points from the filtered data and extract preliminary trunk clusters. Based on the characteristics of the DBSCAN algorithm, the processed output included not only identified noise points but also several clusters with distinct features. For example, because the LiDAR may scan the ground at an inclined angle, the output of the DBSCAN-processed LiDAR data could include ground clusters with linear features. To filter out ground clusters and extract only trunk clusters, the results processed by DBSCAN were further analyzed based on the arc-shaped characteristics of trunk clusters.

Let the scan result of a single LiDAR frame be denoted as $\left(r_i,{\theta }_i\right)$, indicating that the $i$-th point is located at the polar radius $r_i$ and polar angle ${\theta }_i$ in the LiDAR polar coordinate system. Here, $i=1,2,3\dots m$, where $m$ is determined by the LiDAR’s scanning range and angular resolution. The DBSCAN-processed LiDAR scan result is denoted as $\left(r_{i(j)},{\theta }_{i(j)}\right)$, indicating that the $i$-th point is located at the polar radius $r_i$ and polar angle ${\theta }_i$ in the LiDAR polar coordinate system, and that this point belongs to the $j$-th cluster. Here, $j=-1,1,2,3\dots n$, $j=-1$ indicates that the $i$-th point is a noise point, $n$ represents the number of clusters in the LiDAR scan of the frame, and $n>0$. Let $class(i)=j$ indicate that the $i$-th point belongs to the $j$-th cluster. The definitions of $i$ and $j$ are as described above, and we define the following function:

$$\delta \left(x,y\right)=\left\{\begin{array}{c}1\hspace{1em}x=y\\ 0\hspace{1em}x\ne y\end{array}\right.\hspace{1em}(x=1,2,3\dots ,y=1,2,3\dots )$$

(3)

therefore,

$$R(k)={\displaystyle \frac{{\displaystyle \sum _{i=1}^m\delta \left(k,class(i)\right)r_i}}{{\displaystyle \sum _{i=1}^m\delta \left(k,class(i)\right)}}}\hspace{1em}k=j=1,2,3\dots n$$

(4)

$$\Theta (k)={\displaystyle \frac{{\displaystyle \sum _{i=1}^m\delta \left(k,class(i)\right){\theta }_i}}{{\displaystyle \sum _{i=1}^m\delta \left(k,class(i)\right)}}}\hspace{1em}k=j=1,2,3\dots n$$

(5)

Let $R(k)$ denote the polar radius of the $k$-th cluster center in the LiDAR polar coordinate system and $\Theta (k)$ denote the polar angle of the $k$-th cluster center in the LiDAR polar coordinate system. In the LiDAR polar coordinate system, a circular area is defined with the point $\left(R(k),\Theta (k)\right)$ as the center and $radius\_class$ as the radius. When the ratio of points $\left(r_{•(k)},{\theta }_{•(k)}\right)$ in the $k$-th cluster that falls within this circular area over the total number of data points in the $k$-th cluster exceeds a certain threshold, as shown in Equation (6), the $k$-th cluster is considered to be a trunk cluster.

$$ratio\_inCircle={\displaystyle \frac{num(inCircle\_k)}{num(Class\_k)}}>setValue$$

(6)

Here, $num(inCircle\_k)$ represents the number of points in the $k$-th cluster that falls within the circular area, $num(Class\_k)$ is the total number of points in the $k$-th cluster, and $\left(R(k),\Theta (k)\right)$ are the center coordinates of the trunk cluster. The value of $radius\_class$ can be set based on the average radius of the fruit tree trunks in the orchard.

$$dq(i)={\displaystyle \frac{r_i-r_{i+1}}{LiDAR\_AngularResolution}}$$

(7)

Using Equation (7), the fruit tree trunk information in a single frame of LiDAR scan results can be preliminarily extracted, where $r_i$ represents the polar radius of the $i$-th point in the LiDAR polar coordinate system and $LiDAR\_AngularResolution$ Represents the angular resolution of the LiDAR. It is important to note that as a result of the measurement error of the LiDAR, additional detection methods are required to verify the fruit tree trunk information.

2.2.3. Coordinate Transformation of Trunk Cluster Centers into the Orchard’s Local Coordinate System

The center coordinates of the trunk clusters obtained as described above were expressed in the LiDAR polar coordinate system. These coordinates must be transformed into the orchard’s local coordinate system. First, the trunk cluster center coordinates were converted into the LiDAR Cartesian coordinate system. Then, using the coordinate transformation method, these coordinates were transformed into the orchard’s local coordinate system, which represented the fruit tree distribution map. The required rotation angle for the transformation was measured by the dynamic electronic compass, while the translation distance was determined from the prior estimate of the LiDAR scanning center’s current position. Let the center of the platform be the LiDAR scanning center, and define the platform’s state vector as $v={\left[x,y,\varphi \right]}^T$, where $x,y$ are the Cartesian coordinates of the LiDAR scanning center in the orchard’s local coordinate system and $\varphi$ is the azimuth angle of the operating platform in the orchard’s local coordinate system. The azimuth is defined as the angle between the 90° radial direction in the LiDAR polar coordinate system and the positive $x$ axis of the orchard’s local coordinate system. This angle is measured counterclockwise as positive and clockwise as negative from the positive $x$ axis. The prior estimate of the platform’s position and pose at time $k$ is defined as $v_k^{-}={\left[x_k^{-},y_k^{-},{\varphi }_k^{-}\right]}^T$.The posterior estimate of the platform’s position and pose at time $k$ is given by $v_k^{+}={\left[x_k^{+},y_k^{+},{\varphi }_k^{+}\right]}^T$.

From the odometry model, we derive Equations (8) and (9).

$$\left\{\begin{array}{l}\Delta D(k)={\displaystyle \frac{\Delta d_L+\Delta d_R}{2}}\hfill \\ \Delta \varphi (k)={\displaystyle \frac{\Delta d_R-\Delta d_L}{a}}\hfill \end{array}\right.$$

(8)

$$R_{rotate}(k)={\displaystyle \frac{\Delta D(k)}{\Delta \varphi (k)}}$$

(9)

Here, $\Delta d_L$ and $\Delta d_R$ are the distance traveled by the left and right tracks of the platform from time $k-1$ to time $k$, respectively, and $a$ is the distance between the left and right tracks. The radius of the travel trajectory from time $k-1$ to time $k$, denoted as $R_{rotate}(k)$, determines whether we use the arc or straight-line models in the odometry calculation. The prior estimate of the platform’s position and pose using the arc model at time $k$ is expressed as

$$v_k^{-}=f\left(v_{k-1}^{+},u_k\right)=\left[\begin{array}{l}{x}_{k-1}^{+}+\Delta x(k)\hfill \\ y_{k-1}^{+}+\Delta y(k)\hfill \\ {\varphi }_{k-1}^{+}+\Delta \varphi (k)\hfill \end{array}\right]=\left[\begin{array}{c}{x}_{k-1}^{+}+{\displaystyle \frac{\Delta D(k)}{\Delta \varphi (k)}}\left(\sin \left({\varphi }_{k-1}^{+}+\Delta \varphi (k)\right)-\sin {\varphi }_{k-1}^{+}\right)\\ y_{k-1}^{+}-{\displaystyle \frac{\Delta D(k)}{\Delta \varphi (k)}}\left(\cos \left({\varphi }_{k-1}^{+}+\Delta \varphi (k)\right)-\cos {\varphi }_{k-1}^{+}\right)\\ {\varphi }_{k-1}^{+}+\Delta \varphi (k)\end{array}\right]$$

(10)

The prior estimate using the straight-line model is expressed as

$$v_k^{-}=f\left(v_{k-1}^{+},u_k\right)=\left[\begin{array}{c}{x}_{k-1}^{+}+\Delta D(k)\cos {\varphi }_{k-1}^{+}\\ y_{k-1}^{+}+\Delta D(k)\sin {\varphi }_{k-1}^{+}\\ {\varphi }_{k-1}^{+}\end{array}\right]$$

(11)

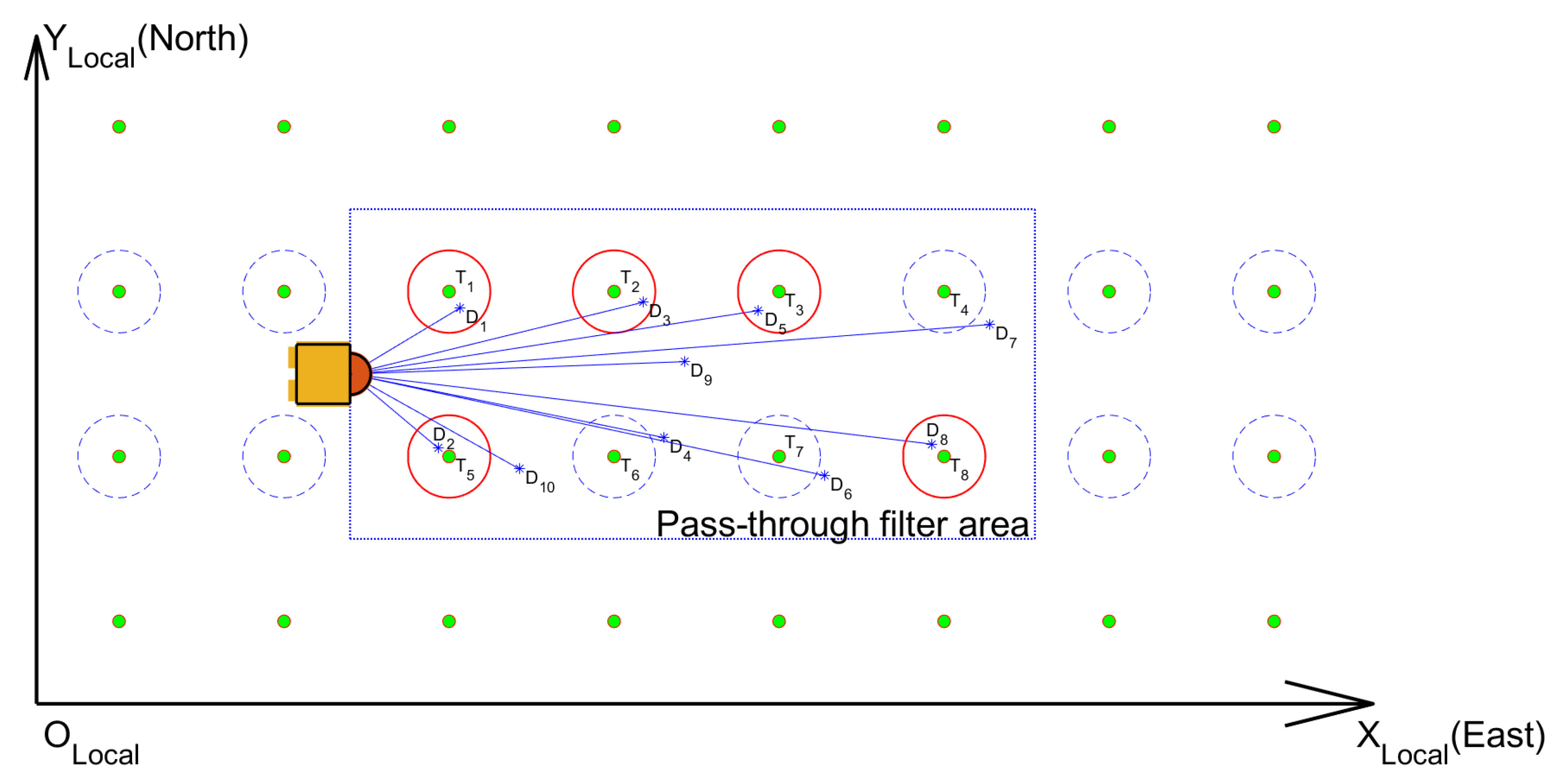
2.2.4. Matching the Trunk Cluster Centers with the Fruit Tree Distribution Map

As described in the previous section, the trunk cluster centers were expressed in Cartesian coordinates within the orchard’s local coordinate system ($O_{Local}-X_{Local}{Y}_{Local}$ in Figure 5). Next, these centers were matched with the fruit tree distribution map (see Section 2.2.1). The matching method is as follows. If a trunk cluster center falls within a circular area centered on a fruit tree in the distribution map with a threshold radius, the trunk cluster center is considered to match the corresponding fruit tree. The polar radius $R(k)$ of the trunk cluster in the LiDAR polar coordinate system is considered as the distance from the LiDAR scanning center to the matched fruit tree. As shown in Figure 5, the trunk cluster center $D_1$ falls within the circular area centered on the fruit tree $T_1$, which confirms a successful match between the two points. The distance from the LiDAR scanning center to point $D_1$ is then considered to be the distance to fruit tree $T_1$. For trunk centers that do not successfully match, such as points $D_4$, $D_7$, and $D_9$, these trunks could be obstacles encountered during the platform’s movement (point $D_9$), unmarked trees in the fruit tree distribution map (point $D_4$), or significant deviations caused by surrounding objects near the fruit trees, preventing the trunk cluster center from matching with the corresponding fruit tree (point $D_7$). The DBSCAN algorithm was used to perform matching between the trunk cluster centers and the fruit tree distribution map. This section of the program outputs the Cartesian coordinates of the successfully matched fruit trees (e.g., trees $T_1$, $T_2$, $T_3$, $T_5$, and $T_8$ in Figure 5) in the orchard’s local coordinate system, as well as the distances from the LiDAR scanning center to the matched trees.

2.2.5. Obtaining a Posterior Estimate

By using the Cartesian coordinates of successfully matched fruit trees within the orchard’s local coordinate system and distances from these trees to the LiDAR scan center, the Cartesian coordinates of the LiDAR scan center within the orchard’s local coordinate system can be calculated based on the relationship between two circles.

For each pair of successfully matched trees, the position of the LiDAR scan center can be computed within the orchard’s local coordinate system. To ensure a unique solution, the posterior estimate of the platform’s position and pose from the previous time step must be used. As shown in Figure 5, the computation of the LiDAR scan center’s position based on two matched trees falls into two scenarios: one in which the two trees are located on opposite sides of the LiDAR scan center (trees $T_1$ and $T_5$ in Figure 5), and another where both trees are on the same side (trees $T_1$ and $T_2$ in Figure 5). As a result of LiDAR measurement errors and the offset between the trunk cluster center and center of the matched tree, each scenario can yield no solution, one solution, or two solutions. Due to the measurement error of LiDAR, it is necessary to confirm the reliability of the current position measurement results further. So, for these three states, the concepts of “valid measurement” and “invalid measurement” were introduced. For example, consider tree $T_1$, tree $T_2$, and the distances $R_{T1}\left(•\right)$ and $R_{T2}\left(•\right)$ from the LiDAR scan center to these trees, respectively. If no solution is obtained, this is considered an “invalid measurement” for tree $T_1$, tree $T_2$, and the distances $R_{T1}\left(•\right)$ and $R_{T2}\left(•\right)$. If a single solution is found and the solution $\left(x^{*},y^{*}\right)$ satisfies,

$${‖\left(x^{*},y^{\ast }\right)-\left(x_{k-1}^{+},y_{k-1}^{+}\right)‖}_2\le C$$

(12)

then this is considered a “valid measurement” for tree $T_1$, tree $T_2$, and the distances $R_{T1}\left(•\right)$ and $R_{T2}\left(•\right)$; otherwise, it is considered an “invalid measurement”. Here, $C$ is a constant, and its value is related to the LiDAR measurement error and ${‖•‖}_2$ denotes the two-norm of the vector. If two solutions $\left(x_i^{*},y_i^{*}\right)\left(i=1,2\right)$ are obtained and the solution $\left(x_i^{*},y_i^{*}\right)$ satisfies

$${‖\left(x_i^{*},y_i^{*}\right)-\left(x_{k-1}^{+},y_{k-1}^{+}\right)‖}_2<{‖\left(x_j^{*},y_j^{*}\right)-\left(x_{k-1}^{+},y_{k-1}^{+}\right)‖}_2\hspace{1em}i,j=1,2;i\ne j$$

(13)

$${‖\left(x_i^{*},y_i^{*}\right)-\left(x_{k-1}^{+},y_{k-1}^{+}\right)‖}_2\le C,$$

(14)

then this is considered a “valid measurement” for tree $T_1$, tree $T_2$, and the distances $R_{T1}\left(•\right)$ and $R_{T2}\left(•\right)$; otherwise, it is considered an “invalid measurement”. The mean of multiple valid measurements for the position of the LiDAR scan center in the orchard’s local coordinate system was used as the positional measurement of the LiDAR scan center. This value was also considered the positional measurement of the platform in the local coordinate system. The platform’s azimuth in the local coordinate system was measured using the dynamic electronic compass. Based on the relevant details of the extended Kalman filter, prior estimate of the position and pose at time $k$, and measurements, the posterior estimate $v_k^{+}$ of the platform’s position and pose at time $k$ can be obtained. Simon [32] provides more details on the extended Kalman filter.

2.2.6. Motion Control

Once the posterior estimate of the platform’s position and pose at time $k$ was obtained, control inputs could be derived, including the vertical distance between the current position and preset path at time $k$, as well as the azimuth deviation between the platform’s heading and preset path at time $k$. The speed difference between the left and right tracks was used as the control output for fuzzy control. The vertical distance between the position at time $k$ and the preset driving path, the azimuth deviation, and the driving speed difference between the left and right tracks of the operating platform were [−2000 mm 2000 mm], [−1.047 rad 1.047 rad], [−400 400], respectively. The input and output quantities were divided into negative big (NB), negative medium (NM), negative small (NS), zero (Z0), positive small (PS), positive medium (PM), and positive big (PB) seven grades. The membership functions and fuzzy control rules for motion control followed the method described by Zhang et al. [2].

2.3. Test Design

2.3.1. Orchard Tests

To verify the autonomous navigation method proposed in this paper, field tests were conducted in July of 2024 in a pear orchard located at the National Experiment Station for Precision Agriculture in Changping District, Beijing, China. The tests mainly focused on two aspects: (1) system localization accuracy tests and (2) orchard navigation tests. The navigation tests included overall system performance evaluation and trajectory tracking tests at different straight-line driving speeds. Following the test design by Shalal et al. [29], an RTK-GNSS system was used to provide ground-truth information for the platform’s position during the tests. Because RTK-GNSS non-fixed solutions (e.g., differential or float solutions) were unable to meet the accuracy requirements of the tests, only fixed RTK-GNSS solutions were used. The ground-truth trajectory was recorded using a NAV-L1 RTK-GNSS receiver manufactured by Suzhou Cenozoic Intelligence Equipment Pty., Ltd., Suzhou, China, which has a localization accuracy of up to 2 cm and a data updating frequency of 1 Hz.

Prior to conducting the tests, the fruit tree distribution map of the orchard needed to be obtained. The map was generated by manually surveying the fruit trees using an RTK-GNSS system. The RTK-GNSS receiver used for this task was a G970II Pro manufactured by Beijing UniStrong Science & Technology Co., Ltd., Beijing, China, with a localization accuracy of 2 cm. After obtaining the spherical coordinates of the trees in the WGS-84 coordinate system, the positional information of the trees in the orchard’s local coordinate system was computed via coordinate transformation to construct the fruit tree distribution map for the orchard. Figure 6 presents a schematic diagram of the fruit tree distribution map, where the green solid circles represent the positions of the tree trunks, and the red solid line indicates the preset path of the platform. The path was generated based on a straight-line driving strategy between the tree rows and semi-circular turns at the headlands. The red solid circles represent the midpoints between the two trees at the ends of each row, while the blue dashed ellipses represent the headland judgment areas. When the platform enters a headland judgment area, it performs a semi-circular turn based on the preset path to complete the row-switching operation.

System Localization Accuracy Tests

During the system localization accuracy tests, the pass-through filter area for LiDAR was defined as a region extending 8 m to both sides of the platform and 13 m along the driving direction. The number of sampling points was determined based on the number of state estimates. The platform’s driving speed was set to 1 km/h, and the total travel distance was set to 100 m. Approximately 8000 state estimates were conducted during the test, and samples were collected at the 2000th, 2500th, 3000th, 3500th, 4000th, 4500th, 5000th, 5500th, and 6000th estimates. After reaching the specified number of estimates, the platform executed a parking command, outputting the state estimate for the current position. Using RTK-GNSS, the platform’s parking location was measured in spherical coordinates under the WGS-84 coordinate system, and these data were converted into the orchard’s local coordinate system to obtain position measurements. The system’s localization accuracy was evaluated using the system localization error $E$, localization error $E_x$ in the $x$-axis direction, and localization error $E_y$ in the $y$-axis direction.

Orchard Navigation Tests

The orchard navigation tests consisted of two parts. For the overall system navigation performance evaluation, the LiDAR pass-through filter area was the same as in the localization accuracy tests. The platform traveled 250 m along the preset path at a speed of 1 km/h. The platform made two left turns and two right turns during the row-switching process. The RTK-GNSS fixed solution was used as the ground truth for the platform’s trajectory, and the preset path generation strategy was identical to that shown in Figure 6. For trajectory tracking tests at different straight-line driving speeds, the arrangements were similar to the overall system navigation tests. The difference was that the platform traveled at speeds of 1 km/h, 2 km/h, and 3 km/h along the straight paths between the tree rows. An encoder was used to monitor the platform’s driving speed, and the system’s navigation performance was evaluated based on trajectory tracking errors.

2.3.2. Data Processing

During the system localization accuracy tests, the system’s estimate of the platform’s current position in the orchard’s local coordinate system was denoted as $\left(x_{estimate},y_{estimate}\right)$ and the RTK-GNSS measurement of the platform’s position was denoted as $\left(x_{measure},y_{measure}\right)$, which was considered to be the ground truth. The system localization error is defined as shown in Equation (15).

$$E=\sqrt{{\left(x_{estimate}-x_{measure}\right)}^2+{\left(y_{estimate}-y_{measure}\right)}^2}$$

(15)

The localization errors in the $x$-axis and $y$-axis directions are defined in Equations (16) and (17), respectively.

$$E_x=x_{estimate}-x_{measure}$$

(16)

$$E_y=y_{estimate}-y_{measure}$$

(17)

In the orchard navigation tests, the trajectory tracking error was defined as the perpendicular distance between the platform’s current ground-truth position and the preset trajectory. If the ground truth was located to the left of the preset trajectory, the tracking error was negative, and if it was located to the right, the tracking error was positive. The ground truth for the platform’s position was defined in the same manner as in the localization accuracy tests. The trajectory tracking error serves as the evaluation metric for the system’s navigation performance.

3. Test Results and Analysis

During our tests, manual RTK-GNSS point-based mapping was used to construct the fruit tree distribution map of the orchard, as shown in Figure 7. In this figure, the red solid line represents the preset driving path of the platform, and the red solid dots denote the midpoints of the lines connecting the two fruit trees at the ends of each row.

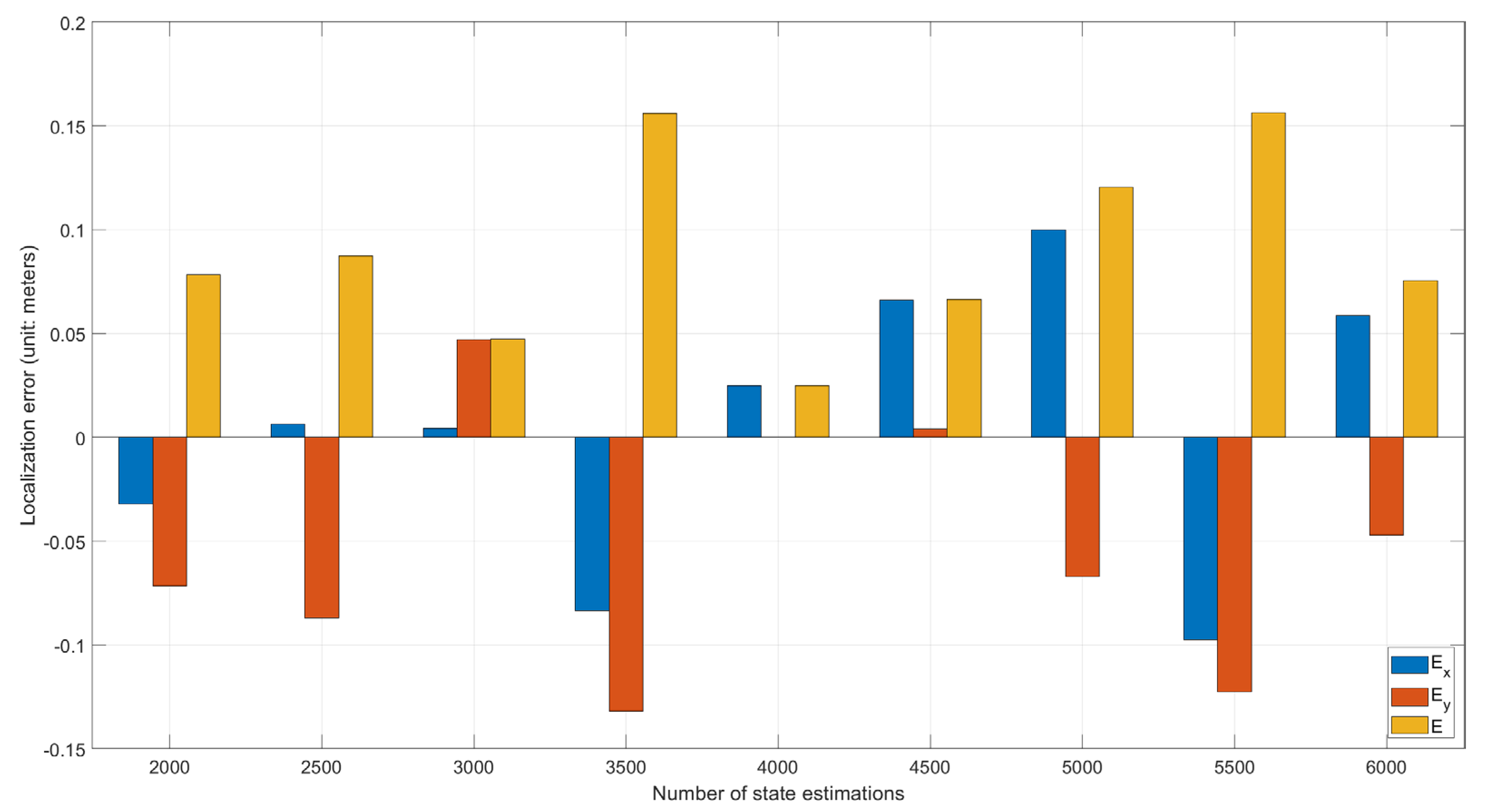
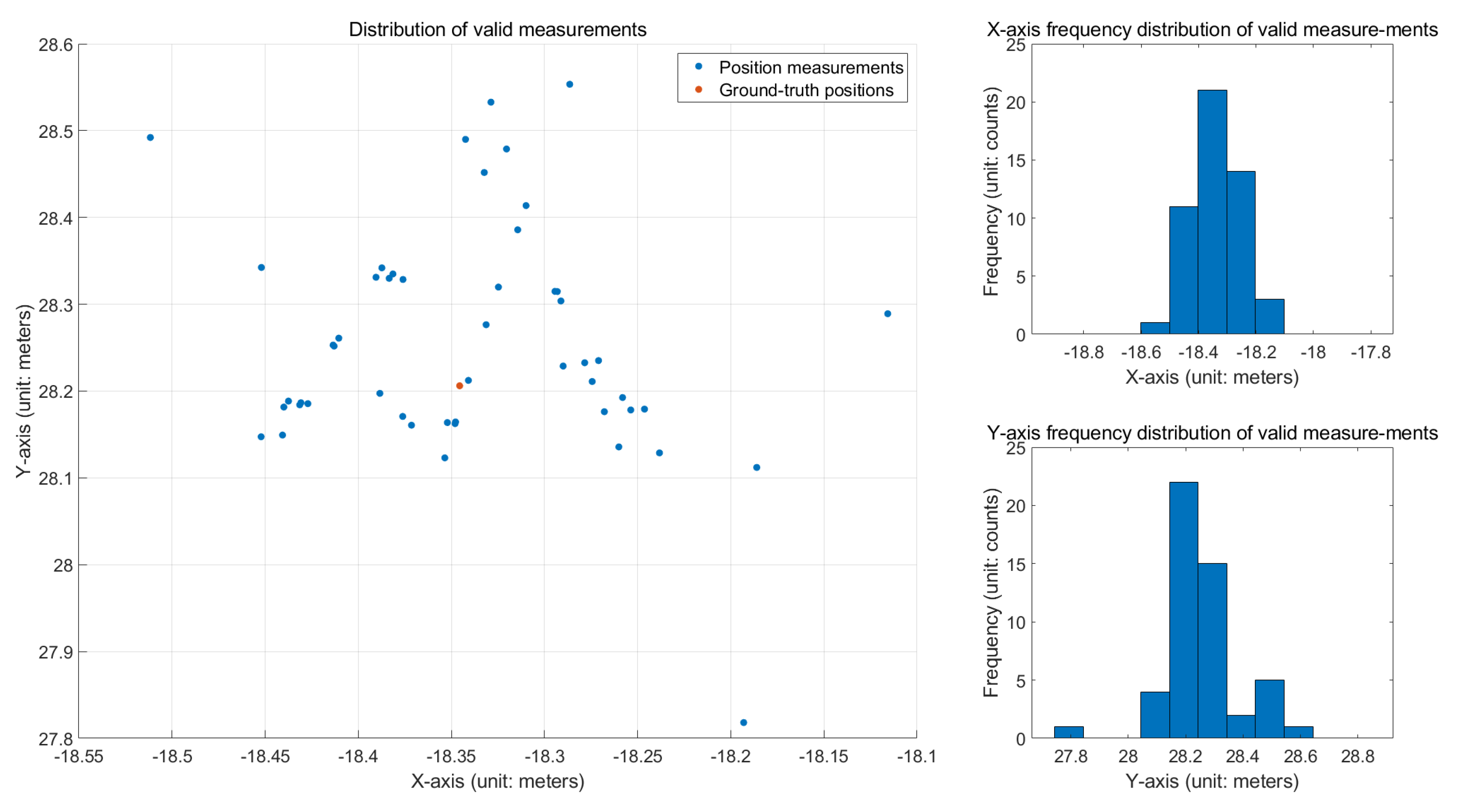
3.1. System Localization Accuracy Tests

The results of the system localization accuracy tests are presented in Figure 8. The sampling points were sequentially located in the orchard’s local coordinate system (as shown in Figure 7) at coordinates of (−31.42, 28.34) for 2000 estimates, (−18.35, 28.29) for 2500 estimates, (−9.30, 28.13) for 3000 estimates, (−0.41, 28.73) for 3500 estimates, (−22.26, 32.40) for 4000 estimates, (−22.66, 32.44) for 4500 estimates, (−31.35, 32.46) for 5000 estimates, (−56.27, 34.19) for 5500 estimates, and (−29.41, 36.04) for 6000 estimates (coordinates are in meters). The test results revealed that the mean absolute value of the localization error $E_x$ in the $x$-axis direction was 0.05 m with a standard deviation of 0.04 m, the mean absolute value of the localization error $E_y$ in the $y$-axis direction was 0.06 m with a standard deviation of 0.05 m, and overall mean localization error $E$ of the system was 0.09 m with a standard deviation of 0.05 m. The results of the system localization accuracy tests indicated that the system meets the navigation accuracy requirements for orchard operations.

By analyzing the system localization accuracy test results, one can see that the valid measurement values for the platform’s position in the orchard’s local coordinate system at the current time follow truncated normal distributions in their projections along the coordinate axes. As an example, consider point 2500 (sampling point coordinates: (−18.35, 28.29), in meters). The distribution of valid measurement values for point 2500 and their projections onto the coordinate axes are presented in Figure 9. The blue solid dots represent valid measurements, while the red solid dots represent the ground truth. A chi-square goodness-of-fit test was conducted, revealing that the projections of the valid measurements along both the X and Y axes follow truncated normal distributions. The observed test statistics were 0.7058 and 6.5432, respectively, while the critical values at the 0.05 significance level were 5.99 and 7.81. Therefore, the projections of the valid measurements along the X and Y axes are considered to follow truncated normal distributions, which can be used to assess the system’s localization accuracy.

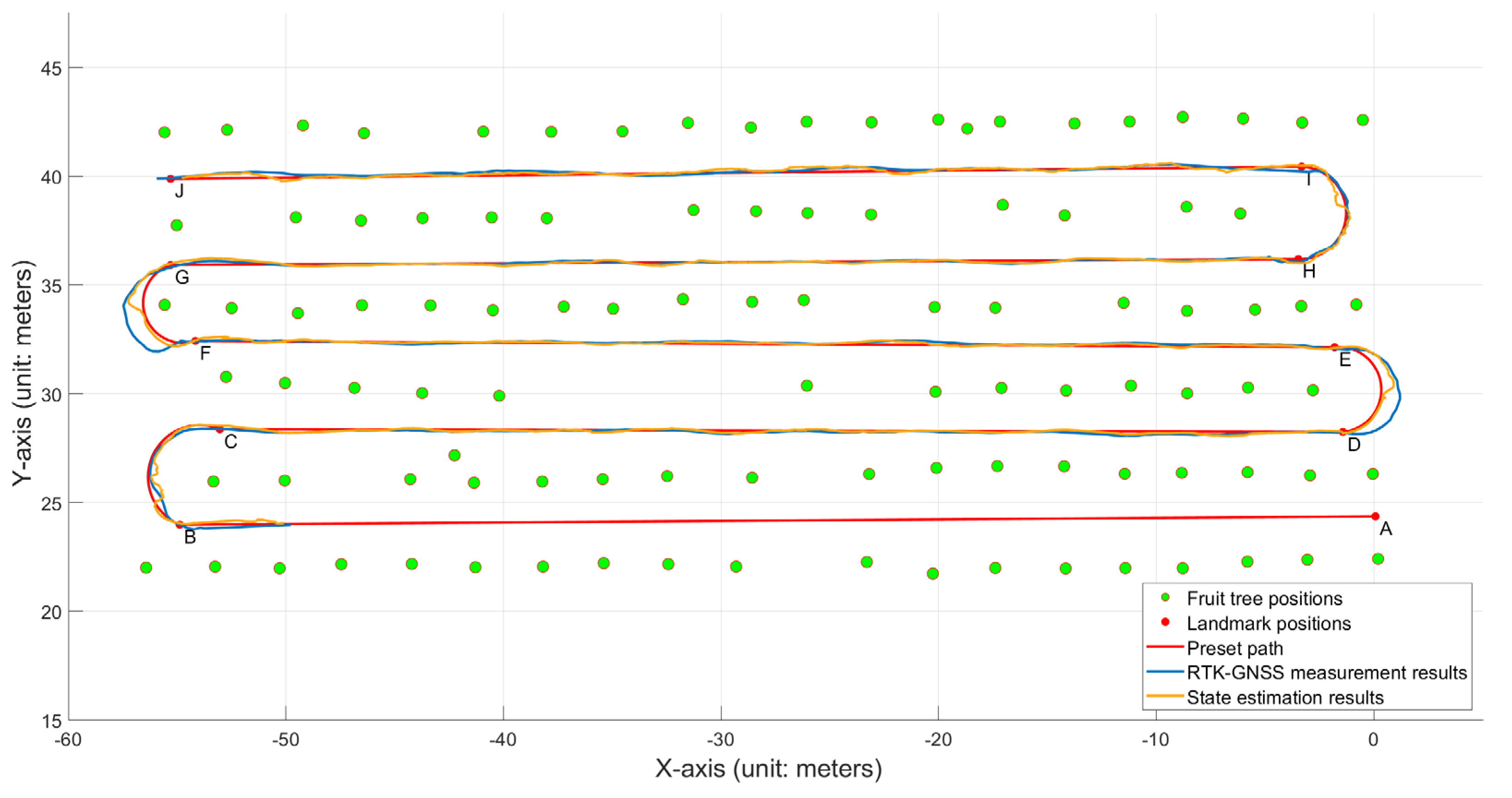
3.2. Orchard Navigation Tests

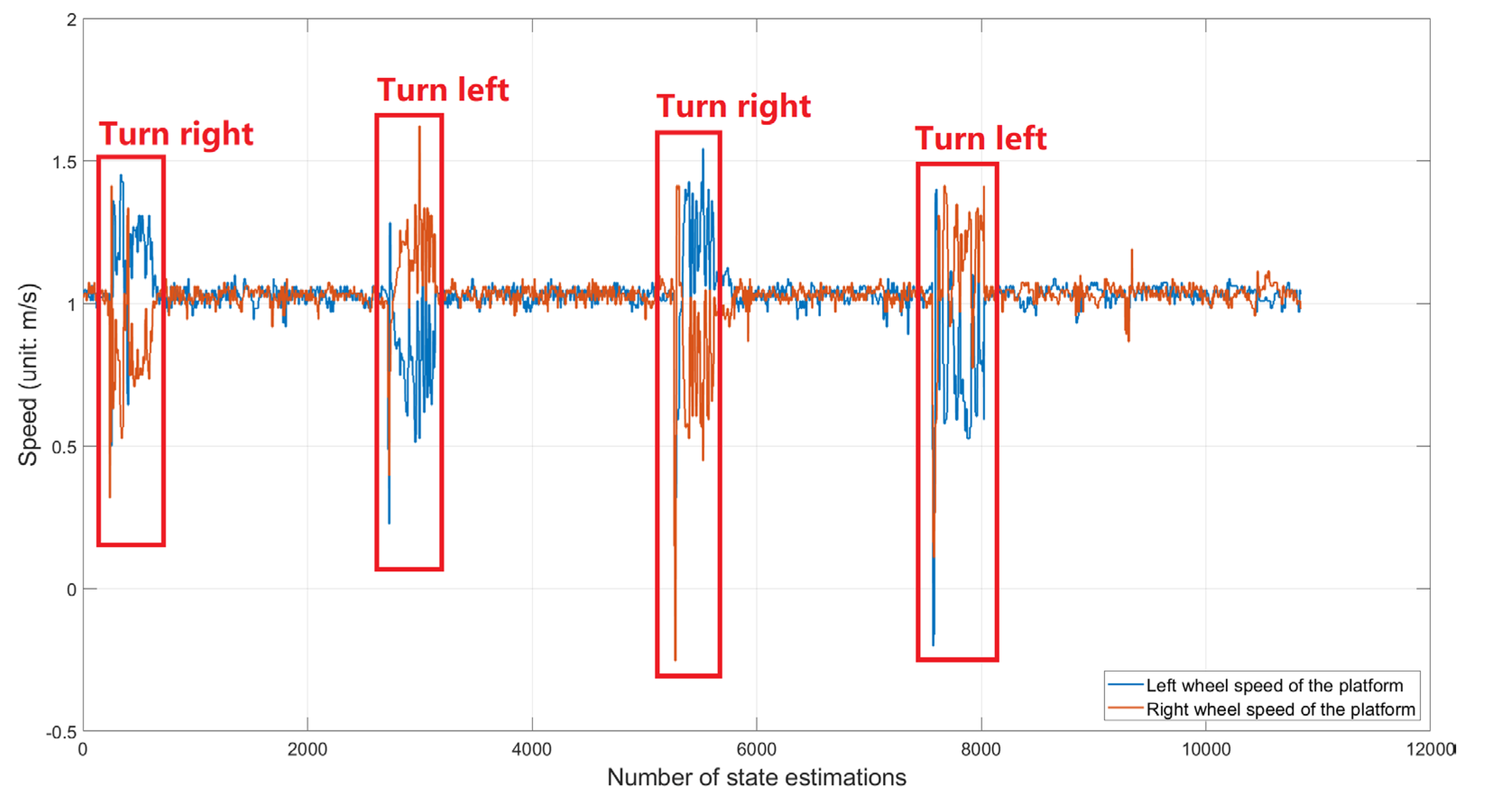
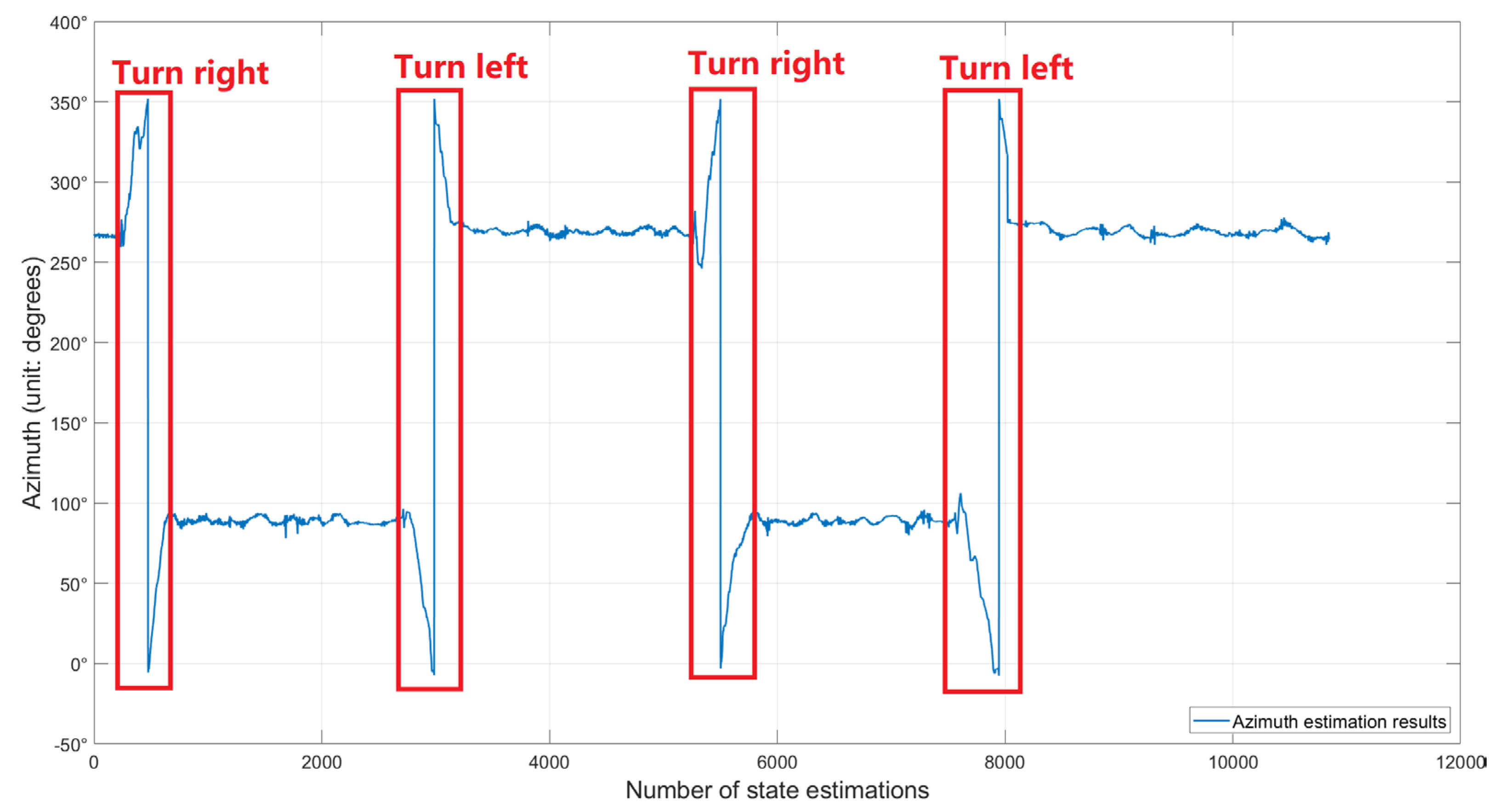
3.2.1. Overall System Navigation Performance Evaluation

The results of the system’s overall navigation performance evaluation, including the ground-truth trajectory, state estimation results, and preset trajectory, are presented in Figure 10. During the straight-line navigation phase (i.e., segments A-B, C-D, etc.), the mean absolute trajectory tracking error was 0.07 m with a standard deviation of 0.06 m. In the turning and row-switching phase (i.e., segments B-C, D-E, etc.), the mean absolute trajectory tracking error was 0.30 m with a standard deviation of 0.30 m. The output frequency of the system state estimation result was approximately 10 Hz.

According to the test results, significant deviations occurred between the system’s estimated and preset trajectories during the turning and row-switching phase, particularly in segments D-E and F-G, as shown in Figure 11. Considering segment D-E as an example, Figure 12 presents the filtered LiDAR data for state estimation points 3200, 3280, 3360, 3380, 3440, and 3560. The localization status and number of valid measurements (see Section 2.2.5) for each point are listed in

Table 1. Localization states in segment D-E.

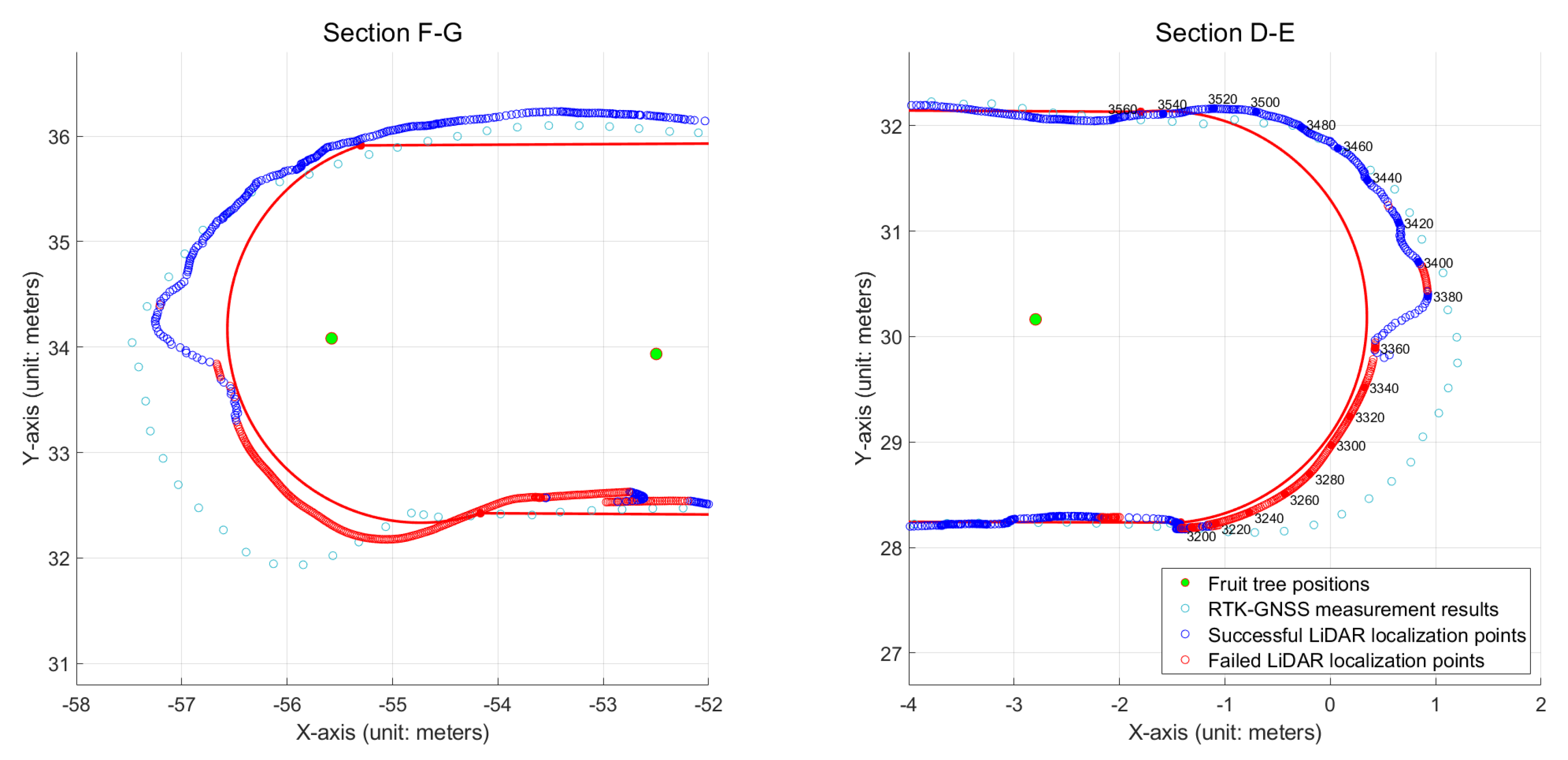
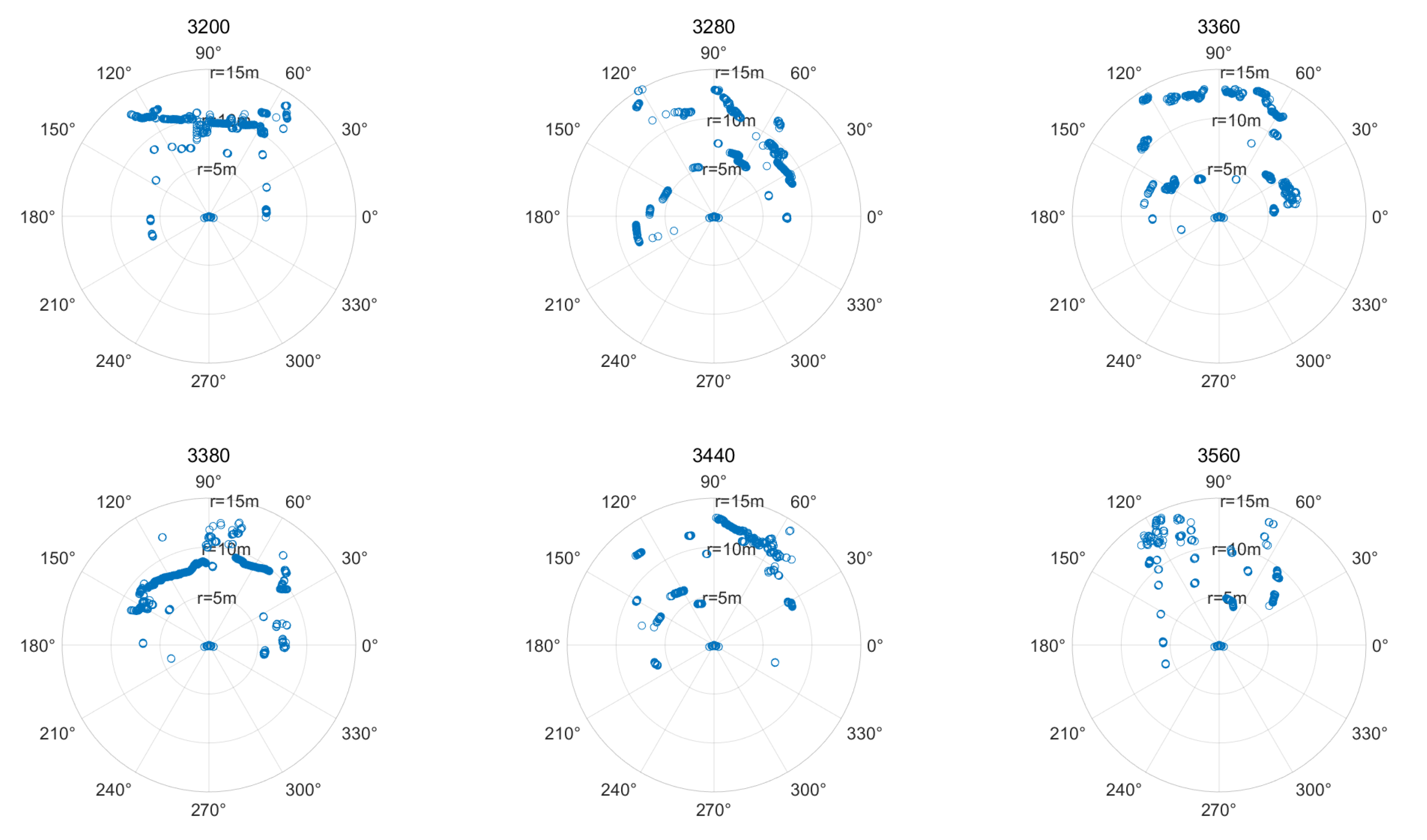
State Estimation Point	Number of Trunk Clusters	Number of Successfully Matched Trunk Clusters	Number of Successfully Matched Fruit Trees	Number of Valid Measurements	Localization State
3200	13	1	1	0	Failed
3280	12	1	1	0	Failed
3360	10	3	3	0	Failed
3380	16	5	5	3	Success
3440	9	8	8	25	Success
3560	13	7	7	21	Success

. From Figure 10 and Table 1, it can be inferred that the primary reasons for localization failures at state estimation points 3200, 3280, and 3360 are twofold: (1) these points are located in the headland, where fewer fruit trees are available for localization; and (2) the LiDAR scanning area was mainly oriented away from the fruit trees. These factors collectively resulted in fewer measurable fruit trees within the LiDAR field of view, leading to a reduced number of valid measurements and ultimately causing localization failures at the current time step. In contrast, at points 3380, 3440, and 3560, the LiDAR scanning area was primarily oriented toward the fruit trees, resulting in more measurable fruit trees and a higher number of valid measurements, allowing for successful localization at these points. As shown in Figure 11, during the period between points 3200 and 3360 in segment D-E, the system was in a state of localization failure most of the time, during which the localization function was taken over by the odometry system. Figure 11 further reveals that during this interval, the deviation between the state estimation results and RTK-GNSS measurements gradually increased. However, between points 3360 and 3380, the system successfully re-localized as more fruit trees became measurable within the LiDAR’s field of view, causing the deviation between the state estimation and RTK-GNSS measurements to decrease gradually. After point 3420, the state estimation results largely coincided with the RTK-GNSS measurements.

In Figure 13 and Figure 14, one can see that during the straight-line travel within the fruit tree rows, the speeds of the left and right wheels remained relatively stable, with no significant fluctuations. Regarding the azimuth angle, only minor variations were observed, and no abrupt changes occurred. However, during the semi-circular turns for row switching, the speeds of both wheels exhibited significant changes to accomplish the differential steering, which was mirrored by substantial variations in the azimuth angle.

In orchard operations, such as spraying and harvesting, the straight-line phase is considered the operational segment, requiring high accuracy in trajectory tracking. In contrast, the turning and row-switching phase is classified as a non-operational segment. In this phase, provided that collisions with fruit trees are avoided, the requirements for trajectory tracking accuracy are relatively relaxed, effectively reducing the cost of navigation equipment. Based on our test results, the proposed system meets the operational requirements of orchard environments.

3.2.2. Trajectory Tracking Tests at Different Straight-Line Driving Speeds

The results of the trajectory tracking tests at different straight-line driving speeds are presented in Figure 15 and

Table 2. Trajectory tracking error results at different straight-line driving speeds.

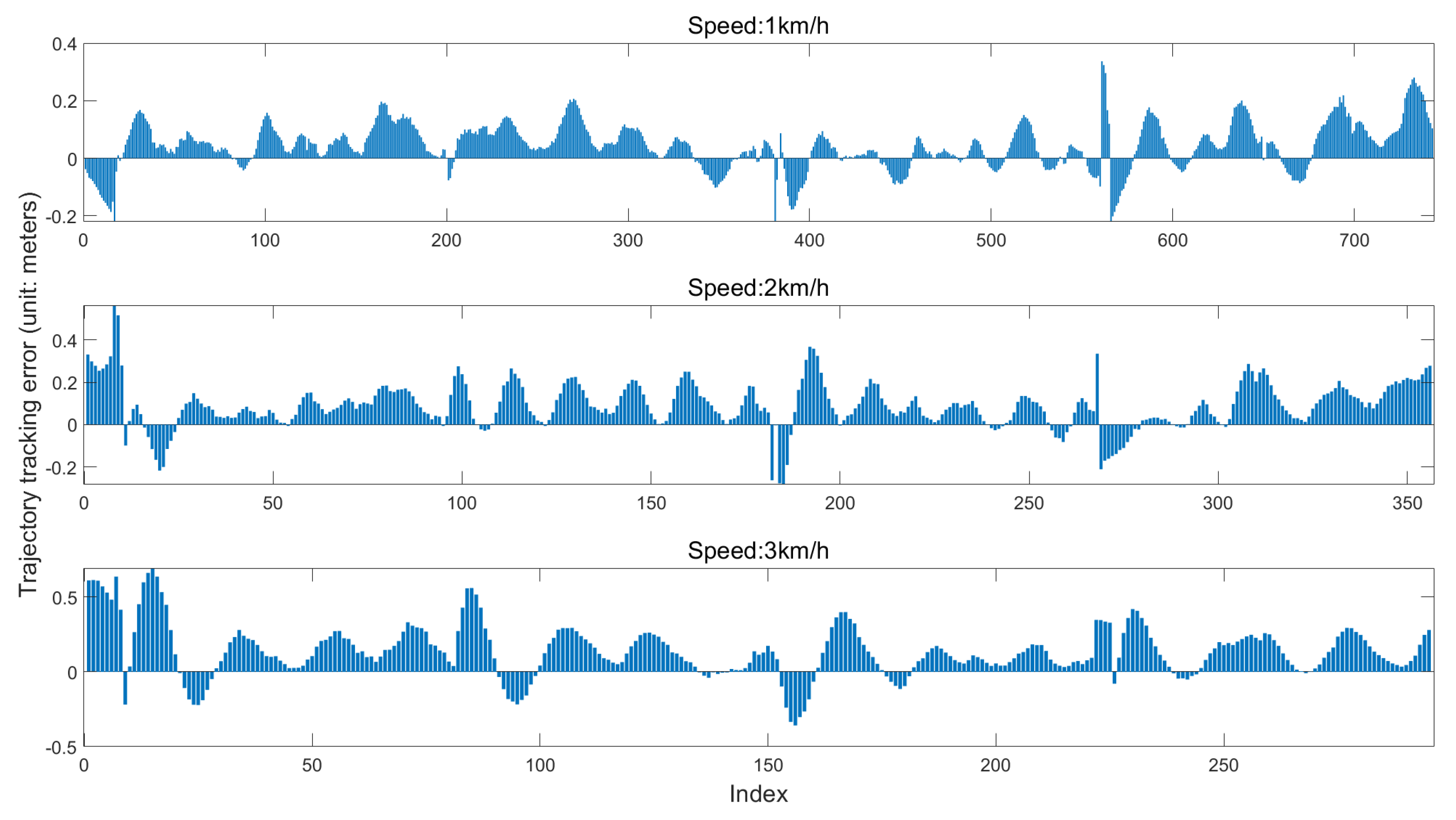
Speed	Mean Absolute Error of Trajectory Tracking	Standard Deviation of Absolute Trajectory Tracking Error	Maximum Absolute Trajectory Tracking Error	RMS	Proportion of Absolute Error ≥5%
1 km/h	0.07 m	0.06 m	0.32 m	0.09 m	≥0.18 m (5.79%)
2 km/h	0.11 m	0.09 m	0.56 m	0.14 m	≥0.27 m (5.06%)
3 km/h	0.18 m	0.14 m	0.64 m	0.22 m	≥0.47 m (5.08%)

.

In Figure 15 and Table 2, one can see that the maximum trajectory tracking errors occurred shortly after the platform started moving. According to Table 2, the maximum absolute trajectory tracking errors at speeds of 1, 2, and 3 km/h were 0.32 m, 0.56 m, and 0.64 m, respectively. The proportion of errors below 0.18 m, 0.27 m, and 0.47 m exceeded 95%, meeting the application requirements for most orchard environments.

Figure 15 also shows that at different straight-line driving speeds, the proportion of positive trajectory tracking errors was relatively high, accounting for 75.64%, 85.96%, and 84.07% at speeds of 1, 2, and 3 km/h, respectively. This indicates that the platform remained on the right side of the pre-set path in more than 75% of the time during straight-line driving.

3.3. Discussion

3.3.1. Discussion of System Localization Results

From the system localization accuracy tests, it can be concluded that in a single-state estimation, the projections of valid measurements on the X and Y axes followed a truncated normal distribution. Taking the projection on the X-axis as an example, according to the central limit theorem, when the number of valid measurements in a single state estimation is large, the mean of the valid measurements approximates a normal distribution $N\left(\mu ,{\sigma }^2/n\right)$. Here, $\mu$ and ${\sigma }^2$ represent the mathematical expectation and variance of the distribution of the valid measurement projections on the X-axis, respectively, and $n$ is the number of valid measurements. Therefore, when the number of valid measurements is large, the positional measurements of the operation platform in the orchard’s local coordinate system approximately follow a normal distribution, allowing for the estimation and prediction of the deviation between the measured values and ground truth.

When computing the platform’s position at time $k$ based on the tree coordinates and distance to the trees, Equation (12) or Equation (14) helps verify the correctness of the solution. Because the constant $C$ is chosen empirically, if $C$ is too small and $x_{true}^k\ne x_{k-1}^{+}$ ($x_{true}^k$ is the X-axis projection of the ground-truth position of the platform at time $k$) is large, this could disrupt the distribution characteristics of valid measurements described in Section 3.1. This disruption would shift the mathematical expectation, introduce systematic errors, and reduce the localization accuracy of the system.

3.3.2. Discussion of System Navigation Performance

As can be seen from Table 2 in Section 3.2.2, the proposed method achieved comparable navigation results with the method “Kalman filter algorithm with line-detection” used by Blok et al. [9]. In this study, the RMS was 0.09 m at a speed of 1 km/h, and the RMS at a speed of 0.25 m/s was 0.087 m, which indicates that the proposed method has a good navigation effect. Compared to Blok et al.’s [9] work, the proposed method has the function of autonomous turning and makes an improvement in localization accuracy (see Section 3.1).

As shown in Table 1 in Section 3.2, the number of successfully matched trunk clusters equaled the number of successfully matched fruit trees. However, theoretical analysis suggests that this relationship is not always valid. According to Section 2.2.4, when multiple trunk cluster centers fall within the threshold area around a single fruit tree, a situation may arise in which a single fruit tree matches multiple trunk cluster centers. In orchard environments, factors such as tree branches, dense weeds around trees, or free-ranging poultry may cause one fruit tree to match multiple trunk cluster centers. When this occurs, the polar radii of the multiple trunk cluster centers in the LiDAR polar coordinate system can be considered as distances from the LiDAR scanning center to the corresponding fruit tree. These distances can then be used to calculate the current position of the operation platform, enhancing the system’s adaptability to the operational environment.

In the trajectory tracking tests at different straight-line driving speeds, the system’s trajectory tracking errors were positive in over 75% of all cases, meaning the platform remained on one side of the preset path during most of the straight-line driving phase. This phenomenon aligns with the findings of Blok et al. [9], although in their study, the platform tended to the left, whereas in our study, it tended to the right. Because this situation did not occur in the offline simulation of the motion control method, this phenomenon was attributable to the following factor: A deviation existed between the measured value of the current position of the operating platform and the true value. In other words, the measured current position value of the operating platform contained a systematic error. The reason for the systematic error of the measured value may be that the distribution characteristics of the effective measurement value described in Section 3.1 have been destroyed, and the mathematical expectation of the distribution followed by the effective measurement value has a deviation from the true value of the current position, thus causing the systematic error. Future research should focus on understanding the causes of the distribution of valid measurements to reduce the system error in the navigation system’s localization function and improve both localization and navigation accuracy.

When the average radius of the fruit tree trunk is small and far from the LiDAR scanning center, only limited laser points may fall on the fruit tree trunk, which may make the autonomous navigation method proposed in this study limited. The same concern was expressed by Higuti et al. [10], but the answer was given in their article: “… However, chances are that the navigation will be unreliable if only LiDAR is used, considering very young plants. When plants are very small, this is not a limiting factor. Indeed, GNSS is usable since there is little multipath error due to cluttered canopies.”

4. Conclusions

We developed an autonomous orchard navigation system that integrated sensor data from 2D LiDAR, an electronic compass, and an encoder. The system’s mean localization error was 0.09 m with a standard deviation of 0.05 m. The mean absolute localization errors in the X and Y axes were 0.05 m and 0.06 m, respectively, with corresponding standard deviations of 0.04 m and 0.05 m. At a driving speed of 1 km/h, the mean absolute trajectory tracking error in the operational segments was 0.07 m with a standard deviation of 0.06 m. At driving speeds of 2 and 3 km/h, the mean absolute trajectory tracking errors were 0.11 m and 0.18 m, respectively, with standard deviations of 0.09 m and 0.14 m. During straight-line driving, the platform remained on the right side of the preset path for more than 75% of the time. These results demonstrate that the proposed method provides effective navigation and is suitable for various orchard environments.