Improving Simulations of Rice Growth and Nitrogen Dynamics by Assimilating Multivariable Observations into ORYZA2000 Model
Abstract
:1. Introduction
2. Materials and Methods
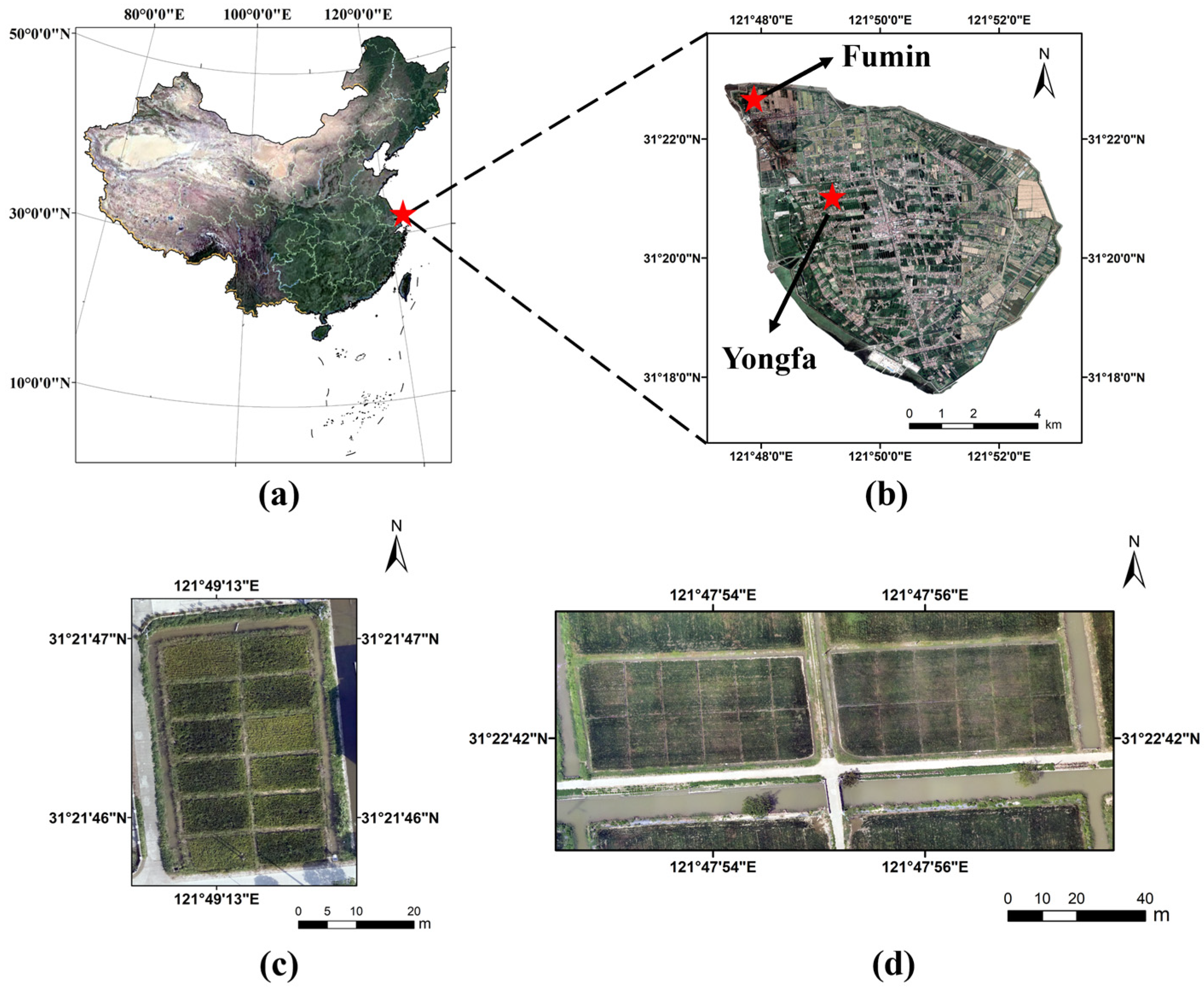
2.1. Description of the Experimental Area
2.2. Field Data Collection
2.3. ORYZA2000 Model
2.3.1. Crop Growth Module
2.3.2. Nitrogen Dynamics
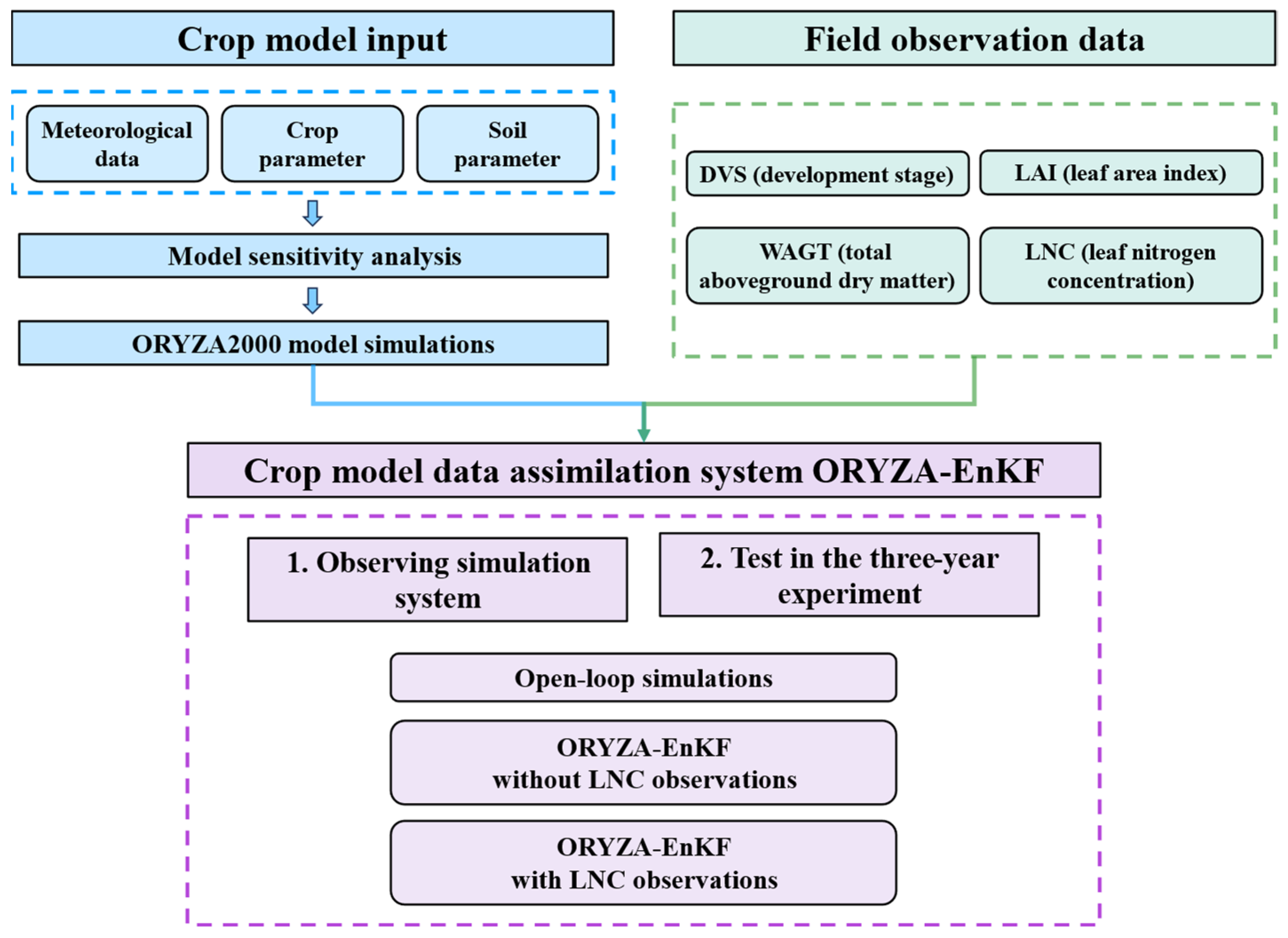
2.4. Parameter Sensitivity Analysis
2.5. ORYZA-EnKF Data Assimilation Framework
2.5.1. Ensemble Kalman Filter
2.5.2. Observing Simulation System
2.6. Evaluation Method
3. Results and Discussion
3.1. ORYZA2000 Model Parameter Sensitivity Analysis
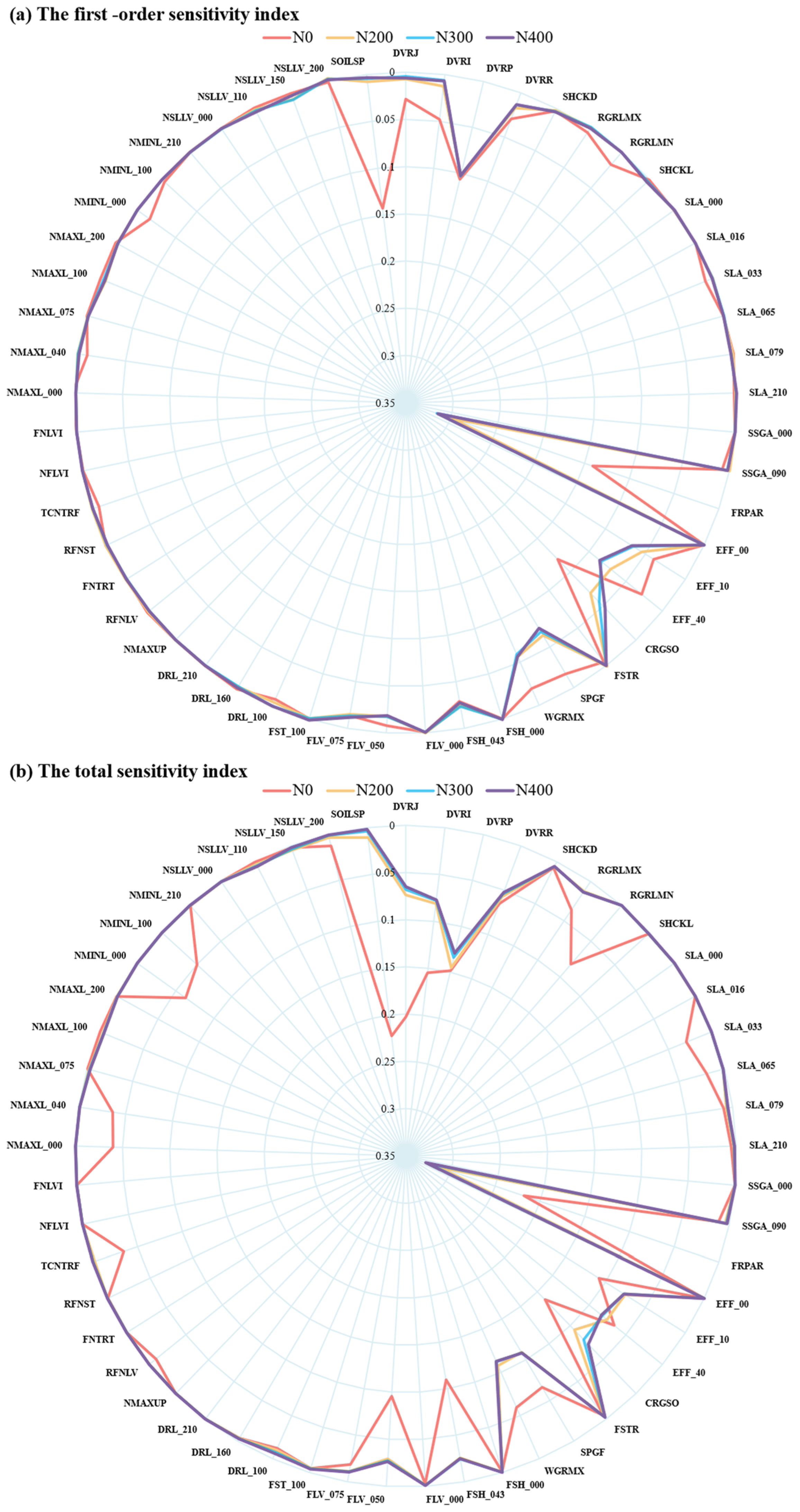
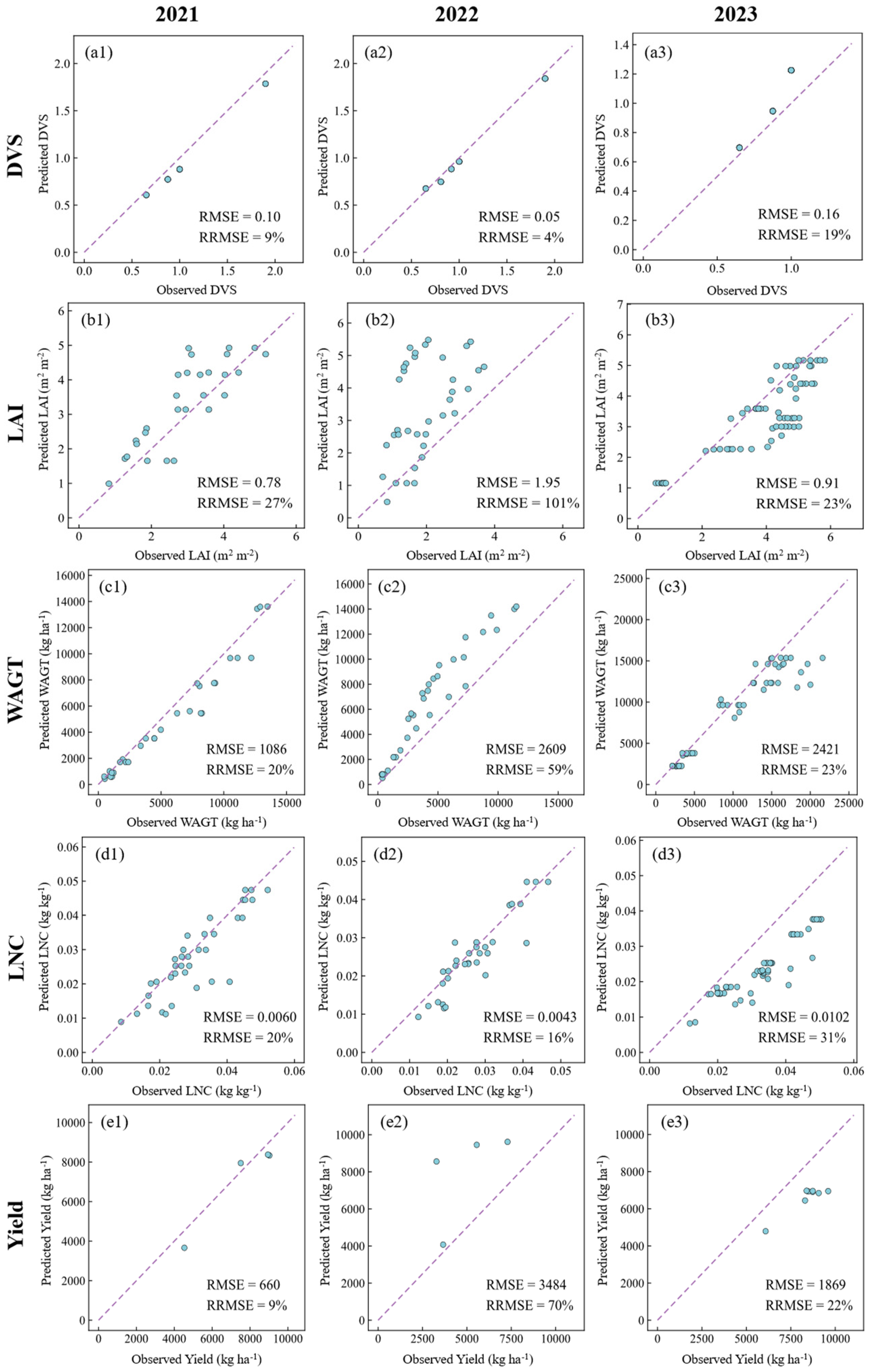
3.2. ORYZA2000 Model Calibration
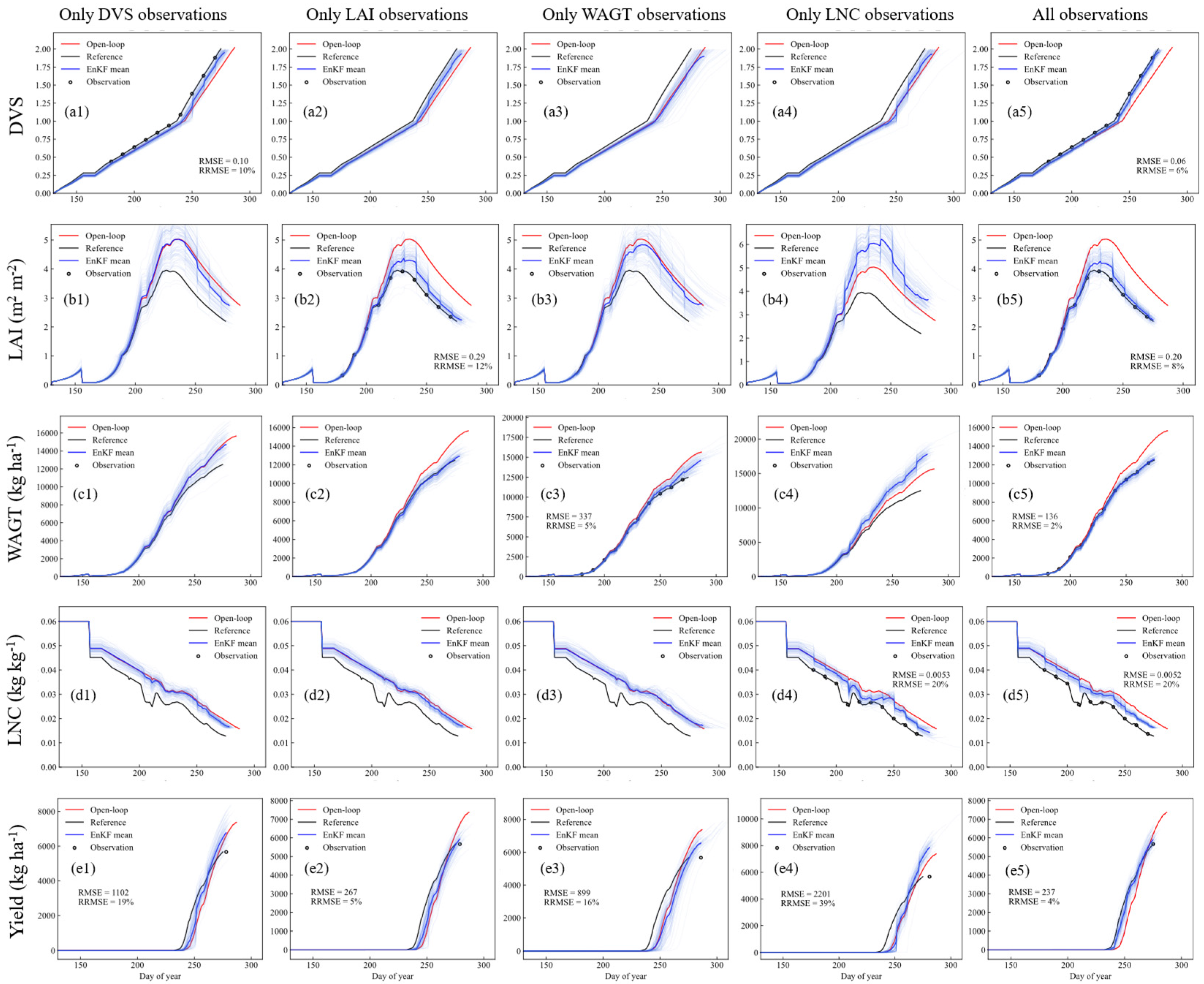
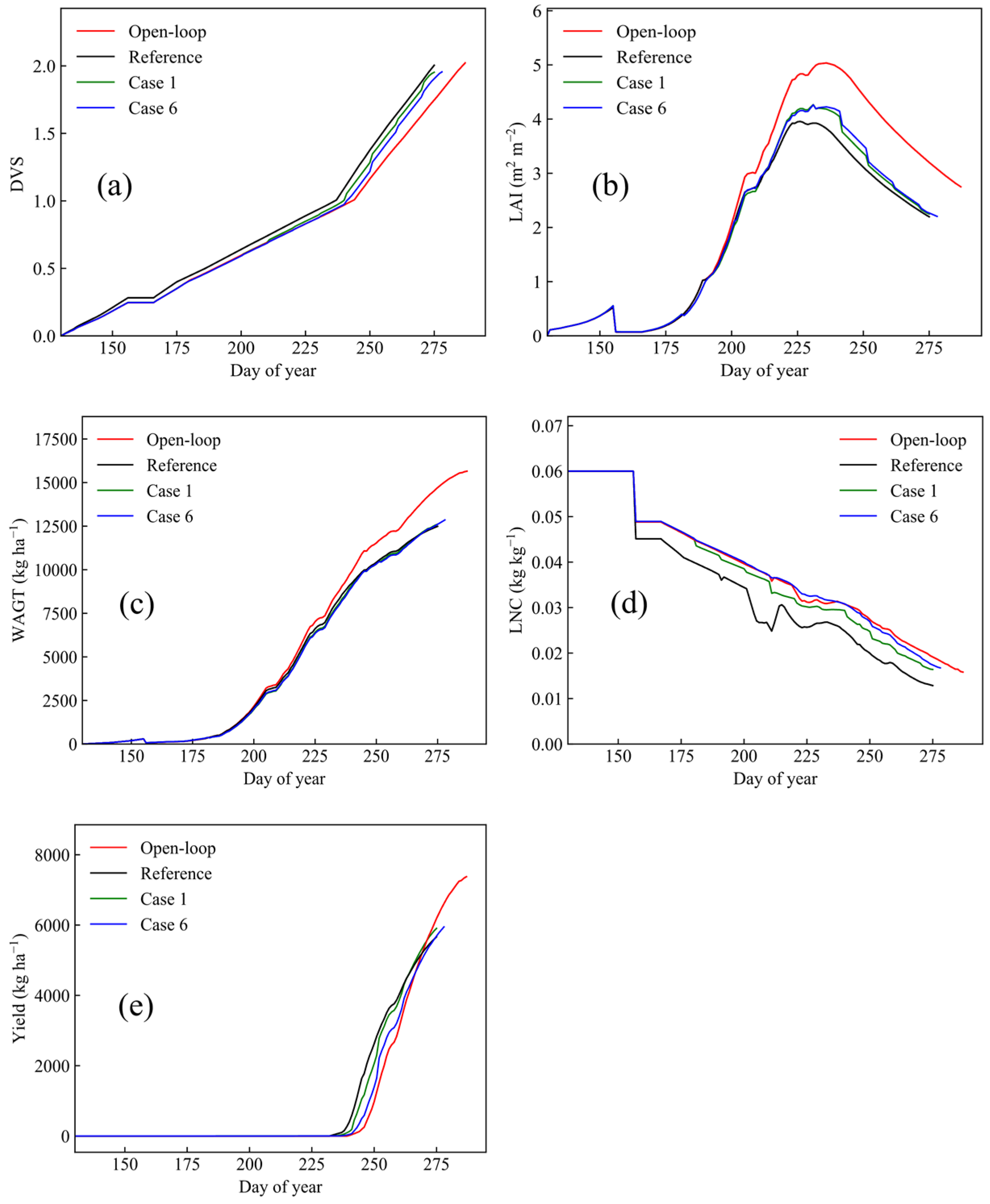
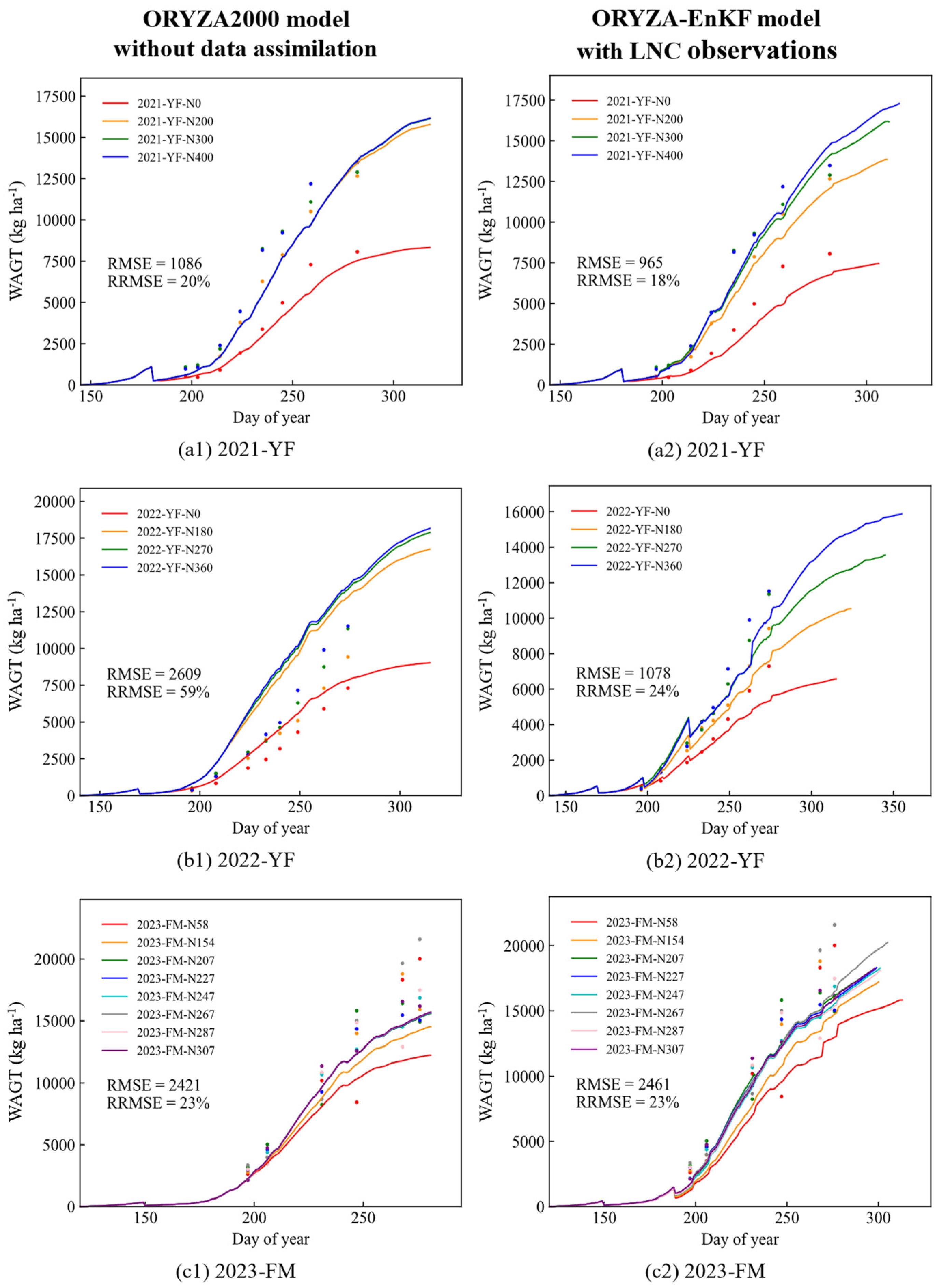
3.3. Value of LNC Observation to ORYZA-EnKF Data Assimilation System
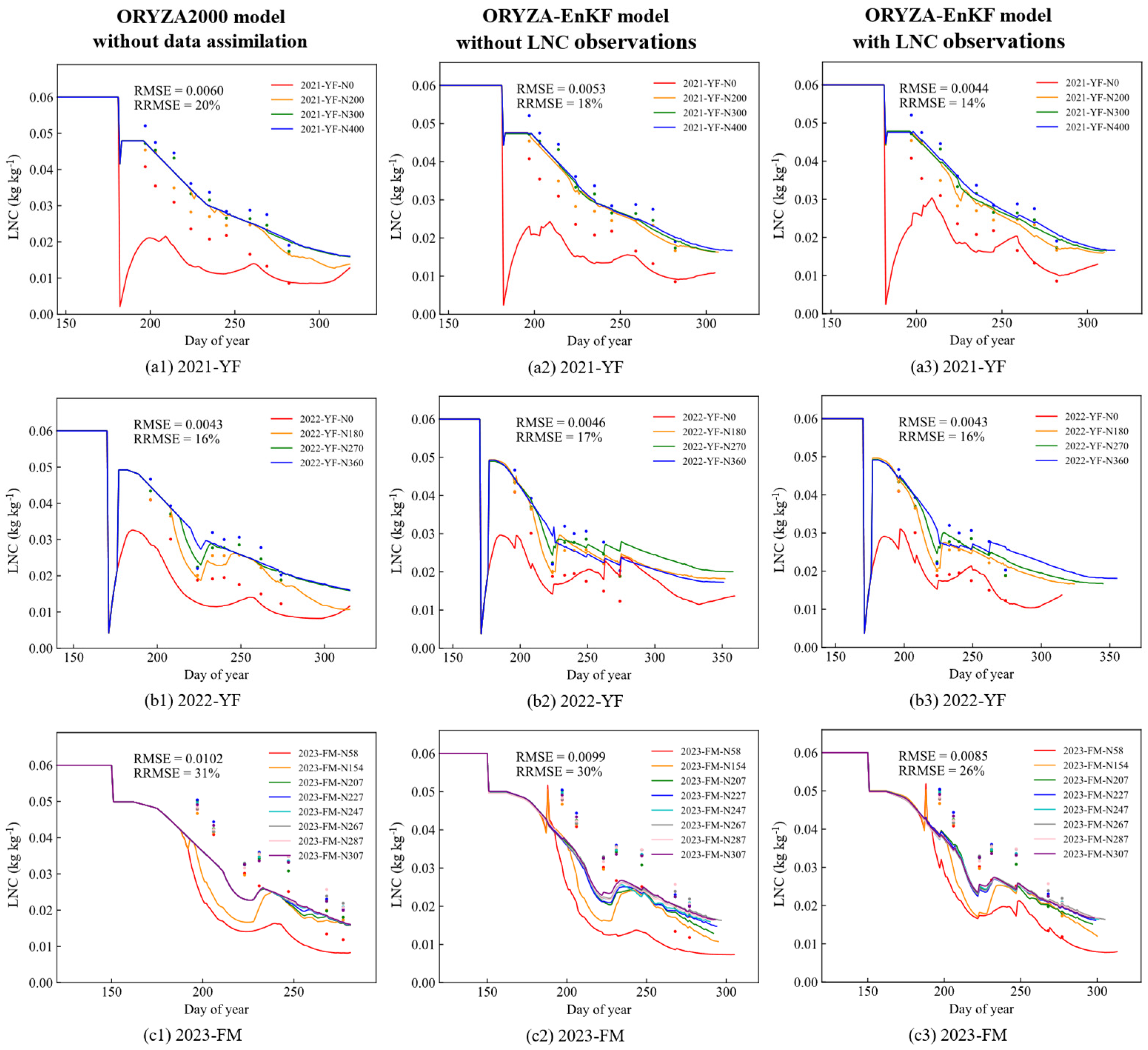
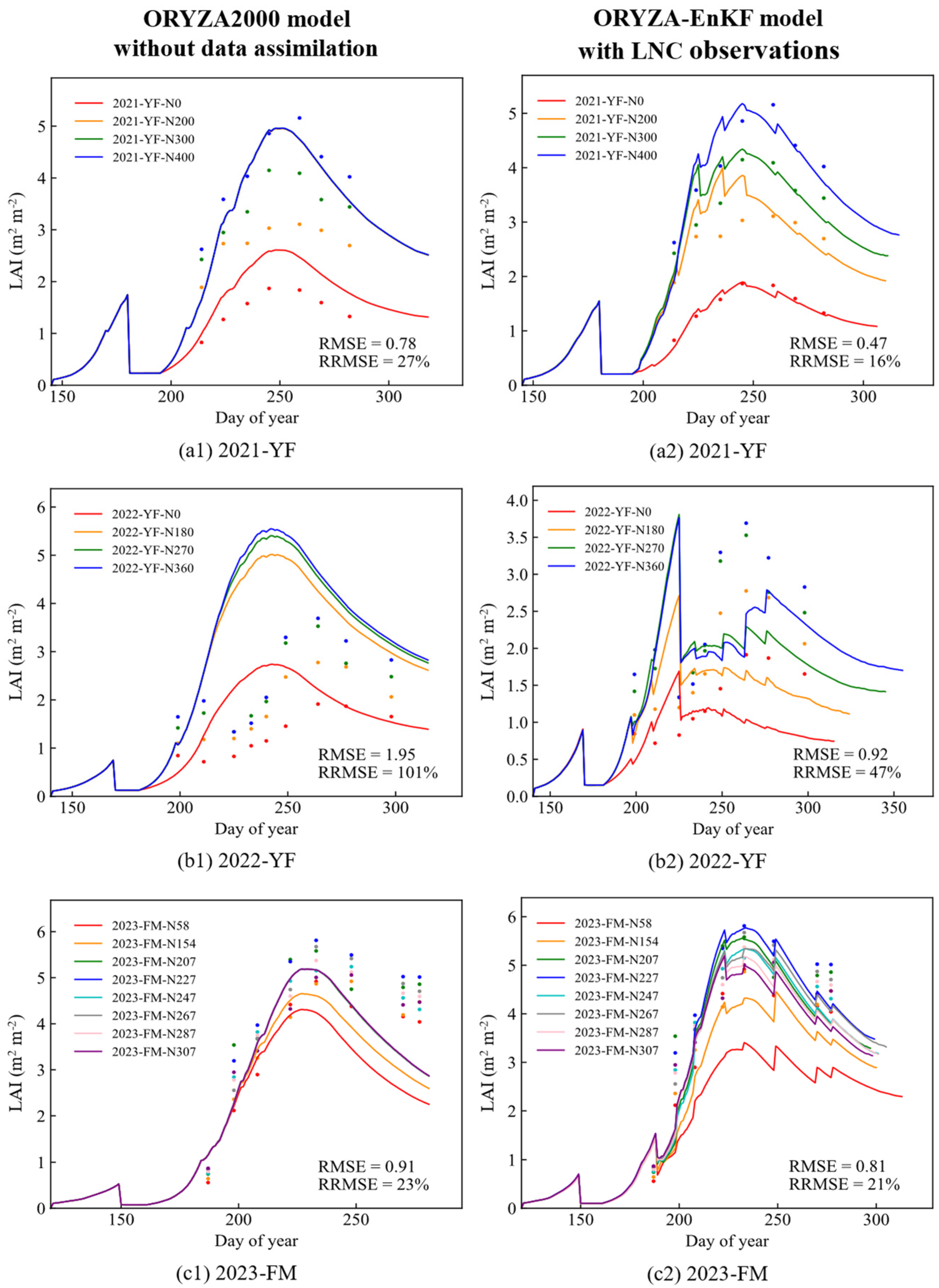
3.4. Test in the Three-Year Experiment
3.5. Potential Applications and Future Work
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yuan, S.; Linquist, B.A.; Wilson, L.T.; Cassman, K.G.; Stuart, A.M.; Pede, V.; Miro, B.; Saito, K.; Agustiani, N.; Aristya, V.E.; et al. Sustainable intensification for a larger global rice bowl. Nat. Commun. 2021, 12, 7163. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, W.; Xu, J.; Wang, Y.; Wu, Z.; Liu, H. Expounding the Effect of Harvest Management on Rice (Oryza sativa L.) Yield and Latent Loss Based on the Accurate Measurement of Grain Data. Agronomy 2024, 14, 1346. [Google Scholar] [CrossRef]
- Cai, S.; Zhao, X.; Pittelkow, C.M.; Fan, M.; Zhang, X.; Yan, X. Optimal nitrogen rate strategy for sustainable rice production in China. Nature 2023, 615, 73–79. [Google Scholar] [CrossRef]
- Xu, J.; Cai, H.; Wang, X.; Ma, C.; Lu, Y.; Ding, Y.; Wang, X.; Chen, H.; Wang, Y.; Saddique, Q. Exploring optimal irrigation and nitrogen fertilization in a winter wheat-summer maize rotation system for improving crop yield and reducing water and nitrogen leaching. Agric. Water Manag. 2020, 228, 105904. [Google Scholar] [CrossRef]
- Zhang, X.; Zou, T.; Lassaletta, L.; Mueller, N.D.; Tubiello, F.N.; Lisk, M.D.; Lu, C.; Conant, R.T.; Dorich, C.D.; Gerber, J.; et al. Quantification of global and national nitrogen budgets for crop production. Nat. Food. 2021, 2, 529–540. [Google Scholar] [CrossRef]
- Morari, F.; Zanella, V.; Gobbo, S.; Bindi, M.; Sartori, L.; Pasqui, M.; Mosca, G.; Ferrise, R. Coupling proximal sensing, seasonal forecasts and crop modelling to optimize nitrogen variable rate application in durum wheat. Precis. Agric. 2021, 22, 75–98. [Google Scholar] [CrossRef]
- Zhao, R.; Ma, Y.; Wu, S. A Review of the Research Status and Prospects of Regional Crop Yield Simulations. Agronomy 2024, 14, 1397. [Google Scholar] [CrossRef]
- Yuan, S.; Saito, K.; van Oort, P.A.J.; van Ittersum, M.K.; Peng, S.; Grassini, P. Intensifying rice production to reduce imports and land conversion in Africa. Nat. Commun. 2024, 15, 835. [Google Scholar] [CrossRef]
- Asseng, S.; Ewert, F.; Martre, P.; Rötter, R.P.; Lobell, D.B.; Cammarano, D.; Kimball, B.A.; Ottman, M.J.; Wall, G.W.; White, J.W.; et al. Rising temperatures reduce global wheat production. Nat. Clim. Chang. 2015, 5, 143–147. [Google Scholar] [CrossRef]
- Wang, B.; Feng, P.; Liu, D.L.; Leary, G.J.O.; Macadam, I.; Waters, C.; Asseng, S.; Cowie, A.; Jiang, T.; Xiao, D.; et al. Sources of uncertainty for wheat yield projections under future climate are site-specific. Nat. Food. 2020, 1, 720–728. [Google Scholar] [CrossRef]
- van Oosterom, E.J.; Borrell, A.K.; Chapman, S.C.; Broad, I.J.; Hammer, G.L. Functional dynamics of the nitrogen balance of sorghum: I. N demand of vegetative plant parts. Field Crop. Res. 2010, 115, 19–28. [Google Scholar] [CrossRef]
- Soufizadeh, S.; Munaro, E.; McLean, G.; Massignam, A.; van Oosterom, E.J.; Chapman, S.C.; Messina, C.; Cooper, M.; Hammer, G.L. Modelling the nitrogen dynamics of maize crops—Enhancing the APSIM maize model. Eur. J. Agron. 2018, 100, 118–131. [Google Scholar] [CrossRef]
- Jing, Q.; Bouman, B.A.M.; Hengsdijk, H.; Van Keulen, H.; Cao, W. Exploring options to combine high yields with high nitrogen use efficiencies in irrigated rice in China. Eur. J. Agron. 2007, 26, 166–177. [Google Scholar] [CrossRef]
- Falconnier, G.N.; Corbeels, M.; Boote, K.J.; Affholder, F.; Adam, M.; MacCarthy, D.S.; Ruane, A.C.; Nendel, C.; Whitbread, A.M.; Justes, É.; et al. Modelling climate change impacts on maize yields under low nitrogen input conditions in sub-Saharan Africa. Glob. Chang. Biol. 2020, 26, 5942–5964. [Google Scholar] [CrossRef]
- Bouman, B.A.M.; van Laar, H.H. Description and evaluation of the rice growth model ORYZA2000 under nitrogen-limited conditions. Agric. Syst. 2006, 87, 249–273. [Google Scholar] [CrossRef]
- Li, T.; Angeles, O.; Marcaida, M.; Manalo, E.; Manalili, M.P.; Radanielson, A.; Mohanty, S. From ORYZA2000 to ORYZA (v3): An improved simulation model for rice in drought and nitrogen-deficient environments. Agric. For. Meteorol. 2017, 237–238, 246–256. [Google Scholar] [CrossRef]
- Charney, J.; Halem, M.; Jastrow, R. Use of Incomplete Historical Data to Infer the Present State of the Atmosphere. J. Atmos. Sci. 1969, 26, 1160–1163. [Google Scholar] [CrossRef]
- Ines, A.V.M.; Das, N.N.; Hansen, J.W.; Njoku, E.G. Assimilation of remotely sensed soil moisture and vegetation with a crop simulation model for maize yield prediction. Remote Sens. Environ. 2013, 138, 149–164. [Google Scholar] [CrossRef]
- Huang, J.; Gómez-Dans, J.L.; Huang, H.; Ma, H.; Wu, Q.; Lewis, P.E.; Liang, S.; Chen, Z.; Xue, J.; Wu, Y.; et al. Assimilation of remote sensing into crop growth models: Current status and perspectives. Agric. For. Meteorol. 2019, 276–277, 107609. [Google Scholar] [CrossRef]
- Jin, X.; Kumar, L.; Li, Z.; Feng, H.; Xu, X.; Yang, G.; Wang, J. A review of data assimilation of remote sensing and crop models. Eur. J. Agron. 2018, 92, 141–152. [Google Scholar] [CrossRef]
- Luo, L.; Sun, S.; Xue, J.; Gao, Z.; Zhao, J.; Yin, Y.; Gao, F.; Luan, X. Crop yield estimation based on assimilation of crop models and remote sensing data: A systematic evaluation. Agric. Syst. 2023, 210, 103711. [Google Scholar] [CrossRef]
- Evensen, G. Sequential data assimilation with a nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics. J. Geophys. Res. Oceans 1994, 99, 10143–10162. [Google Scholar] [CrossRef]
- de Wit, A.J.W.; van Diepen, C.A. Crop model data assimilation with the Ensemble Kalman filter for improving regional crop yield forecasts. Agric. For. Meteorol. 2007, 146, 38–56. [Google Scholar] [CrossRef]
- Hu, S.; Shi, L.; Huang, K.; Zha, Y.; Hu, X.; Ye, H.; Yang, Q. Improvement of sugarcane crop simulation by SWAP-WOFOST model via data assimilation. Field Crop. Res. 2019, 232, 49–61. [Google Scholar] [CrossRef]
- Yang, C.; Lei, H. Evaluation of data assimilation strategies on improving the performance of crop modeling based on a novel evapotranspiration assimilation framework. Agric. For. Meteorol. 2024, 346, 109882. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, H.; Ma, X.; Liu, H. Combining Data Assimilation with Machine Learning to Predict the Regional Daily Leaf Area Index of Summer Maize (Zea mays L.). Agronomy 2023, 13, 2688. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, Z.; Tao, F. Improving regional winter wheat yield estimation through assimilation of phenology and leaf area index from remote sensing data. Eur. J. Agron. 2018, 101, 163–173. [Google Scholar] [CrossRef]
- Jin, X.; Li, Z.; Feng, H.; Ren, Z.; Li, S. Estimation of maize yield by assimilating biomass and canopy cover derived from hyperspectral data into the AquaCrop model. Agric. Water Manag. 2020, 227, 105846. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, Z.; Chen, Y.; Zhang, L.; Tao, F. Improving regional wheat yields estimations by multi-step-assimilating of a crop model with multi-source data. Agric. For. Meteorol. 2020, 290, 107993. [Google Scholar] [CrossRef]
- Yu, D.; Zha, Y.; Shi, L.; Ye, H.; Zhang, Y. Improving sugarcane growth simulations by integrating multi-source observations into a crop model. Eur. J. Agron. 2022, 132, 126410. [Google Scholar] [CrossRef]
- Yang, Q.; Shi, L.; Han, J.; Zha, Y.; Yu, J.; Wu, W.; Huang, K. Regulating the time of the crop model clock: A data assimilation framework for regions with high phenological heterogeneity. Field Crop. Res. 2023, 293, 108847. [Google Scholar] [CrossRef]
- Liang, H.; Gao, S.; Hu, K. Global sensitivity and uncertainty analysis of the dynamic simulation of crop N uptake by using various N dilution curve approaches. Eur. J. Agron. 2020, 116, 126044. [Google Scholar] [CrossRef]
- Li, Z.; Jin, X.; Zhao, C.; Wang, J.; Xu, X.; Yang, G.; Li, C.; Shen, J. Estimating wheat yield and quality by coupling the DSSAT-CERES model and proximal remote sensing. Eur. J. Agron. 2015, 71, 53–62. [Google Scholar] [CrossRef]
- Weiss, M.; Jacob, F.; Duveiller, G. Remote sensing for agricultural applications: A meta-review. Remote Sens. Environ. 2020, 236, 111402. [Google Scholar] [CrossRef]
- Berger, K.; Verrelst, J.; Féret, J.; Wang, Z.; Wocher, M.; Strathmann, M.; Danner, M.; Mauser, W.; Hank, T. Crop nitrogen monitoring: Recent progress and principal developments in the context of imaging spectroscopy missions. Remote Sens. Environ. 2020, 242, 111758. [Google Scholar] [CrossRef]
- Li, J.; Shi, L.; Mo, X.; Hu, X.; Su, C.; Han, J.; Deng, X.; Du, S.; Li, S. Self-correcting deep learning for estimating rice leaf nitrogen concentration with mobile phone images. Comput. Electron. Agric. 2024, 227, 109497. [Google Scholar] [CrossRef]
- Wang, W.; Rong, Y.; Zhang, C.; Wang, C.; Huo, Z. Data assimilation of soil moisture and leaf area index effectively improves the simulation accuracy of water and carbon fluxes in coupled farmland hydrological model. Agric. Water Manag. 2024, 291, 108646. [Google Scholar] [CrossRef]
- Lancashire, P.D.; Bleiholder, H.; Boom, T.V.D.; Langelüddeke, P.; Stauss, R.; Weber, E.; Witzenberger, A. A uniform decimal code for growth stages of crops and weeds. Ann. Appl. Biol. 1991, 119, 561–601. [Google Scholar] [CrossRef]
- Han, J.; Shi, L.; Yang, Q.; Chen, Z.; Yu, J.; Zha, Y. Rice yield estimation using a CNN-based image-driven data as-similation framework. Field Crops Res. 2022, 288, 108693. [Google Scholar] [CrossRef]
- Jung, S.; Rickert, D.A.; Deak, N.A.; Aldin, E.D.; Recknor, J.; Johnson, L.A.; Murphy, P.A. Comparison of Kjeldahl and Dumas methods for determining protein contents of soybean products. J. Am. Oil Chem. Society. 2003, 80, 1169–1173. [Google Scholar] [CrossRef]
- Beljkaš, B.; Matić, J.; Milovanović, I.; Jovanov, P.; Mišan, A.; Šarić, L. Rapid method for determination of protein content in cereals and oilseeds: Validation, measurement uncertainty and comparison with the Kjeldahl method. Accredit. Qual. Assur. 2010, 15, 555–561. [Google Scholar] [CrossRef]
- Aguirre, J. Important Topics Related to the Kjeldahl Method. In The Kjeldahl Method: 140 Years; Aguirre, J., Ed.; Springer: Cham, Switzerland, 2023; pp. 123–145. [Google Scholar]
- Bouman, B. ORYZA2000: Modeling Lowland Rice; IRRI: Los Baños, Philippines, 2001. [Google Scholar]
- Yadav, S.; Li, T.; Humphreys, E.; Gill, G.; Kukal, S.S. Evaluation and application of ORYZA2000 for irrigation scheduling of puddled transplanted rice in North West India. Field Crop. Res. 2011, 122, 104–117. [Google Scholar] [CrossRef]
- Kawakita, S.; Yamasaki, M.; Teratani, R.; Yabe, S.; Kajiya-Kanegae, H.; Yoshida, H.; Fushimi, E.; Nakagawa, H. Dual ensemble approach to predict rice heading date by integrating multiple rice phenology models and machine learning-based genetic parameter regression models. Agric. For. Meteorol. 2024, 344, 109821. [Google Scholar] [CrossRef]
- Chapagain, R.; Remenyi, T.A.; Harris, R.M.B.; Mohammed, C.L.; Huth, N.; Wallach, D.; Rezaei, E.E.; Ojeda, J.J. Decomposing crop model uncertainty: A systematic review. Field Crop. Res. 2022, 279, 108448. [Google Scholar] [CrossRef]
- Tan, J.; Cui, Y.; Luo, Y. Assessment of uncertainty and sensitivity analyses for ORYZA model under different ranges of parameter variation. Eur. J. Agron. 2017, 91, 54–62. [Google Scholar] [CrossRef]
- Li, P.; Ren, L. Evaluating the effects of limited irrigation on crop water productivity and reducing deep groundwater exploitation in the North China Plain using an agro-hydrological model: I. Parameter sensitivity analysis, calibration and model validation. J. Hydrol. 2019, 574, 497–516. [Google Scholar] [CrossRef]
- Sobol’, I.M. On sensitivity estimation for nonlinear mathematical models. Mat. Model. 1990, 2, 112–118. [Google Scholar]
- Thorp, K.R.; DeJonge, K.C.; Marek, G.W.; Evett, S.R. Comparison of evapotranspiration methods in the DSSAT Cropping System Model: I. Global sensitivity analysis. Comput. Electron. Agric. 2020, 177, 105658. [Google Scholar] [CrossRef]
- Yu, J.; Shi, L.; Han, J.; Yang, Q.; Huang, J.; Ye, M. Assessing parametric and nitrogen fertilizer input uncertainties in the ORYZA_V3 model predictions. Agron. J. 2021, 113, 4965–4981. [Google Scholar] [CrossRef]
- Tan, J.; Cui, Y.; Luo, Y. Global sensitivity analysis of outputs over rice-growth process in ORYZA model. Environ. Modell. Softw. 2016, 83, 36–46. [Google Scholar] [CrossRef]
- Hu, S.; Shi, L.; Zha, Y.; Williams, M.; Lin, L. Simultaneous state-parameter estimation supports the evaluation of data assimilation performance and measurement design for soil-water-atmosphere-plant system. J. Hydrol. 2017, 555, 812–831. [Google Scholar] [CrossRef]
- Curnel, Y.; de Wit, A.J.W.; Duveiller, G.; Defourny, P. Potential performances of remotely sensed LAI assimilation in WOFOST model based on an OSS Experiment. Agric. For. Meteorol. 2011, 151, 1843–1855. [Google Scholar] [CrossRef]
- Lu, Y.; Chibarabada, T.P.; Ziliani, M.G.; Onema, J.K.; McCabe, M.F.; Sheffield, J. Assimilation of soil moisture and canopy cover data improves maize simulation using an under-calibrated crop model. Agric. Water Manag. 2021, 252, 106884. [Google Scholar] [CrossRef]
- Gitelson, A.; Arkebauer, T.; Viña, A.; Skakun, S.; Inoue, Y. Evaluating plant photosynthetic traits via absorption coefficient in the photosynthetically active radiation region. Remote Sens. Environ. 2021, 258, 112401. [Google Scholar] [CrossRef]
- Yu, Q.; Cui, Y.; Liu, L. Assessment of the parameter sensitivity for the ORYZA model at the regional scale—A case study in the Yangtze River Basin. Environ. Modell. Softw. 2023, 159, 105575. [Google Scholar] [CrossRef]
- Hyun, S.; Yang, S.M.; Kim, J.; Kim, K.S.; Shin, J.H.; Lee, S.M.; Lee, B.; Beresford, R.M.; Fleisher, D.H. Development of a mobile computing framework to aid decision-making on organic fertilizer management using a crop growth model. Comput. Electron. Agric. 2021, 181, 105936. [Google Scholar] [CrossRef]
- Liu, J.; Liu, Z.; Zhu, A.; Shen, F.; Lei, Q.; Duan, Z. Global sensitivity analysis of the APSIM-Oryza rice growth model under different environmental conditions. Sci. Total Environ. 2019, 651, 953–968. [Google Scholar] [CrossRef]
- Zhao, B.; Ata-Ul-Karim, S.T.; Liu, Z.; Ning, D.; Xiao, J.; Liu, Z.; Qin, A.; Nan, J.; Duan, A. Development of a critical nitrogen dilution curve based on leaf dry matter for summer maize. Field Crop. Res. 2017, 208, 60–68. [Google Scholar] [CrossRef]
- Espe, M.B.; Yang, H.; Cassman, K.G.; Guilpart, N.; Sharifi, H.; Linquist, B.A. Estimating yield potential in temper-ate high-yielding, direct-seeded US rice production systems. Field Crop. Res. 2016, 193, 123–132. [Google Scholar] [CrossRef]
- Li, T.; Raman, A.K.; Marcaida, M.; Kumar, A.; Angeles, O.; Radanielson, A.M. Simulation of genotype performances across a larger number of environments for rice breeding using ORYZA2000. Field Crops Res. 2013, 149, 312–321. [Google Scholar] [CrossRef]
- Gao, Y.; Xu, X.; Sun, C.; Ding, S.; Huo, Z.; Huang, G. Parameterization and modeling of paddy rice (Oryza sativa L. ssp. japonica) growth and water use in cold regions: Yield and water-saving analysis. Agric. Water Manag. 2021, 250, 106864. [Google Scholar] [CrossRef]
- Seidel, S.J.; Palosuo, T.; Thorburn, P.; Wallach, D. Towards improved calibration of crop models—Where are we now and where should we go? Eur. J. Agron. 2018, 94, 25–35. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, J.; Shang, J.; Dong, T.; Tang, M.; Feng, S.; Cai, H. Improving winter wheat biomass and evapotran-spiration simulation by assimilating leaf area index from spectral information into a crop growth model. Agric. Water Manag. 2021, 255, 107057. [Google Scholar] [CrossRef]
- Ata-Ul-Karim, S.T.; Yao, X.; Liu, X.; Cao, W.; Zhu, Y. Development of critical nitrogen dilution curve of Japonica rice in Yangtze River Reaches. Field Crops Res. 2013, 149, 149–158. [Google Scholar] [CrossRef]
- Qiu, Z.; Ma, F.; Li, Z.; Xu, X.; Ge, H.; Du, C. Estimation of nitrogen nutrition index in rice from UAV RGB images coupled with machine learning algorithms. Comput. Electron. Agric. 2021, 189, 106421. [Google Scholar] [CrossRef]
- Jongschaap, R.E.E. Run-time calibration of simulation models by integrating remote sensing estimates of leaf area index and canopy nitrogen. Eur. J. Agron. 2006, 24, 316–324. [Google Scholar] [CrossRef]
- Yu, Q.; Cui, Y. Improvement and testing of ORYZA model water balance modules for alternate wetting and drying irrigation. Agric. Water Manag. 2022, 271, 107802. [Google Scholar] [CrossRef]
- Gao, Y.; Sun, C.; Ramos, T.B.; Huo, Z.; Huang, G.; Xu, X. Modeling nitrogen dynamics and biomass production in rice paddy fields of cold regions with the ORYZA-N model. Ecol. Model. 2023, 475, 110184. [Google Scholar] [CrossRef]
- Mendes, J.; Pinho, T.M.; Neves Dos Santos, F.; Sousa, J.J.; Peres, E.; Boaventura-Cunha, J.; Cunha, M.; Morais, R. Smartphone Applications Targeting Precision Agriculture Practices—A Systematic Review. Agronomy 2020, 10, 855. [Google Scholar] [CrossRef]
- Yu, D.; Zha, Y.; Shi, L.; Jin, X.; Hu, S.; Yang, Q.; Huang, K.; Zeng, W. Improvement of sugarcane yield estimation by assimilating UAV-derived plant height observations. Eur. J. Agron. 2020, 121, 126159. [Google Scholar] [CrossRef]
| Year | Location | Variety | Number of Plots | N application Rate (kg N ha−1) |
|---|---|---|---|---|
| 2021 | Yongfa Village | NJ46 | 12 | N0, N200, N300, N400 |
| 2022 | Yongfa Village | NJ46 | 12 | N0, N180, N270, N360 |
| 2023 | Fumin Village | CXJ201 | 24 | N58, N154, N207, N227, N247, N267, N287, N307 |
| Variable | Unit | Dataset | Number of Observations | RMSE | RRMSE |
|---|---|---|---|---|---|
| DVS | - | Calibration | 8 | 0.08 | 7% |
| Validation | 4 | 0.16 | 19% | ||
| LAI | m2 m−2 | Calibration | 64 | 1.55 | 65% |
| Validation | 64 | 0.91 | 23% | ||
| WAGT | kg ha−1 | Calibration | 64 | 1998 | 40% |
| Validation | 48 | 2421 | 23% | ||
| LNC | kg kg−1 | Calibration | 68 | 0.0053 | 18% |
| Validation | 56 | 0.0102 | 31% | ||
| Yield | kg ha−1 | Calibration | 8 | 2508 | 40% |
| Validation | 8 | 1869 | 22% |
| State Variable | Experiment Name | Number of Observations | ORYZA2000 Model without Data Assimilation | ORYZA-EnKF Model without LNC Observations | ORYZA-EnKF Model with LNC Observations | |||
|---|---|---|---|---|---|---|---|---|
| RMSE | RRMSE | RMSE | RRMSE | RMSE | RRMSE | |||
| DVS | 2021-YF | 4 | 0.10 | 9% | 0.07 | 6% | 0.08 | 7% |
| 2022-YF | 4 | 0.05 | 4% | 0.27 | 26% | 0.15 | 14% | |
| 2023-FM | 4 | 0.16 | 19% | 0.09 | 8% | 0.10 | 9% | |
| LAI | 2021-YF | 28 | 0.78 | 27% | 0.47 | 16% | 0.47 | 16% |
| 2022-YF | 36 | 1.95 | 101% | 0.92 | 48% | 0.92 | 47% | |
| 2023-FM | 64 | 0.91 | 23% | 0.75 | 19% | 0.81 | 21% | |
| WAGT | 2021-YF | 32 | 1086 | 20% | 992 | 18% | 965 | 18% |
| 2022-YF | 32 | 2609 | 59% | 1224 | 28% | 1078 | 24% | |
| 2023-FM | 48 | 2421 | 23% | 2404 | 22% | 2461 | 23% | |
| LNC | 2021-YF | 36 | 0.0060 | 20% | 0.0053 | 18% | 0.0044 | 14% |
| 2022-YF | 32 | 0.0043 | 16% | 0.0046 | 17% | 0.0043 | 16% | |
| 2023-FM | 56 | 0.0102 | 31% | 0.0099 | 30% | 0.0085 | 26% | |
| Yield | 2021-YF | 4 | 660 | 9% | 993 | 13% | 794 | 11% |
| 2022-YF | 4 | 3484 | 70% | 1339 | 27% | 1430 | 29% | |
| 2023-FM | 8 | 1869 | 22% | 1020 | 12% | 860 | 10% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Shi, L.; Han, J.; Hu, X.; Su, C.; Li, S. Improving Simulations of Rice Growth and Nitrogen Dynamics by Assimilating Multivariable Observations into ORYZA2000 Model. Agronomy 2024, 14, 2402. https://doi.org/10.3390/agronomy14102402
Li J, Shi L, Han J, Hu X, Su C, Li S. Improving Simulations of Rice Growth and Nitrogen Dynamics by Assimilating Multivariable Observations into ORYZA2000 Model. Agronomy. 2024; 14(10):2402. https://doi.org/10.3390/agronomy14102402
Chicago/Turabian StyleLi, Jinmin, Liangsheng Shi, Jingye Han, Xiaolong Hu, Chenye Su, and Shenji Li. 2024. "Improving Simulations of Rice Growth and Nitrogen Dynamics by Assimilating Multivariable Observations into ORYZA2000 Model" Agronomy 14, no. 10: 2402. https://doi.org/10.3390/agronomy14102402
APA StyleLi, J., Shi, L., Han, J., Hu, X., Su, C., & Li, S. (2024). Improving Simulations of Rice Growth and Nitrogen Dynamics by Assimilating Multivariable Observations into ORYZA2000 Model. Agronomy, 14(10), 2402. https://doi.org/10.3390/agronomy14102402









