Genotype Selection for Grain Yield of Sorghum through Generalized Linear Mixed Model

Abstract

The classical model only provides a correct analysis if all the effects are fixed. For experiments that include fixed and random effects, the general linear mixed model is appropriate for handling the non-normal distributed response variables. The aim of this study is to perform the genotype selection through a generalized linear mixed model and identify the impact of treatment and the related traits on grain yield. The data were collected using a lattice square design and measured the phenotype traits of sorghum. The result of PCA was used as an input variable for the general linear mixed model. The data analysis was performed using a general linear mixed model with maximum likelihood methods to estimate the parameters of the model. The result showed that the grain yield had a gamma distribution and a treatment effect on grain yield. The first principal component was significant for grain yield. The variability of grain yield due to the random effects of replication within treatment, genotype, and the interaction of genotype by treatment were significant. The best genotypes effective for the mass production of sorghum were G137, G66 and G156 under stress conditions and G55, G41 and G78 under irrigated conditions. Overall, genotype selection using a general linear mixed model for grain yield is recommended for genotype selection of plant breeding.

1. Introduction

Ethiopia is the center of origin for sorghum, where the agroecological district zones significantly contribute to the genetic diversity of the crops. It is the main popular cereal crop in arid and semi-arid areas. In addition, it is the main source of food for humans and fodder for animals [1,2,3]. Therefore, selecting the genotypes that generate better grain yield production is essential for the agrarians who produce sorghum for their feed in semi-arid and arid parts of the world. Various crop researchers have implemented the use of the classical analysis of variance (ANOVA) model or general linear model (GLM) that provides a correct analysis only if all the effects are fixed [4]. However, different agronomy experiments are carried out using complete or incomplete block designs with few replications at multiple sites and/or over several years, and the results of the experiment are influenced by both fixed and random factors that are not directly relevant to the goal of the experiment but cause to mask the effect of the treatment. To account for this phenomenon, statistical models, such as linear mixed models or generalized linear mixed models, must be used [3,4,5,6].

A general linear mixed model developed by [7] to deal with non-normal response variables is an alternative approach for dealing with non-normal distributed response variables. The experiment includes both fixed and random effects. It includes a wide range of random effects that satisfy the standard framework for linear mixed models while retaining the flexibility associated with classic linear models [5,6,7,8]. Moreover, using a general linear mixed model to analyze plant pests and diseases in wheat, grapevine, banana, and sweet potato, where the response variables have incidence nature for wheat and grapevine, binary nature for banana, and count nature for sweet potato. Logit link functions were used for the first three crops, and log link functions for the count nature of the response variable [9].

The study on the characteristics of plants with repeated measure experiments, linear mixed, and general linear mixed models is appropriate to analyze the response variable as the observations were correlated. Therefore, the study was conducted to solve the different problems through the linear mixed model, the response variable is normally distributed, and the general linear mixed model for the response variable is non-normally distributed; for the repeated measure experiment on plant height and stem thickness using various distributions such as Poisson, gamma, lognormal, normal and binomial data distribution [4,9].

Researchers conducted a study to identify the ancestor haplotype-based association mapping for stratification, which used a linear function of different covariates incorporating polygenic and local genomic effects to describe the expected value of the observed phenotype via a link function [10]. The observations with a non-normal nature for the response variable must be examined using various techniques, with the general linear mixed model being the most important to solve such a problem. Furthermore, it is common to use principal component analysis to generate uncorrelated new variables that are important to use as independent variables in the generalized linear mixed model [11]. Furthermore, because the mixed model is more accurate than the general linear model, the general linear mixed model is also useful for the genotype selection of sorghum grain yield.

The aim of this study was to perform the genotype selection through a generalized linear mixed model and identify the impact of treatment and the related traits on the grain yield of sorghum.

The article is organized as follows. First, Section 2 describes the data sources, how the data was collected, and the statistical models used for data analysis. Then, Section 3 explains the main results of the study, while Section 4 discusses and compares the results with other scientific works. Finally, the study’s conclusion and recommendations are presented in Section 5.

2. Methods and Data

2.1. Data and Design Description

The data was collected using an incomplete block design called lattice square design having 14 blocks, and each block contains 14 experimental units (plots) where the genotypes were applied and two replications for each treatment level that are a non-irrigated condition having a lack of water, and the condition having sufficient [12,13]. The experiment was held at the Kobo site of Sirinka agriculture research center in Ethiopia. The experiment was designed to measure the phenotypic characteristics of sorghum, through which 14 phenotypic characteristics were measured. From the measurements, grain yield is considered the response variable. It assumes the treatment and the results of the principal component analysis as a fixed effect since the related yield traits are correlated, which leads to generating an uncorrelated input factor for the model. The result of the principal component analysis decided to generate three components which accounted for 77.46% of the total variance of the originally related yield traits. Additionally, replication within treatment, genotype, and the interaction of genotype by treatment are random effects of the model for the study [11].

2.2. Generalized Linear Mixed Model

Let $\mathit{y}$ represent the vector of the observed phenotypic measured data values, particularly the grain yield of sorghum, which is the non-negative measurement, and the distribution of the grain yield is non-normally distributed. The problem of non-normality of the response variable is solved through the Generalized Linear Mixed Model (GLMM), which is an extension of the general linear model by including the random effects in addition to fixed effects [8,14,15,16]. The advantage of this model is using an exponential family member of a probability distribution that incorporates the link functions for the distributions of the response variables. The vector of the response variable given the vector of the random effect such that the conditional distribution of the response given the random effect is a member of the exponential family with probability density function

$$f_i\left(y_i/\gamma \right)=exp\left\{\frac{y_i{\xi }_i+b\left({\xi }_i\right)}{a\left(\varphi \right)}+c_i\left(y_i;\varphi \right)\right\}$$

(1)

where $b\left(.\right), a\left(.\right), \mathrm{and} c\left(.\right)$ are known functions, and $\varphi$ and $\mu$ are the dispersion parameter and are associated with the condition mean, respectively, on the other hand, related to the linear predictor. GLMM is a linear function of the various covariates to describe the expected value of the observed data and allows the response variable from different distributions which belong to exponential family density [8,14,17], and the conditional mean is formulated as

$$E\left[\raisebox{1ex}{$Y_{ijkl}$}\!\left/ \!\raisebox{-1ex}{${\rho }_{\left(\alpha \right)},\gamma ,\alpha \gamma $}\right.\right]=g^{-1}\left(\omega +{\beta }_1{m}_{1l}+{\beta }_2{m}_{2l}+{\beta }_3{m}_{3l}+{\alpha }_i+{\rho }_{j\left(i\right)}+{\gamma }_k+{\left(\alpha \gamma \right)}_{ik}\right)$$

(2)

where $g\left(.\right)$ is the differentiable monotonic link function having the inverse $g^{-1}\left(.\right)$. Linear predictor of GLMM incorporates the fixed and random effect and excludes the error term and the inverse of the link function [15]. GLMM accommodates the non-normal distributed response, uses the nonlinear link between the mean of the response and the predictors, and allows correlation in the data [18]. The conditional mean is associated with a linear predictor through the link function $g\left(\mu \right)=\eta$ [17], and is given as

$${\eta }_{ijkl}=\omega +{\beta }_1{m}_{1l}+{\beta }_2{m}_{2l}+{\beta }_3{m}_{3l}+{\alpha }_i+{\rho }_{j\left(i\right)}+{\gamma }_k+{\left(\alpha \gamma \right)}_{ik}$$

(3)

where ${\eta }_{ijkl}$ is the linear predictor of the lth observation of ith treatment of jth replication and kth genotype; $\omega$ is the overall mean; ${\beta }_1, {\beta }_2$ and ${\beta }_3$ are the coefficients for the 1st, 2nd and 3rd principal components, respectively, which are considered to be fixed effects for a general linear mixed model; ${\alpha }_i$ is the ith treatment effect, which is a fixed effect; ${\gamma }_k$ is the random effect of the kth genotype; ${\rho }_{j\left(i\right)}$ is the random effect of the jth replication nested within the ith treatment; ${\left(\alpha \gamma \right)}_{ik}$ is the interaction effect of the ith treatment by kth genotype. In this case, ${\rho }_{j\left(i\right)}, {\gamma }_k$, ${\left(\alpha \gamma \right)}_{ik}$ and ${\epsilon }_{ijkt}$ are random effects, and they are uncorrelated to each other. The effect of genotypes, the effect of replication within the treatment, and the effect of the interaction of treatment by genotype are normally distributed with mean zero and variances ${\sigma }_{\gamma }^2 , {\sigma }_{\rho \left(\alpha \right)}^2$ and ${\sigma }_{\alpha \gamma }^2$, respectively.

The variance of the observations given the random effects [19,20], denoted by $var\left(\raisebox{1ex}{$y_{ijkl}$}\!\left/ \!\raisebox{-1ex}{${\rho }_{\left(\alpha \right)},\gamma ,\alpha \gamma $}\right.\right)$, is given as

$$var\left(\raisebox{1ex}{$y_{ijkl}$}\!\left/ \!\raisebox{-1ex}{${\rho }_{\left(\alpha \right)},\gamma ,\alpha \gamma $}\right.\right)=a_i\left(\varphi \right)v\left({\mu }_{ijkl}\right)$$

(4)

where $a_i\left(\varphi \right)$ is a known function and equivalent to $\frac{\varphi }{w_i}$ with $w_i$ being the weight and $v\left(.\right)$ is the variance function. The response variable given the random effect is conditionally independent with mean $E\left[\raisebox{1ex}{$Y_{ijkl}$}\!\left/ \!\raisebox{-1ex}{${\rho }_{\left(\alpha \right)},\gamma ,\alpha \gamma $}\right.\right]={\mu }_{ijkl}$, which is related to the linear predictors via the link function provided above, and variance $var\left(\raisebox{1ex}{$y_{ijkl}$}\!\left/ \!\raisebox{-1ex}{${\rho }_{\left(\alpha \right)},\gamma ,\alpha \gamma $}\right.\right)=a_i\left(\varphi \right)v\left({\mu }_{ijkl}\right)$ [17,20].

The vector notation of the conditional mean, having observed response $\mathit{y}$ and design matrices $\mathit{X}$ and $\mathit{Z}$ for fixed and random effects, respectively, are provided [20] as

$$E\left(\mathit{y}/\mathit{b}\right)=g^{-1}\left(\mathit{X}\mathsf{\beta }+\mathit{Z}\mathit{b}\right)$$

(5)

where $\mathsf{\beta }$ and $\mathit{b}$ are the fixed and random effects parameters. The variance of the random effect is normally distributed with mean 0 and covariance $\mathit{D}$, which is depend on the unknown variance components.

$$var\left(\mathit{y}/\mathit{b}\right)={\mathit{D}}^{\frac{1}{2}}\mathit{R}{\mathit{D}}^{\frac{1}{2}}$$

(6)

where $\mathit{D}$ is the variance that is a function of ${\mu }_{ijkl}$, R is the residual variance.

The estimation method for parameters is estimated by maximum likelihood methods. Still, the marginal distribution for maximum likelihood includes an integration that does not close due to the incorporation of the random effects and non-linearity of the model. Thus, the maximum likelihood has no analytic solution and applies a numeric solution to estimate the parameters of the general linear mixed model [7,17,20,21,22].

The pseudo-likelihood method equivalently penalized quasi-likelihood, which is developed under the assumption that the residuals are well approximated by a normal distribution, estimates the model parameters of GLMM by using a linearization technique, which applies Taylor expressions iteratively to approximate the initial GLMM with a linear mixed model [8,18,20]. The pseudo-likelihood estimation uses the results of the LMM and GLM as starting values of the GLMM. The predictors of the random effects are the estimated best linear unbiased predictors, referred to as EBLUP in the approximated linear mixed model [18,19,23]. The study used the GLIMMIX procedure of SAS version 9.4 for data analysis.

3. Results of the Study

3.1. Descriptive Summary

The overall mean and the standard deviation of the grain yield under the treatments’ levels indicate the difference in grain yield among the treatment levels. Under stress conditions, the grain yield was distributed around the average $2.48\pm 0.71$ t/ha under stress. For irrigated environments, the distribution of grain yield was distributed around $3.17\pm 1.15$ t/ha. The average grain yield varies among the levels of treatment, which explain the influence of drought sorghum production. The overall mean and standard deviation of the log of the grain yield were 0.98106 and 0.3305, respectively.

Figure 1 indicates the distribution of the grain yield, which is skewed distribution (red color denotes the kernel of the data (a)) that explains the non-normality of the grain yield as the normal distribution and the kernel density of grain yield did not overlap or fit a normal distribution as a result of non-normality of the grain yield. On the other hand, the distribution of grain yield approximately tends to the gamma distribution (the blue color curve denotes the gamma density (b)), which is very important to model the skewed datasets. Therefore, the grain yield has no normal distribution and assumes another distribution to fit the observed data.

Figure 2 indicates the distribution of grain yield relative to inverse Gaussian distribution that can be a candidate for the distribution of grain yield. Inverse Gaussian distribution is the other distribution we may use as the distribution of the grain yield and, finally, identify the better distribution that represents the distribution of the grain yield. Figure 1 and Figure 2 above indicate that gamma and inverse Gaussian distributions are closed to represent the grain yield distribution. These distributions will be checked to fit grain yield data using different link functions for the distributions.

3.2. Results of GLMM

The result of GLMM depends on the distribution of the grain yield, which tends to have a gamma or inverse Gaussian distribution. Still, the result of GLMM is based on the inverse Gaussian distribution because the result of GLMM using gamma distribution did not converge for all link functions. Therefore, the main reason for applying a general linear mixed model with the non-normality of the response variable and identifying link functions for the model is performed using the model diagnosis technique. In this case, the link function that provides the best model is preferable for the specified distribution of the response variable, grain yield.

Table 1. Summary results to compare and select the best distribution and link functions for grain yield analysis.

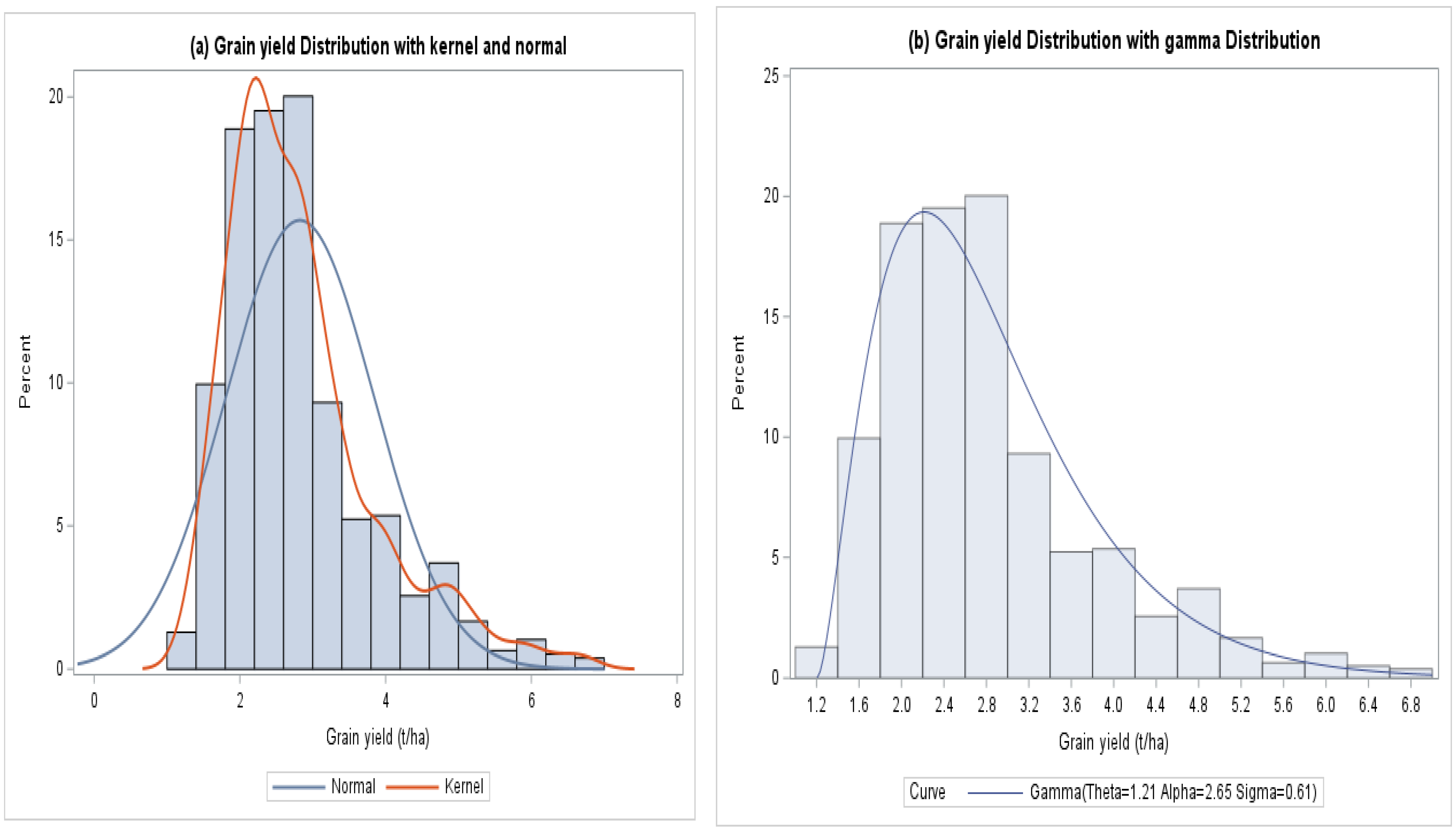
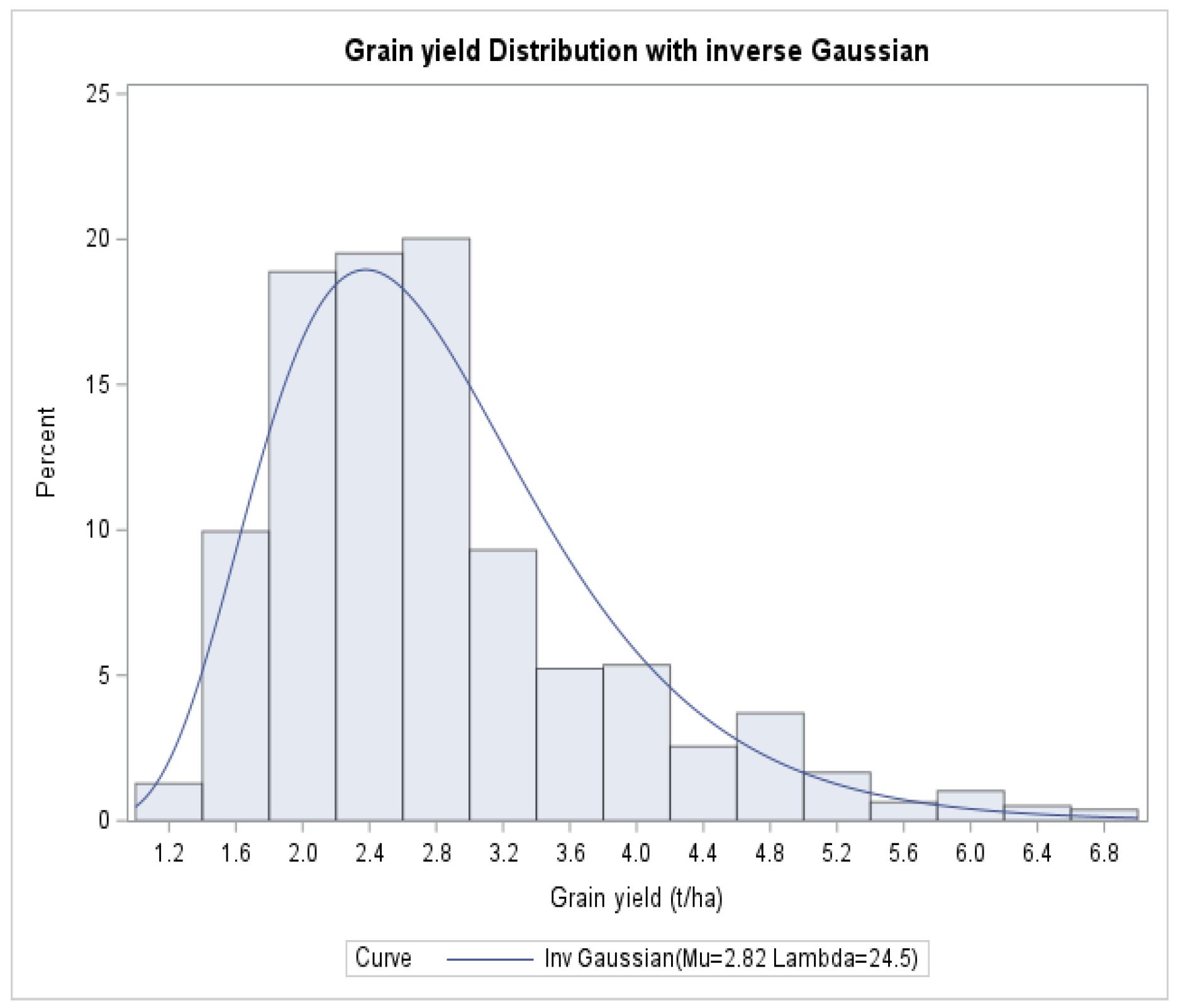
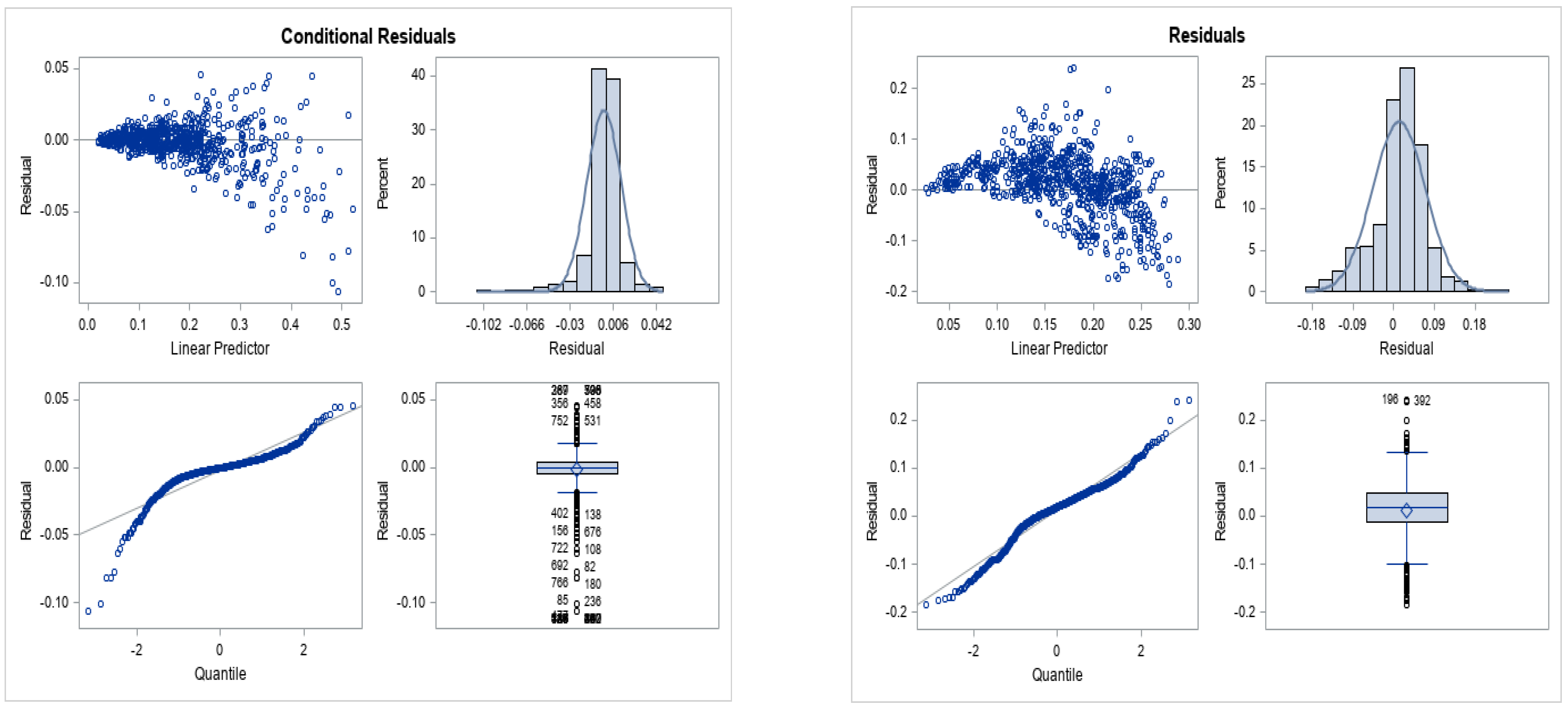
Distribution	Inverse Gaussian			Gamma
Link Function	Inverse	Inverse Square	Log	Inverse	Inverse Square	Log
−2 Res Log PL	−3212.88	−3285.40	−1873.19	−3239.19	−3324.15	−1899.14
Pseudo−AIC	−3204.88	−3277.40	−1865.19	−3231.19	−3316.15	−1891.14
Pseudo−BIC	−3207.34	−3279.85	−1867.64	−3233.64	−3318.61	−1893.60
Pseudo−HQIC	−3210.27	−3282.79	−1870.57	−3236.58	−3321.54	−1896.53
Generalized ${\chi }^2$	0.42	0.51	0.43	1.04	1.23	1.04
Gen. ${\chi }^2$/DF	0.00	0.00	0.00	0.00	0.00	0.00

shows the results of model diagnosis for various link functions using Inverse Gaussian and gamma distribution. The result was manipulated using different link functions (inverse, inverse square and log) by considering inverse Gaussian and gamma distributions for grain yield. Depending on the result, the link function for inverse Gaussian distribution, in which the link function generates the smallest pseudo-AIC, is the inverse square. The link function for the gamma distribution of the grain yield is also inverse square and generates the smallest pseudo-AIC. Finally, the better distribution that can be used for grain yield is compared using information criteria for which the distribution that generates the smallest AIC would be the better one. According to the information criteria, in the general linear mixed model, the grain yield has a gamma distribution that is better than a model with inverse Gaussian distribution for grain yield. For overall analysis, the gamma distribution is the best distribution for the grain yield analysis via GLMM.

Table 2. Covariance Parameter Estimates of the random effects of GLMM.

Covariance Parameter	Estimate	Std. Error
Replication	0.000034	0.000034
Genotype	0.003071	0.000466
Treatment * Genotype	0.000742	0.000101
Residual	0.001583	0.000149

* interaction.

shows the covariance estimates of the random effects with their corresponding standard errors. The result is obtained from the generalized linear mixed model, which considers the grain yield’s gamma distribution and the distribution’s inverse square link function. According to the result, the variability of grain yield associated with the variability of replication within treatment, genotype, and the interaction of genotype are 0.000034, 0.0031 and 0.000742 t/ha with their corresponding standard errors of 0.000043, 0.000383 and 0.000107, respectively. The variability of grain yield is 56.56%, and 13.66%, associated with the random variables related to genotype. The interaction of genotype by treatment is the intraclass correlation of the genotype and the interaction of genotype by treatment to the variability of the grain yield.

Table 3. Tests of Covariance Parameters Based on the residual Pseudo-Likelihood.

Label	DF	−2 Res Log Like	ChiSq	Pr > ChiSq	Note
Diagonal G	0	−3324.15	0.00	1.0000	DF
Independence	3	−2879.16	444.99	<0.0001	MI
No G-side effects	3	−2879.16	444.99	<0.0001	MI

indicates the results of the tests of covariance parameters based on the likelihood. The tests for a diagonal G matrix by setting the Off-diagonal elements in the G matrix to zero against the Off-diagonal elements in G is non-zero, and the R-side structure is not modified. This test uses an inverse square link function based on the grain yield’s gamma distribution. According to the result of the tests of the covariance parameters based on the likelihood, the covariance of the random effect is a diagonal matrix as the chi-square is zero with a small p-value greater than 0.05 indicating the random effects are uncorrelated or independent. As a result, genotype, replication nested with treatment, and interaction of genotype by treatment are independent of each other. The test of independence tests the generalized linear mixed model against a null model of complete independence, which is a general linear model. The result shows that the G-side covariance parameters did not eliminate, and all R-side structures were not reduced to a diagonal model because the null model of complete independence is rejected at a 5% level of significance. Finally, no G-side effects tests whether the covariance matrix of the random effects (G matrix) is reduced to zero or not to indicate the presence of significant random effects in a generalized linear mixed model. The result indicates that the random effects did not eliminate from the general linear mixed model as the test rejected the null hypothesis of no G-side effects with a p-value less than 0.05.

Table 4. Treatment Least Square Means.

Model Scale								Data Scale
Treatment	Estimate	St. Err.	DF	t Value	Pr > |t|	LL	UL	Mean	St Err.	LL	UL
Irrigated	0.1447	0.00613	2	23.62	0.0018	0.1183	0.1710	2.6293	0.05567	2.4182	2.9075
Stress	0.1933	0.00615	2	31.44	0.0010	0.1668	0.2197	2.2748	0.03618	2.1335	2.4485

St. Err. = Standard error, DF = degrees of freedom, LL = Lower Limit, UL = Upper Limit.

presents the least square means of the levels of the treatment with the model scale and data scale form. The mean column indicates the data scale obtained by converting the model scale least square means back to the original data scale using the inverse square link function. For example, the average grain yield of sorghum was 2.275 t/ha under rainfed (non-irrigated) conditions, whereas, under irrigation, the average sorghum production was 2.629 t/ha, which shows the effect of treatment difference on grain yield.

Figure 3 indicates the mean difference of the levels of the treatment that explained the grain yield mean under treatment was significantly different as the least square means plot did not cover the same bar.

Table 5. The estimates and tests of the fixed effects of the GLMM.

Solutions for Fixed Effects
Effect	Estimate	Std. Error	t Value	Pr > |t|
Intercept	0.1933	0.006147	31.44	0.0010
Treatment (Irrigation)	−0.0486	0.006749	−7.20	0.0187
Treatment (Stress)	0
Prin1	−0.01723	0.001066	−16.17	<0.0001
Prin2	0.00196	0.001148	1.71	0.0885
Prin3	−0.00006	0.000618	−0.10	0.9213
Overall Tests of the Fixed effects
Effect	Num DF	Den DF	F Value	Pr > F
Treatment	1	2	51.86	0.0187
Prin1	1	387	261.50	<0.0001
Prin2	1	387	2.92	0.0885
Prin3	1	387	0.01	0.9213

presents the fixed effects estimates for the generalized linear mixed model. The average grain yield is 0.1933 t/ha for production under stress conditions of the treatment while using irrigation for sorghum production; the average grain yield is 0.1447 t/ha. The average change of the grain yield for a unit change of the first, second and third principal components are −0.01723, 0.00196 and −0.00006 t/ha, respectively. The result identified that the first and third principal components have a negative impact on grain yield. In contrast, the second principal component positively correlates with grain yield. The treatment effect and the first principal component were a significant effect on grain yield, while the second and third principal components were insignificant on grain yield at a 5% significance level. The overall test of fixed effect indicates that the treatment effect and first principal components were significant, while the second and third principal components were insignificant for grain yield.

Table 6. Genotype performance for GLMM.

Worst-Performer Genotypes for GLMM					Best-Performer Genotypes for GLMM
Genotype	Estimate	Std.Err.Pred	t Value (Df = 387)	Pr > |t|	Genotype	Estimate	Std.Err.Pred	t Value (Df = 387)	Pr > |t|
G196	−0.08483	0.01905	−4.45	<0.0001	G41	0.2424	0.02547	9.52	<0.0001
G48	−0.07241	0.0191	−3.79	0.0002	G78	0.1772	0.02469	7.18	<0.0001
G186	−0.06368	0.01961	−3.25	0.0013	G66	0.1733	0.02294	7.55	<0.0001
G40	−0.06071	0.01977	−3.07	0.0023	G136	0.1639	0.02383	6.88	<0.0001
G143	−0.06001	0.01906	−3.15	0.0018	G39	0.1588	0.0232	6.84	<0.0001
G187	−0.05132	0.01933	−2.66	0.0082	G108	0.1544	0.02399	6.43	<0.0001
G25	−0.05027	0.01913	−2.63	0.0089	G180	0.1472	0.02287	6.44	<0.0001
G31	−0.04928	0.01972	−2.5	0.0128	G85	0.1244	0.02229	5.58	<0.0001
G23	−0.0479	0.01896	−2.53	0.0119	G56	0.122	0.02277	5.36	<0.0001
G5	−0.04771	0.01899	−2.51	0.0124	G137	0.1161	0.02236	5.19	<0.0001

Std.Err.Pred = standard Error Prediction, Df = degrees of freedom.

presents the worst- and best-performer genotypes on grain yield, which depend on the best linear unbiased genotype prediction. The model results were obtained using gamma distribution with a link function of inverse square. According to the results of BLUP, the last three worst-performer genotypes are G196 (Genotype 196), G48 (Genotype 48) and G186 (Genotype 186) and their estimates are −0.08483, −0.07241 and −0.06368, respectively. The top three best-performer genotypes are G41 (Genotype 41), G78 (Genotype 78) and G66 (Genotype 66), with their estimates of 0.2424, 0.1772 and 0.1733 t/ha, respectively. The worst- and best-performer genotypes significantly affect the grain yield variability, and the estimates are accurate as their standard errors are small.

Table 7. The performance of genotypes under irrigation.

The Worst-Performer Genotype under Irrigation					The Best-Performer Genotypes under Irrigation
Genotype	Estimate	Std.Err.Pred	t Value (Df = 387)	Pr > |t|	Genotype	Estimate	Std.Err.Pred	t Value (Df = 387)	Pr > |t|
G137	−0.06484	0.02134	−3.04	0.0025	G55	0.0658	0.02136	3.08	0.0022
G156	−0.05602	0.02108	−2.66	0.0082	G41	0.0556	0.02309	2.41	0.0166
G157	−0.05325	0.02015	−2.64	0.0085	G78	0.0521	0.02262	2.3	0.0218
G107	−0.0428	0.0196	−2.18	0.0296	G49	0.04216	0.02044	2.06	0.0398
G155	−0.03719	0.02	−1.86	0.0637	G119	0.03617	0.02127	1.7	0.0898
G66	−0.03569	0.02176	−1.64	0.1017	G36	0.03222	0.021	1.53	0.1259
G62	−0.03505	0.01955	−1.79	0.0738	G2	0.03098	0.01967	1.57	0.1161
G167	−0.03412	0.01925	−1.77	0.0771	G108	0.03034	0.02226	1.36	0.1737
G40	−0.0325	0.01915	−1.7	0.0904	G82	0.02641	0.02135	1.24	0.2168
G104	−0.03238	0.01974	−1.64	0.1018	G185	0.02622	0.02097	1.25	0.2119

shows the performance of the genotypes under irrigation that helps to identify the genotype performing better and worse under irrigation. Depending on the result, G137 (Genotype 137), G156 (Genotype 156) and G157 (Genotype 157) are the last three genotypes that perform poorly under irrigation treatment and do not recommend the genotypes for mass production under irrigation conditions. The BLUP estimates of the last three worst-performer genotypes are −0.06484, −0.05602 and −0.05325, respectively, and the estimates have the least standard error that indicates the precision of the estimates. The best-performer genotypes under an irrigated environment are G55 (Genotype 55), G41 (Genotype 41) and G78 (Genotype 78) and these genotypes are recommended for mass production under irrigation-supported production of sorghum. The BLUP estimate of the genotypes that perform better under irrigation-supported sorghum production is 0.0658, 0.0556 and 0.0521, respectively. The result shows that the top three best-performer genotypes are applicable to the irrigated environment, while the last three worst-performer genotypes are not applicable to the irrigated environment.

Table 8. The performance of Genotypes under stress.

The Worst-Performer Genotypes under Stress					The Best-Performer Genotypes under Stress
Genotype	Estimate	Std.Err.Pred	t Value (Df = 387)	Pr > |t|	Genotype	Estimate	Std.Err.Pred	t Value (Df = 387)	Pr > |t|
G55	−0.04783	0.02113	−2.26	0.0242	G137	0.09289	0.02221	4.18	<0.0001
G49	−0.03849	0.0203	−1.9	0.0587	G66	0.07757	0.02232	3.48	0.0006
G8	−0.03324	0.01854	−1.79	0.0737	G156	0.07572	0.02171	3.49	0.0005
G25	−0.02966	0.01841	−1.61	0.108	G157	0.05601	0.02067	2.71	0.007
G196	−0.02804	0.01842	−1.52	0.1287	G147	0.04183	0.02137	1.96	0.051
G26	−0.02736	0.01933	−1.42	0.1577	G155	0.03839	0.0204	1.88	0.0606
G7	−0.02665	0.01851	−1.44	0.1507	G107	0.03838	0.02002	1.92	0.056
G23	−0.02588	0.01843	−1.4	0.1611	G104	0.03144	0.02007	1.57	0.1181
G16	−0.02532	0.01853	−1.37	0.1726	G136	0.03137	0.02242	1.4	0.1625
G3	−0.02514	0.01874	−1.34	0.1806	G138	0.03123	0.02124	1.47	0.1422

shows the performance of genotypes under stress environments, ranked using BLUP estimates of the genotypes in the specified environment. The result indicates that the last three worst-performer genotypes under a stress environment are G55 (Genotype 55), G49 (Genotype 49) and G8 (Genotype 8), which yield the least prediction of grain yield. The BLUP estimates were −0.04783, −0.03849 and −0.03324, respectively; these genotypes did not resist the drought and were not recommended to use as mass production of the sorghum under stress conditions. On the other hand, the top three best-performer genotypes under a stress environment are G137 (Genotype 137), G66 (Genotype 66) and G156 (Genotype 156), which have the best capacity to resist the impact of drought as they performed better under drought conditions/stress. The BLUP estimates are 0.09289, 0.07757 and 0.07572 since the BLUP estimate is large with high precision and the random effect is significant for the variability of the grain yield.

Figure 4 presents the model diagnosis of a general linear mixed model using the conditional residuals (left-hand side of Figure 3) and marginal residuals (right-hand side of Figure 3). According to the plot, the top left of the conditional residual shows that the residual is related to the predictors and shows some trend between the predictor. The residual and the marginal residual plot indicate the presence of some trend which shows the non-normality of the residual. The distribution of the conditional residuals is smaller and tends to be normal relative to the distribution of marginal residuals.

4. Discussion

This study tried to examine the way of genotype selection of sorghum using a general linear mixed model that solves the problem of non-normally distributed response, in this case, grain yield, which violated the assumption of normality, constant variance, and linearity, depending on different fixed and random factors [6,24]. The study showed the influence of fixed and random effects on grain yield through the general linear mixed model that demonstrates the relationship between the grain yield and the treatment, and the new variables created by the principal analysis, which are orthogonal to each other, considered as a fixed effect of the study and replication with the treatment, genotype, and the interaction of genotype by the treatment, which are assumed as random effects [25,26,27].

According to the data exploration of grain yield, the distribution of the grain yield revealed non-normality, and the result showed that the grain yield has a gamma distribution and inverse Gaussian distribution for further analysis. This study agrees with an investigation by [12] that applied a general linear model which required a normality assumption of the grain yield [12]. Therefore, identifying the distribution of the grain yield is essential to model the observed data through a general linear mixed model. Furthermore, this study agreed with the study on longitudinal outcomes using a general linear mixed model by other investigators [28,29].

The result shows that the intraclass correlations of genotype and interaction of genotype by treatment were 56.56% and 13.66%, respectively, which are the total variability of the grain yield associated with the random effects such as genotype, replication within the treatment and the interaction of the genotype by treatment. The test of the covariance parameter indicated the presence of a significant dependence and the G-side effect for grain yield. The study agreed with investigations that explain the association between the grain yield and random effects such as the genotype, replication within the treatment and the interaction of the genotype by treatment [1].

The result showed that the average grain yield is 0.1933 t/ha for production without irrigation treatment, and for irrigation treatment, the average grain yield is 0.2419 t/ha. The average change of the grain yield for a unit alter of the first, second and third principal components analysis are −0.01723, 0.00196 and −0.00006 t/ha, respectively. The effects of the treatment and the first components of the phenotypic traits are highly significant on the grain yield of sorghum. This study agreed with the studies conducted by other investigators that found the impact of climate change on the grain yield of sorghum [1,12,30,31].

The performance of the genotype was evaluated through the empirical restricted maximum likelihood that helps to rank the performance of the genotypes for the grain yield. The results of GLMM indicated that the best- and worst-performer genotypes were selected for sorghum. The best-performer genotypes were G41 (0.2424 t/ha), G78 (0.1772 t/ha) and G66 (0.1733 t/ha), which were recommended for any environment. On the other hand, the worst-performer genotypes were G196 (−0.08483 t/ha), G48 (−0.07241 t/ha) and G186 (−0.06368 t/ha), which are not effective for any environment. This result also agreed with the study conducted on the Genetic diversity study of sorghum (Sorghum bicolor (L.) Moenc) genotypes in Ethiopia [3,25,32].

Under irrigated treatment, identifying the genotypes that outperform grain yield production of sorghum and selecting the best- and worst-performer genotypes are the most important case for genotype selection. For example, genotypes that performed better in grain yield were G55 (0.0658 t/ha), G41 (0.0556 t/ha) and G78 (0.0521 t/ha) and recommended for mass production, whereas G137 (−0.06484 t/ha), G156 (−0.05602 t/ha) and G157 (−0.05325 t/ha) were the worst-performer genotypes under an irrigated environment and were not recommended for such environments [12].

On the other hand, the genotypes that were evaluated for their performance under stress environments and best-performer genotypes for stress environments were G137 (0.1108), G66 (0.1046) and G156 (0.1031), which were recommended for the drought environment. On the other hand, genotypes, which were not recommended for mass production, are G55 (Genotype 55), G49 (Genotype 49) and G8 (Genotype 8) for drought environments [1,12,25].

5. Conclusions

The descriptive summary of the treatment identified that there were differences in grain yield among the treatment level ($2.48\pm 0.71$ t/ha for the stress condition and $3.17\pm 1.15$ t/ha for the irrigated condition) and the first three principal components were significant on grain yield of sorghum.

This study explained the effect of fixed and random factors on the grain yield of sorghum through the generalized linear mixed model. The distribution of the grain yield, which was the response variable for the study, was non-normal. Rather, it considered a gamma distribution and Inverse Gaussian distribution as candidate distributions for the analysis of the general linear mixed model of grain yield. Therefore, the gamma distribution was selected for the analysis using information criteria with the smallest AIC, and the associated link function of the model was inverse square.

The variability of grain yield due to the random effects of replication within treatment, genotype, and the interaction of genotype by treatment, were significant. The best genotypes that are efficient for the mass production of sorghum were G137, G66 and G156 under stress conditions and G55, G41 and G78 under irrigated conditions.

In conclusion, a general linear mixed model for grain yield is recommended when it is non-normally distributed and is important for the genotype selection of plant breeding. Therefore, future work will focus on modeling the grain yield using the general additive mixed model to identify the relationship between the continuous covariates and the grain yield in addition to the random effect.