Smart-Map: An Open-Source QGIS Plugin for Digital Mapping Using Machine Learning Techniques and Ordinary Kriging
Abstract
:1. Introduction
2. Materials and Methods
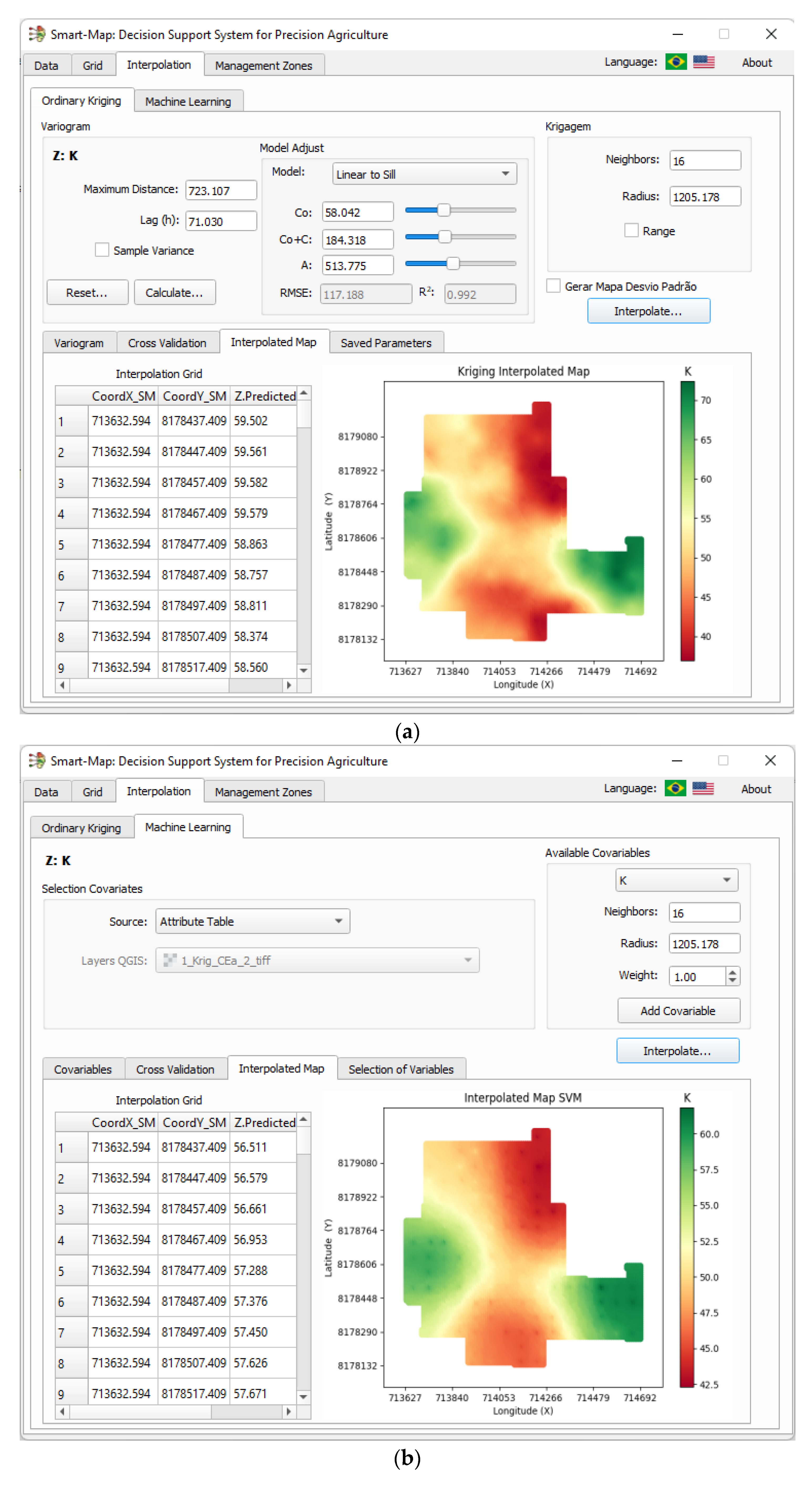
2.1. Smart-Map Implementation
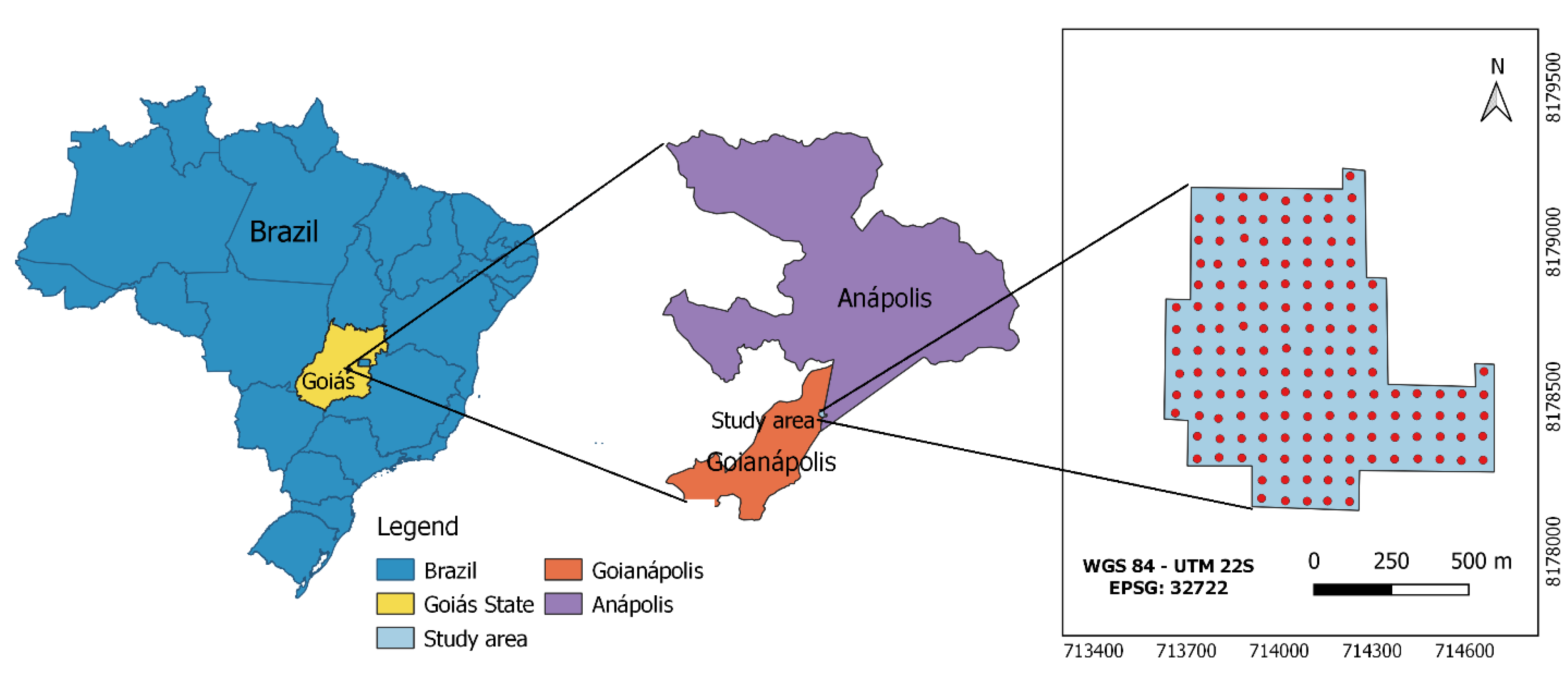
2.2. Case Study for Smart-Map Plugin Evaluation
2.3. Methods of Interpolation and Spatial Correlation Analysis
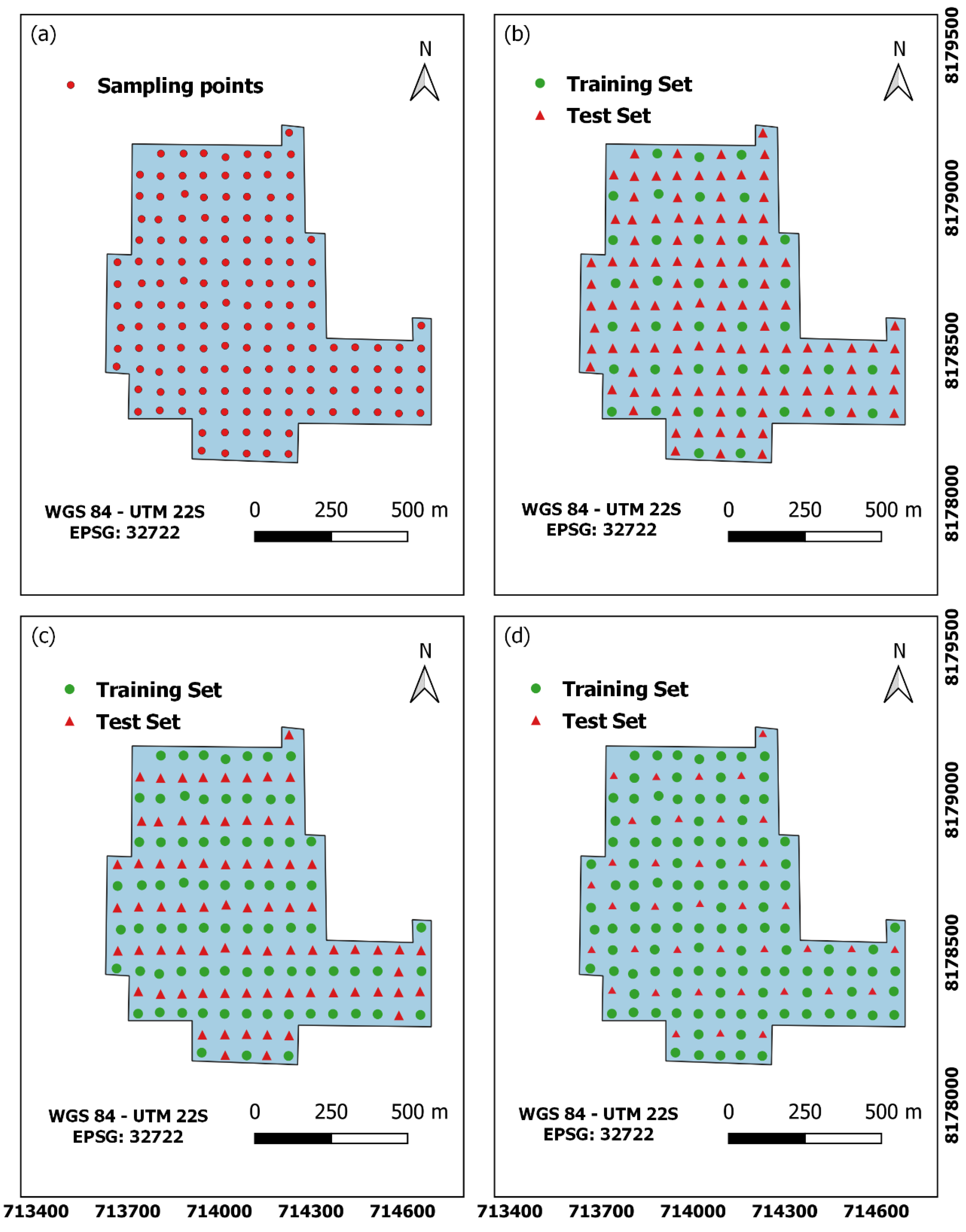
2.4. Generation of Scenarios and Performance Criteria for Comparison between Interpolation Methods
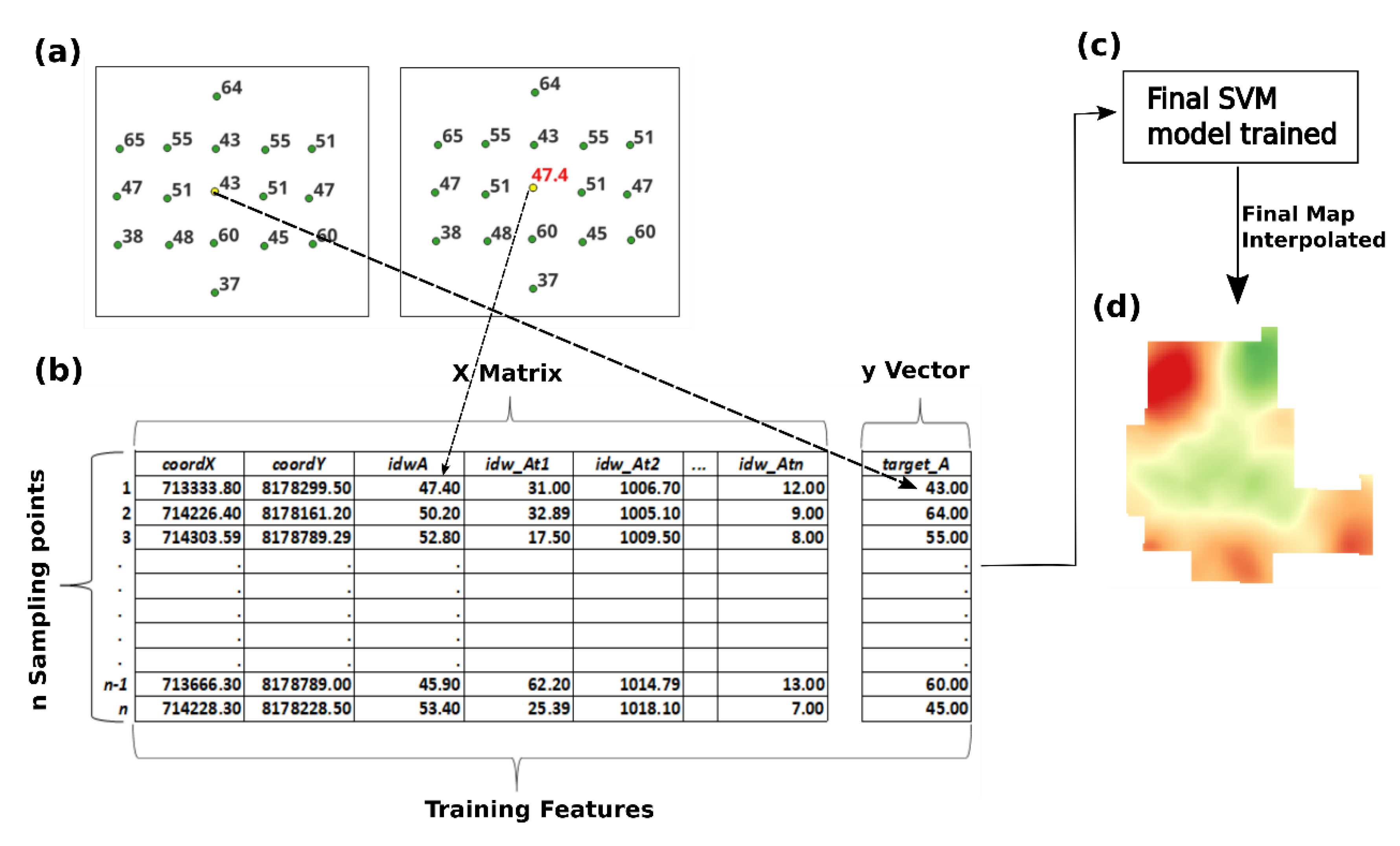
2.5. Definition and Selection of Features for the SVM Model
3. Results and Discussion
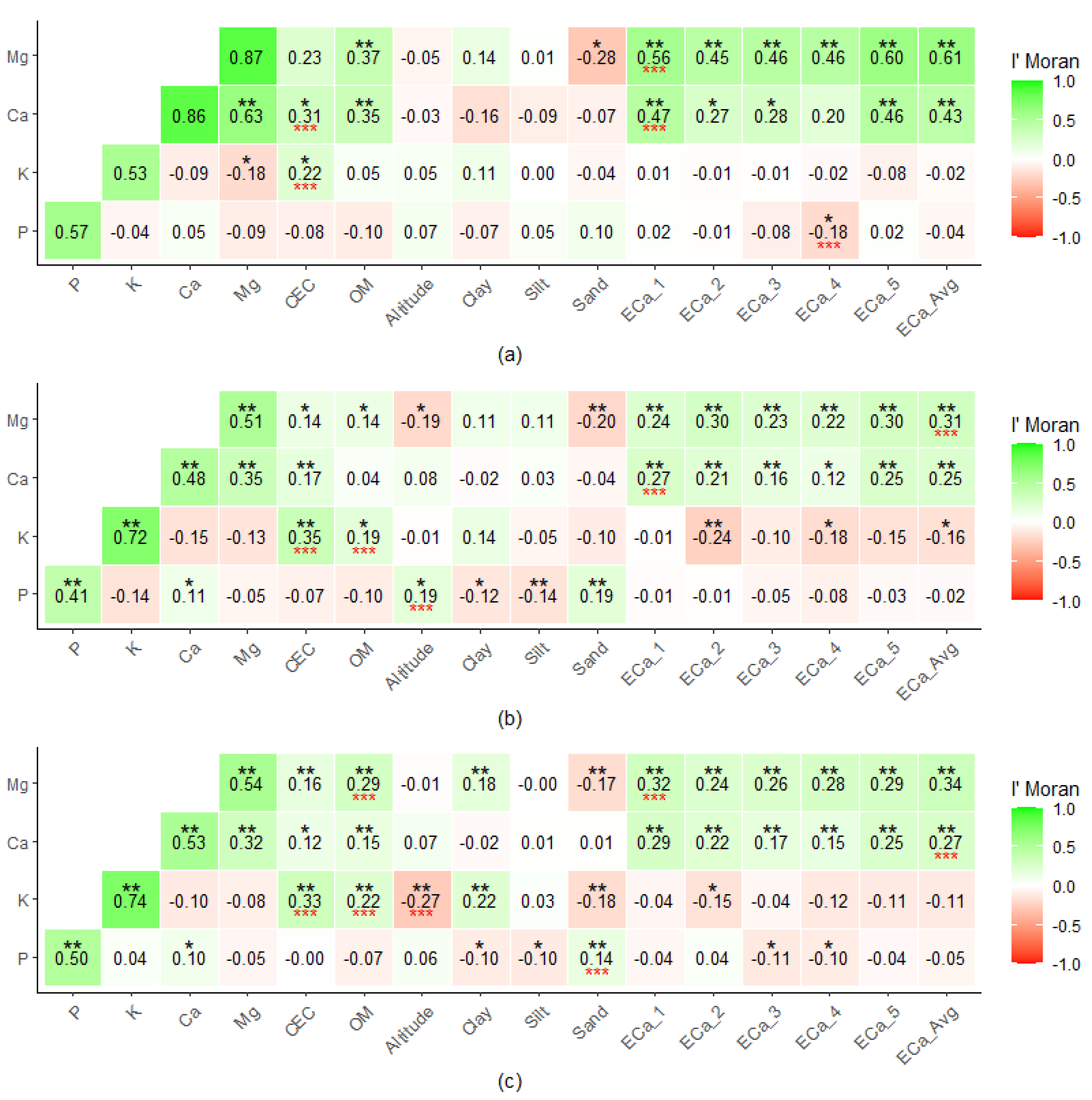
3.1. Spatial Correlation and Selection of Covariates for the SVM Model
3.2. Comparison between OK and SVM Methods
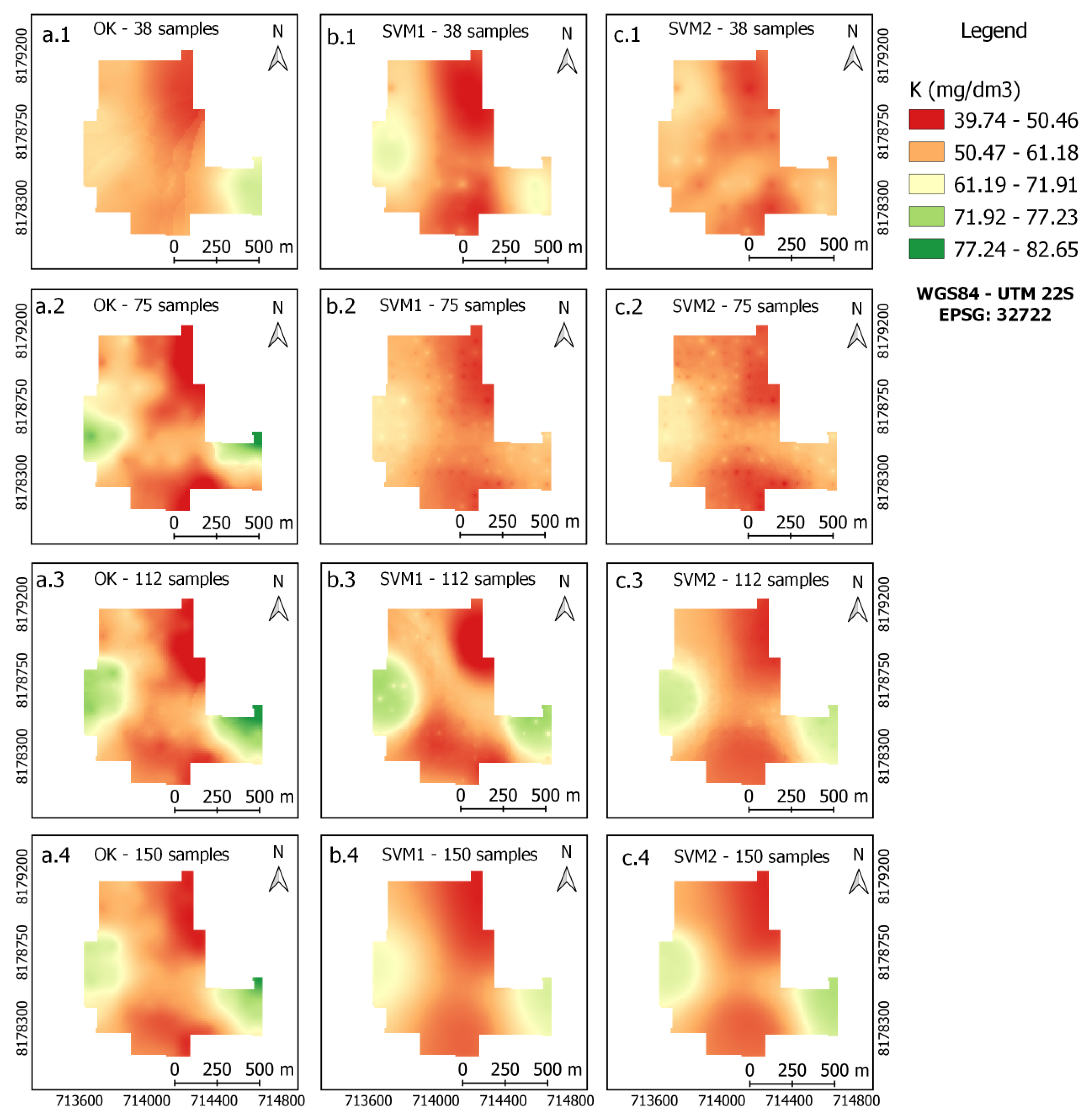
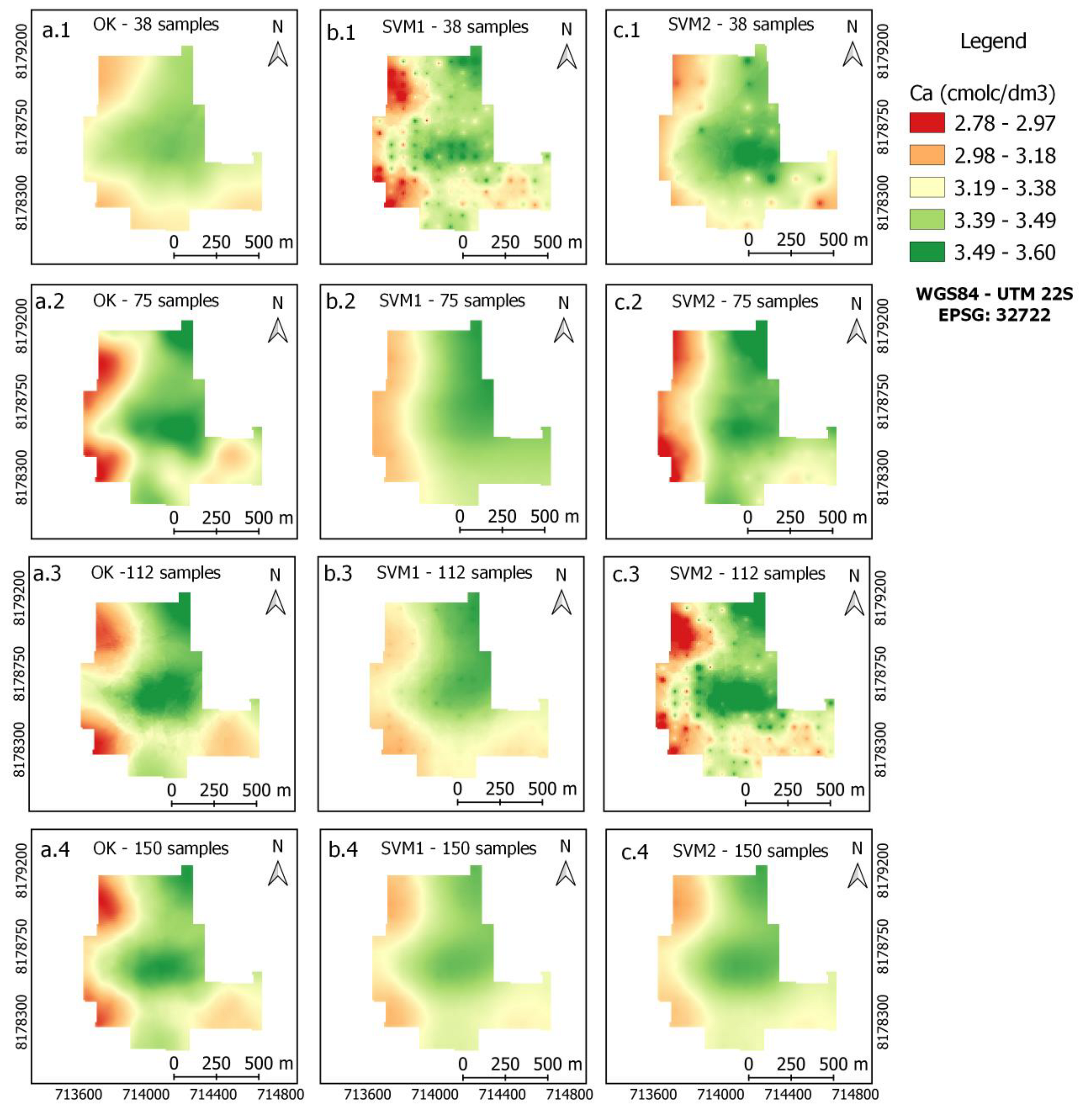
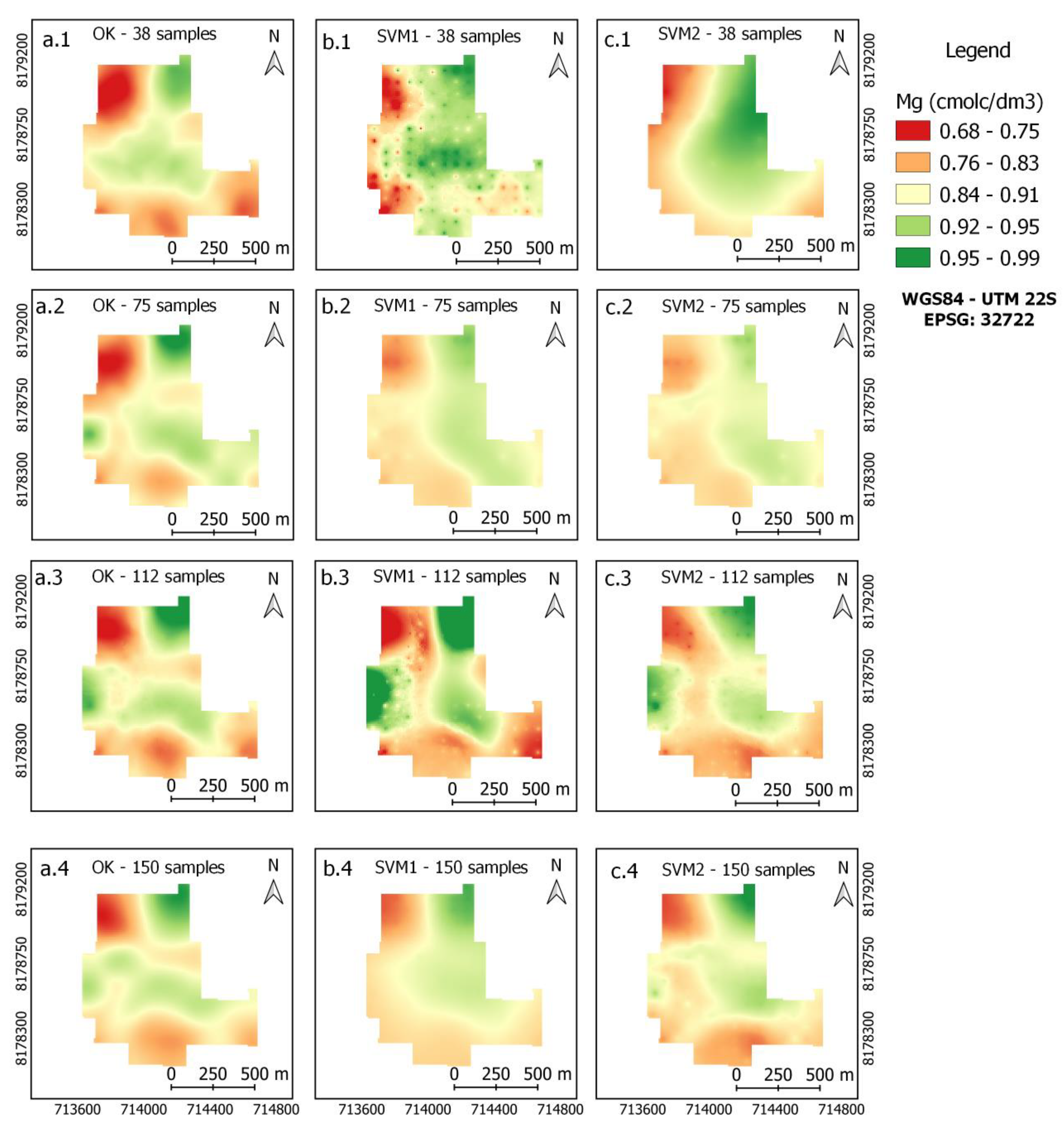
3.3. Maps of Soil Attributes
3.4. Limitations and Future Developments
4. Conclusions
- (1)
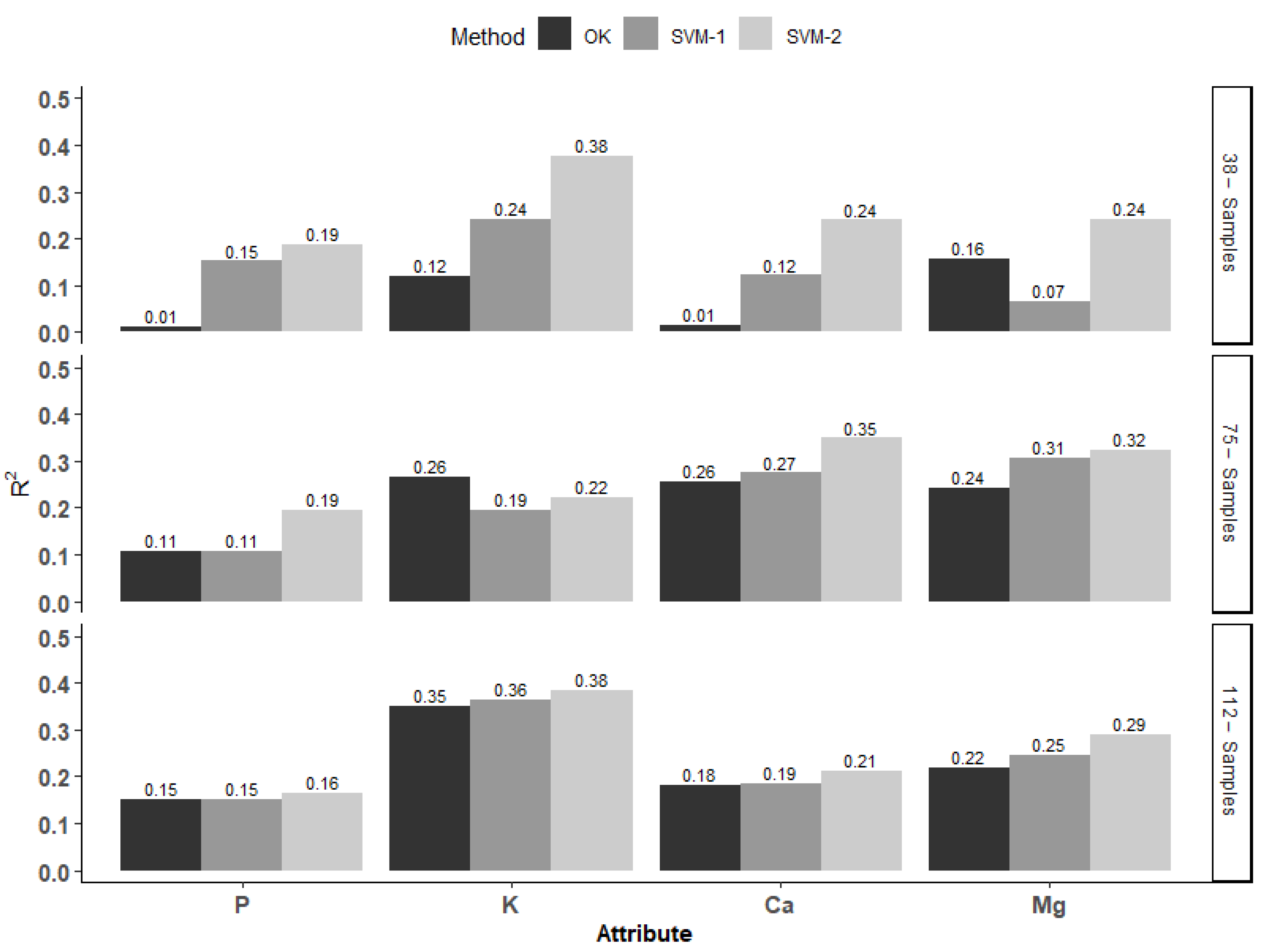
- The SVM2 method was superior to other models in the prediction of soil chemical attributes for the three densities of points in the sampling grids. The R2 values were higher in 11 of the 12 combinations among the four soil attributes interpolated in three densities of points of the sampling grids, considering the training set.
- (2)
- Considering the RMSE of the test set, SVM2 had the lowest error for the prediction of maps obtained by interpolation for the four soil attributes in the three sampling densities, except for the P attribute in the SVM1 method with a grid of 38 points in the test set.
- (3)
- One difficulty encountered by ML algorithms for problems of mapping and prediction of soil attributes is to handle the excessive number of covariates in the model. Spatial correlation of I’Moran proved to be efficient for the selection of covariates of greater importance in the model.
- (4)
- In areas with low spatial correlation of soil attributes and few sampled points, ML techniques are an alternative to the OK method, especially when covariates with a higher number of points and a significant level of correlation with the variables to be interpolated are available. The results in this study confirmed the feasibility and applicability of ML techniques, especially the “Support Vector Machine” method, for prediction and mapping of soil chemical attributes on a regional scale.
- (5)
- The developed Smart-Map plugin is available for download on the GitHub website. Available online: https://github.com/gustavowillam/SmartMapPlugin (accessed on 25 May 2022) and in the QGIS plugin repository Available online: https://plugins.qgis.org/plugins/Smart_Map (accessed on 25 May 2022). With a user-friendly and easy-to-use interface, Smart-Map has over 15,000 downloads according to the QGIS plugin repository. Information on how to use and obtain the software can be found in the “Supplementary Materials” section.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Malla, R.; Shrestha, S.; Khadka, D.; Bam, C.R. Soil fertility mapping and assessment of the spatial distribution of Sarlahi district, Nepal. Am. J. Agric. Sci. 2020, 7, 8–16. [Google Scholar]
- Veronesi, F.; Schillaci, C. Comparison between geostatistical and machine learning models as predictors of topsoil organic carbon with a focus on local uncertainty estimation. Ecol. Indic. 2019, 101, 1032–1044. [Google Scholar] [CrossRef]
- Pouladi, N.; Møller, A.B.; Tabatabai, S.; Greve, M.H. Mapping soil organic matter contents at field level with cubist, random forest and kriging. Geoderma 2019, 342, 85–92. [Google Scholar] [CrossRef]
- Webster, R.; Oliver, M.A. Sample adequately to estimate variograms of soil properties. J. Soil Sci. 1992, 43, 177–192. [Google Scholar] [CrossRef]
- da Matta Campbell, P.M.; Francelino, M.R.; Filho, E.I.F.; de Azevedo Rocha, P.; de Azevedo, B.C. Digital mapping of soil attributes using machine learning. Rev. Cienc. Agron. 2019, 50, 519–528. [Google Scholar] [CrossRef]
- Guo, P.T.; Li, M.F.; Luo, W.; Tang, Q.F.; Liu, Z.W.; Lin, Z.M. Digital mapping of soil organic matter for rubber plantation at regional scale: An application of random forest plus residuals kriging approach. Geoderma 2015, 237–238, 49–59. [Google Scholar] [CrossRef]
- Hengl, T.; Nussbaum, M.; Wright, M.N.; Heuvelink, G.B.M.; Gräler, B. Random forest as a generic framework for predictive modeling of spatial and spatio-temporal variables. PeerJ 2018, 6, e5518. [Google Scholar] [CrossRef] [Green Version]
- Heung, B.; Ho, H.C.; Zhang, J.; Knudby, A.; Bulmer, C.E.; Schmidt, M.G. An overview and comparison of machine-learning techniques for classification purposes in digital soil mapping. Geoderma 2016, 265, 62–77. [Google Scholar] [CrossRef]
- Sekulić, A.; Kilibarda, M.; Heuvelink, G.B.M.; Nikolić, M.; Bajat, B. Random forest spatial interpolation. Remote Sens. 2020, 12, 1–29. [Google Scholar] [CrossRef]
- Khaledian, Y.; Miller, B.A. Selecting appropriate machine learning methods for digital soil mapping. Appl. Math. Model. 2020, 81, 401–418. [Google Scholar] [CrossRef]
- Liakos, K.G.; Busato, P.; Moshou, D.; Pearson, S.; Bochtis, D. Machine learning in agriculture: A review. Sensors 2018, 18, 1–29. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Meier, M.; de Souza, E.; Francelino, M.R.; Fernandes Filho, E.I.; Schaefer, C.E.G.R. Digital soil mapping using machine learning algorithms in a tropical mountainous area. Rev. Bras. de Ciência do Solo 2018, 42, 1–22. [Google Scholar] [CrossRef] [Green Version]
- Parmley, K.A.; Higgins, R.H.; Ganapathysubramanian, B.; Sarkar, S.; Singh, A.K. Machine learning approach for prescriptive plant breeding. Sci. Rep. 2019, 9, 17132. [Google Scholar] [CrossRef] [PubMed]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020; Available online: http://www.r-project.org/ (accessed on 25 May 2022).
- Gomes, L.C.; Faria, R.M.; de Souza, E.; Veloso, G.V.; Schaefer, C.E.G.R.; Filho, E.I.F. Modelling and mapping soil organic carbon stocks in Brazil. Geoderma 2019, 340, 337–350. [Google Scholar] [CrossRef]
- Gregorutti, B.; Michel, B.; Saint-Pierre, P. Correlation and variable importance in random forests. Stat. Comput. 2017, 27, 659–678. [Google Scholar] [CrossRef] [Green Version]
- QGIS Development Team QGIS Geographic Information System. Open Source Geospatial Foundation Project. Available online: http://qgis.org (accessed on 25 May 2020).
- Whelan, B.M.; McBratney, A.B.; Minasny, B. VESPER 1.5-spatial prediction software for precision agriculture. In Proceedings of the 6th International Conference on Precision on Agriculture ASA/CSSA/SSSA, Madison, WI, USA, 14–17 July 2002; Volume 179, pp. 1–14. [Google Scholar]
- Remy, N.; Boucher, A.; Wu, J. Applied Geostatistics with SGeMS: A User’s Guide; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar] [CrossRef]
- Coelho, A.L.F.; Queiroz, D.M.; Valente, D.S.M.; Pinto, F.D.A.D.C. An open-source spatial analysis system for embedded systems. Comput. Electron. Agric. 2018, 154, 289–295. [Google Scholar] [CrossRef]
- Valente, D.S.M.; Queiroz, D.M.; Pinto, F.D.A.D.C.; Santos, N.T.; Santos, F.L. Definition of management zones in coffee production fields based on apparent soil electrical conductivity. Sci. Agric. 2012, 69, 173–179. [Google Scholar] [CrossRef] [Green Version]
- Isaaks, E.H.; Srivastava, R.M. An Introduction to Applied Geostatistics; Oxford University Press: New York, NY, USA, 1989. [Google Scholar]
- Zhou, X.; Zhang, X.; Wang, B. Online support vector machine: A survey. Adv. Intell. Syst. Comput. 2016, 382, 269–278. [Google Scholar] [CrossRef]
- Karamizadeh, S.; Abdullah, S.M.; Halimi, M.; Shayan, J.; Rajabi, M.J. Advantage and drawback of support vector machine functionality. In Proceedings of the 2014 International Conference on Computer, Communications and Control Technology (I4CT), Langkawi, Malaysia, 2–4 September 2014; pp. 63–65. [Google Scholar] [CrossRef]
- Keskin, H.; Grunwald, S.; Harris, W.G. Digital mapping of soil carbon fractions with machine learning. Geoderma 2019, 339, 40–58. [Google Scholar] [CrossRef]
- Xu, S.; Zhao, Y.; Wang, M.; Shi, X. Comparison of multivariate methods for estimating selected soil properties from intact soil cores of paddy fields by Vis–NIR spectroscopy. Geoderma 2018, 310, 29–43. [Google Scholar] [CrossRef]
- Bezdek, J.C.; Ehrlich, R.; Full, W. FCM: The fuzzy c-means clustering algorithm. Comput. Geosci. 1984, 10, 191–203. [Google Scholar] [CrossRef]
- Albornoz, E.M.; Kemerer, A.C.; Galarza, R.; Mastaglia, N.; Melchiori, R.; Martínez, C.E. Development and evaluation of an automatic software for management zone delineation. Precis. Agric. 2018, 19, 463–476. [Google Scholar] [CrossRef]
- Chen, S.; Wang, S.; Shukla, M.K.; Wu, D.; Guo, X.; Li, D.; Du, T. Delineation of management zones and optimization of irrigation scheduling to improve irrigation water productivity and revenue in a farmland of northwest China. Precis. Agric. 2019, 21, 655–677. [Google Scholar] [CrossRef]
- Warner, J.; Sexauer, J.; Unnikrishnan, A. JDWarner/Scikit-Fuzzy: Scikit-Fuzzy, Version 0.4.2. Available online: https://scikit-fuzzy.github.io/scikit-fuzzy/ (accessed on 18 July 2019).
- WRB-IUSS World Reference Base for Soil Resources 2014, update 2015: International soil classification system for naming soils and creating legends for soil maps. World Soil Resource. Report. 2015, 106, 1–191.
- Calamita, G.; Brocca, L.; Perrone, A.; Piscitelli, S.; Lapenna, V.; Melone, F.; Moramarco, T. Electrical resistivity and TDR methods for soil moisture estimation in Central Italy Test-Sites. J. Hydrol. 2012, 454–455, 101–112. [Google Scholar] [CrossRef]
- Costa, M.M.; de Queiroz, D.M.; Pinto, F.D.A.D.C.; dos Reis, E.F.; Santos, N.T. Moisture content effect in the relationship between apparent electrical conductivity and soil attributes. Acta Sci. Agron. 2014, 36, 395–401. [Google Scholar] [CrossRef] [Green Version]
- Muphy, B.; Mullher, S.; Yurchark, R. GeoStat-Framework/PyKrige, Version v1.5.1. Available online: https://github.com/GeoStat-Framework/PyKrige (accessed on 8 January 2020).
- Pedregosa, F.; Varoquaux, G.; Granfort, A.; Michel, V.; Thirion, B. Scikit-Learn: Machine learning in python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar] [CrossRef]
- Huo, X.-N.; Li, H.; Sun, D.-F.; Zhou, L.-D.; Li, B.-G. Combining geostatistics with Moran’s i analysis for mapping soil heavy metals in Beijing, China. Int. J. Environ. Res. Public Health 2012, 9, 995–1017. [Google Scholar] [CrossRef] [Green Version]
- Pereira, G.W.; Valente, D.S.M.; de Queiroz, D.M.; Santos, N.T.; Fernandes-Filho, E.I. Soil mapping for precision agriculture using support vector machines combined with inverse distance weighting. Precis. Agric. 2022, 23. [Google Scholar] [CrossRef]
- Liu, Q.; Xie, W.J.; Xia, J.B. Using semivariogram and Moran’s i techniques to evaluate spatial distribution of soil micronutrients. Commun. Soil Sci. Plant Anal. 2013, 44, 1182–1192. [Google Scholar] [CrossRef]
- Legendre, P.; Fortin, M.-J. Spatial pattern and ecological analysis. Vegetatio 1989, 80, 107–138. [Google Scholar] [CrossRef]
- Lee, S. Developing a bivariate spatial association measure: An integration of Pearson’s r and Moran’s i. Geogr. Syst. 2001, 3, 369–385. [Google Scholar] [CrossRef]
- Rey, S.J.; Anselin, L. PySAL: A Python Library of Spatial Analytical Methods; Fischer, M., Getis, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Celisse, A.; Robin, S. Nonparametric density estimation by exact leave-p-out cross-validation. Comput. Stat. Data Anal. 2008, 52, 2350–2368. [Google Scholar] [CrossRef]
- Cawley, G.C.; Talbot, N.L.C. Efficient leave-one-out cross-validation of kernel fisher discriminant classifiers. Pattern Recognit. 2003, 36, 2585–2592. [Google Scholar] [CrossRef]



| Variable | Unit | Min | Max | Mean | SD (17) | Median | CV(%) (18) |
|---|---|---|---|---|---|---|---|
| P (1) | mg dm−3 | 1.70 | 21.60 | 6.84 | 3.96 | 5.85 | 57.88 |
| K+ (2) | mg dm−3 | 24.00 | 108.00 | 52.63 | 14.20 | 51.00 | 26.98 |
| Ca2+ (3) | cmolc dm−3 | 1.90 | 4.20 | 3.27 | 0.46 | 3.30 | 14.04 |
| Mg2+ (4) | cmolc dm−3 | 0.60 | 1.40 | 0.84 | 0.14 | 0.80 | 16.53 |
| OM (5) | dag kg−1 | 2.50 | 4.30 | 3.06 | 0.30 | 3.10 | 9.85 |
| CEC (6) | cmolc dm−3 | 4.20 | 9.90 | 5.95 | 0.86 | 5.90 | 14.41 |
| Altitude (7) | m | 987 | 1025 | 1011.2 | 7.63 | 1012.1 | 0.75 |
| Clay (8) | g kg−1 | 26.00 | 44.00 | 33.11 | 3.37 | 33.00 | 10.17 |
| Silt (9) | g kg−1 | 6.00 | 20.00 | 10.60 | 2.94 | 10.00 | 27.78 |
| Sand (10) | g kg−1 | 45.00 | 65.00 | 56.28 | 4.41 | 56.50 | 7.84 |
| Eca_1 (11) | mS m−1 | 2.49 | 8.36 | 4.92 | 1.01 | 4.83 | 20.62 |
| Eca_2 (12) | mS m−1 | 2.95 | 10.00 | 5.95 | 1.22 | 5.99 | 20.56 |
| Eca_3 (13) | mS m−1 | 1.71 | 9.11 | 4.54 | 1.13 | 4.51 | 24.86 |
| Eca_4 (14) | mS m−1 | 1.84 | 7.32 | 3.98 | 0.88 | 3.94 | 22.09 |
| Eca_5 (15) | mS m−1 | 0.89 | 5.57 | 2.65 | 0.71 | 2.61 | 26.67 |
| Eca_Avg (16) | mS m−1 | 2.17 | 8.03 | 4.41 | 0.84 | 4.44 | 19.08 |
| Density | 38 Samples | 75 Samples | 112 Samples | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Variable * | OK | SVM1 | SVM2 | OK | SVM1 | SVM2 | OK | SVM1 | SVM2 |
| P | 3.24 | 2.92 | 2.85 | 2.91 | 3.19 | 2.80 | 3.36 | 3.47 | 3.32 |
| K+ | 11.57 | 10.87 | 8.94 | 8.73 | 9.21 | 9.03 | 10.33 | 10.27 | 10.09 |
| Ca2+ | 0.46 | 0.42 | 0.40 | 0.40 | 0.40 | 0.38 | 0.40 | 0.40 | 0.39 |
| Mg2+ | 0.12 | 0.12 | 0.11 | 0.10 | 0.10 | 0.10 | 0.11 | 0.10 | 0.10 |
| Density | 112 Samples | 75 Samples | 38 Samples | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Variable * | OK | SVM1 | SVM2 | OK | SVM1 | SVM2 | OK | SVM1 | SVM2 |
| P | 3.40 | 3.36 | 3.22 | 3.59 | 3.04 | 2.74 | 2.75 | 1.94 | 2.79 |
| K+ | 9.74 | 10.05 | 9.70 | 12.01 | 11.77 | 11.41 | 9.04 | 9.46 | 8.14 |
| Ca2+ | 0.41 | 0.29 | 0.28 | 0.41 | 0.26 | 0.25 | 0.41 | 0.24 | 0.23 |
| Mg2+ | 0.11 | 0.11 | 0.07 | 0.12 | 0.10 | 0.10 | 0.15 | 0.14 | 0.10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pereira, G.W.; Valente, D.S.M.; Queiroz, D.M.d.; Coelho, A.L.d.F.; Costa, M.M.; Grift, T. Smart-Map: An Open-Source QGIS Plugin for Digital Mapping Using Machine Learning Techniques and Ordinary Kriging. Agronomy 2022, 12, 1350. https://doi.org/10.3390/agronomy12061350
Pereira GW, Valente DSM, Queiroz DMd, Coelho ALdF, Costa MM, Grift T. Smart-Map: An Open-Source QGIS Plugin for Digital Mapping Using Machine Learning Techniques and Ordinary Kriging. Agronomy. 2022; 12(6):1350. https://doi.org/10.3390/agronomy12061350
Chicago/Turabian StylePereira, Gustavo Willam, Domingos Sárvio Magalhães Valente, Daniel Marçal de Queiroz, André Luiz de Freitas Coelho, Marcelo Marques Costa, and Tony Grift. 2022. "Smart-Map: An Open-Source QGIS Plugin for Digital Mapping Using Machine Learning Techniques and Ordinary Kriging" Agronomy 12, no. 6: 1350. https://doi.org/10.3390/agronomy12061350
APA StylePereira, G. W., Valente, D. S. M., Queiroz, D. M. d., Coelho, A. L. d. F., Costa, M. M., & Grift, T. (2022). Smart-Map: An Open-Source QGIS Plugin for Digital Mapping Using Machine Learning Techniques and Ordinary Kriging. Agronomy, 12(6), 1350. https://doi.org/10.3390/agronomy12061350







