Using Soil, Plant, Topographic and Remotely Sensed Data to Determine the Best Method for Defining Aflatoxin Contamination Risk Zones within Fields for Precision Management
Abstract
1. Introduction
2. Materials and Methods
2.1. Field Observations
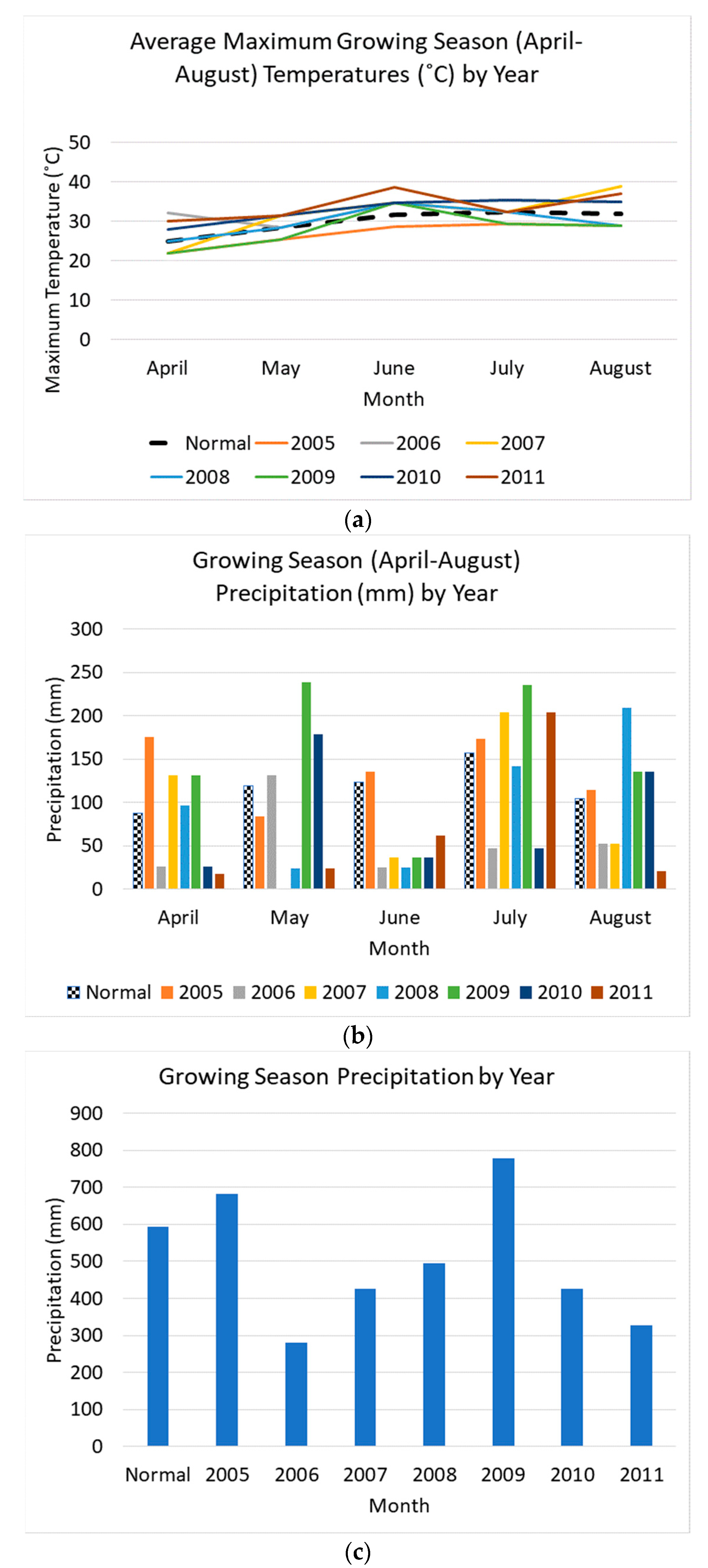
2.2. Weather, Topography and Remotely Sensed Data
2.3. Statistical Analysis
3. Results and Discussion
3.1. Spatial Patterns and Correlation Analysis for 2010
3.2. Regression Analysis for 2010 Growing Season
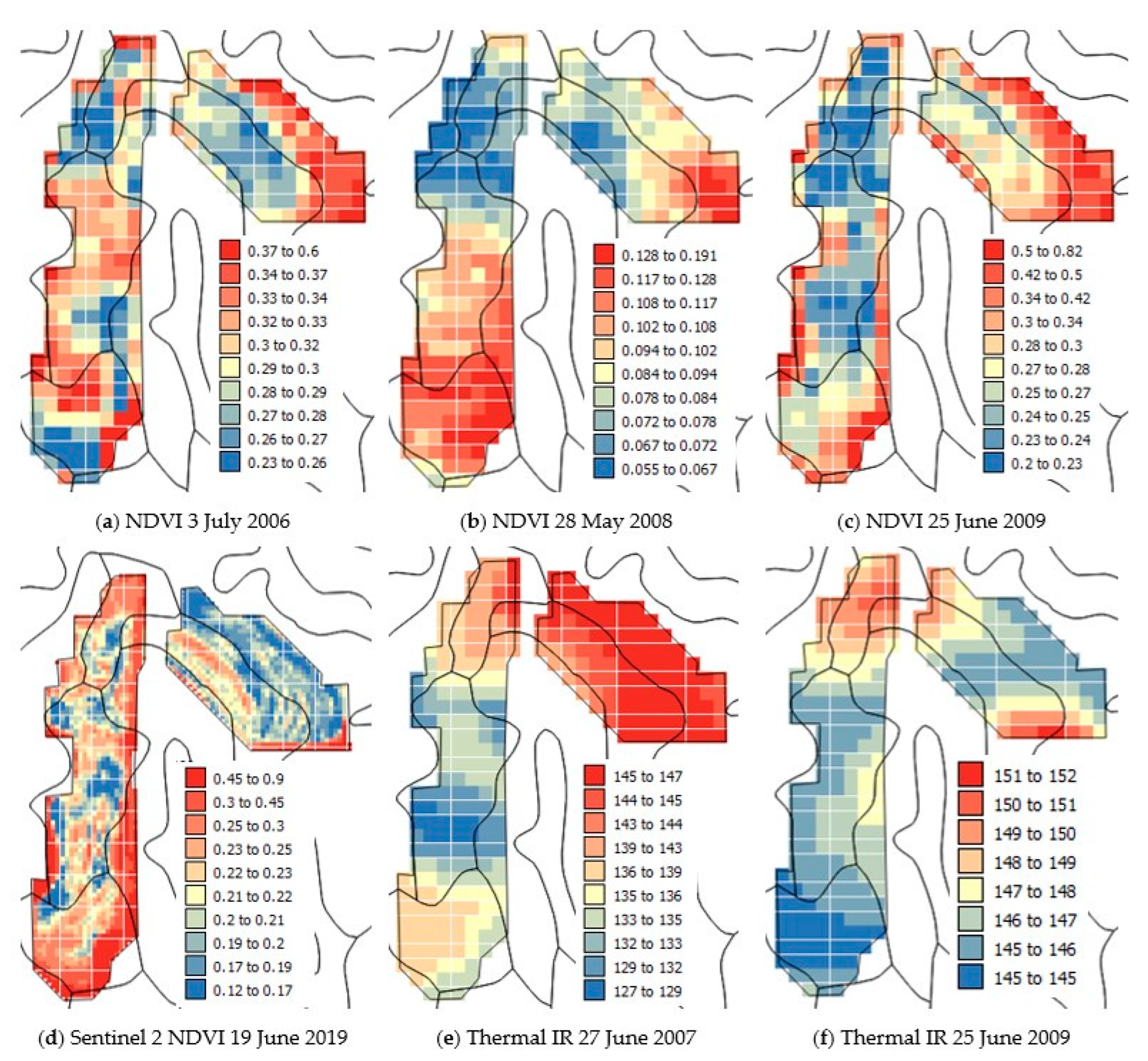
3.3. Imagery Data for the 2006–2011 and 2019 Growing Seasons
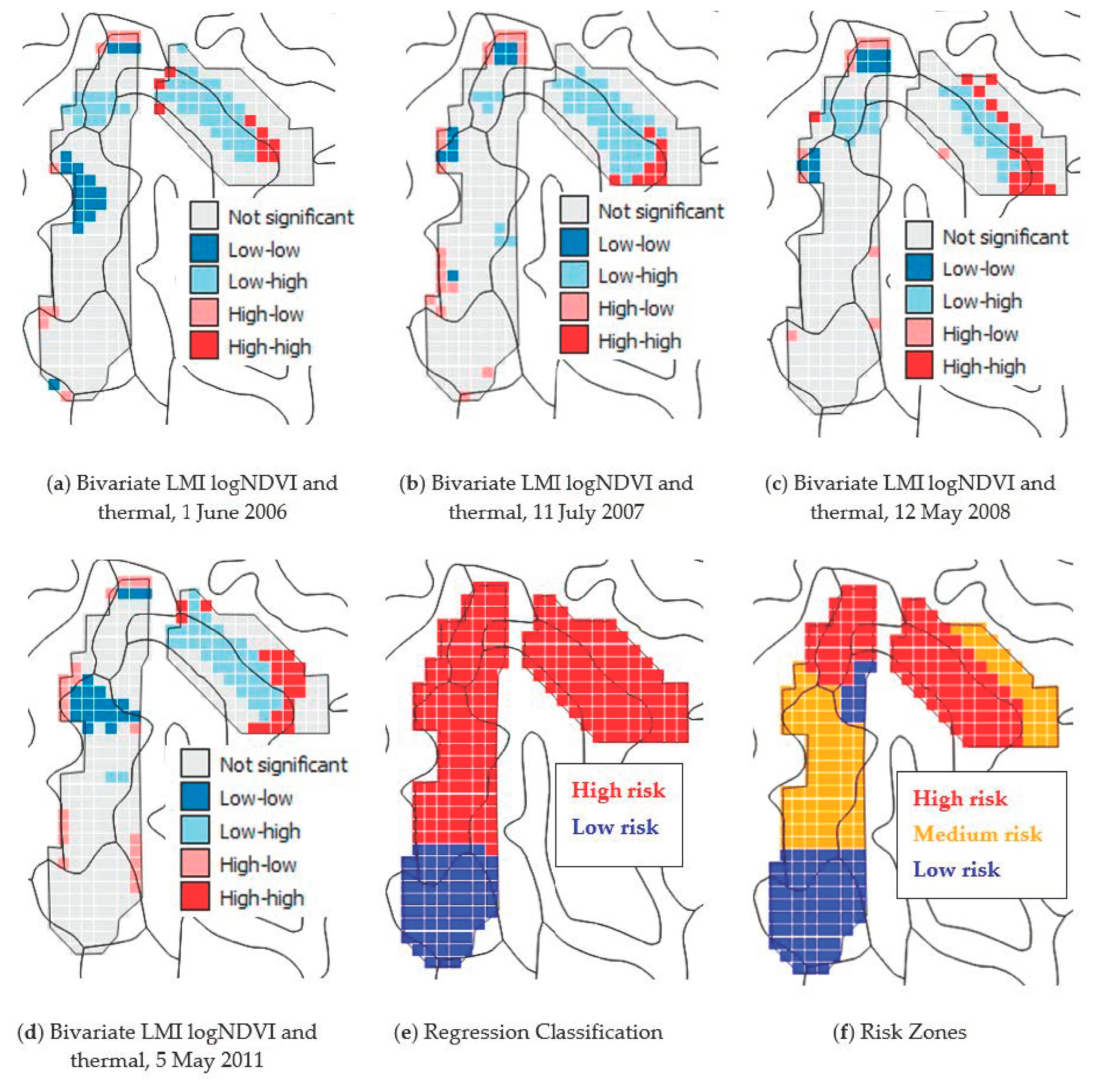
3.4. Local Moran’s I Analysis
3.5. K-Means Classification of Imagery
3.6. Principal Components Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Patriarca, A.; Medina, A.; Pinto, V.F.; Magan, N. Temperature and water stress impacts on growth and production of altetoxin-II by strains of Alternaria tenuissima from Argentinean wheat. World Mycotoxin J. 2014, 7, 329–334. [Google Scholar] [CrossRef]
- Payne, G.A. Aflatoxin in maize. CRC Crit. Rev. Plant Sci. 1992, 10, 423–440. [Google Scholar] [CrossRef]
- Wilson, J.P.; Hanna, W.W.; Wilson, D.M.; Beaver, R.W.; Casper, H.H. Fungal and mycotoxin contamination of pearl-millet grain in response to environmental conditions in Georgia. Plant Dis. 1993, 77, 121–124. [Google Scholar] [CrossRef]
- Abbas, H.K.; Weaver, M.A.; Zablotowicz, R.M.; Horn, B.W.; Shier, W.T. Relationships between aflatoxin production and sclerotia formation among isolates of Aspergillus section Flavi from the Mississippi Delta. Eur. J. Plant Pathol. 2005, 112, 283–287. [Google Scholar] [CrossRef]
- Adegoke, G.O.; Otumu, E.J.; Akanni, A.O. Influence of grain quality, heat, and processing time on the reduction of aflatoxin b-1 levels in tuwo and ogi—2 cereal-based products. Plant Foods Hum. Nutr. 1994, 45, 113–117. [Google Scholar] [CrossRef] [PubMed]
- Barrett, J.R. Liver cancer and aflatoxin: New information from the Kenyan outbreak. Environ. Health Persp. 2005, 113, A837–A838. [Google Scholar] [CrossRef]
- FDA. Bad Bug Book, Foodborne Pathogenic Microorganisms and Natural Toxins, 2nd ed.; Food and Drug Administration: Laurel, MD, USA, 2012. Available online: http://www.fda.gov/downloads/Food/FoodborneIllnessContaminants/UCM297627.pdf (accessed on 12 October 2022).
- FDA. Sec. 683.100 Action Levels for Aflatoxins in Animal Food Compliance Policy Guide. Guidance for FDA Staff; FDA: Rockville, MD, USA, 2019.
- EU. Commission Regulation (EC) No 1881/2006 of 19 December 2006 Setting Maximum Levels for Certain Contaminants in Foodstuffs; EU: Maastricht, The Netherlands, 2006. [Google Scholar]
- Liu, Y.; Wu, F. Global burden of aflatoxin-induced hepatocellular carcinoma: A risk assessment. Environ. Health Perspect. 2010, 118, 818–824. [Google Scholar] [CrossRef] [PubMed]
- FDA. Available online: http://www.fda.gov/ICECI/ComplianceManuals/CompliancePolicyGuidanceManual/ucm074703.htm (accessed on 18 August 2022).
- Papadoyannis, I.N. HPLC in Clinical Chemistry (Chromatographic Science Series), 1st ed.; Marcel Dekker: New York, NY, USA, 2008; p. 504. [Google Scholar]
- EU. Commission Regulation (EC) No 401/2006 of 23 February 2006 Laying Down the Methods of Sampling and Analysis for the Official Control of the Levels of Mycotoxins in Foodstuffs. 2006. Available online: https://eur-lex.europa.eu/legal-content/EN/ALL/?uri=CELEX%3A32006R0401 (accessed on 14 August 2022).
- Maestroni, B.; Cannavan, A. Sampling Strategies to Control Mycotoxins, Joint FAO/IAEA Division of Nuclear Techniques in Food and Agriculture; International Atomic Energy Agency (IAEA): Vienna, Austria, 2011. [Google Scholar]
- Horn, B.W.; Sorensen, R.B.; Lamb, M.C.; Sobolev, V.S.; Olarte, R.A.; Worthington, C.J.; Carbone, I. Sexual reproduction in Aspergillus flavus sclerotia naturally produced in corn. Phytopathology 2014, 104, 75–85. [Google Scholar] [CrossRef] [PubMed]
- Brenneman, T.B.; Wilson, D.M.; Beaver, R.W. Effects of diniconazole on Aspergillus populations and aflatoxin formation in peanut under irrigated and non-irrigated conditions. Plant Dis. 1993, 77, 608–612. [Google Scholar] [CrossRef]
- Salvacion, A.; Ortiz, B.V.; Scully, B.; Wilson, D.M.; Hoogenboom, G.; Lee, D. Effect of rainfall and maximum temperature on corn aflatoxin in the Southeastern U.S. coastal plain. In Proceedings of the Climate Information for Managing Risks, Orlando, FA, USA, 24–27 May 2011. [Google Scholar]
- Kerry, R.; Ortiz, B.V.; Ingram, B.R.; Scully, B.T. A Spatio-Temporal investigation of risk factors for aflatoxin contamination of corn in southern Georgia, USA using geostatistical methods. Crop Prot. 2017, 94, 144–158. [Google Scholar] [CrossRef]
- Yoo, E.; Kerry, R.; Ingram, B.R.; Ortiz, B.; Scully, B. Defining and Characterizing Aflatoxin Contamination Risk Areas for Corn in Georgia, USA: Adjusting for Collinearity and Spatial Correlation. Spat. Stat. 2018, 28, 84–104. [Google Scholar] [CrossRef]
- Battilani, P.; Toscano, P.; Van der Fels-Klerx, H.J.; Moretti, A.; Camardo Leggieri, M.; Brera, C.; Rortais, A.; Goumperis, T.; Robinson, T. Aflatoxin B1 contamination in maize in Europe increases due to climate change. Sci. Rep. 2016, 6, 24328. [Google Scholar] [CrossRef] [PubMed]
- Kerry, R.; Ingram, B.; Garcia-Cela, E.; Magan, N.; Ortiz, B.V.; Scully, B. Determining Future aflatoxin contamination risk scenarios for corn in Southern Georgia, USA using spatio-temporal modelling and future climate simulations. Sci. Rep. 2021, 11, 13522. [Google Scholar] [CrossRef]
- Hell, K.; Cardwell, K.F.; Setamou, M.; Schulthess, F. Influence of insect infestation on aflatoxin contamination of stored maize in four agroecological regions in Benin. Entomol. Afr. Entomol. 2000, 8, 169–177. [Google Scholar]
- Liu, N.; Liu, C.; Dudaš, T.N.; Loc, M.Č.; Bagi, F.F.; Van der Fels-Klerx, H.J. Improved aflatoxins and fumonisins forecasting models for maize (PREMA and PREFUM), using combined mechanistic and Bayesian Network modeling—Serbia as a case study. Front. Microbiol. 2021, 12, 643604. [Google Scholar] [CrossRef] [PubMed]
- Palumbo, J.D.; O’Keeffe, T.L.; Kattan, A.; Abbas, H.K.; Johnson, B.J. Inhibition of aspergillus flavus in soil by antagonistic pseudomonas strains reduces the potential for airborne spore dispersal. Phytopathology 2010, 100, 532–538. [Google Scholar] [CrossRef] [PubMed]
- Damianidis, D.; Ortiz, B.; Windham, G.; Scully, B.; Woli, P. Predicting pre-harvest Aflatoxin corn contamination risk with a rought index. In Precision Agriculture’15; Wageningen Academic Publishers: Wageningen, The Netherlands, 2015; pp. 788–809. [Google Scholar]
- Hatfield, J.L.; Prueger, J.H. Value of using different vegetative indices to quantify agricultural crop characteristics at different growth stages under varying management practices. Remote Sens. 2010, 2, 562–578. [Google Scholar] [CrossRef]
- Wang, R.; Cherkauer, K.; Bowling, L. Corn response to climate stress detected with satellite-based NDVI time series. Remote Sens. 2016, 8, 269. [Google Scholar] [CrossRef]
- Jones, H.G.; Serraj, R.; Loveys, B.R.; Xiong, L.; Wheaton, A.; Price, A.H. Thermal infrared imaging of crop canopies for the remote diagnosis and quantification of plant responses to water stress in the field. Funct. Plant Biol. 2009, 36, 978–989. [Google Scholar] [CrossRef]
- Sepúlveda-Reyes, D.; Ingram, B.; Bardeen, M.; Zúñiga, M.; Ortega-Farías, S.; Poblete-Echeverría, C. Selecting canopy zones and thresholding approaches to assess grapevine water status by using aerial and ground-based thermal imaging. Remote Sens. 2016, 8, 822. [Google Scholar] [CrossRef]
- Kerry, R.; Ingram, B.; Orellana, M.; Ortiz, B.V.; Scully, B.T. Development of a method to assess the risk of aflatoxin contamination of corn within counties in southern Georgia, USA using remotely sensed data. Smart Agric. Technol. 2022, 3, 100124. [Google Scholar] [CrossRef]
- Jaime-Garcia, R.; Cotty, P.J. Aflatoxin contamination of commercial cottonseed in south Texas. Phytopathology 2003, 93, 1190–1200. [Google Scholar] [CrossRef] [PubMed]
- Damianidis, D.; Ortiz, B.V.; Bowen, K.L.; Windham, G.L.; Hoogenboom, G.; Hagan, A.; Knappenberger, T.; Abbas, H.K.; Scully, B.T.; Mourtzinis, S. Minimum Temperature, Rainfall, and Agronomic Management Impacts on Corn Grain Aflatoxin Contamination. Agron. Soils Environ. Qual. 2018, 110, 1697–1708. [Google Scholar] [CrossRef]
- Xiong, D.; Chen, J.; Yu, T.; Gao, W.; Ling, X.; Li, Y.; Peng, S.; Huang, J. SPAD-based leaf nitrogen estimation is impacted by environmental factors and crop leaf characteristics. Sci. Rep.-UK. 2015, 5, 13389. [Google Scholar] [CrossRef]
- Bista, D.R.; Heckathorn, S.A.; Jayawardena, D.M.; Mishra, S.; Boldt, J.K. Effects of Drought on Nutrient Uptake and the Levels of Nutrient-Uptake Proteins in Roots of Drought-Sensitive and -Tolerant Grasses. Plants 2018, 7, 28. [Google Scholar] [CrossRef]
- Tadono, T.; Ishida, H.; Oda, F.; Naito, S.; Minakawa, K.; Iwamoto, H. Precise Global DEM Generation by ALOS PRISM, ISPRS. J. Photogramm. Remote Sens. 2014, 2, 71–76. [Google Scholar]
- Boehner, J.; Selige, T. Spatial prediction of soil attributes using terrain analysis and climate regionalisation. In SAGA-Analyses and Modelling Applications; Boehner, J., McCloy, K.R., Strobl, J., Eds.; Goettinger Geographische Abhandlungen: Goettingen, Germany, 2006; pp. 13–28. [Google Scholar]
- Beven, K.J.; Kirkby, M.J. A physically based, variable contributing area model of basin hydrology/Un modèle à base physique de zone d’appel variable de l’hydrologie du bassin versant. Hydrol. Sci. J. 1979, 24, 43–69. [Google Scholar] [CrossRef]
- Conrad, O.; Bechtel, B.; Bock, M.; Dietrich, H.; Fischer, E.; Gerlitz, L.; Wehberg, J.; Wichmann, V.; Böhner, J. System for Automated Geoscientific Analyses (SAGA) v. 2.1.4. Geosci. Model Dev. 2015, 8, 1991–2007. [Google Scholar] [CrossRef]
- Webster, R.; Oliver, M.A. Sample adequately to estimate variograms of soil properties. J. Soil Sci. 1992, 43, 177–192. [Google Scholar] [CrossRef]
- Kerry, R.; Oliver, M.A. Determining nugget: Sill ratios of standardized variograms from aerial photographs to krige sparse soil data. Precis. Agric. 2008, 9, 33–56. [Google Scholar] [CrossRef]
- Jacquez, G.M.; Goovaerts, P.; Kaufmann, A.; Rommel, R. SpaceStat 4.0 User Manual: Software for the Space-Time Analysis of Dynamic Complex Systems, 4th ed.; BioMedware: Ann Arbor, MI, USA, 2014. [Google Scholar]
- IBM Corp. IBM SPSS Statistics for Windows, Version 25.0; IBM Corp: Armonk, NY, USA, 2017. [Google Scholar]
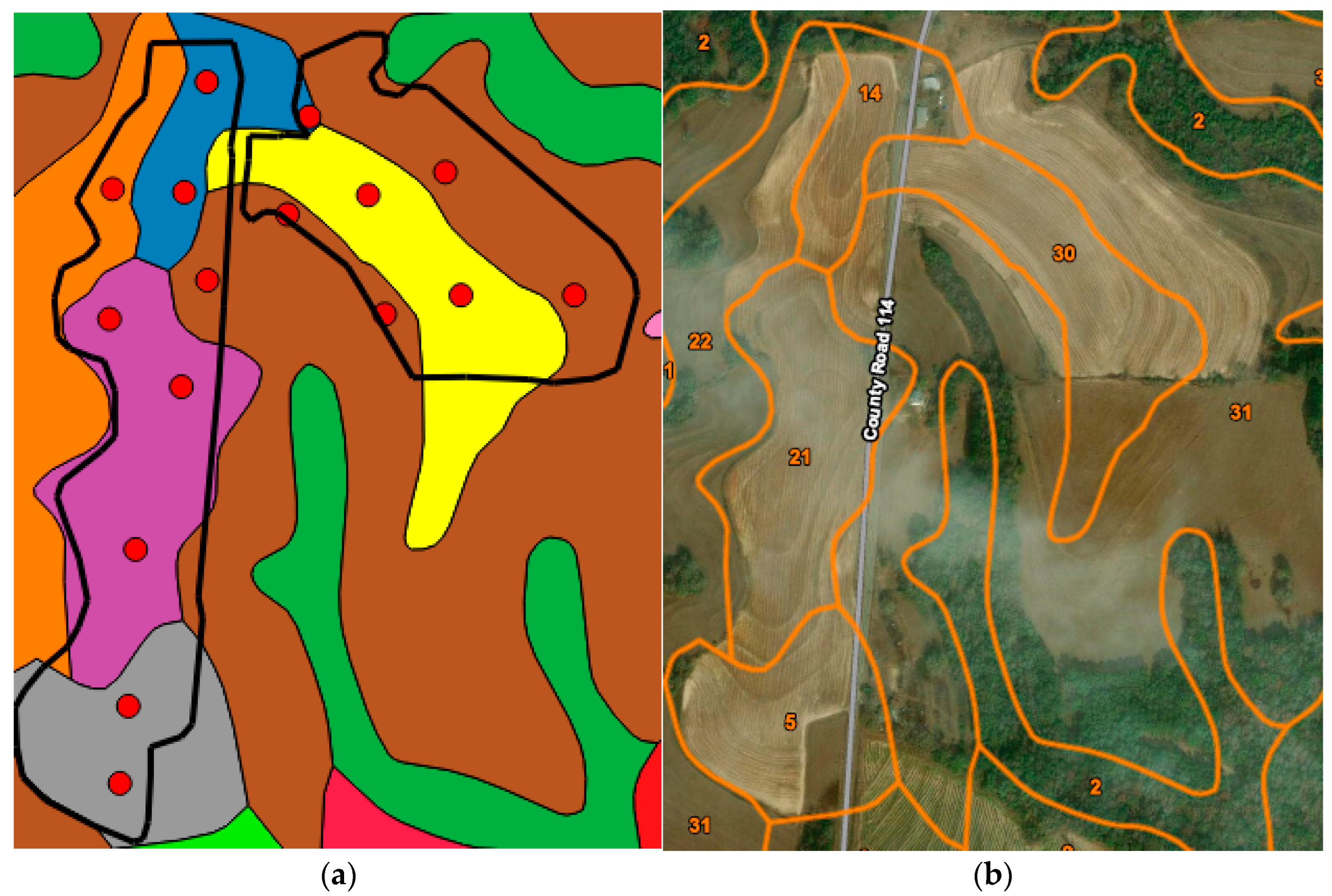


| Soil Series Number | Name | Slope (%) | Drainage Class | Landform | Profile—Horizon Depths (cm) and USDA Textural Class | Prime Farmland? |
|---|---|---|---|---|---|---|
| 5 | Bonifay LS | 1–5 | Well-drained | Ridges | H1—0–115 cm: LS H2—115–180 cm: SCL | No |
| 14 | Fuquay LS | 0–5 | Well-drained | Interfluves | Ap—0–25 cm: LS E1—25–56 cm: LS E2—56–70 cm: LS Bt1—70–90 cm: SCL Bt2—90–110 cm: SCL Btv—110–165 cm: SCL | No |
| 21 | Orangeburg SL | 2–5 | Well-drained | Ridges | A—0–20 cm: SL Bt1—20–150 cm: SCL Bt2—150–200 cm: SCL | Yes |
| 22 | Orangeburg SL | 5–8 | Well-drained | Ridges | A—0–20 cm: SL Bt1—20–150 cm: SCL Bt2—150–200 cm: SCL | Yes |
| 30 | Troup LS | 1–5 | Somewhat excessively drained | Ridges | H1—0–145 cm: LS H2—145–215 cm: SL | No |
| 31 | Troup LS | 5–8 | Somewhat excessively drained | Hillslopes, Ridges | Ap—0–8 cm: LS E—8–130 cm: LS Bt—130–200 cm: SCL | No |
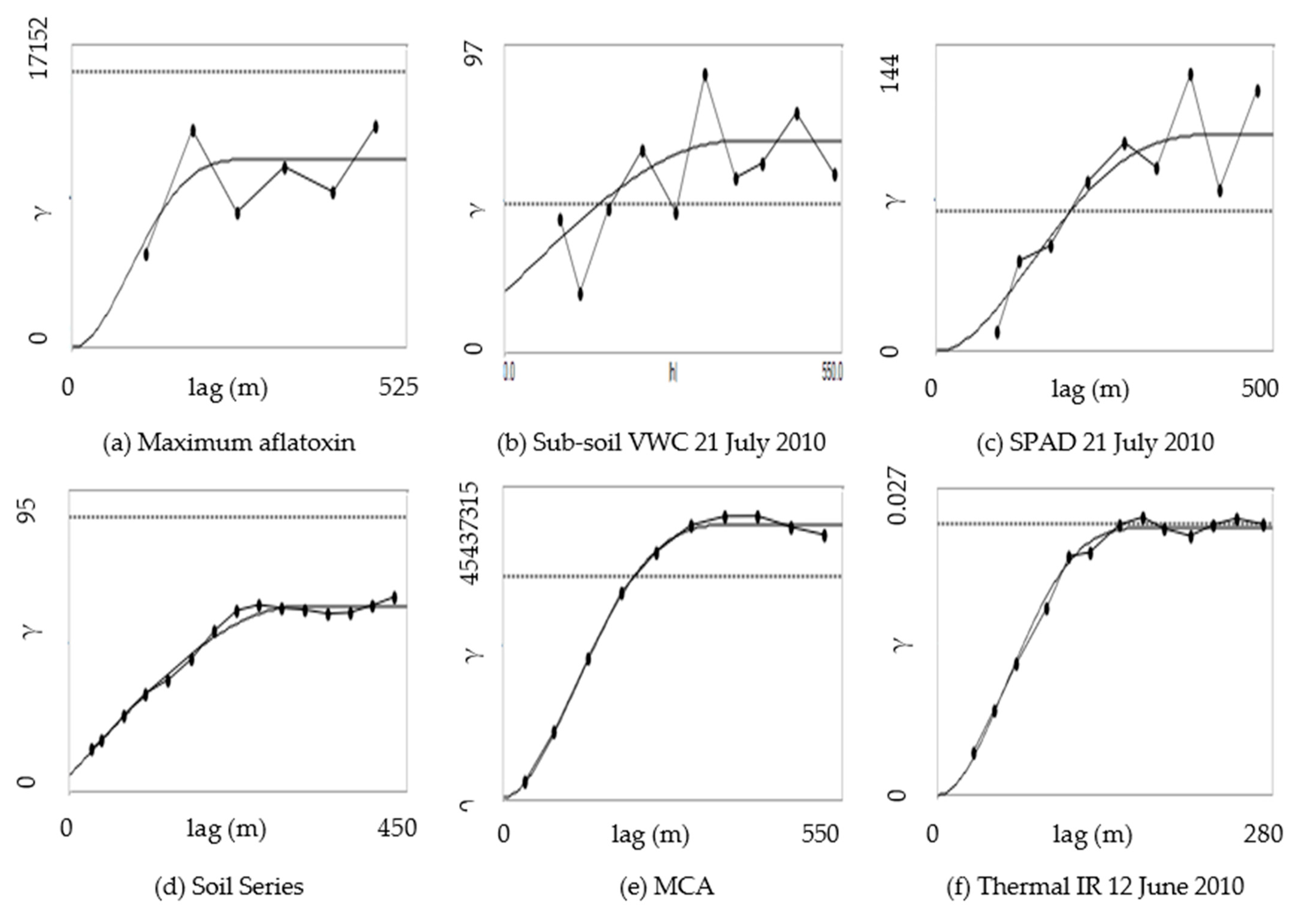
| Variable | Model | Nugget (c0) | Sill (c1) | Range (m) |
|---|---|---|---|---|
| Minimum aflatoxin | Spherical | 0 | 8175.46 | 194.64 |
| Mean aflatoxin | Cubic | 0 | 6435.14 | 273.37 |
| Maximum aflatoxin | Cubic | 0 | 10,713.10 | 293.61 |
| Top-soil VWC (21 July 2010) | Cubic | 0 | 5.93 | 190.86 |
| Sub-soil VWC (21 July 2010) | Spherical | 19.25 | 47.57 | 371.67 |
| SPAD (21 July 2010) | Cubic | 0 | 102.72 | 464.86 |
| Soil series | Spherical | 5.41 | 53.62 | 306.64 |
| MCA | Cubic | 0 | 3572.44 | 401.31 |
| NDVI (12 June 2010) | Spherical | 0.00014 | 0.0013 | 104.68 |
| Thermal IR (12 June 2010) | Cubic | 0 | 0.0237 | 185.08 |
| NDVI (19 June 2010) | Spherical | 0 | 0.0022 | 114.54 |
| Thermal IR (19 June 2010) | Spherical | 0 | 0.0070 | 186.02 |
| Pearson Correlation | Regression | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Variable | Min. Aflatoxin | Mean Aflatoxin | Max. Aflatoxin | Min. Aflatoxin | Mean Aflatoxin | Max. Aflatoxin | |||
| R2 | - | - | - | 0.659 | 0.688 | 0.809 | |||
| Estimate | p-Value | Estimate | p-Value | Estimate | p-Value | ||||
| Intercept | - | - | - | 1,514,279 | 0.00 * | 1,752,835 | 0.00 * | 497,332 | 0.00 * |
| MCA | 0.49 | 0.38 | 0.31 | NA | NA | NA | NA | 0.013 | 0.00 * |
| MUSYM | 0.33 | 0.46 | 0.46 | −4.61 | 0.00 * | −5.34 | 0.00 * | −1.54 | 0.012 * |
| MUKEY | −0.60 | −0.59 | −0.52 | 1.14 | 0.002 * | 3.14 | 0.00 * | 1.46 | 0.0007 * |
| SPAD 21 July 2010 | 0.11 | −0.07 | −0.47 | 1.23 | 0.015 * | NA | NA | −10.51 | 0.00 * |
| VWC 21 July 2010 | −0.56 | −0.59 | −0.41 | −11.6 | 0.00 * | NA | NA | −12.82 | 0.00 * |
| logNDVI 12 June 2010 | −0.01 | −0.01 | 0.05 | 247 | 0.001 * | 126.1 | 0.074 | 244.4 | 0.007 * |
| logNDVI 19 June 2010 | −0.06 | −0.06 | −0.02 | NA | NA | NA | NA | NA | NA |
| logNDVI 14 July 2010 | −0.20 | −0.13 | −0.08 | NA | NA | NA | NA | −615.7 | 0.0004 * |
| logNDVI 21 July 2010 | −0.27 | −0.17 | −0.14 | −333.3 | 0.009 * | NA | NA | NA | NA |
| logNDVI 30 July 2010 | −0.07 | −0.08 | −0.21 | NA | NA | NA | NA | 115.07 | 0.1132 |
| Thermal 12 June 2010 | −0.14 | −0.21 | −0.18 | −6.57 | 0.011 * | NA | NA | −20.71 | 0.00 * |
| Thermal 19 June 2010 | −0.35 | −0.28 | 0.04 | −6.22 | 0.141 | NA | NA | 29.62 | 0.00 * |
| Thermal 14 July 2010 | 0.23 | 0.31 | 0.01 | 6.4 | 0.028 * | 27.58 | 0.00 * | 31.12 | 0.00 * |
| Thermal 21 July 2010 | 0.42 | 0.26 | 0.19 | 6.4 | 0.028 * | NA | NA | 8.29 | 0.0012 * |
| Thermal 30 July 2010 | 0.30 | 0.27 | 0.27 | NA | NA | 14.03 | 0.00 * | 19.67 | 0.00 * |
| logNDVI 28 May 2008 | −0.70 | −0.62 | −0.33 | - | - | - | - | - | - |
| logNDVI 30 May 2011 | 0.61 | 0.74 | 0.73 | - | - | - | - | - | - |
| Thermal 24 June 2006 | −0.54 | −0.36 | −0.30 | - | - | - | - | - | - |
| Thermal 5 May 2008 | 0.63 | 0.73 | 0.64 | - | - | - | - | - | - |
| Thermal 28 May 2008 | −0.62 | −0.63 | −0.48 | - | - | - | - | - | - |
| Thermal 25 June 2009 | 0.64 | 0.53 | 0.57 | - | - | - | - | - | - |
| Thermal 30 May 2011 | 0.74 | 0.70 | 0.54 | - | - | - | - | - | - |
| NDRE June 2019 | −0.48 | −0.65 | −0.64 | - | - | - | - | - | - |
| Kruskal–Wallis H Test Statistic Values | Pearson Correlation | |||||
|---|---|---|---|---|---|---|
| Regression and LMI | PC1 | PC2 | PC1 and PC2 | PC1 | PC2 | |
| Minimum aflatoxin | 150.9 | 74.5 | 137.8 | 172.1 | 0.54 | 0.71 |
| Mean aflatoxin | 192.3 | 68.5 | 138.3 | 167.6 | 0.55 | 0.72 |
| Maximum aflatoxin | 204.8 | 25.5 | 113.5 | 125.9 | 0.39 | 0.65 |
| Variable or Imagery Date | Minimum Aflatoxin | Mean Aflatoxin | Maximum Aflatoxin | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Kappa Statistic | p-Value | % Agreement | Kappa Statistic | p-Value | % Agreement | Kappa Statistic | p-Value | % Agreement | |
| 5 April 2006 | 0.059 | 0.26 | 50.7 | −1.330 | 0.021 | 48.6 | −0.067 | 0.250 | 51.0 |
| 24 June 2006 | 0.184 | 0.001 | 61.8 | −0.205 | 0 | 55.1 | 0.213 | 0 | 56.1 |
| 27 June 2007 | 0.530 | 0 | 77.0 | 0.431 | 0 | 70.3 | 0.343 | 0 | 65.9 |
| 28 May 2008 | 0.402 | 0 | 67.6 | 0.661 | 0 | 85.8 | 0.410 | 0 | 74.7 |
| 8 July 2008 | 0.024 | 0.474 | 44.3 | −0.070 | 0.157 | 61.1 | −0.100 | 0.037 | 58.1 |
| 25 June 2009 | 0.313 | 0 | 73.3 | 0.298 | 0 | 50.4 | 0.327 | 0 | 53.4 |
| 2 July 2009 | 0.223 | 0 | 59.4 | 0.115 | 0.045 | 59.4 | 0.133 | 0.022 | 59.8 |
| 9 April 2010 | −0.044 | 0.419 | 45.9 | −0.147 | 0.01 | 46.6 | −0.129 | 0.025 | 46.9 |
| 12 June 2010 | 0.023 | 0.063 | 42.2 | 0.071 | 0.001 | 69.9 | 0.064 | 0.002 | 67.6 |
| 19 June 2010 | 0.049 | 0.401 | 51.7 | 0.138 | 0.009 | 58.4 | 0.083 | 0.124 | 55.4 |
| 14 July 2010 | 0.169 | 0.002 | 56.8 | 0.076 | 0.187 | 57.4 | 0.050 | 0.391 | 55.7 |
| 21 July 2010 | 0.404 | 0 | 70.3 | 0.220 | 0.000 | 60.8 | 0.172 | 0.002 | 58.4 |
| 30 July 2010 | 0.138 | 0.002 | 52.7 | 0.102 | 0.074 | 63.5 | 0.136 | 0.016 | 63.9 |
| 30 May 2011 | 0.563 | 0 | 83.0 | 0.521 | 0 | 85.8 | 0.416 | 0 | 78.7 |
| 6 June 2011 | 0.049 | 0.189 | 46.3 | 0.163 | 0.002 | 68.6 | 0.103 | 0.045 | 64.9 |
| 15 June 2011 | −0.014 | 0.699 | 42.6 | 0.091 | 0.078 | 66.2 | 0.087 | 0.086 | 64.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kerry, R.; Ingram, B.; Ortiz, B.V.; Salvacion, A. Using Soil, Plant, Topographic and Remotely Sensed Data to Determine the Best Method for Defining Aflatoxin Contamination Risk Zones within Fields for Precision Management. Agronomy 2022, 12, 2524. https://doi.org/10.3390/agronomy12102524
Kerry R, Ingram B, Ortiz BV, Salvacion A. Using Soil, Plant, Topographic and Remotely Sensed Data to Determine the Best Method for Defining Aflatoxin Contamination Risk Zones within Fields for Precision Management. Agronomy. 2022; 12(10):2524. https://doi.org/10.3390/agronomy12102524
Chicago/Turabian StyleKerry, Ruth, Ben Ingram, Brenda V. Ortiz, and Arnold Salvacion. 2022. "Using Soil, Plant, Topographic and Remotely Sensed Data to Determine the Best Method for Defining Aflatoxin Contamination Risk Zones within Fields for Precision Management" Agronomy 12, no. 10: 2524. https://doi.org/10.3390/agronomy12102524
APA StyleKerry, R., Ingram, B., Ortiz, B. V., & Salvacion, A. (2022). Using Soil, Plant, Topographic and Remotely Sensed Data to Determine the Best Method for Defining Aflatoxin Contamination Risk Zones within Fields for Precision Management. Agronomy, 12(10), 2524. https://doi.org/10.3390/agronomy12102524








