Next Article in Journal
Biofortification of Diverse Basmati Rice Cultivars with Iodine, Selenium, and Zinc by Individual and Cocktail Spray of Micronutrients
Previous Article in Journal
Fertilizer Effects on Endosperm Physicochemical Properties and Resistance to Larger Grain Borer, Prostephanus truncatus (Coleoptera: Bostrichidae), in Malawian Local Maize (Zea mays L.) Varieties: Potential for Utilization of Ca and Mg Nutrition
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Agronomy
Volume 12
Issue 1
10.3390/agronomy12010048
agronomy-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Communication

Relating Profile Wall Root-Length Density Estimates to Monolith Root-Length Density Measurements of Cover Crops

by
Tábata Aline Bublitz
1,*,
Roman Kemper
2,
Phillip Müller
3,
Timo Kautz
4,
Thomas F. Döring
2 and
Miriam Athmann
5
1
Department of Soil Biology and Plant Nutrition, Faculty of Organic Agricultural Sciences, University of Kassel, Nordbahnhofstraße 1a, 37213 Witzenhausen, Germany
2
Department of Agroecology and Organic Farming, Faculty of Agriculture, University of Bonn, Auf dem Hügel 6, 53121 Bonn, Germany
3
Cologne Institute of Construction Machinery and Agricultural Engineering (IBL), Faculty of Process Engineering, Energy and Mechanical Systems, Technical University of Cologne, Gustav-Heinemann-Ufer 54, 50968 Cologne, Germany
4
Department of Agronomy and Crop Science, Faculty of Life Sciences, Humboldt University of Berlin, Albrecht-Thaer-Weg 5, 14195 Berlin, Germany
5
Department of Organic Farming and Cropping Systems, Faculty of Organic Agricultural Sciences, University of Kassel, Nordbahnhofstraße 1a, 37213 Witzenhausen, Germany
*
Author to whom correspondence should be addressed.
Agronomy 2022, 12(1), 48; https://doi.org/10.3390/agronomy12010048
Submission received: 9 November 2021 / Revised: 19 December 2021 / Accepted: 24 December 2021 / Published: 27 December 2021
Browse Figures
Review Reports Versions Notes

Abstract

:
Different methods have been proposed for in situ root-length density (RLD) measurement. One widely employed is the time-consuming sampling of soil cores or monoliths (MO). The profile wall (PW) method is a less precise, but faster and less laborious alternative. However, depth-differentiated functions to convert PW RLD estimates to MO RLD measurements have not yet been reported. In this study, we perform a regression analysis to relate PW results to MO results and determine whether calibration is possible for distinct crop groups (grasses, brassicas and legumes) consisting of pure and mixed stands, and whether soil depth affects this calibration. The methods were applied over two years to all crop groups and their absolute and cumulative RLD were compared using a linear (LR) and multiple linear (MLR) regression. PW RLD was found to highly underestimate MO RLD in absolute values and in highly rooted areas. However, a close agreement between both methods was found for cumulative root-length (RL) when applying MLR, highlighting the influence of soil depth. The level of agreement between methods varied strongly with depth. Therefore, the application of PW as the main RLD estimation method can provide reliable estimates of cumulative root distribution traits of cover crops.

1. Introduction

Root-length density (RLD) of cover crops is frequently assessed in crop studies due to its high relevance for crop functions such as nitrogen uptake from deep soil layers [1,2,3,4,5], erosion control [6] and crop productivity [7]. Different quantitative methods have been employed to measure RLD in the field, of which soil core sampling [4,5,8,9,10,11,12], field installation of minirhizotrons [1,2,3,9,13,14,15] and soil monolith (MO) extraction [8,9,16,17] are the most frequently used. These methods are considered to be either very time consuming and/or expensive, but believed to be the most accurate in representing real values [8,18,19].
Böhm [8] suggested that a faster, less expensive and less laborious alternative [20,21,22] could be used for RLD estimation, the profile wall (PW) method. According to Böhm [8], relating PW estimations of RLD with MO measurements could help finding conversion factors to obtain similarly accurate root length. Difficulties related to the PW method, however, include its low RLD estimations compared to other techniques. In his studies to overcome such limitations, Lohmann [23] performed a comparative analysis of PW and MO, and determined a general conversion factor of 1 for faba beans (Vicia faba L.). Köpke [19] in turn, suggested to multiply the PW root lengths of oats (Avena sativa L. cv. Leanda) by 2.06 if PW RLU were counted within 8 weeks after sowing. The author reported a linear decrease of conversion factor at later plant development stages, because of stronger root development at 12 and 13 weeks after sowing. Gäth and Meuser [24] later reported a conversion factor between both methods that varies with the vegetation periods of sugar beets (Beta vulgaris subsp. Vulgaris L.). To have monoliths extracted at several plant stages requires high expenditure of time and labor, and the abovementioned studies demonstrate the unreliability of one mean conversion factor because it cannot do justice to the crops’ temporal dynamics.
When a temporal analysis is not possible, other factors such as the influence of soil depth on the comparison of PW and MO were already shown to be useful. In a novel attempt, Böhm [8] compared root length from PW and MO RLD for maize (Zea mays L.) at different depths and, although he did not develop any calibration tool, his study identified the necessity for finding useful predicting functions between both methods to overcome the difficulties involved in RLD quantification.
Regression analysis has been widely used in comparative studies [23,24] and in the calibration of root quantification methods [14,25,26,27,28,29,30,31]. Böhm performed a regression analysis between root counts from PW and RLD from MO as a function of soil bulk density, however, only within topsoil layers, and only for spring barley (Hordeum vulgare L.). No regression analysis between PW and MO can be found applied to cover crops or that accounts for RLD changes with soil depth.
Cover crops are gaining importance as their use has numerous benefits including improved soil health, reduced soil erosion, and weed suppression [32]. Root data of cover crops are more and more needed to support the knowledge of the positive impacts that a high RLD of cover crops have on the level of shoot nitrogen uptake and nitrate content in the soil [7]. Therefore, the present study works on a novel dataset of RLD recorded for single and mixed cover crops using both PW and MO methods in the same experimental period.
This paper analyzes RLD estimations obtained with the PW method and RLD measurements performed with the MO method by means of a regression analysis of both absolute RLD values (cm/cm3) and relative distribution of root length (RL) across the soil profile; in this paper referred as cumulative RL. The studied crops consist of pure and mixed stands grouped into three different crop families: Gramineae, Leguminosae and Brassicaceae.
The purpose of this study was to relate both methods to each other for each crop group using regression models, and to investigate the role of soil depth in data distribution, evaluating its contribution to the regression functions’ accuracy using absolute and cumulative values. This study aims, as well, at proposing an alternative to the development of a mean conversion factor, demonstrated to be a weak solution when PW and MO are not compared following crops’ temporal dynamics. Thus, because in the present experiment root-length estimation in different plant stages was not possible to record, we hypothesize that a regression model is a good alternative for calibrating PW and MO RLD.

2. Materials and Methods

2.1. Experimental Design and Location

The field experiment was set up as a randomized complete block design with four blocks, of which three blocks (36 plots) were analyzed for root-length density (RLD). The experiment was carried out in 2018/2019 with plot size of 1.5 m × 12.5 m, and in 2019/2020 with plot size 1.5 m × 20 m, inserted within the crop rotation of the farm in which the experiment was performed, as also described by Kemper et al. [33]. A plot seeder with row distance of 17 cm was used on 12 August 2018 and 14 August 2019 for sowing. Separate plots were sown with single and mixed cover crops belonging to three different crop families, and for the present analysis, they were grouped accordingly: Gramineae (grasses group), Brassicaceae (brassicas group) and Leguminosae (legumes group). In mixed stands, crop group was determined on the basis of the dominant crop at the time of root sampling (Table 1). In mixtures, competition mechanisms were attributed to the resulting dominance of one or other mixture component, a process in which plant canopy and/or root system of one crop develops more significantly than the other [34,35,36,37], which for this study, was assessed by determining the partial land equivalent ratio (PLER) [38].
The experiment was performed at the research station for organic farming “Wiesengut”, located in the Sieg lowlands near Hennef (7°17′ East, 50°48′ North) about 65 m above sea level. The site is characterized by a flusivol with a silt-loam soil layer of 60 cm to 120 cm thickness over gravel, in a region with fluctuating groundwater level. The mean annual precipitation at the experimental site is 840 mm with a mean temperature of 10.3 °C over the experimental years. Precrop in both years was faba bean. After harvesting the precrop, the soil was ploughed to 23 cm depth and the seed bed was prepared with a rotary harrow. Hand and mechanical weeding were carried out during crop establishment, and field irrigation was carried out with a sprinkler, applying, in 2018, 50 mm in one application before sowing, and 54 mm in three applications after sowing. In 2019, 30 mm were irrigated in one application before, and 12 mm in one application after sowing.

2.2. Profile Wall Method

The profile wall method was applied according to Böhm [8], as described by Kemper et al. [33], in which a trench of 1.2 m depth and 1.0 m width was opened along the plot’s short end with an excavator. In every plot, the soil profile was manually smoothed with a sharp-edged spade and chisel. Subsequently, a toothed scraper was used to uniformly remove little amounts of soil by making a diagonal scrapping in both directions. Directly afterwards, a battery-operated water sprayer was used to complete the procedure of gently removing around 0.5 cm of soil from the wall to expose its roots. After spraying, a 100 cm × 100 cm metal frame with 5 × 5 cm grids was placed and fixed on the profile wall. The length of the exposed roots was estimated by counting the number of root-length units (RLU) of 0.5 cm inside each grid. Root-length density per soil volume (cm/cm3) was calculated by dividing the RLU sum of each grid by 12.5 cm3 (5 cm × 5 cm × 0.5 cm).
Root counting in the PW method took place from mid to end of October of both experimental years, and was performed by a different person each year. In 2018, the trench was refilled and re-opened between the first and second method repetitions, while in 2019, the trench remained open due to wet conditions. In March 2018, the trench was reopened 50 cm further into the plot and in March 2019, plots within the still open trench had 50 cm of soil removed from the profile wall to have an undisturbed counting surface. RLU were counted separately for large-sized vertical biopores and bulk soil, however, for this study they were combined for the whole plot.

2.3. Monolith Method

The MO method was performed as described by Böhm [18]. Monoliths were extracted on a horizontal plane from each plot in both experimental years in 10 cm depth levels to maximum rooting depth: in October 2018, two monoliths with dimensions of 20 cm × 10 cm × 10 cm, and in October 2019, two monoliths in the topsoil layers (0–30 cm) and three monoliths in the subsoil layers (below 30 cm) with dimensions of 17 cm × 10 cm × 10 cm, always next to each other. The monoliths were extracted until maximum soil depth of each plot before gravel started to appear, and then stored at 5 °C until being washed out for soil removal. The washing process consisted in first soaking the monoliths in water in a 10-liter bucket, then the water was repeatedly poured through a sieve tower with different fine sieves, so straw and finer roots could be caught and separated. This process was repeated with the same bucket, using a hand shower to break soil crumbles and loosen all roots until it was empty. The sieve tower contained sieves of 4.0 mm, 2.0 mm, and 1.0 mm mesh size in 2018, and additional sieves of 0.71 mm, 0.63 mm and 0.5 mm in 2019. After that, the contents of the sieves were transferred to another bucket and poured through a funnel into a small sieve (mesh size 0.5 mm) to facilitate root transfer to small plastic containers that were later (cold) stored. Non-root materials were removed manually with tweezers. To determine the root-length density and the root diameter distribution, each sample was poured on a 297 × 420 mm glass dish and scanned with an Epson Expression 12000XL flatbed scanner, calibrated for determination of RLD with WinRHIZOTM [39].

2.4. Statistical Analysis

R version 4.0.4 [40] was used for data analysis. To determine the best method for estimating MO RLD on the basis of PW RLD, four regression models were applied for both absolute and cumulative RLD values, two of which were linear and two were non-linear models (Tables S1 and S2). The non-linear models were considered to present overfitting (see Supplementary Materials) [41], and are therefore not further presented or discussed. The linear models were:
(1)
Simple linear regression (LR)
Y = a 0 + a 1 ( x )
(2)
Multiple linear regression (MLR)
Y = a 0 + a 1 ( x ) + a 2 ( z )
where Y is root-length density (RLD) in cm/cm3 from MO method,   x is root-length density (RLD) in cm/cm3 from PW method, and z is soil depth in cm, while a 0 , a 1 and a 2 are coefficients to be estimated from the data.
Before the application of the regression models, cumulative RL was calculated by determining each absolute RLD proportion in relation to the total RL of the soil profile, and adding each value to the sum of previous depths. Absolute and cumulative data were then split into two groups, the first one consisting in 2/3 of the dataset, to be used as model training data, and the second, 1/3 of the dataset, to be used as testing data. The data split was performed using a random stratification within crop species and soil depth in order to represent each crop, experimental year and soil depth in both subsets.
The training dataset was used to fit the regression models and assess the best fitting equation using Akaike’s information criterion (AIC) [42] as the evaluation metric in both absolute data (RLD) and cumulative data (RL). The regression equations were then applied to the testing data as a calibration tool to assess their ability in estimating MO RLD or RL using the equation parameters. Root mean squared error (RMSE) [43] and mean absolute error (MAE) were assessed between calculated and measured MO RLD or RL [23]. Additionally, the coefficient of determination (R2) was computed in both training and testing datasets.

3. Results

MO and PW methods resulted in overall higher absolute RLD values, higher standard deviation (sd) and larger deviations between PW and MO methods in the first 30 cm of soil compared to deeper layers. In the topsoil (0–30 cm), grasses presented the highest mean absolute RLD and the greater difference between methods, while legumes had the lowest mean absolute RLD and the smaller difference between methods. In the subsoil (30–100 cm), brassica crops presented higher differences between PW and MO than grasses and legumes. For legumes, methods where similarly close in the subsoil, and for grasses, the agreement tended to increase consistently, up to 100 cm (Table 2). In cumulative data, grasses and legumes reached similar root distribution already at 30 cm, but differed in their level of agreement between methods. Grasses, followed by brassicas, showed the highest agreement between methods at all depths, while legumes had the highest disagreements between methods. Differences in cumulative values between PW and MO, however, were very small for all crops, and values were mostly slightly negative, indicating a certain overestimation from PW (Table 2).

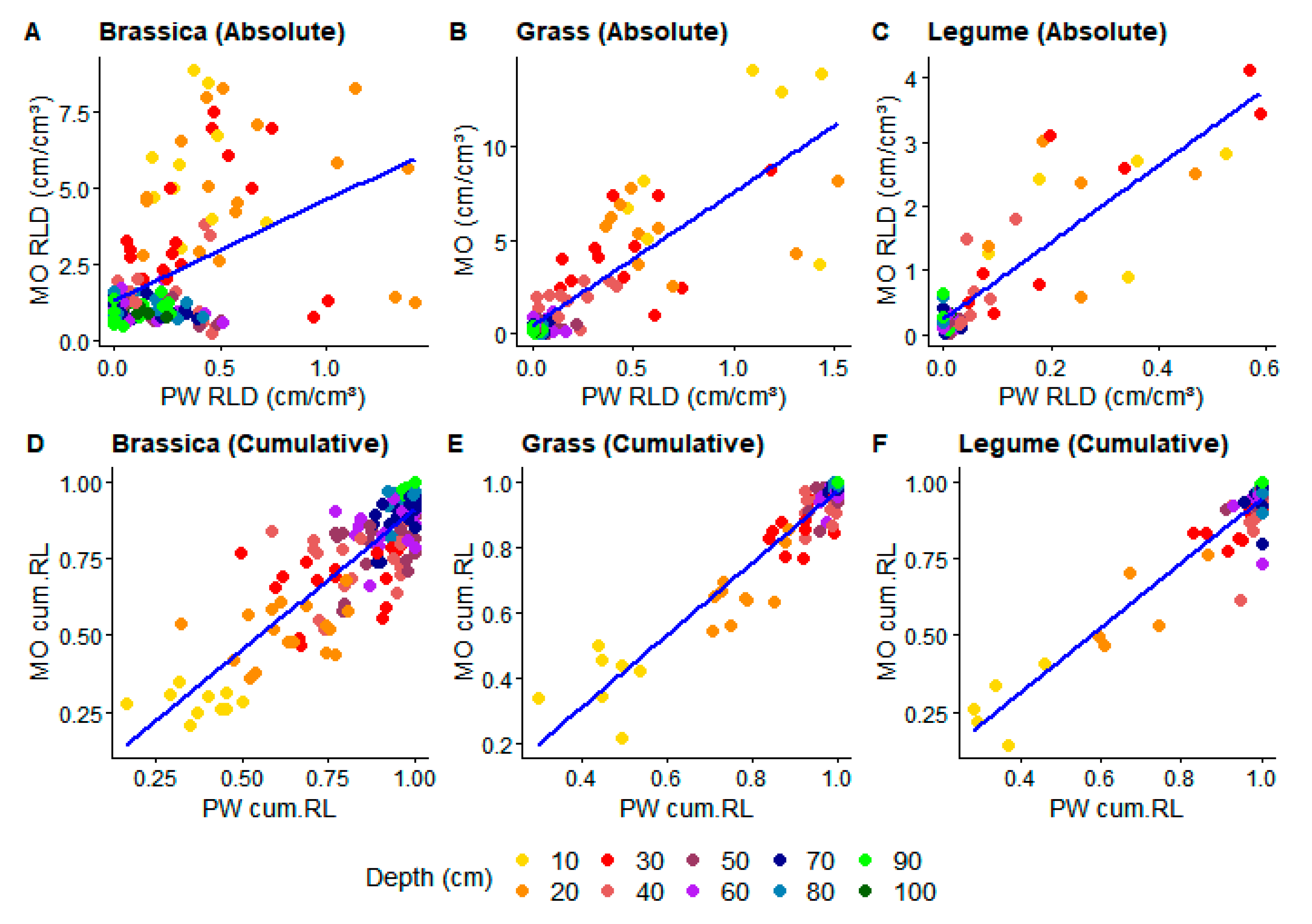
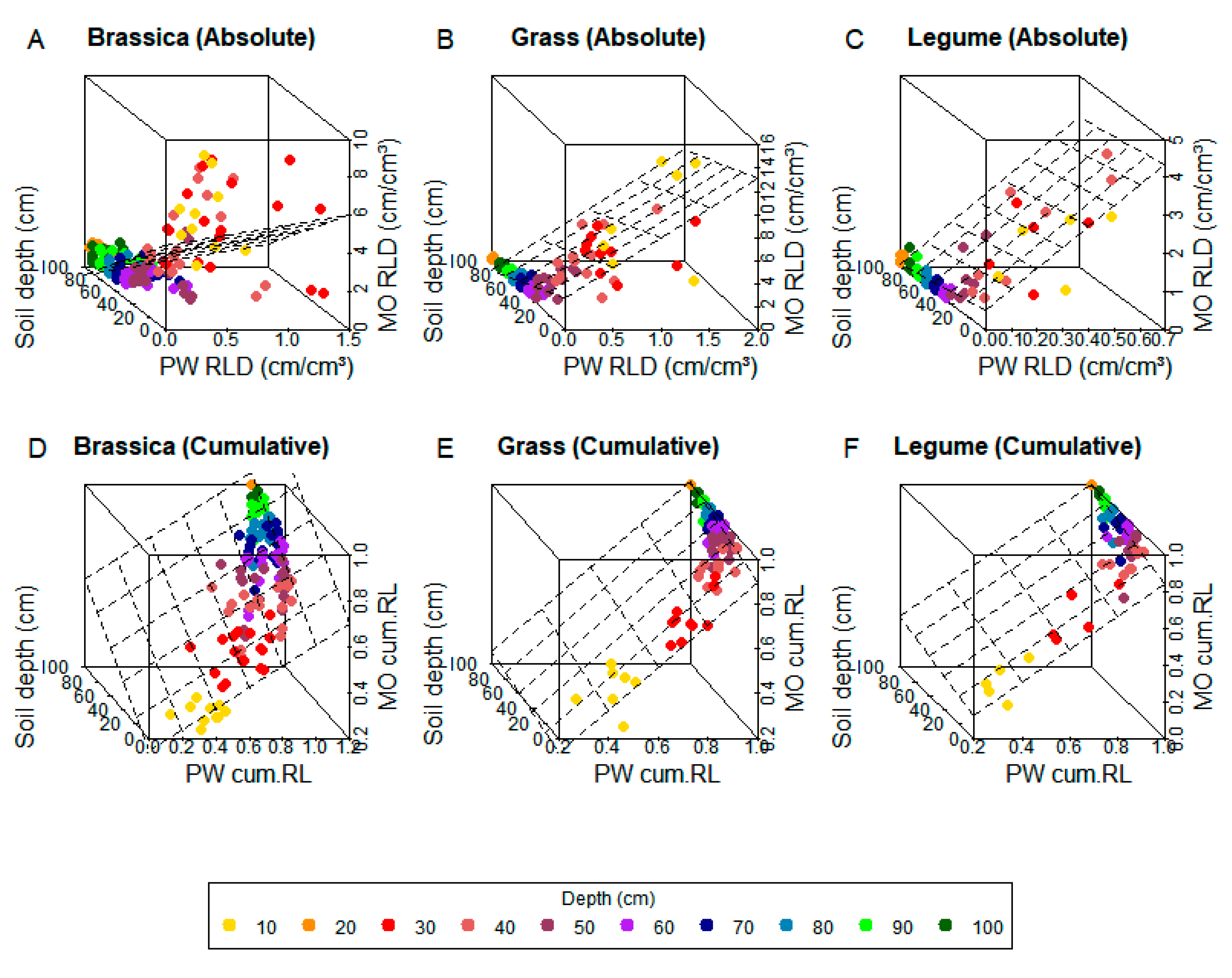
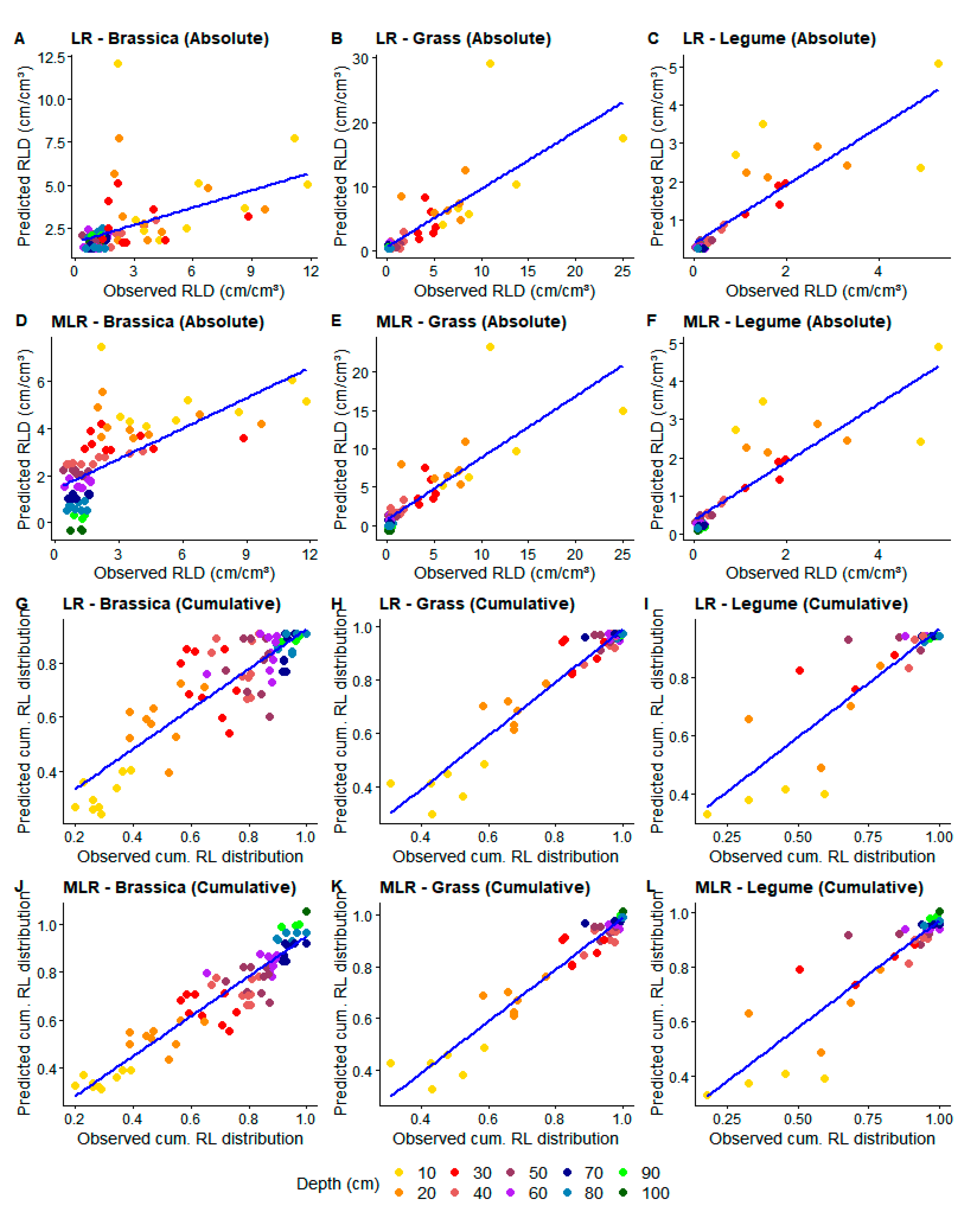
3.1. Model Fitting

The results after data splitting show a significant correlation (p < 0.05) between MO and PW RLD in training data for both LR and MLR and both absolute and cumulative data (Table 3). In absolute data, MLR presented higher R2 and lower AIC as well as higher visual data fitting (Figure 1A,B and Figure 2A,B) than LR for grasses and brassica crops (Table 3). Legumes showed similar data fit for both models in absolute data (Table 3, Figure 1C and Figure 2C).
In cumulative data, all crops showed higher R2 and lower AIC (Table 3) when fitted with MLR, but only for brassica crops was there a pronounced difference compared to LR. Better graphical representation of subsoil RLD was achieved using MLR in all crops (Figure 1D–F and Figure 2D–F) when compared to LR. Cumulative data in general presented better fit than absolute data, independently of regression function. This is visible in the very small or negative intercepts of both models (Table 3), indicating that PW RLD is more predictive of MO RLD for cumulative data than for absolute data.

3.2. Model Testing

Model validation in test data showed a significant correlation (p < 0.05) between predicted and measured RLD from both models in all crop groups and both cumulative and absolute data (Table 4). In absolute data, calculated and measured RLD using MLR presented higher R2, smaller MAE/RMSE and greater accuracy than when using LR for grasses and brassica (Table 4, Figure 3A,B,D,E), even though little agreement is still visible at 10–20 cm (Figure 3D,E).
For legumes, both regression models performed similarly (Table 4), with greater accuracy at subsoil (30–100 cm) and lower accuracy at topsoil (0–30 cm) (Figure 3C,F). In cumulative data, MLR showed higher performance, with higher R2 for all crops than LR, even though MAE and RMSE did not differ much. Calculated and measured cumulative RLD, contrary to the results for absolute data, seem to have a more homogeneous agreement throughout the soil profile for all crops except legumes (Figure 3G–L as compared to Figure 3A–F). When applying MLR in grasses and brassica, the homogeneity and agreement increased even more (Figure 3J,K)

4. Discussion

PW RLD highly underestimated MO RLD and cum. RL in the topsoil, while in the subsoil, values of the two methods were closer. This indicates that highly rooted soil layers tend to have little agreement between methods (Table 2). The results disagree with findings of Böhm [8], regarding root-length estimations from PW being close to half of the MO measurements throughout the whole soil profile. Böhm, however, experimented with maize, and no studies comparing MO and PW results were found for the cover crops, as used in the present study.
Crops within the same group (Table 1) are frequently reported to present similar rooting behavior [1,12,44], but in our study, the low accuracy of the tested models for absolute data indicates that the number of datasets used, or replicates tested for each group, were not sufficient to capture the crop specific features. As it may be assumed that the high deviations between methods in the groups of brassica and grasses might be related to the amount of mixtures present, further tests related to this question were performed, and leaving the mixtures out did not improve the models, as well as comparisons across all crop species resulted in worse fitting (results not shown). Rooting behavior of dominant crops within mixtures might as well need further investigation for future calibration attempts.
Legumes showed high model accuracy and, while this may be related to the absence of mixtures (Table 1), the high accuracy is still surprising. Accuracy of calibration functions often depends on sample size, especially when dealing with mean observations [24], and legumes had the smallest sample size of the three groups analyzed. Also, lupin and crimson clover had contrasting root distributions throughout soil depth [33].
Further limitations in relating PW and MO methods involve human factors intrinsic to RLD estimation with PW. It is common for small roots to clump together in highly rooted regions, an obstacle to individual length estimation [8,26], especially when performed by two different people and at different sites or time points. Such factors mean different soil conditions for each person, affecting the real amount of soil removed by spraying, as well as different root status, influencing visual estimation of RLD.
Additionally, a lack of small sieves (0.71 mm, 0.63 mm, 0.5 mm) in 2018, for the MO root washing step potentially induced MO RLD underestimation. Another potential source of error in our study was the sampling interval. Sinclair and Seligman [45] suggest that model evaluations should be conducted during the entire plant growth cycle such as performed by Kücke et al. [46]. In our study, however, MO RLD was recorded only once due to the method’s labor-intensive nature. While our study attempts to compare methods in a generic sense for a wide scope of crops, it still fails to cover time and space variation, important parameters for real-world representation [45,47].
The reproducibility of the calibration functions here presented for absolute values, therefore, cannot be assured. Regression analysis, however, provided important insights about the influence of soil depth on the comparison between PW and MO. As mentioned before, the level of agreement between methods varies with depth, and can be better seen when visualizing data in a 3D plane (Figure 2). This explains why, for all crops, MLR was able to best describe the relationship between PW and MO in training data (Table 3, Figure 1 and Figure 2) and calculate MO absolute RLD with higher accuracy than LR at the testing phase (Table 4, Figure 3). The highly scattered data of brassicas is also a good indicator that LR might be, as well, less appropriate for deep rooting crops (Figure 1A).
Comparisons between other root-length estimation methods have already highlighted the importance of considering depth distribution [3,14,27,48], and future steps in the development of a calibration function between PW and MO techniques point to this direction. However, as MLR still presented certain limitations in describing depth-dependent variation (Figure 2A–C, Figure 3D–F), its utility for field experiments is limited. MLR fails to calibrate both methods in upper soil layers where RLD is higher, which is possibly why R2 for absolute data in model fitting and testing (Table 3 and Table 4) is low compared to other calibration studies [25,46,49,50].
In training data, high intercept values for MLR (Table 3) and high data scattering (Figure 2A–C) already indicate a general lack of agreement between both methods, while in test data, the error (MAE/RMSE) relative to measured values is high (Table 4). Whether or not such errors are acceptable will depend on the research objectives. Studies focusing on the assessment of root growth differences between crop species might benefit from PW estimations of absolute RLD, while converting it into measurements from other methods using calibration functions can lead to errors. A higher accuracy of absolute value predictions still might be reached with more experimental replications and model validation on unseen data, as performed by Chopart et al. [51].
Relatively high agreement between methods was achieved when comparing cumulative RL values, for which generally high R2 and low MAE/RMSE were found using MLR (Table 3 and Table 4). Grasses and brassica crops showed higher predictive power while legumes had little improvement compared to absolute data, indicating that categories made of more than two crops are recommended for the development of a good conversion model, regarding not only absolute, but also cumulative data.
The good performance for grasses and brassica can be explained by the fact that calculating cumulative RLD through depth minimizes data variation, as it incurs in loss of information, resulting in more subtle changes from one soil layer to another. Cumulative root distribution can be used as a measure of crop performance [3] or as a tool for rooting type characterization [48], demonstrating the utility of such data. In our study, the high depth-dependent RLD variations for grasses and brassica (Figure 3G,H,J,K) seem to reduce in cumulative data when comparing measured and calculated RLD. This demonstrates the potential of root-length estimation with the PW method for studies focusing on crop-specific root-depth frequency.
Further studies on the relationship between PW and MO RLD estimations might benefit from more in-depth analyses about other potential factors involved in PW RLD estimations in highly-rooted areas, such as root orientation [49,51,52], crop management [29] and crop-specific root behavior inside mixtures. When working with absolute data, a more comprehensive approach where a different calibration function is developed for each specific soil layer might as well bring other perspectives to MO and PW comparisons.

5. Conclusions

Profile wall and monolith methods were found to have high disagreements in their root-length density measurements, where values can be greatly underestimated if profile wall is chosen as the main root-length estimation technique. Underestimations were found for crop groups containing more mixtures and crops tested for only one year (Table 1), especially regarding absolute data. Our main findings from the regression analysis are that a simple linear regression is not able to describe the relationship between both employed methods in a sufficiently accurate manner, even though the relationship between PW and MO is significant. It is consequently inefficient in predicting root-length density absolute values. It may still be used to compare cumulative values, but its performance is limited because it is unable to capture root-length density’s covariation with depth.
Soil depth was found in this study to play a very important role in determining the degree of agreement between profile wall estimations and monolith measurements of root-length density. In our study, the level of agreement between methods was inversely proportional to rooting intensity, making it harder to calibrate estimations with simple linear regressions for most crops tested here. All crop groups showed higher mean root-length densities in the topsoil compared to the subsoil, independent on the estimation method used. Applying a multiple linear regression to that data allowed this depth-dependency to be better captured, especially in deep rooted crops. However, its low performance metrics indicated that it cannot be reliable in calibrating both techniques. The difficulties in relating both methods resulting from this study leads us to conclude that profile wall estimations of root-length density from cover crops in absolute values tend to strongly deviate from monolith measurement values, and therefore, are difficult to convert.
On the other hand, when absolute root-length density was converted into cumulative root distribution, all crops presented a very high agreement between methods. A multiple linear regression was able to best describe the relationship, with very small errors and high accuracy between predictions and measurements. These results indicate that, for studies aiming at visualizing root distribution patterns of cover crops, the adoption of the profile wall as the main method can in fact be recommended, especially regarding grasses, because its estimations were very close to that measured when extracting soil monoliths. We found as well that the profile wall method has potential for estimating accurately the cumulative root distribution of mixed cover crops, and of entire crop groups containing mixtures. Although this paper explored possibilities with regression models to compare methods and predict root-length densities, many dataset improvements, and further validations in data acquired from a different experimental site (differing soil and climate conditions), timepoint and/or treatment would be necessary to present them as applicable tools in future crop root studies.

Supplementary Materials

The following are available online at https://www.mdpi.com/article/10.3390/agronomy12010048/s1, Table S1: Coefficients and quality metrics of non-linear regression models in train dataset, by crop group and data type; Table S2: Performance metrics of regression models in test dataset, by crop group and data type.

Author Contributions

M.A. and T.K. conceived the idea, planned the research and designed the experiments. R.K., P.M. and T.A.B. conducted the experiments in the field and collected the data. T.A.B. analyzed the data and wrote the article. M.A., T.F.D., T.K. and R.K. contributed to data interpretation, writing and editing of the article. All authors have read and agreed to the published version of the manuscript.

Funding

The project was supported by funds from the Federal Ministry of Food and Agriculture (BMEL), funding number 28180E024, based on a decision of the parliament of the Federal Republic of Germany via the Federal Office for Agriculture and Food (BLE) under the Federal Program for Ecological Farming and Other Forms of Sustainable Agriculture.

Acknowledgments

We thank the technical staff of the ‘Wiesengut’ organic farming research station and our students for help in the field and laboratory.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Kristensen, H.L.; Thorup-Kristensen, K. Root growth and nitrate uptake of three different catch crops in deep soil layers. Soil Sci. Soc. Am. J. 2004, 68, 529–537. [Google Scholar] [CrossRef]
  2. Thorup-Kristensen, K. Root development of nitrogen catch crops and of a succeeding crop of broccoli. Acta Agric. Scand. B Soil Plant Sci. 1993, 43, 58–64. [Google Scholar] [CrossRef]
  3. Thorup-Kristensen, K. Are differences in root growth of nitrogen catch crops important for their ability to reduce soil nitrate-N content, and how can this be measured? Plant Soil 2001, 230, 185–195. [Google Scholar] [CrossRef]
  4. Barraclough, P.B. Root growth, macro-nutrient uptake dynamics and soil fertility requirements of a high-yielding winter oilseed rape crop. Plant Soil 1989, 119, 59–70. [Google Scholar] [CrossRef]
  5. Wendling, M.; Büchi, L.; Amossé, C.; Sinaj, S.; Walter, A.; Charles, R. Influence of root and leaf traits on the uptake of nutrients in cover crops. Plant Soil 2016, 409, 419–434. [Google Scholar] [CrossRef] [Green Version]
  6. De Baets, S.; Poesen, J.; Gyssels, G.; Knapen, A. Effects of grass roots on the erodibility of topsoils during concentrated flow. Geomorphology 2006, 76, 54–67. [Google Scholar] [CrossRef]
  7. Sainju, U.M.; Singh, B.P.; Whitehead, W.F. Cover crop root distribution and its effects on soil nitrogen cycling. J. Agron. 1998, 90, 511–518. [Google Scholar] [CrossRef]
  8. Böhm, W. In situ estimation of root length at natural soil profiles. J. Agr. Sci. 1976, 87, 365–368. [Google Scholar] [CrossRef]
  9. Böhm, W.; Maduakor, H.; Taylor, H.M. Comparison of five methods for characterizing soybean rooting density and development 1. J. Agr. 1977, 69, 415–419. [Google Scholar] [CrossRef]
  10. Gao, Y.; Duan, A.; Qiu, X.; Liu, Z.; Sun, J.; Zhang, J.; Wang, H. Distribution of roots and root length density in a maize/soybean strip intercropping system. Agr. Water Manag. 2010, 98, 199–212. [Google Scholar] [CrossRef]
  11. Gregory, P.J.; Reddy, M.S. Root growth in an intercrop of pearl millet/groundnut. Field Crops Res. 1982, 5, 241–252. [Google Scholar] [CrossRef] [Green Version]
  12. Yu, Y.; Loiskandl, W.; Kaul, H.-P.; Himmelbauer, M.; Wei, W.; Chen, L.; Bodner, G. Estimation of runoff mitigation by morphologically different cover crop root systems. J. Hydrol. 2016, 538, 667–676. [Google Scholar] [CrossRef] [Green Version]
  13. Upchurch, D.R. Conversion of minirhizotron-root intersections to root length density. In Minirhizotron Observation Tubes: Methods and Applications for Measuring Rhizosphere Dynamics; Taylor, H., Ed.; ASA CSSA SSSA: Madison, WI, USA, 1987; pp. 51–65. [Google Scholar]
  14. Parker, C.J.; Carr, M.K.V.; Jarvis, N.J.; Puplampu, B.O.; Lee, V.H. An evaluation of the minirhizotron technique for estimating root distribution in potatoes. J. Agric. Sci. 1991, 116, 341–350. [Google Scholar] [CrossRef]
  15. Buckland, S.T.; Campbell, C.D.; Mackie-Dawson, L.A.; Horgan, G.W.; Duff, E.I. A method for counting roots observed in minirhizotrons and their theoretical conversion to root length density. Plant Soil 1993, 153, 1–9. [Google Scholar] [CrossRef]
  16. Liao, R.; Bai, Y.; Liang, H.; An, S.; Ren, S.; Cao, Y.; Le, Z.; Lu, J.; Liu, J. Root growth of maize as studied with minirhizotrons and monolith methods. Arch. Agr. Soil Sci. 2015, 61, 1343–1356. [Google Scholar] [CrossRef]
  17. Li, L.; Sun, J.; Zhang, F.; Guo, T.; Bao, X.; Smith, F.A.; Smith, S.E. Root distribution and interactions between intercropped species. Oecologia 2006, 147, 280–290. [Google Scholar] [CrossRef]
  18. Böhm, W. Methods of Studying Root Systems; Springer: Berlin/Heidelberg, Germany, 1979. [Google Scholar]
  19. Köpke, U. Ein Vergleich von Feldmethoden zur Bestimmung des Wurzelwachstums Landwirtschaftlicher Kulturpflanzen. Ph.D. Thesis, University of Göttingen, Göttingen, Germany, 1979. [Google Scholar]
  20. Gregory, P.J. Plant roots: Growth, activity and interaction with soils. Ann. Bot. 2007, 100, 151–152. [Google Scholar]
  21. Gaiser, T.; Perkons, U.; Küpper, P.M.; Puschmann, D.U.; Peth, S.; Kautz, T.; Pfeifer, J.; Ewert, F.; Horn, R.; Köpke, U. Evidence of improved water uptake from subsoil by spring wheat following lucerne in a temperate humid climate. Field Crops Res. 2012, 126, 56–62. [Google Scholar] [CrossRef]
  22. Han, E.; Kautz, T.; Perkons, U.; Uteau, D.; Peth, S.; Huang, N.; Horn, R.; Köpke, U. Root growth dynamics inside and outside of soil biopores as affected by crop sequence determined with the profile wall method. Biol. Fertil. Soils 2015, 51, 847–856. [Google Scholar] [CrossRef]
  23. Yang, J.M.; Yang, J.Y.; Liu, S.; Hoogenboom, G. An evaluation of the statistical methods for testing the performance of crop models with observed data. Agric. Syst. 2014, 127, 81–89. [Google Scholar] [CrossRef]
  24. St-Pierre, N.R. Comparison of model predictions with measurements: A novel model-assessment method. J. Dairy Sci. 2016, 99, 4907–4927. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  25. Delory, B.M.; Weidlich, E.W.A.; Meder, L.; Lütje, A.; Duijnen, R.; Weidlich, R.; Temperton, V.M. Accuracy and bias of methods used for root length measurements in functional root research. Methods Ecol. Evol. 2017, 8, 1594–1606. [Google Scholar] [CrossRef] [Green Version]
  26. Goubran, F.H.; Richards, D. The estimation of root length in samples and sub-samples: Comparison of a visual and an automatic method. Plant Soil 1979, 52, 77–83. [Google Scholar] [CrossRef]
  27. De Ruijter, F.J.; Veen, B.W.; Van Oijen, M. A comparison of soil core sampling and minirhizotrons to quantify root development of field-grown potatoes. Plant Soil 1996, 182, 301–312. [Google Scholar] [CrossRef]
  28. Ephrath, J.E.; Silberbush, M.; Berliner, P.R. Calibration of minirhizotron readings against root length density data obtained from soil cores. Plant Soil 1999, 209, 201–208. [Google Scholar] [CrossRef]
  29. Vepraskas, M.J.; Hoyt, G.D. Comparison of the trench-profile and core methods for evaluating root distributions in tillage studies. J. Agr. 1988, 80, 166–172. [Google Scholar] [CrossRef]
  30. Dusserre, J.; Audebert, A.; Radanielson, A.; Chopart, J.-L. Towards a simple generic model for upland rice root length density estimation from root intersections on soil profile. Plant Soil 2009, 325, 277–288. [Google Scholar] [CrossRef]
  31. Samson, B.K.; Sinclair, T.R. Soil core and minirhizotron comparison for the determination of root length density. Plant Soil 1994, 161, 225–232. [Google Scholar] [CrossRef]
  32. Osipitan, O.A.; Dille, J.A.; Assefa, Y.; Knezevic, S.Z. Cover Crop for Early Season Weed Suppression in Crops: Systematic Review and Meta-Analysis. Agron. J. 2018, 110, 2211–2221. [Google Scholar] [CrossRef] [Green Version]
  33. Kemper, R.; Bublitz, T.A.; Müller, P.; Kautz, T.; Döring, T.F.; Athmann, M. Vertical root distribution of different cover crops determined with the profile wall method. Agriculture 2020, 10, 503. [Google Scholar] [CrossRef]
  34. Klimek-Kopyra, A.; Kulig, B.; Głąb, T.; Zając, T.; Skowera, B.; Kopcińska, J. Effect of plant intercropping and soil type on specific root length. Rom. Agr. Res. 2015, 221–230. [Google Scholar]
  35. De Wit, C.T.; Bergh, J.P.V.D. Competition between herbage plants. J. Agr. Sci. 1965, 13, 212–221. [Google Scholar]
  36. Grace, J.B.; Tilman, D. Perspectives on Plant Competition; Elsevier: Amsterdam, The Netherlands, 1990. [Google Scholar]
  37. Hauggaard-Nielsen, H.; Ambus, P.; Jensen, E.S. Temporal and spatial distribution of roots and competition for nitrogen in pea-barley intercrops—A field study employing 32P technique. Plant Soil 2001, 236, 63–74. [Google Scholar] [CrossRef] [Green Version]
  38. Mead, R.; Willey, R.W. The concept of a ‘Land Equivalent Ratio’ and advantages in yields from intercropping. Ex. Agric. 1980, 16, 217–228. [Google Scholar] [CrossRef] [Green Version]
  39. Regent Instruments Inc. WinRHIZOTM.; Regent Instruments Inc.: Quebec City, QC, Canada, 2017. [Google Scholar]
  40. R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021. [Google Scholar]
  41. Hawkins, D.M. The problem of overfitting. J. Chem. Inf. Comput. Sci. 2004, 44, 1–12. [Google Scholar] [CrossRef]
  42. Akaike, H. Information theory and an extension of the maximum likelihood principle. In Proceedings of the 2nd International Symposium on Information Theory, Tsahkadsor, Armenia, 2–8 September 1971; Petrov, B.N., Csaki, F., Eds.; Akademiai Kiado: Budapest, Hungary, 1998; pp. 267–281. [Google Scholar]
  43. Loague, K.; Green, R.E. Statistical and graphical methods for evaluating solute transport models: Overview and application. J. Contam. Hydrol. 1991, 7, 51–73. [Google Scholar] [CrossRef]
  44. Austin, E.E.; Wickings, K.; McDaniel, M.D.; Robertson, G.P.; Grandy, A.S. Cover crop root contributions to soil carbon in a no-till corn bioenergy cropping system. GCB Bioenergy 2017, 9, 1252–1263. [Google Scholar] [CrossRef] [Green Version]
  45. Sinclair, T.R.; Seligman, N. Criteria for publishing papers on crop modeling. Field Crops Res. 2000, 68, 165–172. [Google Scholar] [CrossRef]
  46. Kücke, M.; Schmid, H.; Spiess, A. A comparison of four methods for measuring roots of field crops in three contrasting soils. Plant Soil 1995, 172, 63–71. [Google Scholar] [CrossRef]
  47. Passioura, J.B. Simulation models: Science, snake oil, education, or engineering? J. Agron. 1996, 88, 690–694. [Google Scholar] [CrossRef]
  48. Bodner, G.; Loiskandl, W.; Hartl, W.; Erhart, E.; Sobotik, M. Characterization of cover crop rooting types from integration of rhizobox imaging and root atlas information. Plants 2019, 8, 514. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  49. Chopart, J.L.; Siband, P. Development and validation of a model to describe root length density of maize from root counts on soil profiles. Plant Soil 1999, 214, 61–74. [Google Scholar] [CrossRef]
  50. Heeraman, D.A.; Juma, N.G. A comparison of minirhizotron, core and monolith methods for quantifying barley (Hordeum vulgare L.) and fababean (Vicia faba L.) root distribution. Plant Soil 1993, 148, 29–41. [Google Scholar] [CrossRef]
  51. Chopart, J.-L.; Sine, B.; Dao, A.; Muller, B. Root orientation of four sorghum cultivars: Application to estimate root length density from root counts in soil profiles. Plant Root 2008, 2, 67–75. [Google Scholar] [CrossRef] [Green Version]
  52. Lopez-Zamora, I.; Falcão, N.; Comerford, N.B.; Barros, N.F. Root isotropy and an evaluation of a method for measuring root distribution in soil trenches. For. Ecol. Manag. 2002, 166, 303–310. [Google Scholar] [CrossRef]
Agronomy 12 00048 g001 550
Figure 1. Linear regression fitting between monolith and profile wall root-length density (RLD) in training data for absolute (A–C) and cumulative (cum.RL) data (D–F). Colors show soil depth (cm) of each value.
Figure 1. Linear regression fitting between monolith and profile wall root-length density (RLD) in training data for absolute (A–C) and cumulative (cum.RL) data (D–F). Colors show soil depth (cm) of each value.
Agronomy 12 00048 g001
Agronomy 12 00048 g002 550
Figure 2. Multiple linear regression 3D fitting between monolith and profile wall root-length density (RLD) with soil depth in training data for absolute (A–C) and cumulative (cum. LR) data (D–F). Colors show soil depth (cm) of each value.
Figure 2. Multiple linear regression 3D fitting between monolith and profile wall root-length density (RLD) with soil depth in training data for absolute (A–C) and cumulative (cum. LR) data (D–F). Colors show soil depth (cm) of each value.
Agronomy 12 00048 g002
Agronomy 12 00048 g003 550
Figure 3. Relationships between observed and predicted root-length density (RLD) using linear (LR) (A–C,G–I) and multiple linear regression (MLR) (D–F,J–L) for absolute (A–F) and cumulative (cum.RL) (G–L) data. Colors show soil depth (cm) of each value.
Figure 3. Relationships between observed and predicted root-length density (RLD) using linear (LR) (A–C,G–I) and multiple linear regression (MLR) (D–F,J–L) for absolute (A–F) and cumulative (cum.RL) (G–L) data. Colors show soil depth (cm) of each value.
Agronomy 12 00048 g003
Table
Table 1. Crops and mixtures used in the experiment. Crop group was determined according to crop family for single crops, and crop family of the dominant crop for mixtures. Grasses, Gramineae family; Brassica, Brassicaceae family and Legumes, Leguminosae family.
Table 1. Crops and mixtures used in the experiment. Crop group was determined according to crop family for single crops, and crop family of the dominant crop for mixtures. Grasses, Gramineae family; Brassica, Brassicaceae family and Legumes, Leguminosae family.
Crop/Mixture SpeciesCultivarDominant CropCrop GroupSeed
Quantity (kg/ha)
Winter rye (Secale cereale L.)Bonfire Grasses120
Bristle oat (Avena strigosa Schreb.)Pratex Grasses80
Blue lupin (Lupinus angustifolius L.)Boruta Legumes120
Crimson clover (Trifolium incarnatum L.)Linkarus Legumes30
Oil radish (Raphanus sativus L. var. oleiformis Pers.)Siletina Brassica25
Tillage radish (Raphanus sativus L. var. oleiformis Pers.)Deeptill Brassica12
Winter turnip rape (Brassica rapa L. var. silvestris (Lam.) Briggs)Jupiter Brassica15
Mixed crops
Oil radish/green rye Oil radishBrassica12.5/60
Oil radish/crimson clover Oil radishBrassica6.25/22.5
Oil radish/crimson clover/winter rye Oil radishBrassica8.5/10/40
Blue lupin/winter rye Winter ryeGrasses60/60
Blue lupin/winter rye Winter ryeGrasses90/30
Table
Table 2. Descriptive statistics of root-length density (RLD) measurements from profile wall (PW) and monolith (MO) methods for different crop categories and soil depths. Mean RLD is the mean value in cm/cm3 of all RLD absolute values, and Sd RLD is the standard deviation in cm/cm3 of all RLD absolute values. Mean cum. RL is the mean cumulative root-length distribution and Sd cum. RL is the standard deviation of the mean cumulative root-length distribution. Mean error is the mean difference between MO and PW. n is the number of observations for each depth.
Table 2. Descriptive statistics of root-length density (RLD) measurements from profile wall (PW) and monolith (MO) methods for different crop categories and soil depths. Mean RLD is the mean value in cm/cm3 of all RLD absolute values, and Sd RLD is the standard deviation in cm/cm3 of all RLD absolute values. Mean cum. RL is the mean cumulative root-length distribution and Sd cum. RL is the standard deviation of the mean cumulative root-length distribution. Mean error is the mean difference between MO and PW. n is the number of observations for each depth.
Crop
Family		Soil Depth
(cm)		Mean RLD
(cm/cm3)		Sd RLD
(cm/cm3)		Mean
cum. RL		Sd
cum. RL		Mean Error (cm/cm3) (abs.)Mean Error (cm/cm3) (cum.)n
MOPWMOPWMOPWMOPW
Brassicas106.401.043.600.890.2880.3620.060.085.36−0.0727
204.830.692.530.480.5070.6320.080.134.15−0.1327
303.780.442.360.330.6730.7930.090.143.34−0.1227
401.680.201.030.180.7490.8500.090.121.48−0.1027
501.000.140.320.150.8010.8910.080.100.86−0.0927
601.050.150.400.160.8560.9250.070.070.91−0.0727
700.990.110.330.130.9080.9500.060.050.88−0.0427
801.060.120.330.140.9560.9720.050.030.93−0.0225
901.050.130.340.100.9730.9860.030.010.91−0.0115
1001.020.120.210.061.0001.0000.000.000.900.009
Grasses1011.561.726.491.400.4420.4760.110.079.84−0.0318
205.680.981.950.630.6870.7730.090.064.70−0.0918
304.330.491.930.310.8660.9230.060.053.84−0.0618
401.540.160.840.140.9310.9650.040.031.38−0.0318
500.430.060.340.070.9490.9790.030.020.37−0.0318
600.370.040.300.050.9640.9880.030.010.32−0.0218
700.290.030.210.030.9760.9940.020.010.26−0.0218
800.250.020.170.020.9860.9970.020.000.23−0.0118
900.250.020.140.020.9920.9990.010.000.23−0.0112
1000.200.010.110.011.0001.0000.000.000.190.009
Legumes102.950.831.660.890.3380.4360.140.102.12−0.1012
202.270.521.020.440.6020.7530.140.121.75−0.1512
301.890.251.230.180.8120.9240.110.061.64−0.1112
400.610.060.520.040.8860.9720.090.030.55−0.0912
500.160.010.100.010.9100.9850.080.030.15−0.0812
600.160.010.090.010.9310.9910.070.020.15−0.0612
700.180.000.110.010.9480.9940.050.010.18−0.0511
800.200.010.150.010.9680.9970.030.010.19−0.0310
900.080.000.660.010.9890.9990.010.000.23−0.018
1000.090.000.320.011.0001.0000.000.000.190.005
Table
Table 3. Coefficients and quality metrics of linear regression models in training dataset, by crop group and data type. RLD, root-length density and cum. RL, cumulative root-length. Models are: simple linear model ( Y = a 0 + a 1 ( x ) ) and multiple linear model ( Y = a 0 + a 1 ( x ) + a 2 ( z ) ), where Y, monolith method RLD or cum. RL, x , profile wall RLD or cum. RL, z , soil depth (cm); a 0 , intercept; a 1 , coefficient to multiply by x and a 2 , coefficient to multiply by z . AIC. Akaike’s information criterion for model comparison. R2, coefficient of determination and * indicates that the correlation between PW and MO was significant, with a p-value < 0.05.
Table 3. Coefficients and quality metrics of linear regression models in training dataset, by crop group and data type. RLD, root-length density and cum. RL, cumulative root-length. Models are: simple linear model ( Y = a 0 + a 1 ( x ) ) and multiple linear model ( Y = a 0 + a 1 ( x ) + a 2 ( z ) ), where Y, monolith method RLD or cum. RL, x , profile wall RLD or cum. RL, z , soil depth (cm); a 0 , intercept; a 1 , coefficient to multiply by x and a 2 , coefficient to multiply by z . AIC. Akaike’s information criterion for model comparison. R2, coefficient of determination and * indicates that the correlation between PW and MO was significant, with a p-value < 0.05.
Data
Type		Crop
Group		ModelAICR2 a 0 a 1 a 2
Absolute
data
(RLD)		BrassicasSimple linear614.360.20 *1.323.28-
Multiple linear552.040.48 *4.411.08−0.05
GrassesSimple linear414.510.68 *0.457.10-
Multiple linear400.590.72 *2.835.18−0.04
LegumesSimple linear100.260.76 *0.255.99-
Multiple linear100.050.77 *0.535.46−0.004
Cumulative
data
(cum. RL)		BrassicasSimple linear−236.340.72 *−0.011.10-
Multiple linear−325.690.85 *0.920.470.004
GrassesSimple linear−309.700.90 *−0.131.10-
Multiple linear−327.270.92 *−0.060.950.001
LegumesSimple linear−160.310.89 *−0.101.05-
Multiple linear−172.190.91 *−0.050.900.002
Table
Table 4. Performance metrics of regression models in test dataset, by crop group and data type. RLD, root-length density and cum. RL, cumulative root-length. R2, coefficient of determination and * indicates that the correlation between predicted and measured RLD or cum. RL was significant, with a p-value < 0.05. MAE, mean absolute error, and RMSE, root mean absolute error.
Table 4. Performance metrics of regression models in test dataset, by crop group and data type. RLD, root-length density and cum. RL, cumulative root-length. R2, coefficient of determination and * indicates that the correlation between predicted and measured RLD or cum. RL was significant, with a p-value < 0.05. MAE, mean absolute error, and RMSE, root mean absolute error.
Data
Type		Crop
Group		ModelR2MAERMSE
Absolute
data
(RLD)		BrassicasSimple linear0.23 *1.372.22
Multiple linear0.42 *1.251.86
GrassesSimple linear0.63 *1.413.13
Multiple linear0.68 *1.352.63
LegumesSimple linear0.73 *0.390.71
Multiple linear0.73 *0.390.70
Cumulative
data
(cum. RL)		BrassicasSimple linear0.76 *0.090.11
Multiple linear0.88 *0.070.08
GrassesSimple linear0.92 *0.040.05
Multiple linear0.93 *0.040.05
LegumesSimple linear0.77 *0.070.11
Multiple linear0.80 *0.060.10
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Bublitz, T.A.; Kemper, R.; Müller, P.; Kautz, T.; Döring, T.F.; Athmann, M. Relating Profile Wall Root-Length Density Estimates to Monolith Root-Length Density Measurements of Cover Crops. Agronomy 2022, 12, 48. https://doi.org/10.3390/agronomy12010048

AMA Style

Bublitz TA, Kemper R, Müller P, Kautz T, Döring TF, Athmann M. Relating Profile Wall Root-Length Density Estimates to Monolith Root-Length Density Measurements of Cover Crops. Agronomy. 2022; 12(1):48. https://doi.org/10.3390/agronomy12010048

Chicago/Turabian Style

Bublitz, Tábata Aline, Roman Kemper, Phillip Müller, Timo Kautz, Thomas F. Döring, and Miriam Athmann. 2022. "Relating Profile Wall Root-Length Density Estimates to Monolith Root-Length Density Measurements of Cover Crops" Agronomy 12, no. 1: 48. https://doi.org/10.3390/agronomy12010048

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop