A Functional Analysis of Pedotransfer Functions Developed for Sri Lankan soils: Applicability for Process-Based Crop Models
Abstract
1. Introduction
2. Materials and Methods
2.1. Meteorological Data
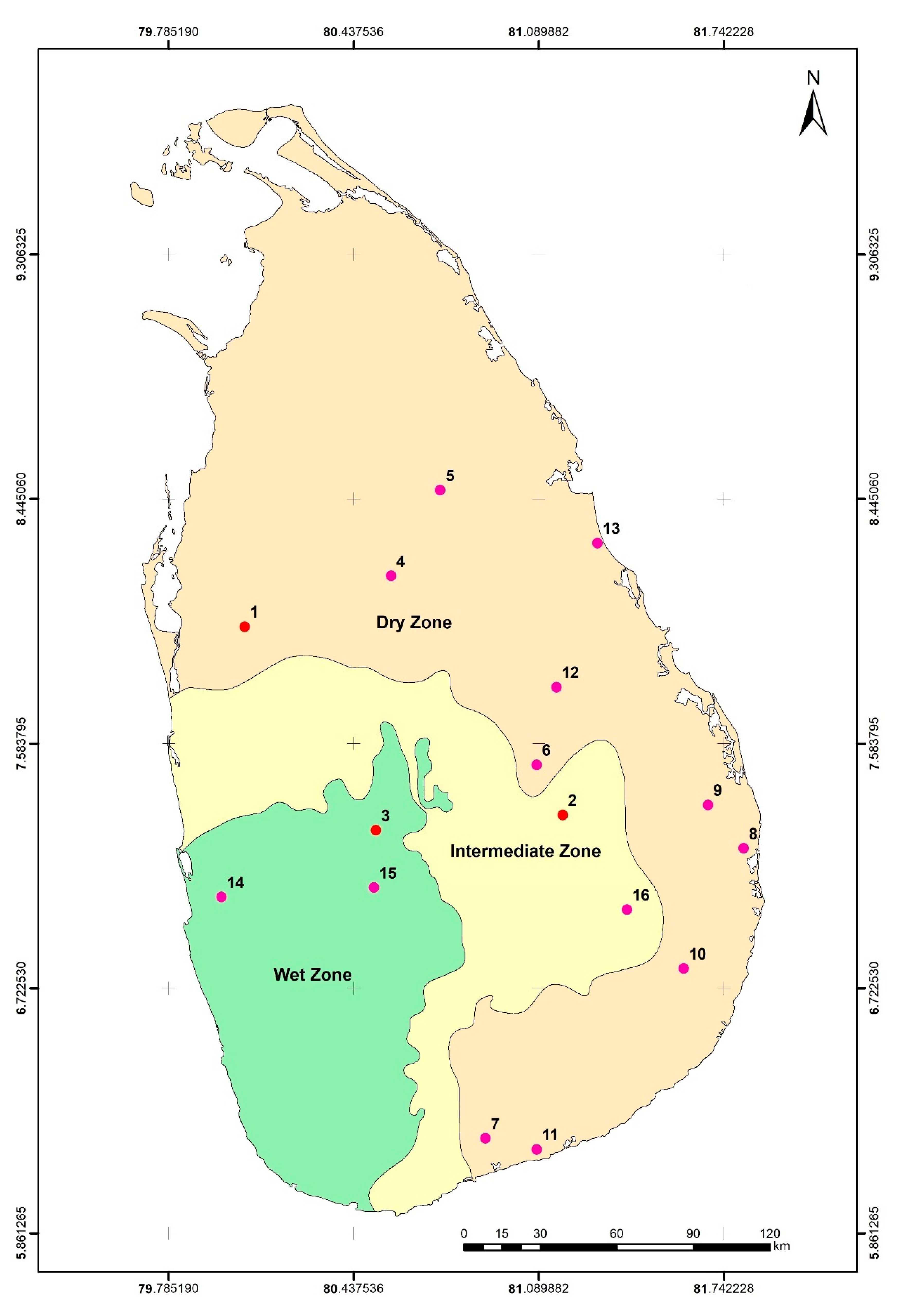
2.2. Soil Data
2.3. APSIM Simulation
2.4. Sensitivity Analysis
2.5. Functional Analysis
3. Results and Discussion
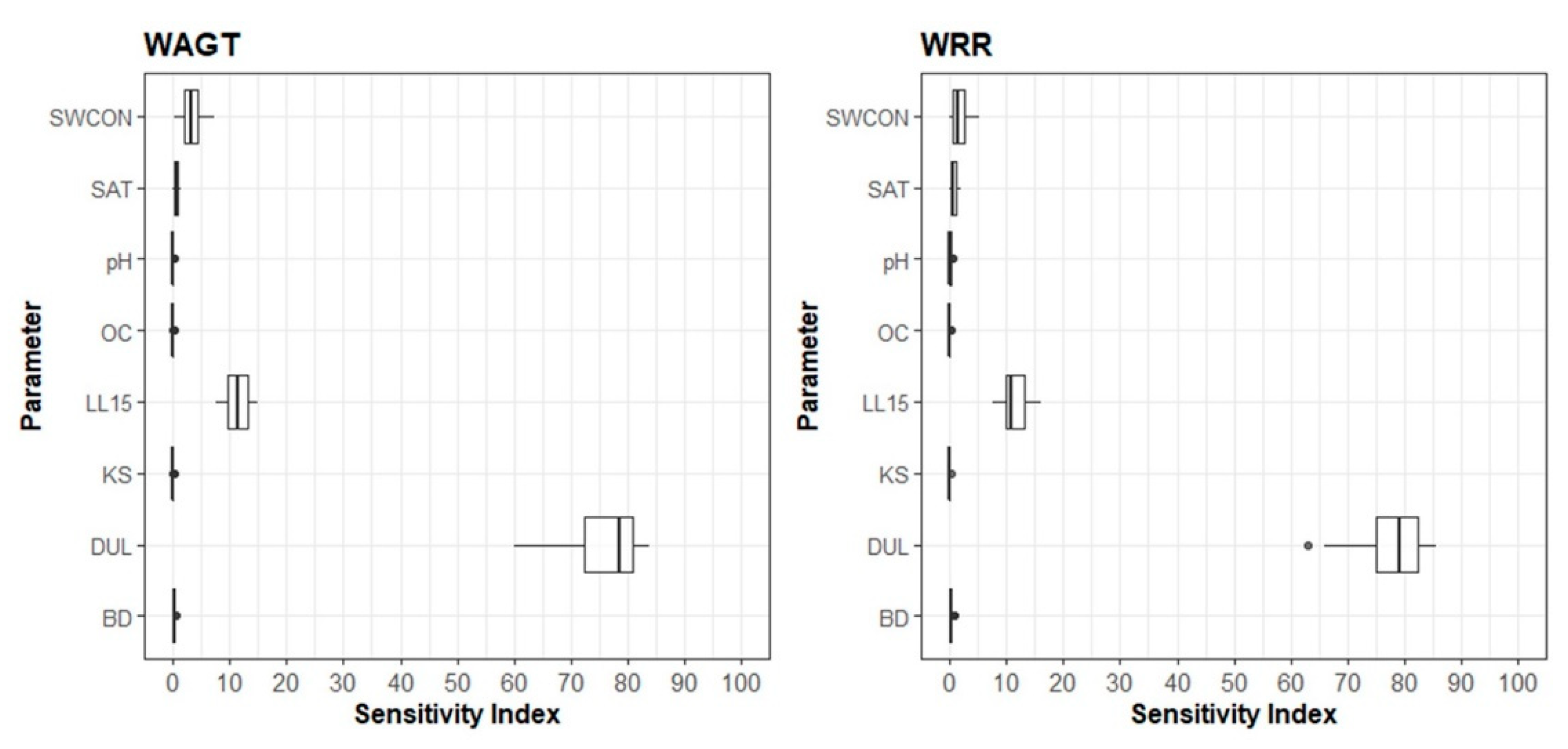
3.1. Sensitivity Analysis
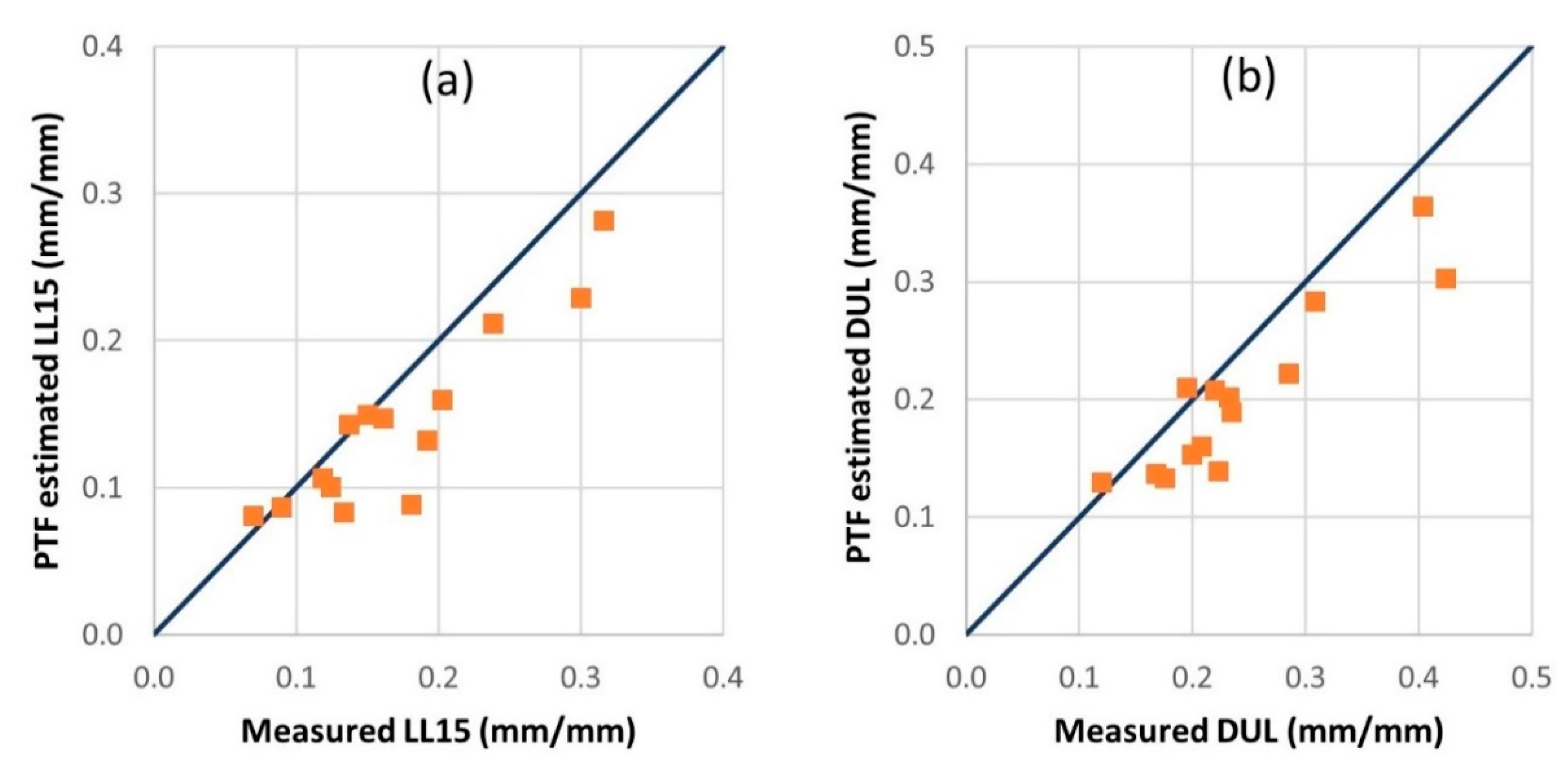
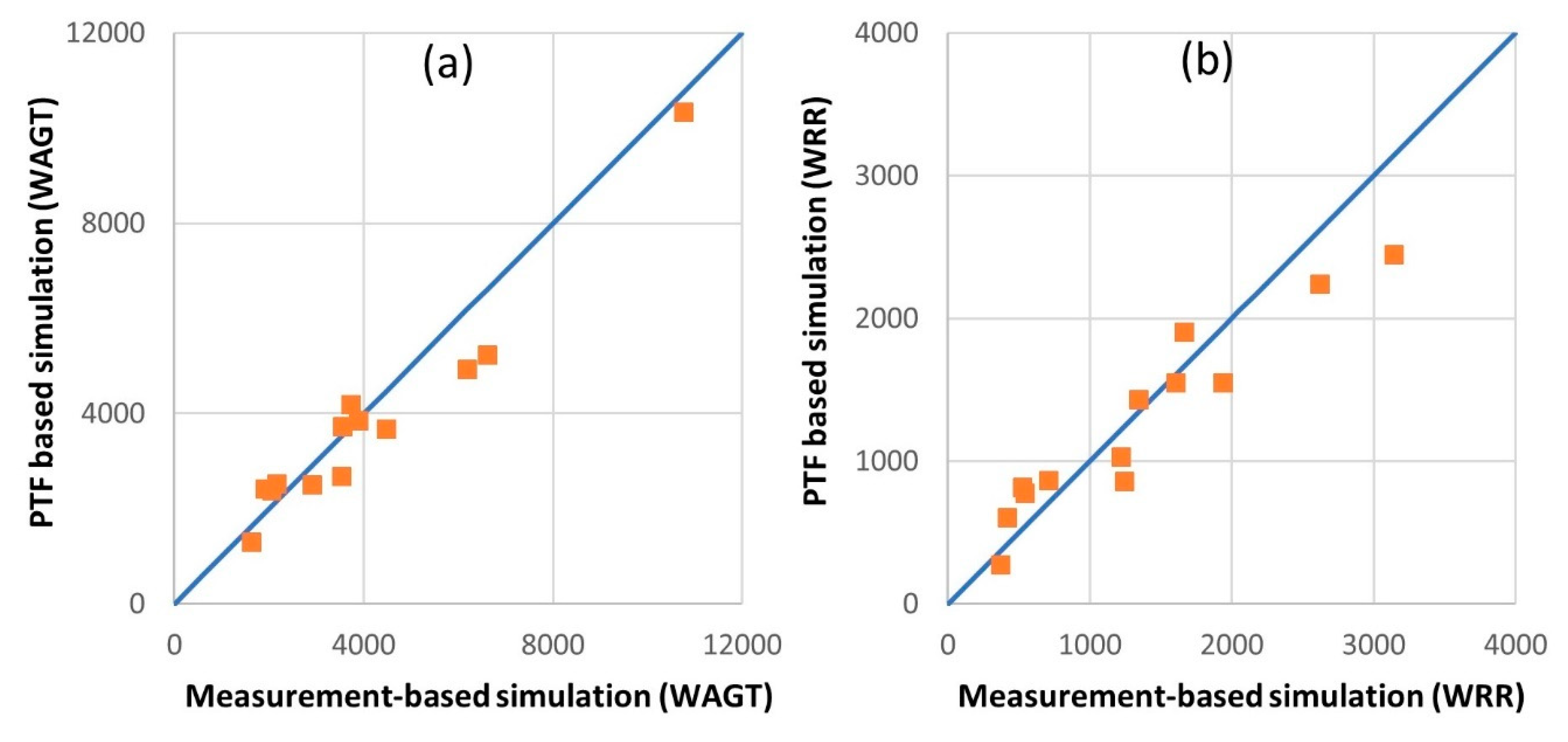
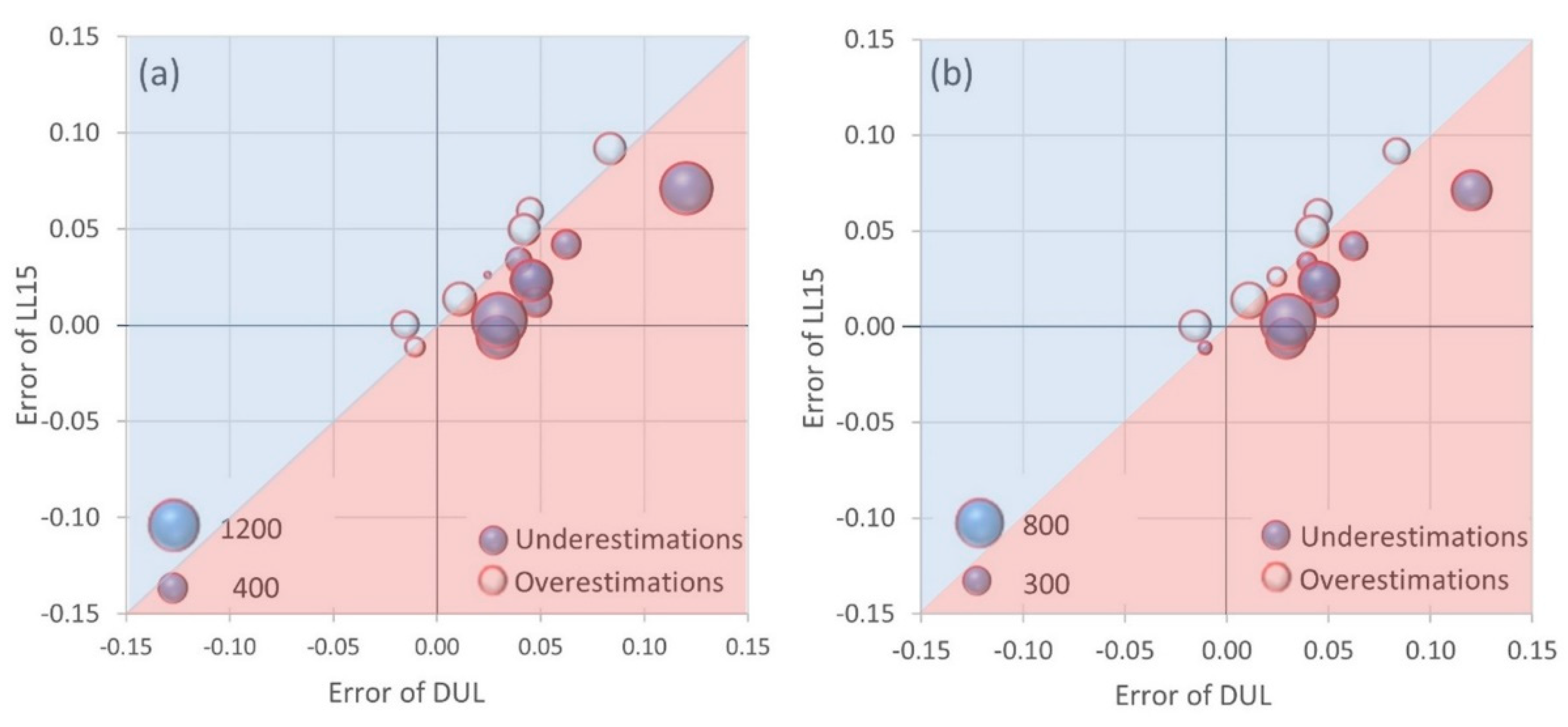
3.2. Functional Analysis
4. Conclusions
5. Limitations
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Year | Dry Zone Soil | Intermediate Zone Soil | Wet Zone Soil | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Sigma sq | CV RMSE | CV RMSSE | Sigma sq | CV RMSE | CV RMSSE | Sigma sq | CV RMSE | CV RMSSE | |
| Year 1 | 0.13 | 615.7 | 1.12 | 0.17 | 1272.3 | 1.04 | 0.17 | 1272.3 | 1.04 |
| Year 2 | 0.03 | 233.1 | 1.11 | 0.14 | 927.1 | 1.06 | 0.14 | 927.1 | 1.06 |
| Year 3 | 0.10 | 732.6 | 1.01 | 0.28 | 1736.4 | 1.04 | 0.28 | 1736.4 | 1.04 |
| Year 4 | 0.03 | 150.9 | 0.92 | 0.04 | 371.2 | 1.11 | 0.04 | 371.2 | 1.11 |
| Year 5 | 0.05 | 450.2 | 1.10 | 0.24 | 1594.6 | 1.06 | 0.24 | 1594.6 | 1.06 |
| Year 6 | 0.13 | 998.2 | 1.11 | 0.37 | 1742.5 | 1.04 | 0.37 | 1742.5 | 1.04 |
| Year 7 | 0.05 | 284.1 | 1.18 | 0.26 | 1346.7 | 1.06 | 0.26 | 1346.7 | 1.06 |
| Year 8 | 0.03 | 373.4 | 1.01 | 0.18 | 1056.5 | 1.09 | 0.18 | 1056.5 | 1.09 |
| Year 9 | 0.06 | 438.5 | 1.08 | 0.11 | 919.4 | 1.03 | 0.11 | 919.4 | 1.03 |
| Year 10 | 0.06 | 268.3 | 1.14 | 0.21 | 1358.2 | 0.96 | 0.21 | 1358.2 | 0.96 |
| Year | Dry Zone Soil | Intermediate Zone Soil | Wet Zone Soil | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Sigma sq | CV RMSE | CV RMSSE | Sigma sq | CV RMSE | CV RMSSE | Sigma sq | CV RMSE | CV RMSSE | |
| Year 1 | 0.14 | 398.2 | 1.16 | 0.21 | 867.9 | 1.04 | 0.14 | 737.8 | 1.05 |
| Year 2 | 0.07 | 182.5 | 1.26 | 0.19 | 631.4 | 1.03 | 0.11 | 546.2 | 1.00 |
| Year 3 | 0.04 | 309.2 | 1.01 | 0.38 | 777.0 | 1.05 | 0.22 | 845.6 | 0.98 |
| Year 4 | 0.12 | 108.3 | 0.99 | 0.11 | 303.1 | 1.04 | 0.09 | 197.1 | 1.13 |
| Year 5 | 0.02 | 195.8 | 1.09 | 0.39 | 942.7 | 1.00 | 0.21 | 720.8 | 1.05 |
| Year 6 | 0.04 | 383.5 | 1.04 | 0.44 | 752.7 | 1.02 | 0.42 | 1009 | 1.05 |
| Year 7 | 0.08 | 169.0 | 1.10 | 0.38 | 970.3 | 1.01 | 0.20 | 584.3 | 1.07 |
| Year 8 | 0.09 | 197.8 | 1.19 | 0.22 | 553.8 | 1.04 | 0.25 | 524.6 | 1.06 |
| Year 9 | 0.12 | 180.5 | 1.13 | 0.26 | 815.3 | 1.06 | 0.11 | 315.1 | 1.10 |
| Year 10 | 0.05 | 176.4 | 1.16 | 0.48 | 778.1 | 0.95 | 0.20 | 616.9 | 1.01 |
References
- Rustanto, A.; Booij, M.J.; Wösten, H.; Hoekstra, A.Y. Application and recalibration of soil water retention pedotransfer functions in a tropical upstream catchment: Case study in Bengawan Solo, Indonesia. J. Hydrol. Hydromech. 2017, 65, 307–320. [Google Scholar] [CrossRef]
- Bouma, J. Using Soil Survey Data for Quantitative Land Evaluation. Adv. Soil Sci. 1989, 9, 177–213. [Google Scholar] [CrossRef]
- Patil, N.G.; Singh, S.K. Pedotransfer Functions for Estimating Soil Hydraulic Properties: A Review. Pedosphere 2016, 26, 417–430. [Google Scholar] [CrossRef]
- Botula, Y.-D.; Van Ranst, E.; Cornelis, W.M. Pedotransfer functions to predict water retention for soils of the humid tropics: A Review. Rev. Bras. Cienc. Solo 2014, 38, 679–698. [Google Scholar] [CrossRef]
- Gunarathna, M.H.J.P.; Sakai, K.; Nakandakari, T.; Momii, K.; Kumari, M.K.N.; Amarasekara, M.G.T.S. Pedotransfer functions to estimate hydraulic properties of tropical Sri Lankan soils. Soil Tillage Res. 2019, 190, 109–119. [Google Scholar] [CrossRef]
- Shein, E.V.; Arkhangel’skaya, T.A. Pedotransfer functions: State of the art, problems, and outlooks. Eurasian Soil Sci. 2006, 39, 1089–1099. [Google Scholar] [CrossRef]
- Wosten, J.H.M.; Bannink, M.H.; Gruijter, J.J.D.E.; Bouma, J. A procedure to identify different groups of hydraulic-conductivity and moisture-retention curves for soil horizons. J. Hydrol. 1986, 86, 133–145. [Google Scholar] [CrossRef]
- Wosten, J.H.M.; van Genuchten, M.T. Using Texture and Other Soil Properties to Predict the Unsaturated Soil Hydraulic Functions. Soil Sci. Soc. Am. J. 1988, 52, 1762–1770. [Google Scholar] [CrossRef]
- Vereecken, H.; Diels, J.; Orshoven, J.; van Feyen, J.; Bouma, J. Functional evaluation of pedotransfer functions for the estimation of soil hydraulic properties. Soil Sci. Soc. Am. J. 1992, 56, 1371–1378. [Google Scholar] [CrossRef]
- Chirico, G.B.; Medina, H.; Romano, N. Functional evaluation of PTF prediction uncertainty: An application at hillslope scale. Geoderma 2010, 155, 193–202. [Google Scholar] [CrossRef]
- Nasta, P.; Romano, N.; Chirico, G.B. Functional evaluation of a simplified scaling method for assessing the spatial variability of soil hydraulic properties at the hillslope scale. Hydrol. Sci. J. 2013, 58, 1059–1071. [Google Scholar] [CrossRef]
- Basile, A.; Bonfante, A.; Coppola, A.; Mascellis, R.; De Bolognesi, S.F.; Terribile, F.; Manna, P. How does PTF interpret soil heterogeneity? A stochastic approach applied to a case study on maize in Northern Italy. Water 2019, 11. [Google Scholar] [CrossRef]
- Moeys, J.; Larsbo, M.; Bergström, L.; Brown, C.D.; Coquet, Y.; Jarvis, N.J. Functional test of pedotransfer functions to predict water flow and solute transport with the dual-permeability model MACRO. Hydrol. Earth Syst. Sci. 2012, 16, 2069–2083. [Google Scholar] [CrossRef]
- Varvaris, I.; Pittaki-Chrysodonta, Z.; Moldrup, P.; de Jonge, L.W.; Iversen, B.V. Combining Visible−Near-Infrared and Pedotransfer Functions for Parameterization of Tile Drain Flow Simulations. Vadose Zone J. 2019, 18. [Google Scholar] [CrossRef]
- Schneider, S.; Jacques, D.; Mallants, D. Inverse modelling with a genetic algorithm to derive hydraulic properties of a multi-layered forest soil. Soil Res. 2013, 51, 372. [Google Scholar] [CrossRef]
- Soet, M.; Stricker, J.N.M. Functional behaviour of pedotransfer functions in soil water flow simulation. Hydrol. Process. 2003, 17, 1659–1670. [Google Scholar] [CrossRef]
- Sun, W.; Yao, X.; Cao, N.; Xu, Z.; Yu, J. Integration of soil hydraulic characteristics derived from pedotransfer functions into hydrological models: Evaluation of its effects on simulation uncertainty. Hydrol. Res. 2016, 47, 964–978. [Google Scholar] [CrossRef]
- Garrigues, S.; Boone, A.; Decharme, B.; Olioso, A.; Albergel, C.; Calvet, J.-C.; Moulin, S.; Buis, S.; Martin, E. Impacts of the Soil Water Transfer Parameterization on the Simulation of Evapotranspiration over a 14-Year Mediterranean Crop Succession. J. Hydrometeorol. 2017, 19, 3–25. [Google Scholar] [CrossRef]
- Baroni, G.; Facchi, A.; Gandolfi, C.; Ortuani, B.; Horeschi, D.; Van Dam, J.C. Uncertainty in the determination of soil hydraulic parameters and its influence on the performance of two hydrological models of different complexity. Hydrol. Earth Syst. Sci. 2010, 14, 251–270. [Google Scholar] [CrossRef]
- Nemes, A.; Czinege, E.; Farkas, C. Use of simulation modeling and pedotransfer functions to evaluate different irrigation scheduling scenarios in a heterogeneous field. In Proceedings of the 19th World Congress of Soil Science, Soil Solutions for a Changing World, Brisbane, Australia, 1–6 August 2010; pp. 186–189. [Google Scholar]
- Lashkari, A.; Salehnia, N.; Asadi, S.; Paymard, P.; Zare, H.; Bannayan, M. Evaluation of different gridded rainfall datasets for rainfed wheat yield prediction in an arid environment. Int. J. Biometeorol. 2018, 62, 1543–1556. [Google Scholar] [CrossRef]
- Shelia, V.; Hansen, J.; Sharda, V.; Porter, C.; Aggarwal, P.; Wilkerson, C.J.; Hoogenboom, G. A multi-scale and multi-model gridded framework for forecasting crop production, risk analysis, and climate change impact studies. Environ. Model. Softw. 2019, 115, 144–154. [Google Scholar] [CrossRef]
- Matthew, O.J.; Abiodun, B.J.; Salami, A.T. Modelling the impacts of climate variability on crop yields in Nigeria: Performance evaluation of RegCM3-GLAM system. Meteorol. Appl. 2015, 22, 198–212. [Google Scholar] [CrossRef]
- Liu, M.; He, B.; Lü, A.; Zhou, L.; Wu, J. Parameters sensitivity analysis for a~crop growth model applied to winter wheat in the Huanghuaihai Plain in China. Geosci. Model Dev. Discuss. 2014, 7, 3867–3888. [Google Scholar] [CrossRef]
- Varella, H.; Buis, S.; Launay, M.; Guerif, M. Global sensitivity analysis for choosing the main soil parameters of a crop model to be determined. Agric. Sci. 2012, 3, 949–961. [Google Scholar] [CrossRef]
- Folberth, C.; Skalský, R.; Moltchanova, E.; Balkovič, J.; Azevedo, L.B.; Obersteiner, M.; Van Der Velde, M. Uncertainty in soil data can outweigh climate impact signals in global crop yield simulations. Nat. Commun. 2016, 7, 1–13. [Google Scholar] [CrossRef]
- Waha, K.; Huth, N.; Carberry, P.; Wang, E. How model and input uncertainty impact maize yield simulations in West Africa. Environ. Res. Lett. 2015, 10, 024017. [Google Scholar] [CrossRef]
- Keating, B.A.; Carberry, P.S.; Hammer, G.L.; Probert, M.E.; Robertson, M.J.; Holzworth, D.; Huth, N.I.; Hargreaves, J.N.G.; Meinke, H.; Hochman, Z.; et al. An overview of APSIM, a model designed for farming systems simulation. Eur. J. Agron. 2003, 18, 267–288. [Google Scholar] [CrossRef]
- Jones, J.W.; Hoogenboom, G.; Porter, C.H.; Boote, K.J.; Batchelor, W.D.; Hunt, L.A.; Wilkens, P.W.; Singh, U.; Gijsman, A.J.; Ritchie, J.T. Eur. J. Agron. 2003, 18, 235–265.
- Brisson, N.; Gary, C.; Justes, E.; Roche, R.; Mary, B.; Ripoche, D.; Zimmer, D.; Sierra, J.; Bertuzzi, P.; Burger, P.; et al. An overview of the crop model STICS. Eur. J. Agron. 2003, 18, 309–332. [Google Scholar] [CrossRef]
- Archontoulis, S.V.; Miguez, F.E.; Moore, K.J. Evaluating APSIM maize, soil water, soil nitrogen, manure, and soil temperature modules in the Midwestern United States. Agron. J. 2014, 106, 1025–1040. [Google Scholar] [CrossRef]
- Holzworth, D.P.; Huth, N.I.; deVoil, P.G.; Zurcher, E.J.; Herrmann, N.I.; McLean, G.; Chenu, K.; van Oosterom, E.J.; Snow, V.; Murphy, C.; et al. APSIM—Evolution towards a new generation of agricultural systems simulation. Environ. Model. Softw. 2014, 62, 327–350. [Google Scholar] [CrossRef]
- Lawless, C.; Semenov, M.A.; Jamieson, P.D. Quantifying the effect of uncertainty in soil moisture characteristics on plant growth using a crop simulation model. Field Crops Res. 2008, 106, 138–147. [Google Scholar] [CrossRef]
- Gijsman, A.; Jagtap, S.; Jones, J. Wading through a swamp of complete confusion: How to choose a method for estimating soil water retention parameters for crop models. Eur. J. Agron. 2002, 18, 77–106. [Google Scholar] [CrossRef]
- Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelli, D.; Saisana, M.; Tarantola, S. Global Sensitivity Analysis: The Primer; John Wiley & Sons: West Sussex, UK, 2008; ISBN 9780470059975. [Google Scholar]
- Saltelli, A.; Annoni, P.; Azzini, I.; Campolongo, F.; Ratto, M.; Tarantola, S. Variance based sensitivity analysis of model output. Design and estimator for the total sensitivity index. Comput. Phys. Commun. 2010, 181, 259–270. [Google Scholar] [CrossRef]
- Confalonieri, R.; Bellocchi, G.; Tarantola, S.; Acutis, M.; Donatelli, M.; Genovese, G. Sensitivity analysis of the rice model WARM in Europe: Exploring the effects of different locations, climates and methods of analysis on model sensitivity to crop parameters. Environ. Model. Softw. 2010, 25, 479–488. [Google Scholar] [CrossRef]
- Lamsal, A.; Amgai, L.; Giri, A. Modeling the sensitivity of CERES-Rice model: An experience of Nepal. Agron. J. Nepal 2013, 3, 11–22. [Google Scholar] [CrossRef]
- Xing, H.M.; Xu, X.G.; Li, Z.H.; Chen, Y.J.; Feng, H.K.; Yang, G.J.; Chen, Z.X. Global sensitivity analysis of the AquaCrop model for winter wheat under different water treatments based on the extended Fourier amplitude sensitivity test. J. Integr. Agric. 2017, 16, 2444–2458. [Google Scholar] [CrossRef]
- Corbeels, M.; Chirat, G.; Messad, S.; Thierfelder, C. Performance and sensitivity of the DSSAT crop growth model in simulating maize yield under conservation agriculture. Eur. J. Agron. 2016, 76, 41–53. [Google Scholar] [CrossRef]
- Eweys, O.A.; Elwan, A.A.; Borham, T.I. Integrating WOFOST and Noah LSM for modeling maize production and soil moisture with sensitivity analysis, in the east of The Netherlands. Field Crops Res. 2017, 210, 147–161. [Google Scholar] [CrossRef]
- Tan, J.; Cui, Y.; Luo, Y. Global sensitivity analysis of outputs over rice-growth process in ORYZA model. Environ. Model. Softw. 2016, 83, 36–46. [Google Scholar] [CrossRef]
- Zhao, G.; Bryan, B.A.; Song, X. Sensitivity and uncertainty analysis of the APSIM-wheat model: Interactions between cultivar, environmental, and management parameters. Ecol. Model. 2014, 279, 1–11. [Google Scholar] [CrossRef]
- Gunarathna, M.H.J.P.; Kumari, M.K.N. Rainfall trends in Anuradhapura: Rainfall analysis for agricultural planning. Rajarata Univ. J. 2013, 1, 38–44. [Google Scholar]
- Ruane, A.C.; Goldberg, R.; Chryssanthacopoulos, J. Climate forcing datasets for agricultural modeling: Merged products for gap-filling and historical climate series estimation. Agric. For. Meteorol. 2015, 200, 233–248. [Google Scholar] [CrossRef]
- Ruane, A.C.; Cecil, L.D.W.; Horton, R.M.; Gordón, R.; McCollum, R.; Brown, D.; Killough, B.; Goldberg, R.; Greeley, A.P.; Rosenzweig, C. Climate change impact uncertainties for maize in Panama: Farm information, climate projections, and yield sensitivities. Agric. For. Meteorol. 2013, 170, 132–145. [Google Scholar] [CrossRef]
- Dassanayake, A.R.; Somasiri, L.L.W.; Mapa, R.B. Benchmark Soils of the Intermediate Zone: Factsheets; Mapa, R.B., Dassanayake, A.R., Nayakekorale, H.B., Eds.; Soil Science Society of Sri Lanka: Kandy, Sri Lanka, 2005. [Google Scholar]
- Dassanayake, A.R.; Silva, G.G.R.; De Mapa, R.B.; Kumaragamage, D. Benchmark Soils of the Dry Zone of Sri Lanka: Factsheets; Mapa, R.B., Somasiri, S., Dassanayake, A.R., Eds.; Soil Science Society of Sri Lanka: Kandy, Sri Lanka, 2010. [Google Scholar]
- Senarath, A.; Dassanayake, A.R.; Mapa, R.B. Bench Mark Soils of the Wet Zone: Factsheets; Mapa, R.B., Somasiri, S., Nagarajah, S.L., Eds.; Soil Science Society of Sri Lanka: Kandy, Sri Lanka, 1999. [Google Scholar]
- Gaydon, D.S.; Probert, M.E.; Buresh, R.J.; Meinke, H.; Suriadi, A.; Dobermann, A.; Bouman, B.; Timsina, J. Rice in cropping systems-Modelling transitions between flooded and non-flooded soil environments. Eur. J. Agron. 2012, 39, 9–24. [Google Scholar] [CrossRef]
- Bouman, B.A.M.; Van Laar, H.H. Description and evaluation of the rice growth model ORYZA2000 under nitrogen-limited conditions. Agric. Syst. 2006, 87, 249–273. [Google Scholar] [CrossRef]
- Amarasingha, R.P.R.K.; Suriyagoda, L.D.B.; Marambe, B.; Gaydon, D.S.; Galagedara, L.W.; Punyawardena, R.; Silva, G.L.L.P.; Nidumolu, U.; Howden, M. Simulation of crop and water productivity for rice (Oryza sativa L.) using APSIM under diverse agro-climatic conditions and water management techniques in Sri Lanka. Agric. Water Manag. 2015, 160, 132–143. [Google Scholar] [CrossRef]
- Zubair, L.; Nissanka, S.P.; Weerakoon, W.M.W.; Herath, D.I.; Karunaratne, A.S.; Agalawatte, P.; Herath, R.M.; Yahiya, S.Z.; Punyawardhene, B.V.R.; Vishwanathan, J.; et al. Climate Change Impacts on Rice Farming Systems in Northwestern Sri Lanka. In Handbook of Climate Change and Agroecosystems; Imperial College Press: London, UK, 2015; pp. 315–352. [Google Scholar]
- Nissanka, S.P.; Karunaratne, A.S.; Perera, R.; Weerakoon, W.M.W.; Thorburn, P.J.; Wallach, D. Calibration of the phenology sub-model of APSIM-Oryza: Going beyond goodness of fit. Environ. Model. Softw. 2015, 70, 128–137. [Google Scholar] [CrossRef]
- Wallach, D.; Makowski, D.; Jones, J.W.; Brun, F. Uncertainty and Sensitivity Analysis. In Working with Dynamic Crop Models; Elsevier B.V.: Amsterdam, The Netherlands, 2014; pp. 161–204. ISBN 9780123970084. [Google Scholar]
- Petropoulos, G.; Wooster, M.J.; Carlson, T.N.; Kennedy, M.C.; Scholze, M. A global Bayesian sensitivity analysis of the 1d SimSphere soil-vegetation-atmospheric transfer (SVAT) model using Gaussian model emulation. Ecol. Model. 2009, 220, 2427–2440. [Google Scholar] [CrossRef]
- O’Hagan, A. Bayesian analysis of computer code outputs: A tutorial. Reliab. Eng. Syst. Saf. 2006, 91, 1290–1300. [Google Scholar] [CrossRef]
- Uusitalo, L.; Lehikoinen, A.; Helle, I.; Myrberg, K. An overview of methods to evaluate uncertainty of deterministic models in decision support. Environ. Model. Softw. 2015, 63, 24–31. [Google Scholar] [CrossRef]
- Kennedy, M.C.; Petropoulos, G.P. GEM-SA: The Gaussian Emulation Machine for Sensitivity Analysis; Elsevier: Amsterdam, The Netherlands, 2017; ISBN 9780128030318. [Google Scholar]
- Sexton, J.; Everingham, Y.L. Global sensitivity analysis of key parameters in a process-based sugarcane growth model—A Bayesian approach. In Proceedings of the 7th International Congress on Environmental Modelling and Software, San Diego, CA, USA, 15–19 June 2014. [Google Scholar]
- Sexton, J.; Everingham, Y.L.; Inman-Bamber, G. A global sensitivity analysis of cultivar trait parameters in a sugarcane growth model for contrasting production environments in Queensland, Australia. Eur. J. Agron. 2017, 88, 96–105. [Google Scholar] [CrossRef]
- Gunarathna, M.H.J.P.; Sakai, K.; Nakandakari, T.; Momii, K.; Kumari, M.K.N. Sensitivity Analysis of Plant- and Cultivar-Specific Parameters of APSIM-Sugar Model: Variation between Climates and Management Conditions. Agronomy 2019, 9, 242. [Google Scholar] [CrossRef]
- Kennedy, M.C.; O’Hagan, A. Bayesian calibration of computer models. J. R. Stat. Soc. Ser. B Stat. Methodol. 2001, 63, 425–464. [Google Scholar] [CrossRef]
- Kennedy, M.C.; Anderson, C.W.; Conti, S.; O’Hagan, A. Case studies in Gaussian process modelling of computer codes. Reliab. Eng. Syst. Saf. 2006, 91, 1301–1309. [Google Scholar] [CrossRef]
- Stanfill, B. Apsimr: Edit, Run and Evaluate APSIM Simulations Easily Using R. R Package Version 1.2. 2015. Available online: https://CRAN.R-project.org/package=apsimr (accessed on 5 February 2019).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018; Available online: https://www.R-project.org/ (accessed on 5 February 2019).
- Oakley, J.E.; O’Hagan, A. Probabilistic sensitivity analysis of complex models: A Bayesian approach. J. R. Stat. Soc. Ser. B Stat. Methodol. 2004, 66, 751–769. [Google Scholar] [CrossRef]
- Wallach, D.; Makowski, D.; Jones, J.W.; Brun, F. Model Evaluation. In Working with Dynamic Crop Models; Elsevier B.V.: Amsterdam, The Netherlands, 2014; pp. 345–406. ISBN 9780123970084. [Google Scholar]
- Krause, P.; Boyle, D.P.; Bäse, F. Advances in Geosciences Comparison of different efficiency criteria for hydrological model assessment. Adv. Geosci. 2005, 5, 89–97. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River Flow Forecasting Through Conceptual Models Part I—A Discussion of Principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Willmott, C.J. On the validation of models. Phys. Geogr. 1981, 2, 184–194. [Google Scholar] [CrossRef]
- Ojeda, J.J.; Volenec, J.J.; Brouder, S.M.; Caviglia, O.P.; Agnusdei, M.G. Evaluation of Agricultural Production Systems Simulator as yield predictor of Panicum virgatum and Miscanthus x giganteus in several US environments. GCB Bioenergy 2017, 9, 796–816. [Google Scholar] [CrossRef]
- McBride, G. A Proposal for Strength-of-Agreement Criteria for Lin’s Concordance Correlation Coefficient; National Institute of Water & Atmospheric Research: Hamilton, New Zealand, 2005. [Google Scholar]
- Stevenson, M.; Nunes, T.; Heuer, C.; Marshall, J.; Sanchez, J.; Thornton, R.; Reiczigel, J.; Robison-Cox, J.; Sebastiani, P.; Solymos, P.; et al. epiR: Tools for the Analysis of Epidemiological Data; R Foundation for Statistical Computing: Vienna, Austria, 2018. [Google Scholar]
- Lee, L.A.; Carslaw, K.S.; Pringle, K.J.; Mann, G.W.; Spracklen, D.V. Emulation of a complex global aerosol model to quantify sensitivity to uncertain parameters. Atmos. Chem. Phys. 2011, 11, 12253–12273. [Google Scholar] [CrossRef]
- Chen, C.; Wu, R.; Fletcher, A.; Lawes, R.; Oliver, Y. Sensitivity of simulated yield of dryland wheat to uncertainty in estimated plant-available water capacity. In Proceedings of the 22nd International Congress on Modelling and Simulation (MODSIM-2017), Hobart, Australia, 3–8 December 2017; pp. 244–249. [Google Scholar]
- Gunarathna, M.H.J.P.; Sakai, K. Evaluation of pedotransfer functions for estimating soil moisture constants: A study on soils in dry zone of tropical Sri Lanka. Int. J. Adv. Sci. Eng. Technol. 2018, 6, 15–19. [Google Scholar]
- Gunarathna, M.H.J.P.; Sakai, K.; Nakandakari, T.; Momii, K.; Kumari, M.K.N. Machine learning approaches to develop pedotransfer functions for tropical Sri Lankan soils. Water 2019, 11, 1940. [Google Scholar] [CrossRef]
- Nemes, A.; Schaap, M.G.; Wösten, J.H.M. Functional Evaluation of Pedotransfer Functions Derived from Different Scales of Data Collection. Soil Sci. Soc. Am. J. 2003, 67, 1093. [Google Scholar] [CrossRef]

| Parameter | Description | Unit | Range | |
|---|---|---|---|---|
| Min | Max | |||
| BD | Bulk density | g/cm3 | 0.8 | 2.0 |
| LL15 | Drained lower limit (equals the permanent wilting point) | mm/mm | 0.05 | 0.30 |
| DUL | Drained upper limit (equals the field capacity) | mm/mm | 0.0 * | 1.0 * |
| SAT | Saturation | mm/mm | 0.0 ** | 1.0 ** |
| KS | Saturated hydraulic conductivity | mm/day | 0.1 | 10,000 |
| OC | Organic carbon | % | 0.1 | 1.5 |
| pH | 4.0 | 9.0 | ||
| SWCON | Drainage coefficient | 0 | 1 | |
| Criteria | WAGT | WRR | SWS(1) | Infiltration | Runoff | EOS |
|---|---|---|---|---|---|---|
| R2 | 0.90 | 0.90 | 0.91 | 0.99 | 0.98 | 0.95 |
| RMSE | 811 kg/ha | 445 kg/ha | 0.05 mm/mm | 0.74 mm | 0.45 mm | 0.35 mm |
| NSE | 0.89 | 0.90 | 0.85 | 0.99 | 0.98 | 0.95 |
| d | 0.97 | 0.97 | 0.95 | 1.00 | 1.00 | 0.99 |
| CCC | 0.94 | 0.95 | 0.91 | 1.00 | 0.98 | 0.99 |
| SD | 2485 kg/ha | 1424 kg/ha | 0.12 mm | 7.84 mm | 3.47 mm | 1.63 mm |
| P(T <=t) | 0.42 | 0.60 | 0.06 | 0.83 | 0.74 | 0.02 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gunarathna, M.H.J.P.; Sakai, K.; Kumari, M.K.N.; Ranagalage, M. A Functional Analysis of Pedotransfer Functions Developed for Sri Lankan soils: Applicability for Process-Based Crop Models. Agronomy 2020, 10, 285. https://doi.org/10.3390/agronomy10020285
Gunarathna MHJP, Sakai K, Kumari MKN, Ranagalage M. A Functional Analysis of Pedotransfer Functions Developed for Sri Lankan soils: Applicability for Process-Based Crop Models. Agronomy. 2020; 10(2):285. https://doi.org/10.3390/agronomy10020285
Chicago/Turabian StyleGunarathna, M. H. J. P., Kazuhito Sakai, M. K. N. Kumari, and Manjula Ranagalage. 2020. "A Functional Analysis of Pedotransfer Functions Developed for Sri Lankan soils: Applicability for Process-Based Crop Models" Agronomy 10, no. 2: 285. https://doi.org/10.3390/agronomy10020285
APA StyleGunarathna, M. H. J. P., Sakai, K., Kumari, M. K. N., & Ranagalage, M. (2020). A Functional Analysis of Pedotransfer Functions Developed for Sri Lankan soils: Applicability for Process-Based Crop Models. Agronomy, 10(2), 285. https://doi.org/10.3390/agronomy10020285







