Mechanical Pulling of Linked Ring Polymers: Elastic Response and Link Localisation
Abstract
:1. Introduction
2. Methods
2.1. Model and Simulation Setups
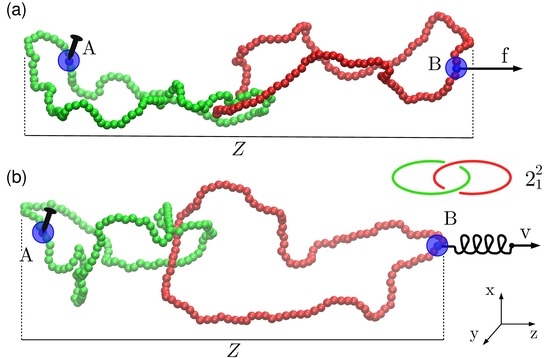
2.1.1. Constant Force Setup
2.1.2. Constant Velocity Setup
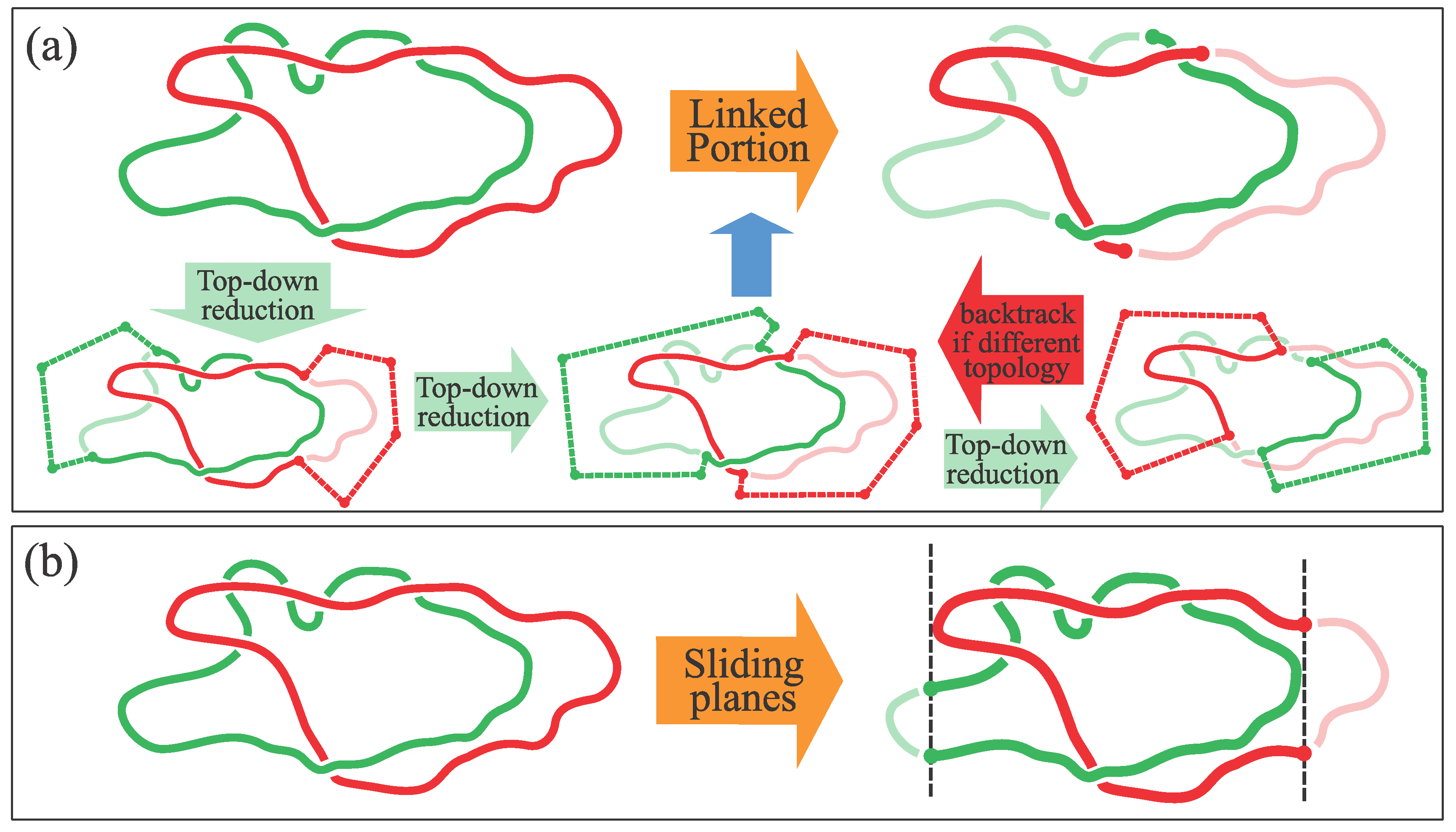
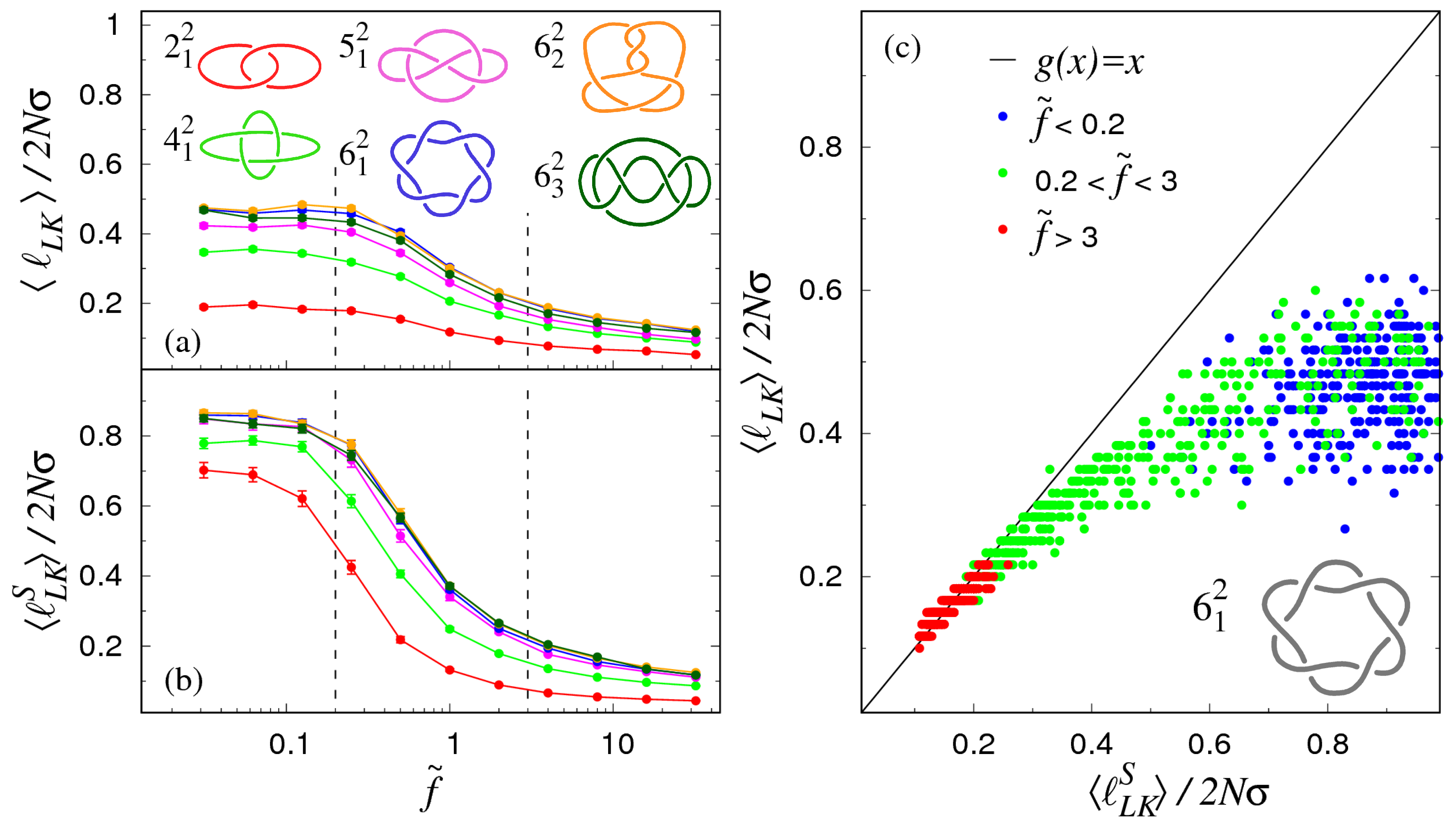
2.2. Locating the Linked Portion
2.2.1. Top-Down Search
2.2.2. Sliding Planes Method
3. Results
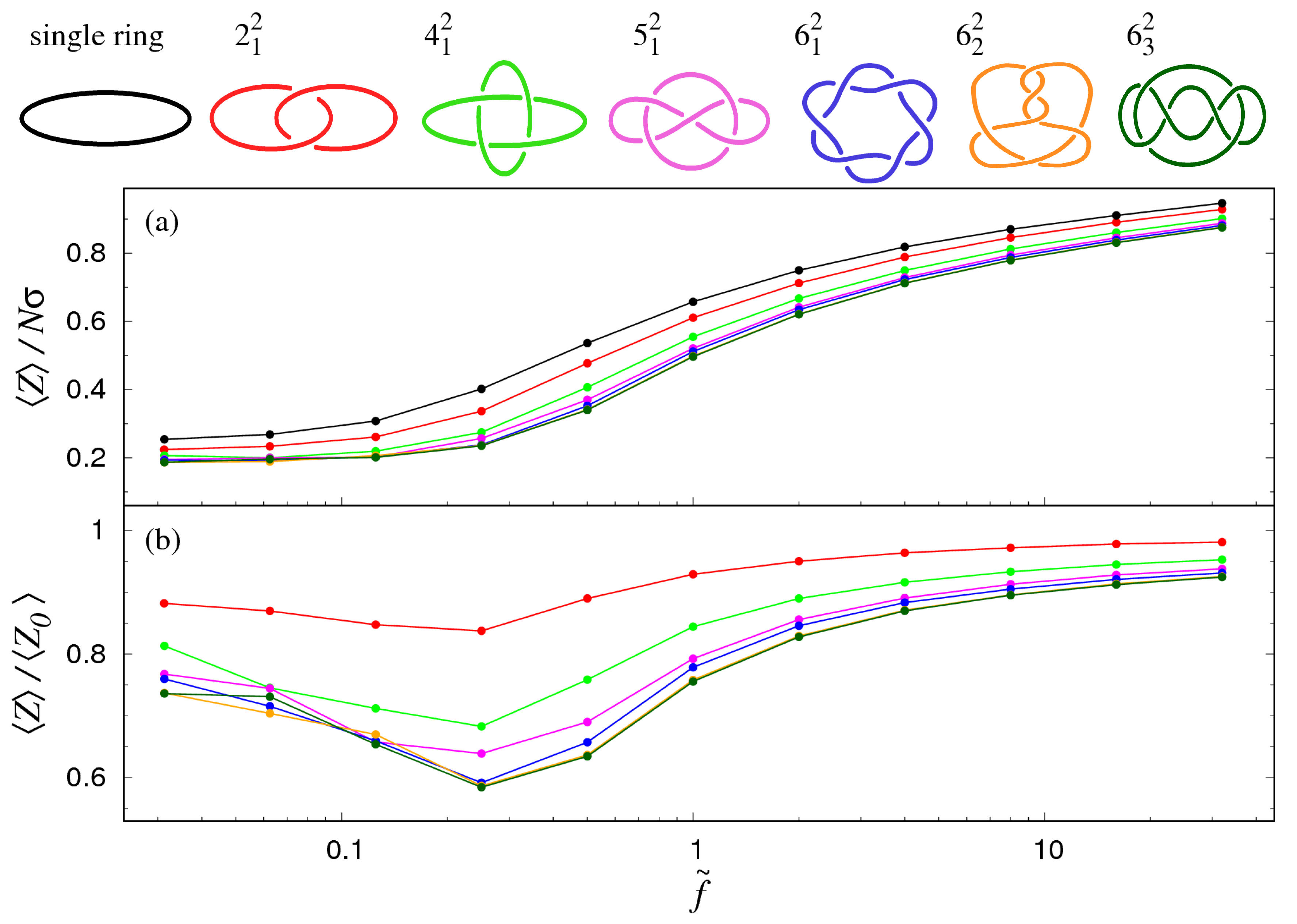
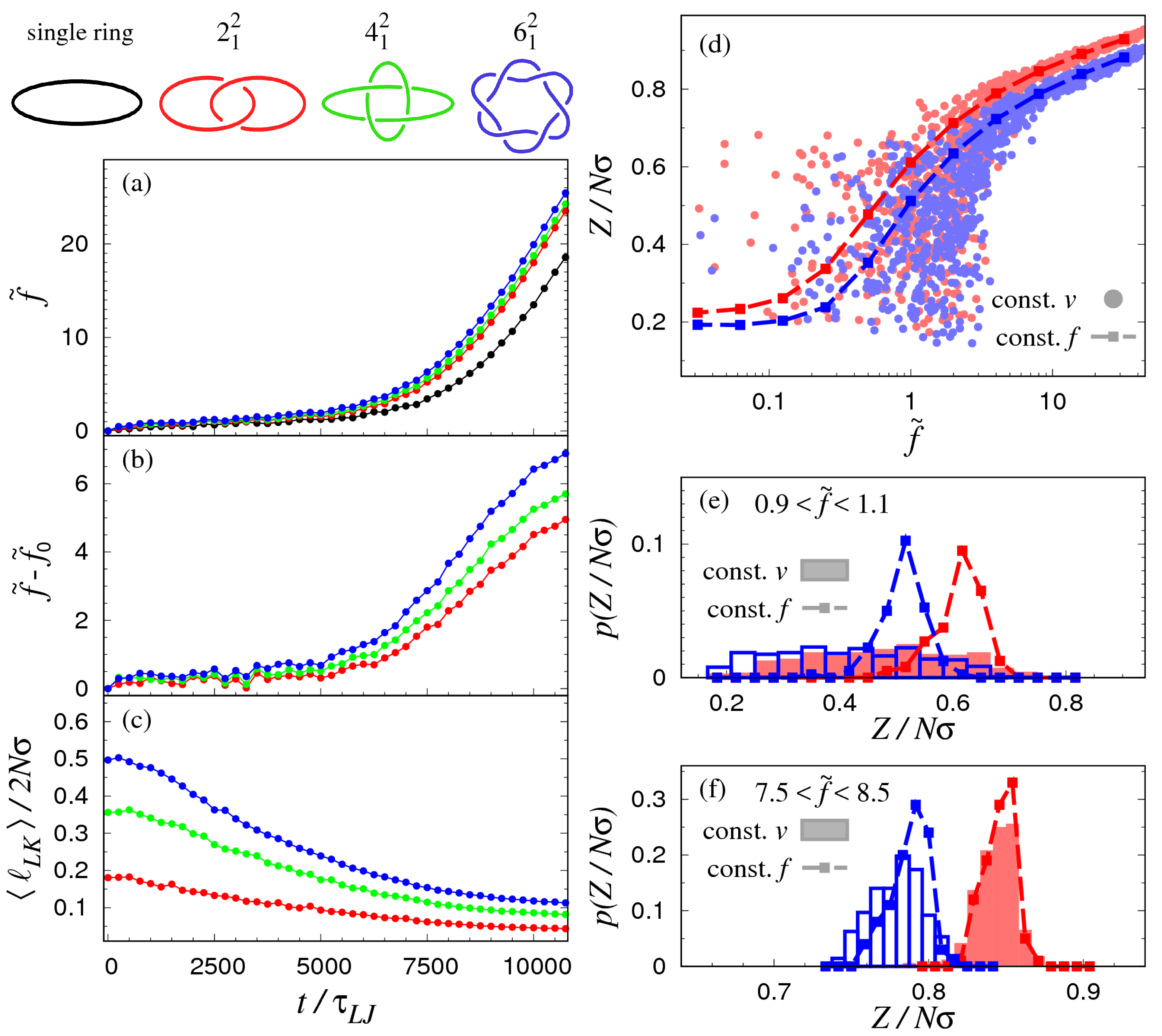
3.1. Pulling at Constant Force
3.2. Pulling at Constant Velocity
4. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Grosberg, A.; Rabin, Y.; Havlin, S.; Neer, A. Crumpled globule model of the three-dimensional structure of DNA. Europhys. Lett. 1988, 23, 373. [Google Scholar] [CrossRef]
- Rosa, A.; Everaers, R. Structure and dynamics of interphase chromosomes. PLoS Comput. Biol. 2008, 4, e1000153. [Google Scholar] [CrossRef] [PubMed]
- Dekker, J.; Marti-Renom, M.A.; Mirny, L.A. Exploring the three-dimensional organization of genomes: Interpreting chromatin interaction data. Nat. Rev. Genet. 2013, 14, 390–403. [Google Scholar] [CrossRef] [PubMed]
- Rolfsen, D. Knots and Links; Mathematics Lecture Series 7; Publish or Perish, Inc.: Houston, TX, USA, 1976. [Google Scholar]
- Chen, J.; Rauch, C.A.; White, J.H.; Englund, P.T.; Cozzarelli, N.R. The topology of the kinetoplast DNA network. Cell 1995, 80, 61–69. [Google Scholar] [CrossRef]
- Michieletto, D.; Marenduzzo, D.; Orlandini, E. Is the kinetoplast DNA a percolating network of linked rings at its critical point? Phys. Biol. 2015, 12, 036001. [Google Scholar] [CrossRef] [PubMed]
- Farago, O.; Kantor, Y.; Kardar, M. Pulling knotted polymers. Europhys. Lett. 2002, 60, 53–59. [Google Scholar] [CrossRef]
- Vologodskii, A. Brownian dynamics simulation of knot diffusion along a stretched DNA molecule. Biophys. J. 2006, 90, 1594–1597. [Google Scholar] [CrossRef] [PubMed]
- Janse van Rensburg, E.J.; Orlandini, E.; Tesi, M.C.; Whittington, S.G. Thermodynamics and entanglements of walks under stress. J. Stat. Mech. 2009, 2009, P07014. [Google Scholar] [CrossRef]
- Matthews, R.; Louis, A.A.; Yeomans, J.M. Effect of topology on dynamics of knots in polymers under tension. Europhys. Lett. 2010, 89, 20001. [Google Scholar] [CrossRef]
- Huang, L.; Makarov, D.E. Langevin dynamics simulations of the diffusion of molecular knots in tensioned polymer chains. J. Phys. Chem. 2007, 111, 10338–10344. [Google Scholar] [CrossRef] [PubMed]
- Di Stefano, M.; Tubiana, L.; Di Ventra, M.; Micheletti, C. Driving knots on DNA with AC/DC electric fields: Topological friction and memory effects. Soft Matter 2014, 10, 6491–6498. [Google Scholar] [CrossRef] [PubMed]
- Aragao de Carvalho, C.; Caracciolo, S.; Fröhlich, J. Polymers and g|ϕ|4 theory in four dimensions. Nucl. Phys. B 1983, 215, 209–248. [Google Scholar] [CrossRef]
- Caraglio, M.; Micheletti, C.; Orlandini, E. Stretching Response of Knotted and Unknotted Polymer Chains. Phys. Rev. Lett. 2015, 115, 188301. [Google Scholar] [CrossRef] [PubMed]
- Arai, Y.; Yasuda, R.; Akashi, K.; Harada, Y.; Miyata, H.; Kinosita, T.; Itoh, H. Tying a molecular knot with optical tweezers. Nature 1999, 399, 446–448. [Google Scholar] [PubMed]
- Bao, X.R.; Lee, H.J.; Quake, S.R. Behavior of complex knots in single DNA molecules. Phys. Rev. Lett. 2003, 91, 265506. [Google Scholar] [CrossRef] [PubMed]
- Rosa, A.; Di Ventra, M.; Micheletti, C. Topological Jamming of Spontaneously Knotted Polyelectrolyte Chains Driven Through a Nanopore. Phys. Rev. Lett. 2012, 109, 118301. [Google Scholar] [CrossRef] [PubMed]
- Plesa, C.; Verschueren, D.; Pud, S.; van der Torre, J.; Ruitenberg, J.W.; Witteveen, M.J.; Jonsson, M.P.; Grosberg, A.Y.; Rabin, Y.; Dekker, C. Direct observation of DNA knots using a solid-state nanopore. Nat. Nanotechnol. 2016, 11, 1093–1097. [Google Scholar] [CrossRef] [PubMed]
- Suma, A.; Micheletti, C. Pore translocation of knotted DNA rings. Proc. Natl. Acad. Sci. USA 2017, 114, E2991–E2997. [Google Scholar] [CrossRef] [PubMed]
- Sulkowska, J.I.; Sulkowski, P.; Szymczak, P.; Cieplak, M. Stabilizing effect of knots on proteins. Proc. Natl. Acad. Sci. USA 2008, 105, 19714–19719. [Google Scholar] [CrossRef] [PubMed]
- Ziegler, F.; Limb, N.C.H.; Mandal, S.S.; Pelz, B.; Ng, W.P.; Schlierf, M.; Jackson, S.E.; Rief, M. Knotting and unknotting of a protein in single molecule experiments. Proc. Natl. Acad. Sci. USA 2016, 113, 7533–7538. [Google Scholar] [CrossRef] [PubMed]
- Caraglio, M.; Micheletti, C.; Orlandini, E. Physical Links: Defining and detecting inter-chain entanglement. Sci. Rep. 2017, 7, 1156. [Google Scholar] [CrossRef] [PubMed]
- Cappella, B.; Dietler, G. Force-distance curves by atomic force microscopy. Surf. Sci. Rep. 1999, 34, 1–104. [Google Scholar] [CrossRef]
- Ritort, F. Single-molecule experiments in biological physics: Methods and applications. J. Phys. 2006, 18, R531–R583. [Google Scholar] [CrossRef] [PubMed]
- Kremer, K.; Grest, G. Dynamics of entangled linear polymer melts: A molecular dynamics simulation. J. Chem. Phys. 1990, 92, 5057–5086. [Google Scholar] [CrossRef]
- Plimpton, S.J. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Janse van Rensburg, E.J.; Sumners, D.W.; Wasserman, E.; Whittington, S.G. Entanglement complexity of self-avoiding walks. J. Phys. A 1992, 25, 6557–6566. [Google Scholar] [CrossRef]
- Marcone, B.; Orlandini, E.; Stella, A.L.; Zonta, F. What is the length of a knot in a polymer? J. Phys. A 2005, 38, L15–L21. [Google Scholar] [CrossRef]
- Millett, K.; Dobay, A.; Stasiak, A. Linear random knots and their scaling behavior. Macromolecules 2005, 38, 601–606. [Google Scholar] [CrossRef]
- Tubiana, L.; Orlandini, E.; Micheletti, C. Profiling the arc entanglement of compact ring polymers: A comparison of different arc-closure schemes with applications to knot localization. Prog. Theor. Phys. 2011, 191, 192–204. [Google Scholar] [CrossRef]
- Baiesi, M.; Orlandini, E.; Trovato, A.; Seno, F. Linking in domain-swapped protein dimers. Sci. Rep. 2016, 6, 33872. [Google Scholar] [CrossRef] [PubMed]
- Dabrowski-Tumanski, P.; Jarmolinska, A.I.; Niemyska, W.; Rawdon, E.J.; Millett, K.C.; Sulkowska, J.I. LinkProt: A database collecting information about biological links. Nucl. Acids Res. 2016. [Google Scholar] [CrossRef] [PubMed]
- Dabrowski-Tumanski, P.; Sulkowska, J.I. Topological knots and links in proteins. Proc. Natl. Acad. Sci. USA 2017, 114, 3415–3420. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Chwastyk, M.; Cieplak, M. Structural entanglements in protein complexes. J. Chem. Phys. 2017, 146, 225102. [Google Scholar] [CrossRef]
- Buck, G.; Simon, J. Energy and length of knots. In Lectures at Knots ’96; Series on Knots and Everything; Suzuki, S., Ed.; World Scientific: Singapore, 1997; Volume 15, pp. 219–235. [Google Scholar]
- D’Adamo, G.; Orlandini, E.; Micheletti, C. Linking of Ring Polymers in Slit-Like Confinement. Macromolecules 2017, 50, 1713–1718. [Google Scholar] [CrossRef]
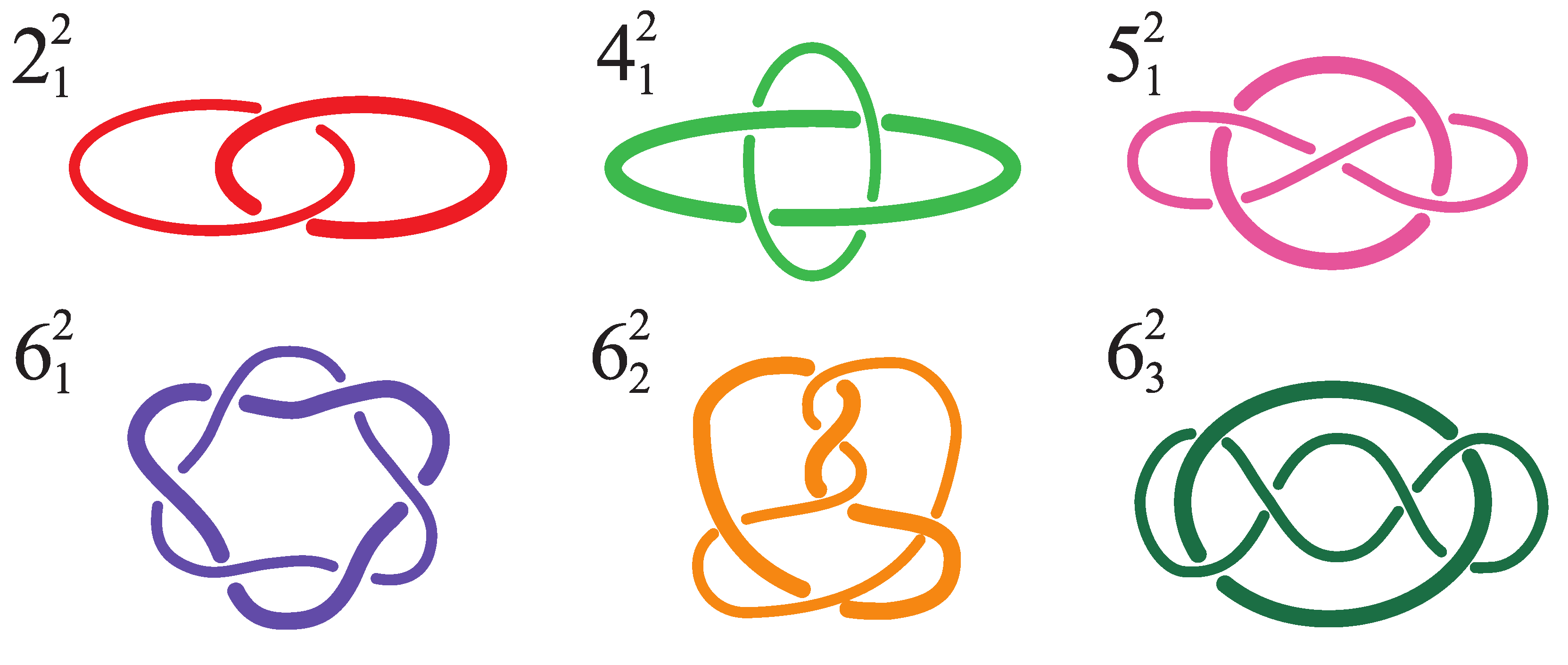
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Caraglio, M.; Micheletti, C.; Orlandini, E. Mechanical Pulling of Linked Ring Polymers: Elastic Response and Link Localisation. Polymers 2017, 9, 327. https://doi.org/10.3390/polym9080327
Caraglio M, Micheletti C, Orlandini E. Mechanical Pulling of Linked Ring Polymers: Elastic Response and Link Localisation. Polymers. 2017; 9(8):327. https://doi.org/10.3390/polym9080327
Chicago/Turabian StyleCaraglio, Michele, Cristian Micheletti, and Enzo Orlandini. 2017. "Mechanical Pulling of Linked Ring Polymers: Elastic Response and Link Localisation" Polymers 9, no. 8: 327. https://doi.org/10.3390/polym9080327
APA StyleCaraglio, M., Micheletti, C., & Orlandini, E. (2017). Mechanical Pulling of Linked Ring Polymers: Elastic Response and Link Localisation. Polymers, 9(8), 327. https://doi.org/10.3390/polym9080327