Statistical and Dynamical Properties of Topological Polymers with Graphs and Ring Polymers with Knots
Abstract
:1. Introduction
1.1. Topological Polymers and Knotted Ring Polymers
1.2. Knotted Ring Polymers in Solution
1.3. Approaches to Topological Polymers with Nontrivial Chemical Connectivity
1.4. Contents of the Review
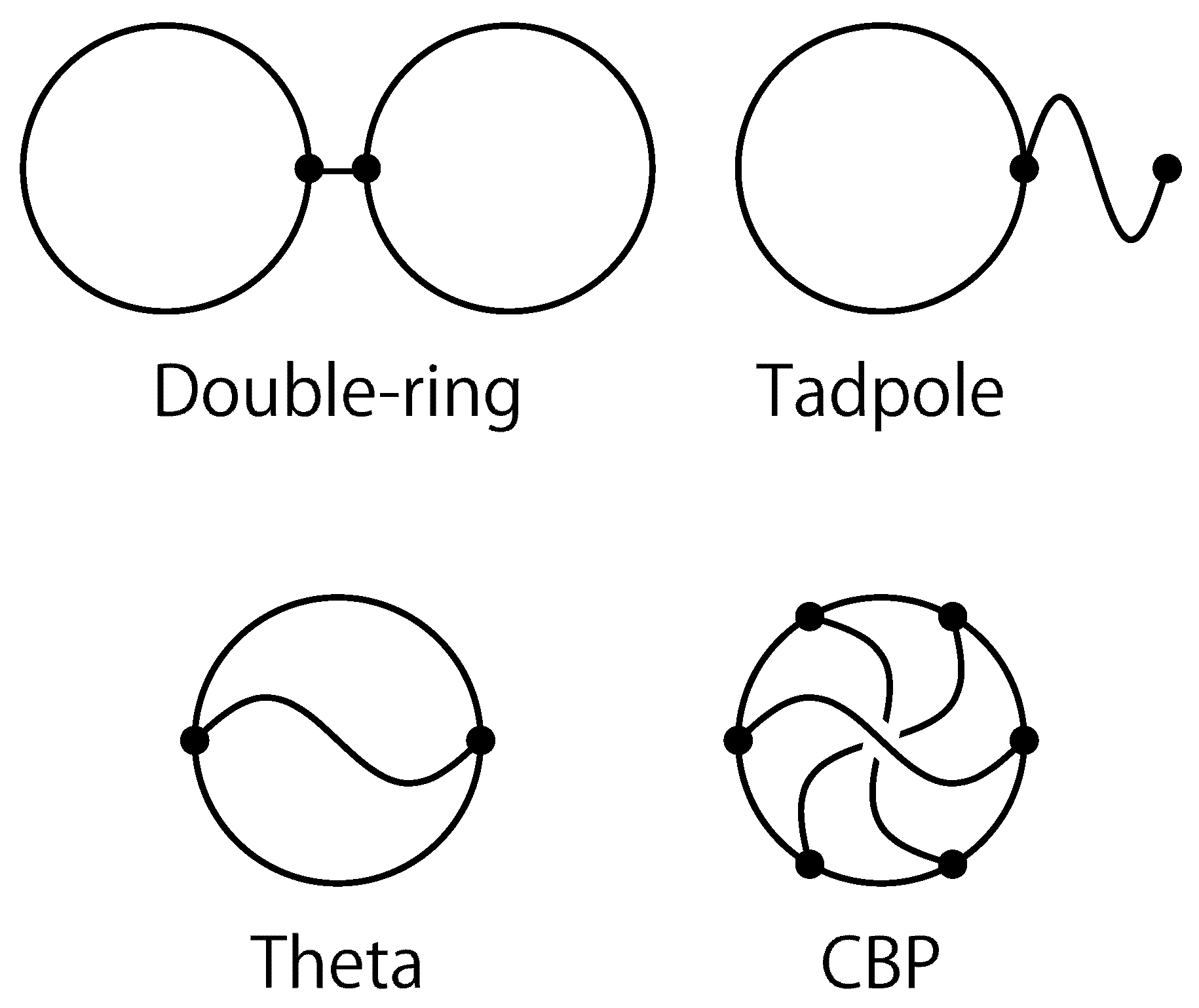
2. Topological Polymers with Various Graphs and Numerical Methods
2.1. Numerical Method I: Ideal Topological Polymers
2.1.1. Linear Time Algorithm Based on Quaternions
2.1.2. Generating Random Configurations of Ideal Topological Polymers
2.2. Numerical Method II: Molecular Dynamics Simulation
The Kremer–Grest Model through LAMMPS
3. Gyration and Hydrodynamic Radii of Topological Polymers
3.1. Mean-Square Radius of Gyration for Topological Polymers
3.2. Diffusion Coefficient via the Hydrodynamic Radius for a Topological Polymer
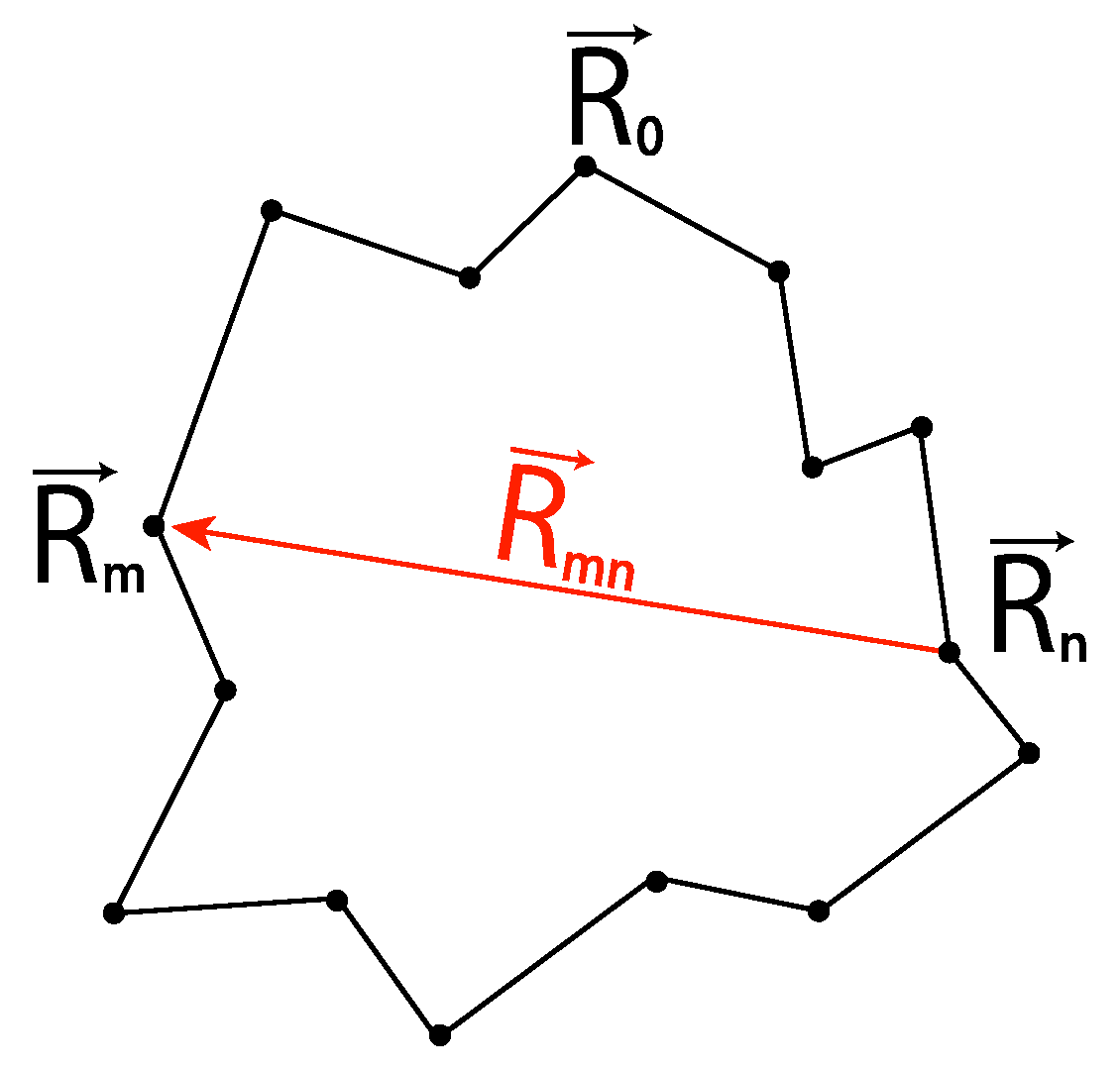
3.3. Ratio in Terms of the Mean-Square Deviations of the Distance between Two Segments: Universality of the Ratio
3.4. Estimates of the Ratio of the Gyration to Hydrodynamic Radii
4. Correlation Functions of Topological Polymers
4.1. Exponents of Short Distance Intrachain Correlation of SAW
4.2. Exact Expression of the Pair Distribution Function of a Gaussian Ring Polymer
4.3. Gyration and Hydrodynamic Radii in Terms of the Distance Distribution Function
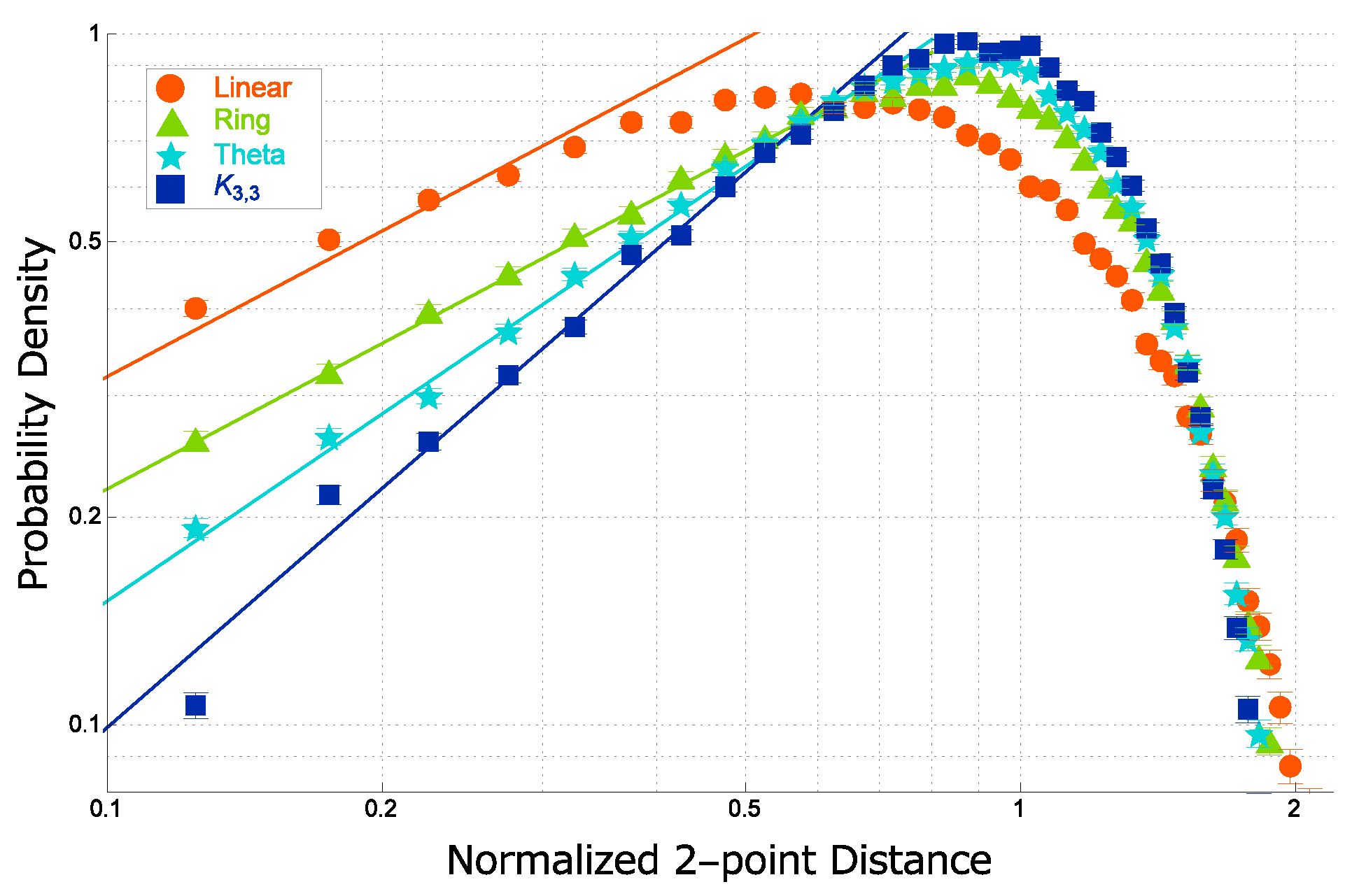
4.4. Real Topological Polymers Showing Enhanced Short-Range Correlation
5. The Probability of Random Knotting
5.1. Definition of the Knotting Probability
5.2. Experiments Measuring the Knotting Probability
5.3. Numerical Method for Evaluating the Knotting Probabilities
5.4. Cylindrical SAPs as the Discrete Worm-Like Chains
5.5. Formula for the N-Dependence of the Knotting Probability
5.6. Unknotting Probability versus Excluded Volume
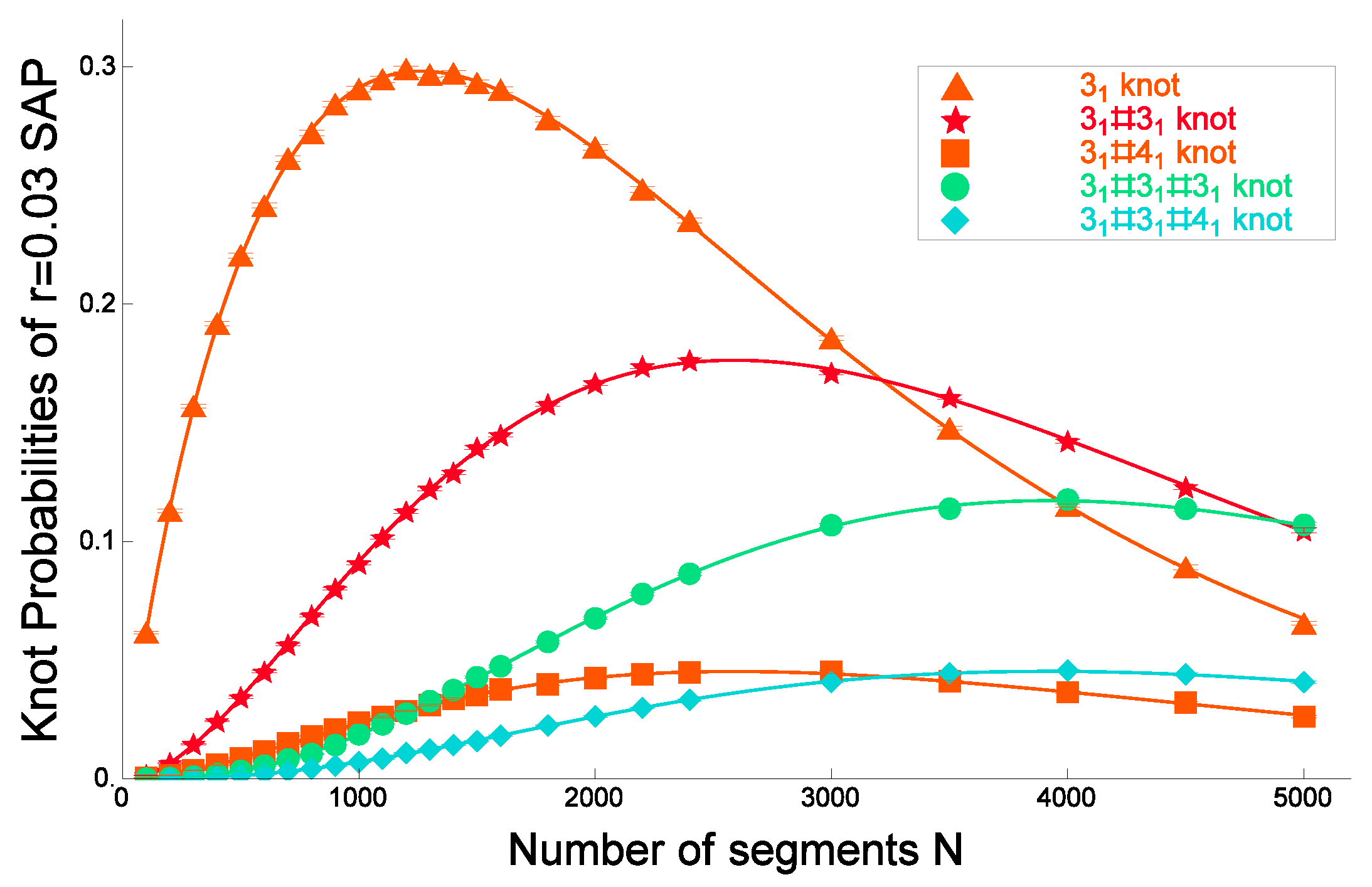
5.7. Random Knotting Probabilities of Composite Knots
6. Scaling Behavior of Random Knots
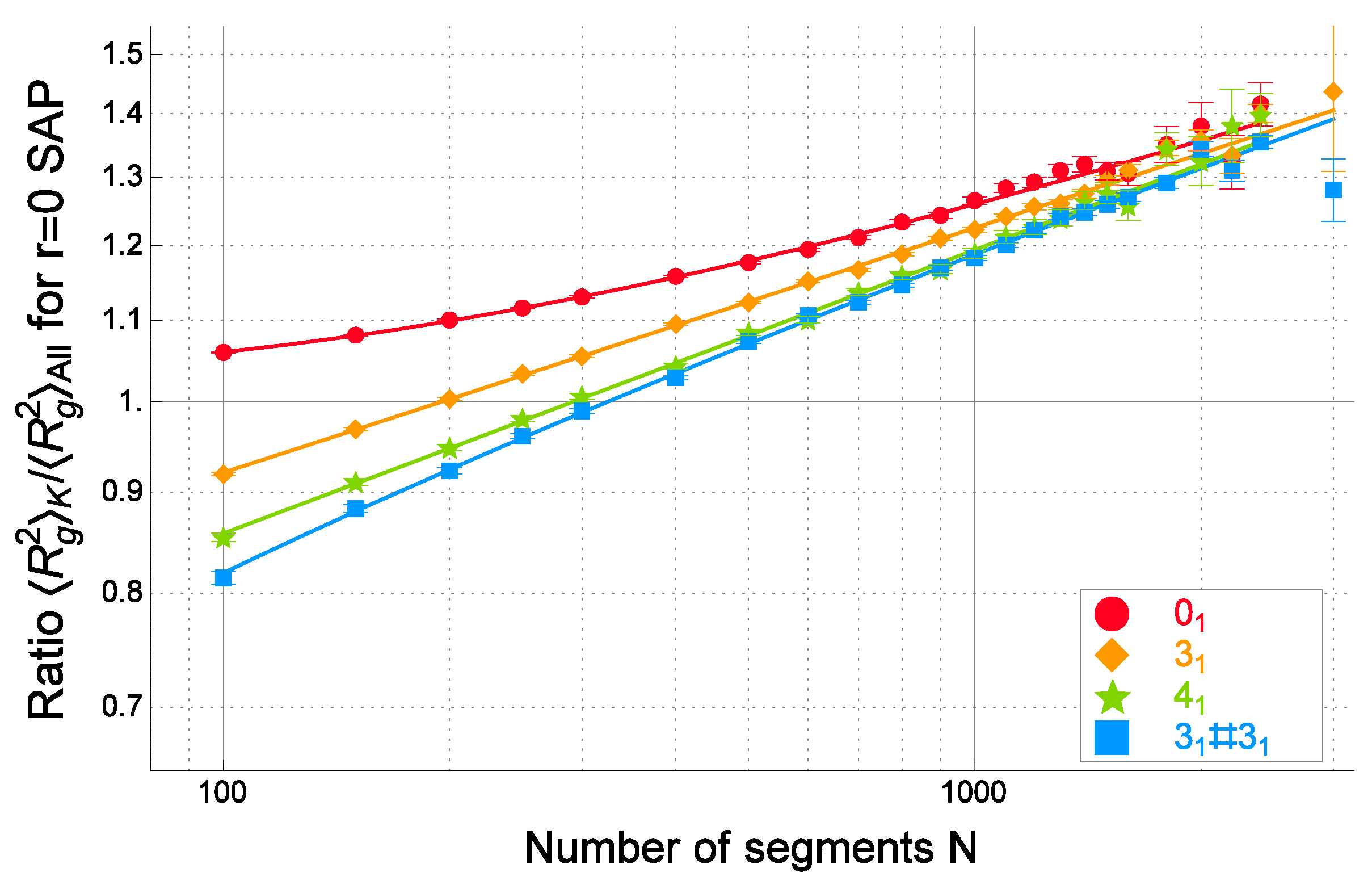
6.1. Mean-Square Radius of Gyration for RP and SAP under Topological Constraints
6.2. Topological Swelling of Random Knots
6.3. Effective Scaling Exponent of RP with Fixed Knot
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Semlyen, J.A. Cyclic Polymers; Elsevier Applied Science Publishers: New York, NY, USA, 1986. [Google Scholar]
- Bates, A.D.; Maxwell, A. DNA Topology; Oxford University Press: Oxford, UK, 2005. [Google Scholar]
- Orlandini, E.; Whittington, S.G. Statistical topology of closed curves: Some applications in polymer physics. Rev. Mod. Phys. 2007, 79, 611. [Google Scholar] [CrossRef]
- Micheletti, C.; Marenduzzo, D.; Orlandini, E. Polymers with spatial or topological constraints: Theoretical and computational results. Phys. Rep. 2011, 504, 1–73. [Google Scholar] [CrossRef]
- Taylor, W.R. A deeply knotted protein structure and how it might fold. Nature 2000, 406, 916–919. [Google Scholar] [CrossRef] [PubMed]
- Stasiak, A.; Shimokawa, K.; Tsurusaki, K.; Takano, H.; Imai, M.; Deguchi, T. Knots and Soft-Matter Physics: Topology of Polymers and Related Topics in Physics, Mathematics and Biology; Bussei-Kenkyu: Kyoto, Japan, 2009; Volume 92, pp. 16–19. [Google Scholar]
- Stasiak, A.; Shimokawa, K.; Tsurusaki, K.; Takano, H.; Deguchi, T. Statistical physics and topology of polymers with ramifications to structure and function of DNA and proteins. Prog. Theor. Phys. Suppl. 2011, 191, 235–244. [Google Scholar]
- Tezuka, Y. Topological Polymer Chemistry: Progress in Cyclic Polymers in Syntheses, Properties and Functions; World Scientific Publishing Company: Singapore, 2013. [Google Scholar]
- Kramers, H.A. The Behavior of Macromolecules in Inhomogeneous Flow. J. Chem. Phys. 1946, 14, 415–424. [Google Scholar] [CrossRef]
- Zimm, B.H.; Stockmayer, W.H. The Dimension of Chain Molecules Containing Branches and Rings. J. Chem. Phys. 1949, 17, 1301–1314. [Google Scholar] [CrossRef]
- Casassa, E.F. Some Statistical Properties of Flexible Ring Polymers. J. Polym. Sci. Part A 1965, 3, 605–614. [Google Scholar] [CrossRef]
- Bloomfield, V.; Zimm, B.H. Viscosity, sedimentation, et cetera, of Ring- and Straight-Chain Polymers in Dilute Solution. J. Chem. Phys. 1966, 44, 315–323. [Google Scholar] [CrossRef]
- Vinograd, J.; Lebowitz, J.; Radloff, R.; Watson, R.; Laipis, P. The twisted circular form of polyoma viral DNA. Proc. Natl. Acad. Sci. USA 1965, 53, 1104–1111. [Google Scholar] [CrossRef] [PubMed]
- Krasnow, M.A.; Stasiak, A.; Spengler, S.J.; Dean, F.; Koller, T.; Cozzarelli, N.R. Determination of the absolute handedness of knots and catenanes of DNA. Nature 1983, 304, 559–560. [Google Scholar] [CrossRef] [PubMed]
- Dean, F.B.; Stasiak, A.; Koller, T.; Cozzarelli, N.R. Duplex DNA Knots Produced by Escherichia coli Topoisomerase I. J. Biol. Chem. 1985, 260, 4975–4983. [Google Scholar] [PubMed]
- Craik, D.J. Seamless Proteins Tie up Their Loose Ends. Science 2006, 311, 1563–1564. [Google Scholar] [CrossRef] [PubMed]
- Oike, H.; Imaizumi, H.; Mouri, T.; Yoshioka, Y.; Uchibori, A.; Tezuka, Y. Designing Unusual Polymer Topologies by Electrostatic Self-Assembly and Covalent Fixation. J. Am. Chem. Soc. 2000, 122, 9592–9599. [Google Scholar] [CrossRef]
- Tezuka, Y.; Oike, H. Topologoical Polymer Chemistry: Systematic Classification of Nonlinear Polymer Topologies. J. Am. Chem. Soc. 2001, 123, 11570–11576. [Google Scholar] [CrossRef] [PubMed]
- Bielawski, C.W.; Benitez, D.; Grubbs, R.H. An “Endles” Route to Cyclic Polymers. Science 2002, 297, 2041–2044. [Google Scholar]
- Cho, D.; Masuoka, K.; Koguchi, K.; Asari, T.; Kawaguchi, D.; Takano, A.; Matsushita, Y. Preparation and Characterization of Cyclic Polystyrenes. Polym. J. 2005, 37, 506–511. [Google Scholar] [CrossRef]
- Takano, A.; Kushida, Y.; Aoki, K.; Masuoka, K.; Hayashida, K.; Cho, D.; Kawaguchi, D.; Matsushita, Y. HPLC Characterization of Cyclization Reaction Product Obtained by End-to-End Ring Closure Reaction of a Telechelic Polystyrene. Macromolecules 2007, 40, 679–681. [Google Scholar] [CrossRef]
- Laurent, B.A.; Grayson, S. An Efficient Route to Well-Defined Macrocyclic Polymers via “Click” Cyclization. J. Am. Chem. Soc. 2006, 128, 4238–4239. [Google Scholar] [CrossRef] [PubMed]
- Sugai, N.; Heguri, H.; Ohta, K.; Meng, Q.; Yamamoto, T.; Tezuka, Y. Effective Click Construction of Bridged- and Spiro-Multicyclic Polymer Topologies with Tailored Cyclic Prepolymers (kyklo-Telechelics). J. Am. Chem. Soc. 2010, 132, 14790–14802. [Google Scholar] [CrossRef] [PubMed]
- Sugai, N.; Heguri, H.; Yamamoto, T.; Tezuka, Y. A Programmed Polymer Folding: Click and Clip Construction of Doubly Fused Tricyclic and Triply Fused Tetracyclic Polymer Topologies. J. Am. Chem. Soc. 2011, 133, 19694–19697. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, T.; Yamamoto, T.; Tezuka, Y. Constructing a Macromolecular K3,3 Graph through Electrostatic Self-Assembly and Covalent Fixation with a Dendric Polymer Precursor. J. Am. Chem. Soc. 2014, 136, 10148–10155. [Google Scholar] [CrossRef] [PubMed]
- Haglund, E.; Sulkowska, J.I.; Noel, J.K.; Lammert, H.; Onuchic, J.N.; Jennings, P.A. Pierced Lasso Bundles Are a New Class of Knot-like Motifs. PLoS Comput. Biol. 2014, 10, e1003613. [Google Scholar] [CrossRef] [PubMed]
- Fukatsu, M.; Kurata, M. Hydrodynamic properties of flexible-ring macromolecules. J. Chem. Phys. 1966, 44, 4539–4545. [Google Scholar] [CrossRef]
- Uehara, E.; Deguchi, T. Statistical and hydrodynamic properties of double-ring polymers with a fixed linking number between twin rings. J. Chem. Phys. 2014, 140, 044902. [Google Scholar] [CrossRef] [PubMed]
- Castle, T.; Evans, M.E.; Hyde, S.T. Ravels: Knot-free but not free. Novel entanglements of graphs in 3-space. New J. Chem. 2008, 32, 1484–1492. [Google Scholar] [CrossRef]
- Bon, M.; Vernizzi, G.; Orland, H.; Zee, A. Topological classification of RNA structures. J. Mol. Biol. 2008, 379, 900–911. [Google Scholar] [CrossRef] [PubMed]
- Uehara, E.; Deguchi, T. Statistical and hydrodynamic properties of topological polymers for various graphs showing enhanced short-range correlation. J. Chem. Phys. 2016, 145, 164905. [Google Scholar] [CrossRef] [PubMed]
- Broedersz, C.P.; MacKintosh, F.C. Modeling semiflexible polymer networks. Rev. Mod. Phys. 2014, 86, 995. [Google Scholar] [CrossRef]
- Stigter, D. Interactions of Highly Charged Colloidal Cylinders with Applications to Double-Stranded DNA. Biopolymers 1997, 16, 1435–1448. [Google Scholar] [CrossRef] [PubMed]
- Ryubenkov, V.V.; Cozzarelli, N.R.; Vologodskii, A. Probability of DNA knotting and the effective diameter of the DNA double helix. Proc. Natl. Acad. Sci. USA 1993, 90, 5307–5311. [Google Scholar] [CrossRef]
- Shaw, S.Y.; Wang, J.C. Knotting of a DNA Chain During Ring Closure. Science 1993, 260, 533–536. [Google Scholar] [CrossRef] [PubMed]
- Grosberg, A.Y.; Khokhlov, A.R. Statistical Physics of Macromolecules; AIP Press: New York, NY, USA, 1994. [Google Scholar]
- Delbrück, M. Knotting problems in biology. In Mathematical Problems in the Biological Sciences; Bellman, R.E., Ed.; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1962; Volume 14, p. 55. [Google Scholar]
- Frisch, H.L.; Wasserman, E. Chemical Topology. J. Am. Chem. Soc. 1961, 83, 3789–3795. [Google Scholar] [CrossRef]
- Rolfsen, D. Knots and Links; Publish or Perish: Wilmington, DE, USA, 1976. [Google Scholar]
- Vologodskii, A.V.; Lukashin, A.V.; Frank-Kamenetskii, M.D.; Anshelevich, V.V. The knot probability in statistical mechanics of polymer chains. Sov. Phys. JETP 1974, 39, 1059–1063. [Google Scholar]
- Vologodskii, A.V.; Lukashin, A.V.; Frank-Kamenetskii, D. Topological interaction between polymer chains. Sov. Phys. JETP 1975, 40, 932–936. [Google Scholar]
- Des Cloizeaux, J.; Mehta, M.L. Topological constraints on polymer rings and critical indices. J. Phys. 1979, 40, 655–670. [Google Scholar] [CrossRef]
- Des Cloizeaux, J. Ring polymers in solution: Topological effects. J. Phys. Lett. 1981, 42, L433–L436. [Google Scholar] [CrossRef]
- Ten Brinke, G.; Hadziioannou, G. Topological Constraints and Their Influence on the Properties of Synthetic Macromolecular Systems. 1. Cyclic Macromolecules. Macromolecules 1987, 20, 480–485. [Google Scholar] [CrossRef]
- Sumners, D.W.; Whittington, S. Knots in self-avoiding walks. J. Phys. A Math. Gen. 1988, 21, 1689–1694. [Google Scholar] [CrossRef]
- Pippenger, N. Knots in random walks. Discret. Appl. Math. 1989, 25, 273–278. [Google Scholar] [CrossRef]
- Shishido, K.; Komiyama, N.; Ikawa, S. Increased Production of a Knotted Form of Plasmid pBR322 DNA in Escherichia coli DNA Topoisomerase Mutants. J. Mol. Biol. 1987, 193, 215–218. [Google Scholar] [CrossRef]
- Vologodskii, A.V.; Crisona, N.J.; Laurie, B.; Pieranski, P.; Katritch, V.; Dubochet, J.; Stasiak, A. Sedimentation and Electrophoretic Migration of DNA Knots and Catenanes. J. Mol. Biol. 1998, 278, 1–3. [Google Scholar] [CrossRef] [PubMed]
- Grosberg, A.Y.; Feigel, A.; Rabin, Y. Flory-type theory of a knotted ring polymer. Phys. Rev. E 1996, 54, 6618–6622. [Google Scholar] [CrossRef]
- Katritch, V.; Bednar, J.; Michoud, D.; Scharein, R.G.; Dubochet, J.; Stasiak, A. Geometry and physics of knots. Nature 1996, 384, 142–145. [Google Scholar] [CrossRef]
- Stasiak, A.; Katritch, V.; Kauffman, L.H. (Eds.) Ideal Knots; World Scientific Publishing Co., Inc.: Singapore, 1999. [Google Scholar]
- Robertson, R.M.; Laib, S.; Smith, D.E. Diffusion of isolated DNA molecules: Dependence on length and topology. Proc. Natl. Acad. Sci. USA 2006, 103, 7310–7314. [Google Scholar] [CrossRef] [PubMed]
- Araki, S.; Nakai, T.; Hizume, K.; Takeyasu, K.; Yoshikawa, K. Hydrodynamic radius of circular DNA is larger than that of linear DNA. Chem. Phys. Lett. 2006, 418, 255–259. [Google Scholar] [CrossRef]
- Roovers, J.R.; Toporowski, P.M. Synthesis of high molecular weight ring polystyrenes. Macromolecules 1983, 16, 843–849. [Google Scholar] [CrossRef]
- Iwata, K. Θ Temperature of ring polymers: Another evidence of topological interaction. Macromolecules 1989, 22, 3702–3706. [Google Scholar] [CrossRef]
- Tanaka, F. Osmotic pressure of ring-polymer solutions. J. Chem. Phys. 1987, 87, 4201. [Google Scholar] [CrossRef]
- Ohta, Y.; Nakamura, M.; Matsushita, Y.; Takano, A. Synthesis, separation and characterization of knotted ring polymers. Polymer 2012, 53, 466–470. [Google Scholar] [CrossRef]
- Virnau, P.; Mirny, L.A.; Kardar, M. Intricate Knots in Proteins: Function and Evolution. PLoS Comput. Biol. 2006, 2, e122. [Google Scholar] [CrossRef] [PubMed]
- Sulkowska, J.I.; Sulkowski, P.; Szymczak, P.; Cieplak, M. Tightening of Knots in Proteins. Phys. Rev. Lett. 2008, 100, 058106. [Google Scholar] [CrossRef] [PubMed]
- Madras, N.; Slade, G. The Self-Avoiding Walk; Birkhäuser: Boston, MA, USA, 1993. [Google Scholar]
- Michels, J.P.J.; Wiegel, F.W. On the topology of a polymer ring. Proc. R. Soc. Lond. Ser. A 1986, 403, 269–284. [Google Scholar] [CrossRef]
- Van Rensburg, E.J.J.; Whittington, S.G. The knot probability in lattice polygons. J. Phys. A Math. Gen. 1990, 23, 3573–3590. [Google Scholar] [CrossRef]
- Koniaris, K.; Muthukumar, M. Knottedness in ring polymers. Phys. Rev. Lett. 1991, 66, 2211–2214. [Google Scholar] [CrossRef] [PubMed]
- Deguchi, T.; Tsurusaki, K. A New Algorithm for Numerical Calculation of Link Invariants. Phys. Lett. A 1993, 174, 29–37. [Google Scholar] [CrossRef]
- Deguchi, T.; Tsurusaki, K. Topology of Closed Random Polygons. J. Phys. Soc. Jpn. 1993, 62, 1411–1414. [Google Scholar] [CrossRef]
- Deguchi, T.; Tsurusaki, K. A Statistical Study of Random Knotting Using the Vassiliev Invariants. J. Knot Theory Ramif. 1994, 3, 321–353. [Google Scholar] [CrossRef]
- Deguchi, T.; Tsurusaki, K. Universality of Random Knotting. Phys. Rev. E 1997, 55, 6245–6248. [Google Scholar] [CrossRef]
- Deguchi, T.; Tsurusaki, K. Random knots and links and applications to polymer physics. In Lectures at Knots’96; Suzuki, S., Ed.; World Scientific: Singapore, 1997; pp. 95–122. [Google Scholar]
- Orlandini, E.; Tesi, M.C.; van Rensburg, E.J.J.; Whittington, S.G. Entropic exponents of lattice polygons with specified knot type. J. Phys. A Math. Gen. 1996, 29, L299–L303. [Google Scholar] [CrossRef]
- Orlandini, E.; Tesi, M.C.; van Rensburg, E.J.J.; Whittington, S.G. Asymptotics of knotted lattice polygons. J. Phys. A Math. Gen. 1998, 31, 5953–5967. [Google Scholar] [CrossRef]
- Shimamura, M.K.; Deguchi, T. Characteristic length of random knotting for cylindrical self-avoiding polygons. Phys. Lett. A 2000, 274, 184–191. [Google Scholar] [CrossRef]
- Shimamura, M.K.; Deguchi, T. Topological entropy of a stiff ring polymer and its connection to DNA knots. J. Phys. Soc. Jpn. 2001, 70, 1523–1536. [Google Scholar] [CrossRef]
- Yao, A.; Matsuda, H.; Tsukahara, H.; Shimamura, M.K.; Deguchi, T. On the dominance of trivial knots among SAP on a cubic lattice. J. Phys. A Math. Gen. 2001, 34, 7563–7577. [Google Scholar] [CrossRef]
- Shimamura, M.K.; Deguchi, T. Knot complexity and the probability of random knotting. Phys. Rev. E 2002, 66, R040801. [Google Scholar] [CrossRef] [PubMed]
- Shimamura, M.K.; Deguchi, T. Geometric complexity of conformations of ring polymers under topological constraints. Phys. Rev. E 2003, 68, 061108. [Google Scholar] [CrossRef] [PubMed]
- Baiesi, M.; Orlandini, E.; Stella, A.L. The entropic cost to tie a knot. J. Stat. Mech. 2010, P06012. [Google Scholar] [CrossRef]
- Akita, Y. Effects of Topology on Statistical Mechanics of Ring Polymers: Distance Distribution and the Knotting Probability of Random Knots. Master’s Thesis, Ochanomizu University, Tokyo, Japan, 2010. (In Japanese). [Google Scholar]
- Van Rensburg, E.J.J.; Rechnitzer, A. On the universality of knot probability ratios. J. Phys. A Math. Theor. 2011, 44, 162002. [Google Scholar] [CrossRef]
- Deguchi, T.; Tsurusaki, K. Topological effects on the statistical and dynamical properties of ring polymers in solution. In Topological Polymer Chemistry: Progress in Cyclic Polymers in Syntheses, Properties and Functions; Tezuka, Y., Ed.; World Scientific Publishing: Singapore, 2013; pp. 221–264. [Google Scholar]
- Tubiana, L. Computational study on the progressive factorization of composite knots into separated prime components. Phys. Rev. E 2014, 89, 052602. [Google Scholar] [CrossRef] [PubMed]
- Uehara, E.; Deguchi, T. Characteristic length of the knotting probability revisited. J. Phys. Condens. Matter 2015, 27, 354104. [Google Scholar] [CrossRef] [PubMed]
- Deutsch, J.M. Equilibrium size of large ring molecules. Phys. Rev. E 1999, 59, R2539. [Google Scholar] [CrossRef]
- Grosberg, A.Y. Critical Exponents for Random Knots. Phys. Rev. Lett. 2000, 85, 3858. [Google Scholar] [CrossRef] [PubMed]
- Quake, S.R. Topological Effects of Knots in Polymers. Phys. Rev. Lett. 1994, 73, 3317–3320. [Google Scholar] [CrossRef] [PubMed]
- Shimamura, M.K.; Deguchi, T. Gyration radius of a circular polymer under a topological constraint with excluded volume. Phys. Rev. E 2001, 64, 020801. [Google Scholar] [CrossRef] [PubMed]
- Shimamura, M.K.; Deguchi, T. Finite-size and asymptotic behaviors of the gyration radius of knotted cylindrical self-avoiding polygons. Phys. Rev. E 2002, 65, 051802. [Google Scholar] [CrossRef] [PubMed]
- Lai, P.-Y. Dynamics of polymer knots at equilibrium. Phys. Rev. E 2002, 66, 021805. [Google Scholar] [CrossRef] [PubMed]
- Shimamura, M.K.; Deguchi, T. Anomalous finite-size effects for the mean-squared gyration radius of Gaussian random knots. J. Phys. A Math. Gen. 2002, 35, L241–L246. [Google Scholar] [CrossRef]
- Dobay, A.; Dubochet, J.; Millett, K.; Sottas, P.E.; Stasiak, A. Scaling behavior of random knots. Proc. Natl. Acad. Sci. USA 2003, 100, 5611–6515. [Google Scholar] [CrossRef] [PubMed]
- Matsuda, H.; Yao, A.; Tsukahara, H.; Deguchi, T.; Furuta, K.; Inami, T. Average size of random polygons with fixed knot topology. Phys. Rev. E 2003, 68, 011102. [Google Scholar] [CrossRef] [PubMed]
- Moore, N.T.; Lua, R.C.; Grosberg, A.Y. Topologically driven swelling of a polymer loop. Proc. Natl. Acad. Sci. USA 2004, 101, 13431–13435. [Google Scholar] [CrossRef] [PubMed]
- Shimamura, M.K.; Deguchi, T. On the mean gyration radius and the radial distribution function of ring polymers with excluded-volume under a topological constraint. In Physical and Numerical Models in Knot Theory; Calvo, J.A., Millett, K.C., Rawdon, E.J., Stasiak, A., Eds.; World Scientific: Singapore, 2005; pp. 399–419. [Google Scholar]
- Marcone, B.; Orlandini, E.; Stella, A.L.; Zonta, F. Size of knots in ring polymers. Phys. Rev. E 2007, 75, 041105. [Google Scholar] [CrossRef] [PubMed]
- Rawdon, E.; Dobay, A.; Kern, J.C.; Millett, K.C.; Piatek, M.; Plunkett, P.; Stasiak, A. Scaling behavior and equilibrium lengths of knotted polymers. Macromolecules 2008, 41, 4444–4451. [Google Scholar] [CrossRef]
- Takano, A.; Ohta, Y.; Masuoka, K.; Matsubara, K.; Nakano, T.; Hieno, A.; Itakura, M.; Takahashi, K.; Kinugasa, S.; Kawaguchi, D.; et al. Radii of Gyration of Ring-Shaped Polystyrenes with High Purity in Dilute Solutions. Macromolecules 2012, 45, 369–373. [Google Scholar] [CrossRef]
- Yao, A.; Tsukahara, H.; Deguchi, T.; Inami, T. Distribution of the distance between opposite nodes of random polygons with a fixed knot. J. Phys. A Math. Gen. 2004, 37, 7993–8006. [Google Scholar] [CrossRef]
- Shimamura, M.K.; Kamata, K.; Yao, A.; Deguchi, T. Scattering functions of knotted ring polymers. Phys. Rev. E 2005, 72, 041804. [Google Scholar] [CrossRef] [PubMed]
- Deguchi, T.; Yao, A. Scattering Functions and Correlation functions of Random Knots. OCAMI Stud. 2007, 1, 165–178. [Google Scholar]
- Yao, A.; Akita, Y.; Deguchi, T. Novel criticality of random knots. 2017; in preparation. [Google Scholar]
- Dünweg, B.; Reith, D.; Steinhauser, M.; Kremer, K. Corrections to scaling in the hydrodynamic properties of dilute polymer solutions. J. Chem. Phys. 2002, 117, 914–924. [Google Scholar] [CrossRef]
- Liu, B.; Dünweg, B. Translational diffusion of polymer chains with excluded volume and hydrodynamic interactions by Brownian dynamics simulation. J. Chem. Phys., 2003, 118, 8061–8072. [Google Scholar] [CrossRef]
- Kanaeda, N.; Deguchi, T. Diffusion of a ring polymer in good solution via the Brownian dynamics with no bond crossing. J. Phys. A Math. Theor. 2008, 41, 145004. [Google Scholar] [CrossRef]
- Kanaeda, N.; Deguchi, T. Universality in the diffusion of knots. Phys. Rev. E 2009, 79, 021806. [Google Scholar] [CrossRef] [PubMed]
- Kanaeda, N.; Deguchi, T. Universal ratios in the dynamics of open and closed chains of linked ring polymers in solution via Brownian dynamics. Prog. Theor. Phys. Suppl. 2011, 191, 146–153. [Google Scholar] [CrossRef]
- Iwata, K.; Kimura, T. Topological distribution functions and the second virial coefficients of ring polymers. J. Chem. Phys. 1981, 74, 2039–2048. [Google Scholar] [CrossRef]
- Deguchi, T. Topological entropic force associated with the topological swelling of random knots and links. In Physical and Numerical Models in Knot Theory; Calvo, J.A., Millett, K.C., Rawdon, E.J., Stasiak, A., Eds.; World Scientific: Singapore, 2005; pp. 343–362. [Google Scholar]
- Hirayama, N.; Tsurusaki, K.; Deguchi, T. Linking probabilities of off-lattice self-avoiding polygons and the effects of excluded volume. J. Phys. A Math. Theor. 2009, 42, 105001. [Google Scholar] [CrossRef]
- Takano, A.; Kushida, Y.; Ohta, Y.; Masuoka, K.; Matsushita, Y. The second virial coefficients of highly-purified ring polystyrenes in cyclohexane. Polymer 2009, 50, 1300–1303. [Google Scholar] [CrossRef]
- Ida, D.; Nakatomi, D.; Yoshizaki, T. A Monte Carlo study of the second virial coefficient of semiflexible ring polymers. Polym. J. 2010, 42, 735–744. [Google Scholar] [CrossRef]
- Hirayama, N.; Tsurusaki, K.; Deguchi, T. General polygonal length dependence of the linking probability for ideal random polygons. Prog. Theor. Phys. Suppl. 2011, 191, 154–164. [Google Scholar] [CrossRef]
- Marcone, B.; Orlandini, E.; Stella, A.L.; Zonta, F. What is the length of a knot in a polygon? J. Phys. A Math. Gen. 2005, 38, L15–L21. [Google Scholar] [CrossRef]
- Orlandini, E.; Stella, A.L.; Vanderzande, C.; Zonta, F. Self-reptation and slow topological time scale of knotted ploymers. J. Phys. A Math. Theor. 2008, 41, 122002. [Google Scholar] [CrossRef]
- Metzler, R.; Hanke, A.; Dommersnes, P.G.; Kantor, Y.; Kardar, M. Equilibrium shapes of flat knots. Phys. Rev. Lett. 2002, 88, 188101. [Google Scholar] [CrossRef] [PubMed]
- Ercolini, E.; Valle, F.; Adamcik, J.; Witz, G.; Metzler, R.; de los Rios, P.; Roca, J.; Dietler, G. Fractal Dimension and Localization of DNA Knots. Phys. Rev. Lett. 2007, 98, 058102. [Google Scholar] [CrossRef] [PubMed]
- Cates, G.E.; Deutsch, J.M. Conjectures on the statistics of ring polymers. J. Phys. 1986, 47, 2121–2128. [Google Scholar] [CrossRef]
- Suzuki, J.; Takano, A.; Matsushita, Y. Topological effect in ring polymers investigated with Monte Carlo simulation. J. Chem. Phys. 2008, 129, 034903. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, J.; Takano, A.; Deguchi, T.; Matsushita, Y. Dimension of ring polymers in bulk studied by Monte-Carlo simulation and self-consistent theory. J. Chem. Phys. 2009, 131, 144902. [Google Scholar] [CrossRef] [PubMed]
- Vettorel, T.; Reigh, S.Y.; Yoon, D.Y.; Kremer, K. Monte-Carlo Method for Simulations of Ring Polymers in the Melt. Macromol. Rapid Commun. 2009, 30, 345–351. [Google Scholar] [CrossRef] [PubMed]
- Vettorel, T.; Grosberg, A.Y.; Kremer, K. Statistics of polymer rings in the melt: A numerical simulation study. Phys. Biol. 2009, 6, 025013. [Google Scholar] [CrossRef] [PubMed]
- Diao, Y. Minimal knotted polygons on the cubic lattice. J. Knot Theory Ramif. 1993, 2, 413–425. [Google Scholar] [CrossRef]
- Scharein, R.; Ishihara, K.; Arsuaga, J.; Diao, Y.; Shimokawa, K.; Vazquez, M. Bounds for the minimum step number of knots in the simple cubic lattice. J. Phys. A Math. Theor. 2009, 42, 475006. [Google Scholar] [CrossRef]
- Saka, S.; Takano, H. Relaxation of a Single Knotted Ring Polymer. J. Phys. Soc. Jpn. 2008, 77, 034001. [Google Scholar] [CrossRef]
- Baiesi, M.; Orlandini, E.; Stella, A.L. Ranking Knots of Random, Globular Polymer Rings. Phys. Rev. Lett. 2007, 99, 058301. [Google Scholar] [CrossRef] [PubMed]
- Hirayama, N.; Tsurusaki, K. Topological Interaction between Loop Structures in Polymer Networks and the Nonlinear Rubber Elasticity. Nihon Reoroji Gakkaishi 2011, 39, 65–73. [Google Scholar] [CrossRef]
- Flapan, E. When Topology Meets Chemistry; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Cantarella, J.; Deguchi, T.; Shonkwiler, C. Probability Theory of Random Polygons from the Quaternionic Viewpoint. Commun. Pure Appl. Math. 2014, 67, 1658–1699. [Google Scholar] [CrossRef]
- Uehara, E.; Tanaka, R.; Inoue, M.; Hirose, F.; Deguchi, T. Mean-square radius of gyration and hydrodynamic radius for topological polymers evaluated through the quaternionic algorithm. React. Funct. Polym. 2014, 80, 48–56. [Google Scholar] [CrossRef]
- Kremer, K.; Grest, G.S. Dynamics of entangled linear polymer melts: A molecular-dynamics simulation. J. Chem. Phys. 1990, 92, 5057. [Google Scholar] [CrossRef]
- Tezuka, Y. Private Communication. In Proceedings of the Grant-in-Aid for Scientific Research No. 26310206, Tokyo, Japan, 11 November 2015. [Google Scholar]
- De Gennes, P.G. Scaling Concepts in Polymer Physics; Cornell University Press: Ithaka, NY, USA; New York, NY, USA, 1979. [Google Scholar]
- Doi, M.; Edwards, S.F. The Theory of Polymer Dynamics; Oxford University Press: Oxford, UK, 1986. [Google Scholar]
- Rubinstein, M.; Colby, R.H. Polymer Physics; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Teraoka, I. Polymer Solutions an Introduction to Physical Properties; John Wiley & Sons: New York, NY, USA, 2002. [Google Scholar]
- Des Cloizeaux, J. Short range correlation between elements of a long polymer in a good solvent. J. Phys. 1980, 41, 223–238. [Google Scholar] [CrossRef]
- Uehara, E.; Deguchi, T. Exponents of intrachain correlation for self-avoiding walks and knotted self-avoiding polygons. J. Phys. A Math. Theor. 2013, 46, 345001. [Google Scholar] [CrossRef]
- Hausmann, J.-C.; Knutson, A. Polygon spaces and Grassmannians. Enseign. Math. 1997, 43, 137–198. [Google Scholar]
- Kapovich, M.; Millson, J.J. The symplectic geometry of polygons in Euclidean space. J. Differ. Geom. 1996, 44, 479–513. [Google Scholar] [CrossRef]
- Howard, B.; Manon, C.; Millson, J. The toric geometry of triangulated polygons in Euclidean space. Can. J. Math. 2011, 63, 878–937. [Google Scholar] [CrossRef]
- Cantarella, J.; Shonkwiler, C. The symplectic geometry of closed equilateral random walks in 3-space. Ann. Appl. Probab. 2016, 26, 549–596. [Google Scholar] [CrossRef]
- Cantarella, J.; Duplantier, B.; Shonkwiler, C.; Uehara, E. A fast direct sampling algorithm for equilateral closed polygons. J. Phys. A Math. Theor. 2016, 49, 275202. [Google Scholar] [CrossRef]
- Cantarella, J.; Deguchi, T.; Shonkwiler, C.; Uehara, E. A weighted algorithm for ideal topological polymers. 2017; in preparation. [Google Scholar]
- Moore, N.; Grosberg, A.Y. Limits of analogy between self-avoidance and topology-driven swelling of polymer loops. Phys. Rev. E 2005, 72, 061803. [Google Scholar] [CrossRef] [PubMed]
- Diao, Y.; Ernst, C.; Montemayor, A.; Ziegler, U. Generating equilateral random polygons in confinement III. J. Phys. A: Math. Theor. 2011, 45, 465003. [Google Scholar] [CrossRef]
- Pimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Compt. Phys. 1995, 117, 1–9. [Google Scholar] [CrossRef]
- Rapaport, D.C. The Art of Molecular Dynamics Simulation; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Suda, I.; Tominaga, Y.; Osa, M.; Yoshizaki, T.; Yamakawa, H. Transport Coefficients of Oligo- and Poly (α-methylstyrene)s in Dilute Solution. Macromolecules 2000, 33, 9322–9328. [Google Scholar] [CrossRef]
- Bishop, M.T.; Langley, K.H.; Karasz, F.E. Dynamic light-scattering studies of polymer diffusion in porous materials: Linear polystyrene in porous glass. Macromolecules 1989, 22, 1220–1231. [Google Scholar] [CrossRef]
- Schäfer, L. Excluded Volume Effects in Polymer Solutions; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1999. [Google Scholar]
- Fisher, M.E. Shape of a Self-Avoiding Walk or Polymer Chain. J. Chem. Phys. 1966, 44, 616–622. [Google Scholar] [CrossRef]
- McKenzie, D.S.; Moore, M.A. Shape of a self-avoiding polymer chain. J. Phys. A Gen. Phys. 1971, 4, L82–L86. [Google Scholar] [CrossRef]
- Des Cloizeaux, J. Lagrangian theory for a self-avoiding random chain. Phys. Rev. A 1974, 10, 1665–1669. [Google Scholar] [CrossRef]
- Oono, Y.; Ohta, T. The distribution function for internal distances in a self-avoding polymer chain. Phys. Lett. A 1981, 85, 480–482. [Google Scholar] [CrossRef]
- Duplantier, B. Swelling of the various parts of a polymer chain in a good solvent. J. Phys. Lett. 1985, 46, 751–758. [Google Scholar] [CrossRef]
- Duplantier, B. Geomertrical properties of a Kuhnian polymer chain. J. Phys. 1986, 47, 1633–1656. [Google Scholar] [CrossRef]
- Baumgärtner, A. Probability Distribution of Internal Distances of a Single Polymer in Good Solvent. Z. Phys. B 1981, 42, 265–270. [Google Scholar] [CrossRef]
- Bishop, M.; Clarke, J.H.R. Investigation of the end-to-end vector distribution function for random and self-avoiding walks in two and three dimensions. J. Chem. Phys. 1991, 94, 3936. [Google Scholar] [CrossRef]
- Bishop, M.; Clarke, J.H.R.; Rey, A.; Freire, J.J. Investigation of the end-to-end vector distribution function for linear polymers in different regimes. J. Chem. Phys. 1991, 95, 4589. [Google Scholar] [CrossRef]
- Valleau, J.P. Distribution of end-to-end length of an excluded-volume chain. J. Chem. Phys. 1996, 116, 3071. [Google Scholar] [CrossRef]
- Timoshenko, E.G.; Kuznetsov, Y.A.; Connolly, R. Intrachain correlation functions and shapes of homopolymers with different architectures in dilute solution. J. Chem. Phys. 2002, 116, 3905–3916. [Google Scholar] [CrossRef]
- Calabrese, P.; Pelissetto, A.; Vicari, E. Structrue factor of dilute ring polymers. J. Chem. Phys. 2002, 116, 8191–8197. [Google Scholar] [CrossRef]
- Plesa, C.; Verschueren, D.; Pud, S.; van der Torre, J.; Ruitenberg, J.W.; Witteveen, M.J.; Jonsson, M.P.; Grosberg, A.Y.; Rabin, Y.; Dekker, C. Direct observation of DNA knots using a solid-state nanopore. Nat. Nanotechnol. 2016, 11, 1093–1097. [Google Scholar] [CrossRef] [PubMed]
- Murasugi, K.; Kurpita, B. Knot Theory and Its Applications; Birkhäuser: Boston, MA, USA, 1996. [Google Scholar]
- Polyak, M.; Viro, O. Gauss Diagram Formulas for Vassiliev Invariants. Int. Math. Res. Not. 1994, 11, 445–453. [Google Scholar] [CrossRef]
- Millett, K.C. Knotting of regular polygons. J. Knot Theory Ramif. 1994, 3, 263–278. [Google Scholar] [CrossRef]
- Alvarado, S.; Calvo, J.A.; Millett, K.C. The Generation of Random Equilateral Polygons. J. Stat. Phys. 2011, 143, 102–138. [Google Scholar] [CrossRef]
- Uehara, E.; Deguchi, T. Knotting probability and the scaling behavior of self-avoiding polygons under a topological constraint. arXiv, 2017; arXiv:1704.07510. [Google Scholar]
- Le Guillou, J.C.; Zinn-Justin, J. Critical exponents from field theory. Phys. Rev. B 1980, 21, 3976. [Google Scholar] [CrossRef]
- Nickel, B.G. One-Parameter Recursion Model for Flexible-Chain Polymers. Macromolecules 1991, 24, 1358–1365. [Google Scholar]
- Li, B.; Madras, N.; Sokal, A.D. Critical Exponentts, Hyperscaling, and Universal Amplitude Ratios for Two- and Three-Dimensional Self-Avoiding Walks. J. Stat. Phys. 1995, 80, 661–754. [Google Scholar] [CrossRef]
- Guida, R.; Zinn-Justin, J. Critical exponents of the N-vector model. J. Phys. A Math. Gen. 1998, 31, 8103–8121. [Google Scholar] [CrossRef]
- Clisby, N. Accurate Estimate of the Critical Exponent nu for Self-Avoiding Walks via a Fast Implementation of the Pivot Algorithm. Phys. Rev. Lett. 2010, 104, 055702. [Google Scholar] [CrossRef] [PubMed]
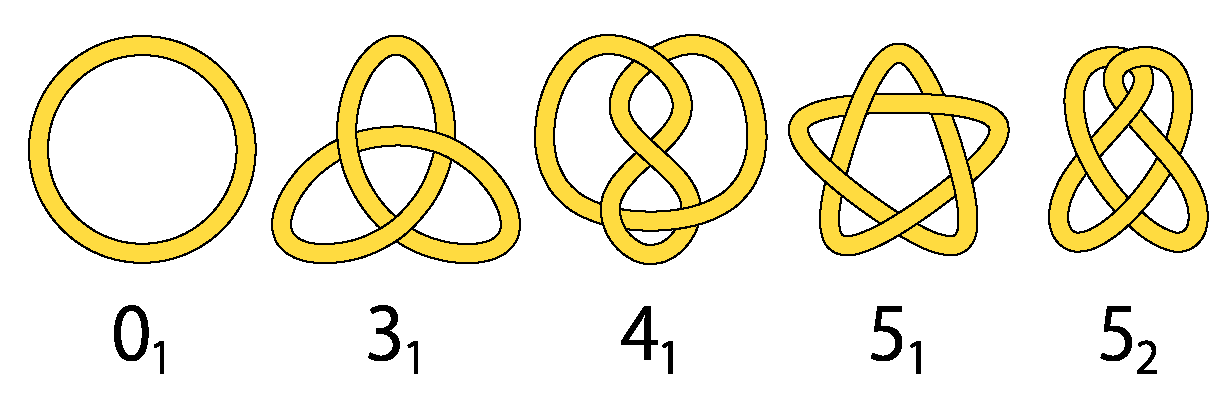
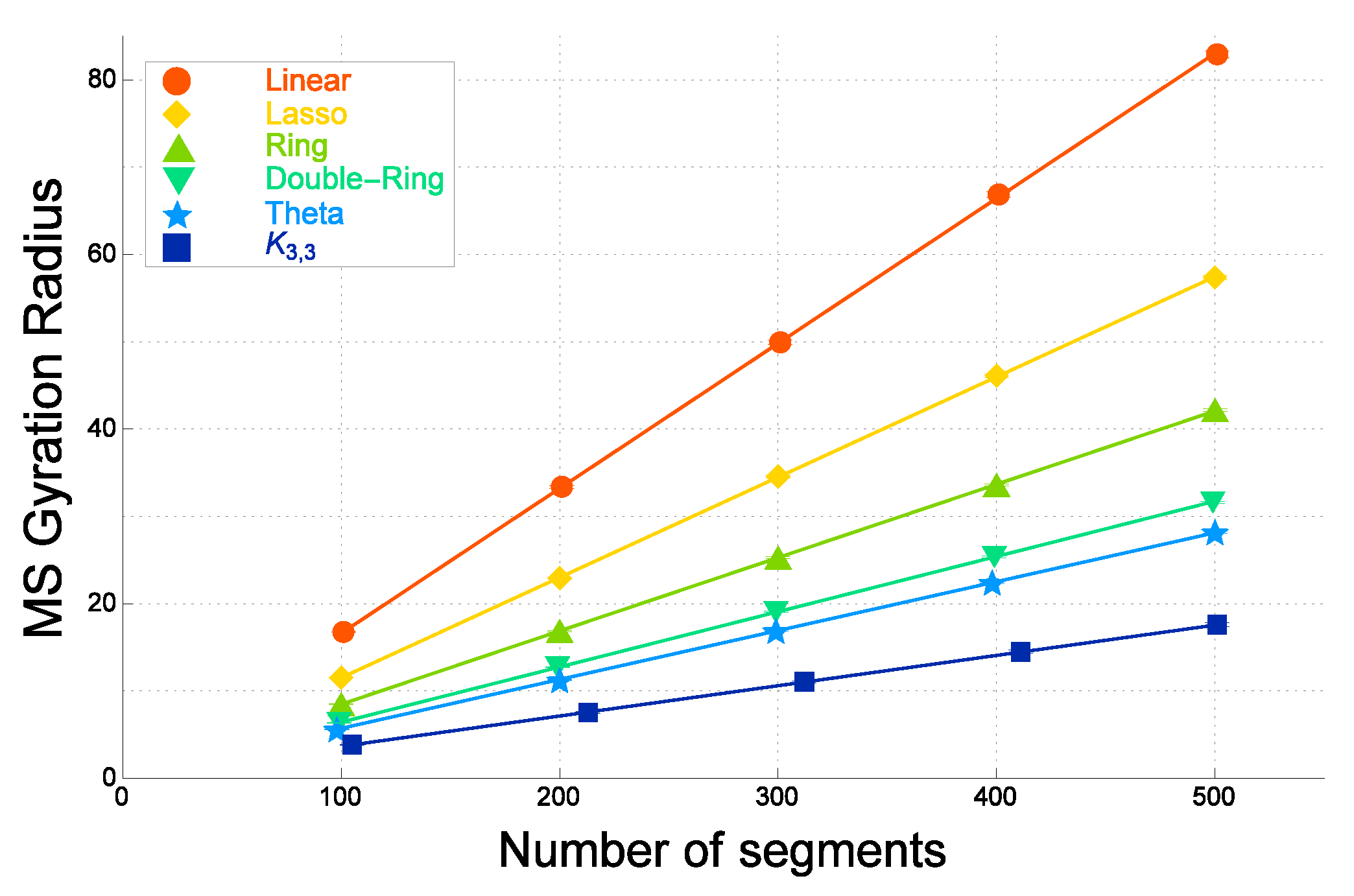
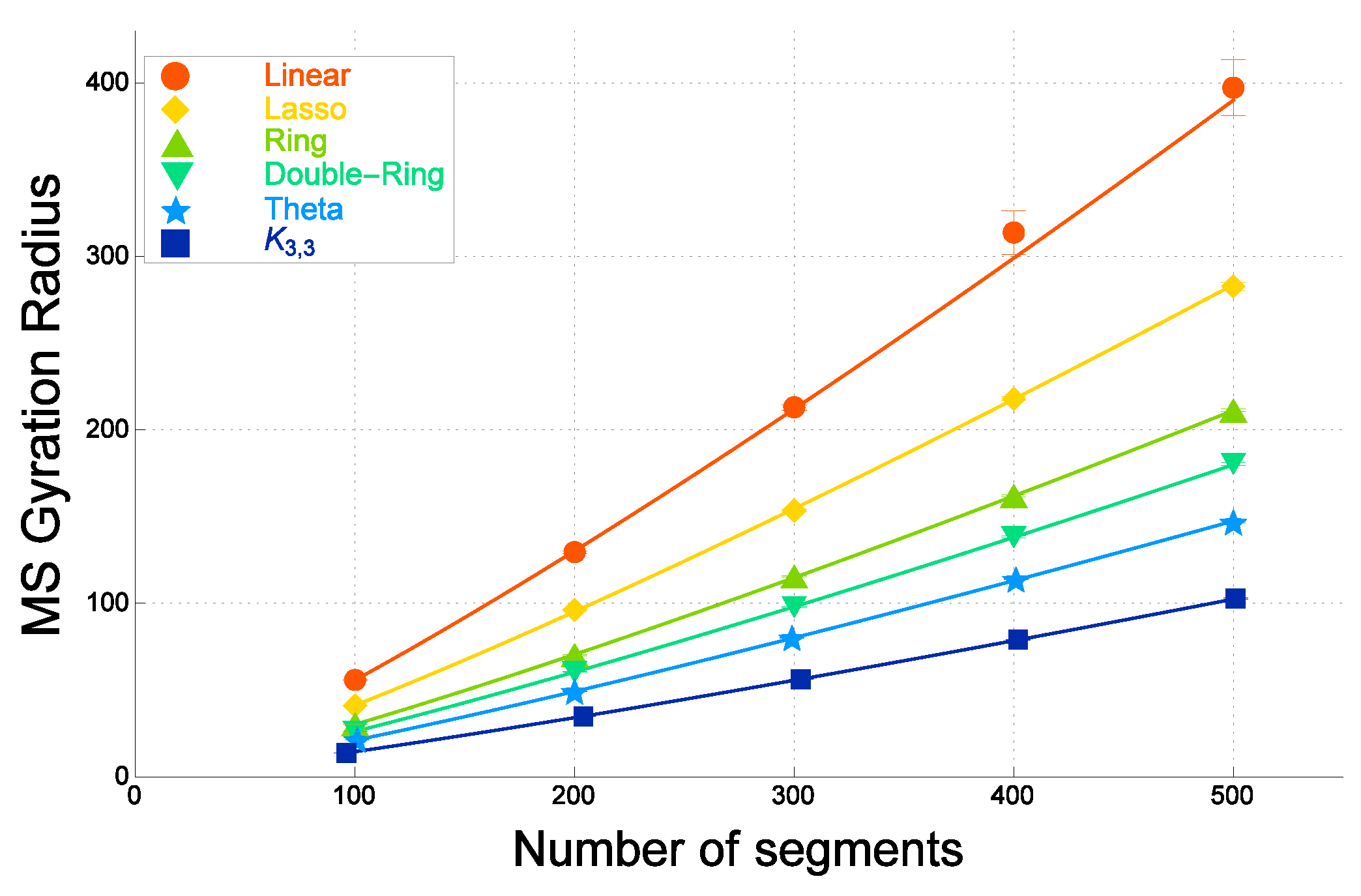
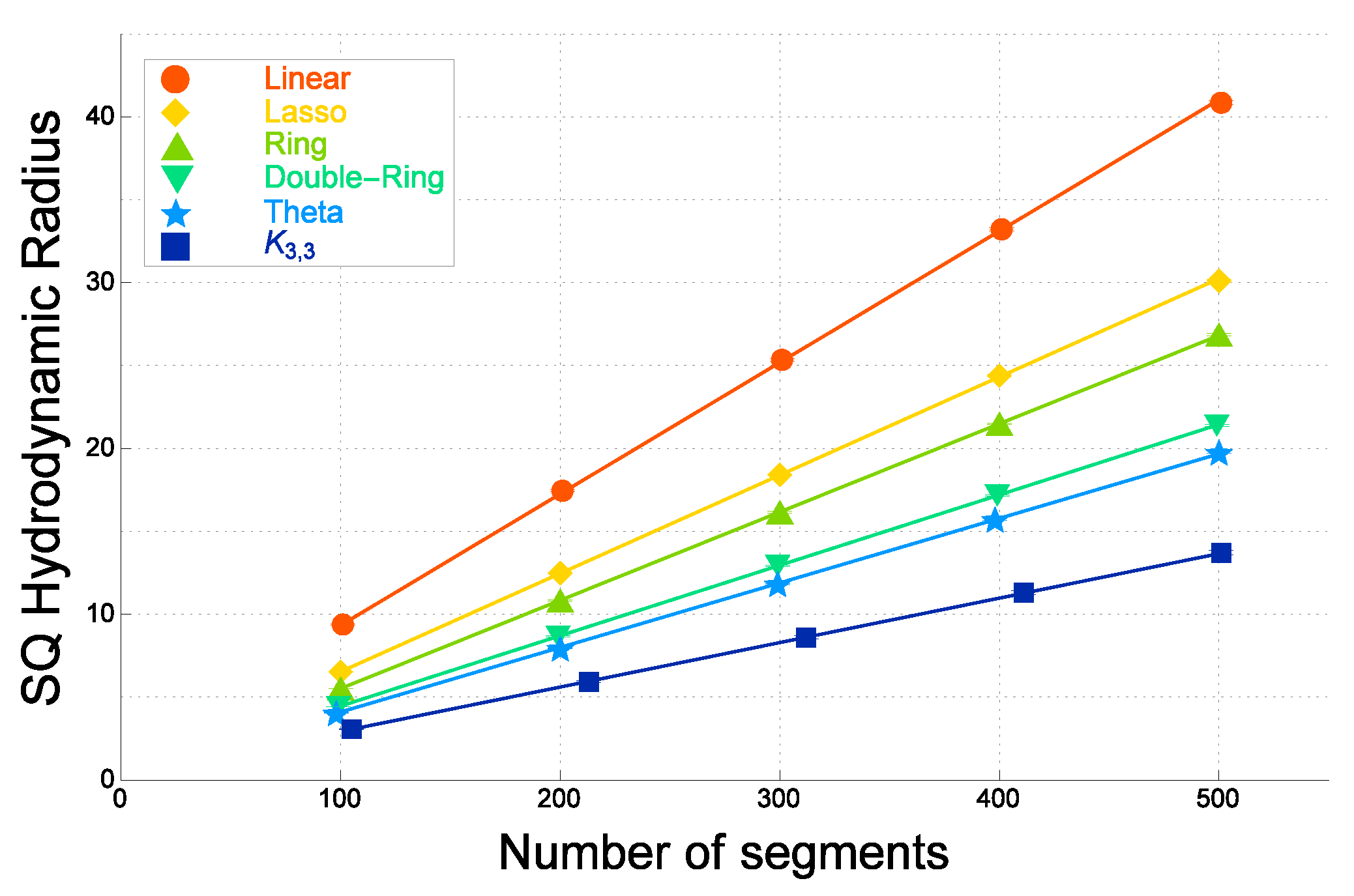
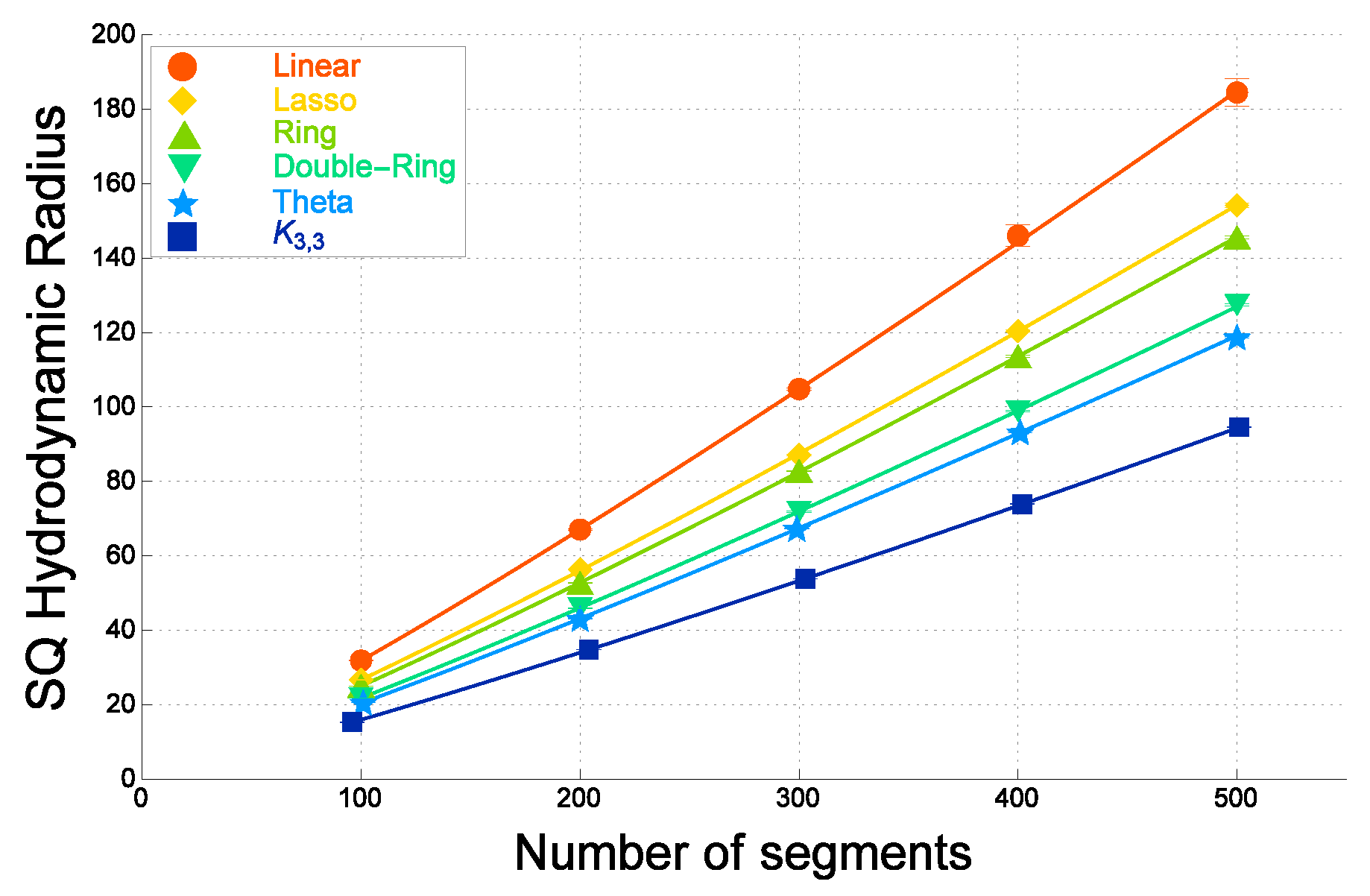
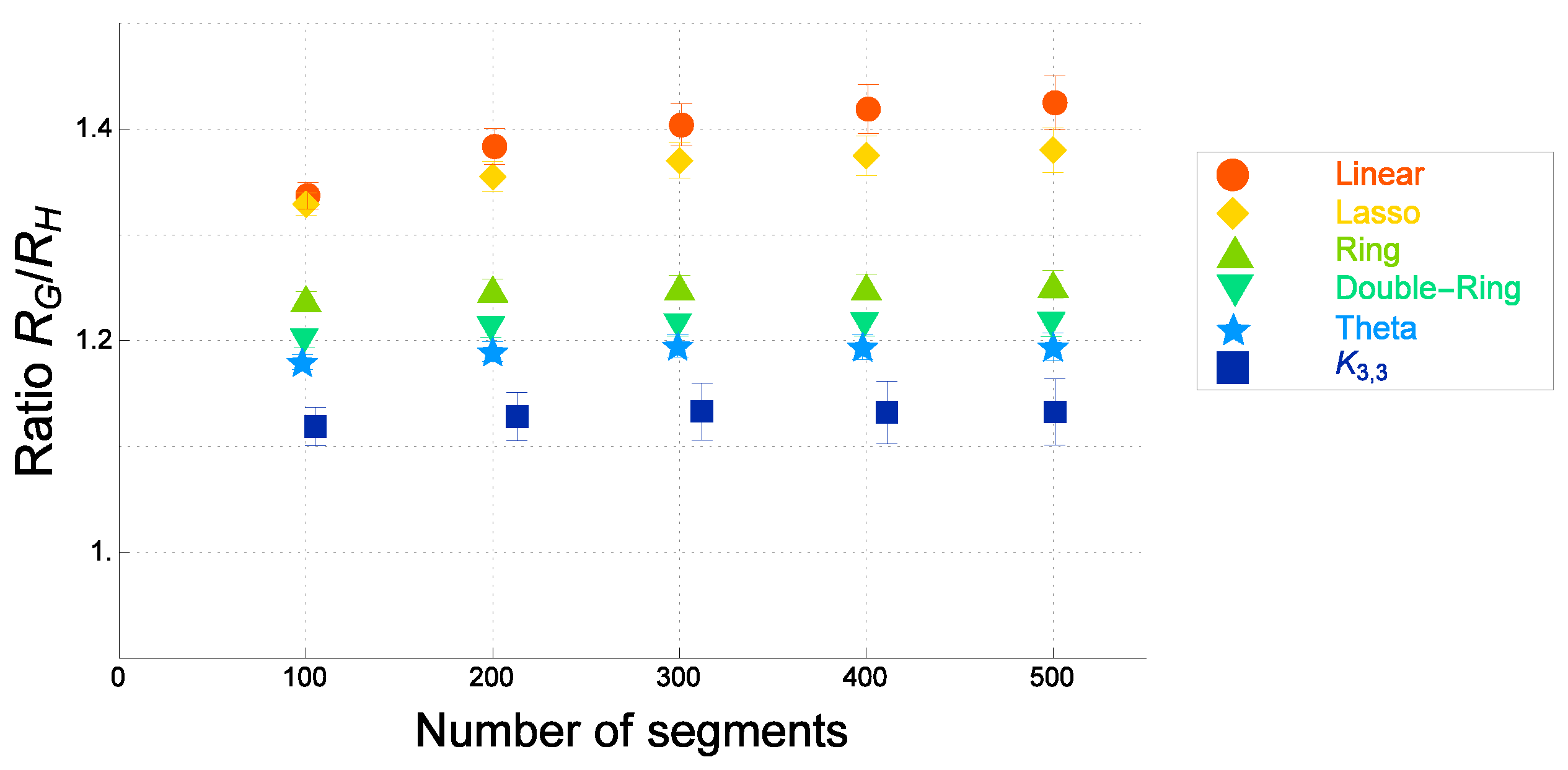
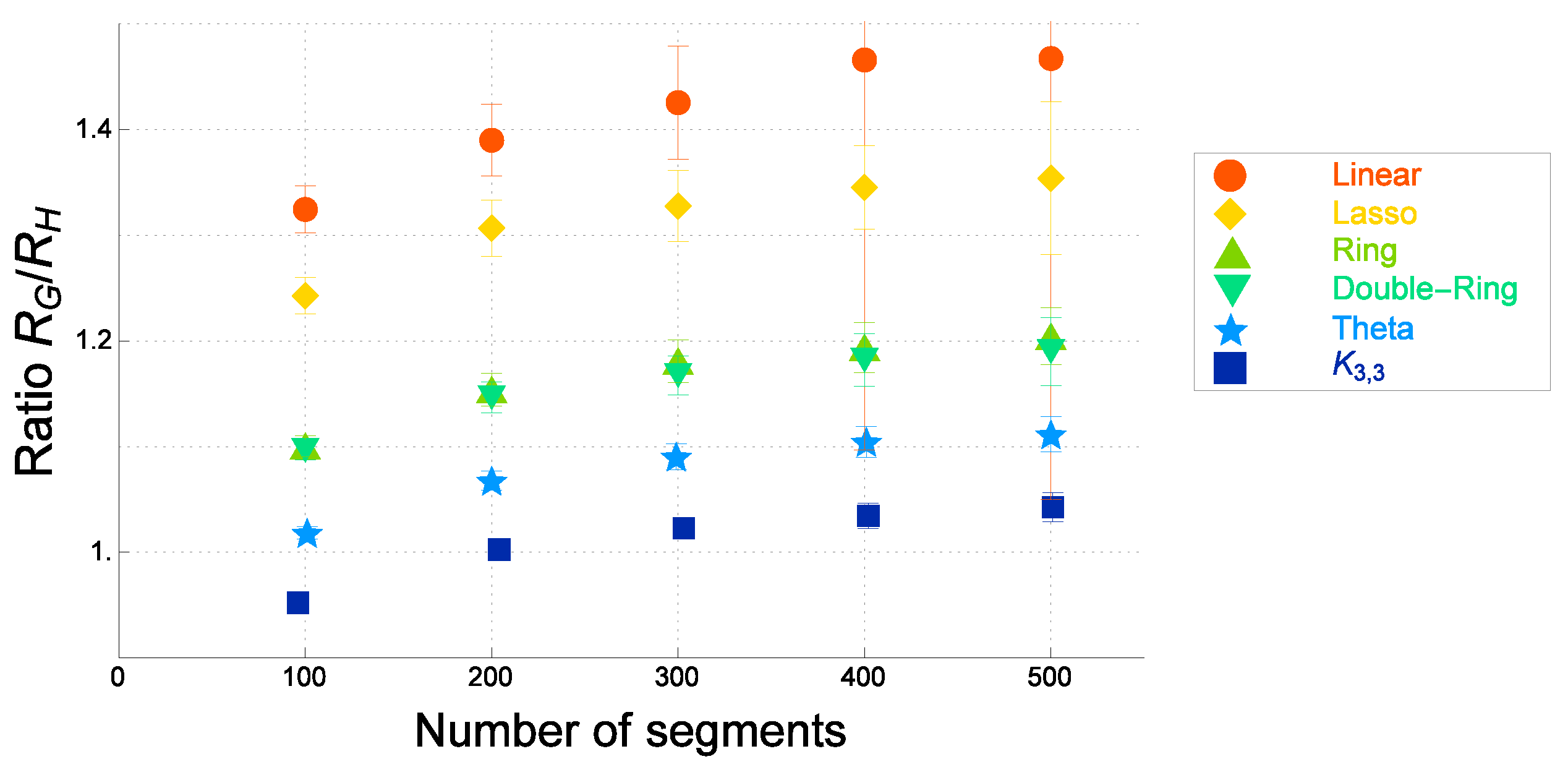



| Graph F | Ratio of (Ideal) | Ratio of (Real) |
|---|---|---|
| linear | ||
| tadpole (lasso) | ||
| ring | ||
| double-ring | ||
| -shaped | ||
| complete |
| Graph F | N | (Ideal) | (Real) |
|---|---|---|---|
| linear | 500 | ||
| tadpole (lasso) | 500 | ||
| ring | 500 | ||
| double-ring | 500 | ||
| -shaped | 500 | ||
| complete | 501 |
| Knot Type | |||||||
|---|---|---|---|---|---|---|---|
| Determinant of knot | 1 | 3 | 5 | 5 | 7 | 9 | 15 |
| 2nd order Vassiliev invariant | 0 | 1 | 3 | 2 | 2 | 0 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deguchi, T.; Uehara, E. Statistical and Dynamical Properties of Topological Polymers with Graphs and Ring Polymers with Knots. Polymers 2017, 9, 252. https://doi.org/10.3390/polym9070252
Deguchi T, Uehara E. Statistical and Dynamical Properties of Topological Polymers with Graphs and Ring Polymers with Knots. Polymers. 2017; 9(7):252. https://doi.org/10.3390/polym9070252
Chicago/Turabian StyleDeguchi, Tetsuo, and Erica Uehara. 2017. "Statistical and Dynamical Properties of Topological Polymers with Graphs and Ring Polymers with Knots" Polymers 9, no. 7: 252. https://doi.org/10.3390/polym9070252
APA StyleDeguchi, T., & Uehara, E. (2017). Statistical and Dynamical Properties of Topological Polymers with Graphs and Ring Polymers with Knots. Polymers, 9(7), 252. https://doi.org/10.3390/polym9070252





