Demixing by a Nematic Mean Field: Coarse-Grained Simulations of Liquid Crystalline Polymers
Abstract
:1. Introduction
2. Model and Simulation Approach
3. Results
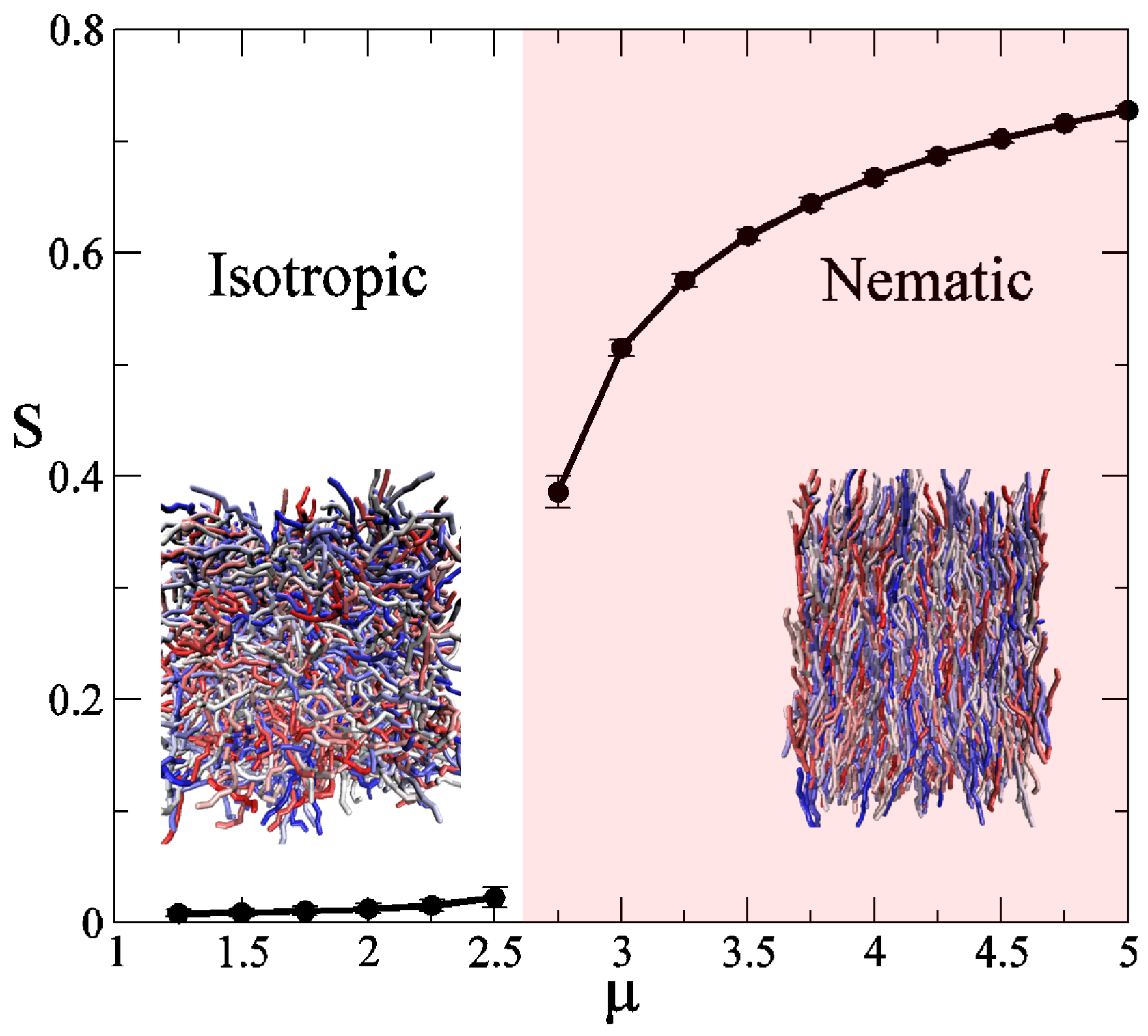
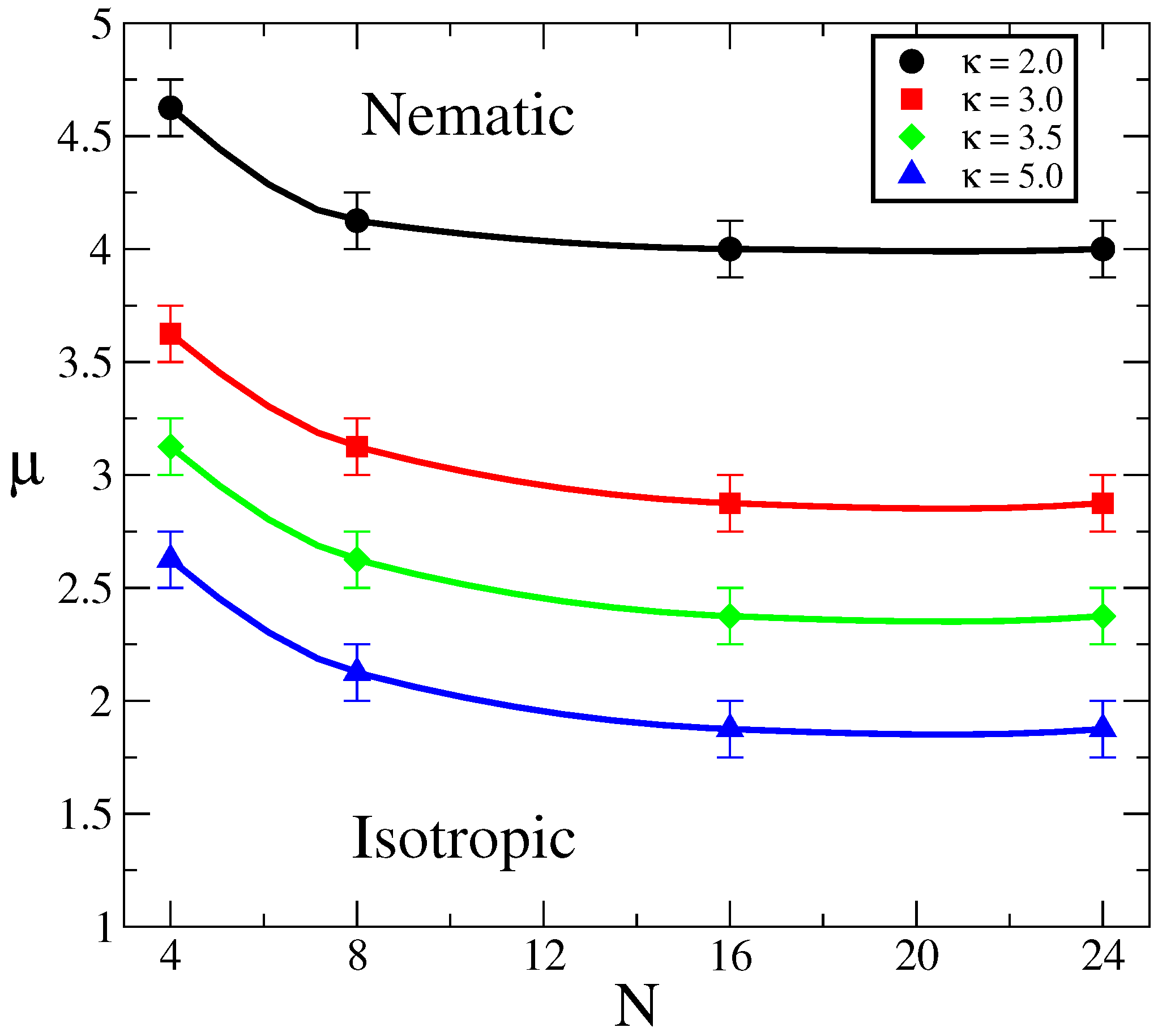
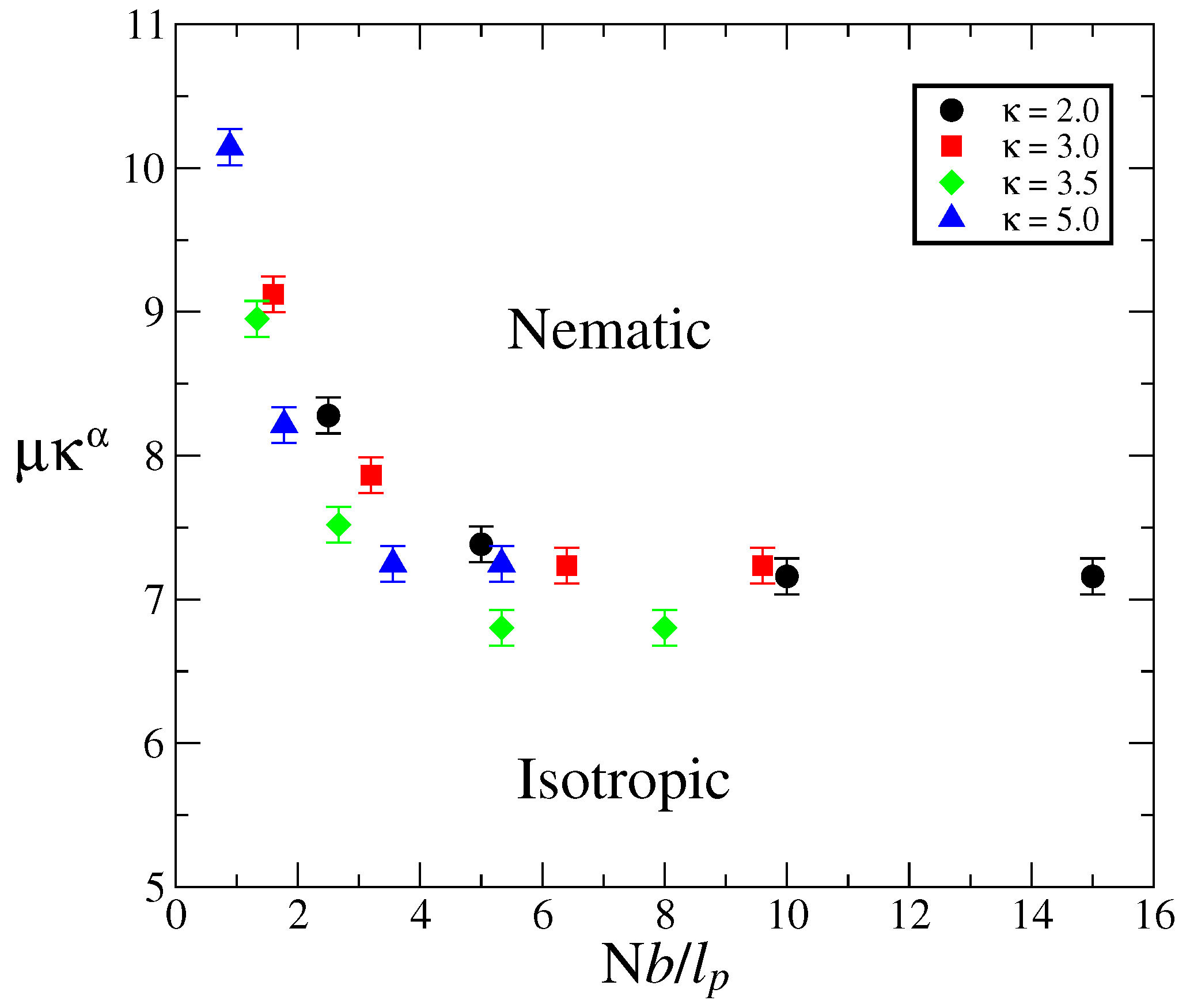
3.1. Pure Systems
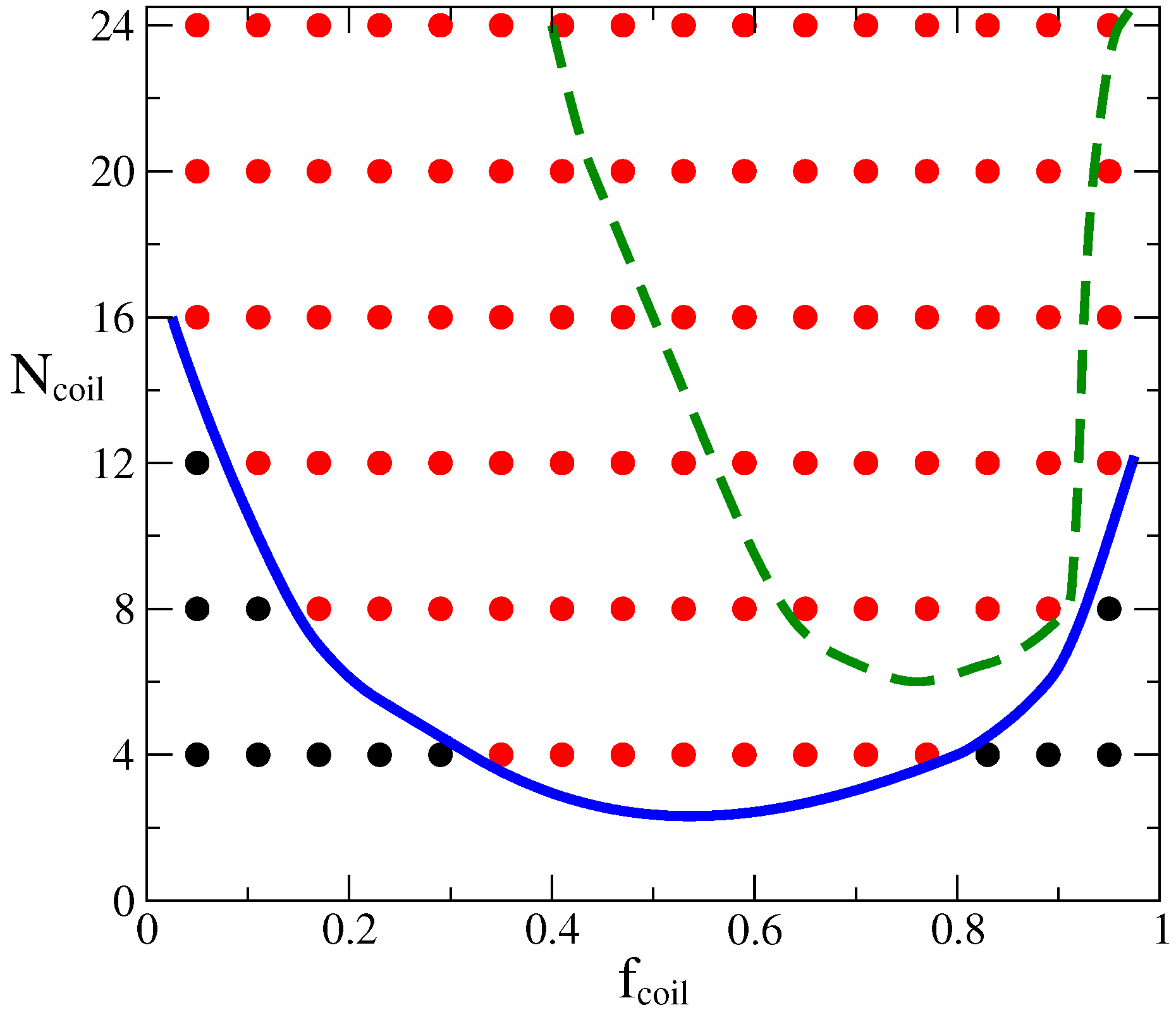
3.2. Mixtures
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Whitesides, G.M.; Grzybowski, B. Self-assembly at all scales. Science 2002, 295, 2418–2421. [Google Scholar] [CrossRef] [PubMed]
- Kato, T. Self-Assembly of Phase-Segregated Liquid Crystal Structures. Science 2002, 295, 2414–2418. [Google Scholar] [CrossRef] [PubMed]
- Larson, R.G. The Structure and Rheology of Complex Fluids; Oxford University Press: Oxford, UK, 1999. [Google Scholar]
- Israelachvili, J.N. Intermolecular and Surface Forces, 3rd ed.; Academic Press: New York, NY, USA, 2011. [Google Scholar]
- Hamley, I.W. The Physics of Block Copolymers; Oxford University Press: Oxford, UK, 1998. [Google Scholar]
- Horsch, M.A.; Zhang, Z.; Glotzer, S.C. Simulation studies of self-assembly of end-tethered nanorods in solution and role of rod aspect ratio and tether length. J. Chem. Phys. 2006, 125, 184903. [Google Scholar] [CrossRef] [PubMed]
- Tang, J.; Jiang, Y.; Zhang, X.; Yan, D.; Chen, J.Z.Y. Phase Diagram of Rod-Coil Diblock Copolymer Melts. Macromolecules 2015, 48, 9060. [Google Scholar] [CrossRef]
- De Gennes, P.G.; Prost, J. The Physics of Liquid Crystals; Clarendon Press: Oxford, UK, 1993. [Google Scholar]
- Bai, P.; Kim, M.I.; Xu, T. Thermally Controlled Morphologies in a Block Copolymer Supramolecule via Nonreversible Order–Order Transitions. Macromolecules 2013, 46, 5531. [Google Scholar] [CrossRef]
- Li, X.; Armas-Perez, J.C.; Martinez-Gonzalez, J.A.; Liu, X.; Xie, H.; Bishop, C.; Hernandez-Ortiz, J.P.; Zhang, R.; de Pablo, J.J.; Nealey, P.F. Directed self-assembly of nematic liquid crystals on chemically patterned surfaces: Morphological states and transitions. Soft Matter 2016, 12, 8595–8605. [Google Scholar] [CrossRef] [PubMed]
- Choo, Y.; Mahajan, L.H.; Gopinadhan, M.; Ndaya, D.; Deshmukh, P.; Kasi, R.M.; Osuji, C.O. Phase Behavior of Polylactide-Based Liquid Crystalline Brushlike Block Copolymers. Macromolecules 2015, 48, 8315–8322. [Google Scholar] [CrossRef]
- Dutta, D.; Fruitwala, H.; Kohli, A.; Weiss, R.A. Polymer Blends Containing Liquid Crystals: A Review. Polym. Eng. Sci. 1990, 30, 1005–1018. [Google Scholar] [CrossRef]
- Gemünden, P.; Poelking, C.; Kremer, K.; Andrienko, D.; Ch. Daoulas, K. Nematic Ordering, Conjugation, and Density of States of Soluble Polymeric Semiconductors. Macromolecules 2013, 46, 5762–5774. [Google Scholar] [CrossRef]
- Lee, Y.; Gomez, E. Challenges and Opportunities in the Development of Conjugated Block Copolymers for Photovoltaics. Macromolecules 2015, 48, 7385–7395. [Google Scholar] [CrossRef]
- Kipp, D.; Wodo, O.; Ganapathysubramanian, B.; Ganesan, V. Achieving Bicontinuous Microemulsion Like Morphologies in Organic Photovoltaics. ACS Macro Lett. 2015, 4, 266–270. [Google Scholar] [CrossRef]
- Vezie, M.S.; Few, S.; Meager, I.; Pieridou, G.; Dorling, B.; Ashraf, R.S.; Goñi, A.R.; Bronstein, H.; McCulloch, I.; Hayes, S.C.; et al. Exploring the origin of high optical absorption in conjugated polymers. Nat. Mater. 2016, 15, 746–753. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Fabiano, S.; Himmelberger, S.; Puzinas, S.; Crispin, X.; Salleo, A.; Berggren, M. Experimental evidence that short-range intermolecular aggregation is sufficient for efficient charge transport in conjugated polymers. Proc. Natl. Acad. Sci. USA 2015, 112, 10599–10604. [Google Scholar] [CrossRef] [PubMed]
- Kipp, D.; Mok, J.; Strzalka, J.; Darling, S.B.; Ganesan, V.; Verduzco, R. Rational Design of Thermally Stable, Bicontinuous Donor/Acceptor Morphologies with Conjugated Block Copolymer Additives. ACS Macro Lett. 2015, 4, 867–871. [Google Scholar] [CrossRef]
- Darling, S.B. Block copolymers for photovoltaics. Energy Environ. Sci. 2009, 2, 1266–1273. [Google Scholar] [CrossRef]
- Müller, M.; de Pablo, J.J. Computational approaches for the dynamics of structure formation in self-assembling polymeric materials. Annu. Rev. Mater. Res. 2013, 43, 1–34. [Google Scholar] [CrossRef]
- Müller, M.; Sun, D.W. Directing the self-assembly of block copolymers into a metastable complex network phase via a deep and rapid quench. Phys. Rev. Lett. 2013, 111, 267801. [Google Scholar] [CrossRef] [PubMed]
- Ten Bosch, A.; Maissa, P.; Sixou, P. A Landau-de Gennes theory of nematic polymers. J. Phys. 1983, 44, 105–111. [Google Scholar] [CrossRef]
- Wang, X.J.; Warner, M. Theory of nematic backbone polymer phases and conformations. J. Phys. A Math. Gen. 1986, 19, 2215–2227. [Google Scholar] [CrossRef]
- Holyst, R.; Schick, M. Mixtures of rigid and flexible nematogenic polymers. J. Chem. Phys. 1992, 96, 721–729. [Google Scholar] [CrossRef]
- Liu, A.J.; Fredrickson, G.H. Free Energy Functionals for Semiflexible Polymer Solutions and Blends. Macromolecules 1993, 26, 2817–2824. [Google Scholar] [CrossRef]
- Liu, A.J.; Fredrickson, G.H. Phase Separation Kinetics of Rod/Coil Mixtures. Macromolecules 1996, 29, 8000–8009. [Google Scholar] [CrossRef]
- Escobedo, F.; de Pablo, J.J. Monte Carlo simulation of athermal mesogenic chains: Pure systems, mixtures, and constrained environments. J. Chem. Phys. 1997, 106, 9858–9868. [Google Scholar] [CrossRef]
- Fukuda, J. Phase separation kinetics of liquid crystalline polymers: Effect of orientational order. Phys. Rev. E 1999, 59, 3275–3288. [Google Scholar] [CrossRef]
- Reenders, M.; ten Brinke, G. Compositional and Orientational Ordering in Rod-Coil Diblock Copolymer Melts. Macromolecules 2002, 35, 3266–3280. [Google Scholar] [CrossRef]
- Pryamitsyn, V.; Ganesan, V. Self-assembly of rod–coil block copolymers. J. Chem. Phys. 2004, 120, 5824–5838. [Google Scholar] [CrossRef] [PubMed]
- Kipp, D.; Ganesan, V. Influence of Block Copolymer Compatibilizers on the Morphologies of Semiflexible Polymer/Solvent Blend. J. Phys. Chem. B 2014, 118, 4425–4441. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Liang, B. Simulation of Phase-Separated Structures of Liquid- Crystalline Polymer/Flexible Polymer Blends. J. Polym. Phys. B Polym. Phys. 2001, 39, 2915–2921. [Google Scholar] [CrossRef]
- Hamm, M.; Goldbeck-Wood, G.; Zvelindovsky, A.V.; Sevink, G.J.A.; Fraaije, J.G.E.M. Structure formation in liquid crystalline polymers. J. Chem. Phys. 2002, 116, 3152–3161. [Google Scholar] [CrossRef]
- Doi, M. Introduction to Polymer Physics; Clarendon Press: Oxford, UK, 1996. [Google Scholar]
- Detcheverry, F.A.; Pike, D.Q.; Nealey, P.F.; Müller, M.; de Pablo, J.J. Monte Carlo simulation of coarse grain polymeric systems. Phys. Rev. Lett. 2009, 102, 197801. [Google Scholar] [CrossRef] [PubMed]
- Helfand, E. Theory of inhomogeneous polymers: Fundamentals of the Gaussian random-walk model. J. Chem. Phys. 1975, 62, 999–1005. [Google Scholar] [CrossRef]
- Ch. Daoulas, K.; Rühle, V.; Kremer, K. Simulations of nematic homopolymer melts using particle-based models with interactions expressed through collective variables. J. Phys. Condens. Matter 2012, 24, 284121. [Google Scholar] [CrossRef] [PubMed]
- Gemünden, P.; Ch. Daoulas, K. Fluctuation spectra in polymer nematics and Frank elastic constants: A coarse-grained modelling study. Soft Matter 2015, 11, 532–544. [Google Scholar] [CrossRef] [PubMed]
- Frenkel, D.; Smit, B. Understanding Molecular Simulations, 2nd ed.; Academic Press: New York, NY, USA, 2002. [Google Scholar]
- Sigaud, G.; Yoon, D.Y.; Griffin, A.C. Order in Nematic Phase of Semiflexible Polymers. Macromolecules 1983, 16, 875–880. [Google Scholar] [CrossRef]
- Zhang, W.; Gomez, E.D.; Milner, S.T. Predicting Nematic Phases of Semiflexible Polymers. Macromolecules 2015, 48, 1454–1462. [Google Scholar] [CrossRef]
- Zhang, W.; Gomez, E.D.; Milner, S.T. Using surface-induced ordering to probe the isotropic-to-nematic transition for semiflexible polymers. Soft Matter 2016, 12, 6141–6147. [Google Scholar] [CrossRef] [PubMed]
- Nakai, A.; Shiwaku, T.; Wang, W.; Hasegawa, H.; Hashimoto, T. Process and Mechanism of Phase Separation in Polymer Mixtures with a Thermotropic Liquid Crystalline Copolyester as One Component. Macromolecules 1996, 29, 5990–6001. [Google Scholar] [CrossRef]
- Bates, C.M.; Bates, F.S. Block Polymers—Pure Potential. Macromolecules 2017, 50, 3–22. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K.J. VMD—Visual Molecular Dynamics. Mol. Graphics 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Images Were Created Using Paraview, an Open-Source Scientific Visualization Software. Available online: http://www.paraview.org/ (accessed on 3 March 2017).


© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramírez-Hernández, A.; Hur, S.-M.; Armas-Pérez, J.C.; Cruz, M.O.d.l.; De Pablo, J.J. Demixing by a Nematic Mean Field: Coarse-Grained Simulations of Liquid Crystalline Polymers. Polymers 2017, 9, 88. https://doi.org/10.3390/polym9030088
Ramírez-Hernández A, Hur S-M, Armas-Pérez JC, Cruz MOdl, De Pablo JJ. Demixing by a Nematic Mean Field: Coarse-Grained Simulations of Liquid Crystalline Polymers. Polymers. 2017; 9(3):88. https://doi.org/10.3390/polym9030088
Chicago/Turabian StyleRamírez-Hernández, Abelardo, Su-Mi Hur, Julio C. Armas-Pérez, Monica Olvera de la Cruz, and Juan J. De Pablo. 2017. "Demixing by a Nematic Mean Field: Coarse-Grained Simulations of Liquid Crystalline Polymers" Polymers 9, no. 3: 88. https://doi.org/10.3390/polym9030088
APA StyleRamírez-Hernández, A., Hur, S.-M., Armas-Pérez, J. C., Cruz, M. O. d. l., & De Pablo, J. J. (2017). Demixing by a Nematic Mean Field: Coarse-Grained Simulations of Liquid Crystalline Polymers. Polymers, 9(3), 88. https://doi.org/10.3390/polym9030088





