Reaction-Multi Diffusion Model for Nutrient Release and Autocatalytic Degradation of PLA-Coated Controlled-Release Fertilizer
Abstract
:1. Introduction
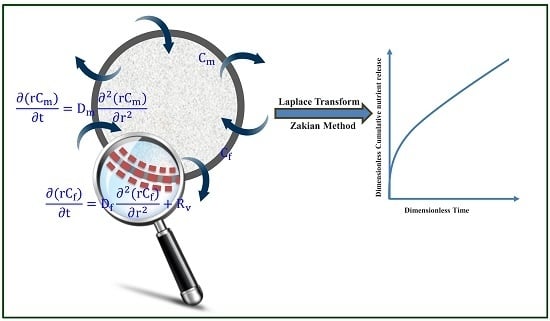
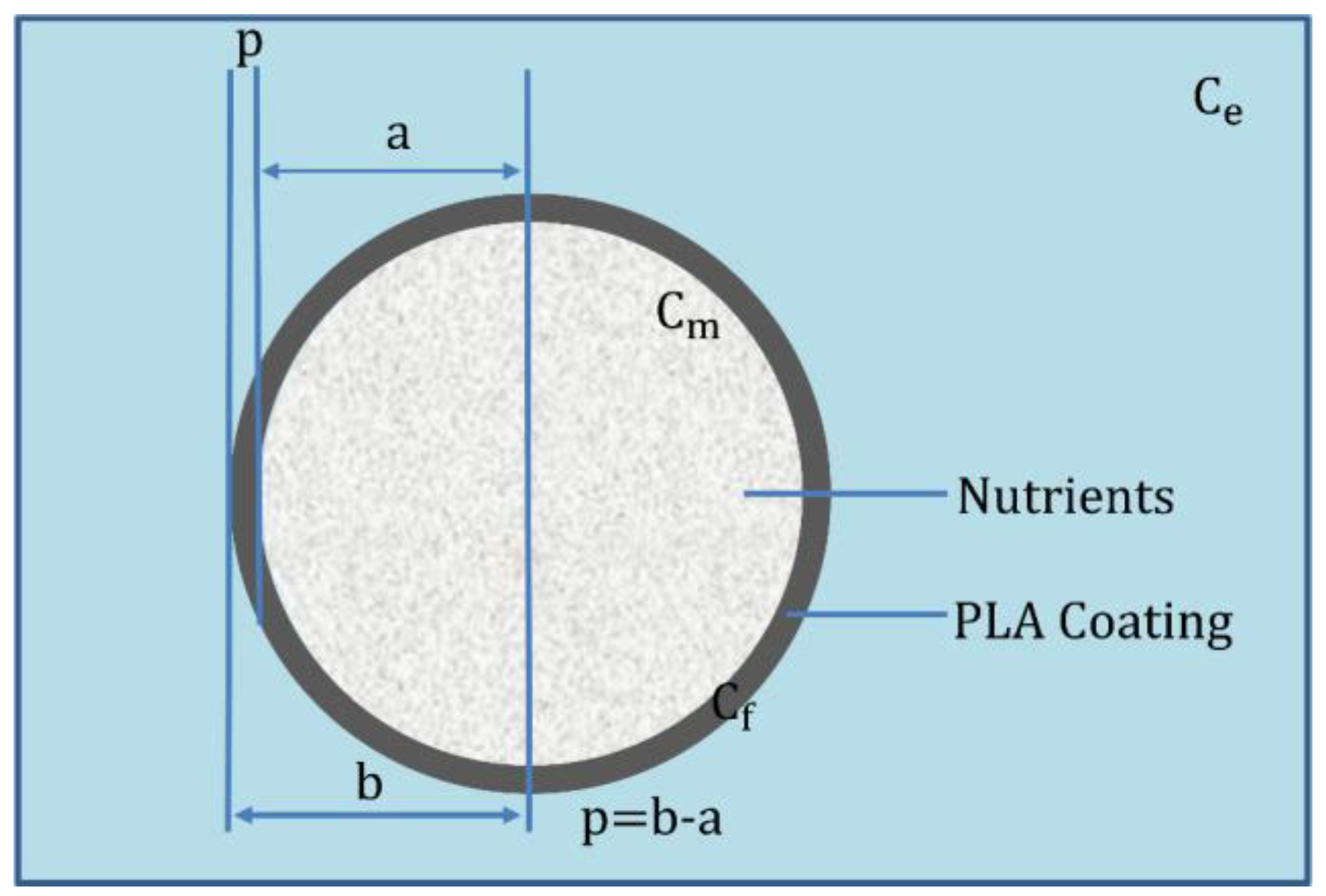
2. Mathematical Model
2.1. Analytical Solution of the Model
2.2. Numerical Inversion of Laplace Transform
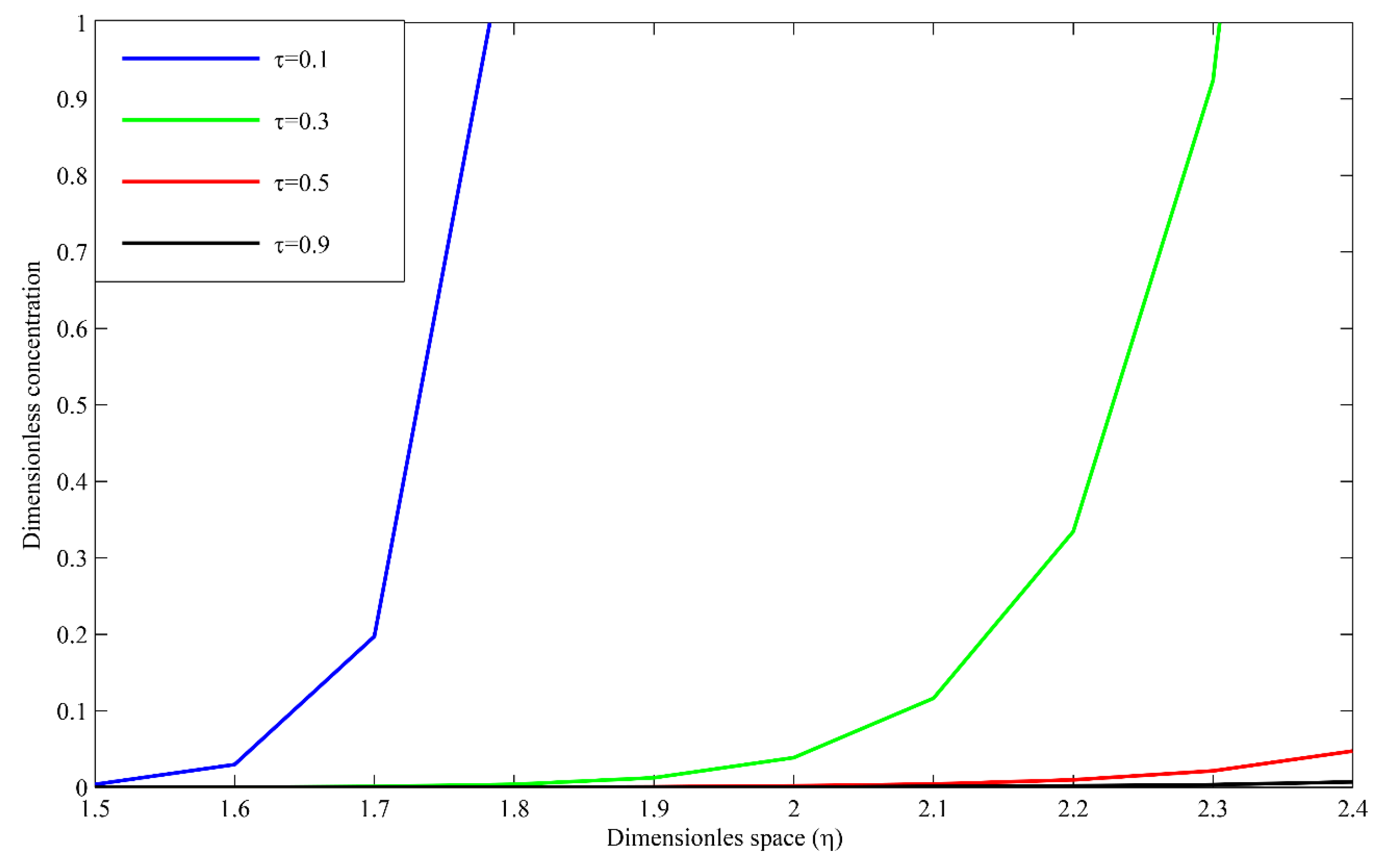
3. Results and Discussion
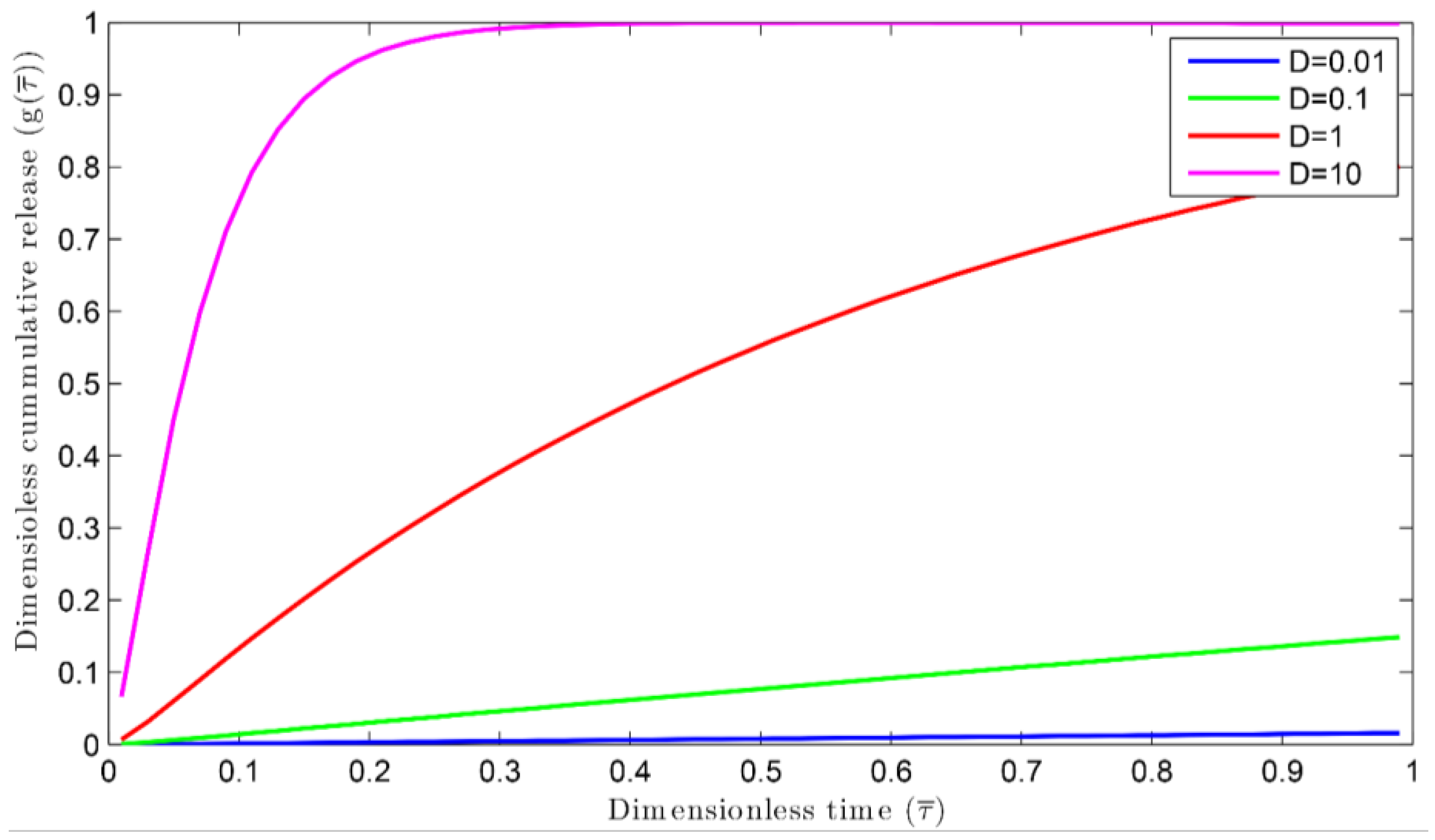
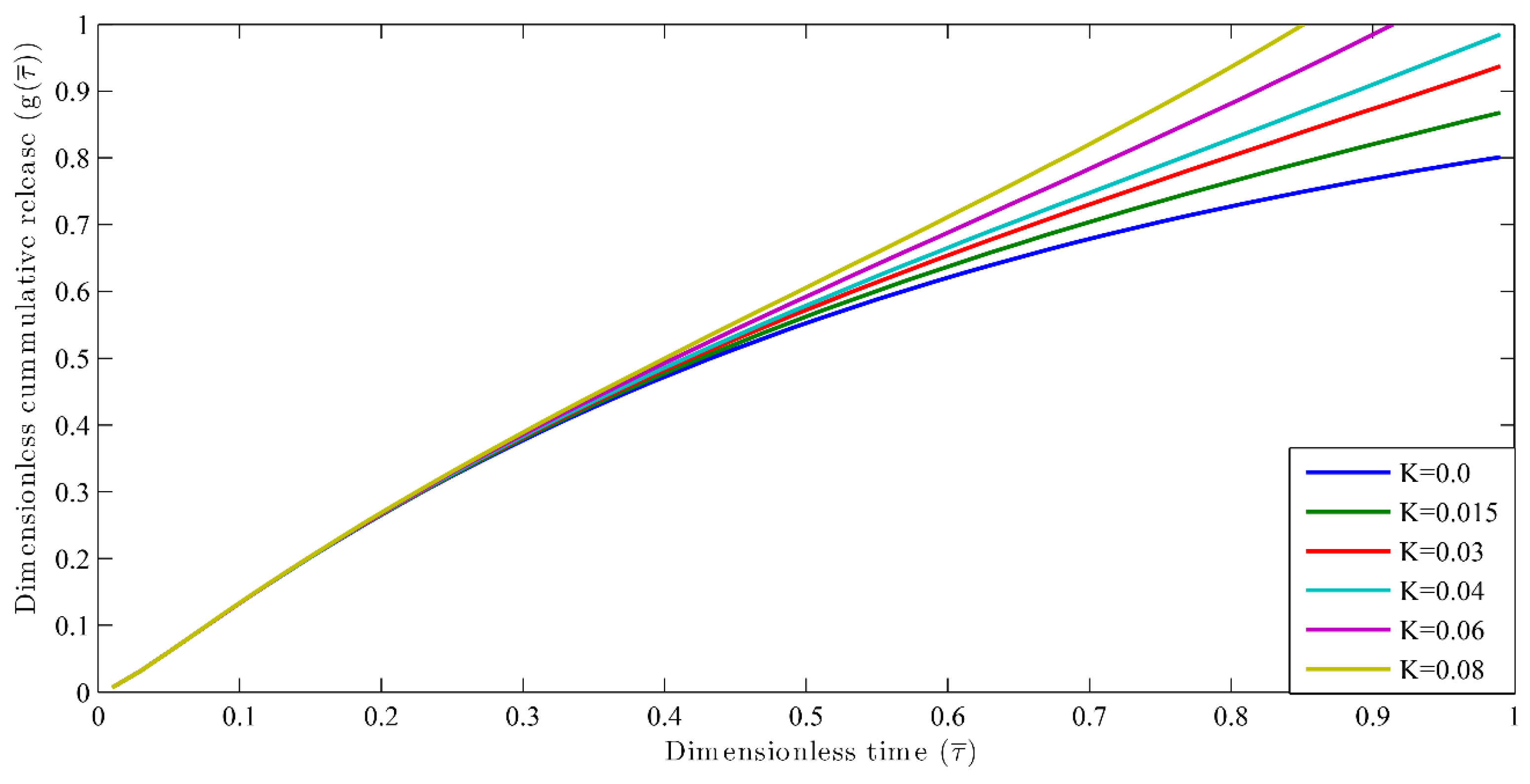
3.1. Nutrient Release Profiles
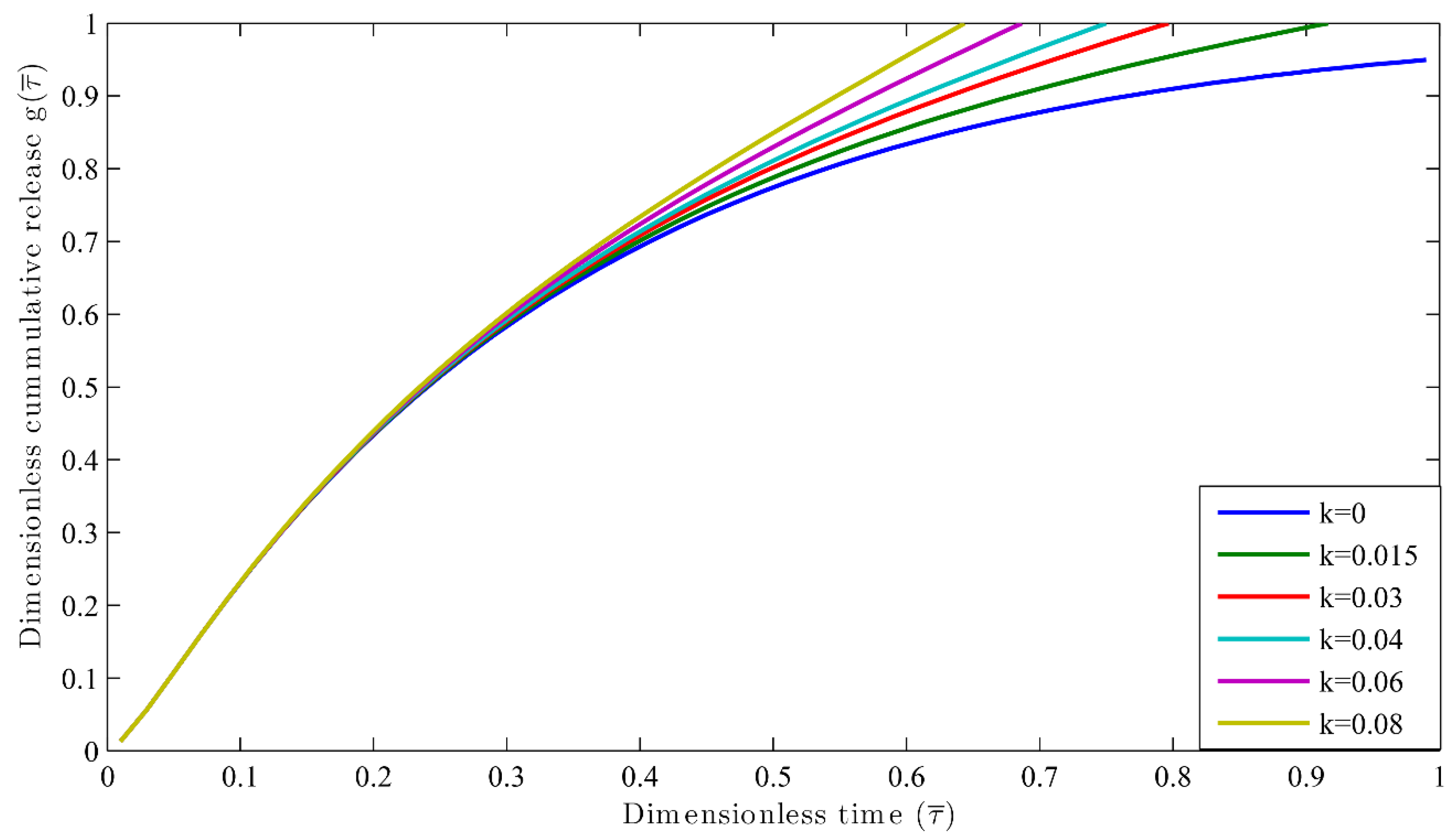
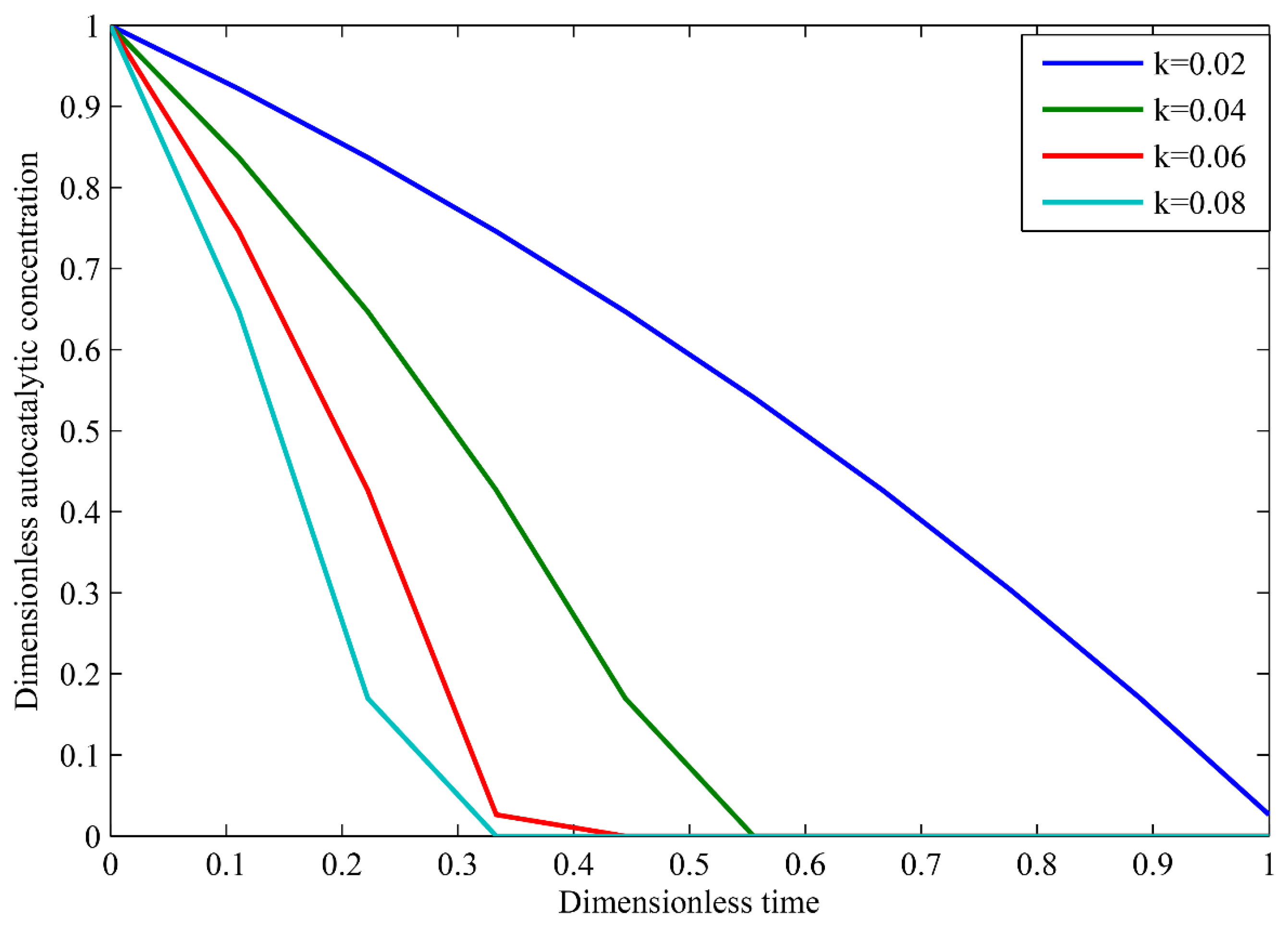
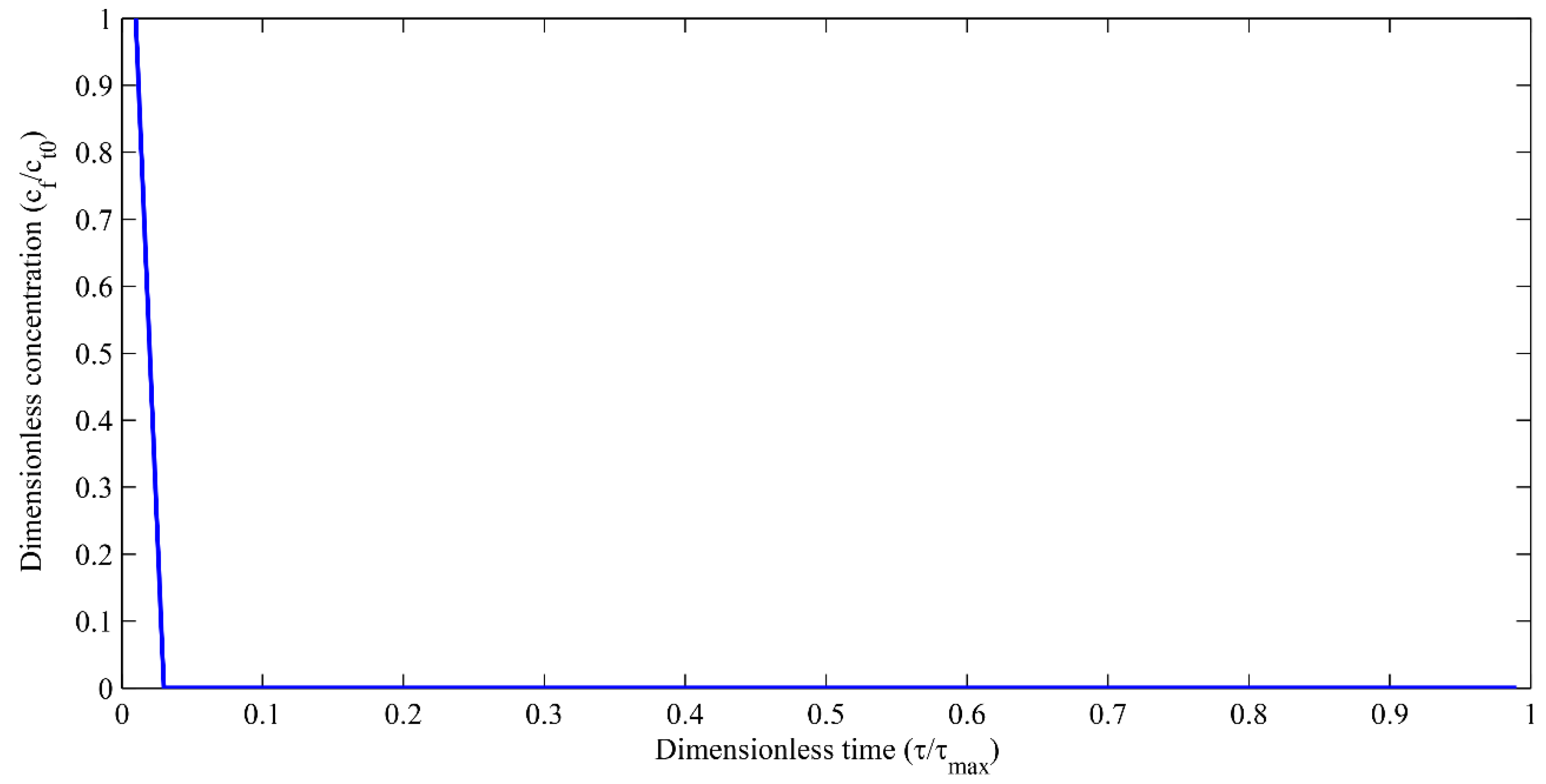
3.2. Autocatalytic Concentration Profiles
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
References
- Trenkel, M.E. Controlled-Release and Stabilized Fertilizers in Agriculture; International fertilizer industry association: Paris, France, 1997. [Google Scholar]
- Shaviv, A. Advances in controlled-release fertilizers. Adv. Agron. 2001, 71, 1–49. [Google Scholar]
- Palivan, C.G.; Goers, R.; Najer, A.; Zhang, X.; Car, A.; Meier, W. Bioinspired polymer vesicles and membranes for biological and medical applications. Chem. Soc. Rev. 2016, 45, 377–411. [Google Scholar] [CrossRef] [PubMed]
- Salman, O.A. Polyethylene-coated urea. I. Improved storage and handling properties. Ind. Eng. Chem. Res. 1989, 28, 630–632. [Google Scholar] [CrossRef]
- Majeed, Z.; Ramli, N.K.; Mansor, N.; Man, Z. A comprehensive review on biodegradable polymers and their blends used in controlled-release fertilizer processes. Rev. Chem. Eng. 2015, 31, 69–95. [Google Scholar] [CrossRef]
- Xiao, X.; Yu, L.; Xie, F.; Bao, X.; Liu, H.; Ji, Z.; Chen, L. One-step method to prepare starch-based superabsorbent polymer for slow release of fertilizer. Chem. Eng. J. 2017, 309, 607–616. [Google Scholar] [CrossRef]
- Tang, X.; Alavi, S. Recent advances in starch, polyvinyl alcohol based polymer blends, nanocomposites and their biodegradability. Carbohydr. Polym. 2011, 85, 7–16. [Google Scholar] [CrossRef]
- Noro, S.; Ochi, R.; Kubo, K.; Nakamura, T. Reversible Structural Changes of Strong Hydrogen Bond-Supported Organic Networks Using Neutral 3,5-Pyridinedicarboxylic Acid N -oxide through Solvent Release/Uptake. Bull. Chem. Soc. Jpn. 2016, 89, 1503–1509. [Google Scholar] [CrossRef]
- Chen, L.; Xie, Z.; Zhuang, X.; Chen, X.; Jing, X. Controlled release of urea encapsulated by starch-g-poly(l-lactide). Carbohydr. Polym. 2008, 72, 342–348. [Google Scholar] [CrossRef]
- Ariga, K.; Li, J.; Fei, J.; Ji, Q.; Hill, J.P. Nanoarchitectonics for Dynamic Functional Materials from Atomic-/Molecular-Level Manipulation to Macroscopic Action. Adv. Mater. 2016, 28, 1251–1286. [Google Scholar] [CrossRef] [PubMed]
- Sanchez-Ballester, N.M.; Rydzek, G.; Pakdel, A.; Oruganti, A.; Hasegawa, K.; Mitome, M.; Golberg, D.; Hill, J.P.; Abe, H.; Ariga, K. Nanostructured polymeric yolk–shell capsules: A versatile tool for hierarchical nanocatalyst design. J. Mater. Chem. A 2016, 4, 9850–9857. [Google Scholar] [CrossRef]
- Calabria, L.; Vieceli, N.; Bianchi, O.; Boff de Oliveira, R.V.; do Nascimento Filho, I.; Schmidt, V. Soy protein isolate/poly(lactic acid) injection-molded biodegradable blends for slow release of fertilizers. Ind. Crops Prod. 2012, 36, 41–46. [Google Scholar] [CrossRef]
- Boontung, W.; Moonmangmee, S.; Chaiyasat, A.; Chaiyasat, P. Preparation of Poly(l-lactic acid) Capsule Encapsulating Fertilizer. Adv. Mater. Res. 2012, 506, 303–306. [Google Scholar] [CrossRef]
- Chaiyasat, P.; Pholsrimuang, P.; Boontung, W.; Chaiyasat, A. Influence of Poly(l-lactic acid) Molecular Weight on the Encapsulation Efficiency of Urea in Microcapsule Using a Simple Solvent Evaporation Technique. Polym. Plast. Technol. Eng. 2016, 55, 1131–1136. [Google Scholar] [CrossRef]
- Ford Versypt, A.N.; Pack, D.W.; Braatz, R.D. Mathematical modeling of drug delivery from autocatalytically degradable PLGA microspheres—A review. J. Control. Release 2013, 165, 29–37. [Google Scholar] [CrossRef] [PubMed]
- Müller, R.-J. Biodegradability of Polymers: Regulations and Methods for Testing. In Biopolymers Online; Steinbüchel, A., Ed.; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2005. [Google Scholar]
- Siparsky, G.L.; Voorhees, K.J.; Miao, F. Hydrolysis of Polylactic Acid (PLA) and Polycaprolactone (PCL) in Aqueous Acetonitrile Solutions: Autocatalysis. J. Polym. Environ. 1998, 6, 31–41. [Google Scholar] [CrossRef]
- Speranza, V.; De Meo, A.; Pantani, R. Thermal and hydrolytic degradation kinetics of PLA in the molten state. Polym. Degrad. Stab. 2014, 100, 37–41. [Google Scholar] [CrossRef]
- Grizzi, I.; Garreau, H.; Li, S.; Vert, M. Hydrolytic degradation of devices based on poly(DL-lactic acid) size-dependence. Biomaterials 1995, 16, 305–311. [Google Scholar] [CrossRef]
- Piemonte, V.; Gironi, F. Kinetics of Hydrolytic Degradation of PLA. J. Polym. Environ. 2013, 21, 313–318. [Google Scholar] [CrossRef]
- Jarrell, W.M.; Pettygrove, G.S.; Boersma, L. Characterization of the Thickness and Uniformity of the Coatings of Sulfur-coated Urea. Soil Sci. Soc. Am. J. 1979, 43, 602. [Google Scholar] [CrossRef]
- Jarrell, W.M.; Boersma, L. Model for the Release of Urea by Granules of Sulfur-Coated Urea Applied to Soil. Soil Sci. Soc. Am. J. 1979, 43, 1044. [Google Scholar] [CrossRef]
- Jarrell, W.M.; Boersma, L. Release of Urea by Granules of Sulfur-Coated Urea. Soil Sci. Soc. Am. J. 1980, 44, 418. [Google Scholar] [CrossRef]
- Al-Zahrani, S.M. Controlled-release of fertilizers: modelling and simulation. Int. J. Eng. Sci. 1999, 37, 1299–1307. [Google Scholar] [CrossRef]
- Shaviv, A.; Raban, S.; Zaidel, E. Modeling controlled nutrient release from polymer coated fertilizers: Diffusion release from single granules. Environ. Sci. Technol. 2003, 37, 2251–2256. [Google Scholar] [CrossRef] [PubMed]
- Shaviv, A.; Raban, S.; Zaidel, E. Modeling Controlled Nutrient Release from a Population of Polymer Coated Fertilizers: Statistically Based Model for Diffusion Release. Environ. Sci. Technol. 2003, 37, 2257–2261. [Google Scholar] [CrossRef] [PubMed]
- Lu, S.M.; Chen, S.R. Mathematical-Analysis of Drug Release from a Coated Particle. J. Control. Release 1993, 23, 105–121. [Google Scholar] [CrossRef]
- Trinh, T.H.; Shaari, K.Z.K.; Suhaila, A.; Shuib, B.; Ismail, L.B. Modeling of Urea Release from Coated Urea for Prediction of Coating Material Diffusivity. Proceeding 6th Int. Conf. Process Syst. Enginerring (PSE ASIA) 2013, 1987, 2261. [Google Scholar]
- Trinh, T.H.; Kushaari, K.; Basit, A.; Azeem, B.; Shuib, A. Use of Multi-Diffusion Model to Study the Release of Urea from Urea Fertilizer Coated with Polyurethane-Like Coating (PULC). APCBEE Procedia 2014, 8, 146–150. [Google Scholar] [CrossRef]
- Trinh, T.H.; Kushaari, K.; Shuib, A.S.; Ismail, L.; Azeem, B. Modelling the release of nitrogen from controlled release fertiliser: Constant and decay release. Biosyst. Eng. 2015, 130, 34–42. [Google Scholar] [CrossRef]
- Trinh, T.H.; KuShaari, K.; Basit, A. Modeling the Release of Nitrogen from Controlled-Release Fertilizer with Imperfect Coating in Soils and Water. Ind. Eng. Chem. Res. 2015, 54, 6724–6733. [Google Scholar] [CrossRef]
- Antheunis, H.; van der Meer, J.-C.; de Geus, M.; Heise, A.; Koning, C.E. Autocatalytic Equation Describing the Change in Molecular Weight during Hydrolytic Degradation of Aliphatic Polyesters. Biomacromolecules 2010, 11, 1118–1124. [Google Scholar] [CrossRef] [PubMed]
- Lyu, S.; Sparer, R.; Untereker, D. Analytical solutions to mathematical models of the surface and bulk erosion of solid polymers. J. Polym. Sci. B 2005, 43, 383–397. [Google Scholar] [CrossRef]
- Wang, Y.; Pan, J.; Han, X.; Sinka, C.; Ding, L. A phenomenological model for the degradation of biodegradable polymers. Biomaterials 2008, 29, 3393–3401. [Google Scholar] [CrossRef] [PubMed]
- Berkland, C.; Pollauf, E.; Pack, D.W.; Kim, K. Uniform double-walled polymer microspheres of controllable shell thickness. J. Control. Release 2004, 96, 101–111. [Google Scholar] [CrossRef] [PubMed]
- Batycky, R.P.; Hanes, J.; Langer, R.; Edwards, D.A. A Theoretical Model of Erosion and Macromolecular Drug Release from Biodegrading Microspheres. J. Pharm. Sci. 1997, 86, 1464–1477. [Google Scholar] [CrossRef] [PubMed]
- Crank, J. The Mathematics of Diffusion, 2nd ed.; Clarendon Press: Oxford, UK, 1975. [Google Scholar]
- Versypt, A.N.F. Modeling of Controlled-Release Drug Delivery from Autocatalytically Degrading Polymer Microspheres; University of Illinois Urbana-Champaign: Champaign, IL, USA, 2012. [Google Scholar]
- Smith, M.G. Laplace Transform Theory; Van Nostrand: London, UK, 1966. [Google Scholar]
- Zakian, V. Numerical inversion of Laplace transform. Electron. Lett. 1969, 5, 120. [Google Scholar] [CrossRef]
- Halsted, D.J.; Brown, D.E. Zakian’s technique for inverting Laplace transforms. Chem. Eng. J. 1972, 3, 312–313. [Google Scholar] [CrossRef]
- Wang, Q.; Zhan, H. On different numerical inverse laplace methods for solute transport problems. Adv. Water Resour. 2015, 75, 80–92. [Google Scholar] [CrossRef]
- Lu, S.M.; Chang, S.L.; Ku, W.Y.; Chang, H.C.; Wang, J.Y.; Lee, D.J. Urea release rate from a scoop of coated pure urea beads: Unified extreme analysis. J. Chinese Inst. Chem. Eng. 2007, 38, 295–302. [Google Scholar] [CrossRef]
- Lu, S.M.; Lee, S.F. Slow release of urea through latex film. J. Control. Release 1992, 18, 171–180. [Google Scholar] [CrossRef]
- Ford Versypt, A.N.; Arendt, P.D.; Pack, D.W.; Braatz, R.D. Derivation of an Analytical Solution to a Reaction-Diffusion Model for Autocatalytic Degradation and Erosion in Polymer Microspheres. PLoS ONE 2015, 10, e0135506. [Google Scholar] [CrossRef] [PubMed]
- Siepmann, J.; Elkharraz, K.; Siepmann, F.; Klose, D. How Autocatalysis Accelerates Drug Release from PLGA-Based Microparticles: A Quantitative Treatment. Biomacromolecules 2005, 6, 2312–2319. [Google Scholar] [CrossRef] [PubMed]
| j | Kj | αj |
|---|---|---|
| 1 | 12.83767675 + 1.666063445i | −36,902.0821 + 196,990.4257i |
| 2 | 12.22613209 + 5.012718792i | 61,277.02524 – 95,408.62551i |
| 3 | 10.93430308 + 8.409673116i | −28,916.56288 + 18,169.18531i |
| 4 | 8.776434715 + 11.92185389i | 4655.361138 − 1.901528642i |
| 5 | 5.2254453361 + 15.72952905i | −118.7414011 − 141.3036911i |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Irfan, S.A.; Razali, R.; KuShaari, K.; Mansor, N. Reaction-Multi Diffusion Model for Nutrient Release and Autocatalytic Degradation of PLA-Coated Controlled-Release Fertilizer. Polymers 2017, 9, 111. https://doi.org/10.3390/polym9030111
Irfan SA, Razali R, KuShaari K, Mansor N. Reaction-Multi Diffusion Model for Nutrient Release and Autocatalytic Degradation of PLA-Coated Controlled-Release Fertilizer. Polymers. 2017; 9(3):111. https://doi.org/10.3390/polym9030111
Chicago/Turabian StyleIrfan, Sayed Ameenuddin, Radzuan Razali, KuZilati KuShaari, and Nurlidia Mansor. 2017. "Reaction-Multi Diffusion Model for Nutrient Release and Autocatalytic Degradation of PLA-Coated Controlled-Release Fertilizer" Polymers 9, no. 3: 111. https://doi.org/10.3390/polym9030111
APA StyleIrfan, S. A., Razali, R., KuShaari, K., & Mansor, N. (2017). Reaction-Multi Diffusion Model for Nutrient Release and Autocatalytic Degradation of PLA-Coated Controlled-Release Fertilizer. Polymers, 9(3), 111. https://doi.org/10.3390/polym9030111