Equilibrium Melting Temperature of Polymorphic Poly(l-lactide) and Its Supercooling Dependence on Growth Kinetics
Abstract
:1. Introduction
2. Theory Background
2.1. Flory–Vrij Approach
2.2. Gibbs–Thomson Approach
2.3. Hoffman–Weeks Approach (Linear Extrapolative Method)
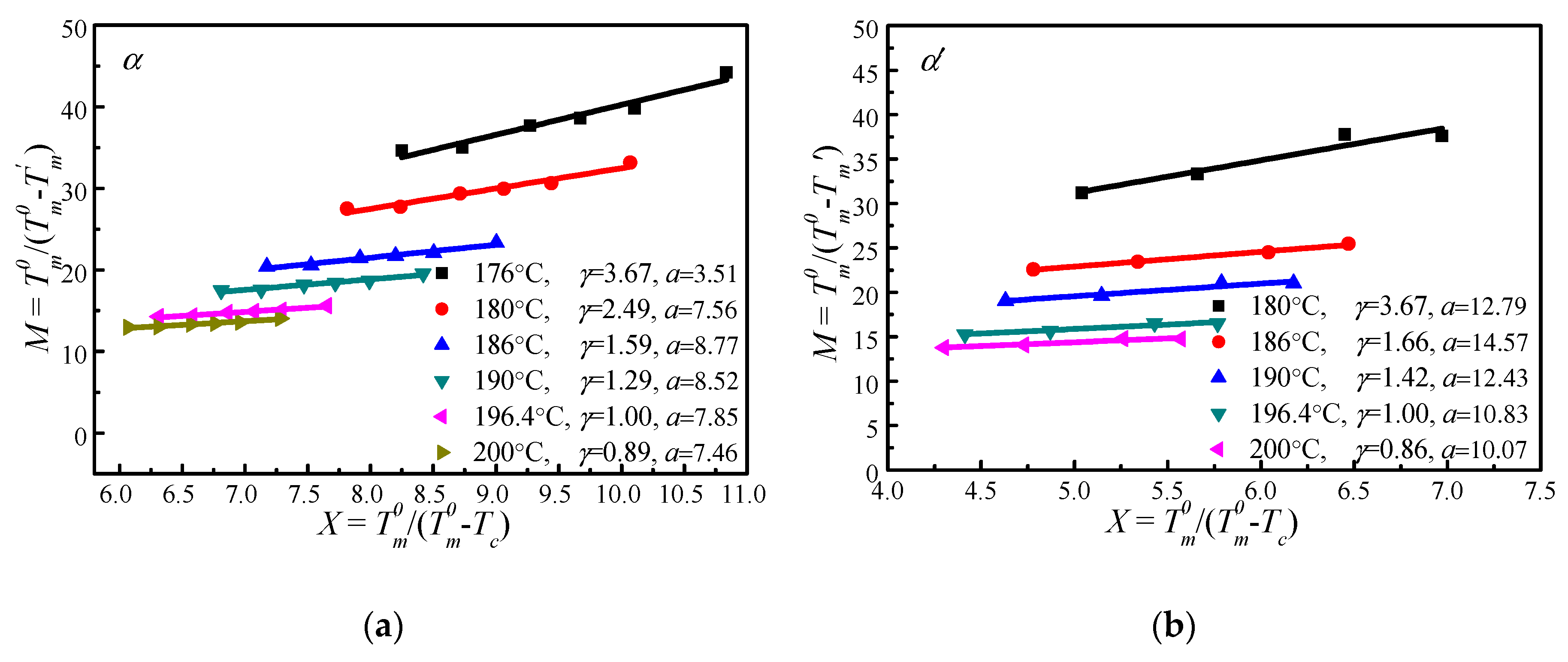
2.4. Nonlinear Extrapolative Method (Marand Herve (MH) Method)
3. Methodology
3.1. Materials
3.2. Isothermal Crystallization Morphology
3.3. X-ray Diffraction (XRD) Analysis
3.4. Differential Scanning Calorimeter (DSC) Measurements
4. Results and Discussion
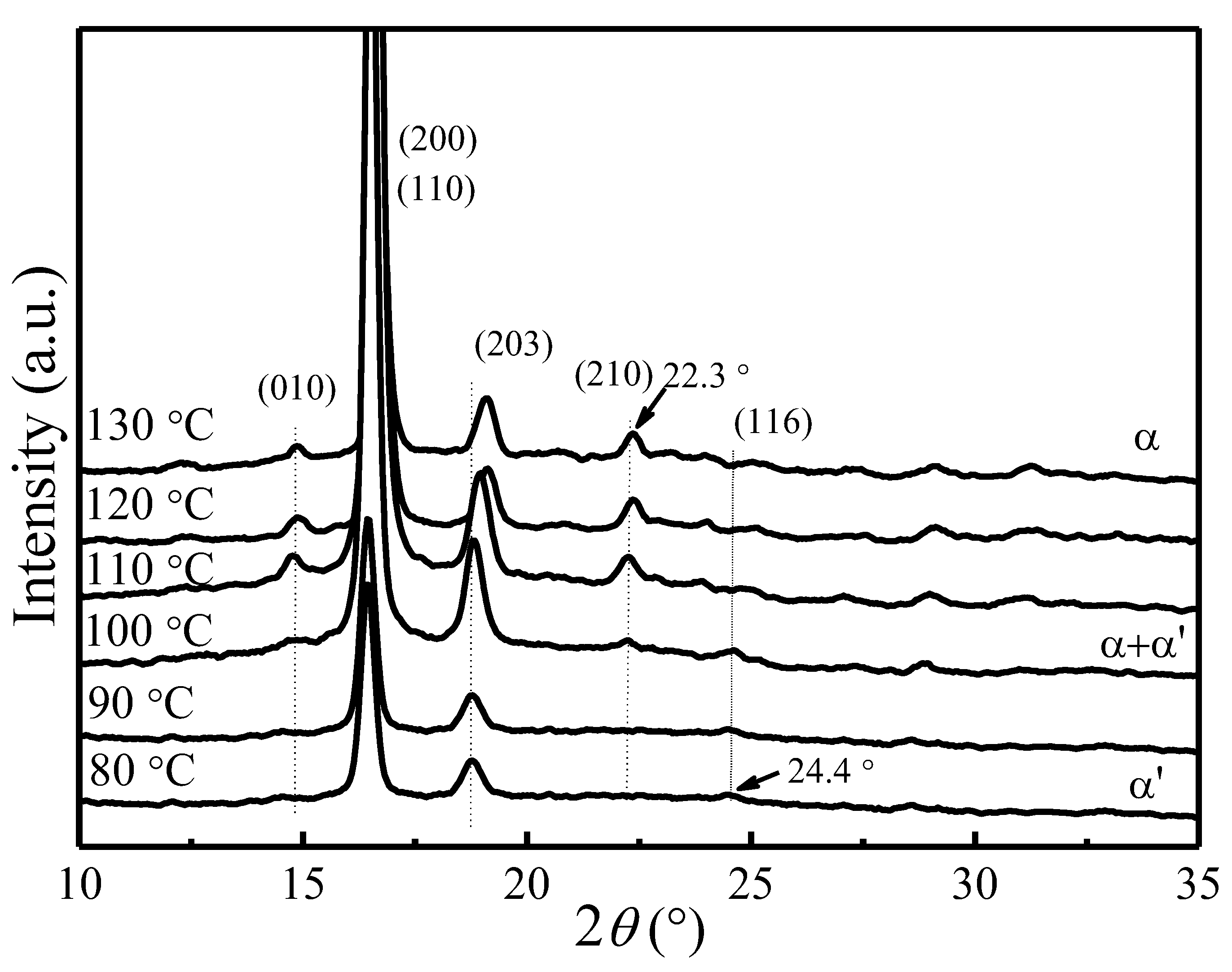
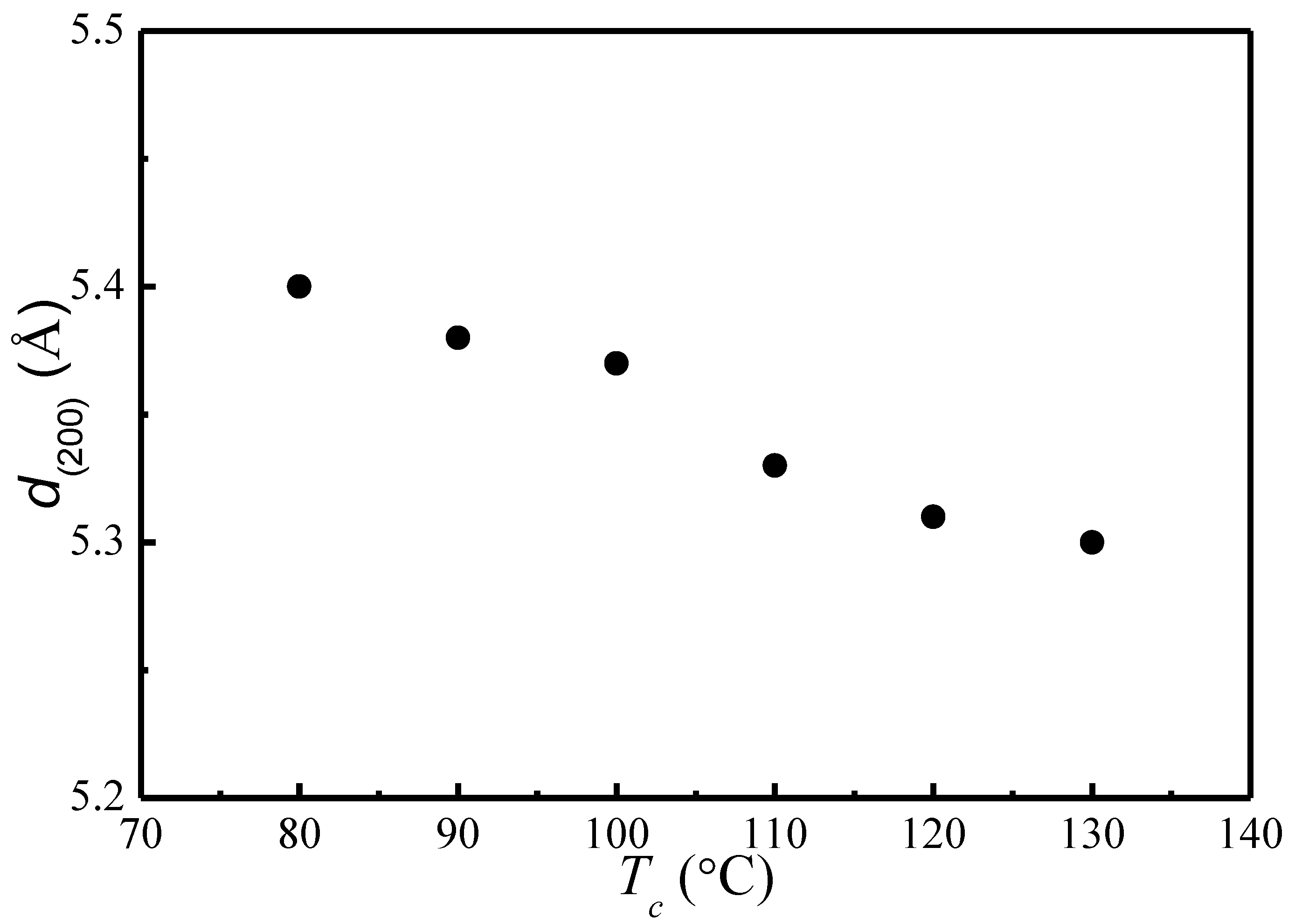
4.1. X-ray Diffraction Patterns of PLLA Crystallized at Different Tc
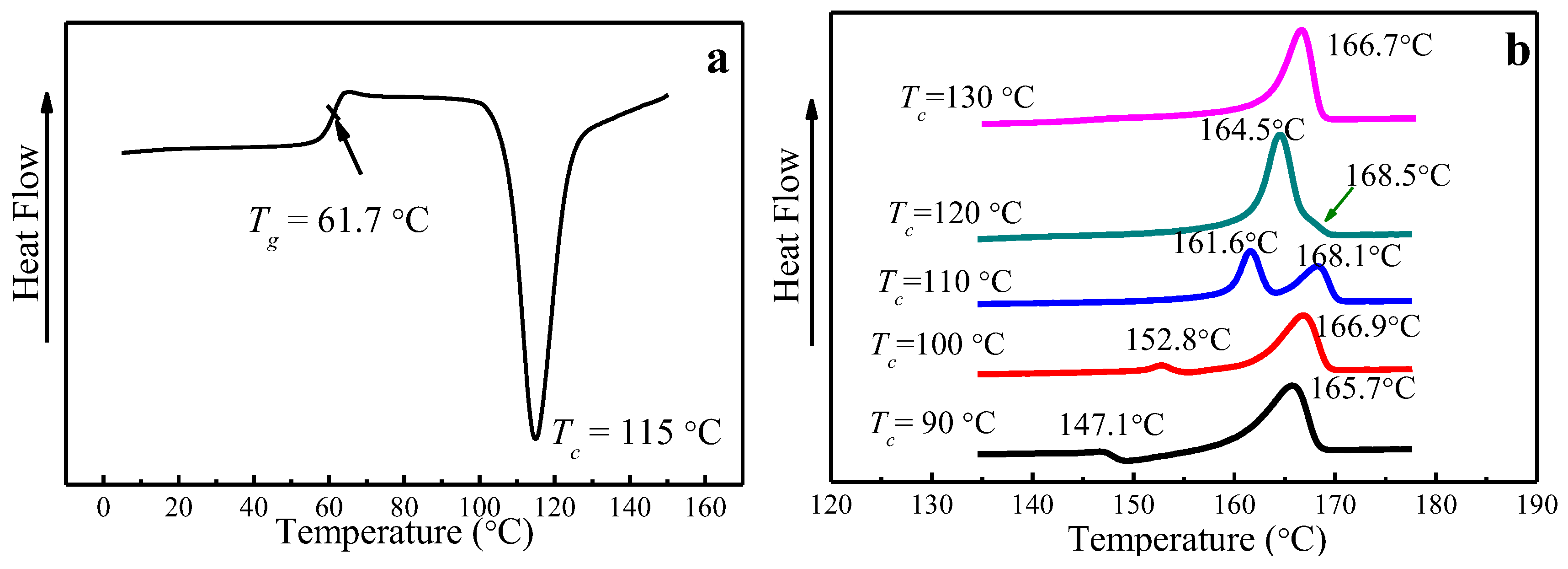
4.2. Multiple-Melting Behavior of PLLA Melt-Crystallized at Various Tc
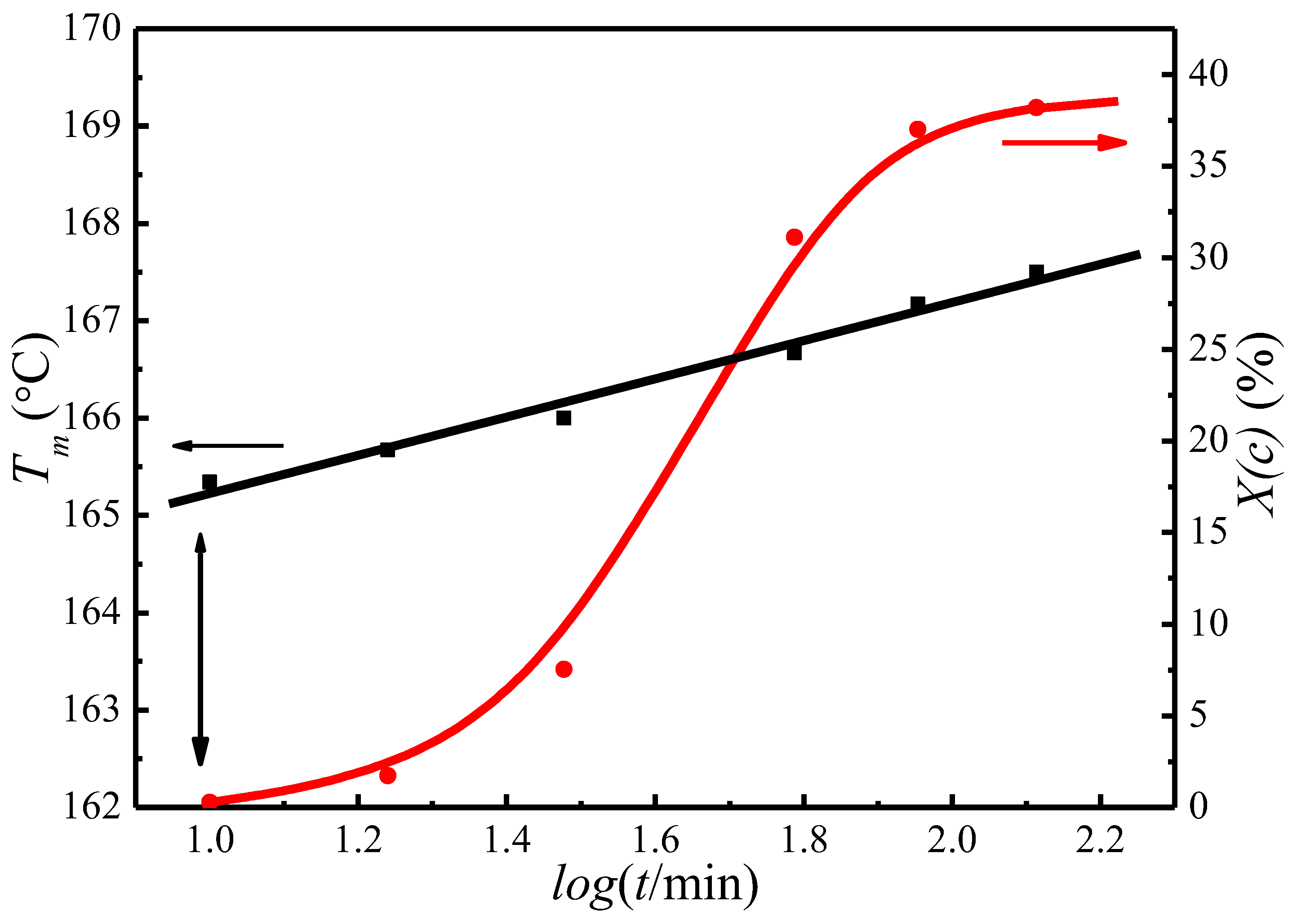
4.3. of Initial Lamellae
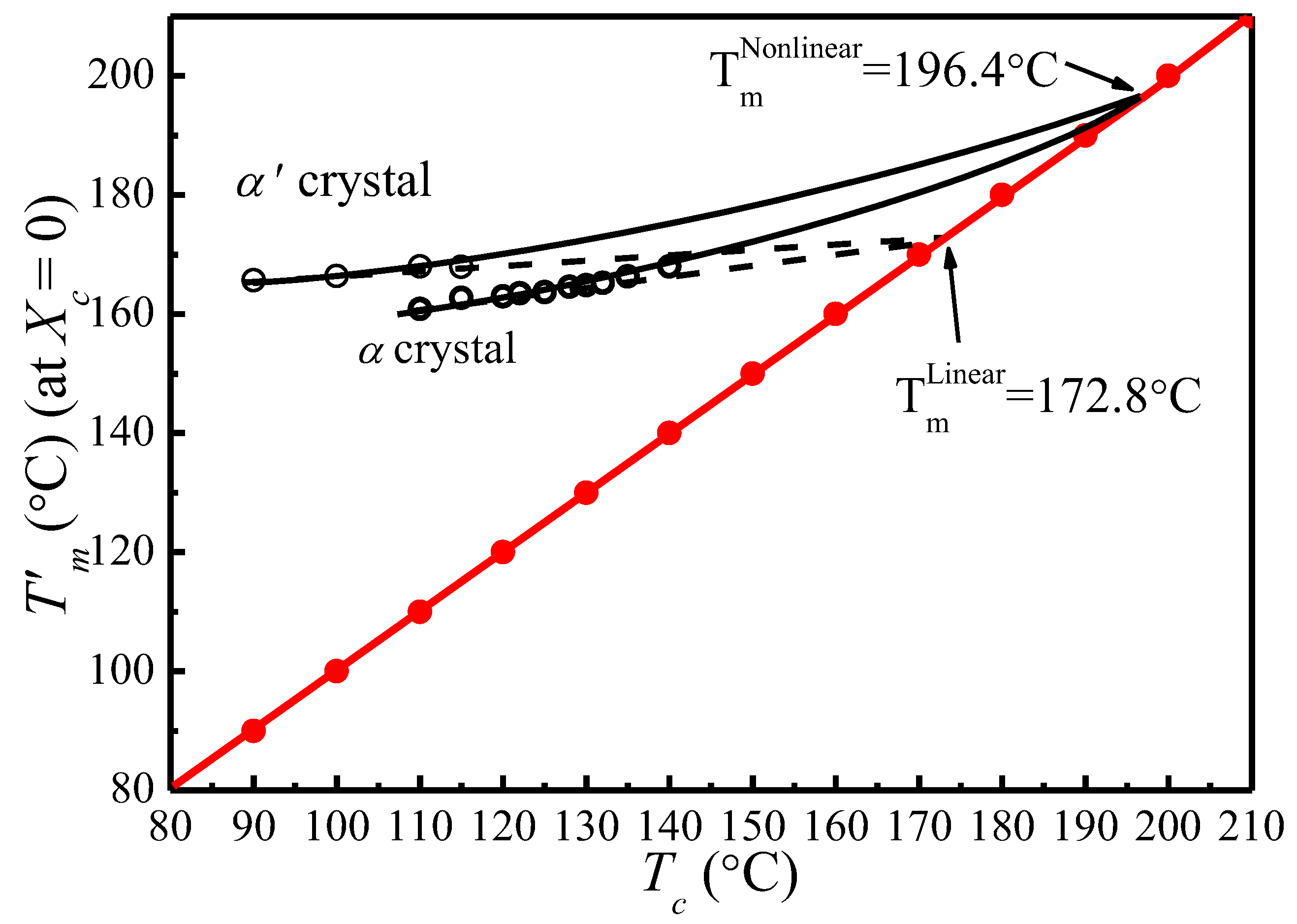
4.4. Determination of by MH and HW Methods
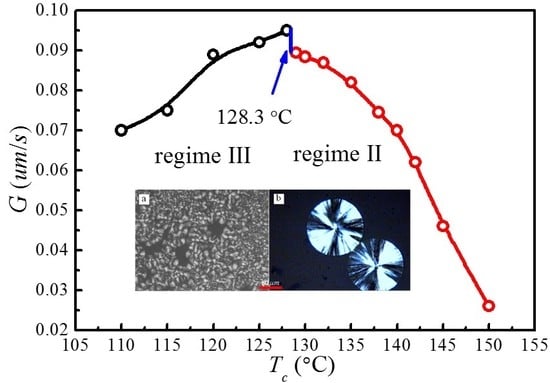
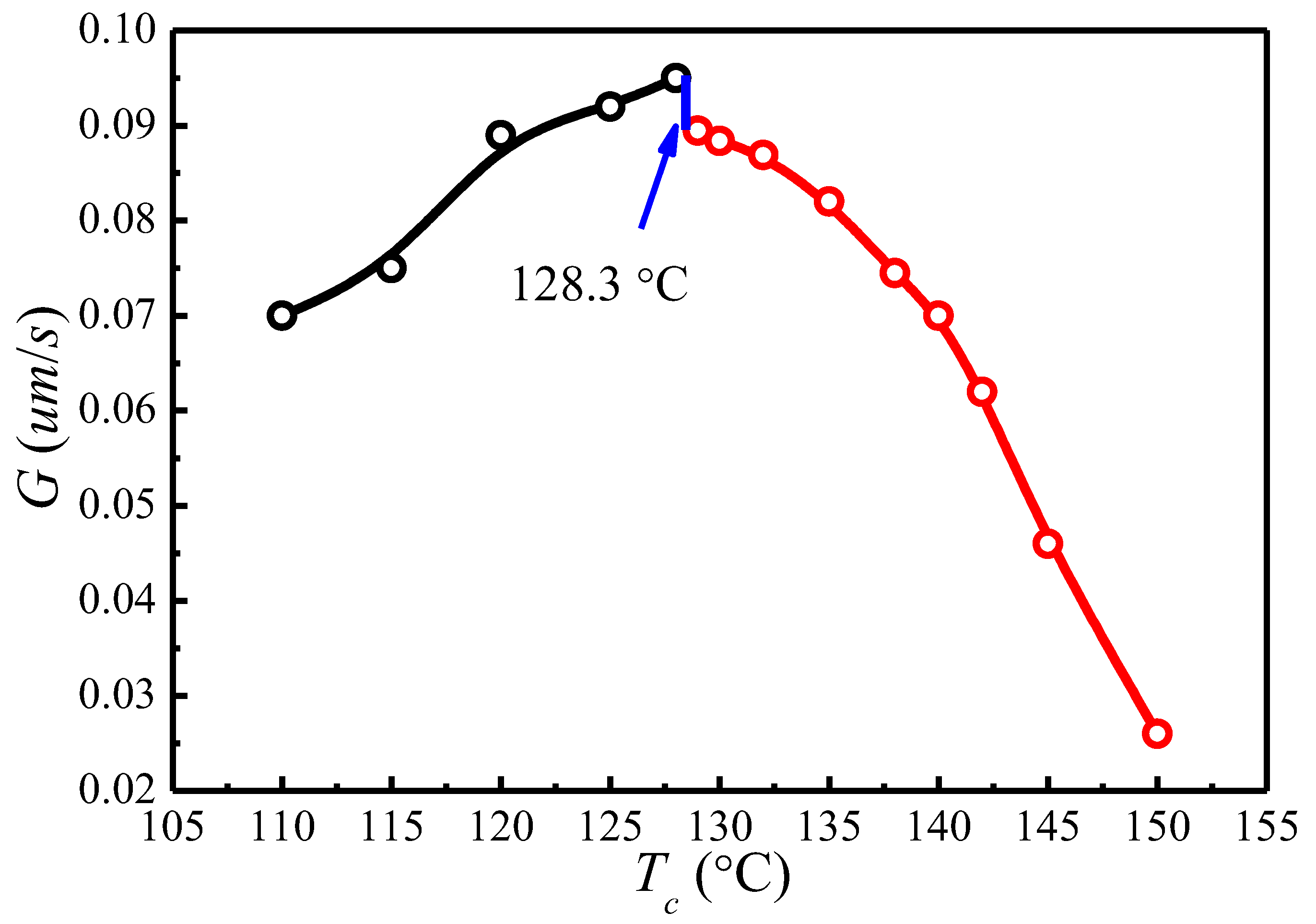
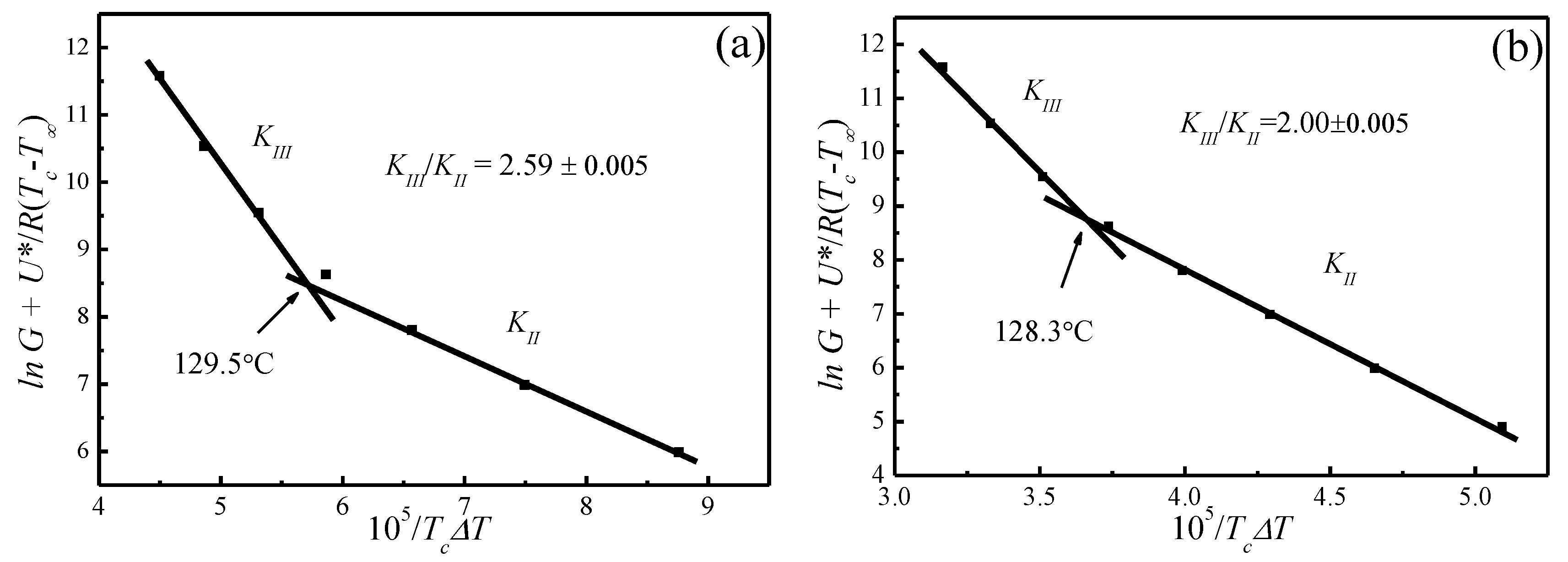
4.5. Temperature Dependence of Spherulitic Growth Rates
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Tsuji, H. Recent Research Developments in Polymer Science; Pandalai, S.G., Ed.; Transworld Research Network: Trivandrum, India, 2000; Volume 4. [Google Scholar]
- Albertsson, A.C. Degradable Aliphatic Polyesters; Advances in Polymer Science; Albertsson, A.C., Ed.; Springer: Berlin, Germany, 2002; Volume 157, p. 180. [Google Scholar]
- Tsuji, H. Polyesters 3; Biopolymers; Doi, Y., Steinbuchel, A., Eds.; Wiley-VCH: Weinheim, Germany, 2002; Volume 4. [Google Scholar]
- Ikada, Y.; Tsuji, H. Biodegradable polyesters for medical and ecological applications. Macromol. Rapid Commun. 2000, 21, 117–132. [Google Scholar] [CrossRef]
- Griffith, L.G. Polymeric biomaterials. Acta Mater. 2000, 48, 263–277. [Google Scholar] [CrossRef]
- Lim, L.T.; Auras, R.; Rubino, M. Processing technologies for poly(lactic acid). Prog. Polym. Sci. 2008, 33, 820–852. [Google Scholar] [CrossRef]
- Gazzotti, S.; Farina, H.; Lesma, G.; Rampazzo, R.; Piergiovanni, L.; Ortenzi, M.A.; Silvani, A. Polylactide/cellulose nanocrystals: The in situ polymerization approach to improved nanocomposites. Eur. Polym. J. 2017, 94, 173–184. [Google Scholar] [CrossRef]
- De Santis, P.; Kovacs, A.J. Molecular conformation of poly(S-lactic acid). Biopolymers 1968, 6, 299–306. [Google Scholar] [CrossRef] [PubMed]
- Eling, B.; Gogolewski, S.; Pennings, A.J. Biodegradable materials of poly(l-lactic acid): 1. Melt-spun and solution-spun fibres. Polymer 1982, 23, 1587–1593. [Google Scholar] [CrossRef]
- Hoogsteen, W.; Postema, A.R.; Pennings, A.J.; Ten Brinke, G.; Zugenmaier, P. Crystal structure, conformation and morphology of solution-spun poly(L-lactide) fibers. Macromolecules 1990, 23, 634–642. [Google Scholar] [CrossRef]
- Cartier, L.; Okihara, T.; Ikada, Y.; Tsuji, H.; Puiggali, J.; Lotz, B. Epitaxial crystallization and crystalline polymorphism of polylactides. Polymer 2000, 41, 8909–8919. [Google Scholar] [CrossRef]
- Zhang, J.; Duan, Y.; Sato, H.; Tsuji, H.; Noda, I.; Yan, S.; Ozaki, Y. Crystal Modifications and Thermal Behavior of Poly(l-lactic acid) Revealed by Infrared Spectroscopy. Macromolecules 2005, 38, 8012–8021. [Google Scholar] [CrossRef]
- Zhang, J.; Tashiro, K.; Domb, A.J.; Tsuji, H. Confirmation of Disorder α Form of Poly(L-lactic acid) by the X-ray Fiber Pattern and Polarized IR/Raman Spectra Measured for Uniaxially-Oriented Samples. Macromol. Symp. 2006, 242, 274–278. [Google Scholar] [CrossRef]
- Zhang, J.; Tashiro, K.; Tsuji, H.; Domb, A.J. Disorder-to-Order Phase Transition and Multiple Melting Behavior of Poly(L-lactide) Investigated by Simultaneous Measurements of WAXD and DSC. Macromolecules 2008, 41, 1352–1357. [Google Scholar] [CrossRef]
- Pan, P.; Kai, W.; Zhu, B.; Dong, T.; Inoue, Y. Polymorphous Crystallization and Multiple Melting Behavior of Poly(L-lactide): Molecular Weight Dependence. Macromolecules 2007, 40, 6898–6905. [Google Scholar] [CrossRef]
- Pan, P.; Zhu, B.; Kai, W.; Dong, T.; Inoue, Y. Polymorphic Transition in Disordered Poly(L-lactide) Crystals Induced by Annealing at Elevated Temperatures. Macromolecules 2008, 41, 4296–4304. [Google Scholar] [CrossRef]
- Pan, P.; Yang, J.; Shan, G.; Bao, Y.; Weng, Z.; Cao, A.; Yazawa, K.; Inoue, Y. Temperature-Variable FTIR and Solid-State 13C NMR Investigations on Crystalline Structure and Molecular Dynamics of Polymorphic Poly(L-lactide) and Poly(L-lactide)/Poly(d-lactide) Stereocomplex. Macromolecules 2012, 45, 189–197. [Google Scholar] [CrossRef]
- Kawai, T.; Rahman, N.; Matsuba, G.; Nishida, K.; Kanaya, T.; Nakano, M.; Okamoto, H.; Kawada, J.; Usuki, A.; Honma, N.; et al. Crystallization and Melting Behavior of Poly (L-lactic Acid). Macromolecules 2007, 40, 9463–9469. [Google Scholar] [CrossRef]
- Wasanasuk, K.; Tashiro, K. Crystal structure and disorder in Poly(L-lactic acid) δ form (α′ form) and the phase transition mechanism to the ordered α form. Polymer 2011, 52, 6097–6109. [Google Scholar] [CrossRef]
- Kalish, J.P.; Aou, K.; Yang, X.; Hsu, S.L. Spectroscopic and thermal analyses of α′ and α crystalline forms of poly(l-lactic acid). Polymer 2011, 52, 814–821. [Google Scholar] [CrossRef]
- Androsch, R.; Schick, C.; Di Lorenzo, M.L. Melting of Conformationally Disordered Crystals (α′-Phase) of Poly(l-lactic acid). Macromol. Chem. Phys. 2014, 215, 1134–1139. [Google Scholar] [CrossRef]
- Righetti, M.C.; Gazzano, M.; Di Lorenzo, M.L.; Androsch, R. Enthalpy of melting of α′- and α-crystals of poly(l-lactic acid). Eur. Polym. J. 2015, 70, 215–220. [Google Scholar] [CrossRef]
- Kalb, B.; Pennings, A.J. General crystallization behaviour of poly(l-lactic acid). Polymer 1980, 21, 607–612. [Google Scholar] [CrossRef]
- Cartier, L.; Okihara, T.; Lotz, B. Triangular Polymer Single Crystals: Stereocomplexes, Twins, and Frustrated Structures. Macromolecules 1997, 30, 6313–6322. [Google Scholar] [CrossRef]
- Huang, Y.F.; Kao, H.L.; Ruan, J.; Su, A.C. Effects of Solution Status on Single-Crystal Growth Habit of Poly(L-lactide). Macromolecules 2010, 43, 7222–7227. [Google Scholar] [CrossRef]
- Sawai, D.; Takahashi, K.; Imamura, T.; Nakamura, K.; Kanamoto, T.; Hyon, S.H. Preparation of oriented β-form poly(L-lactic acid) by solid-state extrusion. J. Polym. Sci. Part B 2001, 40, 95–104. [Google Scholar] [CrossRef]
- Mahendrasingam, A.; Blundell, D.J.; Parton, M.; Wright, A.K.; Rasburn, J.; Narayanan, T.; Fuller, W. Time resolved study of oriented crystallisation of poly(lactic acid) during rapid tensile deformation. Polymer 2005, 46, 6009–6015. [Google Scholar] [CrossRef]
- Li, X.J.; Li, Z.M.; Zhong, G.J.; Li, L.B. Steady–shear-induced Isothermal Crystallization of Poly(L-lactide) (PLLA). J. Macromol. Sci. Part B 2008, 47, 511–522. [Google Scholar] [CrossRef]
- Yamazaki, S.; Itoh, M.; Oka, T.; Kimura, K. Formation and morphology of “shish-like” fibril crystals of aliphatic polyesters from the sheared melt. Eur. Polym. J. 2010, 46, 58–68. [Google Scholar] [CrossRef]
- Huang, S.; Li, H.; Jiang, S.; Chen, X.; An, L. Crystal structure and morphology influenced by shear effect of poly(l-lactide) and its melting behavior revealed by WAXD, DSC and in-situ POM. Polymer 2011, 52, 3478–3487. [Google Scholar] [CrossRef]
- Yang, I.K.; Wu, C.H. Real-time SAXS measurements and rheological behavior of poly(lactic acid) crystallization under continuous shear flow. J. Polym. Res. 2014, 21, 609. [Google Scholar] [CrossRef]
- Mai, F.; Tu, W.; Bilotti, E.; Peijs, T. The Influence of Solid-State Drawing on Mechanical Properties and Hydrolytic Degradation of Melt-Spun Poly(lactic acid) (PLA) Tapes. Fibers 2015, 3, 523. [Google Scholar] [CrossRef]
- Ru, J.F.; Yang, S.G.; Zhou, D.; Yin, H.M.; Lei, J.; Li, Z.M. Dominant β-Form of Poly(L-lactic acid) Obtained Directly from Melt under Shear and Pressure Fields. Macromolecules 2016, 49, 3826–3837. [Google Scholar] [CrossRef]
- Ma, P.; Yu, Q.; Shen, T.; Dong, W.; Chen, M. Strong synergetic effect of fibril-like nucleator and shear flow on the melt crystallization of poly(L-lactide). Eur. Polym. J. 2017, 87, 221–230. [Google Scholar] [CrossRef]
- Xie, X.L.; Sang, Z.H.; Xu, J.Z.; Zhong, G.J.; Li, Z.M.; Ji, X.; Wang, R.; Xu, L. Layer structure by shear-induced crystallization and thermal mechanical properties of injection-molded poly(l-lactide) with nucleating agents. Polymer 2017, 110, 196–210. [Google Scholar] [CrossRef]
- Jalali, A.; Huneault, M.A.; Elkoun, S. Effect of thermal history on nucleation and crystallization of poly(lactic acid). J. Mater. Sci. 2016, 51, 7768–7779. [Google Scholar] [CrossRef]
- Di Lorenzo, M.L.; Rubino, P.; Immirzi, B.; Luijkx, R.; Hélou, M.; Androsch, R. Influence of chain structure on crystal polymorphism of poly(lactic acid). Part 2. Effect of molecular mass on the crystal growth rate and semicrystalline morphology. Colloid Polym. Sci. 2015, 293, 2459–2467. [Google Scholar] [CrossRef]
- Di Lorenzo, M.L.; Rubino, P.; Luijkx, R.; Hélou, M. Influence of chain structure on crystal polymorphism of poly(lactic acid). Part 1: Effect of optical purity of the monomer. Colloid Polym. Sci. 2014, 292, 399–409. [Google Scholar] [CrossRef]
- Lorenzo, M.L.D.; Androsch, R. Melting of α′- and α-crystals of poly(lactic acid). AIP Conf. Proc. 2016, 1736, 020009. [Google Scholar]
- Vasanthakumari, R.; Pennings, A.J. Crystallization kinetics of poly(L-lactic acid). Polymer 1983, 24, 175–178. [Google Scholar] [CrossRef]
- Marega, C.; Marigo, A.; Noto, V.D.; Zannetti, R.; Martorana, A.; Paganetto, G. Structure and crystallization kinetics of poly(L-lactic acid). Die Makromol. Chem. 1992, 193, 1599–1606. [Google Scholar] [CrossRef]
- Tsuji, H.; Tezuka, Y.; Saha, S.K.; Suzuki, M.; Itsuno, S. Spherulite growth of l-lactide copolymers: Effects of tacticity and comonomers. Polymer 2005, 46, 4917–4927. [Google Scholar] [CrossRef]
- Di Lorenzo, M.L. Crystallization behavior of poly(l-lactic acid). Eur. Polym. J. 2005, 41, 569–575. [Google Scholar] [CrossRef]
- Hoffman, J.D.; Miller, R.L. Kinetic of crystallization from the melt and chain folding in polyethylene fractions revisited: Theory and experiment. Polymer 1997, 38, 3151–3212. [Google Scholar] [CrossRef]
- Marand, H.; Xu, J.; Srinivas, S. Determination of the Equilibrium Melting Temperature of Polymer Crystals: Linear and Nonlinear Hoffman−Weeks Extrapolations. Macromolecules 1998, 31, 8219–8229. [Google Scholar] [CrossRef]
- Núñez, E.; Ferrando, C.; Malmström, E.; Claesson, H.; Werner, P.E.; Gedde, U.W. Crystal structure, melting behaviour and equilibrium melting point of star polyesters with crystallisable poly(ε-caprolactone) arms. Polymer 2004, 45, 5251–5263. [Google Scholar] [CrossRef]
- Hoffman, J.D.; Davis, G.T.; Lauritzen, J.I. Treatise on Solid State Chemistry; Hannay, N.B., Ed.; Plenum Press: New York, NY, USA, 1976; Volume 3. [Google Scholar]
- Broadhurst, M.G. Extrapolation of the Orthorhombic n-Paraffin Melting Properties to Very Long Chain Lengths. J. Chem. Phys. 1962, 36, 2578–2582. [Google Scholar] [CrossRef]
- Flory, P.J.; Vrij, A. Melting Points of Linear-Chain Homologs. The Normal Paraffin Hydrocarbons. J. Am. Chem. Soc. 1963, 85, 3548–3553. [Google Scholar] [CrossRef]
- Wunderlich, B. Crystal Melting; Macromolecular Physics; Academic Press: New York, NY, USA, 1980; Volume 3. [Google Scholar]
- Marand, H.; Hoffman, J.D. Determination of the fold surface free energy and the equilibrium melting temperature for .alpha.-phase poly(pivalolactone) crystals. Macromolecules 1990, 23, 3682–3687. [Google Scholar] [CrossRef]
- Xu, J.; Srivatsan Srinivas, A.; Marand, H.; Agarwal, P. Equilibrium Melting Temperature and Undercooling Dependence of the Spherulitic Growth Rate of Isotactic Polypropylene. Macromolecules 1998, 31, 8230–8242. [Google Scholar] [CrossRef]
- Zhang, R.C.; Lu, A.; Xu, Y.; Min, M.; Xia, J.Q.; Zhou, J.H.; Huang, Y.G.; Li, Z.M. Equilibrium melting temperature and spherulitic growth rate of poly(phenylene sulfide). Eur. Polym. J. 2009, 45, 2867–2872. [Google Scholar] [CrossRef]
- Mandelkern, L.; Stack, G.M. Equilibrium melting temperature of long-chain molecules. Macromolecules 1984, 17, 871–878. [Google Scholar] [CrossRef]
- Brizzolara, D.; Cantow, H.J.; Diederichs, K.; Keller, E.; Domb, A.J. Mechanism of the Stereo- complex Formation between Enantiomeric Poly(lactide)s. Macromolecules 1996, 29, 191–197. [Google Scholar] [CrossRef]
- Alemán, C.; Lotz, B.; Puiggali, J. Crystal Structure of the α-Form of Poly(l-lactide). Macromolecules 2001, 34, 4795–4801. [Google Scholar] [CrossRef]
- Sasaki, S.; Asakura, T. Helix Distortion and Crystal Structure of the α-Form of Poly(l-lactide). Macromolecules 2003, 36, 8385–8390. [Google Scholar] [CrossRef]
- Abe, H.; Kikkawa, Y.; Inoue, Y.; Doi, Y. Morphological and Kinetic Analyses of Regime Transition for Poly[(s)-lactide] Crystal Growth. Biomacromolecules 2001, 2, 1007–1014. [Google Scholar] [CrossRef] [PubMed]
- Abe, H.; Harigaya, M.; Kikkawa, Y.; Tsuge, T.; Doi, Y. Crystal growth and solid-state structure of poly(lactide) Stereocopolymers. Biomacromolecules 2005, 6, 457–467. [Google Scholar] [CrossRef] [PubMed]


| Tc (°C) | A (°C) | B | t0 (min) | T′m[Tc, t0] (°C) |
|---|---|---|---|---|
| 122 | 162.8 | 1.22 | 3.83 | 163.52 |
| 125 | 162.5 | 1.49 | 6.16 | 163.66 |
| 128 | 163.62 | 1.12 | 7.18 | 164.57 |
| 130 | 163.18 | 1.69 | 9.43 | 164.86 |
| 132 | 163.26 | 1.97 | 9.63 | 165.2 |
| 135 | 164.77 | 1.58 | 9.71 | 166.33 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, R.-C.; Sun, D.; Lu, A.; Zhong, M.; Xiong, G.; Wan, Y. Equilibrium Melting Temperature of Polymorphic Poly(l-lactide) and Its Supercooling Dependence on Growth Kinetics. Polymers 2017, 9, 625. https://doi.org/10.3390/polym9110625
Zhang R-C, Sun D, Lu A, Zhong M, Xiong G, Wan Y. Equilibrium Melting Temperature of Polymorphic Poly(l-lactide) and Its Supercooling Dependence on Growth Kinetics. Polymers. 2017; 9(11):625. https://doi.org/10.3390/polym9110625
Chicago/Turabian StyleZhang, Ri-Chao, Dan Sun, Ai Lu, Meiling Zhong, Guangyao Xiong, and Yizao Wan. 2017. "Equilibrium Melting Temperature of Polymorphic Poly(l-lactide) and Its Supercooling Dependence on Growth Kinetics" Polymers 9, no. 11: 625. https://doi.org/10.3390/polym9110625
APA StyleZhang, R.-C., Sun, D., Lu, A., Zhong, M., Xiong, G., & Wan, Y. (2017). Equilibrium Melting Temperature of Polymorphic Poly(l-lactide) and Its Supercooling Dependence on Growth Kinetics. Polymers, 9(11), 625. https://doi.org/10.3390/polym9110625