1. Introduction
Polymer chains collapse into compact globules when the solvent condition changes from good to poor. This “coil-globule transition” is relatively well understood for flexible polymers [
1,
2]. The globule state minimizes the area of solvent contact of monomers, and makes the collapsed state energetically more favorable than the extended state. However, many polymers exhibit substantial bending stiffness and are considered to be semiflexible, as described by the worm-like chain model [
3]. For these chains, a globule state minimizes the surface free energy, but involves substantial bending energy. Therefore, these chains collapse into states that are less dense than the globule, which are overall more thermodynamically favorable. In particular, semiflexible polymer chains, such as biopolymers DNA and (methyl)cellulose, tend to collapse into equilibrium states that balance the bending force that resists the collapse with the attractive force that promotes it. Both experiments [
4,
5,
6] and simulations [
7,
8,
9,
10,
11,
12] have detailed collapse pathways, as well as the conformations of semiflexible polymers, once collapse is complete. A typical pathway for the collapse of a semiflexible polymer chain involves long-lived, partially collapsed, “racquet”-shapes, that are intermediates on the path towards a more compact state, such as a torus, folded bundle, or globule [
7,
9,
10,
12].
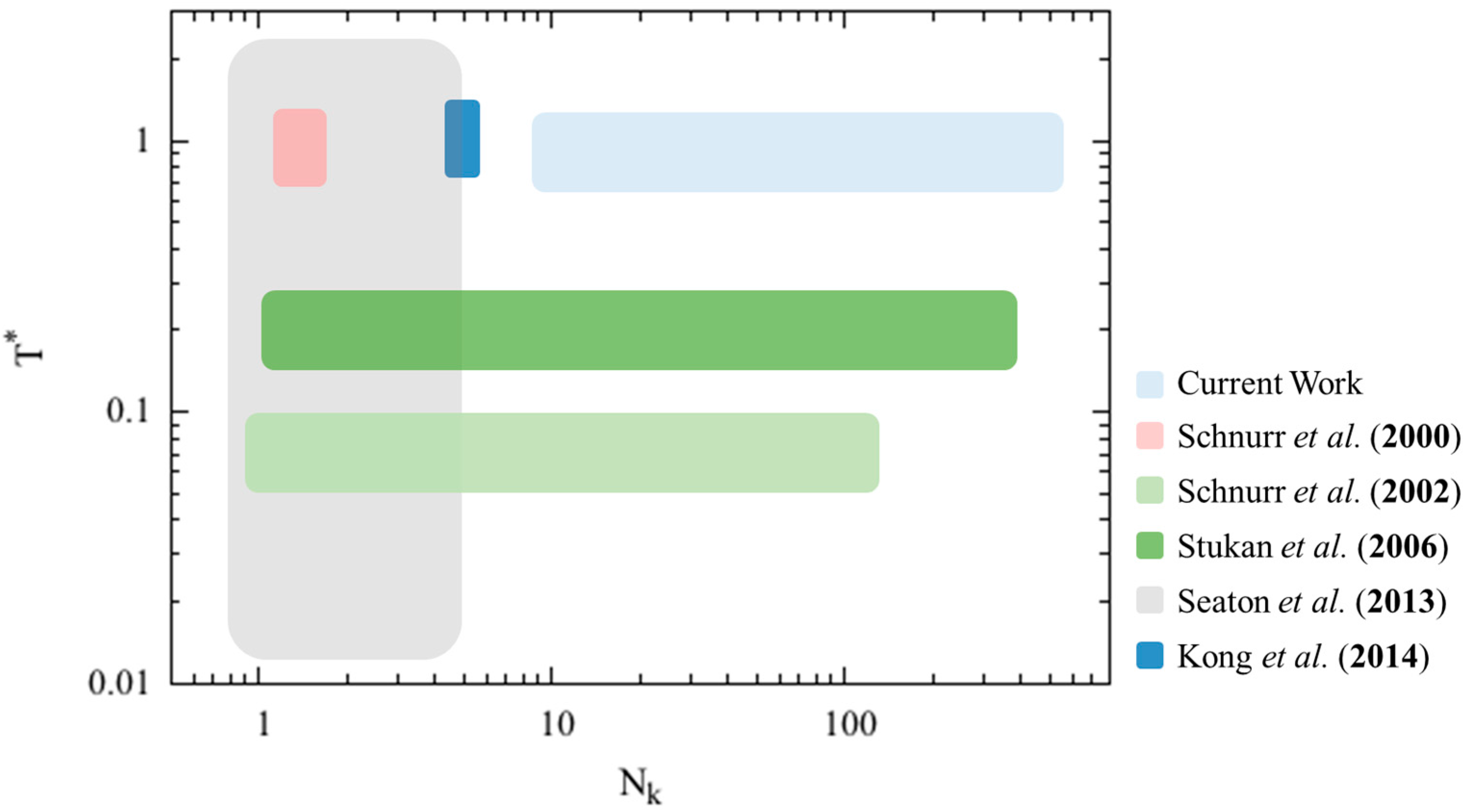
The ability to predict the collapsed state of a given semiflexible polymer chain based on its structural properties (e.g., diameter, bending stiffness, interaction with solvent, etc.) could be a powerful tool to understand the formation of specific collapsed polymer structures. For example, it was recently shown that methylcellulose gel contains fibrillar structures with a uniform diameter [
13]. Such structures are likely to be initiated by the collapse of individual methylcellulose chains when the solution temperature increases [
14]. This collapsed state can be qualitatively predicted based on the structural properties of methylcellulose, as explained in a recent simulation study of methylcellulose by Huang et al. [
11]. In early work, Schnurr et al. [
7] simulated single short stiff chains (2–3 Kuhn steps,
) using bead-spring “pearl necklace” chains and observed the chain evolve from an extended state to various collapsed states. More recently, Seaton et al. [
15] reported the phase behavior of simulated 30-mer semiflexible bead-spring “pearl necklace” chains (
< 10) with various bending stiffnesses over a wide range dimensionless temperatures. With increasing chain stiffness, they observed globules at very small bending stiffness, to bundles of varying aspect ratios at higher bending stiffness, to tori, and to expanded coils at the highest bending stiffness. However, they considered only a single chain length and suggested that the phase diagram could change for much longer chains. In a recent simulation study, Kong et al. [
10] detailed various collapsed states and collapse paths exhibited by semiflexible bead-spring polymers at different chain resolutions (i.e., number of beads per Kuhn length), self-attractive strengths, and chain diameters. A conformational phase diagram for polymer chains with a length of five Kuhn steps (
= 5) as a function of dimensionless self-attraction strength and ratio of chain diameter to Kuhn length was produced. In sum, simulation studies currently available in the literature are limited to bead-spring chains with rather short lengths. However, with the recent advances in computational power, a single chain of length several hundreds of Kuhn steps can now be simulated using standard Brownian Dynamics (BD) simulation model [
11]. Therefore, we would like to re-examine the collapsed phase behavior of semiflexible polymer chains over a wider range of chain lengths.
A few analytical models have been developed to characterize the energy of both metastable intermediates during the collapse and the equilibrated conformations of collapsed semiflexible polymers. Schnurr et al. [
16] calculated the conformational energy of intermediate “racquet” states and showed that this shape is metastable and that semiflexible self-attractive chains will indeed eventually collapse into energetically more favorable bundles and tori. Their model was derived for low dimensionless temperature (
T*, which is the thermal energy
divided by the bead-bead attraction energy) where the tori and bundles with “racquet” heads have crystalline packings of the monomer beads used to model the chain. Thus, the model incorporates the packing order of monomers within the filaments, the completeness of the torus, and number of “racquet” heads in a bundle. Moreover, the shape of an ideal “racquet” head is resolved by introducing additional parameters such as total contour length of the chain within the racquet head and the curvature of the racquet. Stukan et al. [
17] analyzed the stability of a bundle and a torus formed by single chain using a detailed analytical model, including bead packing energies generated by the number of bead-bead contacts. Their model was derived for collapsed structures of bead spring “pearl necklace” chains at low dimensionless temperature, where the packing order (number of bead-bead contacts) of the filaments in both torus and bundle was considered. For both conformations, they found periodicities in the minimum energy state as a function of chain length due to the periodic completion of windings around the torus, or of parallel filaments in the bundle, respectively. They compared the energy of a torus with perfect hexagonal filament packing to a bundle with ideal tight back folding at the ends, and concluded the torus is always energetically more favorable than the bundle. This is a somewhat striking finding, since bundle structures are generally considered to be stable equilibrium collapsed structures for semiflexible polymer chains and have been observed in both simulations and theoretical studies [
10,
15,
18]. However, it is worth noting that in addition to the limitation on bead spring “pearl necklace” model, the chains Stukan et al. modeled were rather stiff. Therefore, it is reasonable that a bundle with ideal tight back folding at the ends is always energetically more costly to form than a torus. Both the analytical models of Schnurr et al. and of Stukan et al. are applicable to long chains (>100 Kuhn steps).
The parameter spaces covered by these previous simulation studies, summarized in
Figure 1, have mostly focused on high dimensionless temperatures and short chain lengths, and the theoretical modeling studies have resolved the conformational space at low dimensionless temperatures and a wide range of chain lengths. While the hexagonal filament packings in collapsed conformations may be important for short oligomer chains with ideal spherically shaped monomers at low dimensionless temperatures, we are interested in providing qualitative prediction of the final collapsed chain conformation at dimensionless temperature value around 1, similar to the condition in Kong et al.’s work. Therefore, we wish to develop a generic analytical model with less emphasis on the actual filament packing details to predict the minimum free energy conformation of semiflexible polymer chains at high dimensionless temperatures with reasonable accuracy, at least for long polymer chains.
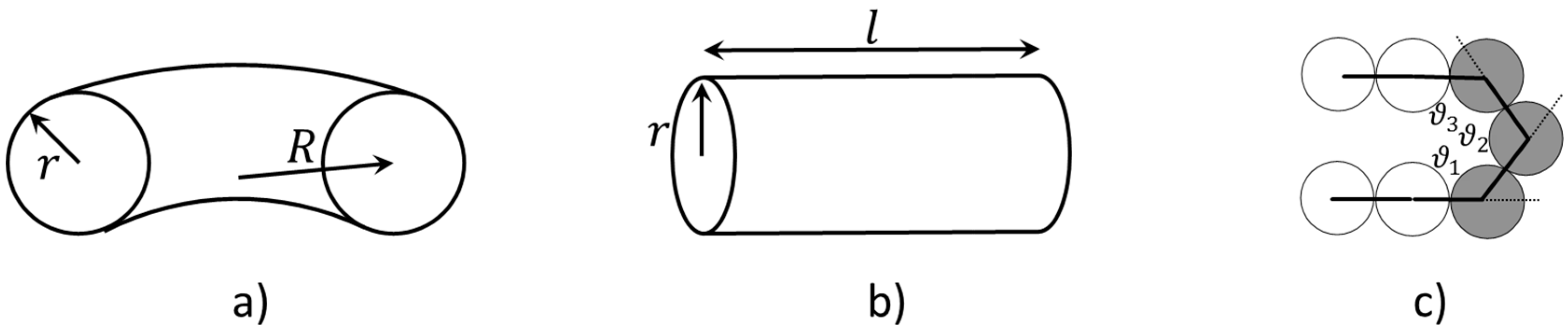
One important consideration in the polymer chain model is the choice of the bending potential. There are two typical bending potentials, namely the harmonic bending potential (
) and the cosine bending potential (
) (Equation (1a,b)). While Schnurr et al. and Kong et al. chose harmonic potential for their model and Seaton et al. chose cosine potential in their work, Stukan et al. have compared the effect of these two bending potentials on the stability of the torus and bundle. They have found that the choice of the bending potential can lead to different stability of the collapsed structures. For example, for large bending angles, such as the ones in the end fold, the cosine potential is “softer” than the harmonic potential (see
Figure S1 at small angle limit), and therefore decreases the overall energy of the end fold. Because Stukan et al. only modeled the chains at low dimensionless temperature with ideal hexagonal packing, we would also like to re-evaluate the effect of the bending potentials on the conformational behavior at higher dimensionless temperature and over a wider range of dimensionless chain length range in this work.
In this work, we develop a much simpler analytical model to predict the formation of torus or bundle states by representing these collapsed states as ideal geometries with specified dimensions, and corresponding surface areas, such as the areas of the folded bundle ends and sides. We then subsume the properties of the chain, namely the number of monomers, monomer diameter, and chain stiffness into surface free energies of both ends and sides, as well as the bending energy per unit length for a chain with a radius of curvature set by the radii of the torus. We then find the geometry of minimum free energy of both torus and bundle for a given set of parameters, and find whether the torus or the bundle has the lower minimum free energy. A phase diagram is produced by recording these minimum free energy conformations. To validate the theoretical derived phase diagram, we also simulate bead-spring “pearl-necklace” chains using Brownian Dynamics (BD) simulations with three different bending potentials. Specifically, in addition to the harmonic and cosine bending potential, we adopt a “stiff” potential () using a linear combination of the two aforementioned potentials (Equation (1c)) to study the effect of bending potential systematically. We show that the predicted phase diagram agrees with the BD simulation results qualitatively.
The paper is organized as follows. We first discuss the development of the analytical model for the collapsed conformations, and the model we use for the BD simulations. We also discuss how to map the parameters used in the analytical model onto the input parameters for the simulations. We then show the calculated phase diagrams for various dimensionless chain lengths, and compare these phase diagrams with the simulation results.
3. Results and Discussion
Within our model, the collapsed state of a single polymer chain is controlled by three dimensionless quantities, namely
,
, and
L*
. A fourth dimensionless parameter, the dimensionless temperature,
, influences when the chain will remain a random coil, rather than collapsing, but we consider long chains here at moderate values of
, and this parameter therefore does not enter our theory. On the “phase diagram” shown in
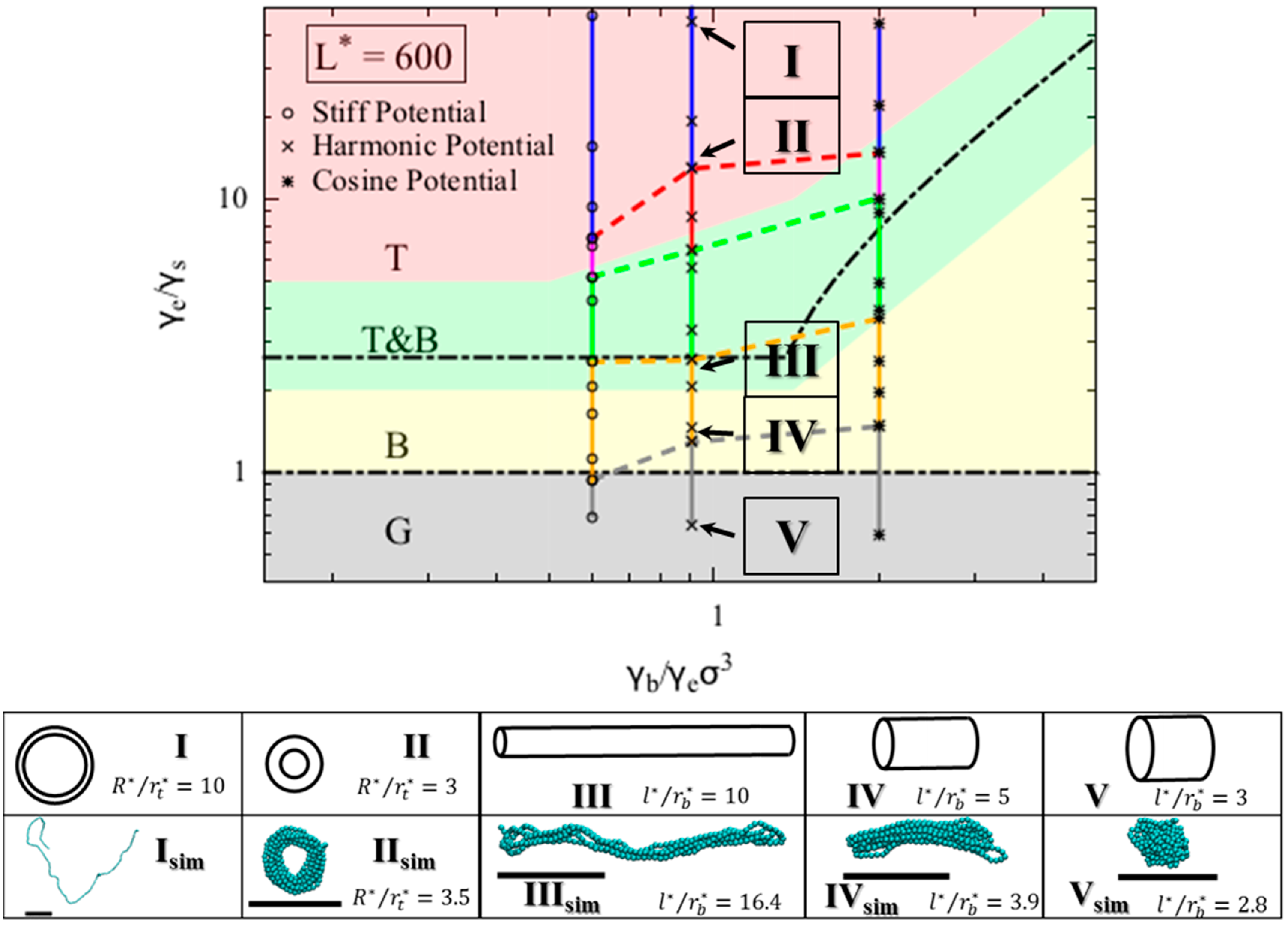
Figure 3, the y-axis is the ratio of the end fold energy to the surface energy, while the x axis is the ratio of the bending energy to the product of end fold energy and bead diameter cubed. We vary the two dimensionless ratios over a range of values to determine a “phase diagram” of lowest energy conformation. Specifically, for each
and
pair, we compute the resulting minimized free energies for all three conformations, and record the lowest energy conformation on the phase diagram. The phase diagram for
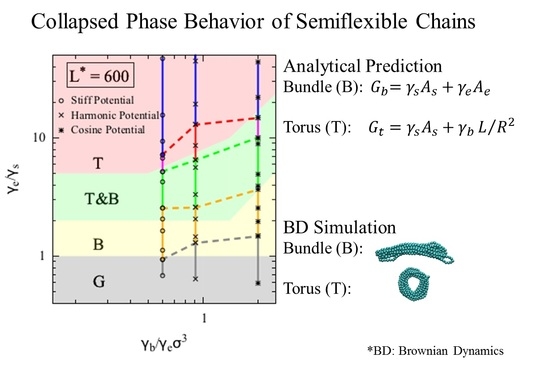
L* = 600 is shown in
Figure 3, which includes regions for each of the three phases that we modeled for a polymer chain. The globule (G) conformation is observed when surface energy penalty dominates (small
values; see inset V in
Figure 3). Chains in this region can be regarded as flexible. The chain adopts either torus or bundle configuration when it has moderate bending and end fold energy penalties. Specifically, when the end surface energy penalty is high but the bending energy penalty is low, the polymer chain collapses into a torus (T). The aspect ratio of this torus (
R*
/r*) increases as the bending energy increases; the cross section of the torus becomes thinner and its radius increases, which helps the chain to reduce the high bending energy penalty. This can be seen from the insets I and II in
Figure 3. On the other hand, when the end fold energy penalty is low but bending energy penalty is high, a bundle (B) is formed. The aspect ratio of the bundle (
l*
/r*) increases as the end fold energy term increases; the bundle becomes thinner and longer, which helps the chain to reduce the end fold energy at an expense of having more beads exposed along its side. Schematics of bundles with different aspect ratios are in the insets III and IV in
Figure 3. We mark the exact solutions to the boundaries between collapsed phases, derived in the theory section on
Figure 3. The boundary between globule and bundle (Equation (4c)) is a horizontal line at
. We note that the upper bound of the boundary between torus and bundle that we present in Equation (7c), namely
, is not visible, because the value of
at the upper bound exceeds the x-axis range. For a small
(
x-axis value), even though the minimum-free-energy torus is self-intersecting at the given
and
pair, a torus with minimum possible
R*
/r* value of 2 can still form and its free energy remains lower than that of a bundle. This results in the horizontal boundary between bundle and torus phase on the phase diagram at small
values. From the simulation trajectories, we observed conformations that fluctuate between two collapsed states, namely torus and bundle. We therefore assume that a chain can fluctuate between two states (i.e., T&B) if the calculated free energy of one state is less than 5% different from that of the other state, and add a transition phase (T&B) on the theoretical phase diagram. The resulting phase diagram captures both the predictions based on theory and the observations from the simulations. Note we expect to see a chain adopting a random coil (RC) conformation when both end fold energy and bending energy penalties dominate (large
and
values), despite its large solvent-exposed surface area. However, because it is challenging to model the entropic contribution in the free energy of the random coil state to a reasonable accuracy, we are not presenting an analytical model for this state in the current work.
We compare the collapsed conformations predicted by the theory with the ones obtained from the simulations. As we noted earlier, because the bending and the end fold are modeled using the same energy potential, the ratio
is constant for a given bending potential in our simulations. We can map the
and
values onto the phase diagram using Equation (9a–c), given a generic end fold (
Figure 2c). From the simulations that use the harmonic bending potential, we observe various collapsed states as
value increases (
Figure 3 inset
Isim through
Vsim). Specifically, for
values less than 1.3, we observe a globule, and for
between 1.3 and 2.7, we observe bundles with various aspect ratios. For
greater than 6.5, tori with various aspect ratios form. In between 2.7 and 6.5, we observe fluctuations between bundle and torus. As expected, simulations show random coils form at large
, here found to be a value greater than 13.
The theoretical diagram is in agreement with the simulation results, and is insensitive to
L* for
L* ≥ 300. The conformations and their corresponding aspect ratios from both theory and simulation using harmonic bending potential under various conditions are presented in
Table 1. The aspect ratios,
l*
/r* and
R*
/r* of the simulated conformation were measured by both visual inspection and an in-house analysis code and agree with the theoretically predicted phases for collapsed states, at least at
L* = 600. We indeed observed both torus and bundle formed in our simulations within the region predicted by the theory. The aspect ratios of the conformations, however, agree only qualitatively. Nevertheless, the aspect ratios of bundles and tori increase with the bending potential coefficient
, as predicted.
We compared the simulation results obtained using different bending potentials. The simulations show transitions from collapsed states to random coil state for all three bending potentials. The transitions from bundle (B) to fluctuation between bundle and torus (T&B) occur at very similar
values for simulations using stiff and harmonic potentials, and at a higher
value for simulations using the cosine potential. This trend is in agreement with theoretical prediction. The transition from fluctuation between bundle and torus (T&B) to torus (T) occurs at a higher
value as
increases. This shows that a chain modeled with a “softer” bending potential that grows less steeply with increasing bending angle is more likely to form a bundle with large aspect ratio. We have marked the upper boundaries of the phases obtained from the simulation results in
Figure 3 (i.e., chain in the simulation with mapped
value between yellow and grey dashed line will result in a bundle as the final collapsed structure). Because we do not model the random coil phase analytically, we simply regard the phase where chain fluctuates between torus and random coil (T&RC) as the torus phase (T). These boundaries obtained from simulations agree qualitatively with the ones predicted by the theory. We note that a globule is merely a very short bundle; therefore, it is often hard to distinguish between a short bundle and a globule from the simulation results, contributing to the deviation on the boundaries between globule and bundle obtained from simulation and theory.
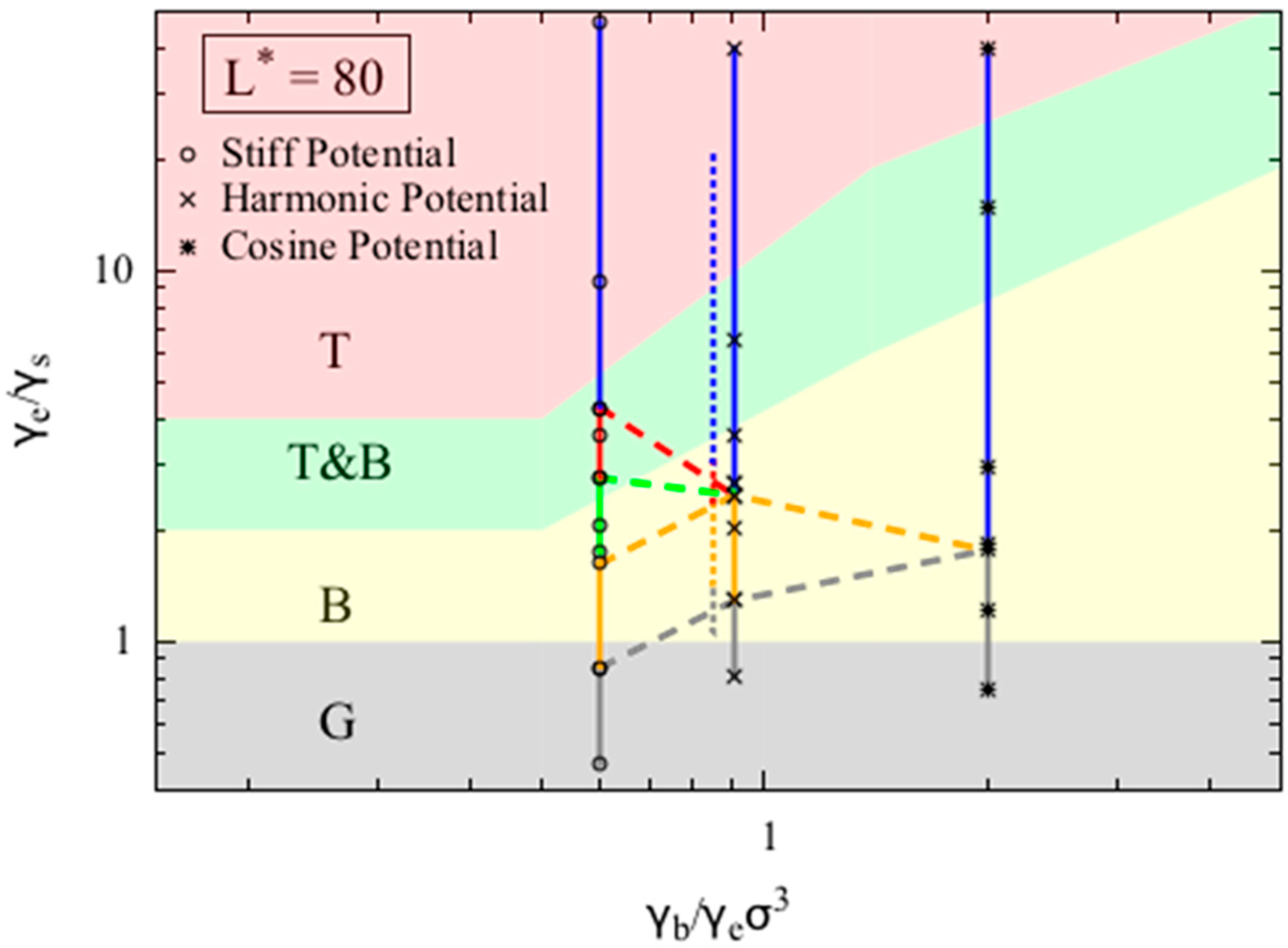
Figure 4 shows that the phase diagrams for dimensionless chain lengths
= 80. For small dimensionless chain lengths
L* (i.e., 80), the phase diagram is more sensitive to chain length, and the model becomes less accurate. In
Figure 4 we assess the accuracy of our model for
= 80, which was chosen to match the value used in the phase behavior reported by Kong et al. [
10] for chains with dimensionless bead diameter
(defined as the ratio of bead diameter to Kuhn length) of 1/16 and five Kuhn lengths long. Kong et al. adopted a harmonic bending potential in their study. To match the conditions reported in Kong et al. we use the harmonic bending potential form, and set the bead diameter to be 1, the chain length to be 80. Unlike other simulations we report in this work, we keep the bending potential strength (
) to be 7.5, corresponding to persistence length (which is half the Kuhn length) to be around 8σ, and then vary the non-bonded interaction strength (ε) to obtain various final equilibrium conformations. We overlay the simulation results from both Kong’s work and our simulations results in
Figure 4. Note that because the both models use harmonic bending potentials to model the bending of polymer chains, the two data sets, when mapped onto the phase diagram (Equation (9a–c)), share the same
x-axis value, and are slightly separated along this axis for clarity only. The two data sets agree well, and the offset along the y-axis is likely caused by the small error in the persistence length estimation.
We also conducted simulations using the other two potentials. Chains with
L* = 80 are more likely to form a random coil (RC) when the
ratio increases, as shown by the smaller value of
at which the random coil state appears. Interestingly, we do not observe either a bundle or a torus for simulations using the cosine bending potential, as the chain transitions directly from the globule state to the random coil state. On the other hand, when using the stiff bending potential, we observe a larger region of torus phase compared to the simulations using harmonic bending potential, which agrees with the theoretical prediction qualitatively. For
L* = 80, although the transition between globule (G) and bundle (B) phase in the simulation is predicted relatively well by the simple theory, the transition from bundle (B) to torus (T) clearly deviates from the prediction. Specifically, in the simulations using the harmonic bending potential, the transition from bundles to tori occurs at
= 2.5, while the model predicts that these transitions occur at around
= 10. This large deviation is expected as our simple continuous model is likely to break down for short chains, for which numbers of folds in the folded state and number of chain wrappings in the torus become few, leading to local minima and maxima in free energy as quantization effects set in. Such effects can indeed by seen in the more detailed models of Schnurr et al. [
16] and Stukan et al. [
15]. We also tested our model for chains with dimensionless chain length
L* = 300 and 1200, and found very similar agreement between theory and simulation as we observed for
L* = 600.