Strengthening of RC Beams Using Externally Bonded Reinforcement Combined with Near-Surface Mounted Technique
Abstract
:1. Introduction
2. Materials and Methods
2.1. Test Matrix
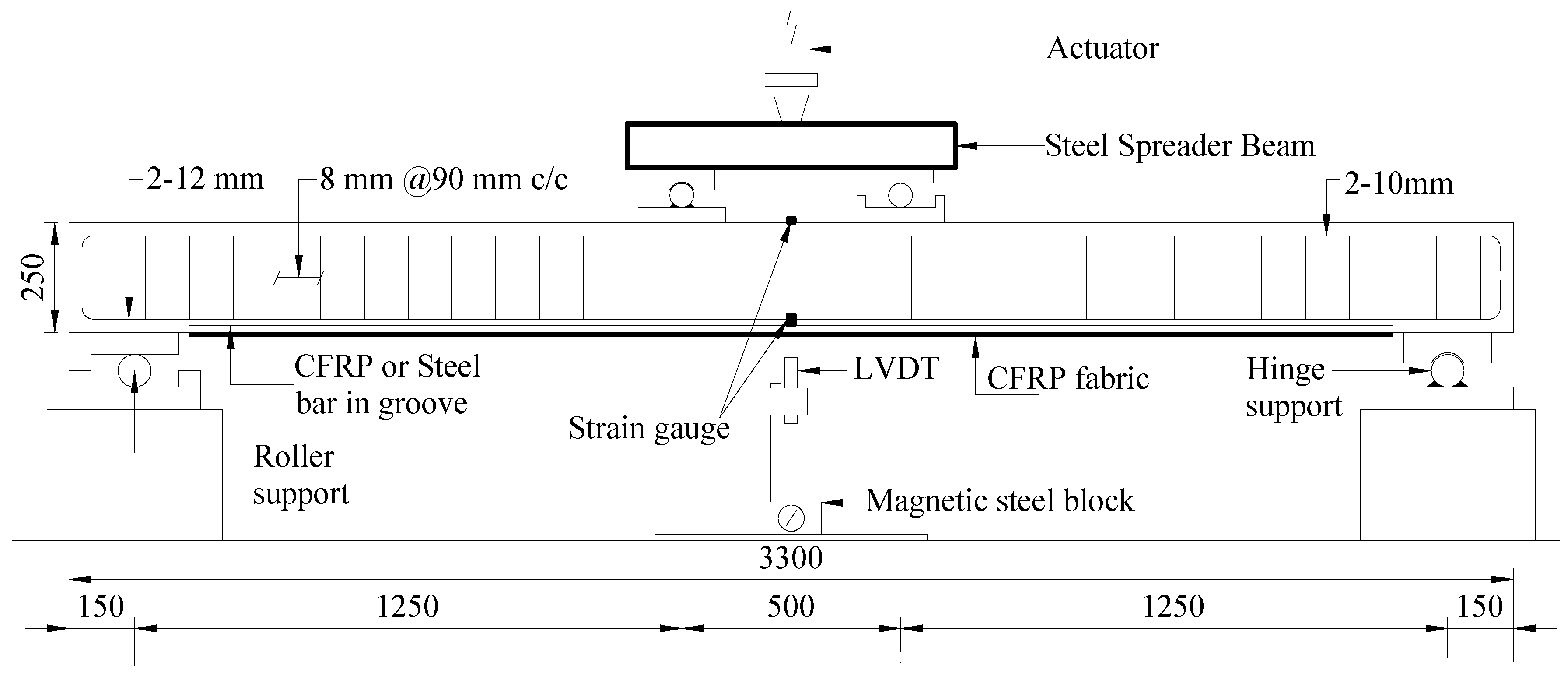
2.2. Specimens and Materials
2.3. Specimen Design and Preparation
3. Results and Discussion
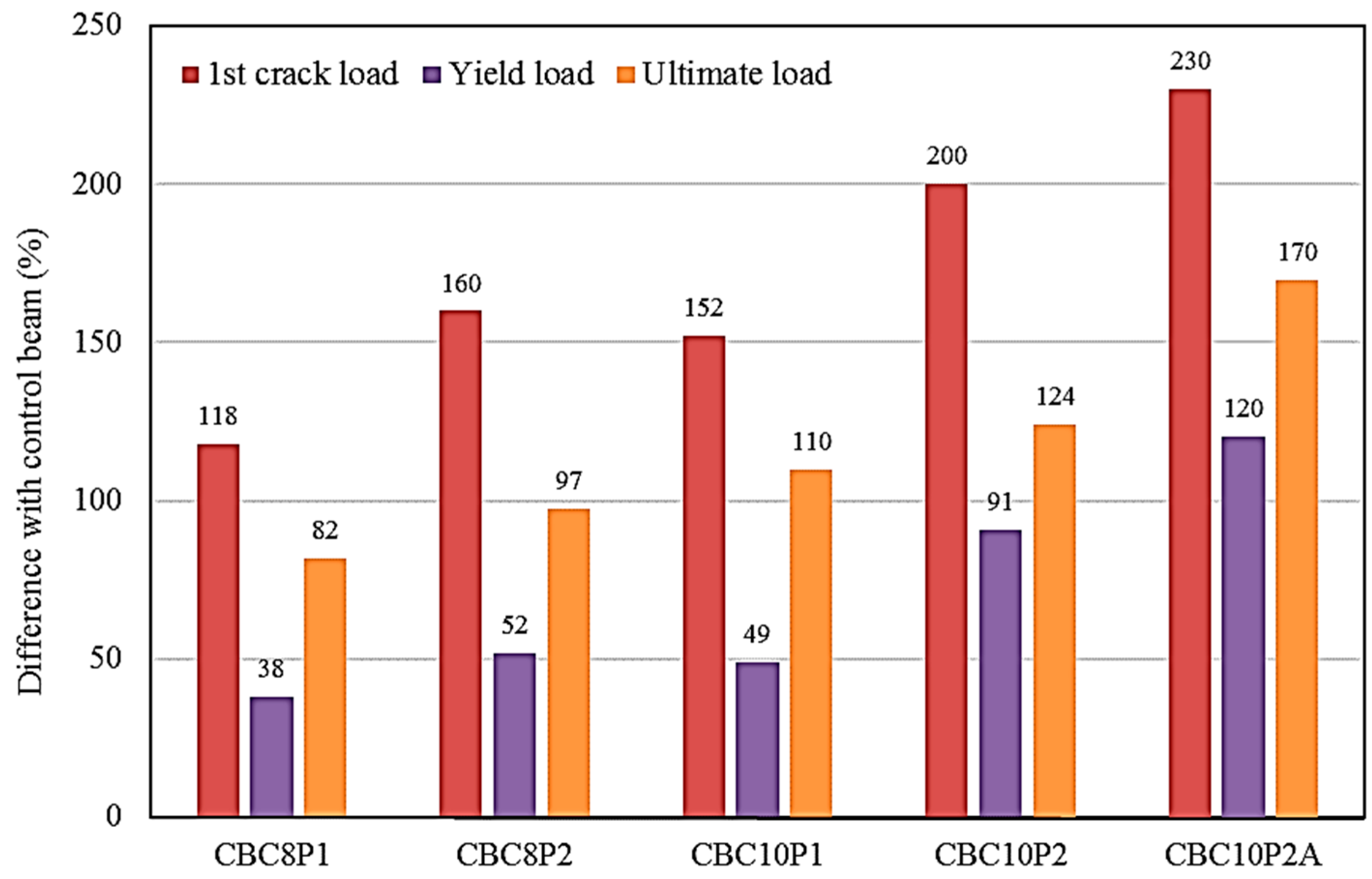
3.1. Load-Carrying Capacity
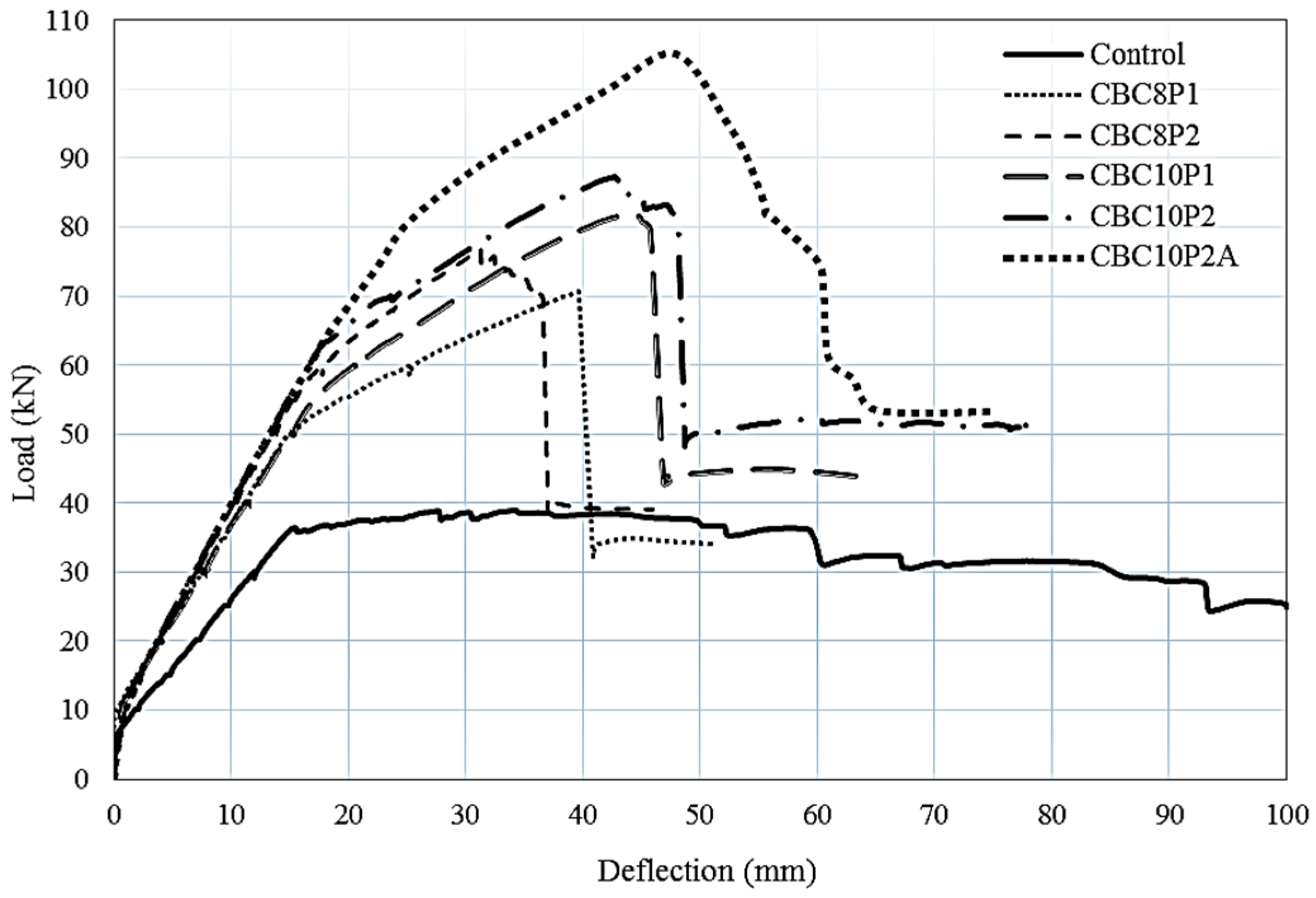
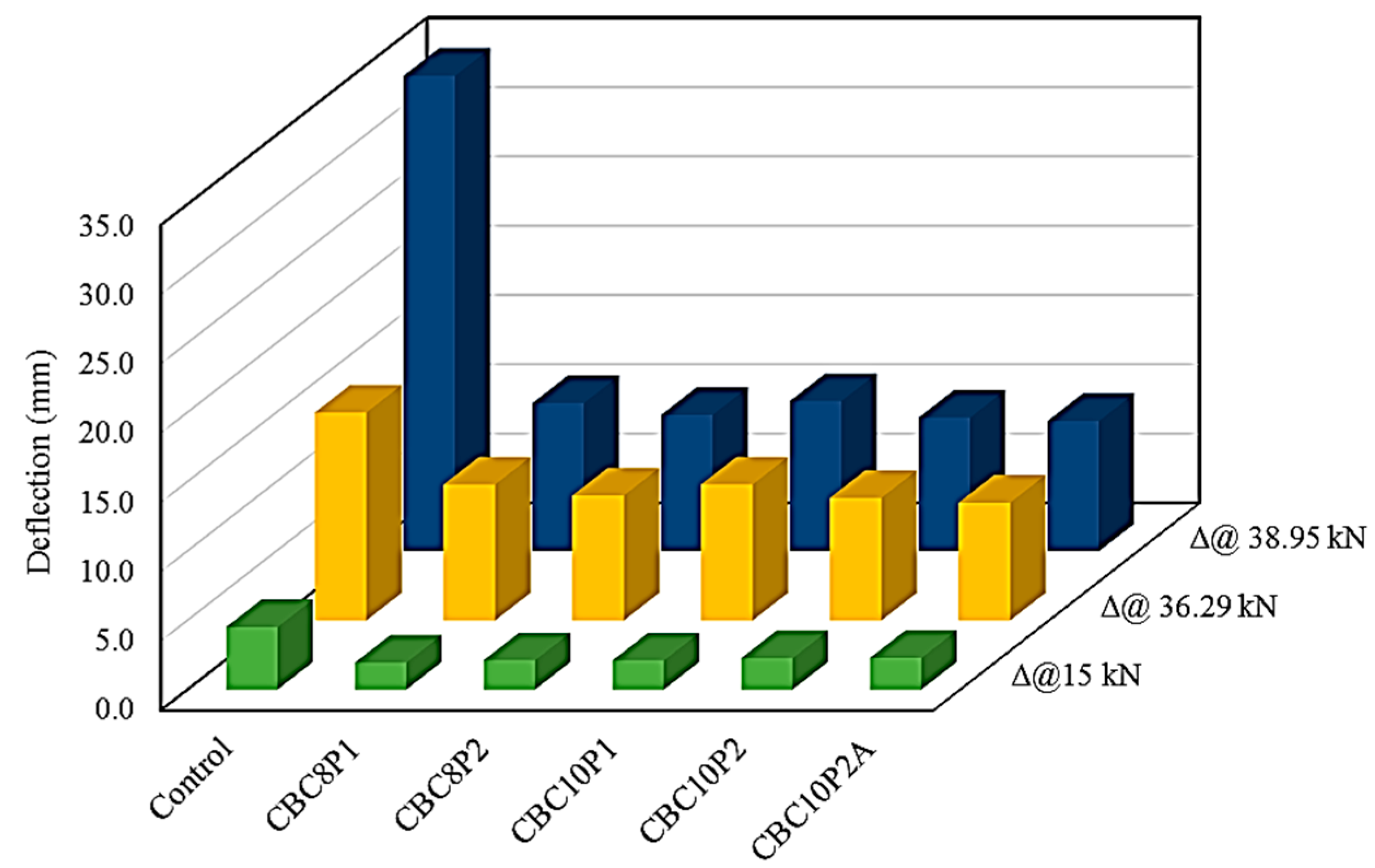
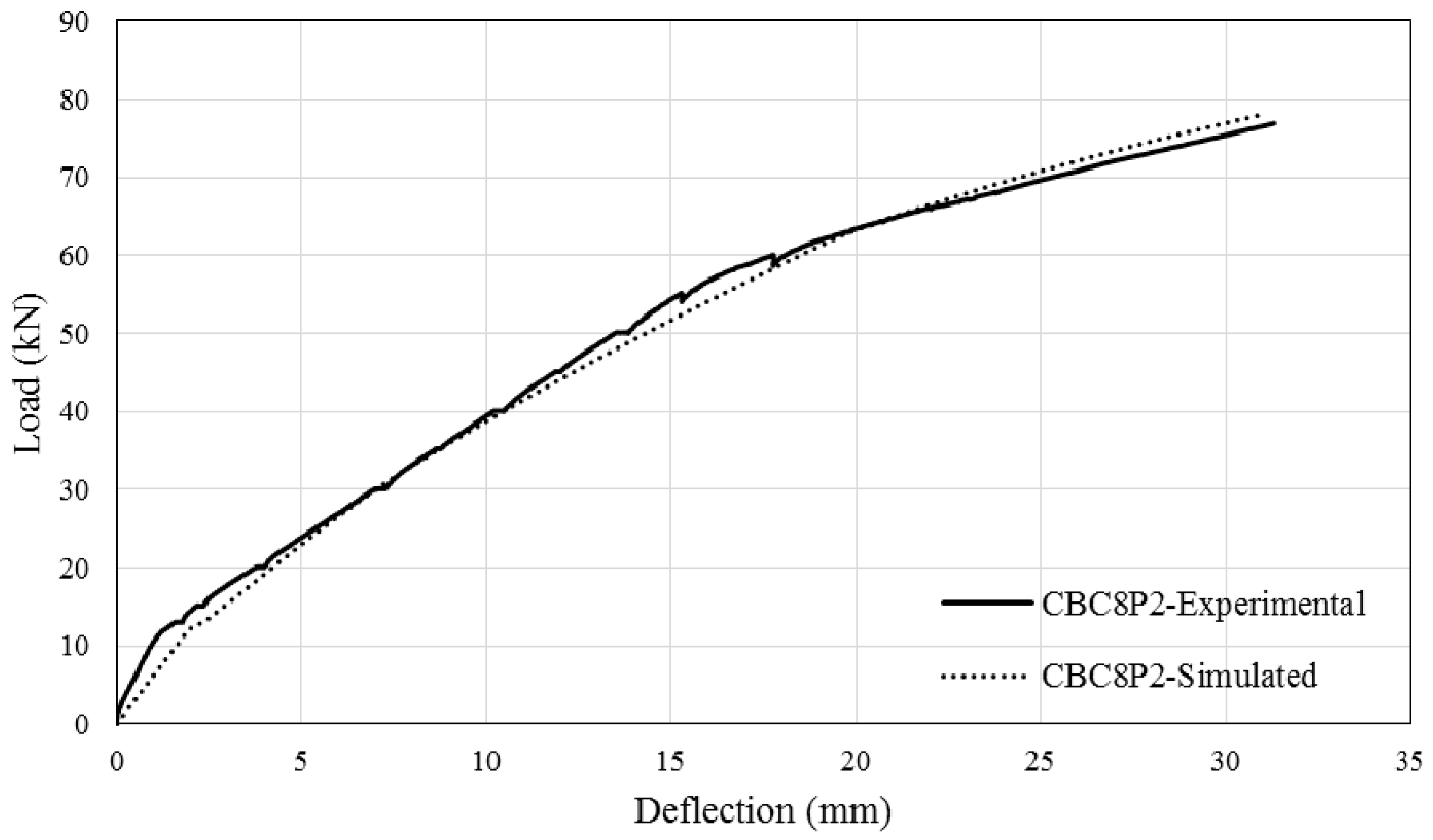
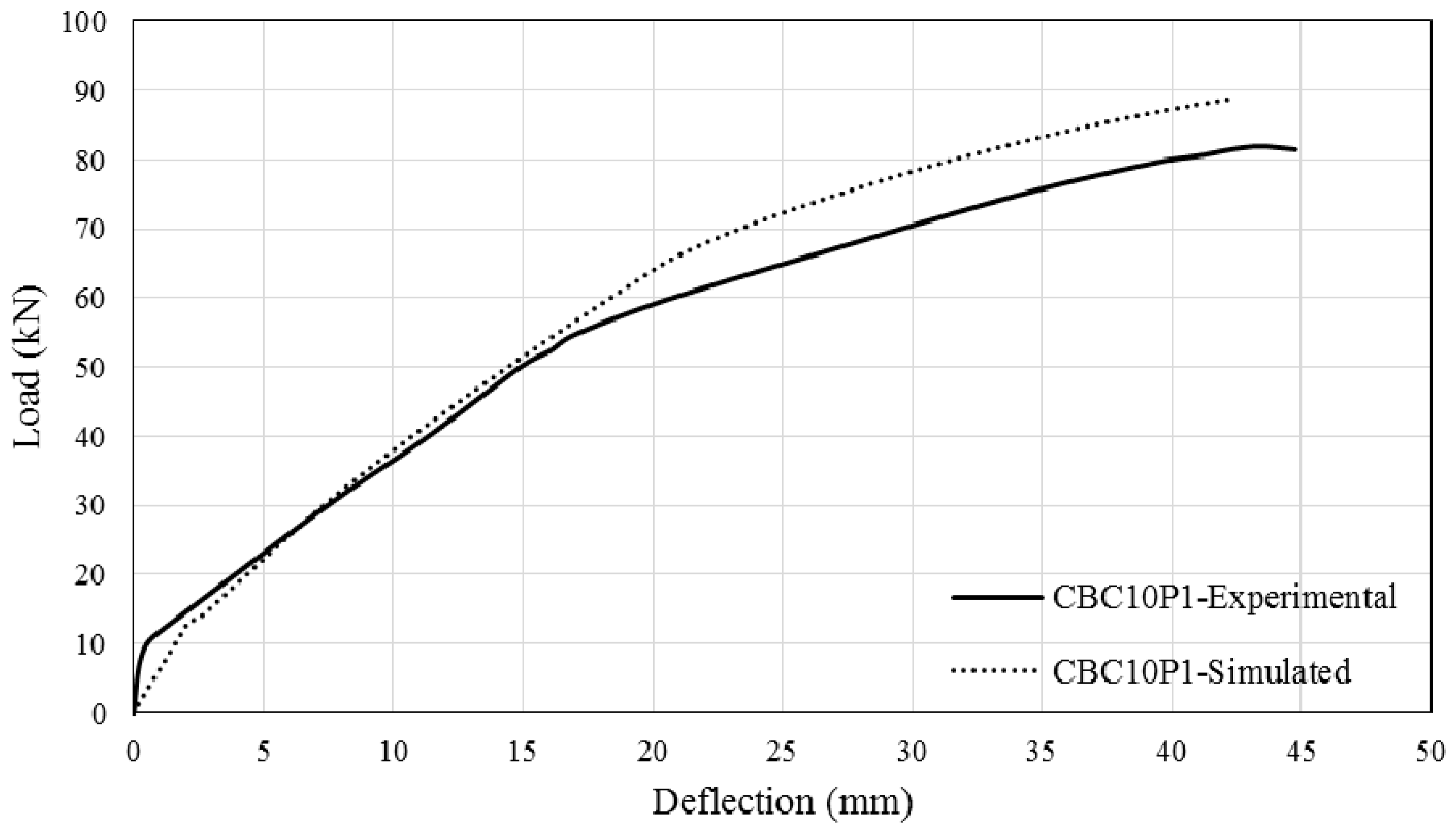
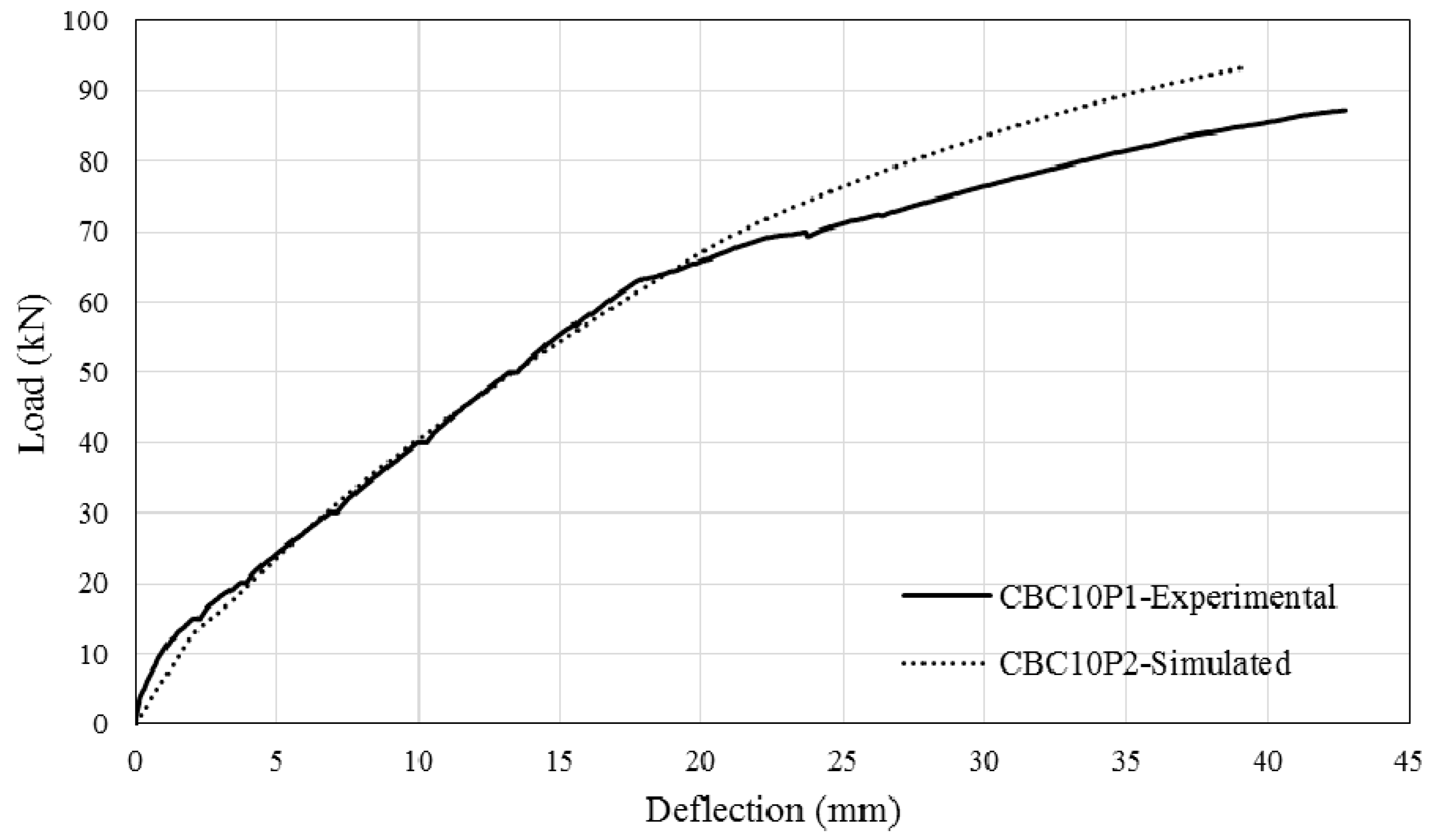
3.2. Load–Deflection Diagram
3.3. Failure Modes
3.4. Cracking Behaviour
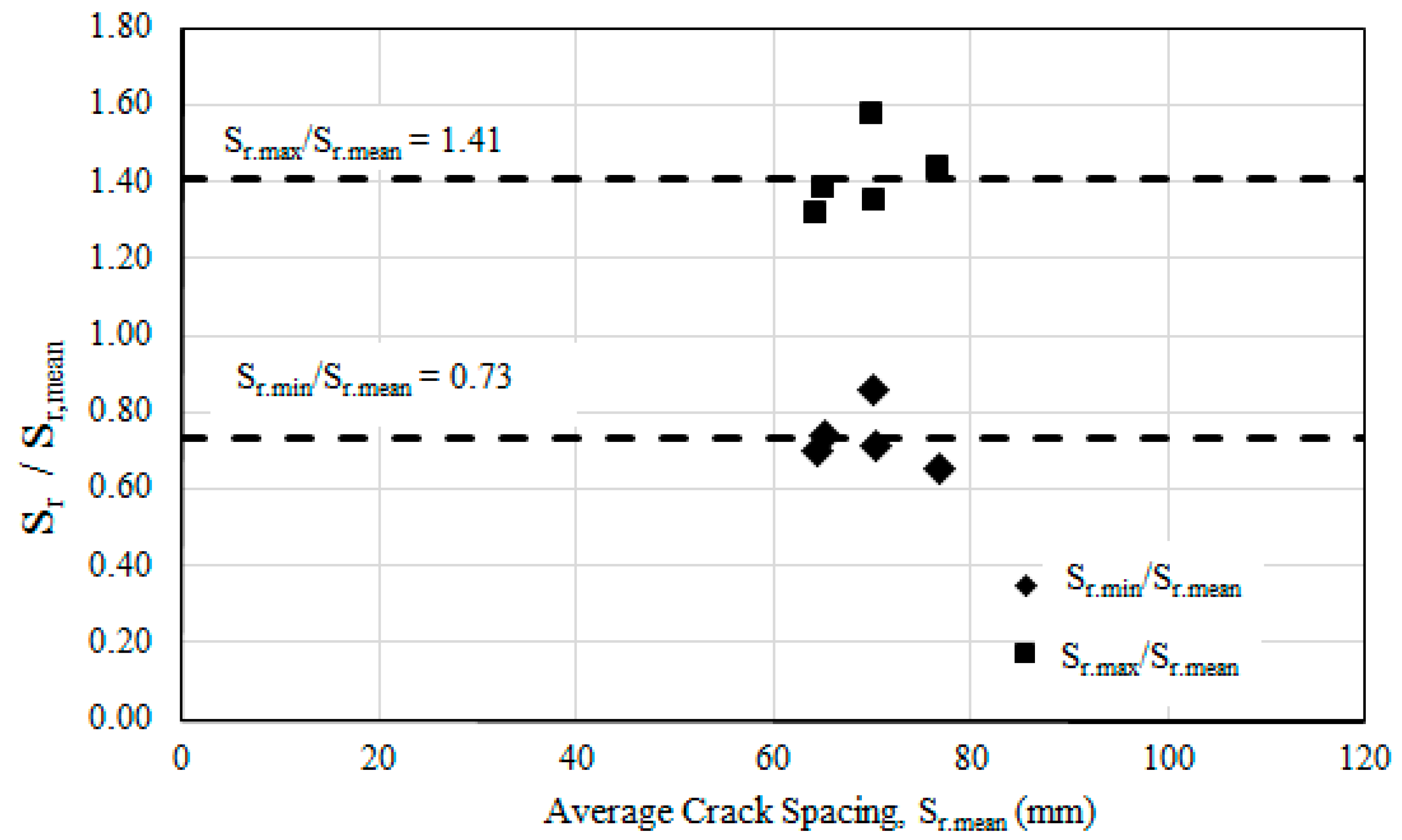
3.4.1. Crack Spacing
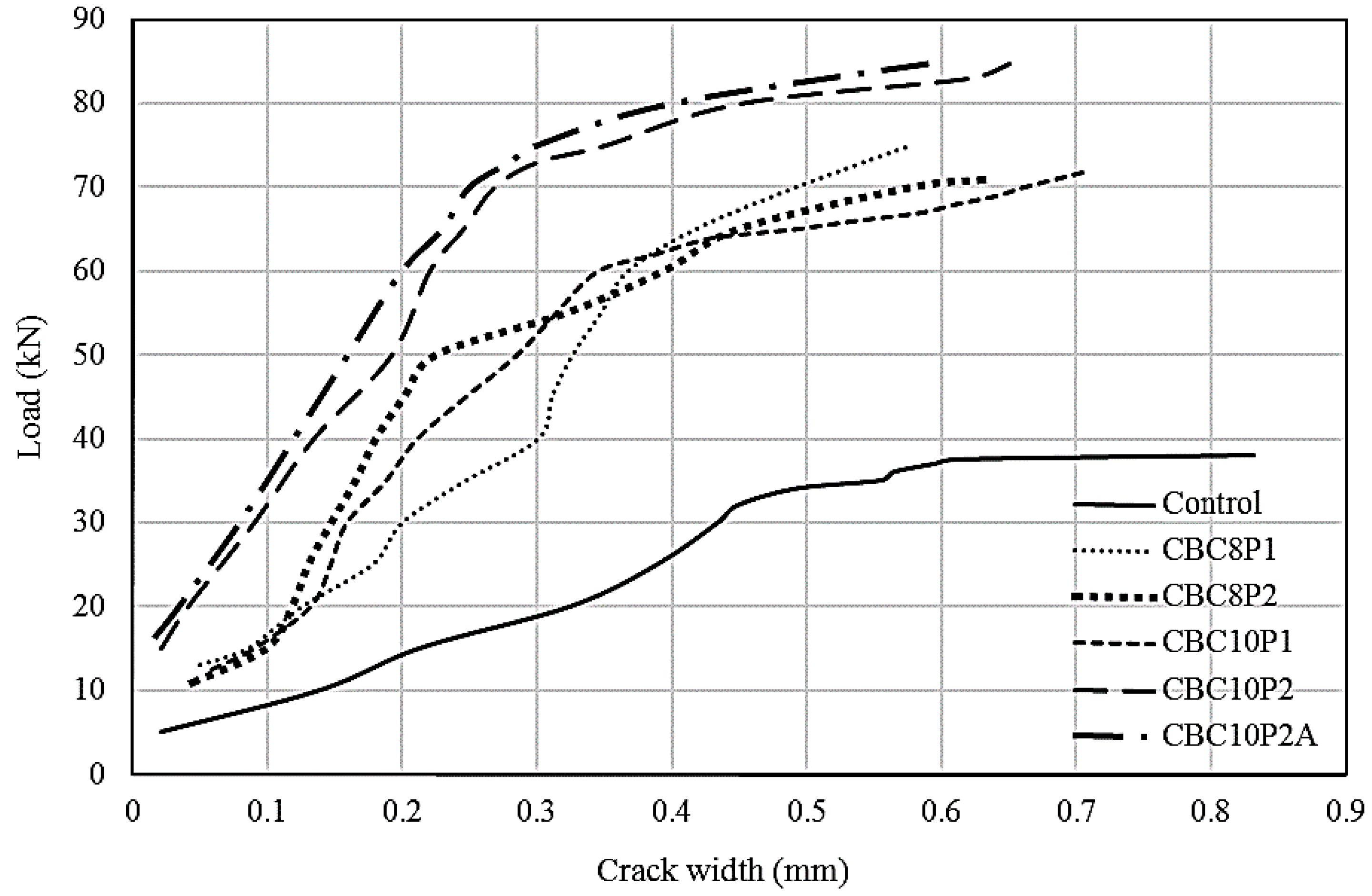
3.4.2. Crack Width
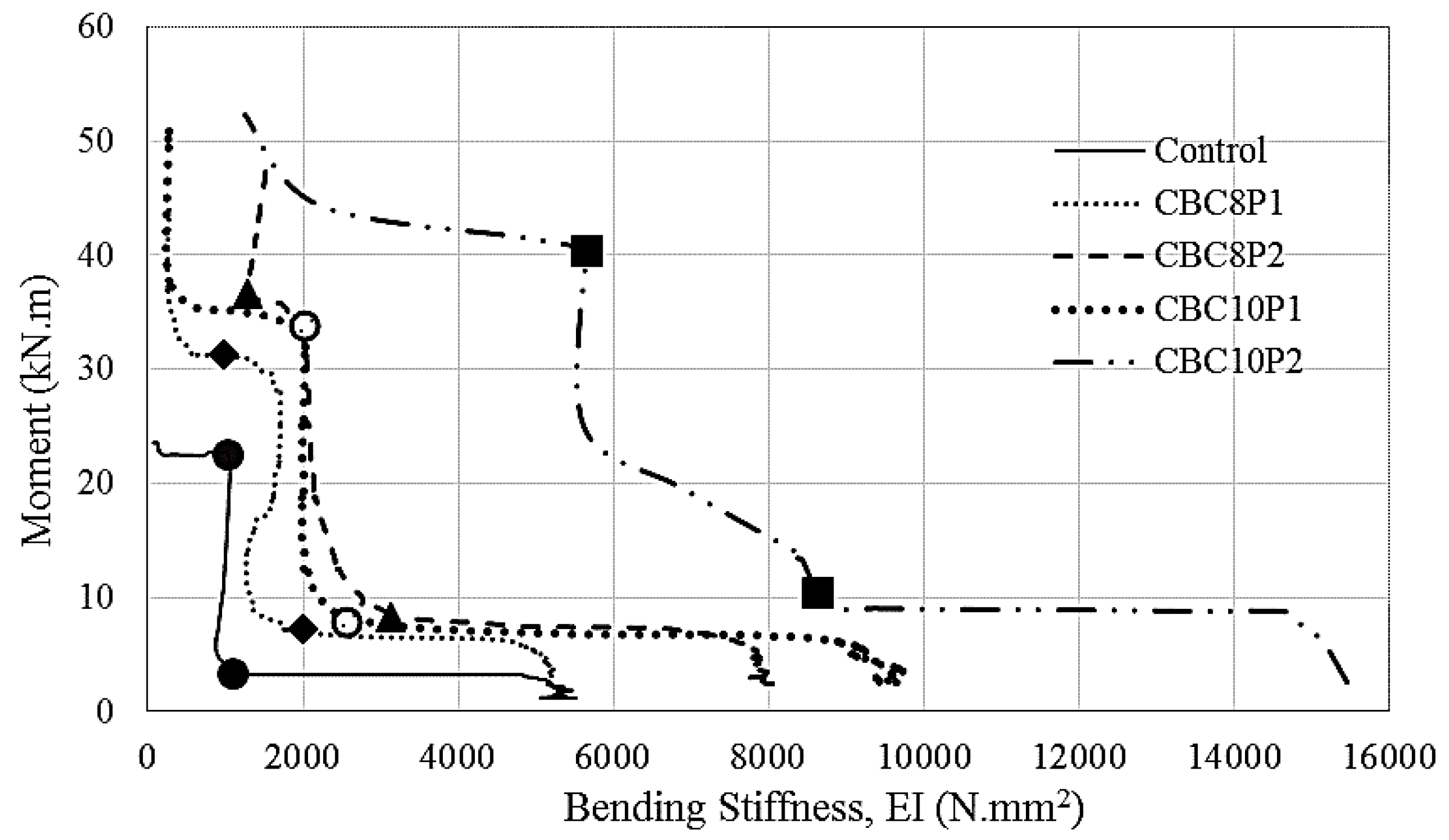
3.5. Stiffness Assessment
4. Simulation Method and Verification
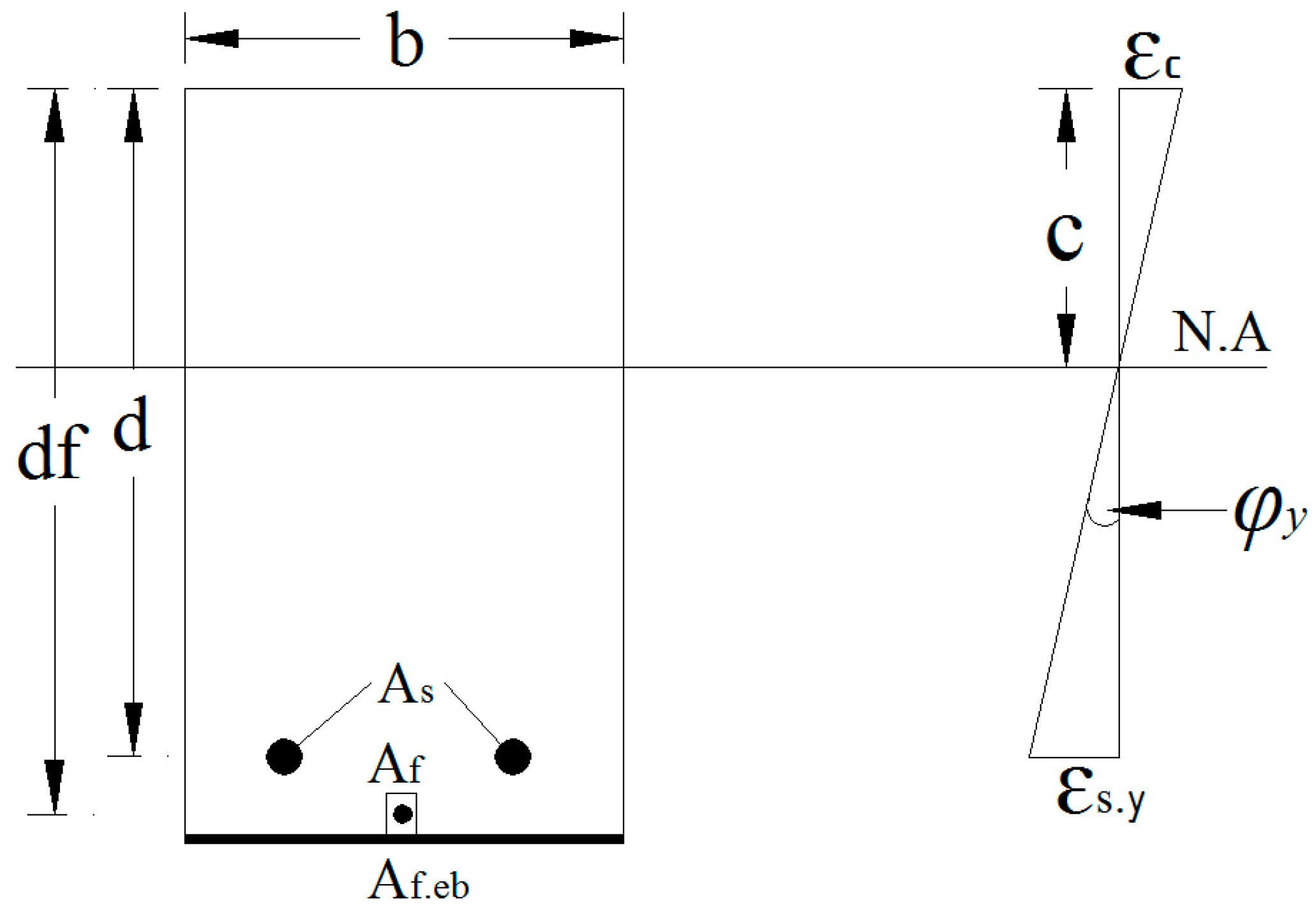
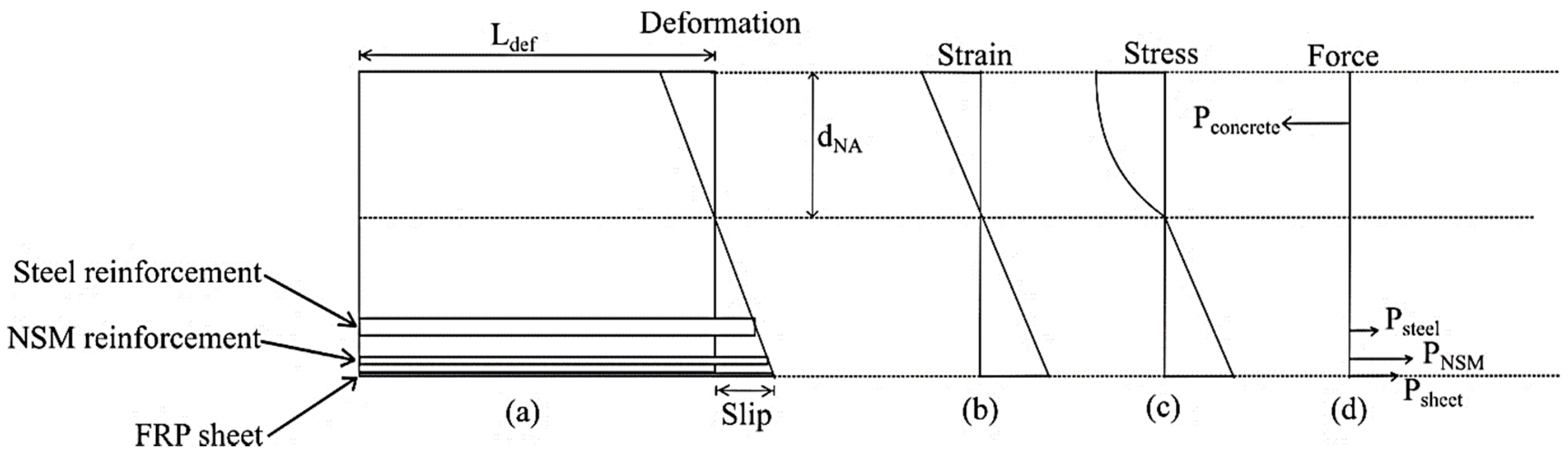
4.1. Moment-Rotation Approach
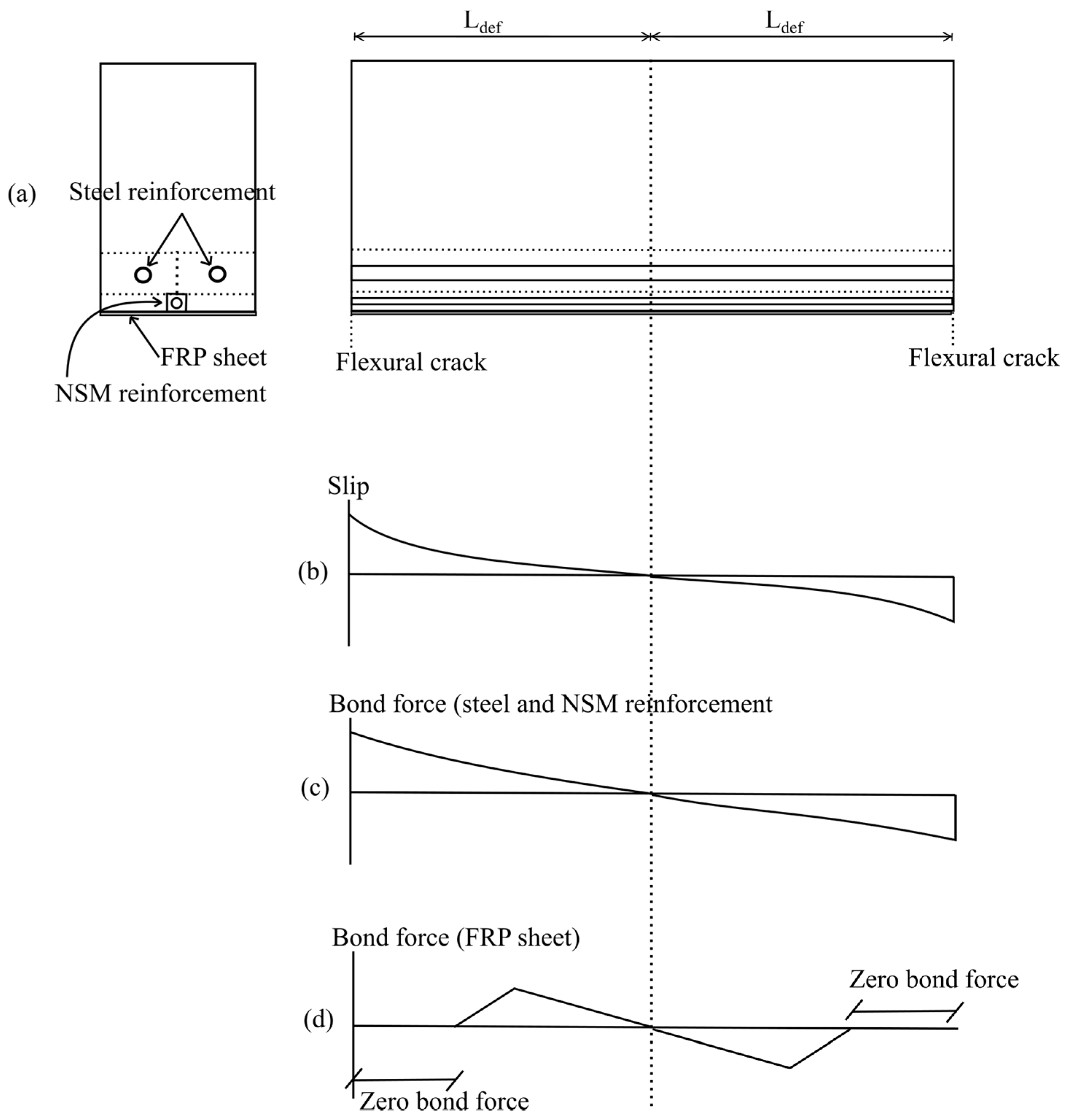
4.1.1. Tension Stiffening Analysis
4.1.2. Moment-Rotation Analysis
5. Conclusions
- The first crack, yield, and ultimate load of the CEBNSM-strengthened beams significantly increased compared with the control beam. The increment of the first crack load was the highest (230%) among the three load levels, which is particularly important for serviceability performance. The maximum ultimate load-carrying capacity increased to 170% over that of the control beam.
- A trilinear load–deflection response was detected, whereas a considerable reduction of the deflection for all of the strengthened beams was witnessed at the ultimate stage. The stiffness of the strengthened beam significantly increased at all levels of load compared with that of the control beam.
- All of the strengthened beams exhibited flexural failure, except for the CBC10P2-strengthened beam, which was strengthened using a double-ply CFRP fabric with a 10 mm-diameter NSM CFRP bar. However, this debonding failure was successfully eliminated by using CFRP U-Wrap anchorage at the fabric curtailment location.
- The average crack spacing of the strengthened beams was 64 to 77 mm, which was smaller than that of the control beam (109 mm). The number of cracks was also more significant (average of 35 cracks) than that of the control beam (21 cracks), which affirmed the enhanced energy dissipation of the strengthened beams. Furthermore, the crack width of the strengthened beams was significantly reduced.
- The strain value of steel and concrete for the strengthened beams was less than that of the control beam. The strain values of the NSM bar and the EBR fabric showed the perfect distribution of the strain by strengthening reinforcement after the yielding of the internal steel bar.
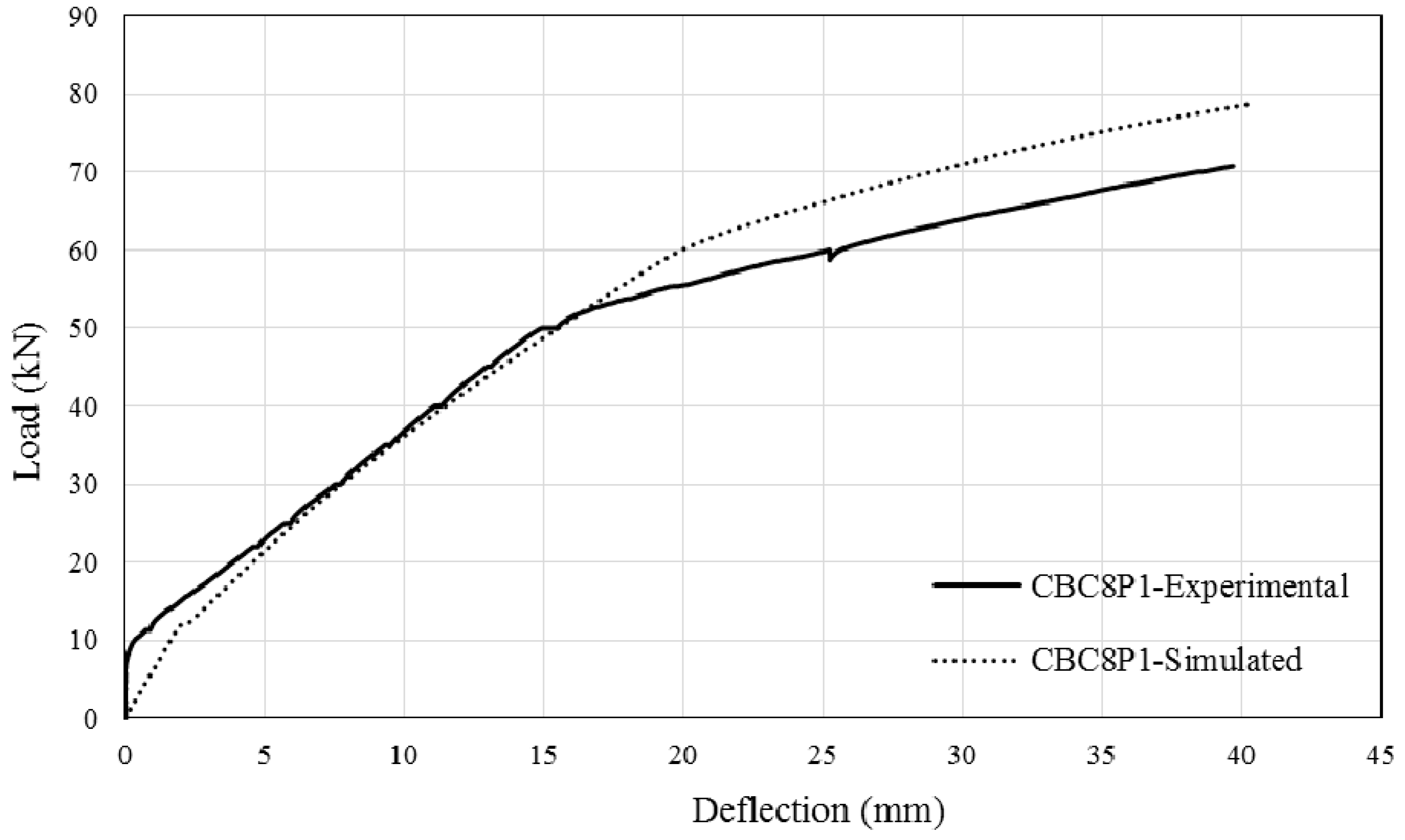
- The moment-rotation approach was applied to simulate the behaviour of CEBNSM-strengthened RC beams and was able to give good accuracy.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Inci, P.; Goksu, C.; Ilki, A.; Kumbasar, N. Effects of reinforcement corrosion on the performance of RC frame buildings subjected to seismic actions. J. Perform. Constr. Facil. 2012, 27, 683–696. [Google Scholar] [CrossRef]
- Aslam, M.; Shafigh, P.; Jumaat, M.Z.; Shah, S. Strengthening of RC beams using prestressed fiber reinforced polymers—A review. Constr. Build. Mater. 2015, 82, 235–256. [Google Scholar] [CrossRef]
- Darain, K.M.; Jumaat, M.Z.; Hossain, M.A.; Hosen, M.A.; Obaydullah, M.; Huda, M.N.; Hossain, I. Automated serviceability prediction of NSM strengthened structure using a fuzzy logic expert system. Expert Syst. Appl. 2015, 42, 376–389. [Google Scholar] [CrossRef]
- Darain, K.M.; Shamshirband, S.; Jumaat, M.Z.; Obaydullah, M. Adaptive neuro fuzzy prediction of deflection and cracking behavior of NSM strengthened RC beams. Constr. Build. Mater. 2015, 98, 276–285. [Google Scholar] [CrossRef]
- Ilki, A.; Bedirhanoglu, I.; Kumbasar, N. Behavior of FRP-retrofitted joints built with plain bars and low-strength concrete. J. Compos. Constr. 2010, 15, 312–326. [Google Scholar] [CrossRef]
- Reza Aram, M.; Czaderski, C.; Motavalli, M. Effects of gradually anchored prestressed CFRP strips bonded on prestressed concrete beams. J. Compos. Constr. 2008, 12, 25–34. [Google Scholar] [CrossRef]
- ACI 440.2R-08. In Guide for the Design and Construction of Externally Bonded FRP Systems for Strengthening Concrete Structures; ACI Committee 440; American Concrete Institute: Farmington Hills, MI, USA, 2008.
- Fédération internationale du béton (fib). Externally bonded FRP reinforcement for RC structures. In Bulletin; fib: Lausanne, Switzerland, 2001; Volume 14, p. 138. [Google Scholar]
- Lou, T.; Lopes, S.M.R.; Lopes, A.V. External CFRP tendon members: Secondary reactions and moment redistribution. Compos. B Eng. 2014, 57, 250–261. [Google Scholar] [CrossRef]
- Lignola, G.P.; Prota, A.; Manfredi, G. Simplified modeling of rectangular concrete cross-sections confined by external FRP wrapping. Polymers 2014, 6, 1187–1206. [Google Scholar] [CrossRef]
- Teng, J.; Chen, J.; Smith, S.T.; Lam, L. Behaviour and strength of FRP-strengthened RC structures: A state-of-the-art review. Proc. ICE Struct. Build. 2003, 156, 51–62. [Google Scholar] [CrossRef]
- De Lorenzis, L.; Teng, J.G. Near-surface mounted FRP reinforcement: An emerging technique for strengthening structures. Compos. B Eng. 2007, 38, 119–143. [Google Scholar] [CrossRef]
- Rosenboom, O.; Rizkalla, S. Behavior of prestressed concrete strengthened with various CFRP systems subjected to fatigue loading. J. Compos. Constr. 2006, 10, 492–502. [Google Scholar] [CrossRef]
- Aram, M.R.; Czaderski, C.; Motavalli, M. Debonding failure modes of flexural FRP-strengthened RC beams. Compos. B Eng 2008, 39, 826–841. [Google Scholar] [CrossRef]
- Martinelli, E.; Napoli, A.; Nunziata, B.; Realfonzo, R. RC beams strengthened with mechanically fastened composites: Experimental results and numerical modeling. Polymers 2014, 6, 613–633. [Google Scholar] [CrossRef]
- Li, G.; Zhang, A.; Jin, W. Effect of shear resistance on flexural debonding load-carrying capacity of RC beams strengthened with externally bonded FRP composites. Polymers 2014, 6, 1366–1380. [Google Scholar] [CrossRef]
- Lousdad, A.; Megueni, A.; Bouchikhi, A. Geometric edge shape based optimization for interfacial shear stress reduction in fiber reinforced polymer plate retrofitted concrete beams. Comput. Mater. Sci. 2010, 47, 911–918. [Google Scholar] [CrossRef]
- Garden, H.; Hollaway, L.; Thorne, A. A preliminary evaluation of carbon fibre reinforced polymer plates for strengthening reinforced concrete members. Proc. Inst. Civil Eng. Struct. Build. 1997, 122, 127–142. [Google Scholar] [CrossRef]
- Oehlers, D.J. Reinforced concrete beams with plates glued to their soffits. J. Struct. Eng. 1992, 118, 2023–2038. [Google Scholar] [CrossRef]
- De Lorenzis, L. Strengthening of RC structures with near surface mounted FRP rods. Ph.D. Thesis, University of Lecce, Lecce, Italy, 2002. [Google Scholar]
- Blaschko, M. Bond behaviour of CFRP strips glued into slits. In Proceedings of the 6th International Symposium on FRP Reinforcement for Concrete Structures (FRPRCS-6), Singapore, 8–10 July 2003; World Scientific: Singapore, 2003; pp. 205–214. [Google Scholar]
- Parretti, R.; Nanni, A. Strengthening of RC members using near-surface mounted FRP composites: Design overview. Adv. Struct. Eng. 2004, 7, 469–483. [Google Scholar] [CrossRef]
- Park, Y.; Kim, Y.H.; Lee, S.-H. Long-term flexural behaviors of GFRP reinforced concrete beams exposed to accelerated aging exposure conditions. Polymers 2014, 6, 1773–1793. [Google Scholar] [CrossRef]
- Bencardino, F.; Condello, A. Innovative solution to retrofit RC members: Inhibiting-Repairing-Strengthening (IRS). Constr. Build. Mater. 2016, 117, 171–181. [Google Scholar] [CrossRef]
- Bencardino, F.; Condello, A. Eco-friendly external strengthening system for existing reinforced concrete beams. Compos. B 2016, 93, 163–173. [Google Scholar] [CrossRef]
- El-Maaddawy, T.; El Refai, A. Innovative repair of severely corroded t-beams using fabric-reinforced cementitious matrix. J. Compos. Constr. 2015, 20, 04015073. [Google Scholar] [CrossRef]
- Rahman, M.; Jumaat, M.Z.; Rahman, M.A.; Qeshta, I.M.I. Innovative hybrid bonding method for strengthening reinforced concrete beam in flexure. Constr. Build. Mater. 2015, 79, 370–378. [Google Scholar] [CrossRef]
- Arduini, M.; Nanni, A. Parametric study of beams with externally bonded FRP reinforcement. ACI Struct. J. 1997, 94, 493–501. [Google Scholar]
- Kotynia, R.; Cholostiakow, S. New proposal for flexural strengthening of reinforced concrete beams using CFRP T-shaped profiles. Polymers 2015, 7, 2461–2477. [Google Scholar] [CrossRef]
- Lim, D.H. Combinations of NSM and EB CFRP strips for flexural strengthening of concrete structures. Mag. Concr. Res. 2009, 61, 633–643. [Google Scholar] [CrossRef]
- Maalej, M.; Bian, Y. Interfacial shear stress concentration in FRP-strengthened beams. Compos. Struct. 2001, 54, 417–426. [Google Scholar] [CrossRef]
- British Standards Institution. BS EN 12390–5. Testing Hardened Concrete—Part 5: Flexural Strength of Test Specimens; British Standards Institution-BSI; CEN European Committee for Standardization: London, UK, 2009. [Google Scholar]
- British Standards Institution. BS EN 12390-3. Testing Hardened Concrete. Compressive Strength of Test Specimens; British Standards Institution-BSI: London, UK, 2009; Volume 19. [Google Scholar]
- ASTM. A615/A615M-14: Standard Specification for Deformed and Plain Carbon-Steel Bars for Concrete Reinforcement; ASTM International: West Conshohocken, PA, USA, 2014. [Google Scholar]
- SikaWrap®-301C. Product Data sheet-woven carbon fibre fabric for structural strengthening. Available online: https://mys.Sika.Com/dms/.../sikawrap-301%20c%202010-12_1.pdf (accessed on 21 May 2016).
- Sikadur®-30. Product Data sheet-adhesive for bonding reinforcement. Available online: https://mys.Sika.Com/dms/...Get/...E6dc.../sikadur-30%202011-10_1.pdf (accessed on 21 May 2016).
- Sikadur®-330. Product Data sheet-adhesive for bonding reinforcement. Available online: https://mys.Sika.Com/dms/...Get/.../sikadur-330%202012-05_1.pdf (accessed on 21 May 2016).
- Barris, C.; Torres, L.; Comas, J.; Mias, C. Cracking and deflections in GFRP RC beams: An experimental study. Compos. B Eng. 2013, 55, 580–590. [Google Scholar] [CrossRef]
- Borosnyói, A. Serviceability of CFRP Prestressed Concrete Beams. Ph.D. Thesis, Budapest University of Technology and Economics, Budapest, Hungary, 2002. [Google Scholar]
- Wight, R.; Green, M.; Erki, M. Prestressed FRP sheets for poststrengthening reinforced concrete beams. J. Compos. Constr. 2001, 5, 214–220. [Google Scholar] [CrossRef]
- Frosch, R.J. Another look at cracking and crack control in reinforced concrete. ACI Struct. J. 1999, 96, 437–442. [Google Scholar]
- American Concrete Institute (ACI). Building Code Requirements for Structural Concrete (ACI 318-14) and Commentary; ACI: Farmington Hills, MI, USA, 2011. [Google Scholar]
- Mohammadhassani, M.; Jumaat, M.Z.B.; Maghsoudi, A.A.; Akib, S.; Jameel, M.; Najmeh, R.; Amin, M.; Hamid, S.; Esmaeil, H.R.; Farhad, G. Bending stiffness and neutral axis depth variation of high strength concrete beams in seismic hazardous areas: Experimental investigation. Int. J. Phys. Sci. 2011, 6, 482–494. [Google Scholar]
- Hosen, M.A.; Jumaat, M.Z.; Alengaram, U.J.; Islam, A.; bin Hashim, H. Near surface mounted composites for flexural strengthening of reinforced concrete beams. Polymers 2016, 8, 67. [Google Scholar] [CrossRef]
- Oehlers, D.; Visintin, P.; Zhang, T.; Chen, Y.; Knight, D. Flexural rigidity of reinforced concrete members using a deformation based analysis. Concr. Aust. 2012, 38, 50–56. [Google Scholar]
- Shukri, A.A.; Darain, K.M.; Jumaat, M.Z. The tension-stiffening contribution of NSM cFRP to the behavior of strengthened RC beams. Materials 2015, 8, 4131–4146. [Google Scholar] [CrossRef]
- Visintin, P.; Oehlers, D.; Wu, C.; Haskett, M. A mechanics solution for hinges in RC beams with multiple cracks. Eng. Struct. 2012, 36, 61–69. [Google Scholar] [CrossRef]
- Muhamad, R.; Ali, M.M.; Oehlers, D.J.; Griffith, M. The tension stiffening mechanism in reinforced concrete prisms. Adv. Struct. Eng. 2012, 15, 2053–2069. [Google Scholar] [CrossRef]
- CEB-FIP. CEB-FIP Model Code 2010; Ernst & Sohn: Berlin, Germany, 2013. [Google Scholar]
- De Lorenzis, L. Anchorage length of near-surface mounted fiber-reinforced polymer rods for concrete strengthening—Analytical modeling. ACI Struct. J. 2004, 101, 375–386. [Google Scholar]
- Lu, X.; Teng, J.; Ye, L.; Jiang, J. Bond–slip models for FRP sheets/plates bonded to concrete. Eng. Struct. 2005, 27, 920–937. [Google Scholar] [CrossRef]
- Chen, Y.; Visintin, P.; Oehlers, D.; Alengaram, U. Size-dependent stress–strain model for unconfined concrete. J. Struct. Eng. 2013, 140, 04013088. [Google Scholar] [CrossRef]
- Popovics, S. A numerical approach to the complete stress–strain curve of concrete. Cem. Concr. Res. 1973, 3, 583–599. [Google Scholar] [CrossRef]
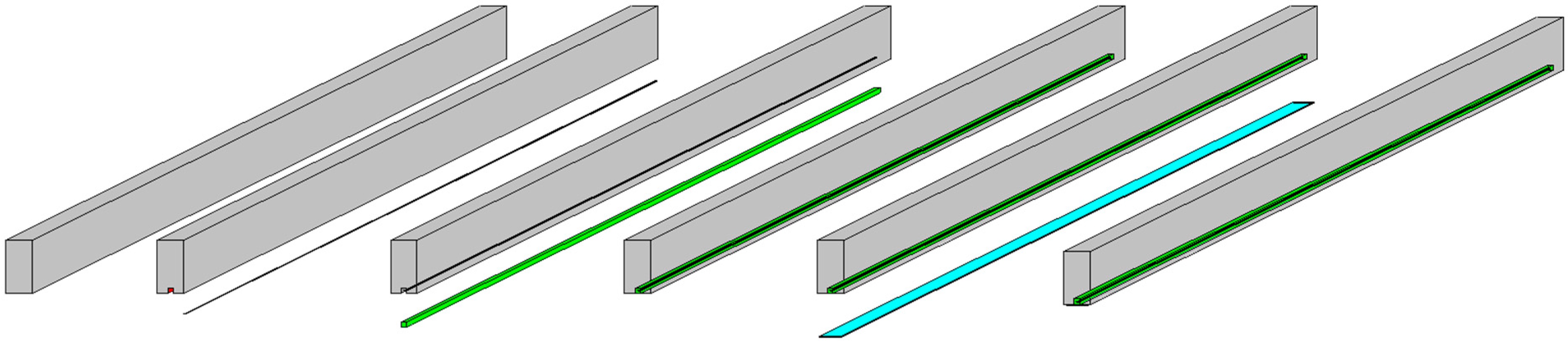


| Serial. No. | Notation | Description | Strengthening details |
|---|---|---|---|
| 1 | CB | Control RC beam | Without strengthening |
| 2 | CBC8P1 | 8 mm φ NSM CFRP bar and 1 ply of EBR CFRP fabric | CFRP bar: 1–8 mm φ (L = 2900 mm) CFRP fabric: 2900 × 125 × 0.17 mm3 |
| 3 | CBC8P2 | 8 mm φ NSM CFRP bar and 2 ply of EBR CFRP fabric | CFRP bar: 1–8 mm φ (L = 2900 mm) CFRP 1st fabric: 2900 × 125 × 0.17 mm3 CFRP 2nd fabric: 2600 × 125 × 0.17 mm3 |
| 4 | CBC10P1 | 10 mm φ NSM CFRP bar and 1 ply of EBR CFRP fabric | CFRP bar: 1–10 mm φ (L = 2900 mm) CFRP fabric: 2900 × 125 × 0.17 mm3 |
| 5 | CBC10P2 | 10 mm φ NSM CFRP bar and 2 ply of EBR CFRP fabric | CFRP bar: 1–10 mm φ (L = 2900 mm) CFRP 1st fabric: 2900 × 125 × 0.17 mm3 CFRP 2nd fabric: 2600 × 125 × 0.17 mm3 |
| 6 | CBC10P2A | NSM CFRP bar, EB 2 ply CFRP fabric and 2 ply U-wrap end anchorage | CFRP bar: 1–10 mm φ (2900 mm) CFRP fabric: 2900 × 125 × 0.34 mm3 CFRP U-wrap anchorage: 2 ply (625 × 125 × 0.34 mm3) |
| Material | Mechanical property | Result |
|---|---|---|
| Concrete | Compressive strength (MPa) | 50.1 |
| Flexure strength (MPa) | 5.5 | |
| Elastic modulus (GPa) | 33.26 | |
| Steel 12 mm φ (Internal bottom reinforcement) | Yield stress (MPa) | 529 |
| Ultimate strength (MPa) | 587 | |
| Elastic modulus (GPa) | 200 | |
| Elongation (%) | 21 | |
| Steel 10 mm φ (Internal top reinforcement) | Yield stress (MPa) | 521 |
| Ultimate strength (MPa) | 578 | |
| Elastic modulus (GPa) | 200 | |
| Elongation (%) | 20 | |
| Steel 8 mm φ (Internal shear reinforcement) | Yield stress (MPa) | 380 |
| Ultimate strength (MPa) | 450 | |
| Elastic modulus (GPa) | 200 | |
| Elongation (%) | 29 | |
| CFRP bar-12 mm φ | Ultimate strength (MPa) | 2,400 |
| Elastic modulus (GPa) | 165 | |
| Ultimate strain (%) | 1.6 | |
| CFRP Fabric (SikaWrap-301C) [35] | Ultimate strength (MPa) | 4,900 |
| Elastic modulus (GPa) | 230 | |
| Ultimate strain (%) | 2.1 | |
| Epoxy (Sikadur®) 30 [36] | Compressive strength | 70–80 MPa (15 °C); 85–95 MPa (35 °C) |
| Tensile strength | 14–17 MPa (15 °C); 16–19 MPa (35 °C) | |
| Shear strength | 24–27 MPa (15 °C); 26–31 MPa (35 °C) | |
| Epoxy (Sikadur®) 330 [37] | Tensile strength (MPa) | 30 |
| Elastic modulus–Flexural (MPa) | 3,800 | |
| Elastic modulus–Tensile (MPa) | 4,500 |
| Beam ID | Pcr (kN) | Δcr (mm) | Py (kN) | Δy (mm) | Pu (kN) | Δu (mm) | Failure modes |
|---|---|---|---|---|---|---|---|
| CB | 5 | 0.5 | 36 | 15.0 | 39 | 34.3 | FFC |
| CBC8P1 | 11 | 1.5 | 50 | 14.9 | 71 | 39.7 | FFF |
| CBC8P2 | 13 | 1.9 | 55 | 15.2 | 77 | 31.3 | FFF |
| CBC10P1 | 13 | 1.6 | 54 | 16.6 | 82 | 43.3 | FFF |
| CBC10P2 | 15 | 2.3 | 69 | 23.7 | 87 | 42.7 | CFD |
| CBC10P2A | 16 | 2.8 | 80 | 24.7 | 105 | 47.9 | FFC |
| Beam No. | Sr.max (mm) | Sr.min (mm) | Sr.mean (mm) | No. cracks |
|---|---|---|---|---|
| CB | 140 | 75 | 109 | 21 |
| CBC8P1 | 85 | 45 | 64 | 39 |
| CBC8P2 | 110 | 50 | 77 | 31 |
| CBC10P1 | 95 | 50 | 70 | 38 |
| CBC10P2 | 90 | 48 | 65 | 34 |
| CBC10P2A | 110 | 60 | 70 | 33 |
| Beam ID | Pcr (kN) | Pserv (kN) | wserv (mm) | Load (kN) at w = 0.33 mm | % of Pu |
|---|---|---|---|---|---|
| Control | 5.0 | 23.4 | 0.34 | 22 | 56 |
| CBC8P1 | 10.9 | 42.5 | 0.18 | 56 | 79 |
| CBC8P2 | 13.0 | 46.1 | 0.31 | 54 | 70 |
| CBC10P1 | 12.6 | 49.0 | 0.28 | 58 | 71 |
| CBC10P2 | 15.0 | 52.4 | 0.19 | 74 | 85 |
| CBC10P2A | 16.5 | 63.1 | 0.21 | 76 | 72 |
| Parameter | Value |
|---|---|
| δmax (mm) | 0.319 |
| τmax−n (mm) | 21 |
| α | 0.65 |
| α’ | −0.88 |
© 2016 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Darain, K.M.u.; Jumaat, M.Z.; Shukri, A.A.; Obaydullah, M.; Huda, M.N.; Hosen, M.A.; Hoque, N. Strengthening of RC Beams Using Externally Bonded Reinforcement Combined with Near-Surface Mounted Technique. Polymers 2016, 8, 261. https://doi.org/10.3390/polym8070261
Darain KMu, Jumaat MZ, Shukri AA, Obaydullah M, Huda MN, Hosen MA, Hoque N. Strengthening of RC Beams Using Externally Bonded Reinforcement Combined with Near-Surface Mounted Technique. Polymers. 2016; 8(7):261. https://doi.org/10.3390/polym8070261
Chicago/Turabian StyleDarain, Kh Mahfuz ud, Mohd Zamin Jumaat, Ahmad Azim Shukri, M. Obaydullah, Md. Nazmul Huda, Md. Akter Hosen, and Nusrat Hoque. 2016. "Strengthening of RC Beams Using Externally Bonded Reinforcement Combined with Near-Surface Mounted Technique" Polymers 8, no. 7: 261. https://doi.org/10.3390/polym8070261
APA StyleDarain, K. M. u., Jumaat, M. Z., Shukri, A. A., Obaydullah, M., Huda, M. N., Hosen, M. A., & Hoque, N. (2016). Strengthening of RC Beams Using Externally Bonded Reinforcement Combined with Near-Surface Mounted Technique. Polymers, 8(7), 261. https://doi.org/10.3390/polym8070261








