Mechanical Properties of Composites Used in High-Voltage Applications
Abstract
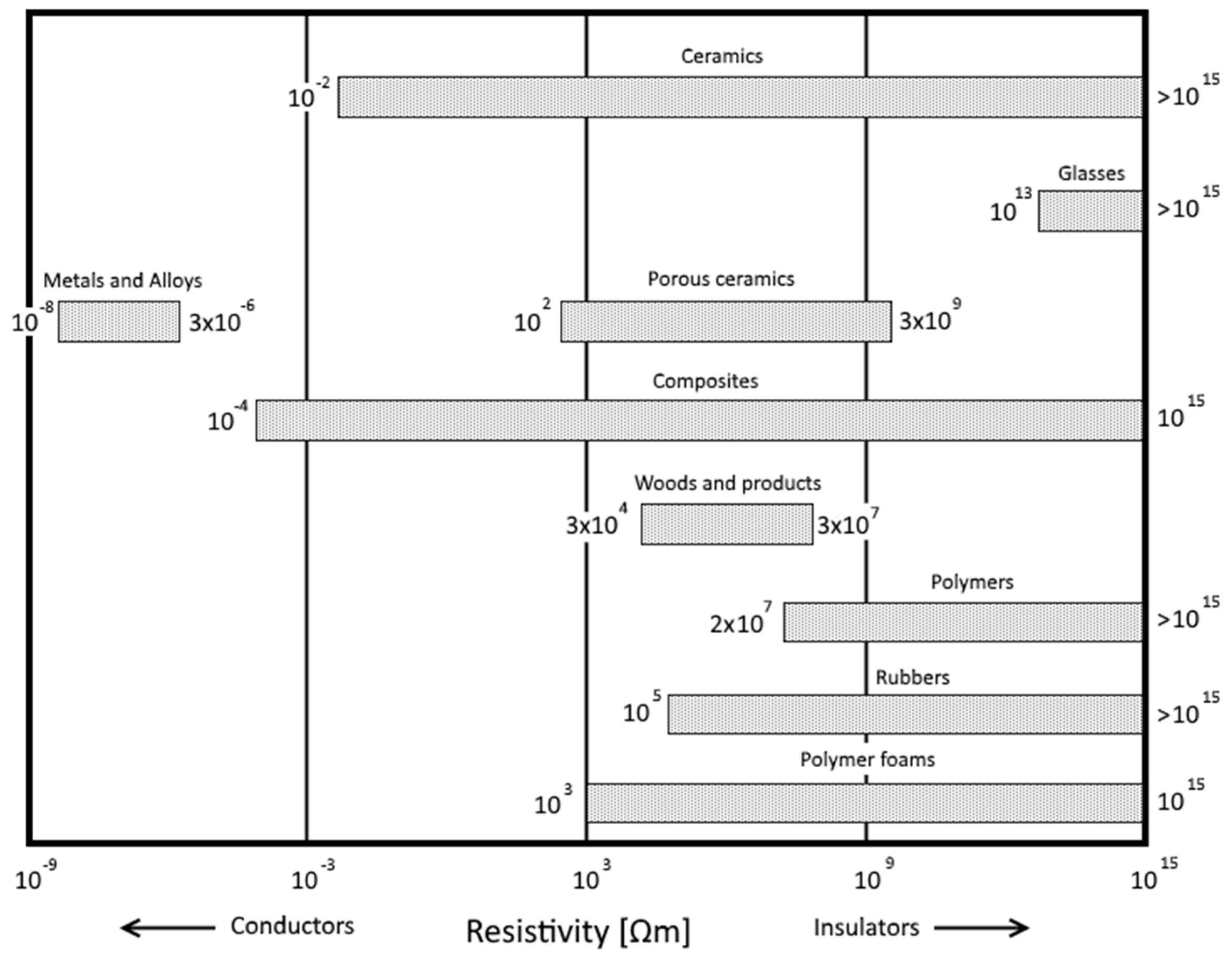
:1. Introduction
2. Characterization of Thermo-Mechanical Properties of Thermosets
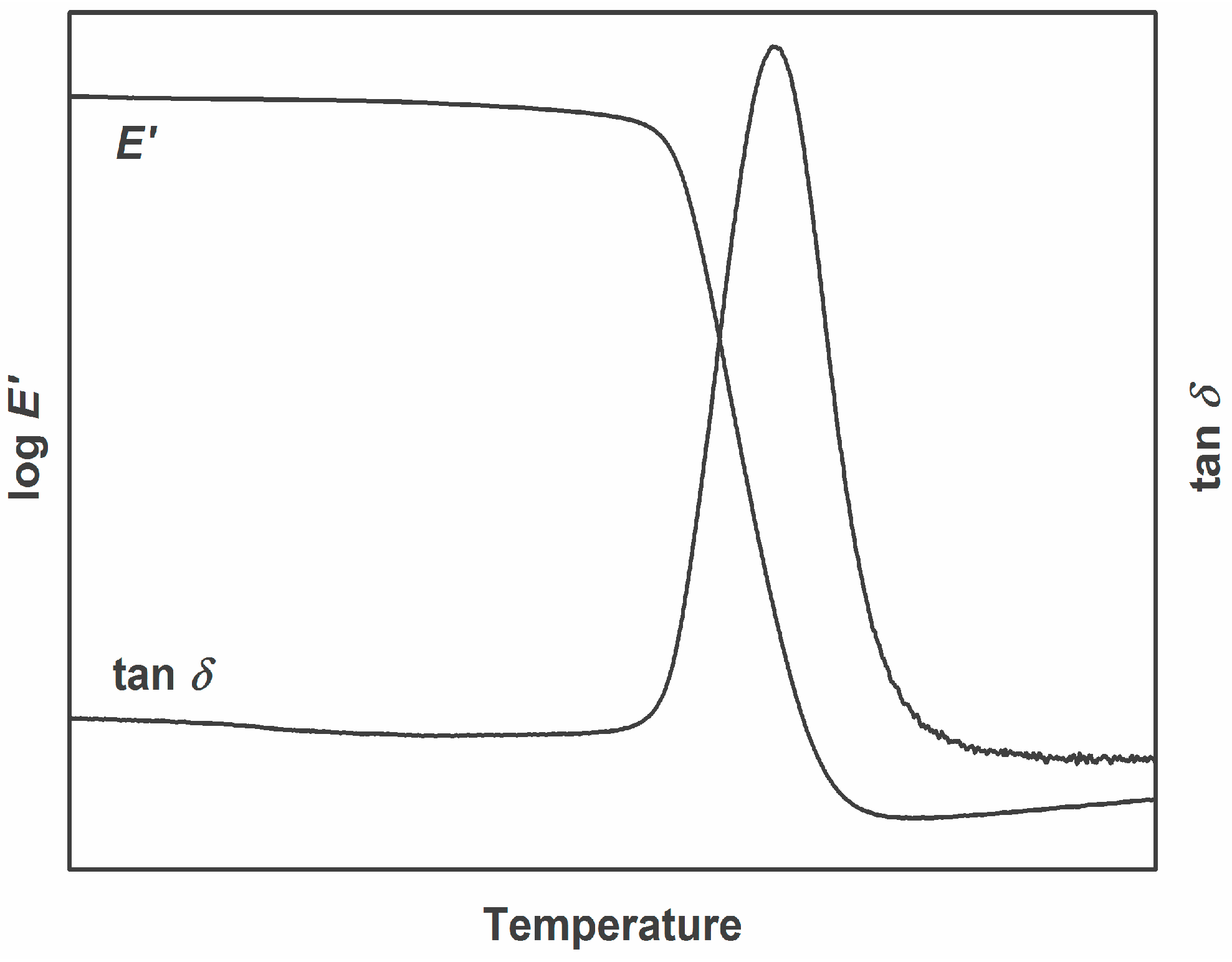
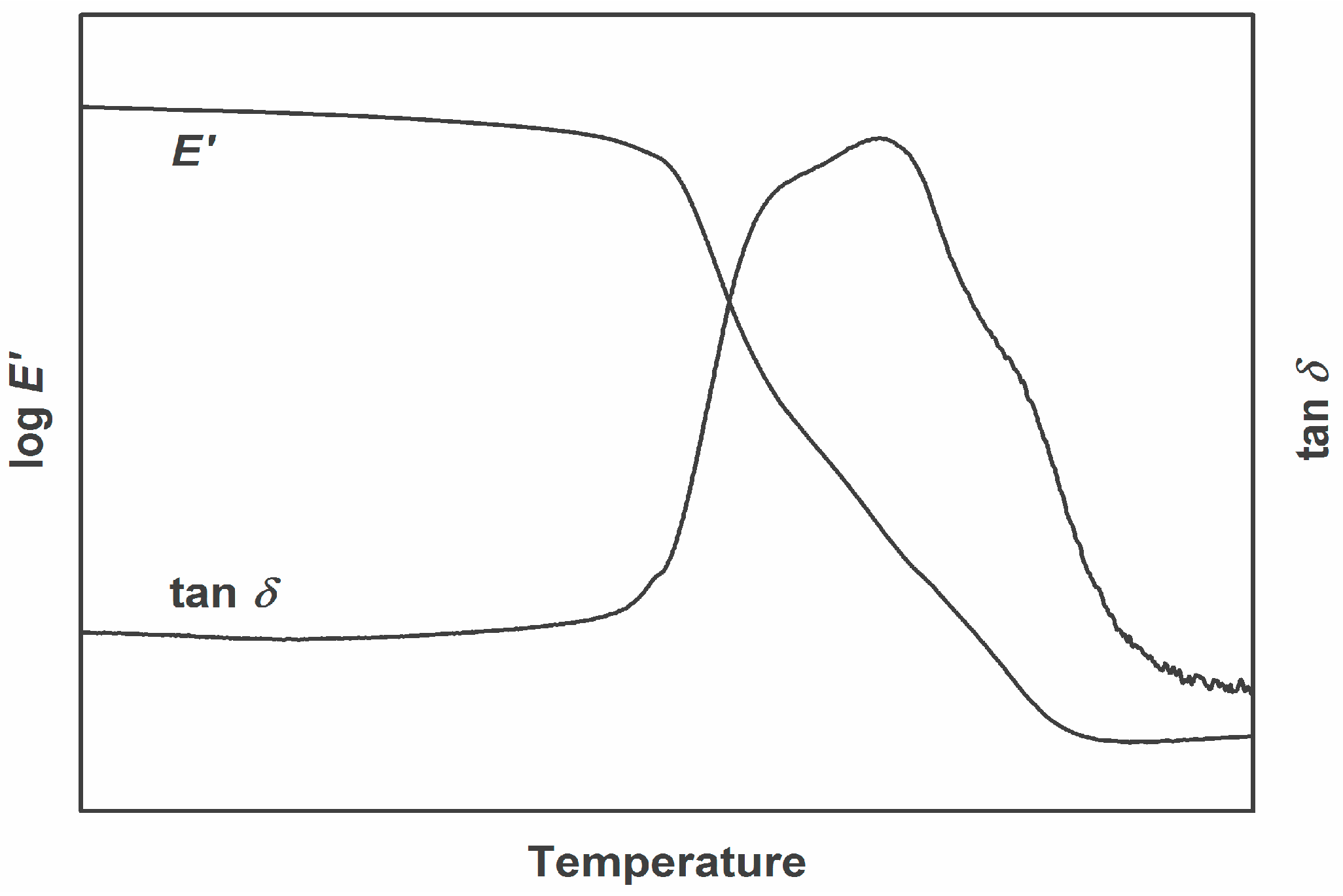
2.1. Dynamic Mechanical Analysis
2.2. Structure Property Relationships in the Glass Transition Region
2.3. Homogenous Network
2.4. Inhomogeneous Network
2.5. Application of DMA Analysis on Epoxy Based Materials
3. Mechanical Properties of Thermosets
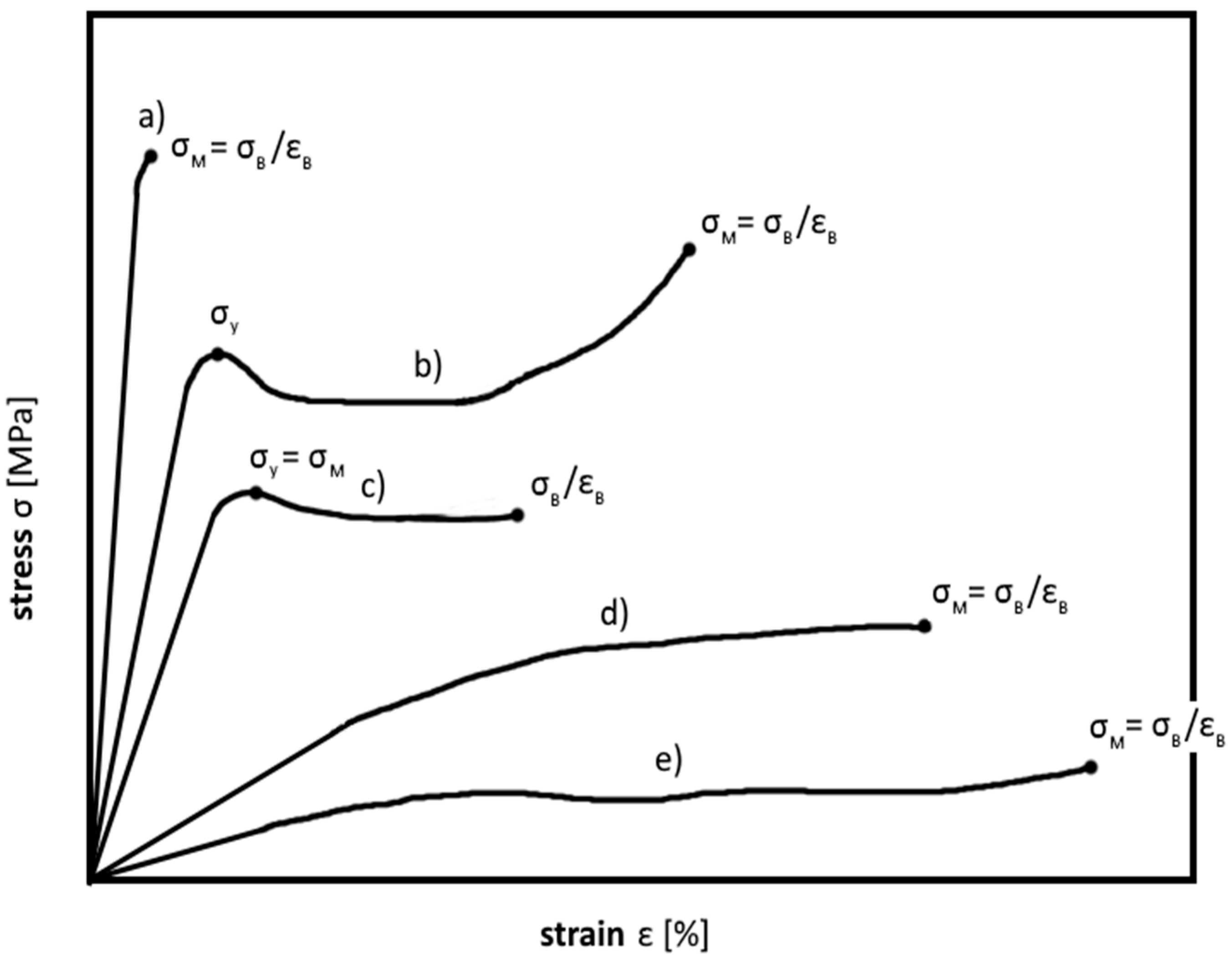
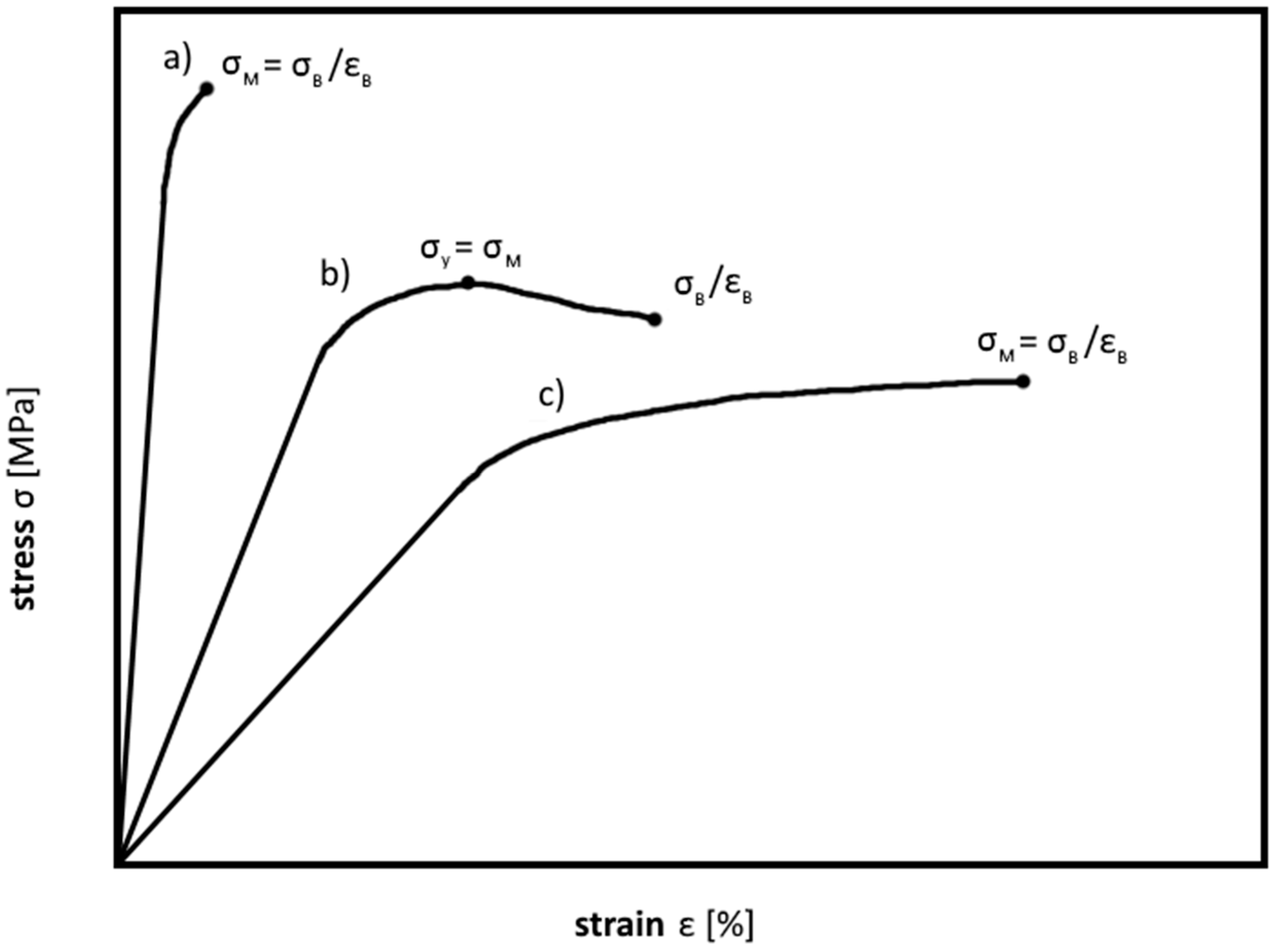
3.1. Tensile tests on Thermosets
3.2. Application of Tensile Tests on Epoxy Based Materials
3.3. Bending Test on Thermosets
3.4. Application of Bending Tests on Epoxy Based Materials
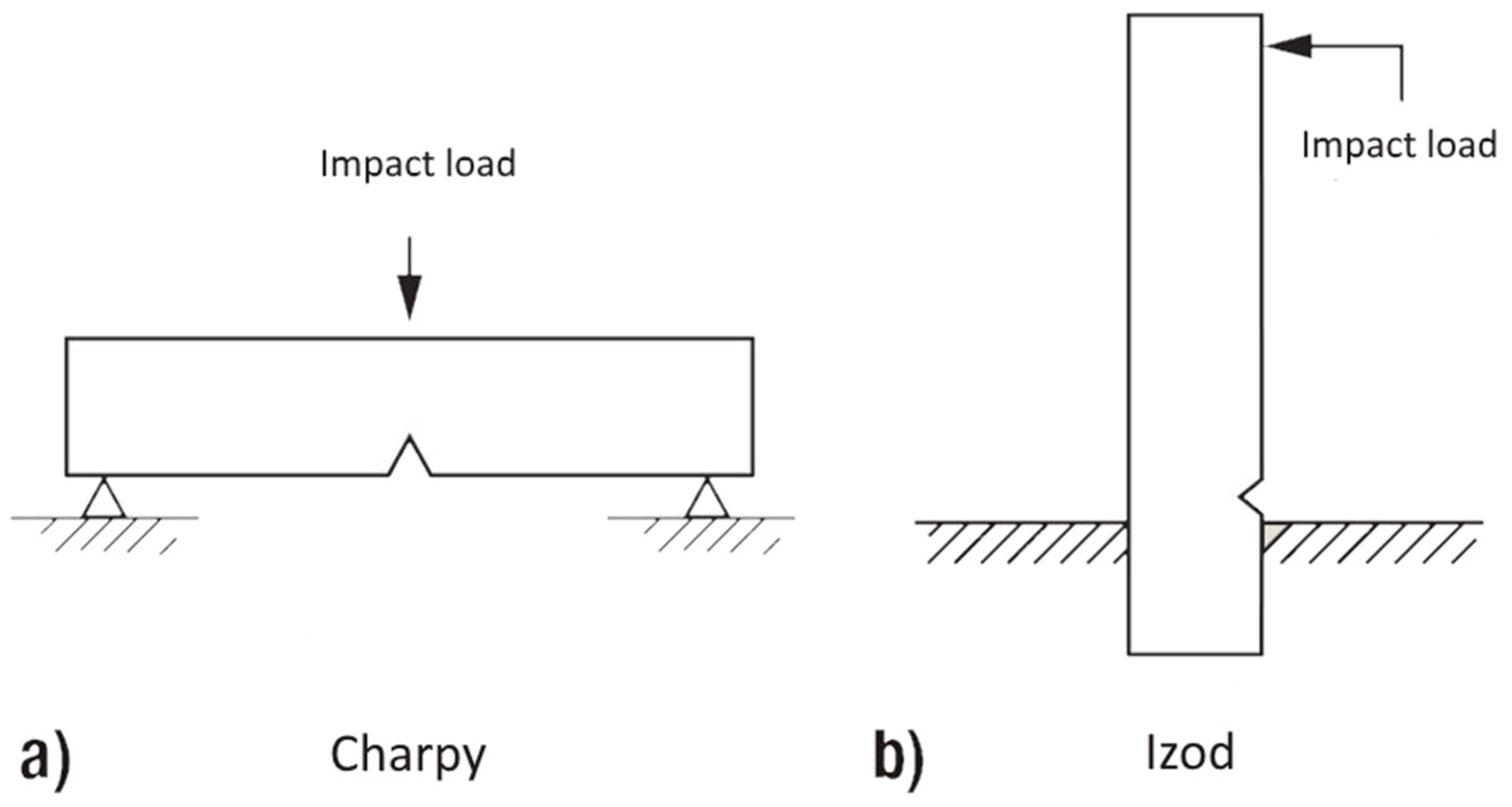
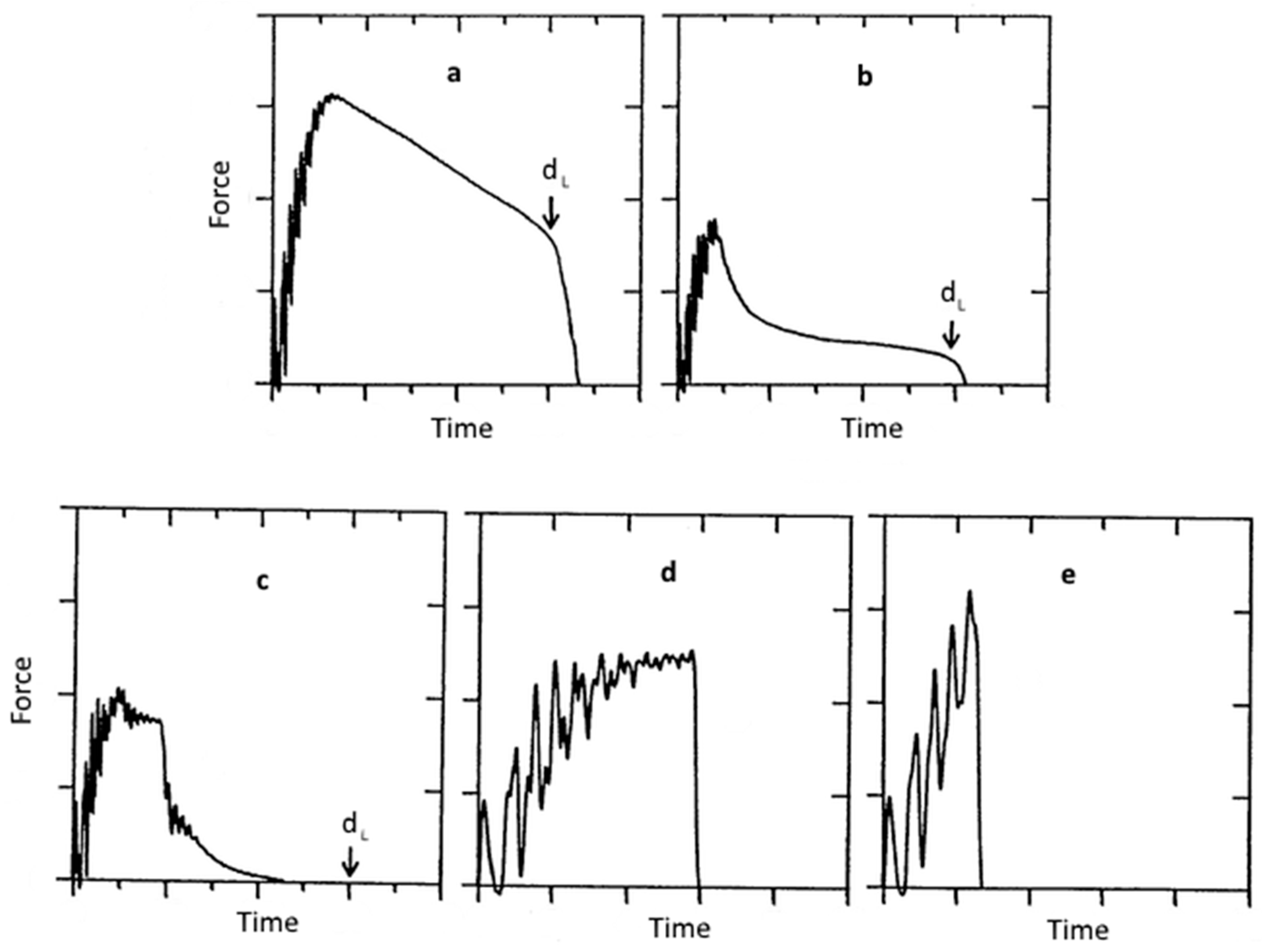
3.5. Impact Behavior of Thermosets
3.6. Application of Impact Tests on Epoxy Based Materials
4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Ashby, M.; Shercliff, H.; Cebon, D. Dynamic Materials Engineering, Science, Processing and Design, 1st ed.; Butterworth-Heinemann: Oxford, UK, 2007. [Google Scholar]
- Arora, R.; Mosch, W. High Voltage and Electrical Insulation Engineering, 1st ed.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2011. [Google Scholar]
- Mohanty, A.; Srivastava, V.K. Dielectric breakdown performance of alumina/epoxy resin nanocomposites under high voltage application. Mater. Des. 2013, 47, 711–716. [Google Scholar] [CrossRef]
- Guo, Q. Thermosets Structure, Properties and Application, 1st ed.; Woodhead Publishing Limited: Cambridge, UK, 2012. [Google Scholar]
- Menard, K.P. Dynamic Mechanical Analysis a Practical Introduction, 2nd ed.; CRC Press: New York, NY, USA, 2008. [Google Scholar]
- Ehrenstein, G.W.; Riedel, G.; Trawiel, P. Praxis der Thermischen Analyse, 2nd ed.; Carl Hanser Verlag: München, Germany, 2003. [Google Scholar]
- Pascault, J.P.; Sautereau, H.; Verdu, J.; Williams, R.J.J. Thermosetting Polymers, 1st ed.; Marcel Dekker Inc.: New York, NY, USA, 2002. [Google Scholar]
- Vanalandingham, M.R.; Eduljee, R.F.; Gillespie, J.W. Relationships between stoichiometry, microstructure, and properties for amine-cured epoxies. J. Appl. Polym. Sci. 1999, 71, 699–712. [Google Scholar]
- Palmese, G.R.; McCullough, R.L. Effect of epoxy-amine stoichiometry on cured resin material properties. J. Appl. Polym. Sci. 1992, 46, 1863–1873. [Google Scholar] [CrossRef]
- Guo, Q. Effect of curing agent on the phase behavior of epoxy resin/phenoxy blends. Polymer 1995, 36, 4753–4760. [Google Scholar] [CrossRef]
- Guo, Q.; Peng, X. The miscibility and morphology of epoxy resin/poly(ethylene oxide) blends. Polymer 1991, 32, 53–57. [Google Scholar]
- Guo, Q.; Jinyu, H.; Liaohai, H.; Zhiliu, F. Phase separation in anhydride-cured epoxy resin containing phenolphthalein poly(ether ether ketone). Eur. Polym. J. 1992, 28, 405–409. [Google Scholar]
- Clark, J.N.; Daly, J.H.; Garton, A. Hydrogen bonding in epoxy resin/poly(ϵ-caprolactone) blends. J. Appl. Polym. Sci. 1984, 29, 3381–3390. [Google Scholar] [CrossRef]
- Kosmidou, T.V.; Vatalis, A.S.; Delides, C.G.; Logakis, E.; Pissis, P.; Papanicolaou, G.C. Structural, mechanical and electrical characterization of epoxy-amine/carbon black nanocomposites. eXPRESS Polym. Lett. 2008, 2, 364–372. [Google Scholar] [CrossRef]
- Ma, J.; Mo, M.S.; Du, X.S.; Rosso, P.; Friedrich, K.; Kuan, H.C. Effect of inorganic nanoparticles on mechanical property, fracture toughness and toughening mechanism of two epoxy systems. Polymer 2008, 49, 3510–3523. [Google Scholar] [CrossRef]
- Rodriguez, M.T.; Garcia, S.J.; Cabello, R.; Suay, J.J.; Gracenea, J.J. Effect of plasticizer on the thermal, mechanical, and anticorrosion properties of an epoxy primer. J. Coat. Technol. Res. 2008, 2, 557–564. [Google Scholar] [CrossRef]
- Shabeer, A.; Sundararaman, S.; Chandrashekhara, K.; Dharani, L.R. Physicochemical properties and fracture behavior of soy-based resin. J. Appl. Polym. Sci. 2007, 105, 656–663. [Google Scholar] [CrossRef]
- Gupta, A.P.; Ahmad, S.; Dev, A. Modification of novel bio-based resin-epoxidized soybean oil by conventional epoxy resin. Polym. Eng. Sci. 2011, 51, 1087–1091. [Google Scholar] [CrossRef]
- Rochester, J.R. Bisphenol A and human health: A review of the literature. Reprod. Toxicol. 2013, 42, 132–155. [Google Scholar] [CrossRef] [PubMed]
- Tsai, W.T. Human health risk on environmental exposure to bisphenol-A: A review. J. Environ. Sci. Health 2006, 24, 225–255. [Google Scholar] [CrossRef] [PubMed]
- Park, S.J.; Jin, F.L.; Lee, J.R. Effect of biodegradable epoxidized castor oil on physicochemical and mechanical properties of epoxy resins. Macromol. Chem. Phys. 2004, 205, 2048–2054. [Google Scholar] [CrossRef]
- Miyagawa, H.; Misra, M.; Drzal, L.T. Fracture toughness and impact strength of anhydride-cured biobased epoxy. Polym. Eng. Sci. 2005, 45, 487–495. [Google Scholar] [CrossRef]
- Chrysanthos, M.; Galy, J.; Pascault, J.P. Preparation and properties of bio-based epoxy networks derived from isosorbide diglycidyl ether. Polymer 2011, 52, 3611–3620. [Google Scholar] [CrossRef]
- Bell, J.P. Mechanical properties of a glassy epoxide polymer: effect of molecular weight between crosslinks. J. Appl. Polym. Sci. 1970, 14, 1901–1906. [Google Scholar] [CrossRef]
- Grellmann, W.; Seidler, S. Polymer Testing, 2nd ed.; Hanser Gardner Publications Inc.: Cincinnaty, OH, USA, 2013. [Google Scholar]
- Bonten, C. Kunststofftechnik Einführung und Grundlagen, 1st ed.; Carl Hanser Verlag: München, Germany, 2014. [Google Scholar]
- Kim, S.L.; Skibo, M.D.; Manson, J.A.; Hertzberg, R.W.; Janiszewski, J. Tensile, impact and fatigue behavior of an amine-cured epoxy resin. Polym. Eng. Sci. 1978, 18, 1093–1100. [Google Scholar] [CrossRef]
- Urbaczewski-Espuche, E.; Galy, J.; Gerard, J.F.; Pascault, J.P.; Sautereau, H. Influence of chain flexibility and crosslink density on mechanical properties of epoxy/amine networks. Polym. Eng. Sci. 1991, 32, 1572–1580. [Google Scholar] [CrossRef]
- Daly, J.; Britten, A.; Garton, A.; McLean, P.D. An additive for increasing the strength and modulus of amine-cured epoxy resins. J. Appl. Polym. Sci. 1984, 29, 1403–1414. [Google Scholar] [CrossRef]
- Gojny, F.H.; Wichmann, M.H.G.; Köpke, U.; Fiedler, B.; Schulte, K. Carbon nanotube-reinforced epoxy-composites: Enhanced stiffness and fracture toughness at low nanotube content. Compos. Sci. Technol. 2004, 64, 2363–2371. [Google Scholar] [CrossRef]
- Kornmann, X.; Thomann, R.; Mülhaupt, R.; Finter, J.; Berglund, L. Synthesis of amine-cured, epoxy-layered silicate nanocomposites: The influence of the silicate surface modification on the properties. J. Appl. Polym. Sci. 2002, 86, 2643–2652. [Google Scholar] [CrossRef]
- Wang, R.; Schumann, T.; Vuppalapati, R.R.; Chandrashekhara, K. Fabrication of bio-based epoxy-clay nanocomposites. Gr. Chem. 2014, 16, 1871–1882. [Google Scholar] [CrossRef]
- Rong, M.Z.; Zhang, M.Q.; Ruan, W.H. Surface modification of nanoscale fillers for improving properties of polymer nanocomposites: A review. Mater. Sci. Technol. 2006, 22, 787–797. [Google Scholar] [CrossRef]
- Xu, Y.; Hoa, S.V. Mechanical properties of carbon fiber reinforced epoxy/clay nanocomposites. Compos. Sci. Technol. 2008, 68, 854–861. [Google Scholar] [CrossRef]
- Rong, M.Z.; Ming, M.Q.; Liu, Y.; Yang, G.C.; Zeng, H.M. The effect of fiber treatment on the mechanical properties of unidirectional sisal-reinforced epoxy composites. Compos. Sci. Technol. 2001, 61, 1437–1447. [Google Scholar] [CrossRef]
- Sgricca, N.; Hawley, M.C.; Misra, M. Characterization of natural fiber surfaces and natural fiber composites. Compos. Part A 2008, 39, 1632–1637. [Google Scholar] [CrossRef]
- Wambua, P.; Ivens, J.; Verpoest, I. Natural fibres: Can they replace glass in fibre reinforced plastics? Compos. Sci. Technol. 2003, 63, 1259–1264. [Google Scholar] [CrossRef]
- Tjong, S.C. Structural and mechanical properties of polymer nanocomposites. Mater. Sci. Eng. Rep. 2006, 53, 73–197. [Google Scholar] [CrossRef]
- Wang, J.; Fang, Z.; Gu, A.; Xu, L.; Liu, F. Effect of amino-functionalization of multi-walled carbon nanotubes on the dispersion with epoxy resin matrix. J. Appl. Polym. Sci. 2006, 100, 97–104. [Google Scholar] [CrossRef]
- Sharma, S.P.; Lakkad, S.C. Impact behavior and fractographic study of carbon nanotubes grafted carbon fiber-reinforced epoxy matrix multi-scale hybrid composites. Compos. Part A 2015, 69, 124–131. [Google Scholar] [CrossRef]
- Czub, P. Application of modified natural oils as reactive diluents for epoxy resins. Macromol. Symp. 2006, 242, 60–64. [Google Scholar] [CrossRef]

| Epoxy base | Tg measured at maximum tan δ (°C) | Reference |
|---|---|---|
| DGEBA | 161 | [8] |
| DGEBA + carbon black | 169 | [14] |
| Epoxidized allyl soyate | 90 | [17] |
| Epoxidized soybean oil | 80 | [18] |
| Epoxy base | Young’s modulus (MPa) | Reference |
|---|---|---|
| DGEBA | 2,750 | [15] |
| DGEBA + Carbon nanotubes | 3,500 | [30] |
| DGEBA + sisal fibers | 15,000 | [33] |
| Epoxidized soybean oil | 648 | [18] |
© 2016 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moser, A.; Feuchter, M. Mechanical Properties of Composites Used in High-Voltage Applications. Polymers 2016, 8, 260. https://doi.org/10.3390/polym8070260
Moser A, Feuchter M. Mechanical Properties of Composites Used in High-Voltage Applications. Polymers. 2016; 8(7):260. https://doi.org/10.3390/polym8070260
Chicago/Turabian StyleMoser, Andreas, and Michael Feuchter. 2016. "Mechanical Properties of Composites Used in High-Voltage Applications" Polymers 8, no. 7: 260. https://doi.org/10.3390/polym8070260
APA StyleMoser, A., & Feuchter, M. (2016). Mechanical Properties of Composites Used in High-Voltage Applications. Polymers, 8(7), 260. https://doi.org/10.3390/polym8070260






