Predicting the Flory-Huggins χ Parameter for Polymers with Stiffness Mismatch from Molecular Dynamics Simulations
Abstract
:1. Introduction
1.1. Flory–Huggins χ Parameter
1.2. Entropic Contributions to χ
1.3. Challenges of Calculating χ from Simulation
1.4. Novel Method for Determining χ from Simulation
2. Method
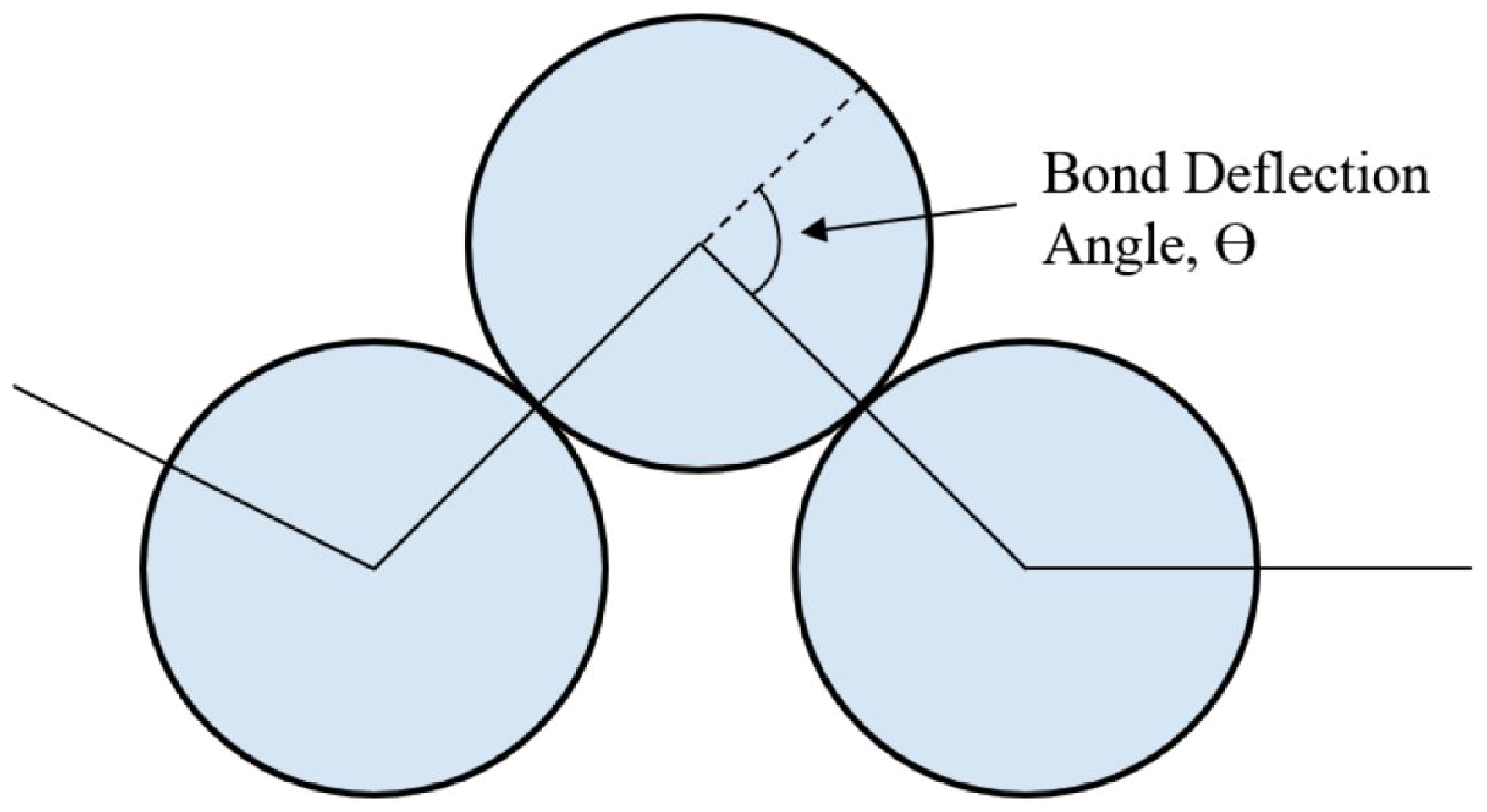
2.1. Theory for Determining χ
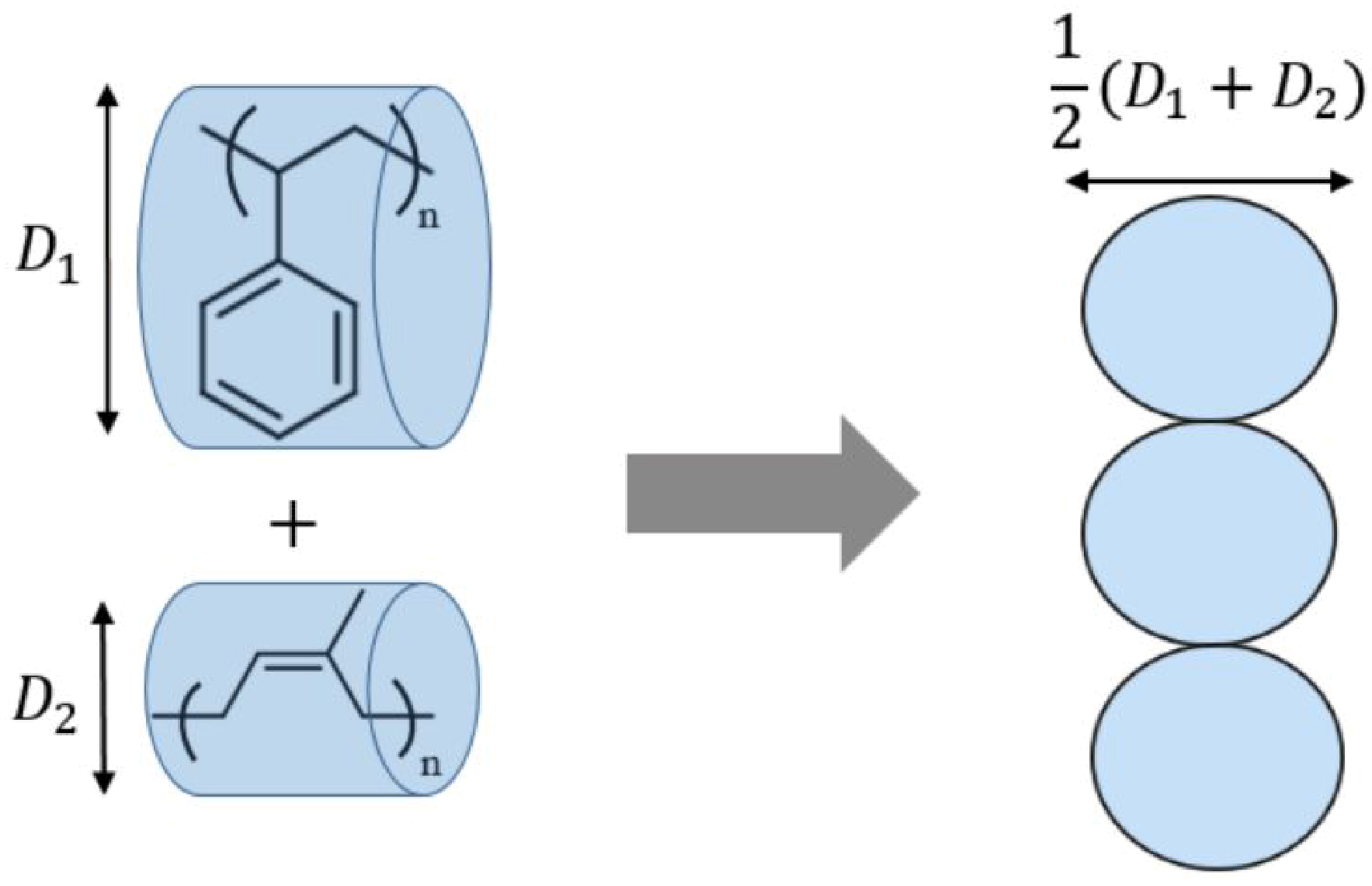
2.2. Simulation Details
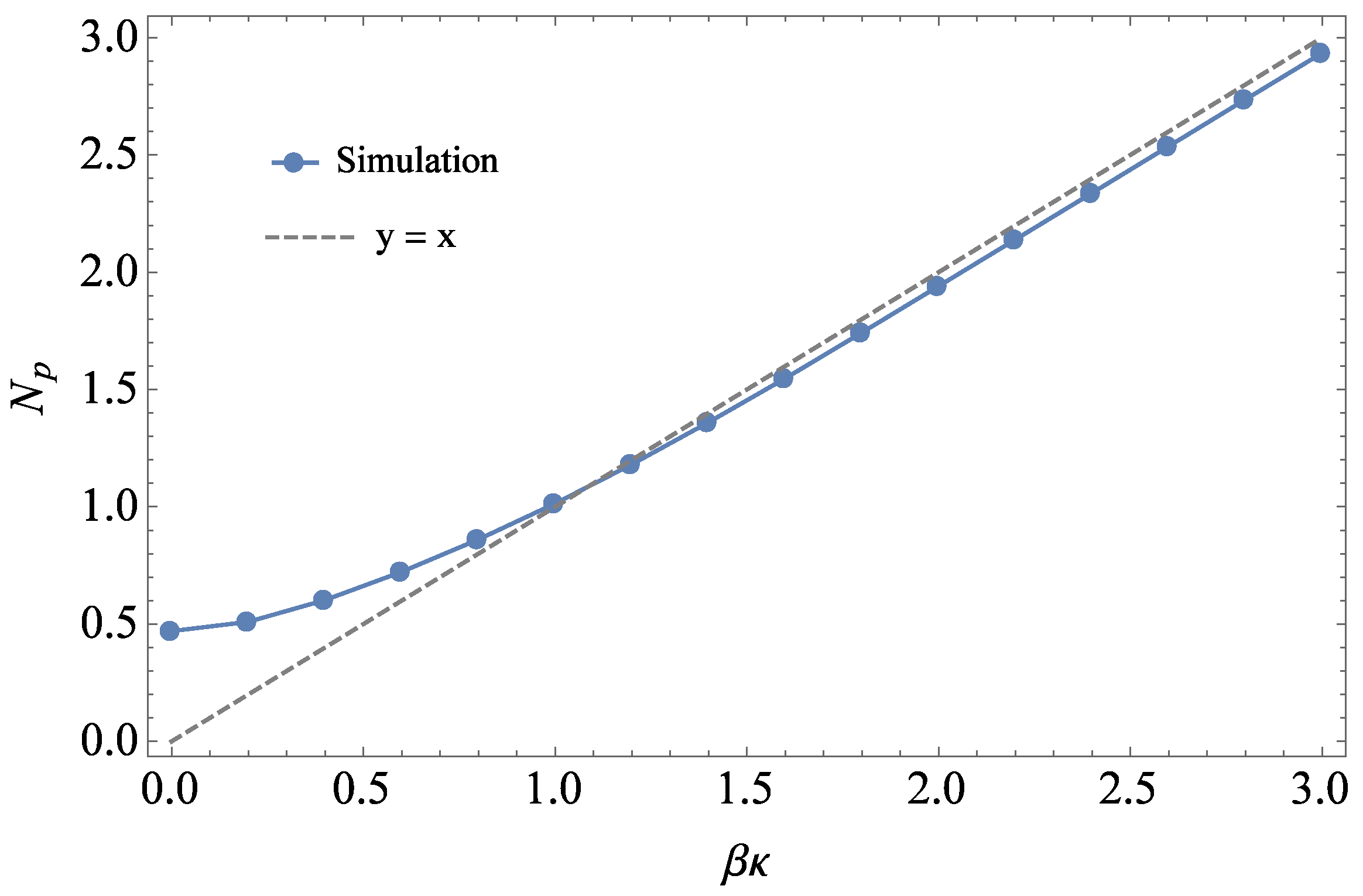
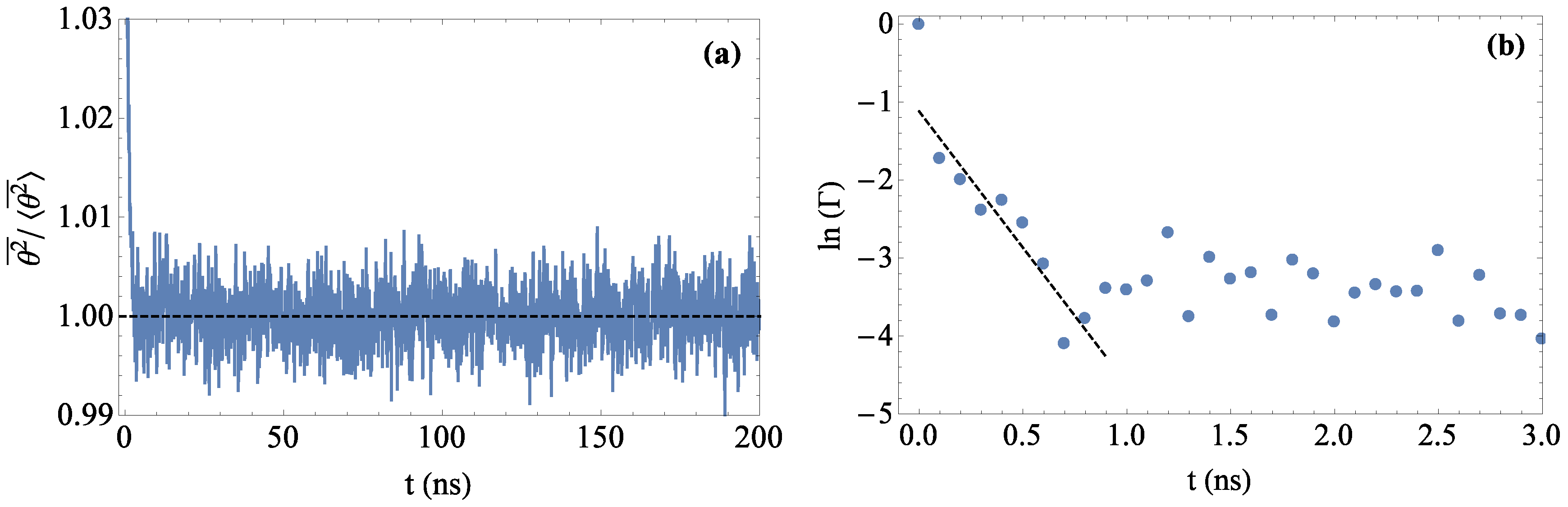
2.3. Analysis of Simulation Data
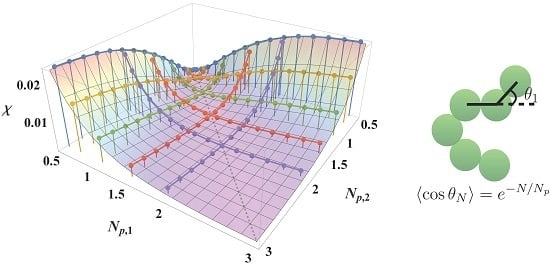
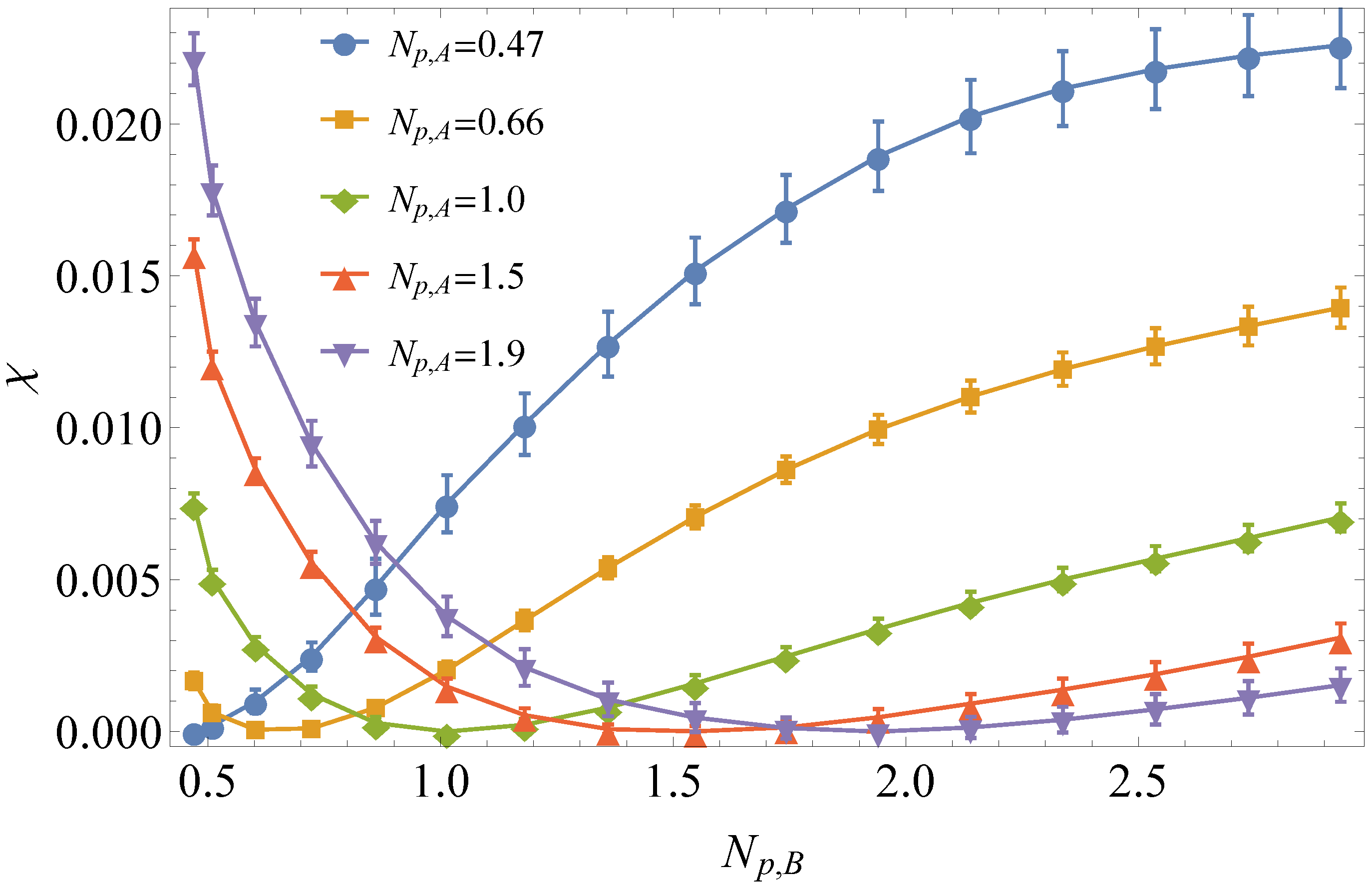
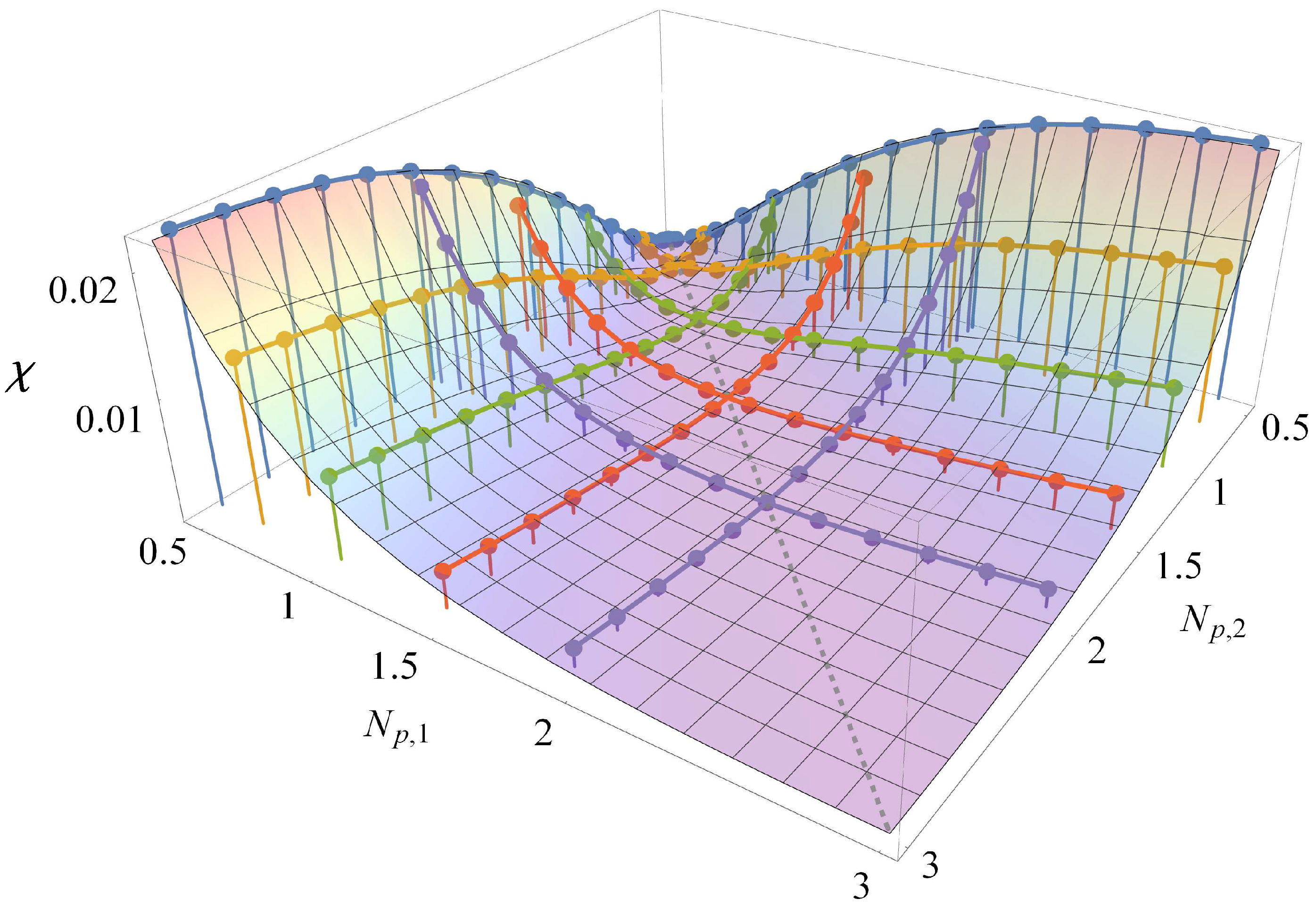
3. Results
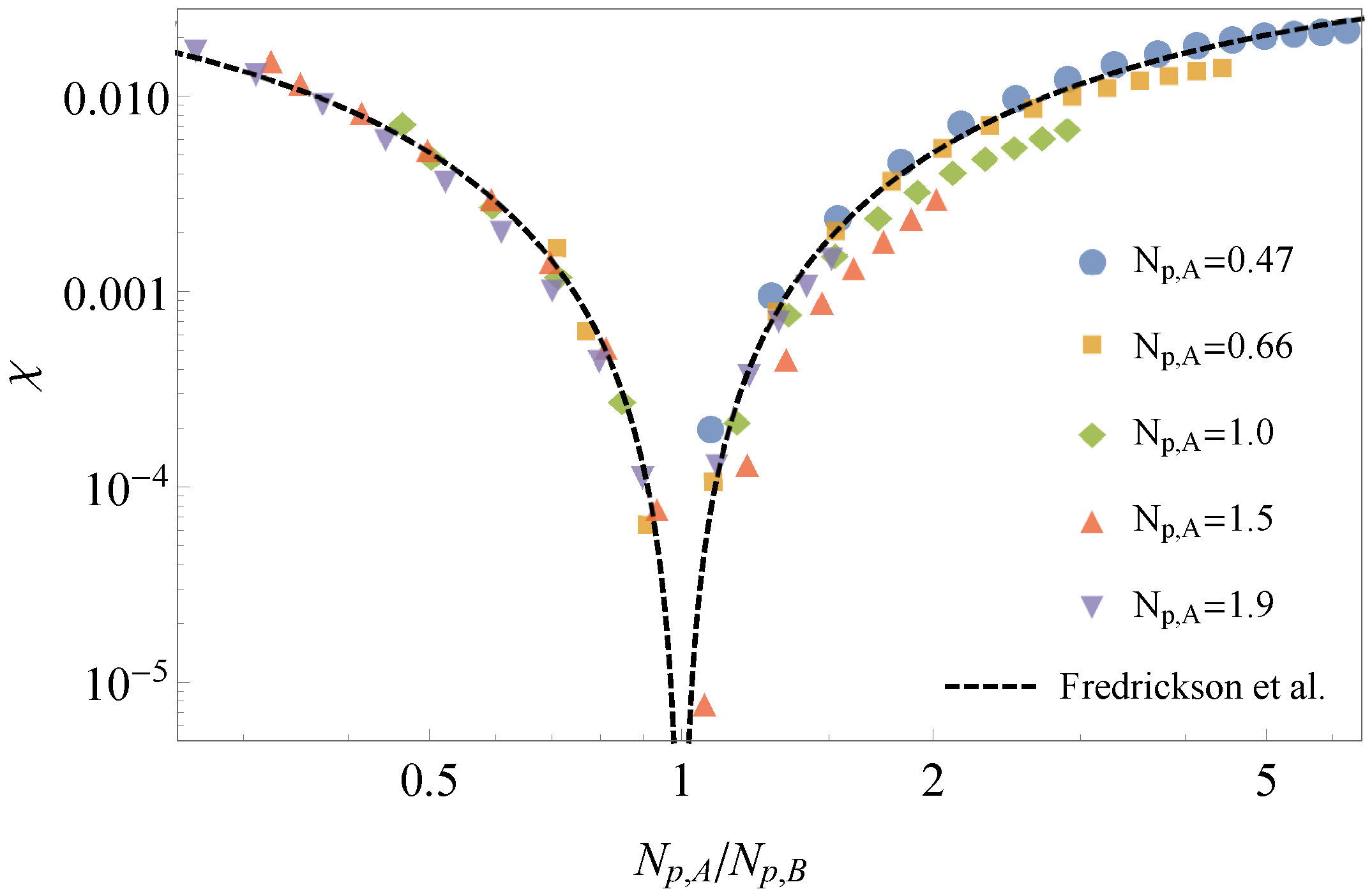
3.1. Comparison to Field Theory
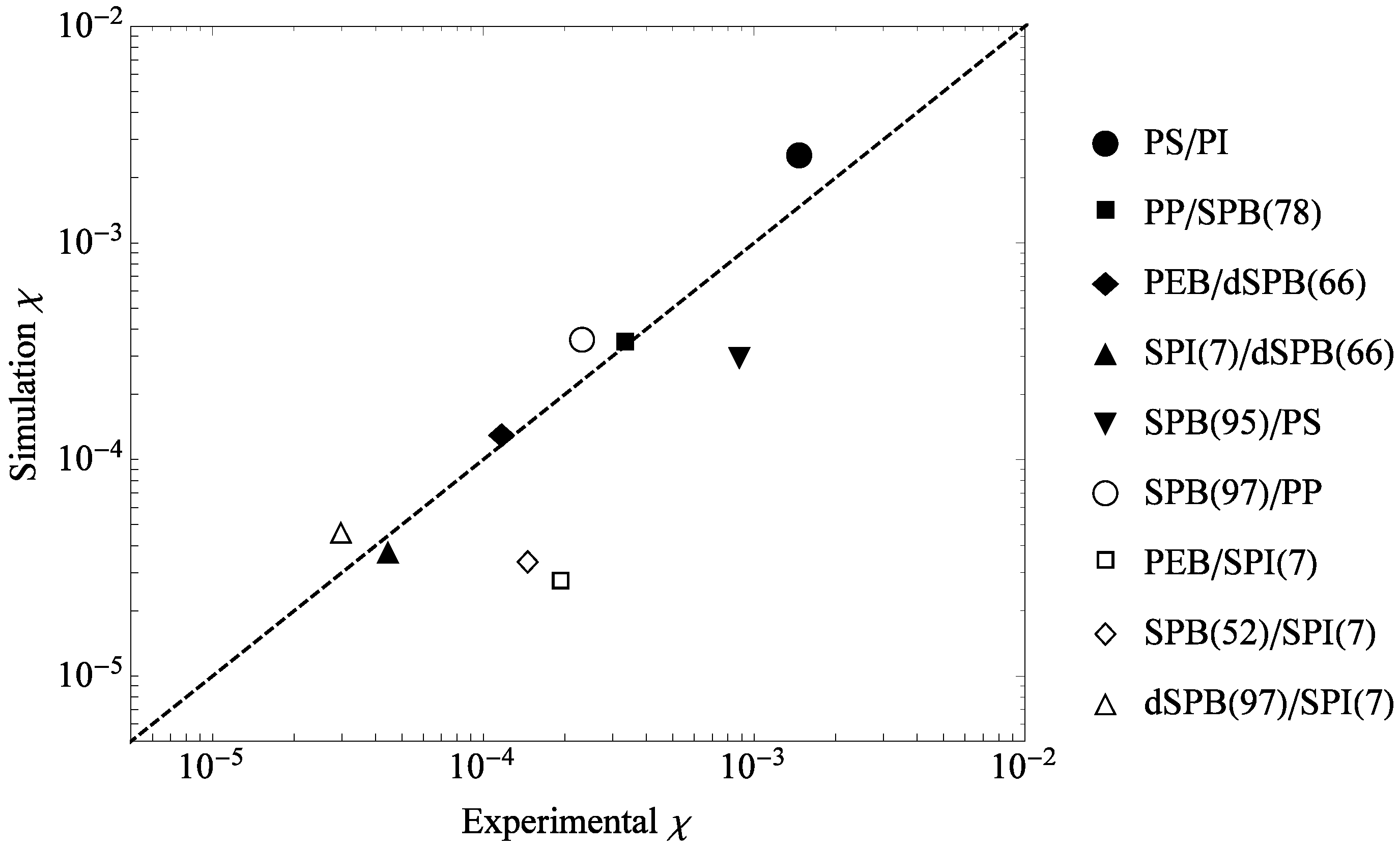
3.2. Comparison to Experiments
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Robeson, L.M. Applications of polymer blends: Emphasis on recent advances. Polym. Eng. Sci. 1984, 24, 587–597. [Google Scholar] [CrossRef]
- Goettler, L.A.; Scobbo, J.J. Applications of Polymer Blends. In Polymer Blends Handbook, 2nd ed.; Utracki, L.A., Wilkie, C.A., Eds.; Springer: London, UK, 2014; pp. 1434–1457. [Google Scholar]
- Hamley, I.W. Nanostructure fabrication using block copolymers. Nanotechnology 2003, 14, R39–R54. [Google Scholar] [CrossRef]
- Sommer, M.; Huettner, S.; Thelakkat, M. Donor acceptor block copolymers for photovoltaic applications. J. Mater. Chem. 2010, 20, 10788–10797. [Google Scholar] [CrossRef]
- Kim, H.C.; Park, S.M.; Hinsberg, W.D.; Division, I.R. Block copolymer based nanostructures: Materials, processes, and applications to electronics. Chem. Rev. 2010, 110, 146–177. [Google Scholar] [CrossRef] [PubMed]
- Tao, Y.; McCulloch, B.; Kim, S.; Segalman, R.A. The relationship between morphology and performance of donor–acceptor rod–coil block copolymer solar cells. Soft Matter 2009, 5, 4219–4230. [Google Scholar] [CrossRef]
- Bates, F.S. Polymer-polymer phase behavior. Science 1991, 251, 898–905. [Google Scholar] [CrossRef] [PubMed]
- Hiemenz, P.C.; Lodge, T.P. Polymer Chemistry, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Flory, P.J. Principles of Polymer Chemistry; Cornell University Press: Ithaca, NY, USA, 1953; pp. 495–540. [Google Scholar]
- De Gennes, P.G. Scaling Concepts in Polymer Physics; Cornell University Press: Ithaca, NY, USA, 1979. [Google Scholar]
- Murray, C.T.; Gilmer, J.W.; Stein, S.S. Neutron-scattering investigation of the interaction between components in concentrated, miscible, amorphous polymer blends. Macromolecules 1985, 18, 996–1002. [Google Scholar] [CrossRef]
- Russell, T.P. X-Ray and Neutron reflectivity for the investigation. Mater. Sci. Rep. 1990, 5, 171–271. [Google Scholar] [CrossRef]
- Bates, F.S.; Fredrickson, G.H. Block copolymer thermodynamics: Theory and experiment. Annu. Rev. Phys. Chem. 1990, 41, 525–557. [Google Scholar] [CrossRef] [PubMed]
- Graessley, W.W. Polymeric Liquids and Networks: Structure and Properties; Garland Science: New York, NY, USA, 2004. [Google Scholar]
- Fredrickson, G.H.; Liu, A.J.; Bates, F.S. Entropic corrections to the Flory–Huggins Theory of polymer blends—Architectural and conformational effects. Macromolecules 1994, 27, 2503–2511. [Google Scholar] [CrossRef]
- Helfand, E.; Tagami, Y. Theory of the interface between immiscible polymers. J. Polym. Sci. B Polym. Lett. 1971, 9, 741–746. [Google Scholar] [CrossRef]
- Helfand, E.; Tagami, Y. Theory of the interface between immiscible polymers. II. J. Chem. Phys. 1972, 56, 3592–3601. [Google Scholar] [CrossRef]
- Groot, R.D.; Warren, P.B. Dissipative particle dynamics: Bridging the gap between atomistic and mesoscopic simulation. J. Chem. Phys. 1997, 107, 4423–4435. [Google Scholar] [CrossRef]
- Chremos, A.; Nikoubashman, A.; Panagiotopoulos, A.Z. Flory–Huggins parameter χ, from binary mixtures of Lennard-Jones particles to block copolymer melts. J. Chem. Phys. 2014, 140, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Qin, J.; Milner, S.T. Tubes, topology, and polymer entanglement. Macromolecules 2014, 47, 6077–6085. [Google Scholar] [CrossRef]
- Allen, M.P.; Tildesley, D.J. Computer Simulations of Liquids; Oxford University Press: New York, NY, USA, 1987. [Google Scholar]
- Kumar, S.K.; Szleifer, I.; Panagiotopoulos, A.Z. Determination of the chemical potentials of polymeric systems from Monte Carlo simulations. Phys. Rev. Lett. 1991, 66, 2935–2938. [Google Scholar] [CrossRef] [PubMed]
- Frenkel, D.; Smit, B. Understanding Molecular Simulation: From Algorithms to Applications; Academic Press: San Diego, CA, USA, 1996. [Google Scholar]
- Villa, A.; Mark, A.E. Calculation of the free energy of solvation for neutral analogs of amino acid side chains. J. Comput. Chem. 2002, 23, 548–553. [Google Scholar] [CrossRef] [PubMed]
- Flory, P.J.; Krigbaum, W.R. Thermodynamics of high polymer solutions. Annu. Rev. Phys. Chem. 1951, 2, 383–402. [Google Scholar] [CrossRef]
- Gujrati, P.D. Composition dependence of chi from neutron scattering, compressibility, and a purely interaction chi. J. Chem. Phys. 2000, 112, 4806–4821. [Google Scholar] [CrossRef]
- Berendsen, H.; van der Spoel, D.; van Drunen, R. GROMACS: A message-passing parallel molecular dynamics implementation. Comput. Phys. Commun. 1995, 91, 43–56. [Google Scholar] [CrossRef]
- Hess, B.; Kutzner, C.; Van Der Spoel, D.; Lindahl, E. GROMACS 4: Algorithms for highly efficient, load-balanced, and scalable molecular simulation. J. Chem. Theory Comput. 2008, 4, 435–447. [Google Scholar] [CrossRef] [PubMed]
- Weeks, J.D.; Chandler, D.; Andersen, H.C. Role of repulsive forces in determining the equilibrium structure of simple liquids. J. Chem. Phys. 1971, 54, 5237–5247. [Google Scholar] [CrossRef]
- Pedersen, U.R.; Christensen, T.; Schroder, T.B.; Dyre, J.C. Feasibility of a single-parameter description of equilibrium viscous liquid dynamics. Phys. Rev. E 2008, 77, 1–5. [Google Scholar] [CrossRef] [PubMed]
- Qin, J.; Milner, S.T. Tube diameter of oriented and stretched polymer melts. Macromolecules 2013, 46, 1659–1672. [Google Scholar] [CrossRef]
- Eitouni, H.B.; Balsara, N.P. Thermodynamics of polymer blends. In Physical Properties of Polymers Handbook, 2nd ed.; Springer: New York, NY, USA, 2007; Chapter 19; pp. 349–355. [Google Scholar]
- Hanwell, M.D.; Curtis, D.E.; Lonie, D.C.; Vandermeerschd, T.; Zurek, E.; Hutchison, G.R. Avogadro: An advanced semantic chemical editor, visualization, and analysis platform. J. Cheminform. 2012, 4, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Fetters, L.J.; Lohse, D.J.; Richter, D.; Witten, T.A.; Zirkel, A. Connection between polymer molecular weight, density, chain dimensions, and melt visoelastic properties. Macromolecules 1994, 27, 4639–4647. [Google Scholar] [CrossRef]


| Parameter | ||||
|---|---|---|---|---|
| Value | 0.162 | 5.40 | 0.0563 | 2.59 |
| Polymer | Temperature (K) | ρ (g·cm) | (g·mol) | L (nm) | (nm) | (nm·mol·g) | (nm) | D (nm) | (nm) |
|---|---|---|---|---|---|---|---|---|---|
| PS | 413 | 0.969 | 104 | 0.252 | 0.178 | 0.896 | 0.402 | ||
| SPS | 413 | 0.920 | 109 | 0.252 | 0.197 | 0.699 | 0.442 | ||
| PI | 298 | 0.913 | 68.1 | 0.501 | 0.124 | 0.462 | 0.1976 | ||
| SPI(75) | 413 | 0.810 | 70.2 | 0.252 | 0.144 | 0.735 | 0.324 | ||
| SPI | 298 | 0.856 | 70.2 | 0.506 | 0.136 | 0.640 | 0.216 | ||
| PB(100) | 300 | 0.890 | 54.1 | 0.252 | 0.101 | 0.709 | 0.226 | ||
| PB | 298 | 0.900 | 54.1 | 0.501 | 0.100 | 0.410 | 0.159 | ||
| SPB(98) | 298 | 0.784 | 56.1 | 0.252 | 0.119 | 0.712 | 0.266 | ||
| SPB | 413 | 0.784 | 56.1 | 0.506 | 0.119 | 0.693 | 0.1886 | ||
| PEB | 298 | 0.861 | 84.2 | 0.506 | 0.162 | 0.603 | 0.258 | ||
| PP | 298 | 0.852 | 84.2 | 0.506 | 0.164 | 0.552 | 0.262 |
| Polymer Pair | (nm) | (nm) | (nm) | (nm) | χ (Experimental) | χ (Simulation) | |||
|---|---|---|---|---|---|---|---|---|---|
| PS/PI | 0.896 | 0.462 | 0.299 | 2.99 | 1.54 | ||||
| PP/SPB(78) | 0.552 | 0.708 | 0.255 | 2.17 | 2.78 | ||||
| PEB/dSPB(66) | 0.603 | 0.705 | 0.249 | 2.42 | 2.83 | ||||
| SPI(7)/dSPB(66) | 0.647 | 0.705 | 0.236 | 2.75 | 2.99 | ||||
| SPB(95)/PS | 0.711 | 0.896 | 0.332 | 2.14 | 2.70 | ||||
| SPB(97)/PP | 0.711 | 0.552 | 0.262 | 2.71 | 2.10 | ||||
| PEB/SPI(7) | 0.603 | 0.647 | 0.244 | 2.47 | 2.65 | ||||
| SPB(52)/SPI(7) | 0.703 | 0.647 | 0.230 | 3.05 | 2.81 | ||||
| dSPB(97)/SPI(7) | 0.711 | 0.647 | 0.248 | 2.87 | 2.61 |
| Abbreviation | Polymer |
|---|---|
| PS | polystyrene |
| SPS | saturated polystyrene; poly(vinylcyclohexane) |
| PI | 1,4 polyisoprene |
| SPI | saturated 1,4 polyisoprene; alternating poly ethylene-co-propylene |
| PB | 1,4 polybutadiene |
| SPB | saturated 1,4 polybutadiene; polyethylene |
| PEB | poly(ethyl butylene) |
| PP | polypropylene |
© 2016 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kozuch, D.J.; Zhang, W.; Milner, S.T. Predicting the Flory-Huggins χ Parameter for Polymers with Stiffness Mismatch from Molecular Dynamics Simulations. Polymers 2016, 8, 241. https://doi.org/10.3390/polym8060241
Kozuch DJ, Zhang W, Milner ST. Predicting the Flory-Huggins χ Parameter for Polymers with Stiffness Mismatch from Molecular Dynamics Simulations. Polymers. 2016; 8(6):241. https://doi.org/10.3390/polym8060241
Chicago/Turabian StyleKozuch, Daniel J., Wenlin Zhang, and Scott T. Milner. 2016. "Predicting the Flory-Huggins χ Parameter for Polymers with Stiffness Mismatch from Molecular Dynamics Simulations" Polymers 8, no. 6: 241. https://doi.org/10.3390/polym8060241
APA StyleKozuch, D. J., Zhang, W., & Milner, S. T. (2016). Predicting the Flory-Huggins χ Parameter for Polymers with Stiffness Mismatch from Molecular Dynamics Simulations. Polymers, 8(6), 241. https://doi.org/10.3390/polym8060241