Turbulent Drag Reduction with Polymers in Rotating Disk Flow
Abstract
:1. Introduction
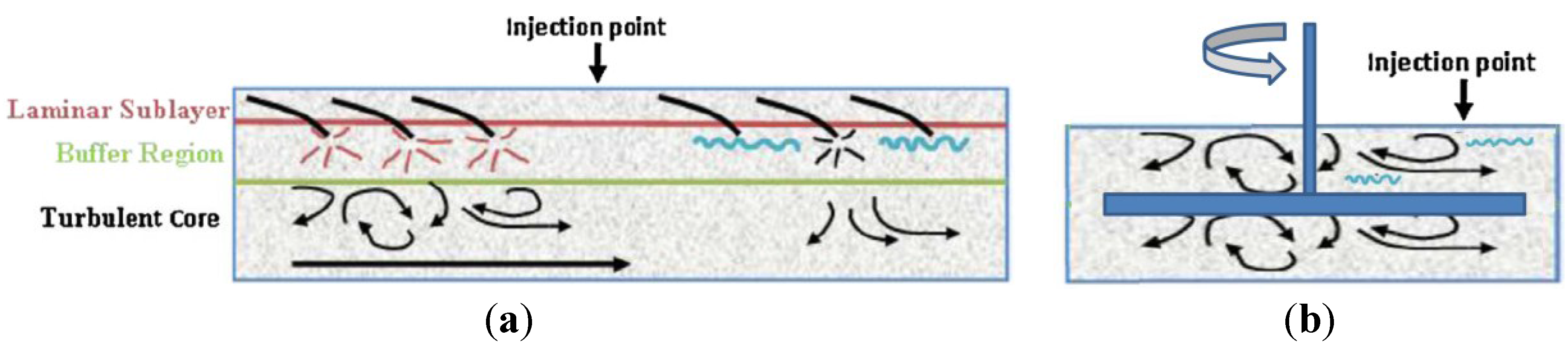
2. Mechanism of DR
= w1e−at + 2w2(1 − e−at) + c
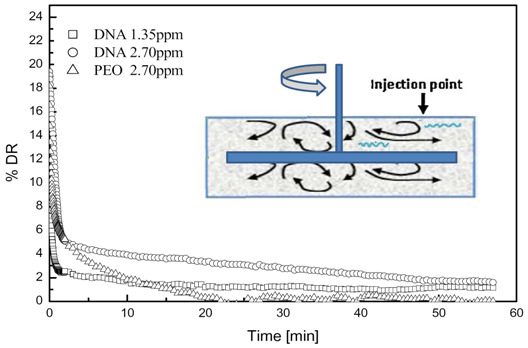
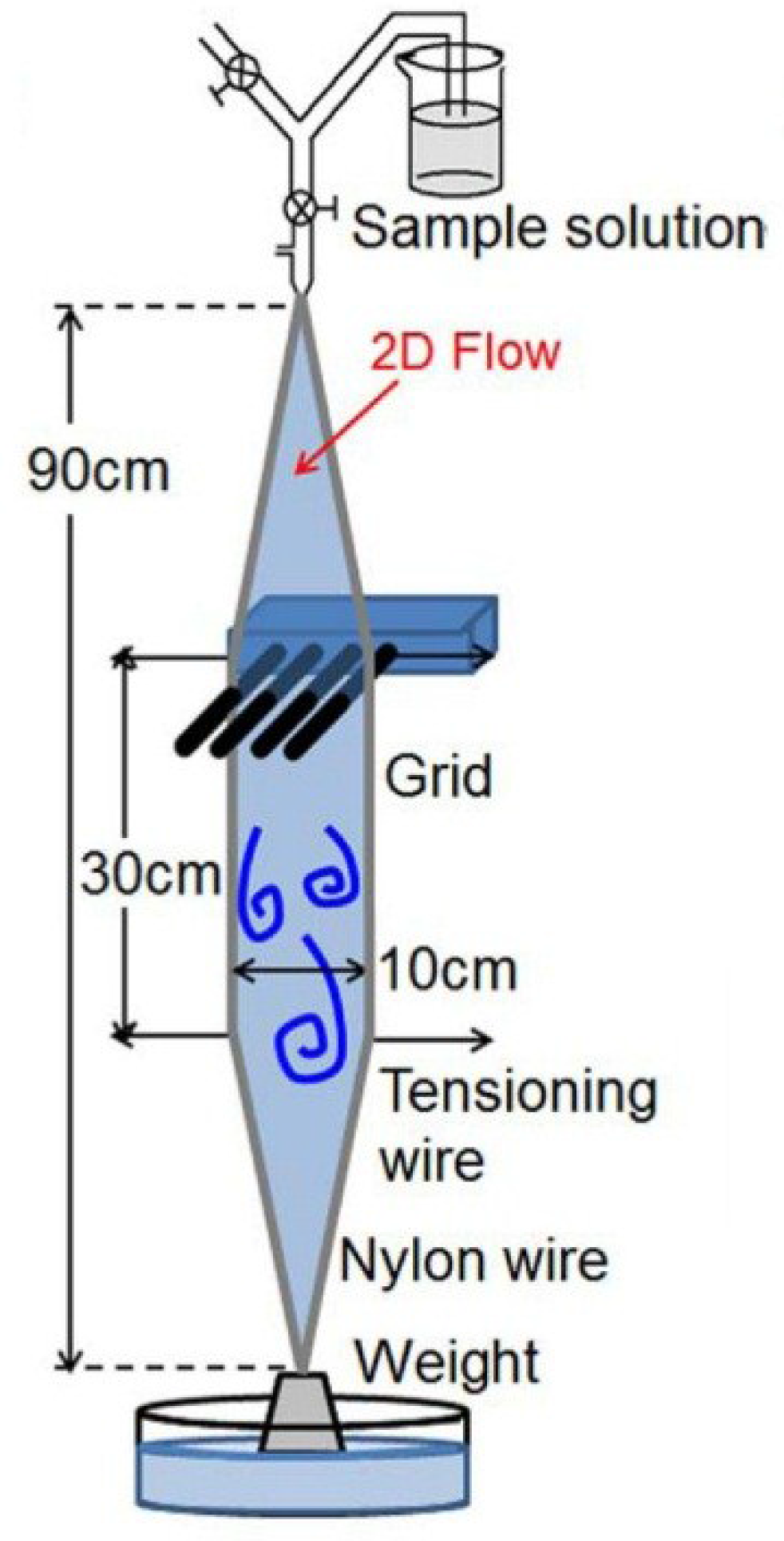
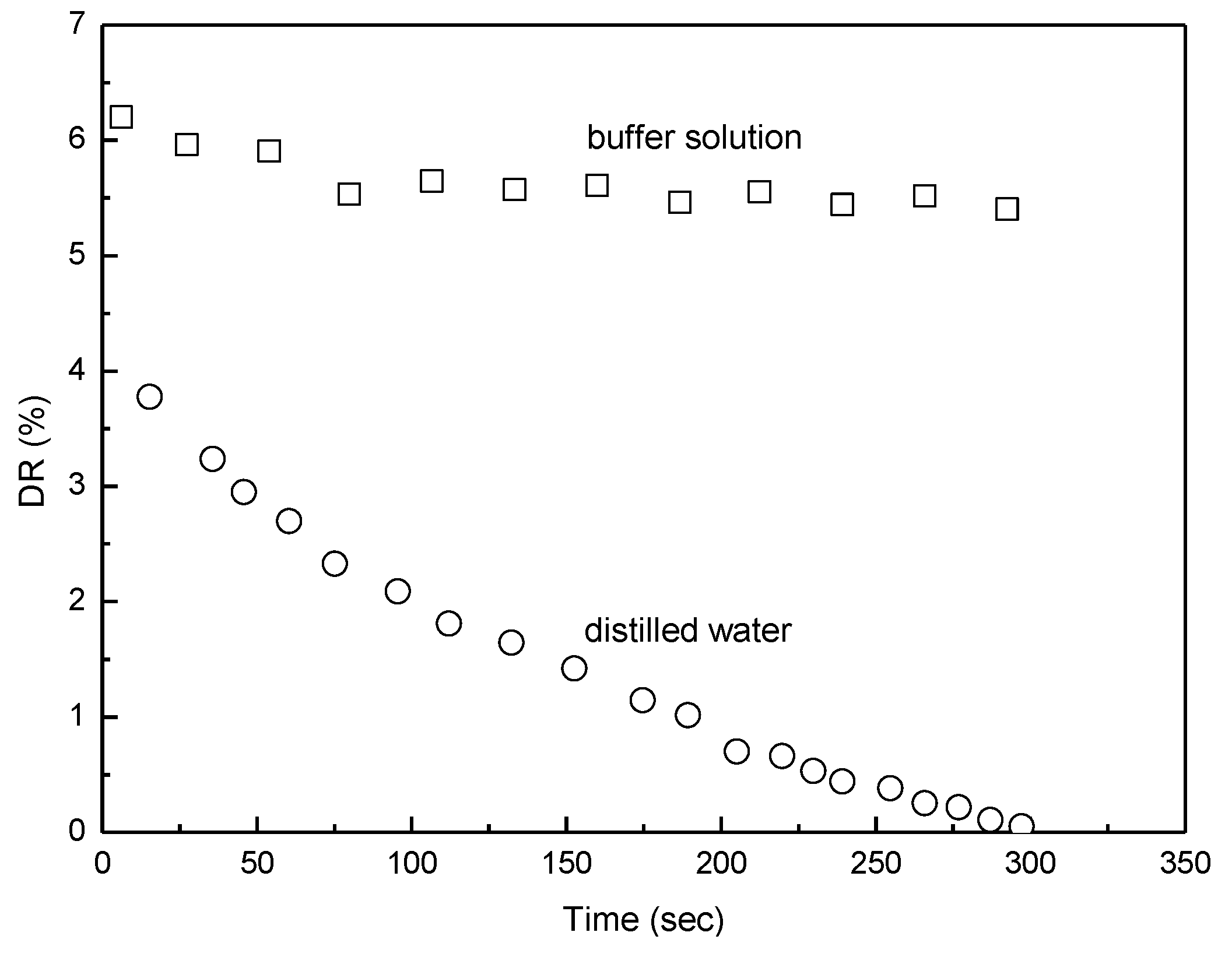
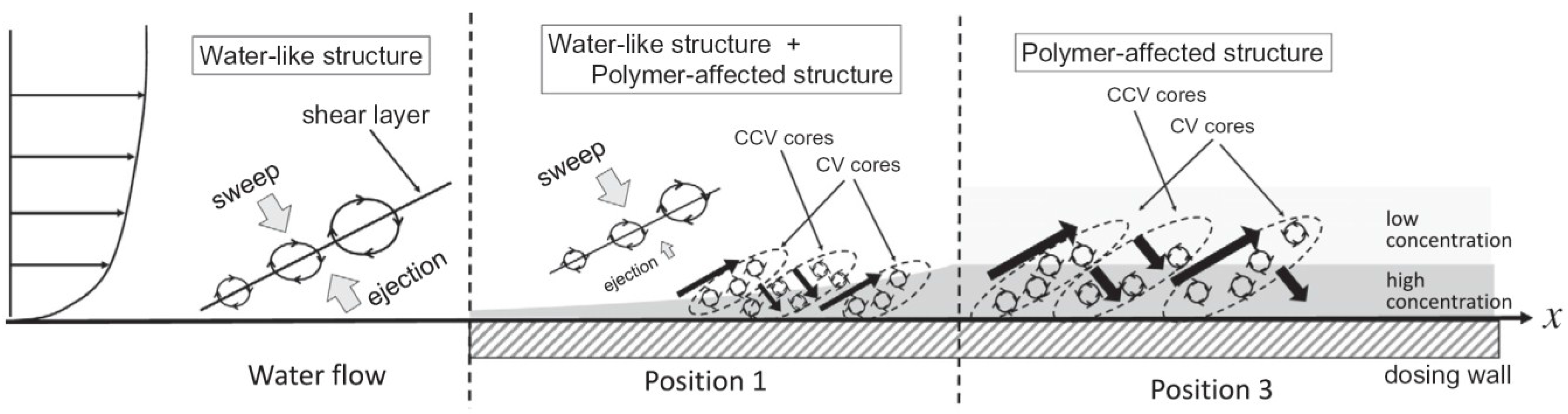
3. Rotating Disk Flow
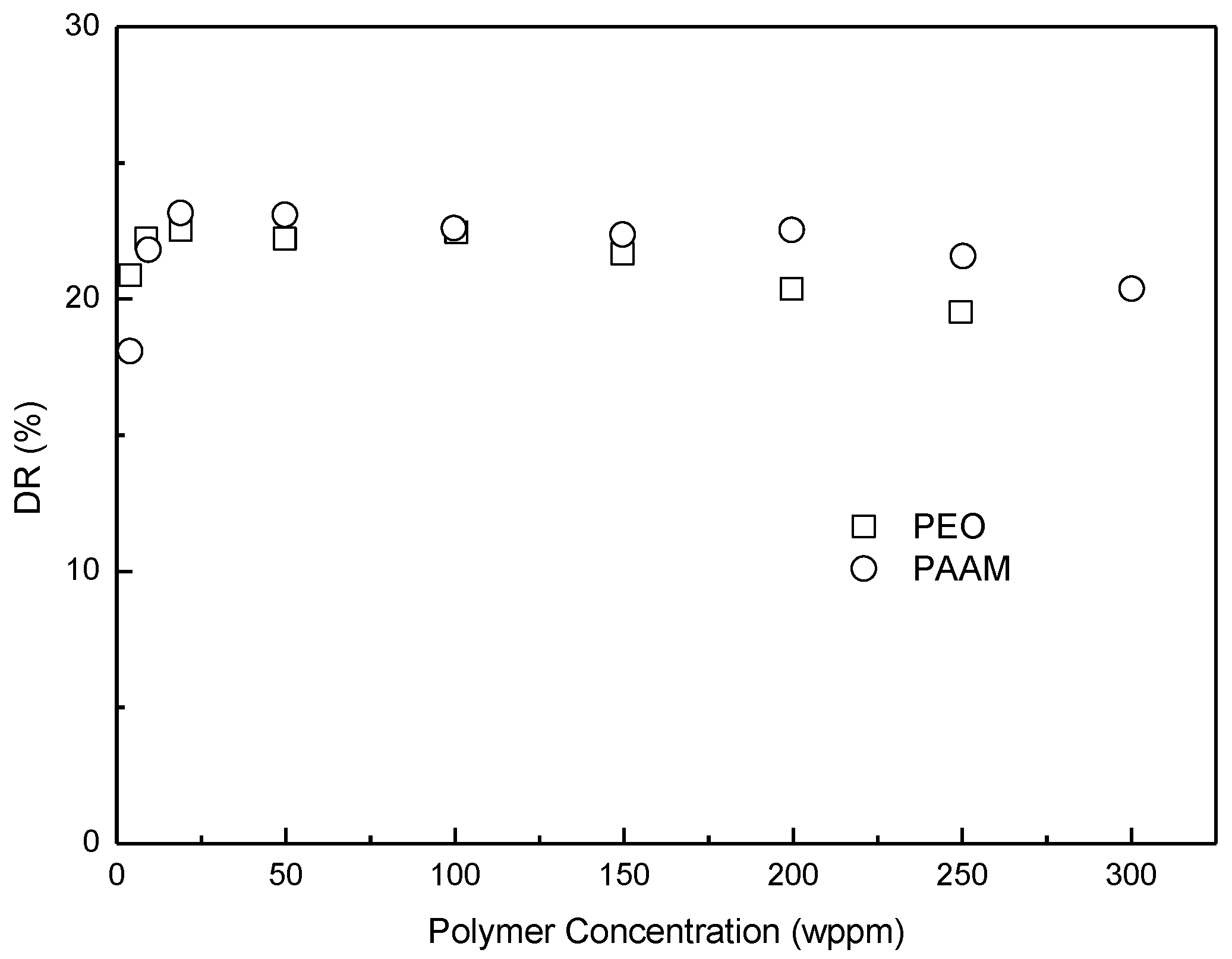
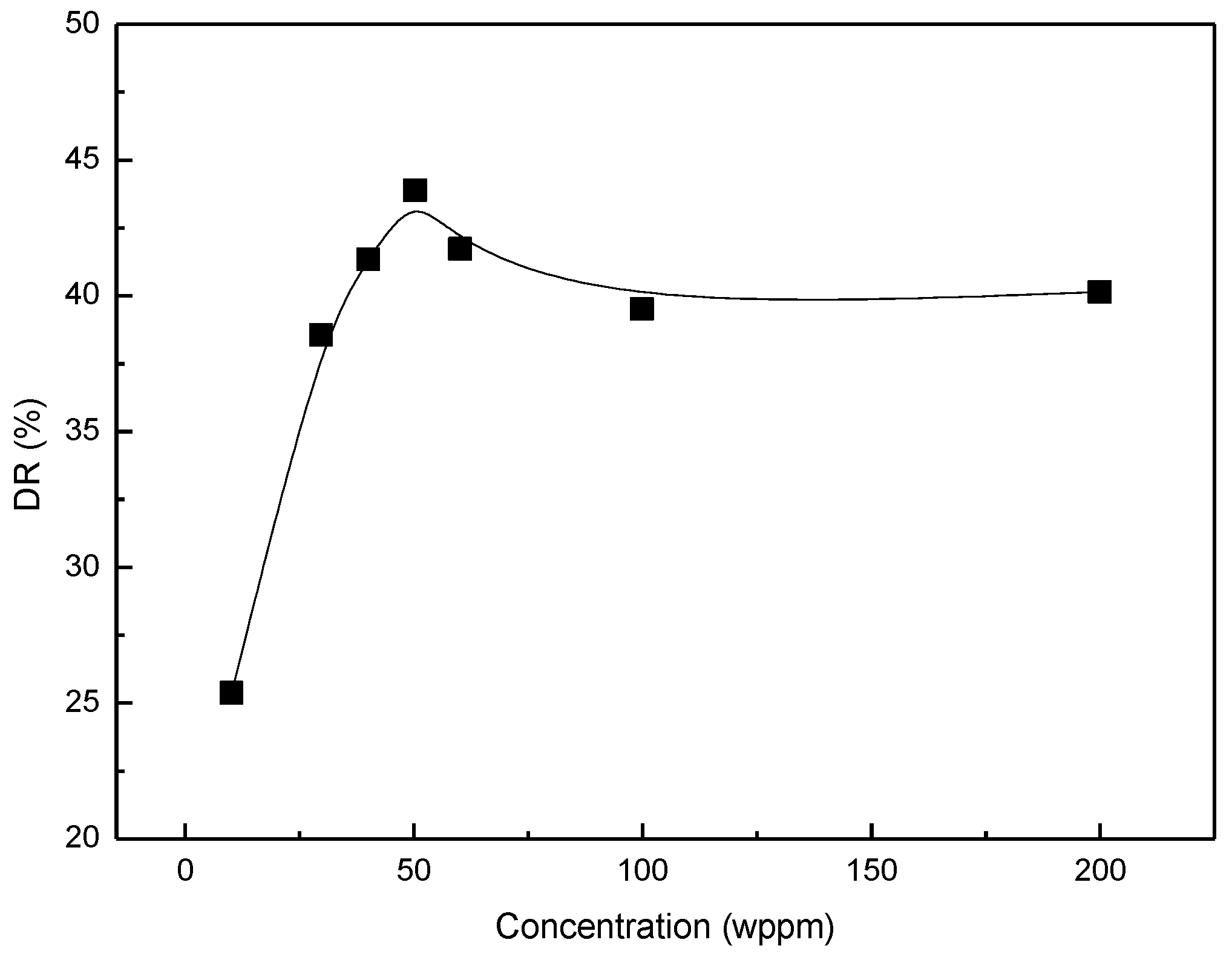
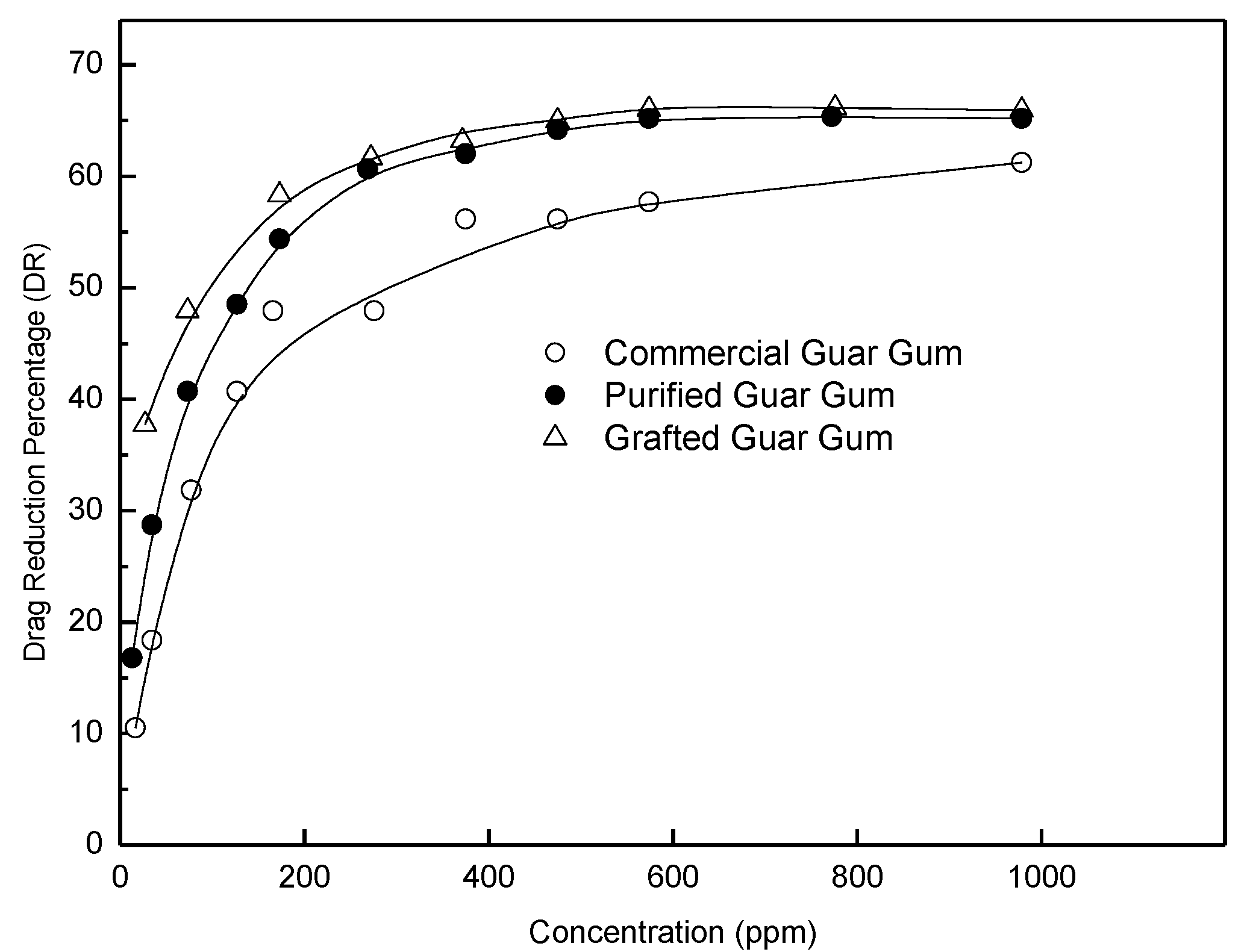
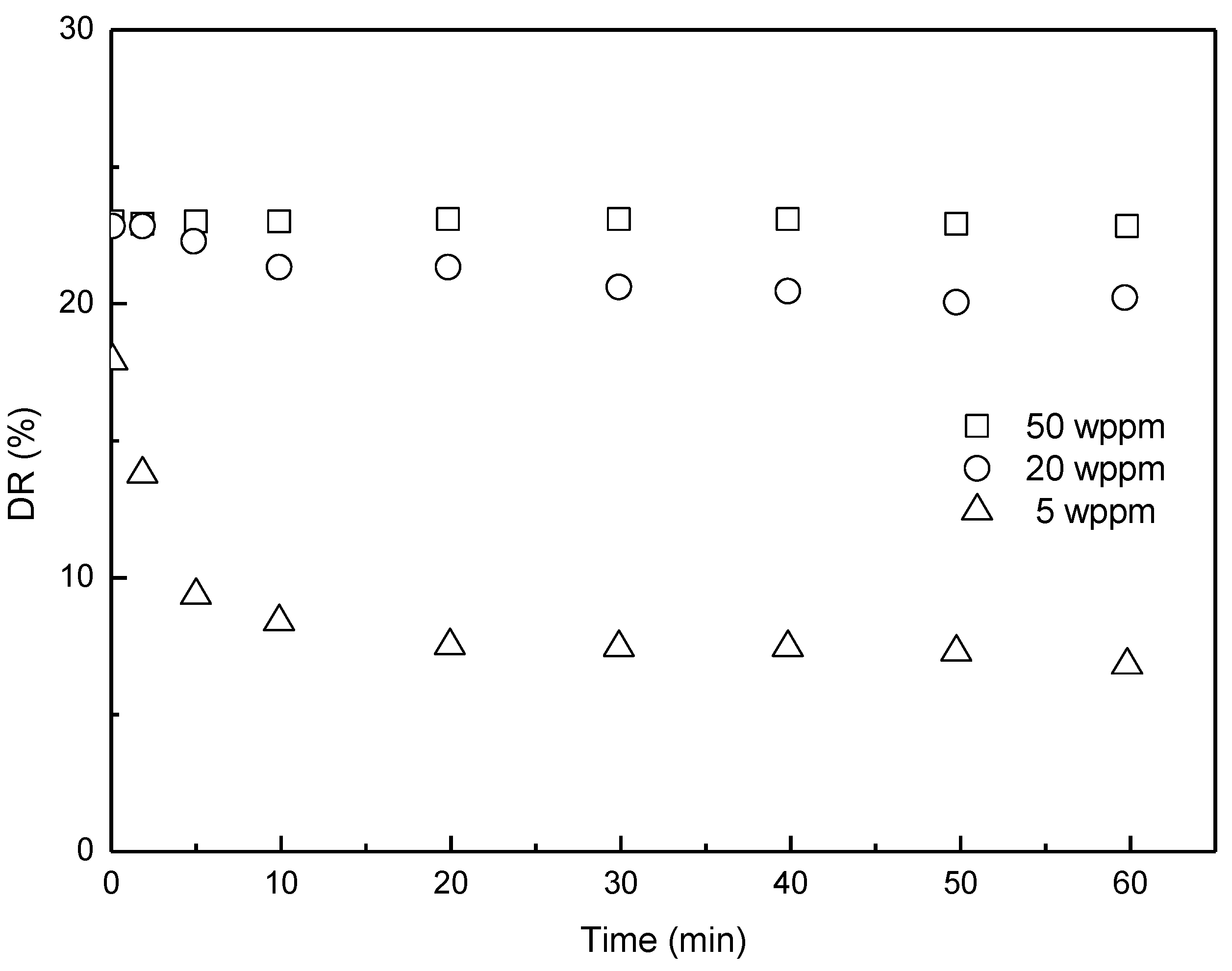
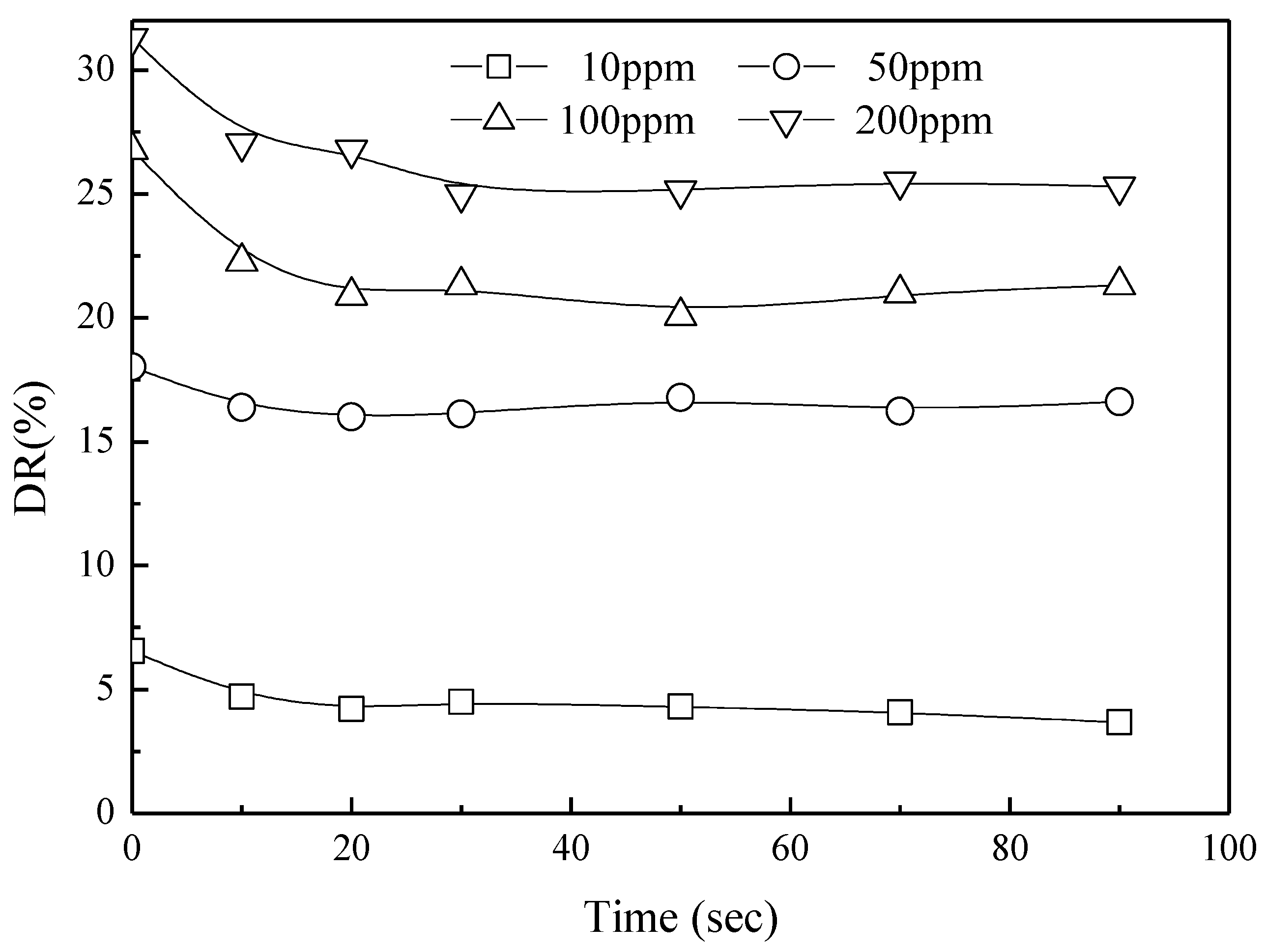
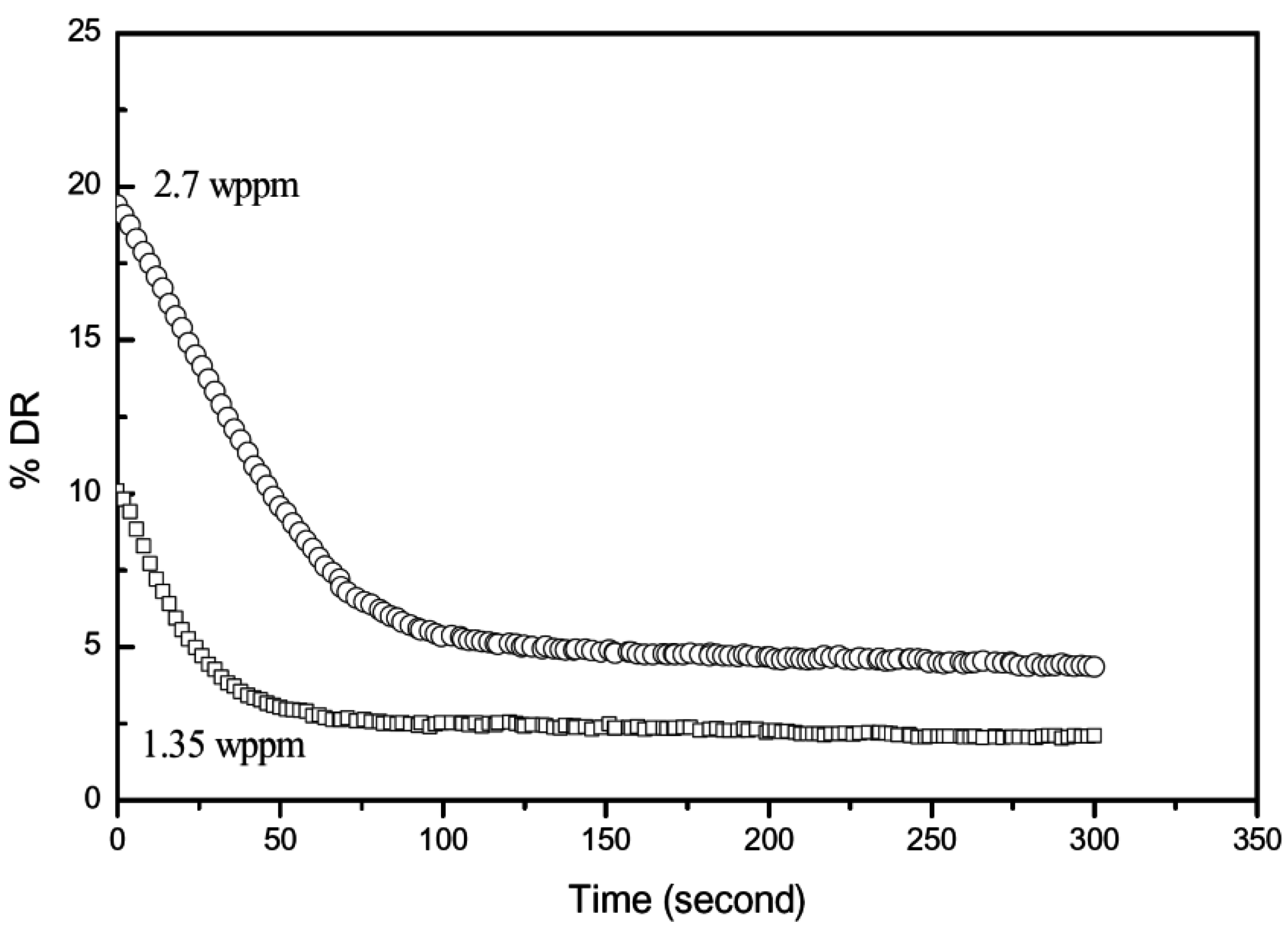
4. Polymer Concentration Effect
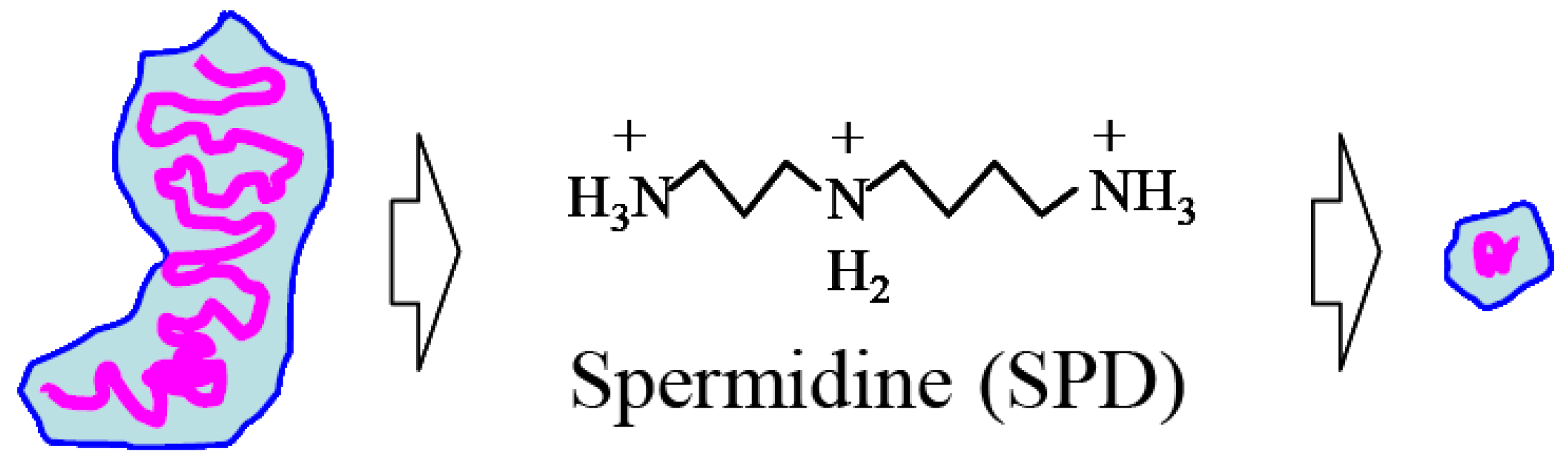
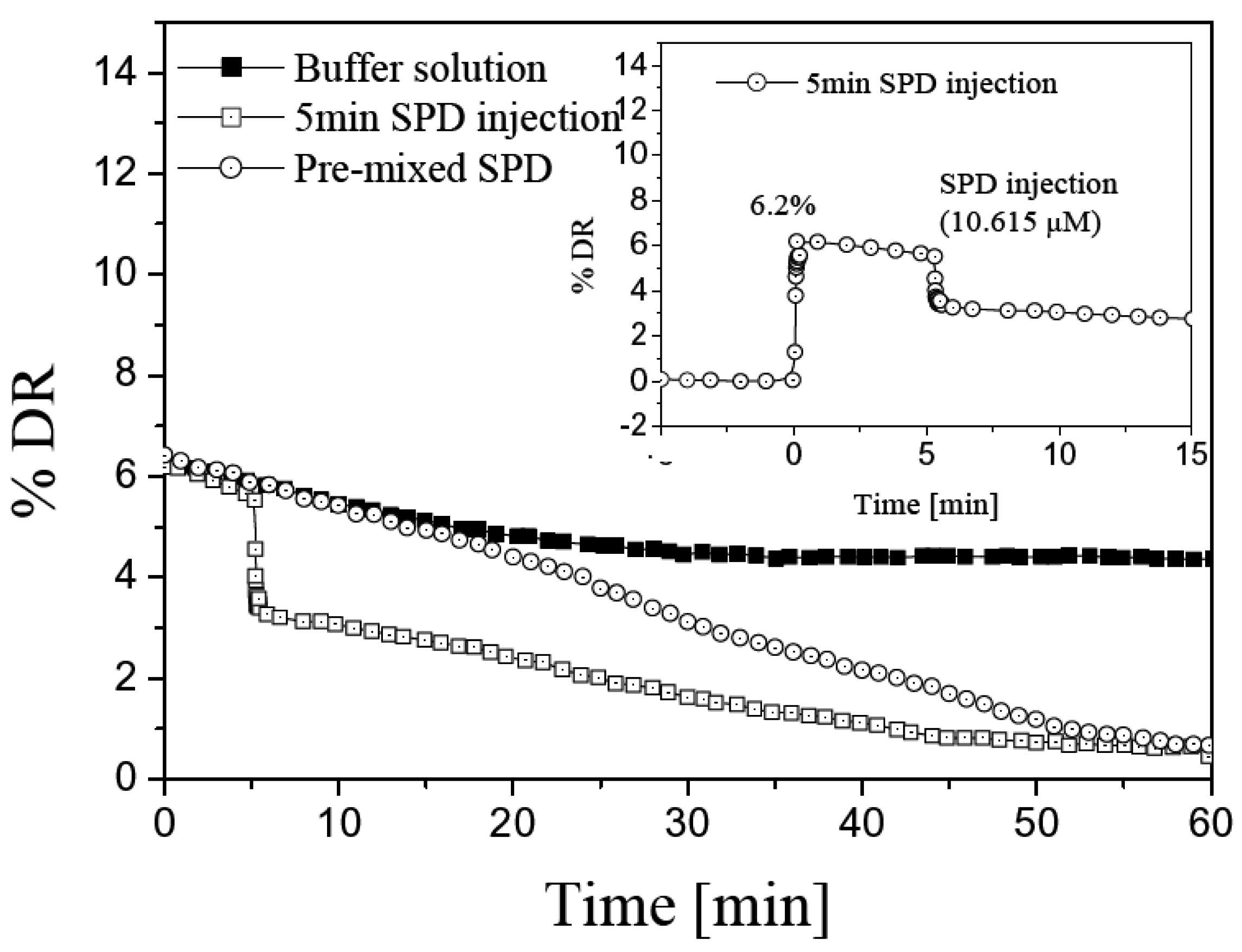
5. Polymer Chain Conformation Effect
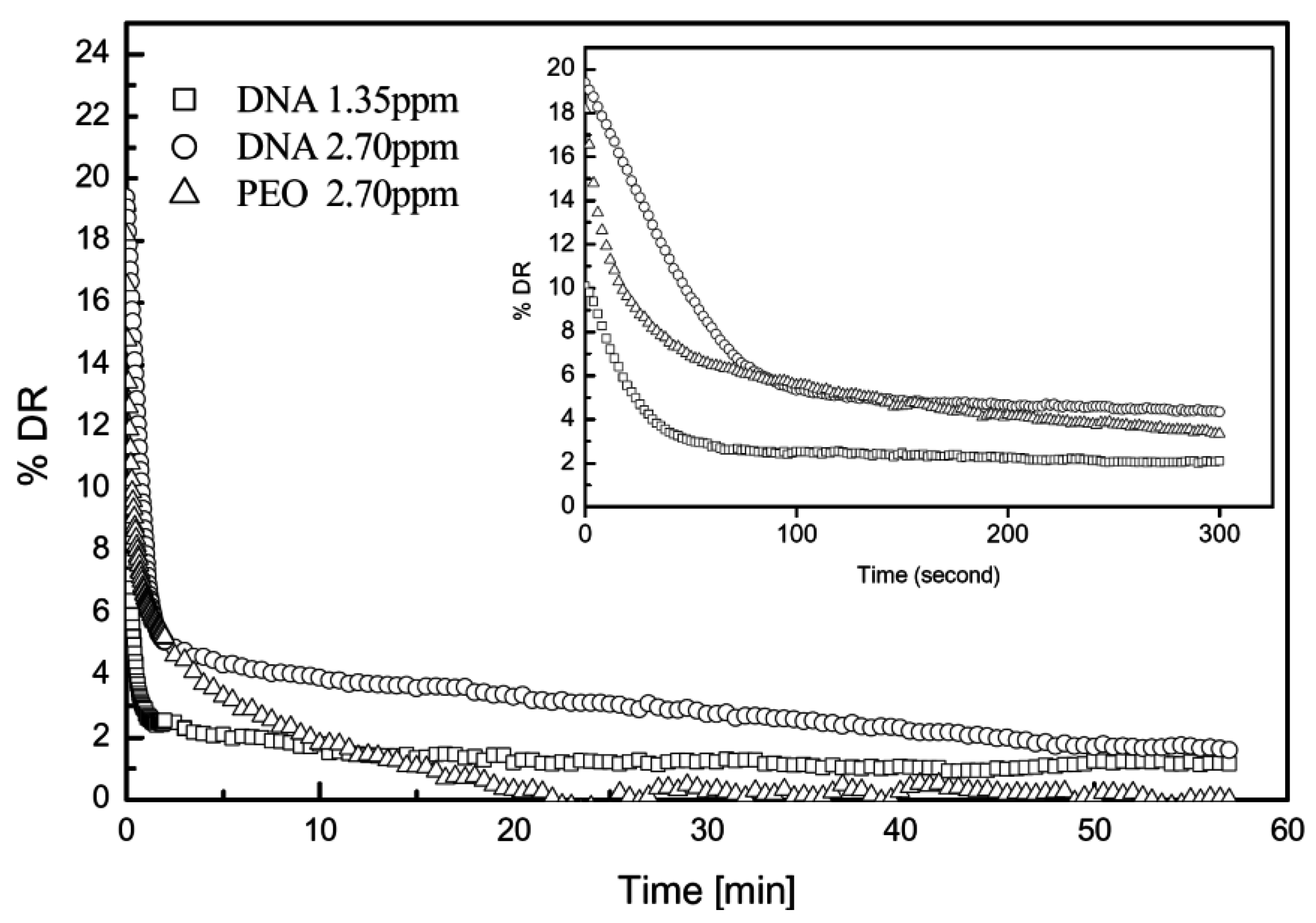
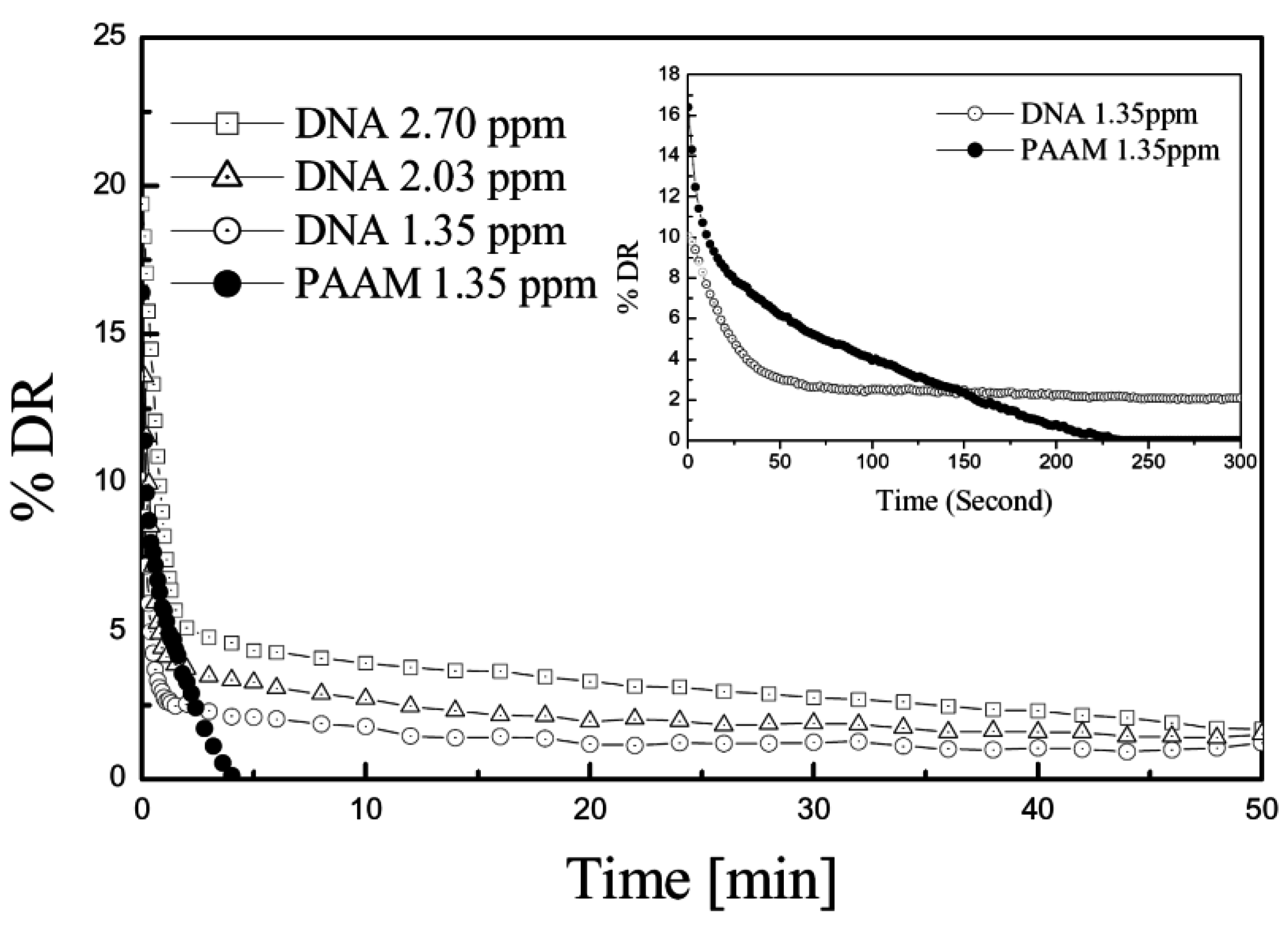
6. Molecular Weight and Polydispersity Effect
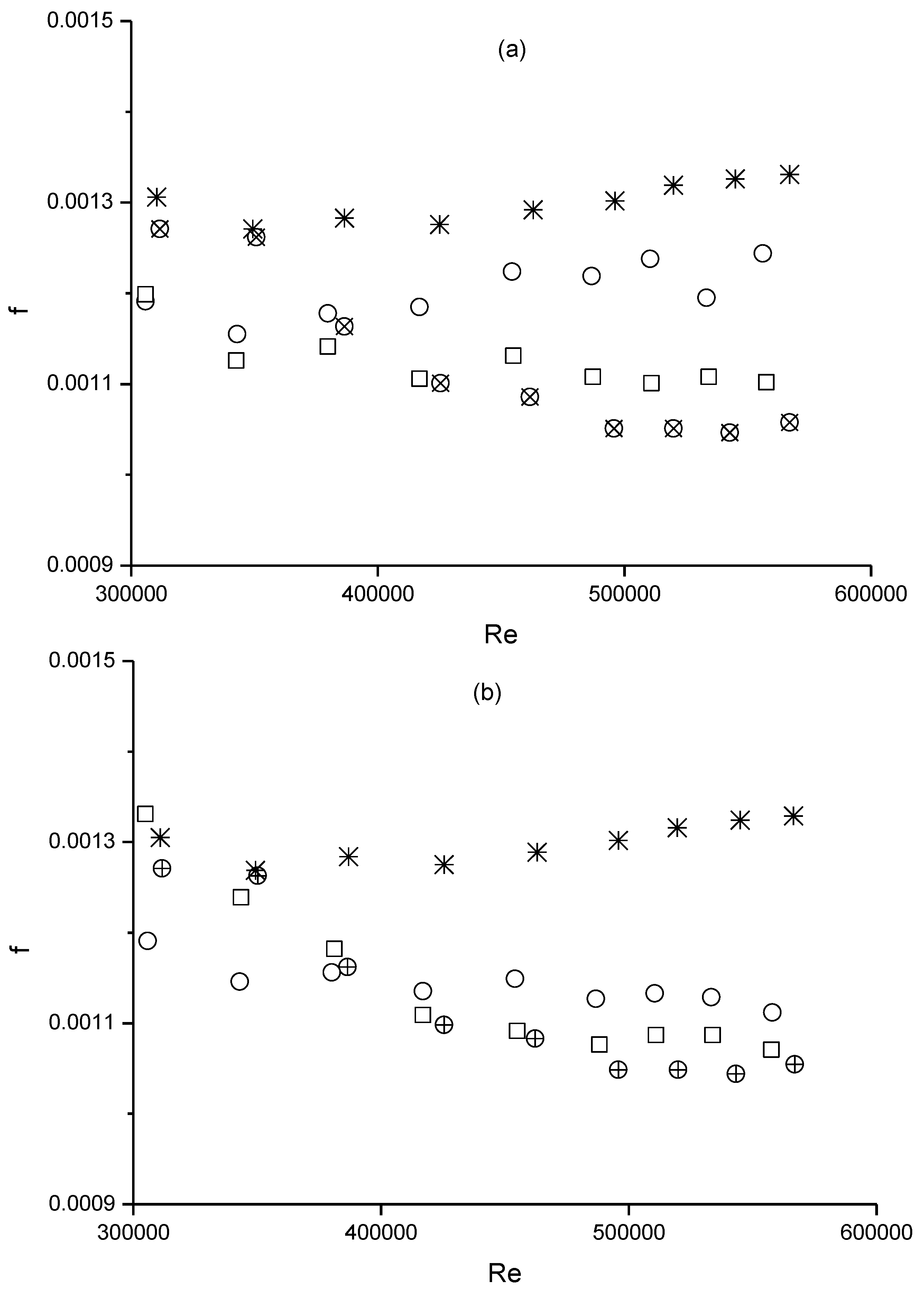
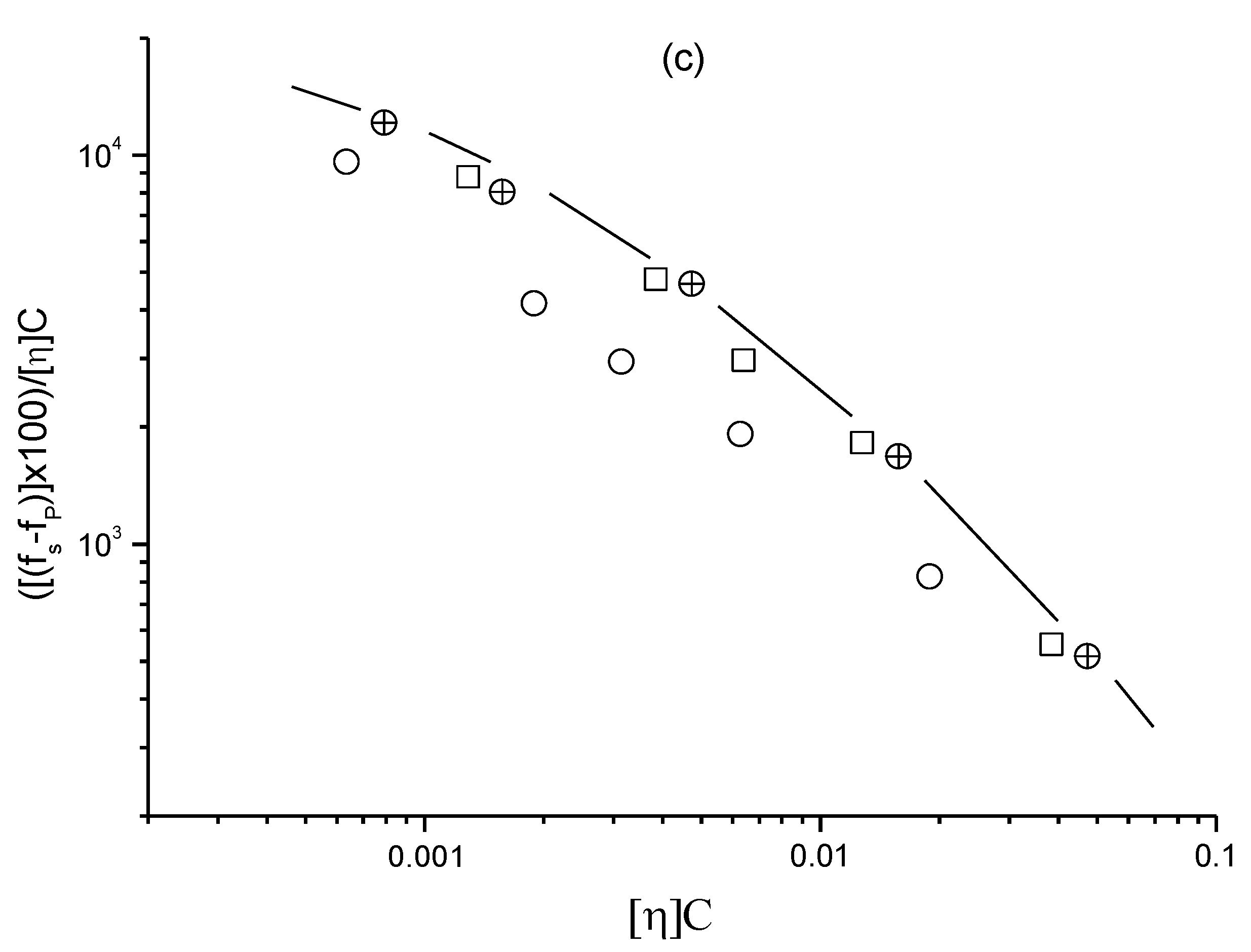
7. Reynolds Number Effect
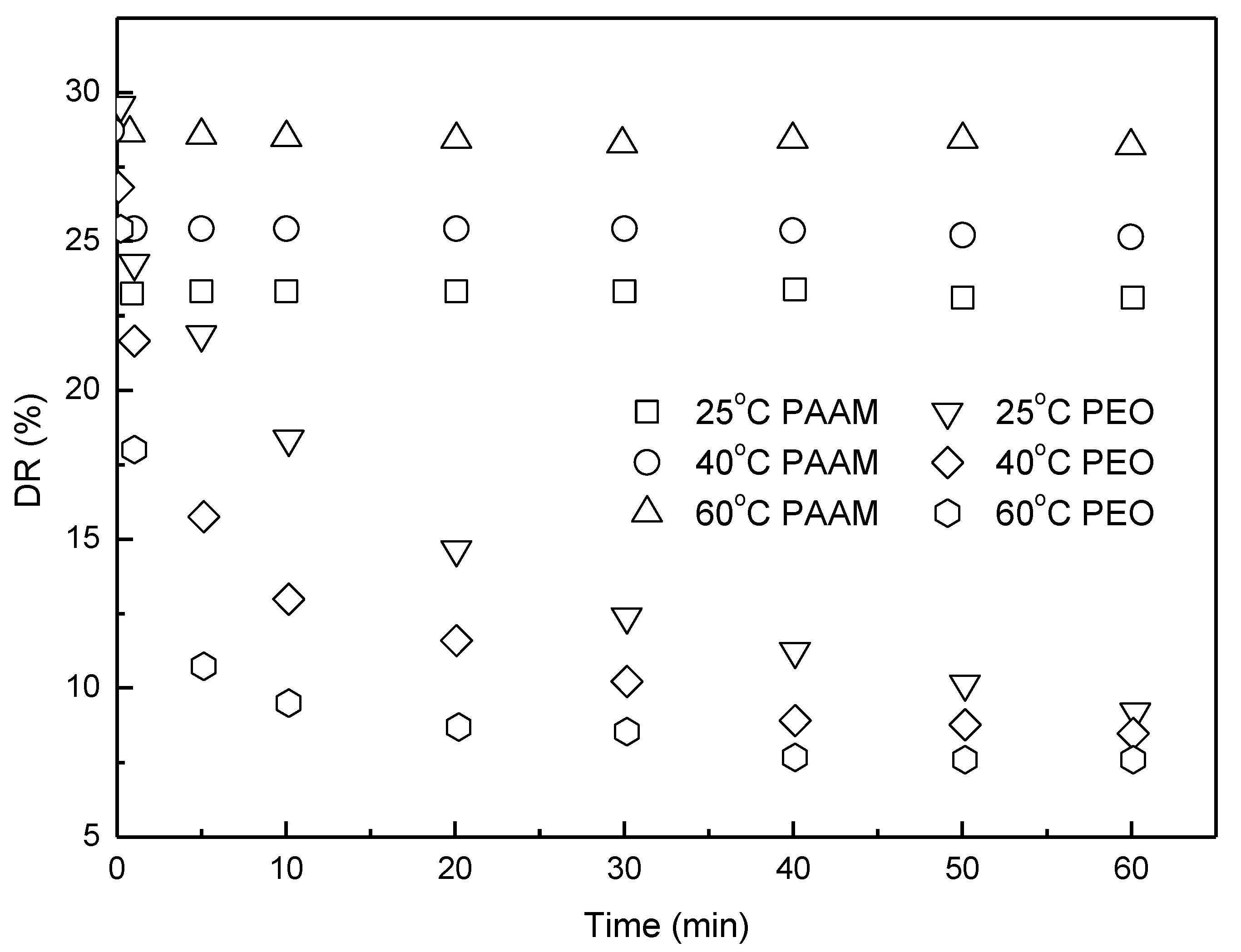
8. Temperature Effect
9. Conclusion
Acknowledgments
References
- Ranade, V.V.; Mashelkar, R.A. Turbulent mixing in dilute polymer-solutions. Chem. Eng. Sci. 1993, 48, 1619–1628. [Google Scholar] [CrossRef]
- Abdulbari, H.A.; Shabirin, A.; Abdurrahman, H.N. Bio-polymers for improving liquid flow in pipelines—A review and future work opportunities. J. Ind. Eng. Chem. 2014, 20, 1157–1170. [Google Scholar] [CrossRef]
- Abubakar, A.; Al-Wahaibi, T.; Al-Wahaibi, Y.; Al-Hashmi, A.R.; Al-Ajmi, A. Roles of drag reducing polymers in single- and multi-phase flows. Chem. Eng. Res. Des. 2014, 92, 2153–2181. [Google Scholar] [CrossRef]
- Ilg, P.; de Angelis, E.; Karlin, I.V.; Casciola, C.M.; Succi, S. Polymer dynamics in wall turbulent flow. Europhys. Lett. 2002, 58, 616–622. [Google Scholar] [CrossRef]
- Manzhai, V.N.; Nasibullina, Y.R.; Kuchevskaya, A.S.; Filimoshkin, A.G. Physico-chemical concept of drag reduction nature in dilute polymer solutions (the Toms effect). Chem. Eng. Process. 2014, 80, 38–42. [Google Scholar] [CrossRef]
- Dosunmu, I.T.; Shah, S.N. Turbulent flow behavior of surfactant solutions in straight pipes. J. Petrolem Sci. Eng. 2014, 124, 323–330. [Google Scholar] [CrossRef]
- Yang, J.W.; Park, H.; Chun, H.H.; Ceccio, S.L.; Perlin, M.; Lee, I. Development and performance at high Reynolds number of a skin-friction reducing marine paint using polymer additives. Ocean Eng. 2014, 84, 183–193. [Google Scholar] [CrossRef]
- Fu, Z.; Otsuki, T.; Motozawa, M.; Kurosawa, T.; Yu, B.; Kawaguchi, Y. Experimental investigation of polymer diffusion in the drag-reduced turbulent channel flow of inhomogeneous solution. Int. J. Heat. Mass. Trans. 2014, 77, 860–873. [Google Scholar] [CrossRef]
- Tamano, S.; Kitao, T.; Morinishi, Y. Turbulent drag reduction of boundary layer flow with non-ionic surfactant injection. J. Fluid Mech. 2014, 749, 367–403. [Google Scholar] [CrossRef]
- Tamano, S.; Ikarashi, H.; Morinishi, Y.; Taga, K. Drag reduction and degradation of nonionic surfactant solutions with organic acid in turbulent pipe flow. J. Non-Newton. Fluid Mech. 2015, 215, 1–7. [Google Scholar] [CrossRef]
- Suzuki, H.; Shingo, T.; Komoda, Y. Direct numerical simulation of the turbulent channel flow of a polymer solution. Int. J. Refrig. 2010, 33, 1632–1638. [Google Scholar] [CrossRef]
- Steele, A.; Bayer, I.S.; Loth, E. Pipe flow drag reduction effects from carbon nanotube additives. Carbon 2014, 77, 1183–1186. [Google Scholar] [CrossRef]
- Boffetta, G.; Mazzino, A.; Musacchio, S.; Vozella, L. Polymer heat transport enhancement in thermal convection: The case of Rayleigh-Taylor turbulence. Phys. Rev. Lett. 2010, 104, 184501. [Google Scholar] [CrossRef] [PubMed]
- Burger, E.D.; Chorn, L.G. Studies of drag reduction conducted over a broad range of pipeline conditions when flowing prudhoe bay crude oil. J. Rheol. 1980, 24, 603–626. [Google Scholar] [CrossRef]
- Usui, H.; Li, L.; Suzuki, H. Rheology and pipeline transportation of dense fly ash-water slurry. Korea-Aust. Rheol. J. 2001, 13, 47–54. [Google Scholar]
- Greene, H.L.; Mostardi, R.F.; Nokes, R.F. Effects of drag reducing polymers on initiation of atherosclerosis. Polym. Eng. Sci. 1980, 20, 499–504. [Google Scholar] [CrossRef]
- Marhefka, J.N.; Marascalco, P.J.; Chapman, T.M.; Russell, A.J.; Kameneva, M.V. Poly(N-vinylformamide)—A drag-reducing polymer for biomedical applications. Biomacromolecules 2006, 7, 1597–1603. [Google Scholar] [CrossRef] [PubMed]
- Fontaine, A.A.; Deutsch, S.; Brungart, T.A.; Petrie, H.L.; Fenstermacker, M. Drag reduction by coupled systems: Microbubble injection with homogeneous polymer and surfactant solutions. Exp. Fluids 1999, 26, 397–403. [Google Scholar] [CrossRef]
- Lumley, J.L. Drag reduction in turbulent flow by polymer additives. J. Polym. Sci. 1973, 7, 263–290. [Google Scholar] [CrossRef]
- Astarita, G. Possible interpretation of mechanism of drag reduction in viscoelastic liquids. Ind. Eng. Chem. Fundam. 1965, 4, 354–356. [Google Scholar] [CrossRef]
- Gadd, G.E. Turbulence damping and drag reduction produced by certain additives in water. Nature 1965, 206, 463–467. [Google Scholar] [CrossRef]
- Walsh, M. Theory of drag reduction in dilute high-polymer flows. Int. Shipbuilding Prog. 1967, 14, 134. [Google Scholar]
- Gadd, G.E. Reduction of turbulent drag in liquids. Nat. Phys. Sci. 1971, 230, 29–31. [Google Scholar] [CrossRef]
- Kuo, Y.; Tanner, R.I. A burgers-type model of turbulent decay in a non-newtonian fluid. J. Appl. Mech. 1972, 39, 661–666. [Google Scholar] [CrossRef]
- Gordon, R.J.; Balakrishnan, C. Vortex inhibition: A new viscoelastic effect with importance in drag reduction and polymer characterization. J. Appl. Polym. Sci. 1972, 16, 1629–1639. [Google Scholar] [CrossRef]
- Armstrong, R.; Jhon, M.S. Turbulence induced change in the conformation of polymer molecules. J. Chem. Phys. 1983, 79, 3143–3147. [Google Scholar] [CrossRef]
- Fraenkel, G.K. Visco-elastic effect in solutions of simple particles. J. Chem. Phys. 1952, 20, 642–647. [Google Scholar] [CrossRef]
- Brostow, W. Drag reduction and mechanical degradation in polymer solutions in flow. Polymer 1983, 24, 631–638. [Google Scholar] [CrossRef]
- Brostow, W.; Majumdar, S.; Singh, R.P. Drag reduction and solvation in polymer solutions. Macromol. Rapid. Commun. 1999, 20, 144–147. [Google Scholar] [CrossRef]
- Tabor, M.; de Gennes, P.G. A cascade theory of drag reduction. Europhys. Lett. 1986, 2, 519–522. [Google Scholar] [CrossRef]
- Valente, P.C.; da Silva, C.B.; Pinho, F.T. The effect of viscoelasticity on the turbulent kinetic energy cascade. J. Fluid Mech. 2014, 760, 39–62. [Google Scholar] [CrossRef]
- Jourdan, L.; Knapp, Y.; Oliver, F.; Guibergia, J.P. The effect of drag-reducing polymer additives on wall-pressure fluctuations in turbulent channel flows. Eur. J. Mech. B-Fluid. 1998, 17, 105–136. [Google Scholar] [CrossRef]
- Gillissen, J.J.J.; Boersma, B.J.; Mortensen, P.H.; Andersson, H.I. Fibre-induced drag reduction. J. Fluid Mech. 2008, 602, 209–218. [Google Scholar] [CrossRef]
- Paschkewitz, J.S.; Dimitropoulos, C.D.; Hou, Y.X.; Somandepalli, V.S.R.; Mungal, M.G.; Shaqfeh, E.S.G.; Moin, P. An experimental and numerical investigation of drag reduction in a turbulent boundary layer using a rigid rodlike polymer. Phys. Fluids 2005, 17. [Google Scholar] [CrossRef]
- Choi, H.J.; Lim, S.T.; Lai, P.Y.; Chan, C.K. Turbulent drag reduction and degradation of DNA. Phys. Rev. Lett. 2002, 89, 088302. [Google Scholar] [CrossRef] [PubMed]
- Brostow, W. Drag reduction in flow: Review of applications, mechanism and prediction. J. Ind. Eng. Chem. 2008, 14, 409–416. [Google Scholar] [CrossRef]
- Pereira, A.S.; Soares, E.J. Polymer degradation of dilute solutions in turbulent drag reducing flows in a cylindrical double gap rheometer device. J. Non-Newton. Fluid Mech. 2012, 179, 9–22. [Google Scholar]
- Chemloul, N.S. Experimental study of the drag reduction in turbulent pipe flow. Energy 2014, 64, 818–827. [Google Scholar] [CrossRef]
- Karami, H.R.; Mowla, D. A general model for predicting drag reduction in crude oil pipelines. J. Petrol. Sci. Eng. 2013, 111, 78–86. [Google Scholar] [CrossRef]
- Motozawa, M.; Sawada, T.; Ishitsuka, S.; Iwamoto, K.; Ando, H.; Senda, T.; Kawaguchi, Y. Experimental investigation on streamwise development of turbulent structure of drag-reducing channel flow with dosed polymer solution from channel wall. Int. J. Heat Fluid Flow 2014, 50, 51–62. [Google Scholar] [CrossRef]
- Moussa, T.; Tiu, C.; Sridhar, T. Effect of solvent on polymer degradation in turbulent-flow. J. Non-Newton. Fluid Mech. 1993, 48, 261–284. [Google Scholar] [CrossRef]
- Kim, C.A.; Jo, D.S.; Choi, H.J.; Kim, C.B.; Jhon, M.S. A high-precision rotating disk apparatus for drag reduction characterization. Polym. Test. 2001, 20, 43–48. [Google Scholar] [CrossRef]
- Ricco, P.; Hahn, S. Turbulent drag reduction through rotating discs. J. Fluid Mech. 2013, 722, 267–290. [Google Scholar] [CrossRef]
- Wise, D.J.; Alvarenga, C.; Ricco, P. Spinning out of control: Wall turbulence over rotating discs. Phys. Fluids 2014, 26. [Google Scholar] [CrossRef]
- Wise, D.J.; Ricco, P. Turbulent drag reduction through oscillating discs. J. Fluid Mech. 2014, 746, 536–564. [Google Scholar] [CrossRef]
- Sreedhar, I.; Jain, G.; Srinivas, P.; Reddy, K.S.K. Polymer induced turbulent drag reduction using pressure and gravity-driven methods. Korean J. Chem. Eng. 2014, 31, 568–573. [Google Scholar] [CrossRef]
- Burnishev, Y.; Steinberg, V. Early turbulence in von Karman swirling flow of polymer solutions. Europhys. Lett. 2015, 109. [Google Scholar] [CrossRef]
- Eskin, D. Applicability of a Taylor-Couette device to characterization of turbulent drag reduction in a pipeline. Chem. Eng. Sci. 2014, 116, 275–283. [Google Scholar] [CrossRef]
- Moosaie, A.; Manhart, M. Direct Monte Carlo simulation of turbulent drag reduction by rigid fibers in a channel flow. Acta Mech. 2013, 224, 2385–2413. [Google Scholar] [CrossRef]
- Wang, S.N.; Graham, M.D.; Hahn, F.J.; Xi, L. Time-series and extended Karhunen-Loeve analysis of turbulent drag reduction in polymer solutions. AIChE J. 2014, 60, 1460–1475. [Google Scholar] [CrossRef]
- Amrouchene, Y.; Kellay, H. Polymer in 2D turbulence: Suppression of large scale fluctuation. Phys. Rev. Lett. 2002, 89. [Google Scholar] [CrossRef]
- Hidema, R.; Suzuki, H.; Hisamatsu, S.; Komoda, Y. Characteristic scales of two-dimensional turbulence in polymer solutions. AIChE J. 2014, 60, 1854–1862. [Google Scholar] [CrossRef]
- Jun, Y.; Zhang, J.; Wu, X.L. Polymer effect on small and large scale two-dimensional turbulece. Phys. Rev. Lett. 2006, 96. [Google Scholar] [CrossRef]
- Sung, J.H.; Kim, C.A.; Choi, H.J.; Hur, B.K.; Kim, J.G.; Jhon, M.S. Turbulent drag reduction efficiency and mechanical degradation of poly(acrylamide). J. Macromol. Sci. Phys. 2004, B43, 507–518. [Google Scholar] [CrossRef]
- Zhang, K.; Choi, H.J.; Jang, C.H. Turbulent drag reduction characteristics of poly(acrylamide-co-acrylic acid) in a rotating disk apparatus. Colloid Polym. Sci. 2011, 289, 1821–1827. [Google Scholar] [CrossRef]
- Brostow, W.; Drewniak, M. Computer simulations of chain conformations in dilute polymer solutions under shear flow. J. Chem. Phys. 1996, 105, 7135–7139. [Google Scholar] [CrossRef]
- Ram, P.S.; Pal, S.; Krishnamoorthy, S.; Adhikary, P.; Ali, A.S. High-technology materials based on modified polysaccharides. Pure Appl. Chem. 2009, 81, 525–547. [Google Scholar]
- Halake, K.; Birajdar, M.; Kim, B.S.; Bae, H.; Lee, C.C.; Kim, Y.J.; Kim, S.; Kim, H.J.; Ahn, S.; An, Y.; et al. Recent application developments of water-soluble synthetic polymers. J. Ind. Eng. Chem. 2014, 20, 3913–3918. [Google Scholar] [CrossRef]
- Kim, C.A.; Choi, H.J.; Kim, C.B.; Jhon, M.S. Drag reduction characteristics of polysaccharide xanthan gum. Macromol. Rapid Commun. 1998, 19, 419–422. [Google Scholar] [CrossRef]
- Lim, S.T.; Choi, H.J.; Biswal, D.; Singh, R.P. Turbulent drag reduction characteristics of amylopectin and its derivative. E-Polymers 2004, 4. [Google Scholar] [CrossRef]
- Lim, S.T.; Choi, H.J.; Lee, S.Y.; So, J.S.; Chan, C.K. Gamma-DNA induced turbulent drag reduction and its characteristics. Macromolecules 2003, 36, 5348–5354. [Google Scholar] [CrossRef]
- Hong, C.H.; Zhang, K.; Choi, H.J.; Yoon, S.M. Mechanical degradation of polysaccharide guar gum under turbulent flow. J. Ind. Eng. Chem. 2010, 16, 178–180. [Google Scholar] [CrossRef]
- White, C.M.; Somandepalli, V.S.R.; Mungal, M.G. The turbulence structure of drag-reduced boundary layer flow. Exp. Fluids 2004, 36, 62–69. [Google Scholar] [CrossRef]
- Kim, C.A.; Choi, H.J.; Sung, J.H.; Lee, H.M.; Jhon, M.S. Effect of solubility parameter of polymer-solvent pair on turbulent drag reduction. Macromol. Symp. 2005, 222, 169–174. [Google Scholar] [CrossRef]
- Sohn, J.I.; Kim, C.A.; Choi, H.J.; Jhon, M.S. Drag-reduction effectiveness of xanthan gum in a rotating disk apparatus. Carbohyd. Polym. 2001, 45, 61–68. [Google Scholar] [CrossRef]
- Lim, S.T.; Choi, H.J.; Chan, C.K. Effect of turbulent flow on coil-globule transition of lambda-DNA. Macromol. Rapid. Commun. 2005, 26, 1237–1240. [Google Scholar] [CrossRef]
- Virk, P.S. Drag reduction fundamentals. AIChE J. 1975, 21, 625–656. [Google Scholar] [CrossRef]
- McCormick, C.L.; Hester, R.D.; Morgan, S.E.; Safieddine, A.M. Water-soluble copolymers .31. Effects of molecular-parameters, solvation, and polymer associations on drag reduction performance. Macromolecules 1990, 23, 2132–2139. [Google Scholar] [CrossRef]
- McCormick, C.L.; Hester, R.D.; Morgan, S.E.; Safieddine, A.M. Water-soluble copolymers .30. Effects of molecular structure on drag reduction efficiency. Macromolecules 1990, 23, 2124–2131. [Google Scholar] [CrossRef]
- Gampert, B.; Wagner, P. The Influence of Polymer Additives on Velocity and Temperature Fields; Springer-Verlag: Berlin, Germany, 1985. [Google Scholar]
- Morgan, S.E.; McCormick, C.L. Water-Soluble copolymers XXXII: Macromolecular drag reduction. A review of predictive theories and the effects of polymer structure. Prog. Polym. Sci. 1990, 15, 507–549. [Google Scholar] [CrossRef]
- Liaw, G.C.; Zakin, J.L.; Patterson, G.K. Effect of molecular parameters, solvation, and polymer associations on drag reductioin. AIChE J. 1971, 17, 391–397. [Google Scholar] [CrossRef]
- Zakin, J.L.; Hunston, D.L. Effect of polymer molecular variables on drag reduction. J. Macromol. Sci. Phys. 1980, 18, 795–814. [Google Scholar] [CrossRef]
- Choi, H.J.; Kim, C.A.; Jhon, M.S. Universal drag reduction characteristics of polyisobutylene in a rotating disk apparatus. Polymer 1999, 40, 4527–4530. [Google Scholar] [CrossRef]
- Virk, P.S.; Merrill, E.W.; Mickley, H.S.; Smith, K.A.; Mollo-Christensen, E.L. The Toms phenomenon: Turbulent pipe flow polymer solutions. J. Fluid Mech. 1967, 20, 305–328. [Google Scholar] [CrossRef]
- Myagchenkov, V.A.; Chichkanov, S.V. Toms effect in model and real systems. Russ. J. Appl. Chem. 2005, 78, 521–537. [Google Scholar] [CrossRef]
- Choi, H.J.; Jhon, M.S. Polymer-induced turbulent drag reduction. Ind. Eng. Chem. Res. 1996, 35, 2993–2998. [Google Scholar] [CrossRef]
- Koury, E.; Virk, P.S. Drag reduction by polymer solutions in a riblet-lined pipe. Appl. Sci. Res. 1995, 54, 323–347. [Google Scholar] [CrossRef]
- Interthal, W.; Wilski, H. Drag reduction experiments with very large pipes. Colloid Polym. Sci. 1985, 263, 217–229. [Google Scholar] [CrossRef]
- Lim, S.T.; Hong, C.H.; Choi, H.J.; Lai, P.-Y.; Chan, C.K. Polymer turbulent drag reduction near the theta point. Europhys. Lett. 2007, 80, 58003. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hong, C.H.; Jang, C.H.; Choi, H.J. Turbulent Drag Reduction with Polymers in Rotating Disk Flow. Polymers 2015, 7, 1279-1298. https://doi.org/10.3390/polym7071279
Hong CH, Jang CH, Choi HJ. Turbulent Drag Reduction with Polymers in Rotating Disk Flow. Polymers. 2015; 7(7):1279-1298. https://doi.org/10.3390/polym7071279
Chicago/Turabian StyleHong, Cheng Hai, Chun Hag Jang, and Hyoung Jin Choi. 2015. "Turbulent Drag Reduction with Polymers in Rotating Disk Flow" Polymers 7, no. 7: 1279-1298. https://doi.org/10.3390/polym7071279
APA StyleHong, C. H., Jang, C. H., & Choi, H. J. (2015). Turbulent Drag Reduction with Polymers in Rotating Disk Flow. Polymers, 7(7), 1279-1298. https://doi.org/10.3390/polym7071279