Surface-Induced Ordering on Model Liquid Crystalline Dendrimers

Abstract

The surface alignment of liquid crystalline dendrimers (LCDrs) is a key factor for many of their potential applications. Here, we present results from Monte Carlo simulations of LCDrs adsorbed on flat, impenetrable aligning substrates. A tractable coarse-grained force field for the inter-dendritic and the dendrimer-substrate interactions is introduced. We investigate the conformational and ordering properties of single, end-functionalized LCDrs under homeotropic, random (or degenerate) planar and unidirectional planar aligning substrates. Depending on the anchoring constrains to the mesogenic units of the LCDr and on temperature, a variety of stable ordered LCDr states, differing in their topology, are observed and analyzed. The influence of the dendritic generation and core functionality on the surface-induced ordering of the LCDrs are examined.

1. Introduction

Dendrimers are a class of monodisperse polymeric macromolecules with a well defined and highly branched three-dimensional architecture. Their well-defined structure and structural precision makes them outstanding candidates for the development of new types of multifunctional super-molecules and materials with applications in medicine and pharmacy [1,2,3], catalysis [4], electronics, optoelectronics, etc. [1,2,3,4,5,6,7].

Liquid crystalline dendrimers (LCDrs) are usually derived through functionalization of common dendrimers with low molar mass liquid crystal molecules (mesogens) [8,9,10,11]. The resulting super-molecules have proven to be an interesting new family of mesogenic compounds with dimensions and molecular weights between low molar mass mesogens and polymers [12]. Dendritic properties, like the absence of entanglements and the high local concentration of mesogenic groups, explain the interest in dendritic supermesogens as LC materials with an interesting balance in viscosity and thermodynamic stability [13,14]. Intensive research work has been conducted in recent years in the synthesis and characterization [15,16,17,18,19,20], as well as in the theory of self-organization [21,22,23] and the molecular simulations of these materials [24,25,26,27,28].

The ability to control the macroscopic alignment of LCDrs is a key factor for many of their potential applications. For low molar mass LCs, robust and well-established techniques/materials are available for the precise alignment of the LC medium through surface-mediated interactions. Through controlling the surface-LC interactions, usually by means of chemical and/or mechanical treatment of the substrate, a variety of alignments (homeotropic, planar, tilted, etc.) of the LC medium with respect to the substrate are possible. In the case of LC dendrimers, however, the mechanism behind surface alignment does not involve only the orientational restrictions imposed by the substrate to its surrounding mesogens, but also the positional/orientational correlations among mesogens that belong to the same dendrimer.

Several different models for common dendrimers (isolated and confined) [29,30,31,32,33], liquid crystal dendrimers [24,25,26,27,28] and dendronized polymers [34,35,36] have been proposed for computer simulation studies of their properties. These models range from detailed atomistic to coarse grained. In atomistic models, detailed interaction potentials between individual atoms should be considered, rendering them computationally expensive. Alternatively, in coarse-grained models, groups of atoms are represented as united interacting sites, preserving, at the same time, the architectural characteristics of the dendrimer.

In this work, we establish tractable coarse-grained (CG) models for LCDrs in order to study their molecular properties near impenetrable flat substrates under various anchoring conditions. In the next section, we present a coarse-grained model for LCDrs and the force field we have developed for the intra-dendritic bonded and non-bonded interactions. In Section 3, we introduce the interaction model between the dendrimer and the flat substrate. Next, in Section 4, we briefly mention some details of our Monte Carlo simulations, and in Section 5, we present and discuss our results on the dendritic structure near substrates, directional or not. Our conclusions are given in Section 6.

2. Coarse Grain Modeling of LCDrs

A generic coarse-grained picture of an end-functionalized LC dendron is shown in Figure 1a. The spherical beads are united atoms representing the branching sites and groups of atoms of the flexible spacers connecting the branching points. The ellipsoids denote the terminal mesogenic units. The dashed lines around groups of branching and spacer sites denote the minimum number of united atoms that are needed to produce a primitive model of a dendrimer, preserving the dendritic architecture and flexibility. The functionality, f_b, of the branching points of the dendrons is a chemically controlled property that could be generation dependent. The number of the terminal mesogens of a G-generation dendron is ${\displaystyle {\prod }_{g=1}^G{f}_b(g)}$. The length of the flexible spacer connecting two adjacent branching sites is another parameter that influences the size and the degree of deformability of the individual dendrons and of the dendrimer. In this work, we assume that these spacers are the same for each generation.

Figure 1. (a) Coarse grain representation of an end-functionalized second generation liquid crystalline (LC) dendron with f_c = 2. The dashed lines around groups of dendritic units indicate coarse-gained united atoms; and (b) coarse-grained model for a third generation liquid crystalline dendrimer (LCDr) composed of three dendrons linked on a spherical core (G₂D₃).

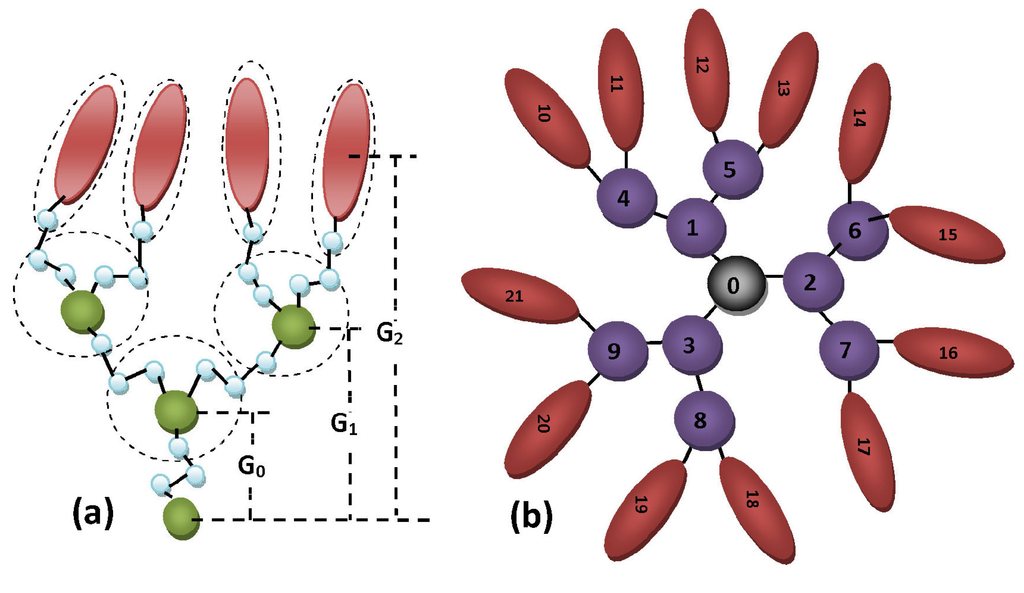
Figure 1. (a) Coarse grain representation of an end-functionalized second generation liquid crystalline (LC) dendron with f_c = 2. The dashed lines around groups of dendritic units indicate coarse-gained united atoms; and (b) coarse-grained model for a third generation liquid crystalline dendrimer (LCDr) composed of three dendrons linked on a spherical core (G₂D₃).

The dendritic supermesogen is composed of a number of dendrons. This number is determined by the connectivity or multiplicity f_c of the multifunctional core moiety (in Figure 1b, we have assumed f_c = 3). In the rest of the paper, we denote by G_kD_n a dendrimer that is composed of n dendrons of generation G. Such a dendrimer, with the branching functionality of the dendrons f_b, contains N_m = nf_b^g terminal mesogenic units.

In this work, our primary interest is to investigate the impact of the dendritic architecture on the surface alignment of a single dendrimer. To do this, the detailed structure of the spacer chains is not considered explicitly. In our model, the branching units are united atoms, which represent collectively the atoms around each branching point. These junction super-atoms are connected with virtual bonds with a variable length. This preserve the precise connectivity and the substantial intrinsic conformational flexibility of the dendrimer. With this assumption, the dendrimer is composed of two different spherically symmetric sites (denoted with b) representing the junction points and one representing the core of the dendrimer. The mesogenic units (denoted with m) are assumed to be cylindrically symmetric and are connected by one of their ends to the junction beads in the periphery of the dendrimer with bonds having the same properties with the internal virtual bonds (Figure 1).

At the level of structural resolution described above, a dendritic conformation is fully described by the positions of the junction sites {r_b} and the positions and orientations of the mesogenic units {r_m, uˆ}. The total intra-molecular potential energy of a single dendrimer is the sum of the bonded (B) and non-bonded (N-B) interactions,

$$\begin{array}{c}U=U^B+U^{N-B}\\ ={\displaystyle \sum _{i,j}{U}^B(l_{ij})}+{\displaystyle \sum _{i,j}{U}_{pq}^{N-B}(r_{ij},u_i,u_j)}\end{array}$$

(1)

Here, l_ij is the length of the virtual bond connecting the segments i, j. The indexes p, q in $U_{pq}^{N-B}$ may be either b or m, denoting branching and mesogenic segments, respectively. r_ij is the vector that connects the centers of the non-boded sites i, j, and the unit vector u_i denotes the orientation of the i−th mesogenic unit.

For the bonded potential, we have adopted a simple form, which corresponds to a freely fluctuating bond. For a pair of bonded sites, we have:

$$U^B(l)=\{\begin{array}{l}0,\text{ for }{l}_{min}<l<l_{max}\\ \infty ,\text{ otherwise}\end{array}$$

(2)

where l_min and l_max are the minimum and maximum allowed separation distances between two bonded segments. The interaction potential of two non-bonded sites of type p and q is given by:

$$U_{pq}^{N-B}({\text{r}}_{ij},{\text{u}}_i,{\text{u}}_j)=\{\begin{array}{l}{U}_{bb}^{N-B}(r_{ij}),p=q=b\\ U_{mm}^{N-B}({\text{r}}_{ij},{\text{u}}_i,{\text{u}}_j),p=q=m\\ U_{bm}^{N-B}({\text{r}}_{ij},{\text{u}}_j),p=b,q=m\end{array}$$

(3)

The junction beads are modeled as Lennard–Jones spheres interacting through:

$$U_{bb}^{N-B}=4{ϵ}_{0bb}\left[{\left(\frac{{\sigma }_{0bb}}{r_{ij}}\right)}^{12}-{\left(\frac{{\sigma }_{0bb}}{r_{ij}}\right)}^6\right]$$

(4)

and the mesogens are modeled as cylindrically symmetric soft ellipsoids interacting with the widely used Gay–Berne (GB) interaction potential [37]:

$$U_{mm}^{N-B}=4{ϵ}_{mm}({\text{r}}_{ij},{\text{u}}_i,{\text{u}}_j)\times \left[{\left(\frac{{\sigma }_{0mm}}{r_{ij}-{\sigma }_{mm}({\widehat{\text{r}}}_{ij},{\text{u}}_i,{\text{u}}_j)+{\sigma }_{0mm}}\right)}^{12}-{\left(\frac{{\sigma }_{0mm}}{r_{ij}-{\sigma }_{mm}({\widehat{\text{r}}}_{ij},{\text{u}}_i,{\text{u}}_j)+{\sigma }_{0mm}}\right)}^6\right]$$

(5)

with:

$${\sigma }_{mm}({\widehat{\text{r}}}_{ij},{\text{u}}_i,{\text{u}}_j)={\sigma }_{0mm}{\left[1-\frac{\chi }{2}\left(\frac{{({\widehat{\text{r}}}_{ij}.{\text{u}}_i+{\widehat{\text{r}}}_{ij}.{\text{u}}_j)}^2}{1+\chi ({\text{u}}_i.{\text{u}}_j)}\right)+\left(\frac{{({\widehat{\text{r}}}_{ij}.{\text{u}}_i-{\widehat{\text{r}}}_{ij}.{\text{u}}_j)}^2}{1-\chi ({\text{u}}_i.{\text{u}}_j)}\right)\right]}^{-1/2}$$

(6)

In the last Equation, $\chi =\frac{k^2-1}{k^2+1}$ with k the shape anisotropy (length to diameter ratio) of the ellipsoidal particle. The strength of the intermolecular potential in the Gay–Berne model depends also on the relative positions and orientations of the interacting ellipsoids according to:

$${ϵ}_{mm}({\widehat{\text{r}}}_{ij},{\text{u}}_i,{\text{u}}_j)={ϵ}_{0mm}{\left[{ϵ}_1({\text{u}}_i,{\text{u}}_j)\right]}^{\nu }\times {\left[{ϵ}_2({\widehat{\text{r}}}_{ij},{\text{u}}_i,{\text{u}}_j)\right]}^{\mu }$$

(7)

with:

$${ϵ}_1({\text{u}}_i,{\text{u}}_j)={\left[1-{\chi }^2{({\text{u}}_i.{\text{u}}_j)}^2\right]}^{-1/2}$$

(8)

and:

$${ϵ}_2({\widehat{\text{r}}}_{ij},{\text{u}}_i,{\text{u}}_j)=1-\frac{\chi ’}{2}\left[\frac{{{(\widehat{\text{r}}}_{ij}.{\text{u}}_i+{\widehat{\text{r}}}_{ij}.{\text{u}}_j)}^2}{1+\chi ’({\text{u}}_i.{\text{u}}_j)}+\frac{{{(\widehat{\text{r}}}_{ij}.{\text{u}}_i-{\widehat{\text{r}}}_{ij}.{\text{u}}_j)}^2}{1-\chi ’({\text{u}}_i.{\text{u}}_j)}\right]$$

(9)

where $\chi ’=\frac{k{’}^{1/\mu }-1}{k{’}^{1/\mu }+1}$ with k’ a measure of the anisotropy of the soft interactions. In the present study, we have used, µ = 2, ν = 1, k = 3 and k’ = 5, which correspond to a parameterization of the GB potential, which has been extensively studied [38,39,40,41,42,43]. With this parametrization, the Gay–Berne particles in the bulk exhibit a stable nematic phase between the isotropic fluid and the crystalline phase [43]. No smectic phases have been detected with this parametrization.

The interaction potential between the spherical branching units and the mesogens is modeled by the GB potential of Equation (5), where the orientation of the spherical segment is considered zero. The parametrization is shown in Table 1.

Table 1. Force field parameters for the coarse-grained liquid crystalline dendrimer (LCDr) model.

Parameter	Description	Values
D = σ0mm	diameter of mesogen	1.0 (unit length)
L	length of mesogen	3 D
σ0bb	diameter of bead	1:2 D
σ0bm	mesogen-bead diameter	$\frac{{\mathrm{\&\#x03C3;}}_{0bb}+{\mathrm{\&\#x03C3;}}_{0mm}}{2}$
σ0bw	bead-wall diameter	σ0bm
σ0mw	mesogen-wall diameter	σ0mm
ϵ0mm	energy unit	1
ϵ0bb	bead-bead interaction strength	0.5 ϵ0mm
ϵ0bm	mesogen-bead interaction strength	$\sqrt{{ϵ}_{0mm}{ϵ}_{0bb}}$
ϵ0bw	bead-wall interaction strength	ϵ0bm
ϵ0mw	mesogen-wall interaction strength	ϵ0mm
lmax	maximum bond length	1:8 σ0mm
lmin	minimum bond length	1:2 σ0mm

Table 1. Force field parameters for the coarse-grained liquid crystalline dendrimer (LCDr) model.

Parameter	Description	Values
D = σ0mm	diameter of mesogen	1.0 (unit length)
L	length of mesogen	3 D
σ0bb	diameter of bead	1:2 D
σ0bm	mesogen-bead diameter	$\frac{{\mathrm{\&\#x03C3;}}_{0bb}+{\mathrm{\&\#x03C3;}}_{0mm}}{2}$
σ0bw	bead-wall diameter	σ0bm
σ0mw	mesogen-wall diameter	σ0mm
ϵ0mm	energy unit	1
ϵ0bb	bead-bead interaction strength	0.5 ϵ0mm
ϵ0bm	mesogen-bead interaction strength	$\sqrt{{ϵ}_{0mm}{ϵ}_{0bb}}$
ϵ0bw	bead-wall interaction strength	ϵ0bm
ϵ0mw	mesogen-wall interaction strength	ϵ0mm
lmax	maximum bond length	1:8 σ0mm
lmin	minimum bond length	1:2 σ0mm

3. Dendrimer-Substrate Interaction Potential

To model various anchoring conditions of the LCDr, we have assumed that the spherical segments of the dendrimer are repelled softly by the wall according to U^bw(r) = 4ϵ_0bw(σ_0bw/r_ij)⁹, with r denoting the vertical distance between the spherical segment and the confining surface located at z = 0. The values of the interaction parameters σ_0bw and ϵ_0bw used in the present simulations are listed in Table 1.

Several descriptions for the interactions of a Gay–Berne particle with solid surfaces have been proposed [44,45,46]. In our study, we use a modification of the interaction model introduced in [46]. Each mesogenic unit of the dendrimer with coordinates (x, y, z) interacts with a phantom mesogen centered at (x, y, 0). The orientation of the phantom particle with respect to the surface determines the anchoring constraints that the substrate imposes on the mesogenic units of the adsorbed dendrimer. Homeotropic (vertical) anchoring is modeled assuming the phantom particle being normal to the surface. In this case, the energetically preferred orientation of the dendritic mesogens is when the mesogenic unit is normal to the confining substrate. Random planar anchoring is achieved assuming that the phantom ellipsoid lies parallel to the substrate having (cos ϕ, sin ϕ, 0) on the x − y plane with ϕ a uniformly distributed angle in the range 0 < ϕ < π. Similarly, the uniform (unidirectional) planar anchoring condition is achieved assuming that the phantom mesogen points along a given direction on the surface, which, without loss of generality, is chosen to be the macroscopic x-axis.

The mesogen-surface interaction effective potential is given by:

$$U^{mw}=\frac{2\pi }{3}{ϵ}_{mw}(r_{ii’},u_i,u_{i’})\times \left[\frac{2}{15}{\left(\frac{{\sigma }_{0mw}}{r_{ii’}-{\sigma }_{mw}({\widehat{\text{r}}}_{ii’},u_i,u_{i’})+{\sigma }_{0mw}}\right)}^9-{\left(\frac{{\sigma }_{0mw}}{r_{ii’}-{\sigma }_{mw}({\widehat{\text{r}}}_{ii’},u_i,u_{i’})+{\sigma }_{0mw}}\right)}^3\right]$$

(10)

where, ${\widehat{\text{u}}}_i$ is the orientation of the mesogenic unit i and ${\widehat{\text{u}}}_{i’}$ is the orientation of the phantom ellipsoid. r_ii’ is the intermolecular vector, which connects the mesogenic unit with its phantom counterpart. The latter is centered at the less distant point of the surface to the actual mesogen. For a homeotropic substrate, ${\widehat{\text{u}}}_{i’}=\widehat{\text{z}}$; for random planar, ${\widehat{\text{u}}}_{i’}=\cos (\varphi )\widehat{\text{x}}+sin(\varphi )\widehat{\text{y}}$, (with ϕ a randomly chosen angle from a uniform distribution) and ${\widehat{\text{u}}}_{i’}=\widehat{\text{x}}$ for unidirectional planar anchoring conditions. The definitions for σmw and ϵmw are the same with those of Equations (6) and (7) with parametrization νw = 1, µw = 2, χw = 0.8 and ${\chi }_w^{’}=0.382$, for the planar anchoring, and νw = 3, µw = 1, χw = 0.8 and ${\chi }_w^{’}=0.667$, for the homeotropic. In Figure 2, we present plots of the mesogen-surface interaction potential as a function of the distance, r, from the surface for various orientations of the mesogens with respect to the substrate, assuming unidirectional planar (Figure 2a) and homeotropic (Figure 2b) anchoring conditions.

Figure 2. Mesogenic unit-surface potential at four specific values of the polar angle θ between the mesogenic axis and the surface normal as the function of distance under (a) unidirectional planar and (b) homeotropic anchoring conditions.

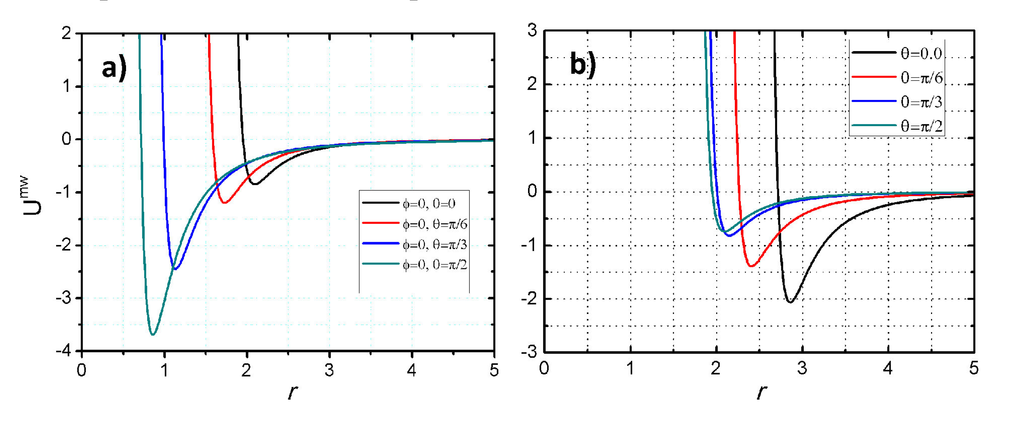
Figure 2. Mesogenic unit-surface potential at four specific values of the polar angle θ between the mesogenic axis and the surface normal as the function of distance under (a) unidirectional planar and (b) homeotropic anchoring conditions.

4. Simulation Details

We have used standard Metropolis Monte Carlo (MC) computer simulations to investigate the conformational behavior and the possibility of alignment of the model LCDr adsorbed on flat surfaces. At a given reduced temperature T^∗= Tk_B/ϵ_0mm, an MC cycle consists of one random displacement for each molecular segment and one random reorientation for each mesogenic segment. The random translations/reorientations are tuned to give an overall acceptance ratio of the random moves of about 30%. We start with a well-equilibrated state, at a relatively high temperature T^∗, with the LCDr located initially well above the substrate. The dendrimer is then brought gradually close to the surface with the help of an auxiliary gravitational-like force applied to the core segment of the dendrimer. During this procedure, the conformation of the dendrimer is allowed to change, taking into account the dendrimer-surface interactions. Once the LCDr is close to the surface, we cool the system gradually to a low enough temperature, at which spontaneous thermal detachment of the adsorbed dendrimer is not possible. Long simulations (O(10⁶) MC cycles) are performed afterwards for the calculation of the equilibrium properties of the system both in heating and cooling series to ensure that the studied systems are not trapped in metastable states. During the heating runs, the temperature is increased gradually up to the characteristic temperature, T_D, at which the dendrimer spontaneously detaches from the surface. The absence of any noticeable hysteresis, during the heating and cooling runs, for all of the studied properties, suggests that the simulated systems were brought to thermodynamic equilibrium.

5. Results and Discussion

5.1. Homeotropic Anchoring

In Figure 3, we present characteristic snapshots from equilibrated states of a G = 3 LCDr with core multiplicity f_c = 3–5 (top row) and of G = 3–5 dendrimers with fc = 3 (bottom row). All of the snapshots are taken at T^∗= 0.4, which is well bellow the detachment temperature T_D ≈ 2.5. From the visual inspection of the snapshots, it is clear that at low enough temperatures, the mesogenic units align, as expected, normal to the substrate. However, above a certain generation and depending on the core functionality, due to geometrical and packing restrictions, a fraction of mesogenic units are not allowed to be in contact with the substrate. This is clearly demonstrated in the snapshots of the G₃D₅ and G₅D₃ LCDrs in Figure 3c,d.

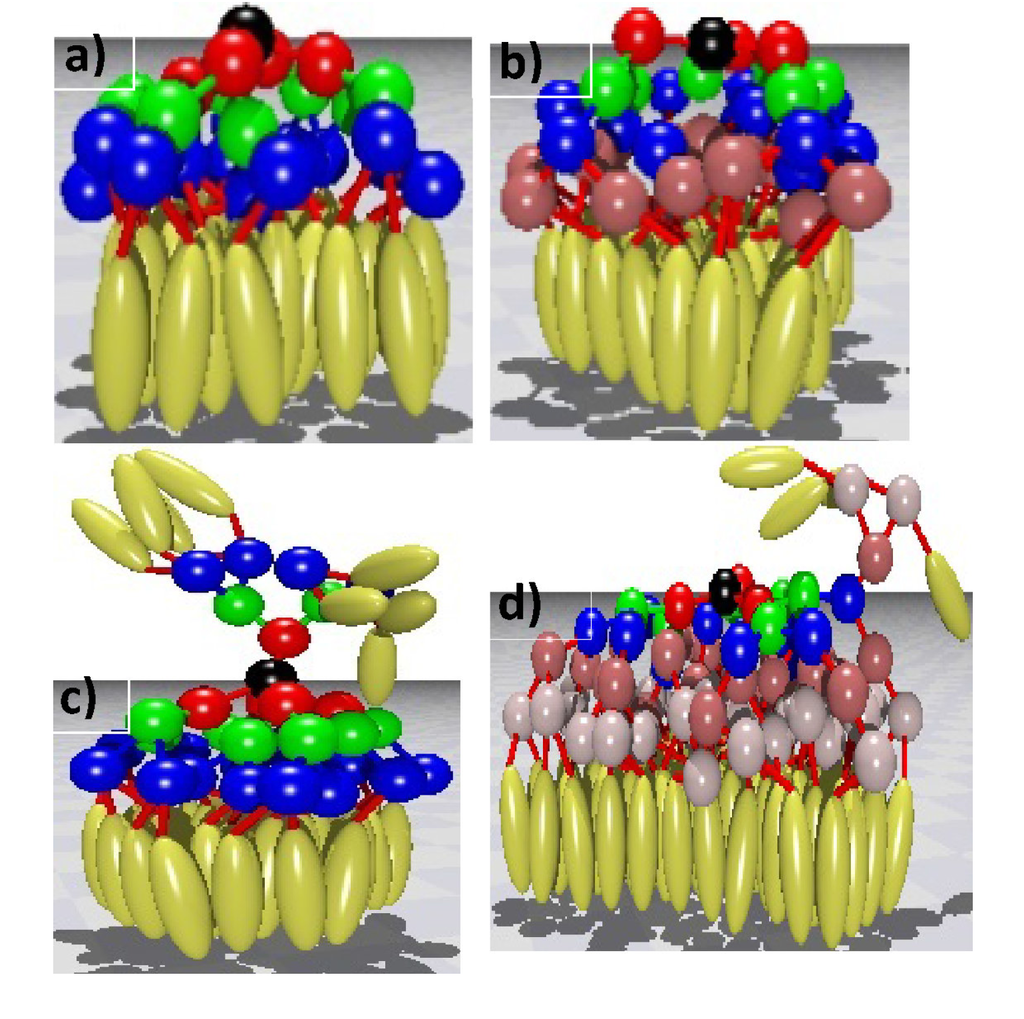
Figure 3. Representative snapshots of LCDrs under homeotropic anchoring condition at T^∗ = 0.4. (a) G₃D₄; (b) G₄D₃; (c) G₃D₅; and (d) G₅D₃ LCDrs.

Figure 3. Representative snapshots of LCDrs under homeotropic anchoring condition at T^∗ = 0.4. (a) G₃D₄; (b) G₄D₃; (c) G₃D₅; and (d) G₅D₃ LCDrs.

To quantify the mass distribution of the mesogenic and spherical segments as a function of their distance from the substrate, we have calculated the average density profile of the LCDrs above the substrate:

$${\rho }^{(w)}(z)=\frac{1}{N_w}\langle {\displaystyle \sum \delta (z-r_i\cdot \widehat{\text{z}})}\rangle$$

(11)

where w denotes either the mesogenic (w = m) or the spherical bead (w = b) segments of the LCDr; here, N_w is the total number of the corresponding segments and r_i is the position vector of segment i. Representative plots of the density profiles at various temperatures for high generation and core functionality LCDrs are shown in Figure 4b,d for the mesogenic units and in Figure 4a,c for the branching beads. These plots reveal a clear, anchoring driven, submolecular partitioning of the LCDrs. The mesogenic units are adsorbed homeotropically on the substrate at a distance slightly less than half their length, as indicated by the strong peak in the plots of Figure 4b,d. The G₃D₅ LCDrs exhibit also a secondary weak density maximum (see the inset of Figure 4d), which is located well above the adsorbed layer. This maximum, present for the whore range of temperatures, corresponds to the mesogenic units, which, due to the intra-molecular geometrical constrains, are not allowed to be in contact with the substrate. A similar density modulation, much weaker though, is observed for the G₅D₃ dendrimer (see Figure 4b). The plots of the density profile of the branching segments (Figure 4a,c) indicate that the inner flexible part of the LCDrs is separated from the mesogenic units, forming well-defined layers above them.

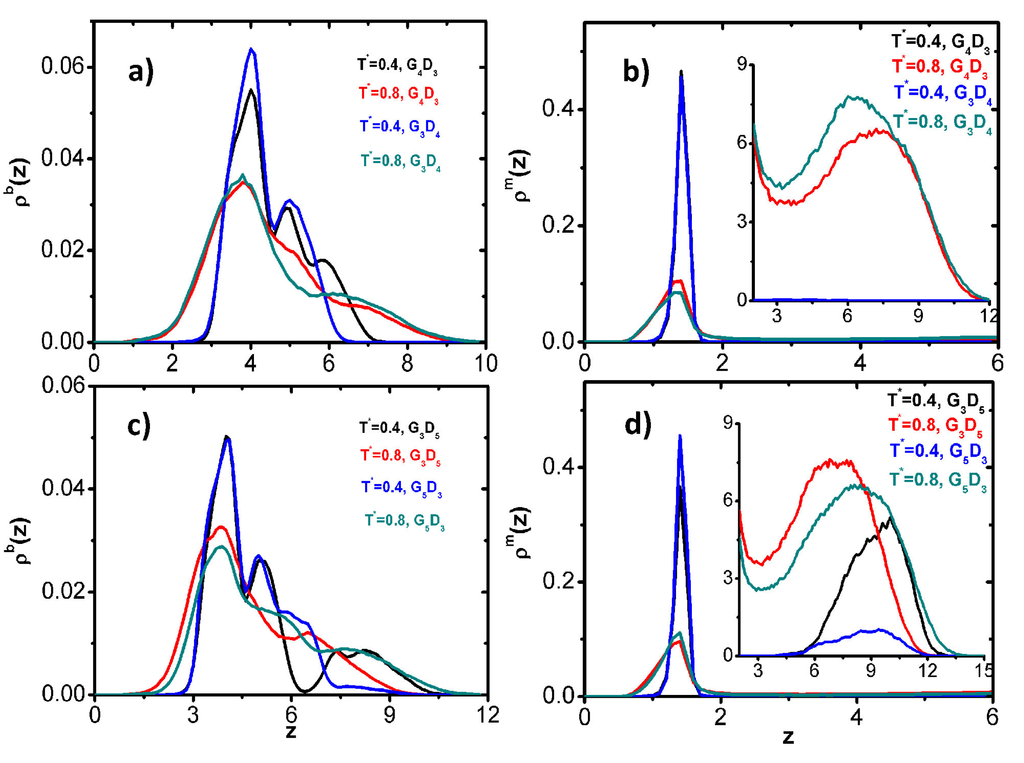
Figure 4. Calculated density profiles of the spherical beads (a,c) and the mesogens (b,d) of LCDrs under homeotropic the anchoring condition as a function of the distance z from the surface. The values of ρ^m in the insets are scaled by 10³.

Figure 4. Calculated density profiles of the spherical beads (a,c) and the mesogens (b,d) of LCDrs under homeotropic the anchoring condition as a function of the distance z from the surface. The values of ρ^m in the insets are scaled by 10³.

The orientational order of the mesogenic units of the LCDrs has been quantified by calculating their order parameter through, $S_z=\langle P_2(cos\theta )\rangle$, where P₂ is the second Legendre polynomial and θ the angle between the direction of the mesogenic segment and the normal to the substrate. The temperature dependence of the orientational order for homeotropic anchoring is shown in Figure 5. From this figure, it is clear that the LCDr develops a substantial orientational order at temperatures below T^∗ ≈ 0.9. The LCDrs become highly oriented, S_z > 0.9, for T^∗ < 0.6. However, in the case of G₃D₅ and G₅D₃ LCDrs, S_z stays below unity, even at very low temperatures. This, as discussed above, happens because a number of mesogens stay well above the substrate in the high generation or core-functionality LCDrs. Clearly, these distant mesogens do not “feel” the aligning effects of the substrate.

Taking into account that the detaching temperature for all of the studied systems is higher than T^∗ = 2, it becomes clear that the adsorbed LCDrs under homeotropic anchoring can be found in two different states on the substrate: an orientationally ordered state with S_zz > 0 and an “isotropic” with S_zz ≈ 0. The transition between the two states takes place at T^∗ ≈ 0.8 and has the features of a continuous order-disorder transition, associated with substantial conformational changes of the LCDr. We note that simulations of isolated (not-confined) LCDrs do not indicate any significant conformational change at this particular temperature. This kind of temperature activated surface anchoring transition has been observed recently in systems of organo-siloxane tetrapods [20] under homeotropic alignment.

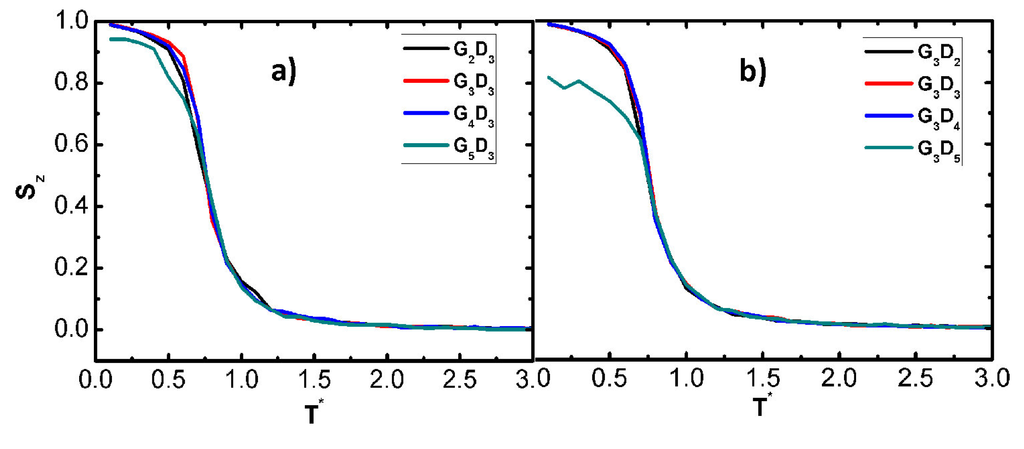
Figure 5. Average orientational order parameter as a function of temperature, T^∗ for LCDrs with (a) fixed f_c = 3 and G = 2–5 and (b) fixed G = 3 and f_c= 2–5.

Figure 5. Average orientational order parameter as a function of temperature, T^∗ for LCDrs with (a) fixed f_c = 3 and G = 2–5 and (b) fixed G = 3 and f_c= 2–5.

Extrapolating the behavior of a single LCDr under homeotropic anchoring conditions to a system of LCDrs confined by such a surface, we believe that the transmission of the alignment from the adsorbed layer to the bulk, if at all present, will be mainly due to the submolecular partitioning, thus favoring smectic or columnar-like ordering close to the substrate.

5.2. Random Planar Anchoring

The alignment of the mesogenic units under random planar anchoring conditions favor mesogenic orientations parallel to the substrate. In this case, all of the in-plane directions are equivalent. As we can observe from the typical snapshots presented in Figure 6, the adsorbed mesogens at low temperatures are distributed radially, and they do dot seem to align along any particular direction. In addition, the beads are well separated from the mesogens, forming a thin layer above them.

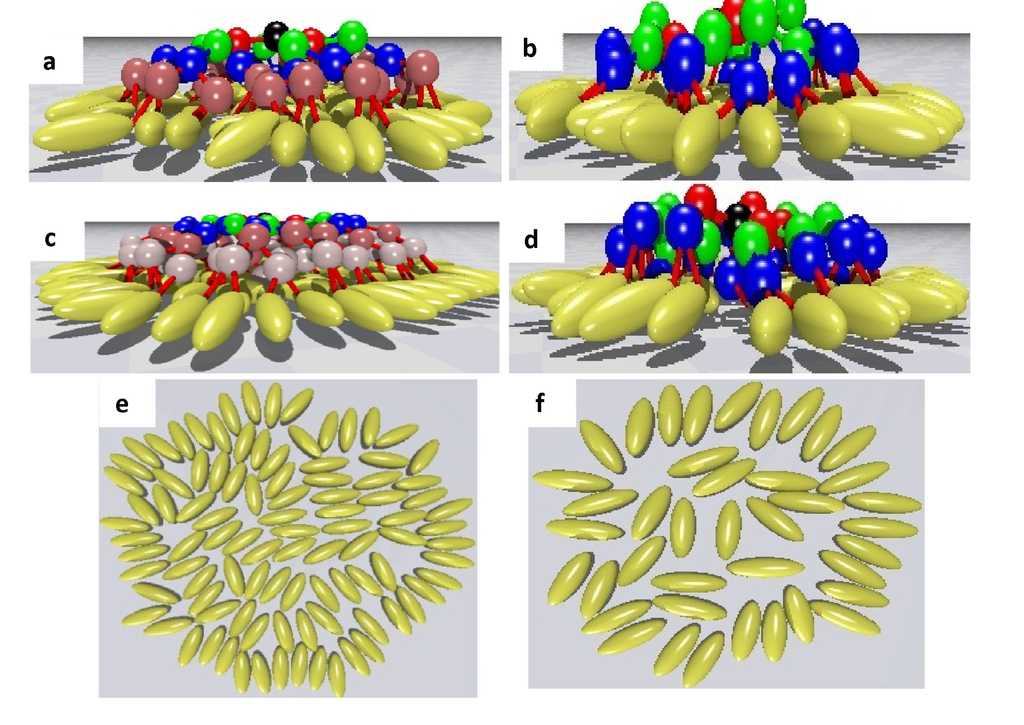
Figure 6. Snapshots of adsorbed LCDrs under random planar anchoring conditions at T^∗= 0.6. (a) G₄D₃; (b) G₃D₄; (c) G₅D₃; (d) G₃D₅. In the bottom row, the junction beads are not shown. (e) G₅D₃; and (f) G₃D₅.

Figure 6. Snapshots of adsorbed LCDrs under random planar anchoring conditions at T^∗= 0.6. (a) G₄D₃; (b) G₃D₄; (c) G₅D₃; (d) G₃D₅. In the bottom row, the junction beads are not shown. (e) G₅D₃; and (f) G₃D₅.

The radial topology of the mesogenic units of the LCDr under random planar anchoring conditions is nicely confirmed in the means of the calculated radial mass distribution of the dendritic units with respect to its center of mass, ${\rho }^{(w)}(r)=\langle {\displaystyle {\sum }_i\delta (r-r_i)}\rangle$, with w denoting either beads or mesogens. This distribution is calculated using the projections of the position of the dendritic segments on the x − y-plane. Calculated results at various temperatures are presented in Figure 7. From these plots and with the help of the visual inspection of snapshots, we can draw the following important conclusions: (i) both the junction and mesogenic units are symmetrically distributed around the center of mass of the LCDr; (ii) the outer mesogenic units form a well-defined shell with a radial (along their position vector) orientation; (iii) the mesogenic units of the high generation and/or core-functionality LCDrs show a clear tendency to form secondary internal radial shells, as indicated by the secondary maxima in Figure 7c; and (iv) the branching beads exhibit a well-defined, modulated mass distribution in the radial direction (see Figure 7a,b). Not surprisingly, the number of peaks in Figure 7a,b corresponds to the generation number. The inner peak stands for the zeroth generation branching segments; the second peak is for generation one; and so on. The spacing between the peaks slowly decreases as we go from the center to the periphery. In the range of temperatures for which the LCDrs are adsorbed on the surface, all of the calculated radial mass distributions of the dendritic segments vary smoothly without any abrupt change going from high to low temperatures or vice versa.

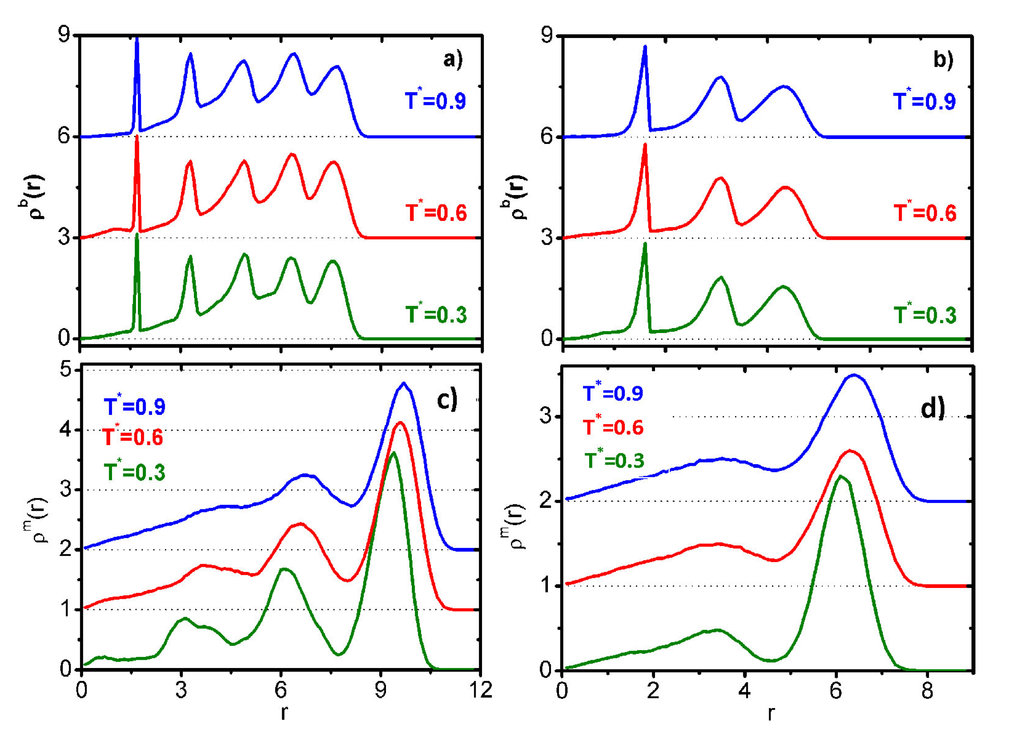
Figure 7. Radial distribution of monomers about the center of mass of LCDrs. (a) G₅D₃; (b) G₃D₅; (c) G₅D₃; and (d) G₃D₅. In all plots, the traces are offset for clarity; horizontal dashed lines show zero levels for the functions.

Figure 7. Radial distribution of monomers about the center of mass of LCDrs. (a) G₅D₃; (b) G₃D₅; (c) G₅D₃; and (d) G₃D₅. In all plots, the traces are offset for clarity; horizontal dashed lines show zero levels for the functions.

To study the orientational order of the mesogenic units in more detail, we calculated several orientational-dependent radial distribution functions. These distributions reveal how mesogens are oriented with respect to the projection on the x −y-plane of their position vector (calculated with respect to the center of mass of the LCDr) and are defined as:

$$g^l(r)=\frac{\langle {\displaystyle {\sum }_i{P}_l({\widehat{r}}_i\cdot {\widehat{\text{u}}}_i)\delta (r-r_i)}\rangle }{\langle \delta (r-r_i)\rangle }$$

(12)

with P_l(x) the Legendre polynomial of rank l. Here, r_i denotes the distance of the i − th segment from the center of mass of the LCDr.

The function g¹(r) takes explicitly into account the non-equivalence of the +rˆ and −rˆ orientations of the mesogenic units. This asymmetry stems from the fact that the apolar (by construction) mesogenic segments become polar, since one of their ends is bonded to the outer junction beads of the dendrimer. The plots of Figure 8a,b indicate clearly that the more distant outer mesogens have orientations that practically coincide with the direction of their position vector, i.e., g¹(r) ≈ +1. However moving towards the center of the LCDr, g¹ decreases gradually and vanishes to the center, indicating the absence of any polar correlations. The non-vanishing g²(r) for distances close to the center of the LCDr indicates that the densely-packed inner mesogens have developed a small degree of persisting nematic-like orientational order. The degree of the orientational order remains practically constant for the inner mesogens for temperatures above T^∗ = 0.8 (see Figure 8c,d). At lower temperatures, the modulation of both g¹(r) and g²(r) at distances smaller than the radius of the outer shell is attributed to the formation of frozen and practically immobile groups of mesogens. The overall picture of the LCDrs under random planar anchoring conditions resembles a two-dimensional analogue of nematic droplets with radial boundary conditions [47].

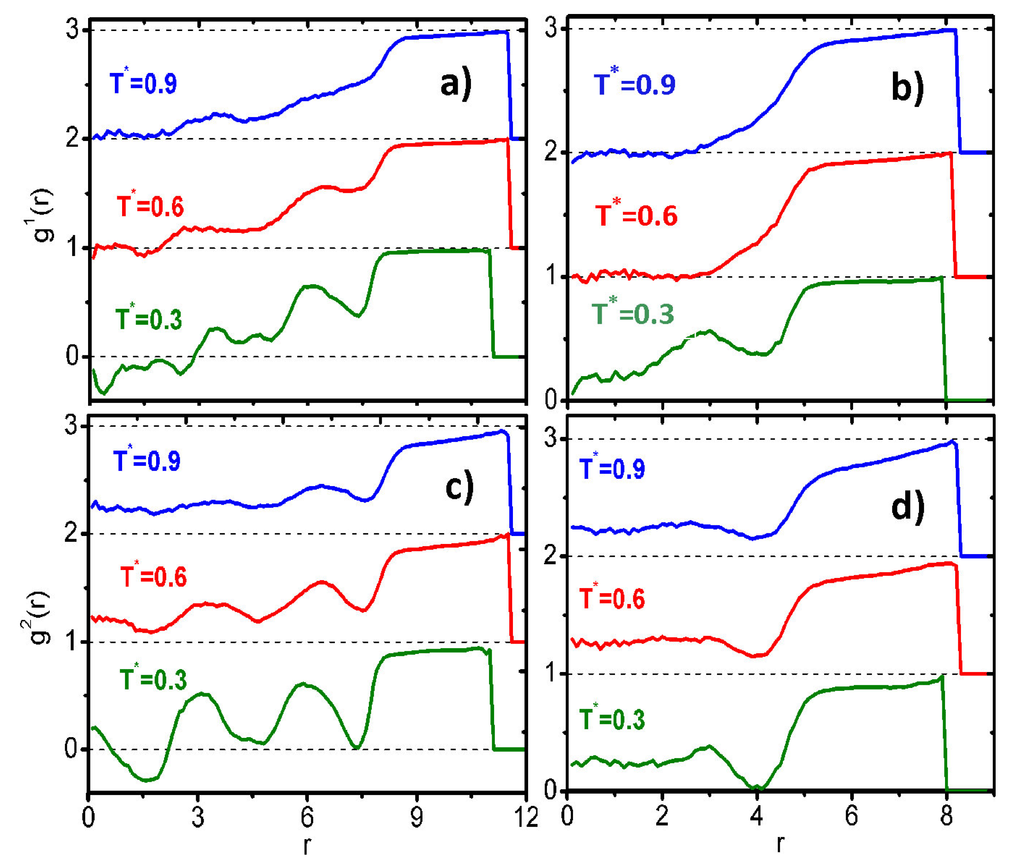
Figure 8. Calculated radial correlation functions, g¹(r) and g²(r) (see Equation (12)) for G₅D₃ (a,c) and G₃D₅ (b,d) LCDrs at various temperatures. In all plots, the traces are offset for clarity; horizontal dashed lines show zero levels for the correlation functions.

Figure 8. Calculated radial correlation functions, g¹(r) and g²(r) (see Equation (12)) for G₅D₃ (a,c) and G₃D₅ (b,d) LCDrs at various temperatures. In all plots, the traces are offset for clarity; horizontal dashed lines show zero levels for the correlation functions.

5.3. Unidirectional Planar Anchoring

Unidirectional planar anchoring conditions are usually achieved by mechanical rubbing of polymer-treated planar surfaces. To model this type of anchoring, the phantom ellipsoids are assumed to be parallel to the plane, and in addition, their symmetry axis is oriented along the macroscopic x-axis (rubbing direction). Representative snapshots of simulated LCDrs under this anchoring are shown in Figure 9.

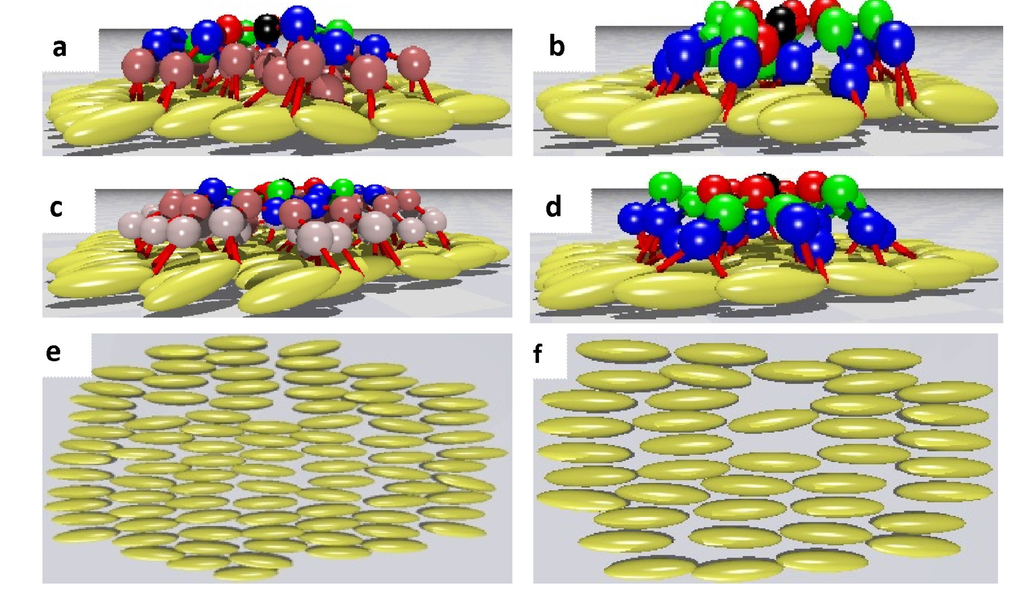
Figure 9. Snapshots of LCDrs under uniform planar anchoring conditions at T^∗ = 0.6. (a) G₄D₃; (b) G₃D₄; (c) G₅D₃ and (d) G₃D₅. Snapshots (e) and (f) are, respectively, G₅D₃ and G₃D₅ LCDrs without the junction beads.

Figure 9. Snapshots of LCDrs under uniform planar anchoring conditions at T^∗ = 0.6. (a) G₄D₃; (b) G₃D₄; (c) G₅D₃ and (d) G₃D₅. Snapshots (e) and (f) are, respectively, G₅D₃ and G₃D₅ LCDrs without the junction beads.

As can be clearly seen in the snapshots in Figure 9, the mesogenic units of the LCDr form two-dimensional (2D) smectic-like layers. This layering becomes more pronounced at low temperatures. In order to confirm this observation and to quantify the layer spacing of these 2D smectic layers, we have calculated the average mass distribution along the rubbing direction of both branching segments and mesogenic units through the density profiles:

$${\rho }^w(x)=\langle {\displaystyle \sum _i\delta (x-{\text{r}}_i\cdot \widehat{\text{x}})}\rangle$$

(13)

where r_i is the position vector of site i with respect to the center of mass of the LCDr. The calculated density modulation suggest that, at low temperatures, LCDrs form well-defined smectic-like structures with the layer normal along the rubbing direction and with layer spacing close to the mesogenic length. As temperature increases, the density modulation becomes weaker, and at high temperatures, the 2D smectic organization transforms to a 2D nematic ordering with the mesogenic units oriented on average along the rubbing direction. The range of thermal stability of the smectic-like dendritic organization is connected with the number of mesogenic units of the dendrimer. This can be clearly seen in the plots of Figure 10a,b; the smectic-like organization of the G₃D₅ LCDr becomes less pronounced at T^∗ = 0.9, while the fifth generation dendrimer, G₅D₃, at the same temperature, preserves its smectic organization.

Figure 10. (a,b) Calculated mass distribution (Equation (14)); and (c,d) polar correlations (Equation (14)) of the mesogenic units along the rubbing direction. The plots are for G₅D₃ (a,c) and G₃D₅ (b,d) LCDrs. In all plots, the traces are offset for clarity.

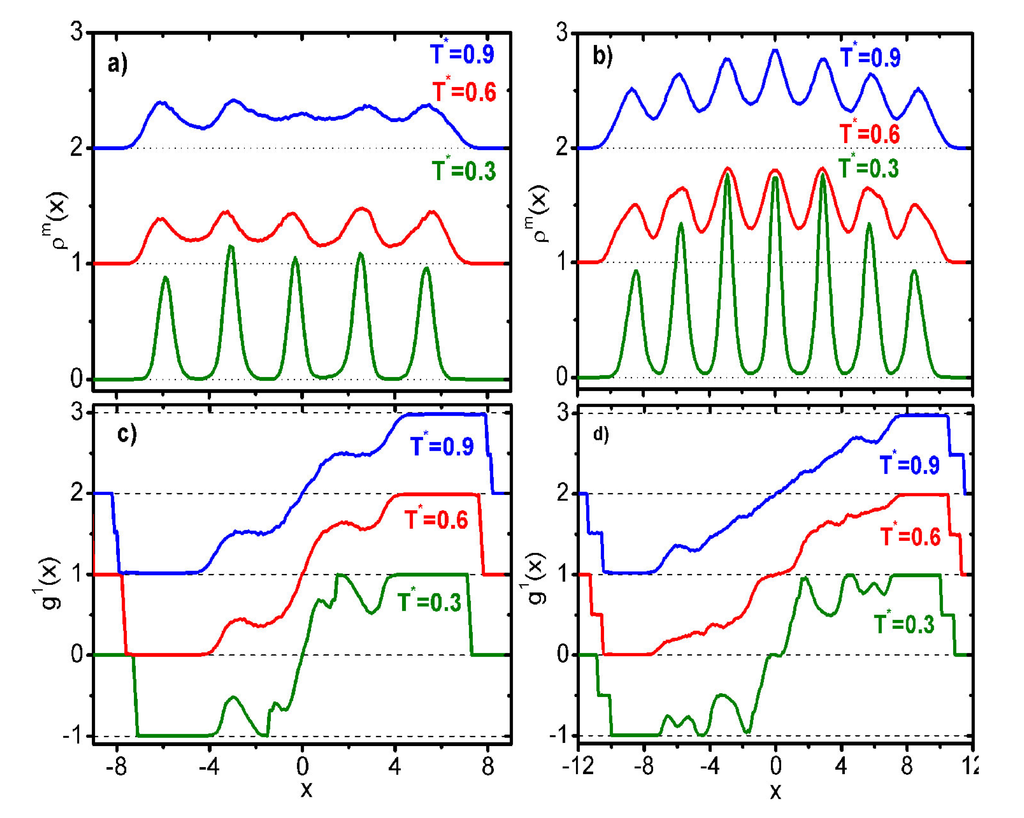
Figure 10. (a,b) Calculated mass distribution (Equation (14)); and (c,d) polar correlations (Equation (14)) of the mesogenic units along the rubbing direction. The plots are for G₅D₃ (a,c) and G₃D₅ (b,d) LCDrs. In all plots, the traces are offset for clarity.

In addition to mass distribution functions, the following one-dimensional mixed positional/orientational correlation function defined as:

$$g_{\left|\right|}^1(x)=\frac{\langle {\displaystyle {\sum }_i(\widehat{\text{x}}\cdot {\widehat{\text{u}}}_i)\delta (x-({\text{r}}_i-{\text{r}}_{cm})\cdot \widehat{\text{x}})}\rangle }{\langle \delta (x-({\text{r}}_i-{\text{r}}_{cm})\cdot \widehat{\text{x}})\rangle }$$

(14)

provides significant information on the positional dependence of the mesogenic polar order with respect to the rubbing direction. According to the plots in Figure 10b,c, the smectic layers, with the exception of the central one at x = 0, are polar $(g_{\left|\right|}^1(x)\ne 0)$ with $g_{\left|\right|}^1(x)=-g_{\left|\right|}^1(-x)$. In the central layer, the number of mesogens pointing at the +xˆ and at the −xˆ directions are equal on average. Clearly, LCDrs under uniform planar alignment consist of two structurally symmetric parts of opposite polarity, therefore rendering the whole LCDr apolar. To quantify the degree of the nematic-like order of the LCDrs, we calculated the $S_x=\langle P_2(cos(\widehat{\text{u}}\cdot \widehat{\text{x}})\rangle$. As can be seen in Figure 11, in the case of uniform planar anchoring, the orientational order develops smoothly with temperature, not exhibiting the abrupt change observed in the case of homeotropic anchoring.

Figure 11. Average orientational order parameter as a function of temperature, T^∗ for (a) G₃D_2-5 and (b) G_3-5D₃ LCDrs under uniform planar anchoring.

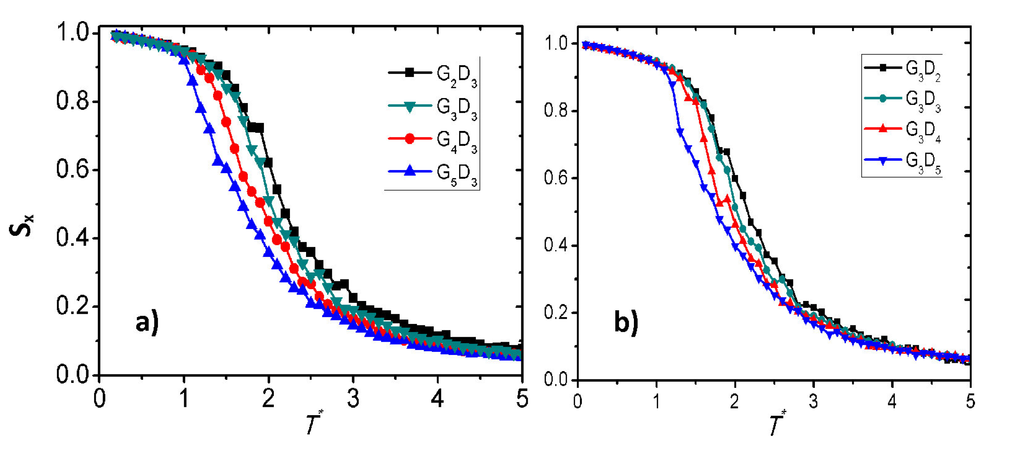
Figure 11. Average orientational order parameter as a function of temperature, T^∗ for (a) G₃D_2-5 and (b) G_3-5D₃ LCDrs under uniform planar anchoring.

6. Conclusions

In this work, we introduced a tractable coarse-grained model for simulating the conformational properties and the structure of single liquid crystalline dendrimers near aligning substrates. The developed force field is based on modifications of well-known interaction potentials that can be used either with MC or with molecular dynamics simulations.

We studied three different anchoring modes: homeotropic, random (or degenerate) planar and unidirectional planar. Our findings indicate that the conformational properties of LCDrs in the proximity of aligning substrates depend strongly on the dendritic architecture (generation and core functionality), as well as on the type of anchoring of the mesogenic units. In thermal equilibrium, the structure of the confined LCDrs is determined by the interplay between the anchoring driven alignment and the positional/orientational constraints the dendritic connectivity imposes on the mesogenic units.

Our results demonstrate clearly that different anchoring constraints give rise to specific types of submolecular partitioning and ordering on the adsorbed dendrimers. Random planar anchoring leads to the radial distribution of the mesogenic units, having their orientations along the radial direction. On the other hand, the directional planar anchoring results in well-defined smectic-like ordering with layer spacing comparable with the length of the mesogenic units. Finally, in the case of homeotropic anchoring, the degree of orientational order is a sensitive function of the temperature. At low temperatures, the adsorbed mesogenic units stay, on average, normal to the substrate. Above a critical temperature, the LCDrs loose their orientational order, although they stay adsorbed on the substrate.

We note here that, in the case of high generation dendrimers under homeotropic anchoring, a number of mesogenic units are not permitted to stay adsorbed on the substrate. This is not the case for planar anchoring. This observation indicates that the architectural intramolecular constraints have different effects, not only on the ordering of the dendrimers, but also on the portion of the mesogenic units, which are allowed to be in contact with the aligning substrate.

An observation worth noting is that the confinement-induced submolecular segregation results in dendritic structures with the mesogenic units “isolated” between the substrate and a layer formed above them from the flexible internal dendritic part. This is the case for LCDrs with g ≥ 3 for all of the anchoring conditions. This insulation of the mesogenic units prevents the direct interactions of the dendritic mesogens with other molecules above the adsorbed LCDr layer. As a result, it is expected that the alignment effects of the substrate to an ensemble of LCDrs above it are not transmitted into the bulk directly through the mesogenic units, but rather through the dendritic sub-layer formed by the non-mesogenic internal dendritic segments. In addition, taking into account that the adsorbed LCDrs exhibit well-defined and persisting conformational motifs, we argue that the surface-induced order to the bulk, especially in the case of high generation LCDrs, will be determined mainly by the substrate-induced microphase separation in the proximity of the substrate. Work on the molecular origins of the surface-induced order to the bulk phases of LCDrs is in progress.