Long-Term Bending Creep Behavior of Thin-Walled CFRP Tendon Pretensioned Spun Concrete Poles
Abstract
:1. Introduction
2. Materials
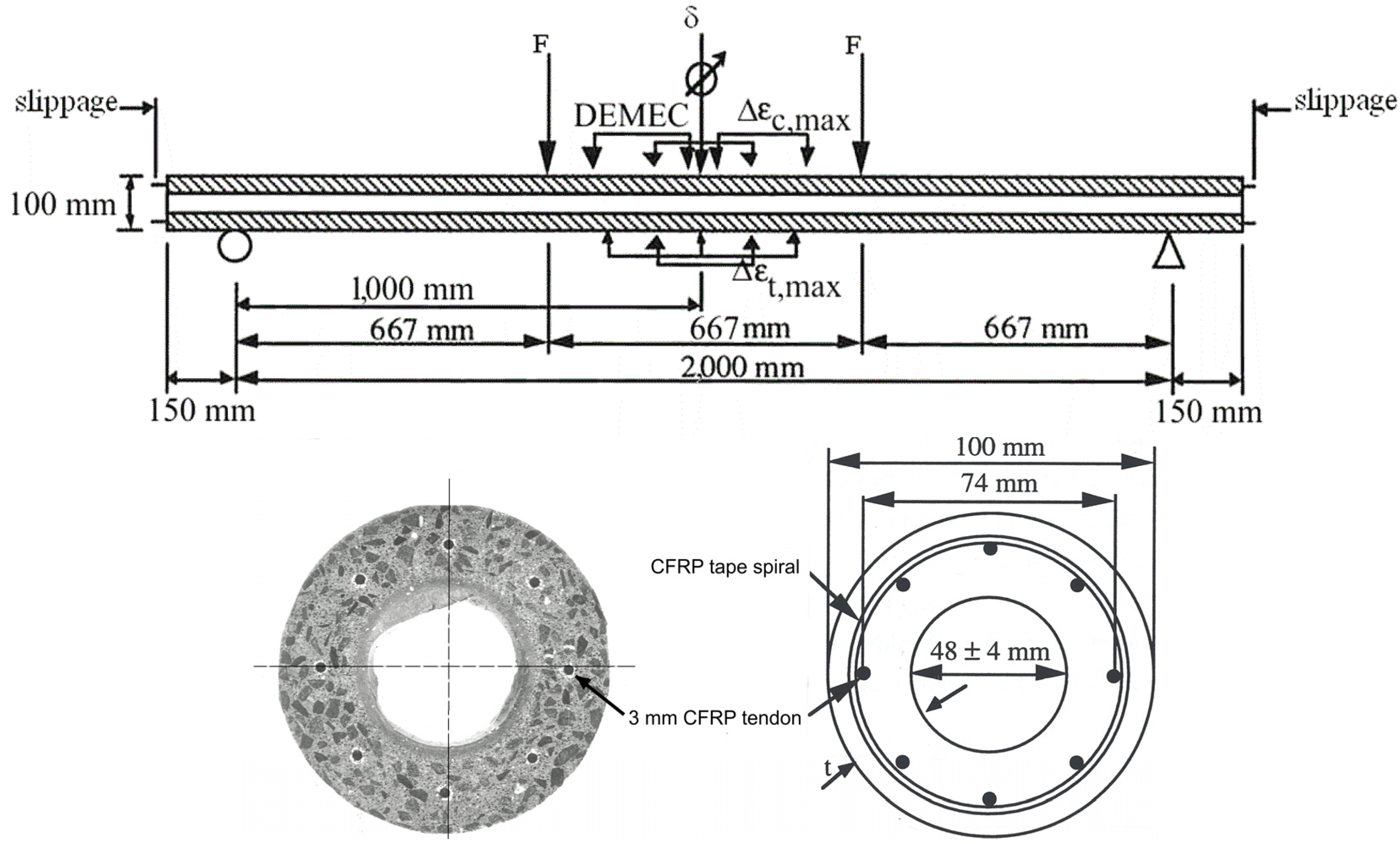
3. Experimental Specimens and Bending Test Setup

| Pole No. | Initial CFRP prestress (MPa) | Bending test | Cracking moment (kNm) | Creep moment (kNm) | Failure moment (kNm) | Time to failure | Midspan deflection at failure (mm) | Δεc,max (‰) | ΔεCFRP, max (‰) | Failure mode |
|---|---|---|---|---|---|---|---|---|---|---|
| 7 | 1600 | quasi-static | 2.58 | n.a. | 5.76 | 1 h | 66.4 | −5.37 | 10.55 | HPSC crushing |
| 8 | 1600 | quasi-static | 2.41 | n.a. | 5.53 | 1 h | 70.6 | −5.90 | 11.33 | HPSC crushing |
| 12 | 1600 | creep | 2.07 | 2.07 | none | running | n.a. | −2.37 | 1.55 | none |
| 13 | 1600 | creep | n.a . | 2.80 | none | running | n.a. | −4.14 | 3.92 | none |
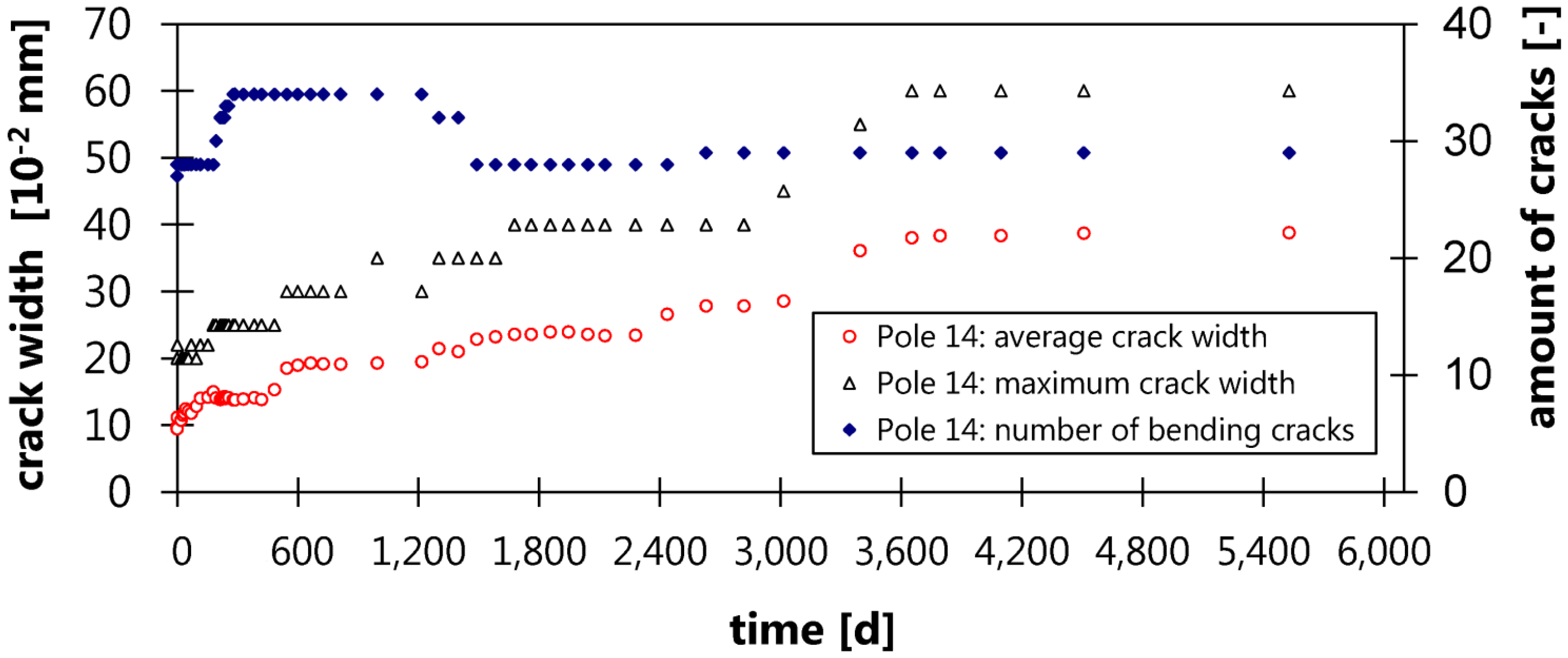
| 14 | 1600 | creep | n.a. | 4.07 | 4.07 | 16.54 y | 68.6 * | −6.84 * | 9.27 * | bond |
4. Results and Discussion
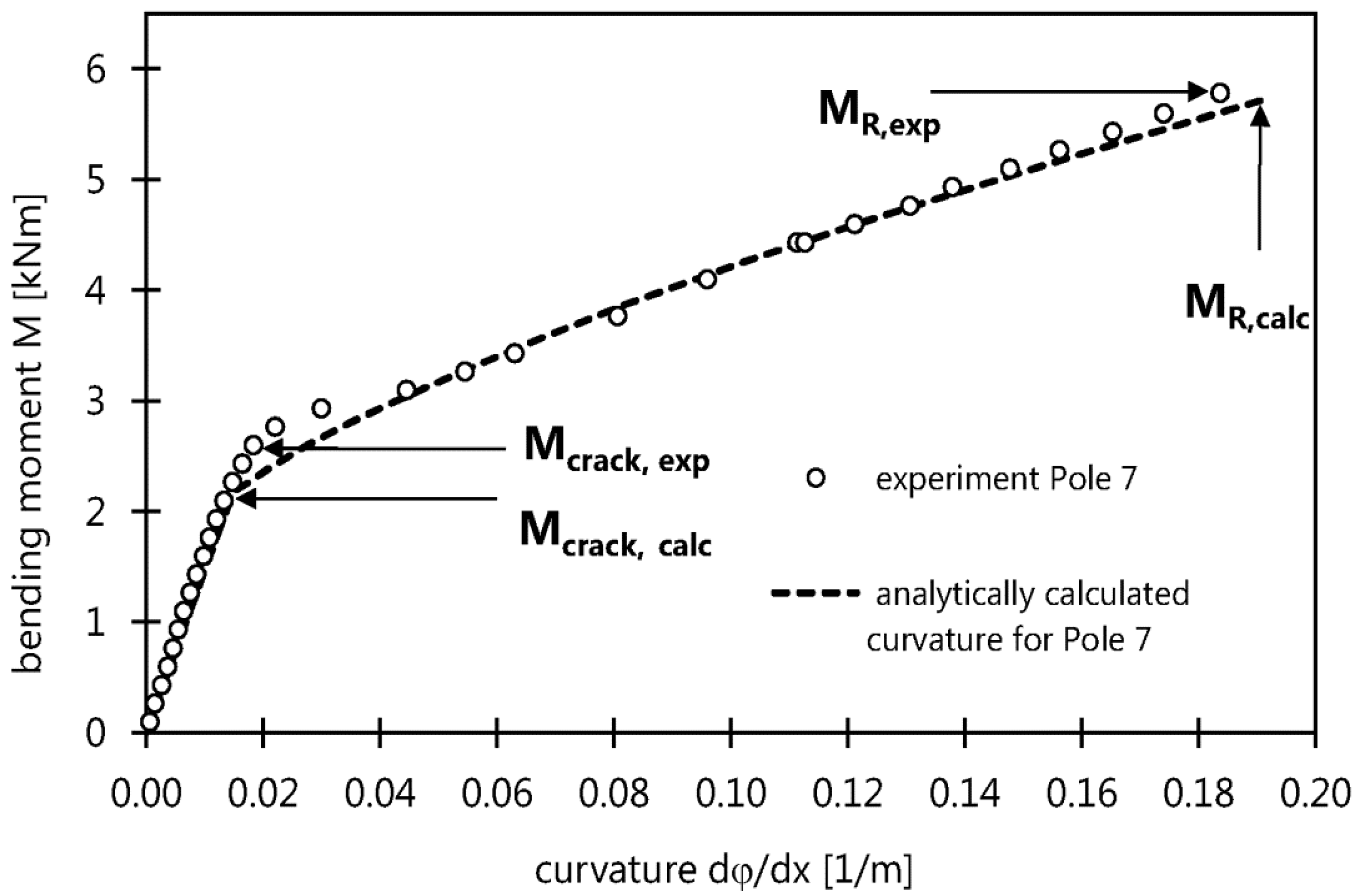
4.1. Short-Term Bending Behavior
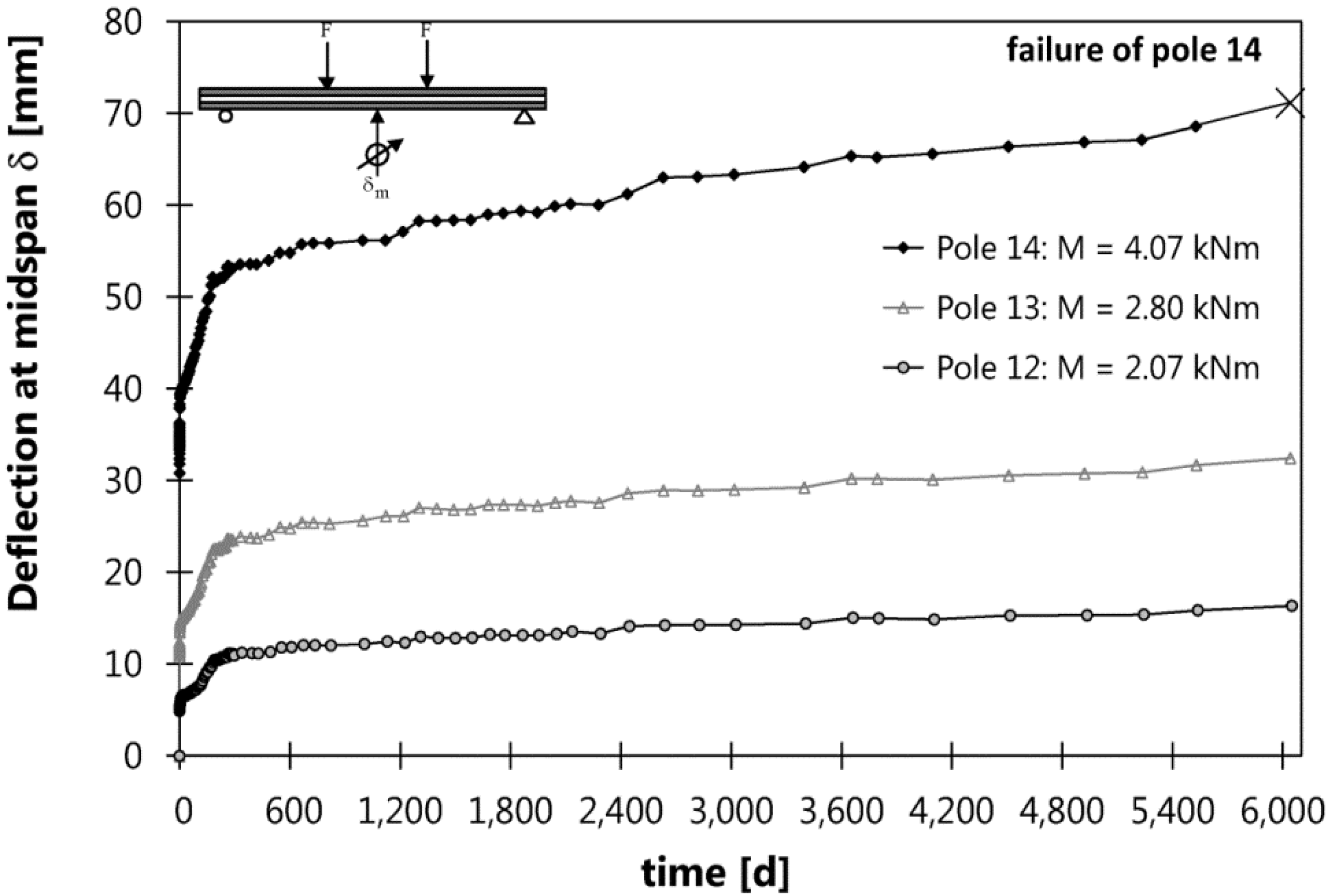
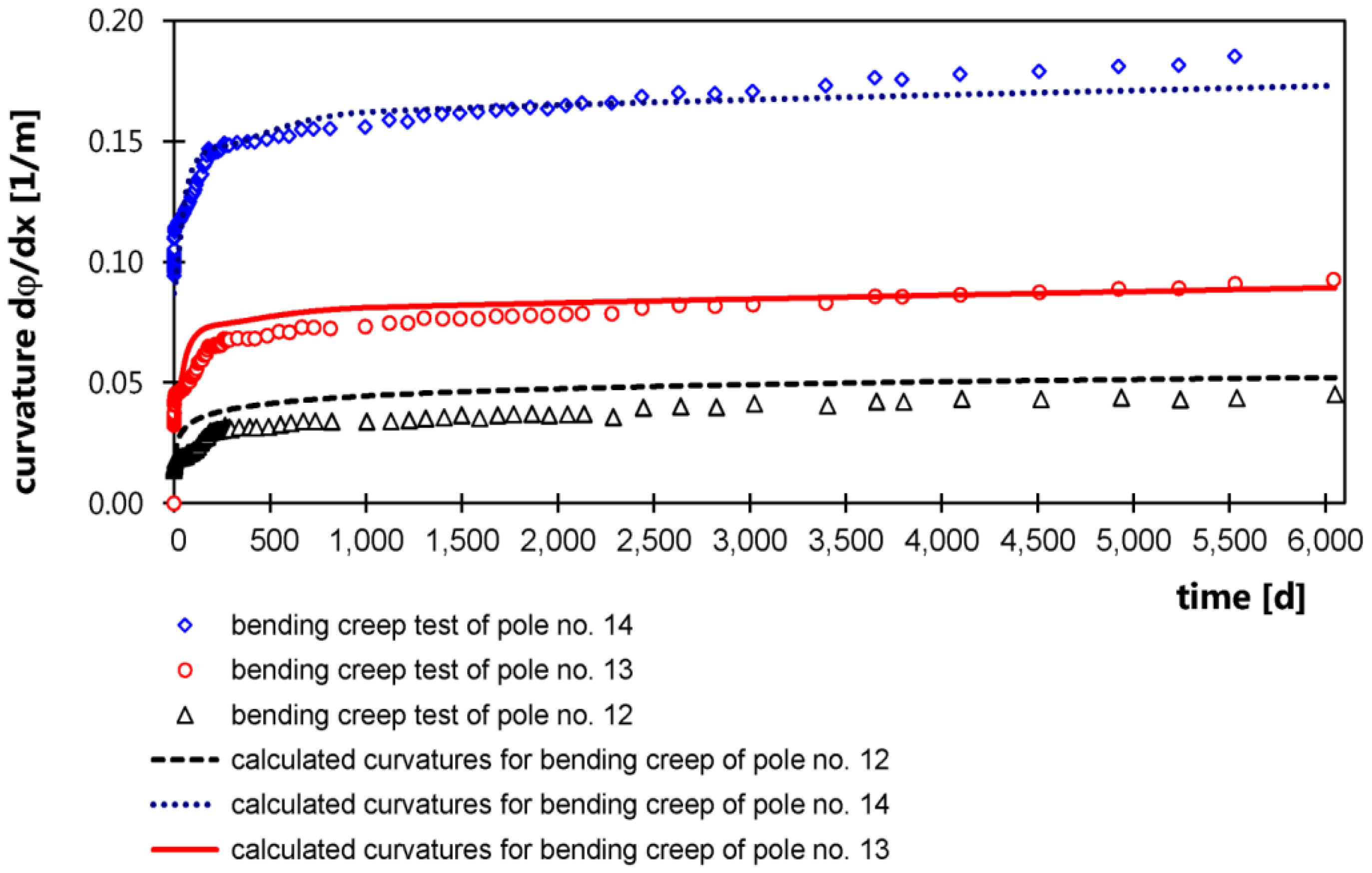
4.2. Long-Term Bending Behavior Outdoors



5. Conclusions
- The short-term bending behavior of CFRP prestressed HPSC poles is bilinear with considerable rotation capacity at failure. The moment vs. curvature behavior and the failure moment for HPSC crushing can be modeled by a simple cross-sectional analysis following the beam theory of hybrid prestressed cross-sections.
- The long-term bending serviceability of CFRP prestressed HPSC poles is satisfactory for realistic service moments, represented by the lowest loaded pole, No. 12, in the test series presented. Long-term curvatures and deflections stabilize after six months of sustained loading. Furthermore, pole specimens under realistic long-term service moments showed crack patterns that were stable over time and minimal slippage of the tendons with respect to the pole’s end faces. The latter proves the successful and durable anchorage of the Al2O3 sand-coated CFRP prestressing tendons of this study in thin-walled precast concrete members under realistic long-term service loads.
- Pole No. 14, which was loaded with twice the maximum long-term service moment, failed after 16.5 years, due to bond failure of the highest loaded CFRP tendon. The debonding of the Al2O3 sand coating from the CFRP tendon surface could be clearly observed.
- The long-term evolution of curvatures due to bending creep of the poles could be modeled analytically with reasonable accuracy using a simple, direct analysis based on the assumption that HPSC creep governs the strain and stress redistribution over the cross-section with time.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Gerritse, A.; Schürhoff, H.J. Prestressing with Aramid Tendons. In Proceedings of the 10th FIP Congress, New Delhi, India, 16–20 February 1986.
- Rostásy, F.S.; Budelmann, H. High strength fiber composites for prestressing. Mater. Eng. 1990, 3, 779–792. [Google Scholar]
- Lees, J.M.; Burgoyne, C.J. Experimental study of influence of bond on flexural behavior of concrete beams pretensioned with aramid fiber reinforced plastics. ACI Struct. J. 1999, 96, 377–385. [Google Scholar]
- Lees, J.M.; Burgoyne, C.J. Transfer bond stresses generated between FRP tendons and concrete. Mag. Concr. Res. 1999, 51, 229–239. [Google Scholar] [CrossRef]
- Sen, R.; Shahawy, M.; Sukumar, S.; Rosas, J. Durability of carbon fiber reinforced polymer (CFRP) pretensioned elements under tidal/thermal cycles. ACI Struct. J. 1999, 96, 450–457. [Google Scholar]
- Nanni, A.; Tanigaki, M. Pretensioned prestressed concrete members with bonded fiber reinforced plastic tendons: development and flexural bond lengths (static). ACI Struct. J. 1992, 89, 433–441. [Google Scholar]
- Terrasi, G.P.; Bättig, G.; Brönnimann, R. Pylons made of high-strength spun concrete and prestressed with carbon fibre reinforced plastic for high power transmission lines. Int. J. Matter. Prod. Technol. 2002, 17, 32–45. [Google Scholar] [CrossRef]
- Portnov, G.; Bakis, C.E.; Lackey, E.; Kulakov, V. FRP Reinforcing bars designs and methods of manufacture (Review of Patents). Mech. Compos. Mater. 2013, 49, 1–20. [Google Scholar] [CrossRef]
- Sayed Ahmad, F.; Foret, G.; Le Roy, R. Bond between carbon fibre-reinforced polymer (CFRP) bars and ultra high performance fibre reinforced concrete (UHPFRC): Experimental study. Constr. Build. Mater. 2011, 25, 479–485. [Google Scholar] [CrossRef]
- Nanni, A.; Bakis, C.E.; O’Neil, E.F.; Dixon, T.O. Performance of FRP tendon-anchor systems for prestressed concrete structures. PCI J. 1996, 41, 34–44. [Google Scholar]
- Toutanji, H.; Saafi, M. Performance of concrete beams prestressed with aramid fiber-reinforced polymer tendons. Compos. Struct. 1999, 44, 63–70. [Google Scholar] [CrossRef]
- Campbell, T.I.; Shrive, N.G.; Soudki, K.A.; Al-Mayah, A.; Keatley, J.P.; Reda, M.M. Design and evaluation of a wedge-type anchor for fibre reinforced polymer tendons. Ca. J. Civil Eng. 2000, 27, 985–992. [Google Scholar] [CrossRef]
- Cosenza, E.; Manfredi, G.; Realfonzo, R. Behavior and modeling of bond of FRP rebars to concrete. J. Compos. Constr. 1997, 1, 40–51. [Google Scholar] [CrossRef]
- De Lorenzis, L.; Miller, B.; Nanni, A. Bond of fiber-reinforced polymer laminates to concrete. ACI Mater. J. 2001, 98, 256–264. [Google Scholar]
- Bakis, C.E.; Uppuluri, V.S.; Nanni, A.; Boothby, T.E. Analysis of bonding mechanisms of smooth and lugged frp rods embedded in concrete. Compos. Sci. Technol. 1998, 58, 1307–1319. [Google Scholar] [CrossRef]
- Mahmoud, Z.I.; Rizkalla, S.H. Bond of CFRP prestressing reinforcement. In Proceedings of 2nd International Conference on Advanced Composite Materials in Bridges and Structures, Montreal, Canada, 11–14 August 1996.
- Gerritse, A.; Den Uijl, J. Long term behaviour of arapree. In Proceedings of Non-Metallic (FRP) Reinforcement for Concrete Structures (FRPRCS-2), Ghent, Belgium, 23–25 August 1995; pp. 57–66.
- Shahidi, F. Bond degradation between FRP bars and concrete under sustained loads. Ph.D. Thesis, University of Saskatchewan, Saskatoon, Canada, 2003. [Google Scholar]
- Fornůsek, J.; Konvalinka, P.; Sovják, R.; Vítek, J.L. Long-term behaviour of concrete structures reinforced with pre-stressed GFRP tendons. WIT Trans. Model. Simul. 2009, 1, 535–545. [Google Scholar]
- Terrasi, G.P.; Brönnimann, R.; Bättig, G. CFRP tendon prestress monitoring by resistance measurement in a spun concrete powerline pylon. In Proceedings of the first middle east conference on smart monitoring, assessment and rehabilitation of civil structures (SMAR 2011), American University, Dubai, UAE, 8–10 February 2011.
- Zou, P.X.W. Long-term deflection and cracking behavior of concrete beams prestressed with carbon fiber-reinforced polymer tendons. J. Compos. Constr. 2003, 7, 187–193. [Google Scholar]
- Zou, P.X.W.; Shang, S. Time-dependent behaviour of concrete beams pretensioned by carbon fibre-reinforced polymers (CFRP) tendons. Constr. Build. Mater. 2007, 21, 777–788. [Google Scholar] [CrossRef]
- Youakim, S.A.; Karbhari, V.M. An approach to determine long-term behavior of concrete members prestressed with FRP tendons. Constr. Build. Mater. 2007, 21, 1052–1060. [Google Scholar] [CrossRef]
- Rodriguez-Gutierrez, J.A.; Aristizabal-Ochoa, J.D. Short- and long-term deflections in reinforced, prestressed, and composite concrete beams. J. Struct. Eng. 2007, 133, 495–506. [Google Scholar] [CrossRef]
- Terrasi, G.P. Mit Kohlenstoffasern vorgespannte Schleuderbetonrohre. Ph.D. Thesis, Eidgenössische Technische Hochschule (ETH), Zurich, Switzerland, 1998. [Google Scholar]
- Agyei, B.B.; Lees, J.M.; Terrasi, G.P. Fatigue of high strength concrete beams pretensioned with CFRP tendons. In Proceedings of 6th International Symposium on Fibre-Reinforced Polymer (FRP) Reinforcement for Concrete Structures (FRPRCS-6), Singapore, 8–10 July 2003.
- Roberts, E.E.; Lees, J.M.; Hoult, N.A. Flexural fatigue performance of CFRP prestressed concrete poles. Adv. Struct. Eng. 2012, 15, 575–588. [Google Scholar] [CrossRef]
- Uomoto, T. Durability considerations of FRP reinforcement. In Proceedings of the Non-Metallic (FRP) Reinforcement for Concrete Structures (FRPRCS-5), Cambridge, UK, 16–18 July 2001.
- Burgoyne, C.J. Rational use of advanced composites in concrete. In Proceedings of the Non-Metallic (FRP) Reinforcement for Concrete Structures (FRPRCS-3), Sapporo, Japan, 14–16 October 1997.
- Terrasi, G.P. Prefabricated Thin-walled Structural Elements Made from High Performance Concrete Prestressed with CFRP Wires. J. Mater. Sci. Res. 2013, 2. [Google Scholar] [CrossRef]
- Terrasi, G.P.; Lees, J.M. CFRP Prestressed Concrete Lighting Columns. Am. Concr. Inst. Int. 2003, 215, 55–74. [Google Scholar]
- American Concrete Institute (ACI). Prestressing Concrete Structures with FRP Tendons; ACI 440. 4R-04; Detroit, MI, USA, 2004. [Google Scholar]
- Swiss Standard. SN 505 160, Loads on Structures; SIA 160; Swiss Engineers and Architects Society: Zurich, Switzerland, 1989. [Google Scholar]
- Saadatmanesh, H.; Tannous, F.E. Relaxation, creep, and fatigue behavior of carbon fiber reinforced plastic tendons. ACI Mater. J. 1999, 96, 143–153. [Google Scholar]
- Bachmann, H. Spannbeton II (Prestressed Concrete); Vdf university publishers of ETH (Eidgenössische Technische Hochschule): Zurich, Switzerland, 1991. (In German) [Google Scholar]
- Held, M. A Contribution to the Production and Design of Compressive Members made of High Strength Concrete. Ph.D. Thesis, Technische Universität Darmstadt, Darmstadt, Germany, 1992. [Google Scholar]
- Deskovic, N.; Meier, U.; Triantafillou, T.C. Innovative design of FRP combined with concrete: Long-term behavior. J. Struct. Eng. NY 1995, 121, 1079–1089. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Terrasi, G.P.; Meier, U.; Affolter, C. Long-Term Bending Creep Behavior of Thin-Walled CFRP Tendon Pretensioned Spun Concrete Poles. Polymers 2014, 6, 2065-2081. https://doi.org/10.3390/polym6072065
Terrasi GP, Meier U, Affolter C. Long-Term Bending Creep Behavior of Thin-Walled CFRP Tendon Pretensioned Spun Concrete Poles. Polymers. 2014; 6(7):2065-2081. https://doi.org/10.3390/polym6072065
Chicago/Turabian StyleTerrasi, Giovanni P., Urs Meier, and Christian Affolter. 2014. "Long-Term Bending Creep Behavior of Thin-Walled CFRP Tendon Pretensioned Spun Concrete Poles" Polymers 6, no. 7: 2065-2081. https://doi.org/10.3390/polym6072065
APA StyleTerrasi, G. P., Meier, U., & Affolter, C. (2014). Long-Term Bending Creep Behavior of Thin-Walled CFRP Tendon Pretensioned Spun Concrete Poles. Polymers, 6(7), 2065-2081. https://doi.org/10.3390/polym6072065




