Behavior of FRP-Confined Concrete-Filled Steel Tube Columns
Abstract
:1. Introduction
2. Experimental Program
2.1. Test Specimens
| Specimens | L (mm) | D (mm) | FRP type | nf | ts (mm) | fcu (MPa) | fy (MPa) | ξs | ξf |
|---|---|---|---|---|---|---|---|---|---|
| t4C40 | 400 | 128 | – | – | 4.0 | 44.9 | 248 | 0.95 | 0.00 |
| CF1t4C40 | 400 | 128 | CFRP | 1 | 4.0 | 44.9 | 248 | 0.95 | 0.39 |
| CF2t4C40 | 400 | 128 | CFRP | 2 | 4.0 | 44.9 | 248 | 0.95 | 0.78 |
| CF3t4C40 | 400 | 128 | CFRP | 3 | 4.0 | 44.9 | 248 | 0.95 | 1.17 |
| GF1t4C40 | 400 | 128 | GFRP | 1 | 4.0 | 44.9 | 248 | 0.95 | 0.48 |
| GF2t4C40 | 400 | 128 | GFRP | 2 | 4.0 | 44.9 | 248 | 0.95 | 0.97 |
| GF3t4C40 | 400 | 128 | GFRP | 3 | 4.0 | 44.9 | 248 | 0.95 | 1.45 |
| CF2t3C40 | 400 | 126 | CFRP | 2 | 3.0 | 44.9 | 243 | 0.69 | 0.77 |
| CF2t5C40 | 400 | 130 | CFRP | 2 | 5.0 | 44.9 | 242 | 1.17 | 0.79 |
| CF2t4C50 | 400 | 128 | CFRP | 2 | 4.0 | 54.2 | 248 | 0.79 | 0.65 |
| CF2t4C60 | 400 | 128 | CFRP | 2 | 4.0 | 60.0 | 248 | 0.71 | 0.58 |
2.2. Material Properties
2.3. Preparation of Specimens
2.4. Test Setup and Instrumentation
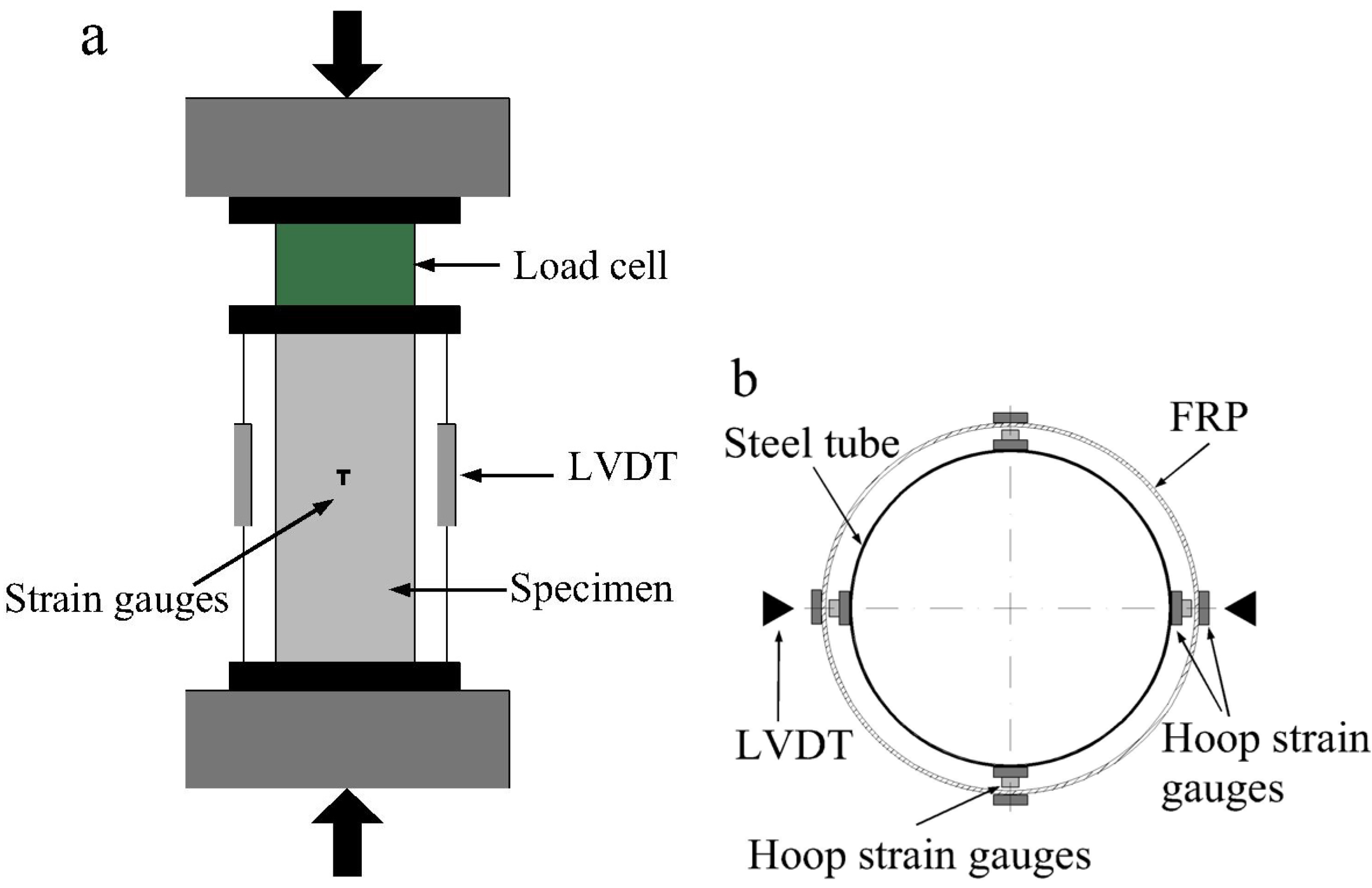
3. Experimental Results and Discussions
3.1. General Observations

3.2. Axial Load-Axial Shortening Behavior
| Specimens | Ny (kN) | Nf (kN) | εf (με) | Nu (kN) | δu (mm) | kε2 | Nup (kN) | Nu/Nup |
|---|---|---|---|---|---|---|---|---|
| t4C40 | 800 | – | – | 1,130 | 3.5 | – | 1,101 | 1.03 |
| CF1t4C40 | 850 | 1,200 | 10,227 | 1,300 | 5.2 | 0.76 | 1,283 | 1.01 |
| CF2t4C40 | 900 | 1,400 | 11,025 | 1,440 | 6.5 | 0.82 | 1,466 | 0.98 |
| CF3t4C40 | 900 | 1,670 | 10,821 | 1,685 | 9.4 | 0.81 | 1,648 | 1.02 |
| GF1t4C40 | 900 | 900 | 19,890 | 1,355 | 9.5 | 0.77 | 1,327 | 1.02 |
| GF2t4C40 | 850 | 1,350 | 22,288 | 1,693 | 11.8 | 0.86 | 1,554 | 1.09 |
| GF3t4C40 | 950 | 1,450 | 24,282 | 1,845 | 13. 6 | 0.94 | 1,780 | 1.04 |
| CF2t3C40 | 800 | 1,330 | 10,816 | 1,330 | 7.1 | 0.81 | 1,271 | 1.05 |
| CF2t5C40 | 1,150 | 1,550 | 11,104 | 1,650 | 7.3 | 0.83 | 1,631 | 1.01 |
| CF2t4C50 | 900 | 1,430 | 10,189 | 1,548 | 8.3 | 0.76 | 1,550 | 1.00 |
| CF2t4C60 | 950 | 1,658 | 8,853 | 1,658 | 8.5 | 0.66 | 1,602 | 1.03 |
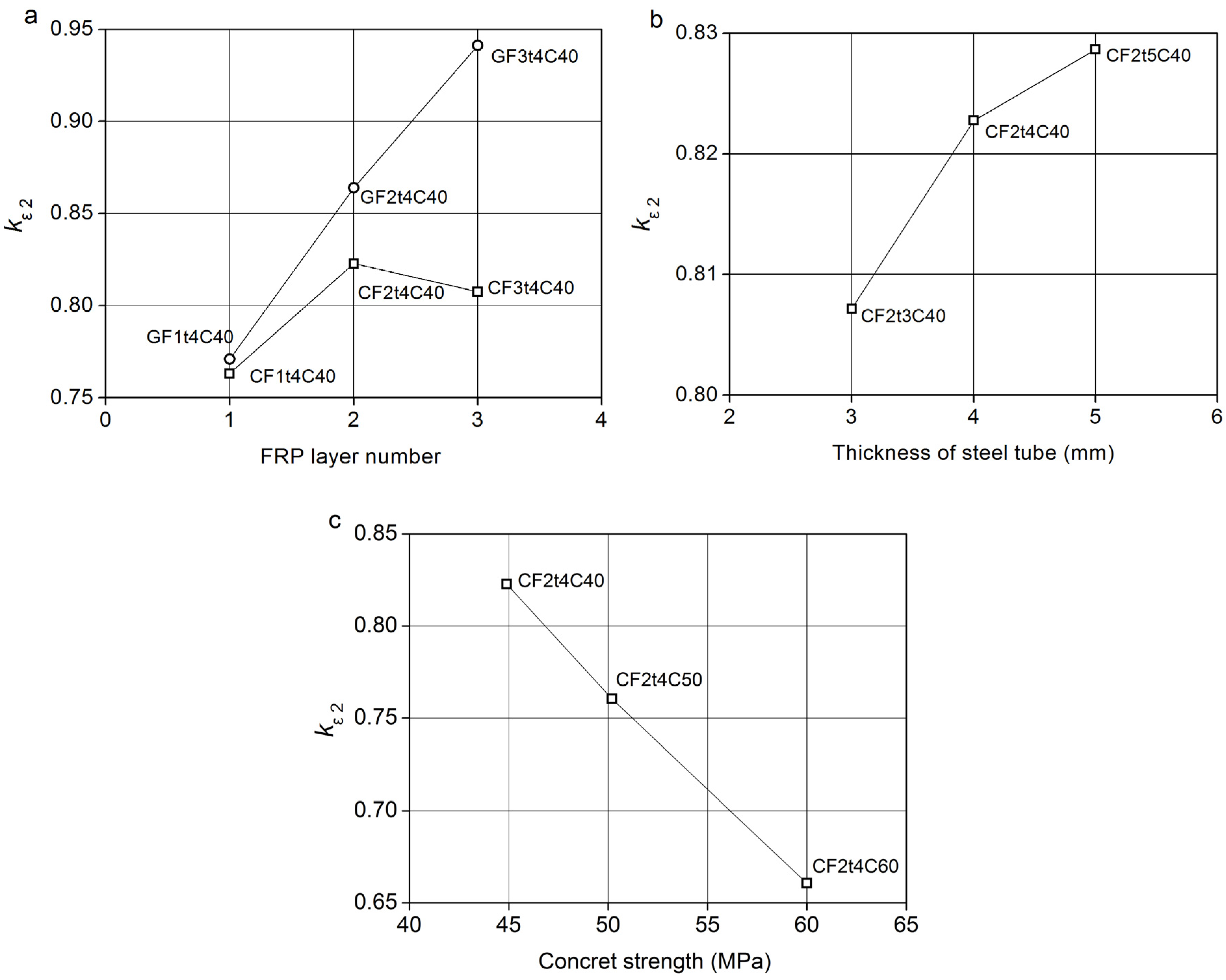
3.2.1. Effect of Fiber-Reinforced Polymer (FRP) Confinement
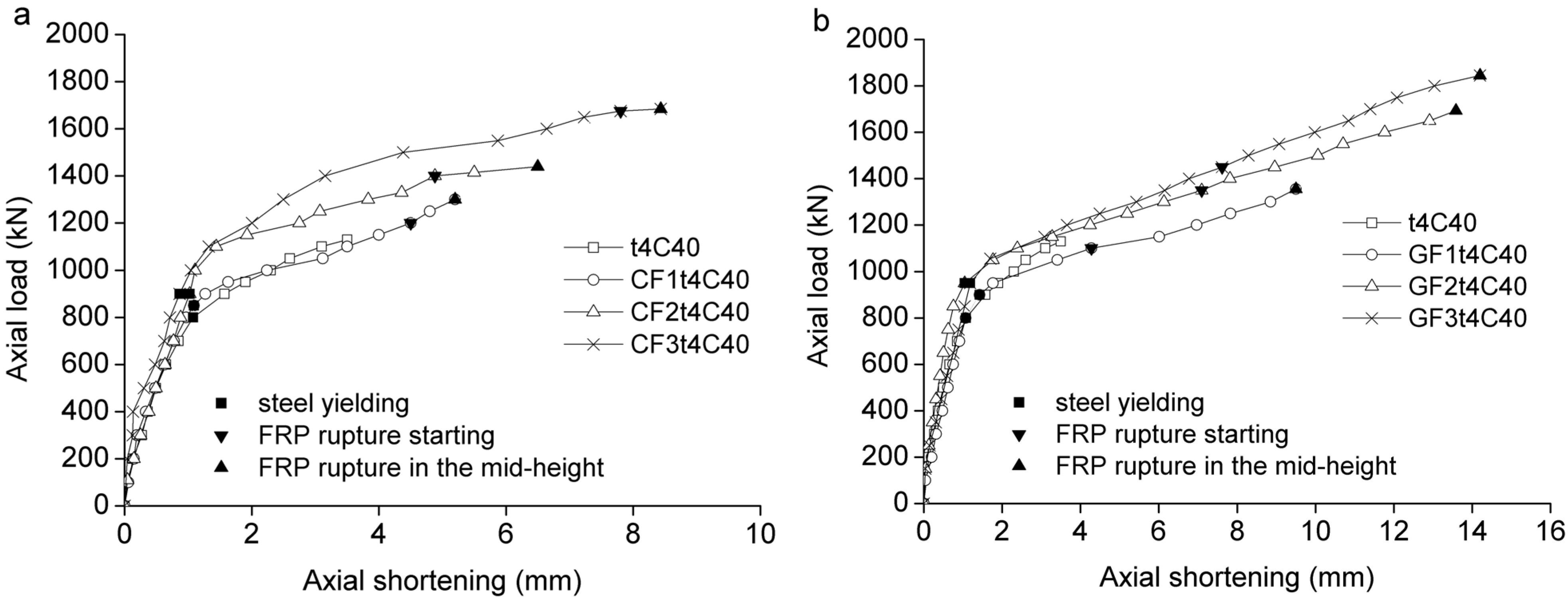
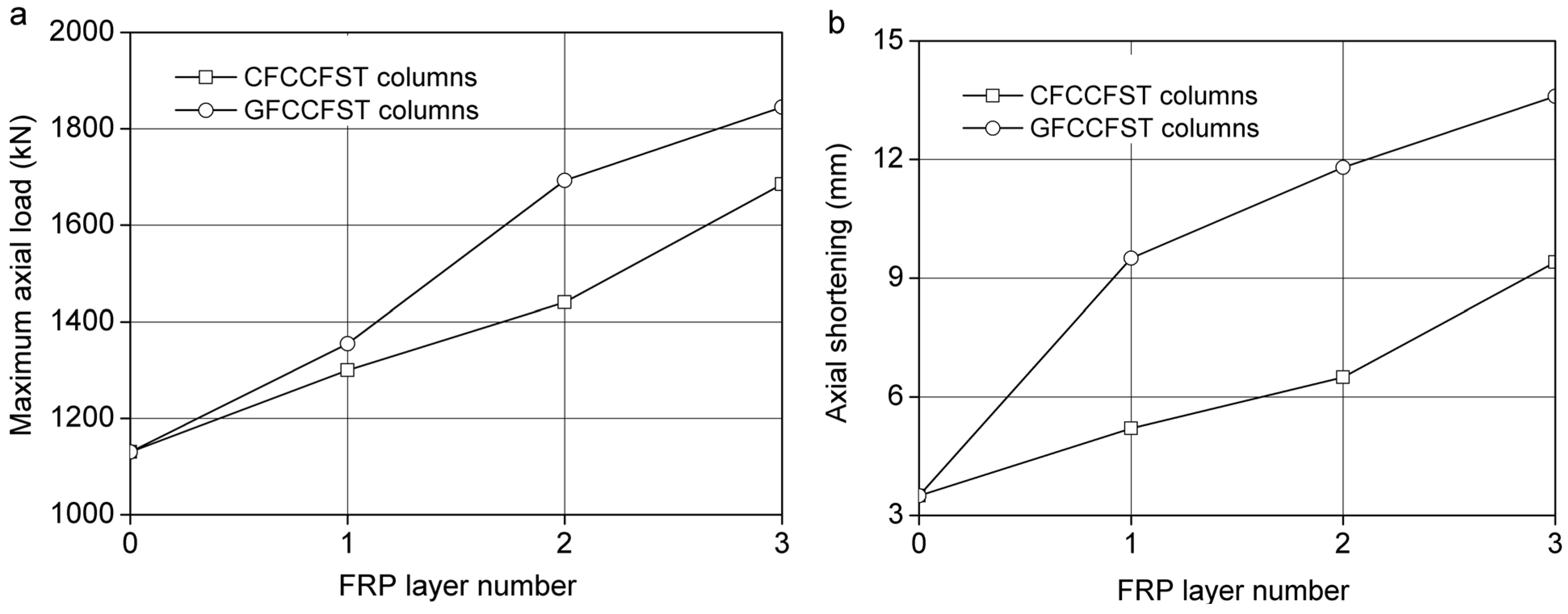
3.2.2. Effect of the Thickness of the Steel Tube
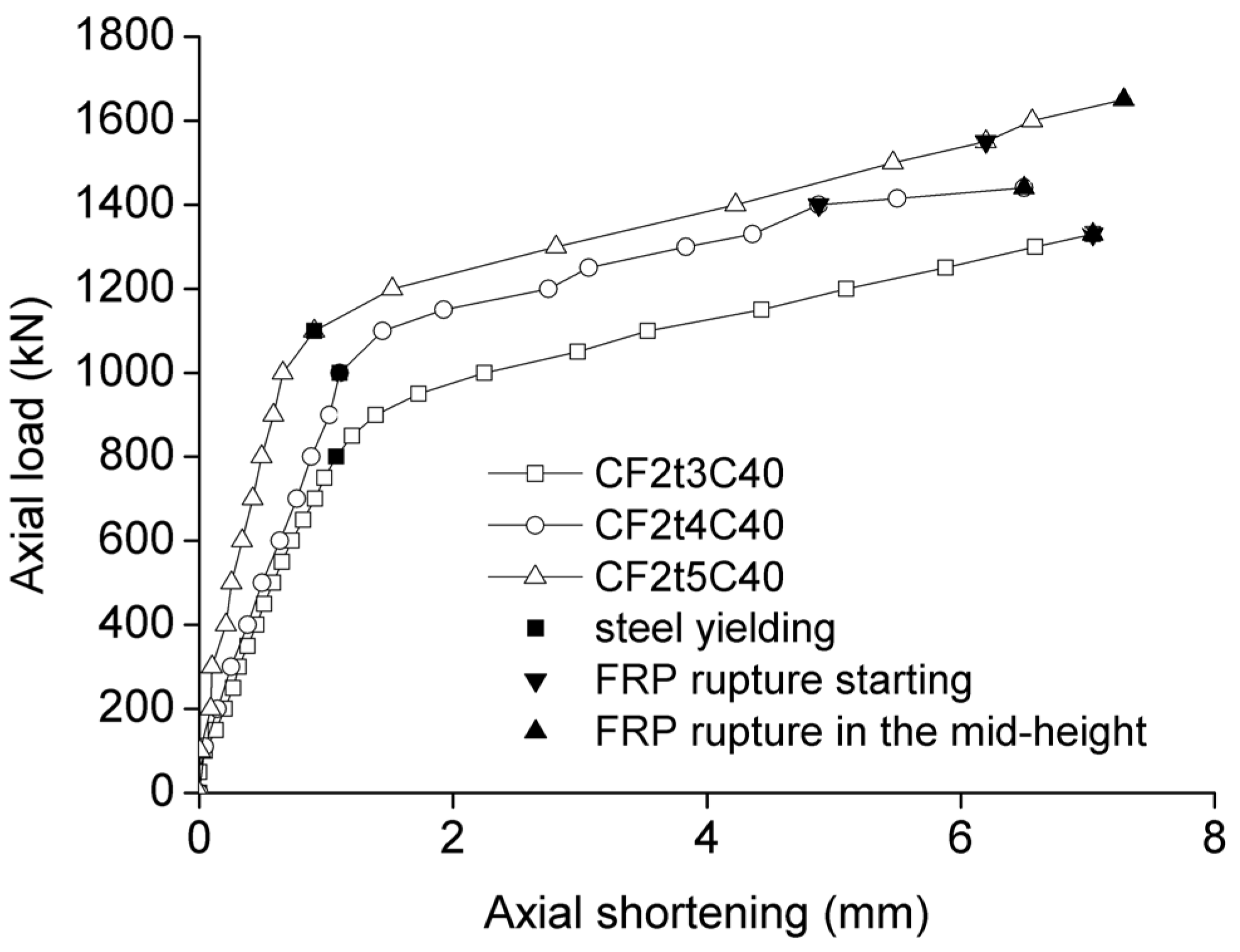
3.2.3. Effect of Concrete Strength

3.3. Behavior of Confined Concrete
| Specimens | fcc, fccf | fcc/fccf | εcc, εccf | εcc/εccf |
|---|---|---|---|---|
| t4C40 | 65.80 | – | 0.0088 | – |
| CF1t4C40 | 80.83 | 1.23 | 0.0130 | 1.49 |
| CF2t4C40 | 93.22 | 1.42 | 0.0163 | 1.86 |
| CF3t4C40 | 114.89 | 1.75 | 0.0235 | 2.69 |
| GF1t4C40 | 85.70 | 1.30 | 0.0238 | 2.71 |
| GF2t4C40 | 115.60 | 1.76 | 0.0295 | 3.37 |
| GF3t4C40 | 129.05 | 1.96 | 0.0340 | 3.89 |
3.3.1. Confining Pressure

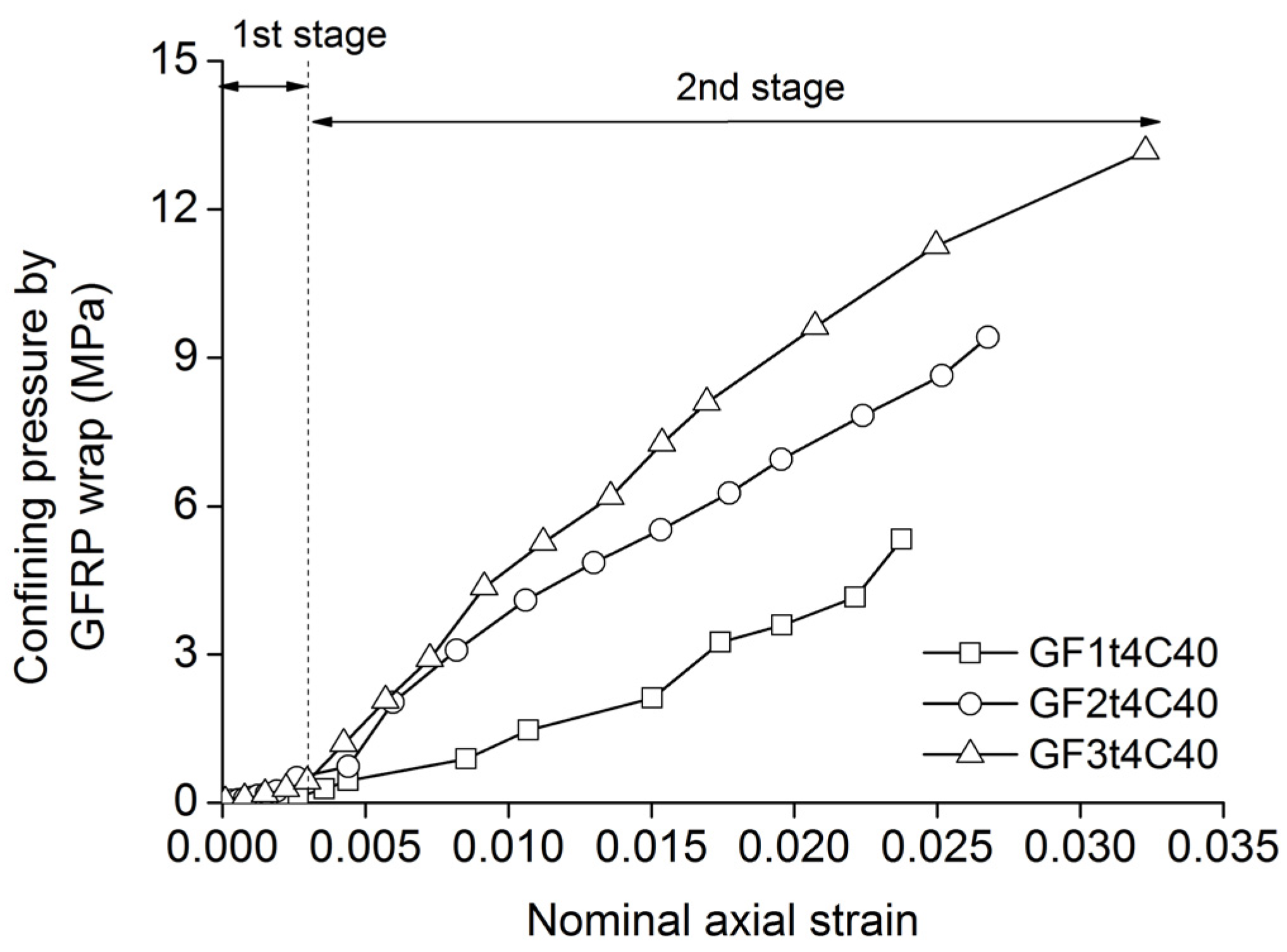
3.3.2. Lateral Expansion Behavior

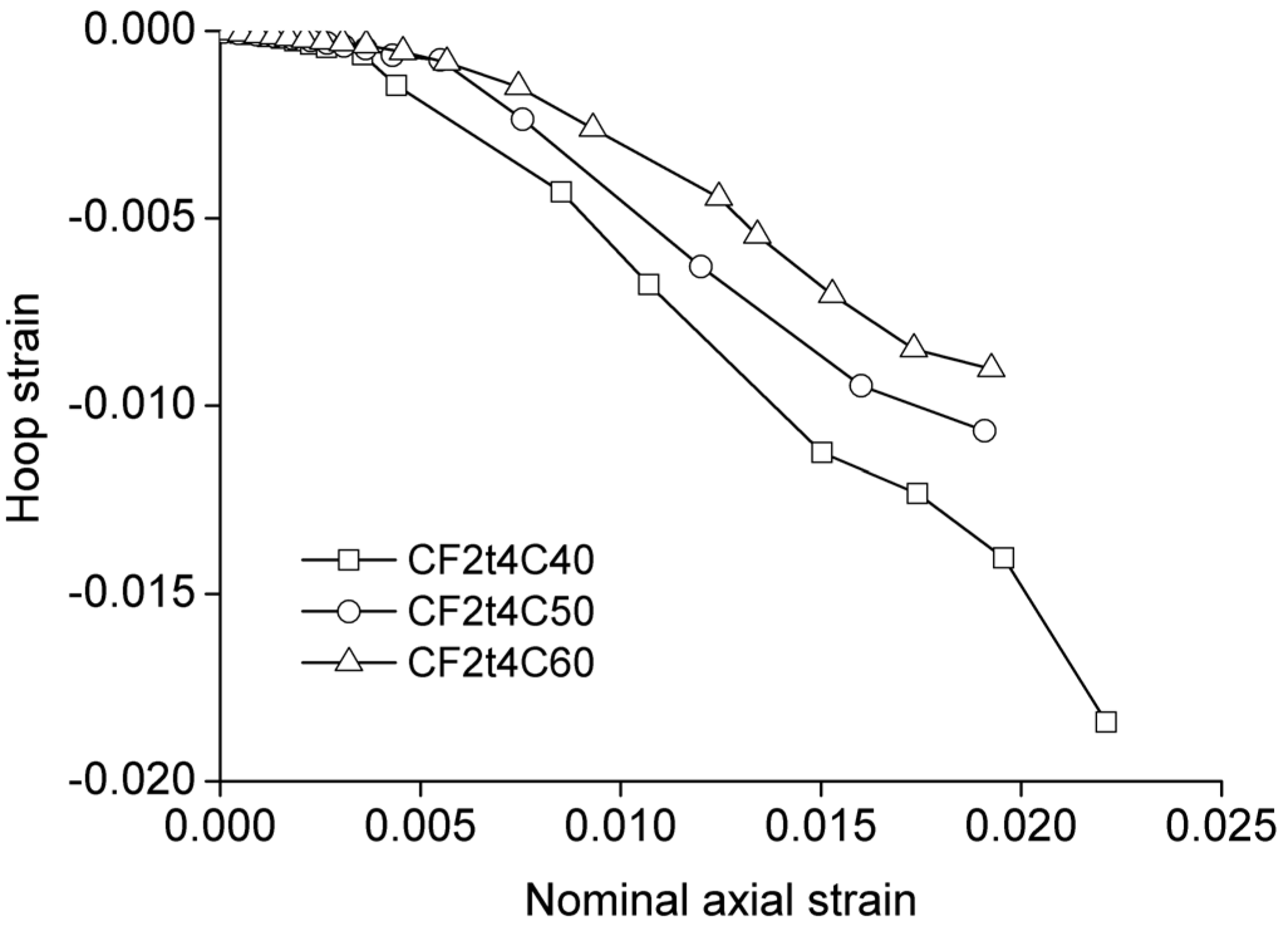
3.3.3. Strain Efficiency of FRP Wrap
3.4. Local Behavior of Steel Tube
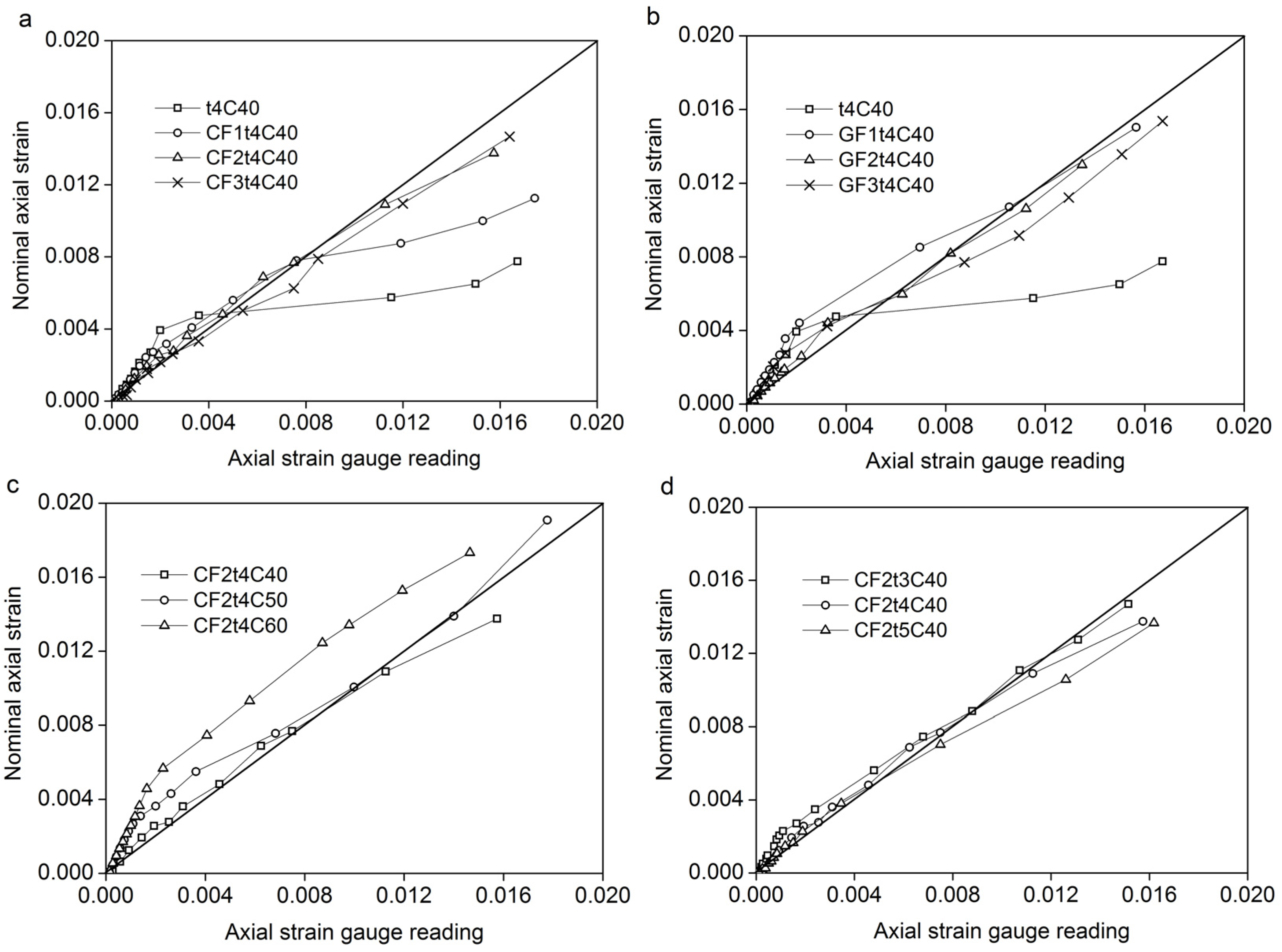
4. Prediction of Load Capacity


| Specimens | D (mm) | ts (mm) | fy (MPa) | fcu (MPa) | fc (MPa) | nf | tf | ff (MPa) | ξs | ξf | Nu (kN) | Nup (kN) | Nu/Nup |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Xiao et al. [6] | |||||||||||||
| CFT | 152 | 2.95 | 356 | – | 47 | 0 | – | – | 0.69 | – | 1453 | 1593 | 0.91 |
| CCFT-2L-1 | 152 | 2.95 | 356 | – | 47 | 2 | 2.8 | 897 | 0.69 | 1.69 | 2233 | 2972 | 0.75 |
| CCFT-2L-2 | 152 | 2.95 | 356 | – | 47 | 2 | 2.8 | 897 | 0.69 | 1.69 | 2266 | 2972 | 0.76 |
| CCFT-4L-1 | 152 | 2.95 | 356 | – | 47 | 4 | 5.6 | 897 | 0.69 | 3.38 | 3439 | 4351 | 0.79 |
| CCFT-4L-2 | 152 | 2.95 | 356 | – | 47 | 4 | 5.6 | 897 | 0.69 | 3.38 | 3439 | 4351 | 0.79 |
| Tao et al. [9] | |||||||||||||
| C1-0 | 156 | 3.0 | 230 | – | 46 | 0 | – | 4212 | 0.45 | – | 1245 | 1328 | 0.94 |
| C1-1 | 156 | 3.0 | 230 | – | 46 | 1 | 0.170 | 4212 | 0.45 | 0.48 | 1649 | 1731 | 0.95 |
| C1-2 | 156 | 3.0 | 230 | – | 46 | 2 | 0.340 | 4212 | 0.45 | 0.96 | 2053 | 2135 | 0.96 |
| C2-0 | 250 | 3.0 | 230 | – | 46 | 0 | – | 4212 | 0.28 | – | 2831 | 2898 | 0.98 |
| C2-1 | 250 | 3.0 | 230 | – | 46 | 1 | 0.170 | 4212 | 0.28 | 0.29 | 3478 | 3545 | 0.98 |
| C2-2 | 250 | 3.0 | 230 | – | 46 | 2 | 0.340 | 4212 | 0.28 | 0.58 | 4126 | 4191 | 0.98 |
| Hu et al. [7] | |||||||||||||
| F0-102 | 204 | 2 | 226 | – | 42 | 0 | 0.17 | 1826 | 0.24 | 0.00 | 1864 | 1703 | 1.09 |
| F1-102 | 204 | 2 | 226 | – | 42 | 1 | 0.17 | 1826 | 0.24 | 0.17 | 1993 | 1932 | 1.03 |
| F2-102 | 204 | 2 | 226 | – | 42 | 2 | 0.17 | 1826 | 0.24 | 0.34 | 2127 | 2160 | 0.98 |
| F3-102 | 204 | 2 | 226 | – | 42 | 3 | 0.17 | 1826 | 0.24 | 0.50 | 2427 | 2389 | 1.02 |
| F0-135 | 203 | 1.5 | 242 | – | 42 | 0 | 0.17 | 1826 | 0.19 | 0.00 | 1699 | 1600 | 1.06 |
| F2-135 | 203 | 1.5 | 242 | – | 42 | 2 | 0.17 | 1826 | 0.19 | 0.33 | 2014 | 2055 | 0.98 |
| F3-135 | 203 | 1.5 | 242 | – | 42 | 3 | 0.17 | 1826 | 0.19 | 0.50 | 2244 | 2283 | 0.98 |
| F4-135 | 203 | 1.5 | 242 | – | 42 | 4 | 0.17 | 1826 | 0.19 | 0.67 | 2561 | 2511 | 1.02 |
| F0-202 | 202 | 1 | 231 | – | 36 | 0 | 0.17 | 1826 | 0.14 | 0.00 | 1380 | 1280 | 1.08 |
| Hu et al. [7] | |||||||||||||
| F2-202 | 202 | 1 | 231 | – | 36 | 2 | 0.17 | 1826 | 0.14 | 0.39 | 1749 | 1733 | 1.01 |
| F3-202 | 202 | 1 | 231 | – | 36 | 3 | 0.17 | 1826 | 0.14 | 0.58 | 1961 | 1959 | 1.00 |
| F4-202 | 202 | 1 | 231 | – | 36 | 4 | 0.17 | 1826 | 0.14 | 0.77 | 2265 | 2185 | 1.04 |
| Gu et al [29] | |||||||||||||
| 0-1.5 | 127 | 1.5 | 350 | 55 | – | 0 | – | – | 0.39 | – | 890 | 903 | 0.99 |
| 0-2.5 | 129 | 2.5 | 350 | 55 | – | 0 | – | – | 0.65 | – | 1140 | 1157 | 0.99 |
| 0-3.5 | 131 | 3.5 | 310 | 55 | – | 0 | – | – | 0.82 | – | 1293 | 1313 | 0.98 |
| 0-4.5 | 133 | 4.5 | 310 | 55 | – | 0 | – | – | 1.06 | – | 1528 | 1544 | 0.99 |
| 1-1.5 | 127 | 1.5 | 350 | 55 | – | 1 | 0.167 | 1260 | 0.39 | 0.16 | 1086 | 1000 | 1.09 |
| 1-2.5 | 129 | 2.5 | 350 | 55 | – | 1 | 0.167 | 1260 | 0.65 | 0.16 | 1294 | 1255 | 1.03 |
| 1-3.5 | 131 | 3.5 | 310 | 55 | – | 1 | 0.167 | 1260 | 0.82 | 0.16 | 1348 | 1413 | 0.95 |
| 1-4.5 | 133 | 4.5 | 310 | 55 | – | 1 | 0.167 | 1260 | 1.06 | 0.17 | 1689 | 1645 | 1.03 |
| 2-1.5 | 127 | 1.5 | 350 | 55 | – | 2 | 0.334 | 1260 | 0.39 | 0.32 | 1283 | 1096 | 1.17 |
| 2-2.5 | 129 | 2.5 | 350 | 55 | – | 2 | 0.334 | 1260 | 0.65 | 0.32 | 1506 | 1353 | 1.11 |
| 2-3.5 | 131 | 3.5 | 310 | 55 | – | 2 | 0.334 | 1260 | 0.82 | 0.33 | 1593 | 1512 | 1.05 |
| 2-4.5 | 133 | 4.5 | 310 | 55 | – | 2 | 0.334 | 1260 | 1.06 | 0.33 | 1846 | 1746 | 1.06 |
5. Conclusions
- The load capacity and the axial deformation capacity of concrete-filled steel tube columns can be effectively improved by the FRP wrap. All specimens failed by the explosive rupture of the FRP in the mid-height region because of the lateral expansion of the concrete.
- The FRP wrap can delay the outward local buckling deformation of the steel tube and suppress the lateral expansion of the concrete in the CFST column. The strength and the strain capacity of the concrete can be enhanced by the additional confinement from the FRP wrap.
- The GFRP wrap has higher strain efficiency than the CFRP wrap. The CFRP efficiency increases with the increasing of the CFRP layer number, but decreases with the increasing of the concrete strength.
- A simple model is proposed to predict the load capacity of the FCCFST columns. The model can accurately predict the load capacity of the FCCFST columns with not too strong FRP confinement. However, it overestimates that of the FCCFST columns with strong FRP confinement. Therefore, there is further research needed to develop a more accurate design approach when strong FRP confinement is exerted on CFST columns.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Fam, A.; Qie, F.; Rizkalla, S. Concrete-filled steel tubes subjected to axial compression and lateral cyclic loads. J. Struct. Eng. 2004, 130, 631–640. [Google Scholar] [CrossRef]
- O’Shea, M.D.; Bridge, R.Q. Design of circular thin-walled concrete-filled steel tubes. J. Struct. Eng. 2000, 126, 1295–1303. [Google Scholar] [CrossRef]
- Xiao, Y. Applications of FRP Composites in Concrete Columns. Adv. Struct. Eng. 2004, 7, 335–343. [Google Scholar] [CrossRef]
- Teng, J.G.; Yu, T.; Ferando, D. Strengthening of steel structures with fiber-reinforced polymer composites. J. Constr. Steel Res. 2012, 78, 131–143. [Google Scholar] [CrossRef]
- Smith, S.T.; Kim, M.S.J.; Zhang, H.W. Behavior and Effectiveness of FRP Wrap in the Confinement of Large Concrete Cylinders. J. Compos. Constr. 2010, 14, 573–582. [Google Scholar] [CrossRef]
- Xiao, Y.; He, W.H.; Choi, K.K. Confined concrete-filled tubular columns. J. Struct. Eng. 2005, 131, 488–497. [Google Scholar] [CrossRef]
- Hu, Y.M.; Yu, T.; Teng, J.G. FRP-Confined Circular Concrete-Filled Thin Steel Tubes under Axial Compression. J. Compos. Constr. 2011, 15, 850–860. [Google Scholar] [CrossRef]
- Sundarraja, M.C.; Prabhu, G.G. Experimental study on CFST members strengthened by CFRP composites under compression. J. Constr. Steel Res. 2012, 72, 75–83. [Google Scholar] [CrossRef]
- Tao, Z.; Han, L.H.; Zhuang, J.P. Axial Loading Behavior of CFRP Strengthened Concrete-Filled Steel Tubular Stub Columns. Adv. Struct. Eng. 2007, 10, 37–46. [Google Scholar] [CrossRef]
- Dong, J.F.; Wang, Q.Y.; Guan, Z.W. Structural behaviour of recycled aggregate concrete-filled steel tube columns strengthened by CFRP. Eng. Struct. 2013, 48, 532–542. [Google Scholar] [CrossRef]
- Choi, K.K.; Xiao, Y. Analytical model of circular CFRP confined concrete-filled steel tubular columns under axial compression. J. Compos. Constr. 2010, 14, 125–133. [Google Scholar] [CrossRef]
- Liu, L.; Lu, Y.Y. Axial bearing capacity of short FRP confined concrete-filled steel tubular columns. J. Wuhan Univ. Technol. Mater. Sci. Ed. 2010, 25, 454–458. [Google Scholar] [CrossRef]
- Teng, J.G.; Hu, Y.M. Stress-strain model for concrete in FRP-confined steel tubular columns. Eng. Struct. 2013, 49, 156–167. [Google Scholar] [CrossRef]
- Li, S.Q.; Chen, J.F.; Bisby, L.A. Strain efficiency of FRP jackets in FRP-confined concrete-filled circular steel tubes. Int. J. Struct. Stab. Dy. 2012, 12, 75–94. [Google Scholar] [CrossRef]
- Yu, T; Hu, Y.M.; Teng, J.G. FRP-confined circular concrete-filled steel tubular columns under cyclic axial compression. J. Constr. Steel Res. 2014, 94, 33–48. [Google Scholar] [CrossRef]
- Che, Y.; Wang, Q.L.; Shao, Y.B. Experimental study on hysteretic behaviors of concrete-filled circular CFRP-steel tubular beam-columns. China Civ. Eng. J. 2011, 44, 46–54. (In Chinese) [Google Scholar]
- Mao, X.Y.; Xiao, Y. Seismic behavior of confined square CFT columns. Eng. Struct. 2006, 28, 1378–1386. [Google Scholar] [CrossRef]
- Li, S.; Lu, Y.Y.; Li, N. Experimental study on shear resistance performance of concrete-filled circular FRP-steel tube columns. J. Build. Struct. 2012, 33, 107–114. [Google Scholar]
- Shan, J.H.; Chen, R.; Zhang, W.X. Behavior of Concrete-Filled Tubes and Confined Concrete-Filled Tubes under High Speed Impact. Adv. Struct. Eng. 2007, 10, 209–218. [Google Scholar] [CrossRef]
- Xiao, Y.; Shen, Y.L. Impact Behaviors of CFT and CFRP-confined CFT Stub Columns. J. Compos. Constr. 2012, 16, 662–670. [Google Scholar] [CrossRef]
- Tao, Z.; Han, L.H.; Wang, L.L. Compressive and flexural behaviour of CFRP-repaired concrete-filled steel tubes after exposure to fire. J. Constr. Steel Res. 2007, 63, 1116–1126. [Google Scholar] [CrossRef]
- Standard Test Method for Tensile Properties of Polymer Matrix Composite Material; ASTM D3039/D3039M-08; American Society for Testing and Materials (ASTM): West Conshohocken, PA, USA, 2006.
- Pessiki, S.; Harries, K.; Kestner, J. Axial Behavior of Reinforced Concrete Columns Confined with FRP Jackets. J. Compos. Constr. 2001, 5, 237–245. [Google Scholar] [CrossRef]
- Lam, L.; Teng, J.G. Ultimate Condition of Fiber Reinforced Polymer-Confined Concrete. J. Compos. Constr. 2004, 8, 539–548. [Google Scholar] [CrossRef]
- Han, L.H. Theoretical analysis and experimental researches for the behaviors high strength concrete-filled steel tubes. Ind. Constr. 1997, 27, 39–44. (In Chinese) [Google Scholar]
- Lam, L.; Teng, J.G. Strength Models for Fiber-Reinforced Plastic-Confined Concrete. J. Struct. Eng. 2002, 128, 612–623. [Google Scholar] [CrossRef]
- Samaan, M.; Mirmiran, A.; Shahawy, M. Model of Concrete Confined by Fiber Composites. J. Struct. Eng. 1998, 124, 1025–1031. [Google Scholar] [CrossRef]
- Yu, Q. Behaviors of FRP-Confined Concrete Columns. Master’s Degree, Harbin Institute of Technology, Harbin, China, 2002. [Google Scholar]
- Gu, W., Guan; Zhao, Y.H.; Cao, H. Experimental study on concentrically-compressed circular concrete filled CFRP steel composite tubular short columns. J. Shenyang Archit. Civ. Eng. Univ. (Nat. Sci.) 2004, 20, 118–120. (In Chinese) [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Lu, Y.; Li, N.; Li, S. Behavior of FRP-Confined Concrete-Filled Steel Tube Columns. Polymers 2014, 6, 1333-1349. https://doi.org/10.3390/polym6051333
Lu Y, Li N, Li S. Behavior of FRP-Confined Concrete-Filled Steel Tube Columns. Polymers. 2014; 6(5):1333-1349. https://doi.org/10.3390/polym6051333
Chicago/Turabian StyleLu, Yiyan, Na Li, and Shan Li. 2014. "Behavior of FRP-Confined Concrete-Filled Steel Tube Columns" Polymers 6, no. 5: 1333-1349. https://doi.org/10.3390/polym6051333
APA StyleLu, Y., Li, N., & Li, S. (2014). Behavior of FRP-Confined Concrete-Filled Steel Tube Columns. Polymers, 6(5), 1333-1349. https://doi.org/10.3390/polym6051333




