Abstract
Collagen molecules are the primary structural proteins of many biological systems. Much progress has been made in the study of the structure and function of collagen, but fundamental understanding of its electronic structures at the atomic level is still lacking. We present the results of electronic structure and bonding calculations of a specific model of type I collagen using the density functional theory-based method. Information on density of states (DOS), partial DOS, effective charges, bond order values, and intra- and inter-molecular H-bonding are obtained and discussed. We further devised an amino-acid-based potential method (AAPM) to circumvent the full self-consistent field (SCF) calculation that can be applied to large proteins. The AAPM is validated by comparing the results with the full SCF calculation of the whole type I collagen model with three strands. The calculated effective charges on each atom in the model retained at least 95% accuracy. This technique provides a viable and efficient way to study the electronic structure of large complex biomaterials at the ab initio level.
1. Introduction
Collagen molecules are the primary structural proteins found in animals. Together with mineral bioceramics such as hydroxyapatite (HA) and tricalcium phosphate (TCP), these macromolecules constitute the major components of bones and teeth [1]. The structure and properties of the triple helix molecule in type I collagen is an area of intense investigation because the interactions between collagen, mineral bioceramics, and their surrounding environment are important to many bio-related systems. Collagen is a complex multifunctional protein whose various forms are based on different amino acid (residue) sequences contained therein [2,3,4,5]. The most abundant collagen, type I, has a long rod-like triple helix structure [4,6] consisting of three intertwined polypeptide chains, called α-chains, of approximately 3000 Å in length and 15 Å in diameter. Most type I collagen is in the heterotrimer [α1(I)]2[α2(I)] form, where α1(I) and α2(I) are polypeptide chains. The primary structures of the α-chains consist of an amino acid sequence of the general form (Gly-X-Y)n [7,8]. Although the residues X and Y can be any of the 20 canonical amino acids, the glycine (Gly) residue at every third position in the chain is considered to be a prerequisite for the correct formation of the triple helical structure [9,10,11,12,13]. Each α-chain is coiled into a helical secondary structure and the three separate chains are super coiled around a common axis into a triple helical tertiary structure. The collagen molecules are aligned to form microfibrils which are then bundled together to form collagen fibers that are the key to biomineralization [14,15]. Because collagen molecules do not mineralize by themselves, this complicated process is thought to occur through interaction with HA crystallites [16].
The structure of collagen molecules determines their properties and functions. The first triplet position is usually occupied by a Gly residue with a single H-atom for the side chain [17,18,19] whereas the X and Y residues usually have side chains of different lengths with some of them being aromatic. The Gly-Pro-Hyp triplet fits well into the triple helix structure because it has relatively small side chains, however other residues with more substantial side chains can still be accommodated by directing the side chains away from the central axis. They are easily accessible to the surrounding solvent and allow for polar and charged side chains to form additional (water mediated) intra-molecular bridges via H-bonding [10,12,17]. The side chains are also accessible to other molecules, biominerals, or proteins in the biological environment. Hence, the identities of the residues at the X and Y positions to some extent govern the interaction properties of the collagen molecule. Regions along the collagen triple helix with a high degree of substitution of Pro and Hyp for charged and hydrophobic residues often function as binding sites. Finally, the interaction of the collagen molecule with crystalline bioceramics is also largely determined by the domains of specific residues at the X or Y position, and its attraction to a particular surface site of the crystal [20]. It has been known for some time that the presence of specific substitutions or abnormal sequences in the collagen can be related to certain diseases. Indeed, many collagen related diseases such as osteogenesis imperfecta are caused by the single substitution of a Gly residue in the primary sequence, resulting in local deformations of the triple helix [21]. The electronic influence of such substituted structures vs. the “normal” structure may play a role in the interaction of the collagen molecule with its surrounding solvent or substrate. Information on the electronic structure of collagen molecules in relation to different amino acid sequences will thus be very helpful.
Most computational studies on complex biomolecules rely on empirical methods which are less adequate for addressing issues such as interatomic interactions, charge transfer, bond breaking, excited states, spectral response intensity, long range interactions, etc. Current computational efforts on collagen molecules focus mostly on their structures and mechanical properties under various assumptions and approximations [22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39], and less on the electronic structure at the level of amino acids. Nevertheless, a classical description in biomolecular simulations has contributed tremendously in this area because they can be applied to much larger systems [36,37,38,39,40]. The molecular mechanic (MM) and molecular dynamics (MD) simulations based on force field models [41] have been very useful for structural optimizations and elastic properties. These models are extremely valuable in providing plausible structural models based on which more robust ab initio calculations can be demonstrated. Our main goal in this paper is to initiate such investigations by calculating the electronic structure of a specific model of a dry collagen molecule provided by Dr. Simone Vesentini [30] based on classical simulation. More recently, calculations based on density functional theory (DFT) in the local density approximation (LDA) [42,43] have been attempted for a single peptide chain [44]. This study, using a parameterized form for the LDA potential [45,46,47], concentrates on the low energy configurations of dihedral angles of the triplets. Jalkanen et al. [48] used a semi-empirical wave function method to calculate a close-packed structural motif for the triple helix [49]. To the best of our knowledge, no detailed electronic structure calculation on collagen models has been attempted. We also make it very clear from the beginning that it is not our aim to comment on the validity or the appropriateness of the collagen structures which is still quite controversial, and we make no claims on the influence or connections of the electronic structures to the biological functions of collagen and its interaction with biominerals or solvents.
In this paper, we report the ab initio self-consistent field (SCF) calculation on a realistic triple helix model of collagen using the orthogonalized linear combination of atomic orbitals (OLCAO) method [50,51] which is well-suited for complex crystals and biomolecular systems. In Section 2, we report the results of ab initio calculations on a 7-2 heterostructural model of type I collagen. The electronic structure, density of states (DOS) and amino-acid resolved partial DOS (PDOS), interatomic bonding including hydrogen bonding (H-bonding) and charge distributions are presented. In Section 3, we present an efficient method, or amino acid potential method (AAPM), that can be applied to large protein models. The method uses the self-consistent potential functions obtained for each individual amino acid in the protein. This AAPM is validated by comparing the results with the fully self-consistent results of the collagen model presented in Section 2. We conclude the paper with a summary and a vision for future studies on the electronic structures of complex biomaterials.
2. Electronic Structure of a Model of 7-2 Heterostructural Type I Collagen
2.1. Description of the 7-2 Heterostructural Model
The availability of a reliable structural model is the basic necessity for any ab initio calculation. Based on X-ray diffraction studies, two models for type I collagen molecules have been proposed [52,53]. They are referred to as the 7-2 and 10-3 helices which differ in the number of residues per turn around the central axis. In both models, the three α-chains are staggered by exactly one residue along the main helical axis and an angular displacement around the main axis. These models were further refined based on x-ray crystallographic studies of collagen-like models of peptides [16,17,18], together with careful statistical analysis of the secondary and tertiary structures [54]. More recent work seems to suggest that the 7-2 model may be a more frequent structural segment than the 10-3 model [54,55,56,57].
In the present work, the triple-helix collagen model was provided by Dr. Simon Vesentini [30]. He and his collaborators used the HyperChem molecular mechanics software package with the AMBER force field model to construct models for type I collagen and estimate the binding force of the collagen molecule-decorin core protein complex in collagen fibril [58]. The initial primary structure of the α1(I) chain was from GenBank (No. NP000079). All solvent effects for collagen are ignored in this model. This polymeric model is a reasonable representation for a segment of the real collagen molecule. It is sufficiently large to capture the basic features of type I collagen but still within the capability of the OLCAO method for full SCF ab initio calculation of its electronic structure and bonding. Table 1 lists the three single strand molecules (each with 30 trimers and 90 amino acids) in the 7-2 heterostructural model. Figure 1a shows the structure of the α2(I) chain. The other two strands (α1(I) chains) have identical amino acid sequences but with slightly different twists. This model (Figure 1b) contains a total of 1135 atoms and 3246 valence electrons. For the electronic structure calculation, the model was put into a box of 30 Å × 30 Å × 100 Å which is sufficiently large to avoid spurious interactions among replicated molecules in adjacent cells (The closest separation of atoms between adjacent cells is greater than 9 Å). Six H atoms (three on each end) were added to the end of each chain to pacify the dangling bonds. This is a reasonably effective means to avoid the dangling bond effect in the calculation with a model of finite size because the real collagen molecule could be approximately 3000 Å long.

Table 1.
List of amino acids in the 7-2 heterostructural model.
| Chain 1: α2[I] | Chain 2: α1[I] | Chain 3: α1[I] |
|---|---|---|
| Gly-Pro-Met | Gly-Pro-Met | Gly-Pro-Met |
| Gly-Leu-Met | Gly-Pro-Ser | Gly-Pro-Ser |
| Gly-Pro-Arg | Gly-Pro-Arg | Gly-Pro-Arg |
| Gly-Pro-Hyp | Gly-Leu-Hyp | Gly-Leu-Hyp |
| Gly-Ala-Ala | Gly-Pro-Hyp | Gly-Pro-Hyp |
| Gly-Ala-Hyp | Gly-Ala-Hyp | Gly-Ala-Hyp |
| Gly-Pro-Gln | Gly-Pro-Gln | Gly-Pro-Gln |
| Gly-Phe-Gln | Gly-Phe-Gln | Gly-Phe-Gln |
| Gly-Pro-Ala | Gly-Pro-Hyp | Gly-Pro-Hyp |
| Gly-Glu-Hyp | Gly-Glu-Hyp | Gly-Glu-Hyp |
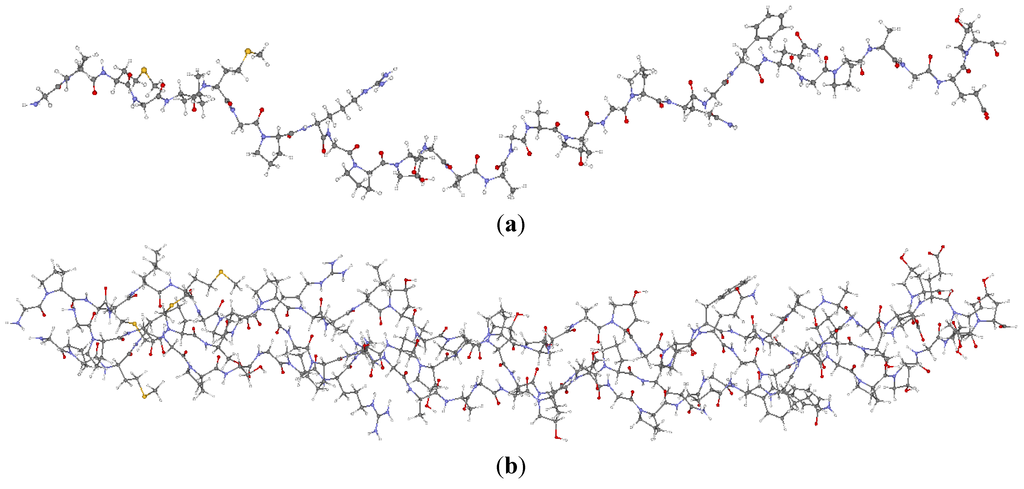
Figure 1.
(Color on-line) (a) The single strand of α2(I) chain in the 7-2 heterostructural model with the positions of Arg and Glu residues marked; and (b) The 7-2 heterostructural model with three strands, [α1(I)]2 α2(I)].
2.2. Method of Calculation
The method we used for the electronic structure calculation is the first-principles OLCAO method [50,51] within the local density approximation (LDA) of density functional theory (DFT). This method was developed in our own laboratory and has been successfully used to study the electronic and spectroscopic properties of many crystalline and non-crystalline materials including biomaterials and bioceramics with complex structures [59,60,61,62,63,64,65,66,67]. In the OLCAO method, the wave function 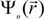 is expanded in terms of atomic orbitals uiα centered at the atomic site Rα. The uiα are expanded as products of Gaussian-type-orbitals (GTOs) and spherical harmonics [51].
is expanded in terms of atomic orbitals uiα centered at the atomic site Rα. The uiα are expanded as products of Gaussian-type-orbitals (GTOs) and spherical harmonics [51].
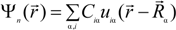
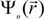 is expanded in terms of atomic orbitals uiα centered at the atomic site Rα. The uiα are expanded as products of Gaussian-type-orbitals (GTOs) and spherical harmonics [51].
is expanded in terms of atomic orbitals uiα centered at the atomic site Rα. The uiα are expanded as products of Gaussian-type-orbitals (GTOs) and spherical harmonics [51].
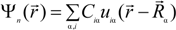
The use of atomic orbitals greatly facilitates the investigation of the electronic structure and bonding of complex biomolecular systems. Quantitative information on interatomic bonding and charge transfer can be obtained via the Mulliken scheme [68]. The effective charge (Qα*) on an atom α and the bond order (BO) values ραβ between each atomic pair (α, β) which quantify the strength of a bond can be evaluated according to:
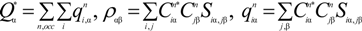 where
where 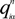 is the fractional charge of the ith orbital in the αth atom of the nth state which contains two electrons (one if the spin quantum number is included in i) and Siα,jβ are the overlap integrals. The calculation of Qα* and BO values enables us to quantitatively assess the charge transfer and bond strength in various parts of the system. The self-consistent potential for the collagen model was obtained by iteratively solving the Kohn-Sham equation with a full basis (FB) set (1s, 2s, 3s, 2p, 3p atomic orbitals for C, O, and N and 1s, 2s, 2p orbitals for H). A minimal basis (MB) set (1s, 2s, 2p for C, O, and N and 1s orbitals for H) was used for effective charge and BO calculations since Mulliken scheme works only for the more localized basis set.
is the fractional charge of the ith orbital in the αth atom of the nth state which contains two electrons (one if the spin quantum number is included in i) and Siα,jβ are the overlap integrals. The calculation of Qα* and BO values enables us to quantitatively assess the charge transfer and bond strength in various parts of the system. The self-consistent potential for the collagen model was obtained by iteratively solving the Kohn-Sham equation with a full basis (FB) set (1s, 2s, 3s, 2p, 3p atomic orbitals for C, O, and N and 1s, 2s, 2p orbitals for H). A minimal basis (MB) set (1s, 2s, 2p for C, O, and N and 1s orbitals for H) was used for effective charge and BO calculations since Mulliken scheme works only for the more localized basis set.
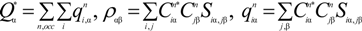
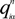 is the fractional charge of the ith orbital in the αth atom of the nth state which contains two electrons (one if the spin quantum number is included in i) and Siα,jβ are the overlap integrals. The calculation of Qα* and BO values enables us to quantitatively assess the charge transfer and bond strength in various parts of the system. The self-consistent potential for the collagen model was obtained by iteratively solving the Kohn-Sham equation with a full basis (FB) set (1s, 2s, 3s, 2p, 3p atomic orbitals for C, O, and N and 1s, 2s, 2p orbitals for H). A minimal basis (MB) set (1s, 2s, 2p for C, O, and N and 1s orbitals for H) was used for effective charge and BO calculations since Mulliken scheme works only for the more localized basis set.
is the fractional charge of the ith orbital in the αth atom of the nth state which contains two electrons (one if the spin quantum number is included in i) and Siα,jβ are the overlap integrals. The calculation of Qα* and BO values enables us to quantitatively assess the charge transfer and bond strength in various parts of the system. The self-consistent potential for the collagen model was obtained by iteratively solving the Kohn-Sham equation with a full basis (FB) set (1s, 2s, 3s, 2p, 3p atomic orbitals for C, O, and N and 1s, 2s, 2p orbitals for H). A minimal basis (MB) set (1s, 2s, 2p for C, O, and N and 1s orbitals for H) was used for effective charge and BO calculations since Mulliken scheme works only for the more localized basis set.The OLCAO calculation was originally developed for crystalline solids [51] so the electronic structures of molecules are usually presented in the form of electronic density of states (DOS) instead of discrete molecular levels as is often the case in quantum chemical calculations. The usual HOMO (highest occupied molecular orbital) to LUMO (lowest unoccupied molecular orbital) gap corresponds to the separation of the top of the valence band (VB) and the bottom of the conduction band (CB) in the DOS. We will use the HOMO–LUMO gap description in this paper for collagen. The total DOS (TDOS) can be conveniently resolved into partial components (PDOS) arising from different subunits of atoms (residues, group of residues, individual atoms and their orbital components, etc.). Such decomposition is very useful since it can interpret the electronic structure and complex interactions in a more illustrative way instead of simply using numbers. This will be illustrated when the results are presented.
An important feature in the OLCAO method is the analytical evaluation of the 2-center and 3-center integrals between Gaussian type orbitals (GTOs) [51]. The GTOs are used in the expansion of both the radial part of the atomic basis function and in the atom-centered potential function 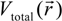 and total charge density
and total charge density  :
:
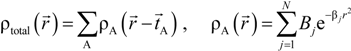
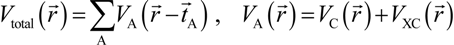
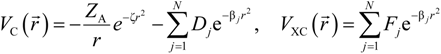
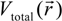 and total charge density
and total charge density  :
:
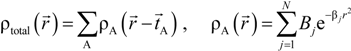
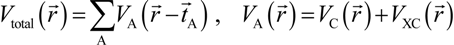
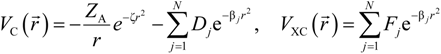
Here, VC and VXC are the Coulomb and exchange-correlation part of the potential. A crucial approximation is introduced which is central to the efficiency of the method [51]. The same set of Gaussian exponentials {βj} is used in both Equations (3) and (5). This reduces the number of multicenter integrals between GTOs by several orders of magnitude and enables the OLCAO method to be applied to very large systems and still retain the ab initio character of the method. The exponential set {βj} is predetermined for each atom and tabulated in the OLCAO data base [51] whereas the coefficients Bj, Dj, Fj, etc. are updated in each cycle of the self-consistent iterations using a linear fitting procedure to 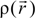 . Because the accuracy of the calculation depends largely on how accurately the true charge density can be represented by Equations (3)–(5), the optimal choice of the fitting set {βj} is extremely important. When carefully constructed, these site-specific atom-centered potential functions are transferable. Thus, it is possible to obtain a self-consistent potential from the calculation of a simpler system (say quartz, α-SiO2) and then use it in the calculation of a similar but larger and more complicated system (amorphous SiO2 glass) without needing to perform self-consistent calculations. It should be noted that although the atom-centered functions
. Because the accuracy of the calculation depends largely on how accurately the true charge density can be represented by Equations (3)–(5), the optimal choice of the fitting set {βj} is extremely important. When carefully constructed, these site-specific atom-centered potential functions are transferable. Thus, it is possible to obtain a self-consistent potential from the calculation of a simpler system (say quartz, α-SiO2) and then use it in the calculation of a similar but larger and more complicated system (amorphous SiO2 glass) without needing to perform self-consistent calculations. It should be noted that although the atom-centered functions 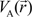 and
and 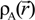 consist of spherical Gaussians around each atom, the superposition of them is non-spherical in real space and can accurately represent different types of bonding in different types of structural configurations without shape approximation [51]. For large biomolecules with more than several thousand of atoms, the self-consistent procedure described above is still not feasible but we can make use of the accurately calculated
consist of spherical Gaussians around each atom, the superposition of them is non-spherical in real space and can accurately represent different types of bonding in different types of structural configurations without shape approximation [51]. For large biomolecules with more than several thousand of atoms, the self-consistent procedure described above is still not feasible but we can make use of the accurately calculated 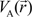 and
and 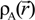 obtained from smaller subunits and apply them in the calculation of the larger system. We will return to this part later when we present the simplified method for large proteins using the self-consistent charge densities and potentials obtained from individual amino acids. We list the important parameters that enter into the OLCAO calculation for the 7-2 heterostructural model of collagen as follows: (1) number of chains 3; (2) number of trimmers 30; (3) number of amino acids 90; (4) number of atoms 1135; (5) number of valence electrons 3246; (6) size of total potential column data 12,706; (7) size of secular equation (FB) 7456.
obtained from smaller subunits and apply them in the calculation of the larger system. We will return to this part later when we present the simplified method for large proteins using the self-consistent charge densities and potentials obtained from individual amino acids. We list the important parameters that enter into the OLCAO calculation for the 7-2 heterostructural model of collagen as follows: (1) number of chains 3; (2) number of trimmers 30; (3) number of amino acids 90; (4) number of atoms 1135; (5) number of valence electrons 3246; (6) size of total potential column data 12,706; (7) size of secular equation (FB) 7456.
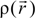 . Because the accuracy of the calculation depends largely on how accurately the true charge density can be represented by Equations (3)–(5), the optimal choice of the fitting set {βj} is extremely important. When carefully constructed, these site-specific atom-centered potential functions are transferable. Thus, it is possible to obtain a self-consistent potential from the calculation of a simpler system (say quartz, α-SiO2) and then use it in the calculation of a similar but larger and more complicated system (amorphous SiO2 glass) without needing to perform self-consistent calculations. It should be noted that although the atom-centered functions
. Because the accuracy of the calculation depends largely on how accurately the true charge density can be represented by Equations (3)–(5), the optimal choice of the fitting set {βj} is extremely important. When carefully constructed, these site-specific atom-centered potential functions are transferable. Thus, it is possible to obtain a self-consistent potential from the calculation of a simpler system (say quartz, α-SiO2) and then use it in the calculation of a similar but larger and more complicated system (amorphous SiO2 glass) without needing to perform self-consistent calculations. It should be noted that although the atom-centered functions 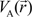 and
and 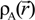 consist of spherical Gaussians around each atom, the superposition of them is non-spherical in real space and can accurately represent different types of bonding in different types of structural configurations without shape approximation [51]. For large biomolecules with more than several thousand of atoms, the self-consistent procedure described above is still not feasible but we can make use of the accurately calculated
consist of spherical Gaussians around each atom, the superposition of them is non-spherical in real space and can accurately represent different types of bonding in different types of structural configurations without shape approximation [51]. For large biomolecules with more than several thousand of atoms, the self-consistent procedure described above is still not feasible but we can make use of the accurately calculated 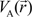 and
and 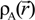 obtained from smaller subunits and apply them in the calculation of the larger system. We will return to this part later when we present the simplified method for large proteins using the self-consistent charge densities and potentials obtained from individual amino acids. We list the important parameters that enter into the OLCAO calculation for the 7-2 heterostructural model of collagen as follows: (1) number of chains 3; (2) number of trimmers 30; (3) number of amino acids 90; (4) number of atoms 1135; (5) number of valence electrons 3246; (6) size of total potential column data 12,706; (7) size of secular equation (FB) 7456.
obtained from smaller subunits and apply them in the calculation of the larger system. We will return to this part later when we present the simplified method for large proteins using the self-consistent charge densities and potentials obtained from individual amino acids. We list the important parameters that enter into the OLCAO calculation for the 7-2 heterostructural model of collagen as follows: (1) number of chains 3; (2) number of trimmers 30; (3) number of amino acids 90; (4) number of atoms 1135; (5) number of valence electrons 3246; (6) size of total potential column data 12,706; (7) size of secular equation (FB) 7456.2.3. Results and Discussions on the Collagen Model
The electronic structure of the 7-2 heterostructural model was calculated using the ab initio OLCAO method. The self-consistent calculations were done only for the individual chains of the triple helix while the full helix was studied with an alternate approach to be detailed in Section 3.2. Figure 2 shows the calculated total DOS (TDOS) for the single stranded α2(I) chain in the 7/2 heterotrimer model of Figure 1a. The zero of the energy is set at the HOMO state, or the top of the VB. The HOMO–LUMO gap of this peptide is only about 2.0 eV with a defect-like state at 1.3 eV within the gap. The lowest occupied non-core level is at −24.0 eV. The TDOS is further resolved into PDOS of the 10 triplets in the α2(I) chain shown in Figure 3. Please note that the HOMO–LUMO gaps for each of the triplets are very different but are at least 3.5 eV which may be related to the relative strengths in the peptide chain. The rich spectra in the DOS and PDOS contain information about the electronic structure and bonding for individual triplets. For example, the deep levels below −18 eV are all from O-2s orbitals with peak structures that depict the various energy levels for the O atoms in different amino acids with different local bonding configurations. The highest occupied state is associated with the H-terminated Gly from the first trimer Gly-Pro-Met, and thus may be considered as a defect-like state. However, the next highest state is also localized on the first trimer it is associated with the other residues and could thus be recognized as the HOMO for the trimer. The LUMO comes from the eighth triplet Gly-Phe-Gln. In the 10th triplet Gly-Glu-Hyp, we again recognize an additional defect-like state in the gap that may originate from the H termination effect in Hyp. Each triplet has rather different peak positions in their PDOS which can be further delineated. It is also expedient to resolve the PDOS further down into the individual residue level or even atoms to obtain atomic details.
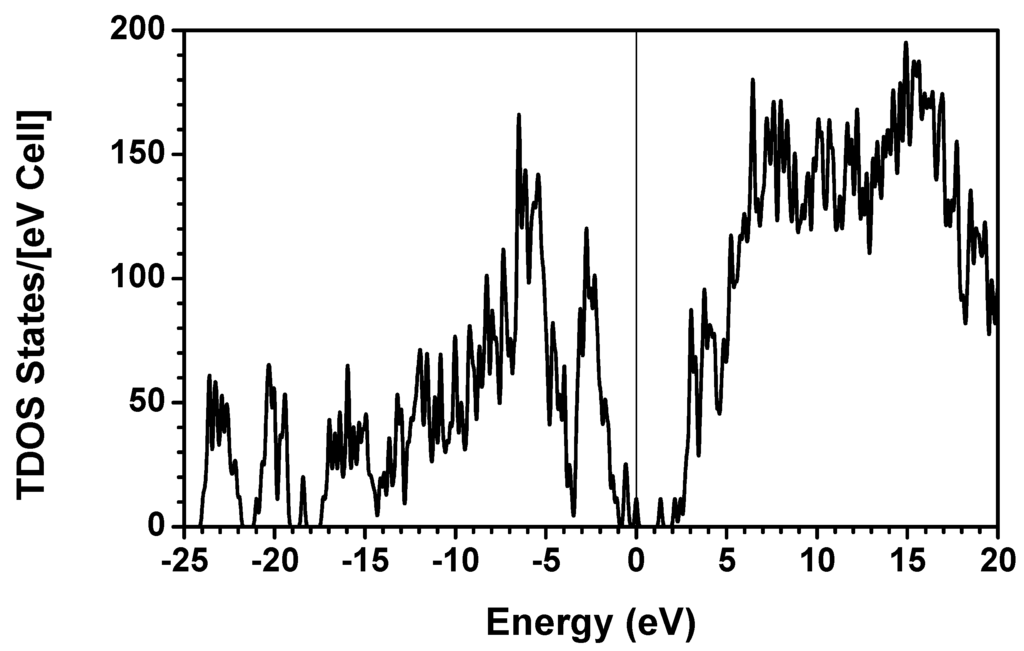
Figure 2.
Calculated total DOS of the α2(I) chain in the 7-2 heterostructural model.
Figure 4a shows the PDOS of Gly, Pro, and Met in the first triplet and Figure 4b the PDOS of Gly, Glu, Hyp of the 10th residue. It shows that the HOMO for this triplet comes from Gly and the defect-like state in the gap for the 10th triplet is from Hyp. The LUMO in the eighth triplet originates from Gln (not shown). In this way, all electronic structures down to the amino acid levels and even to individual atoms within the amino acids can be displayed. According to the principle of maximum hardness (PMH) [69,70], the HOMO–LUMO gap (εLUMO − εHOMO) can be related to maximum hardness η = ½ (εLUMO − εHOMO) and used to roughly estimate the stability of each molecular fragment [71,72]. Based on this simple rule, the fifth trimer (Gly-Ala-Ala) and the sixth trimer (Gly-Ala-Hyp) in the middle part of the α2(I) chain should be more stable than the other trimers.
Figure 5 shows in graphic form the calculated charge transfer ΔQ* (also called the partial charge or the deviation of charge from the neutral atom) associated with each individual atom in the same strand according to the Mulliken effective charge Q*. There are differences in ΔQ* for atoms in different residues. In classical simulations or other DFT methods where plane waves are used in the basis expansion, the calculation of effective charge on each atom in a large complex biomolecule can be quite onerous and may require additional procedures, making the method less effective. The efficient evaluation of partial charge is very useful in explaining different geometric conformation and interaction in biomolecular systems. We will return to the distribution of effective charges Q* later where it will be used as a quantitative measure to validate the simpler AAPM in Section 3.
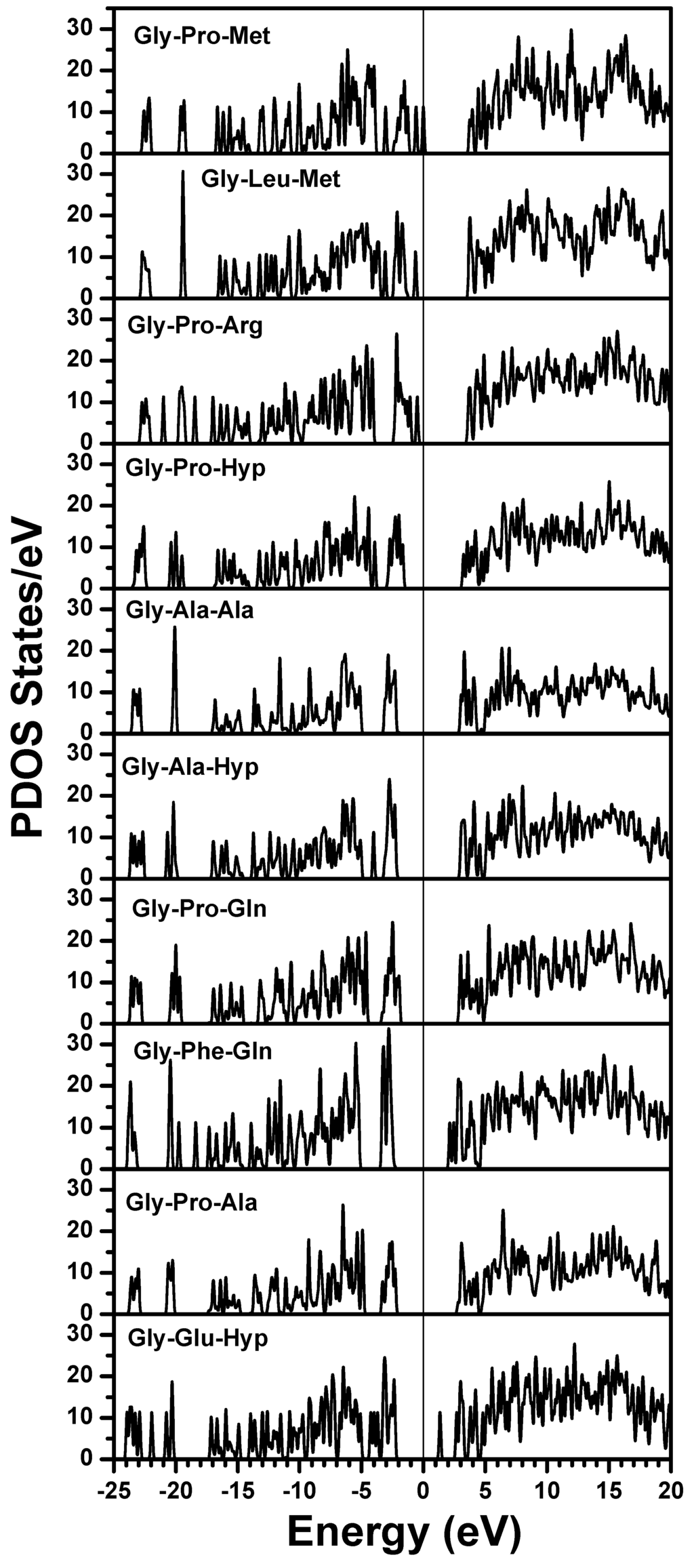
Figure 3.
Calculated PDOS for each triplet in the α2(I) chain. Note the difference in the HOMO–LUMO gaps for different triplets.
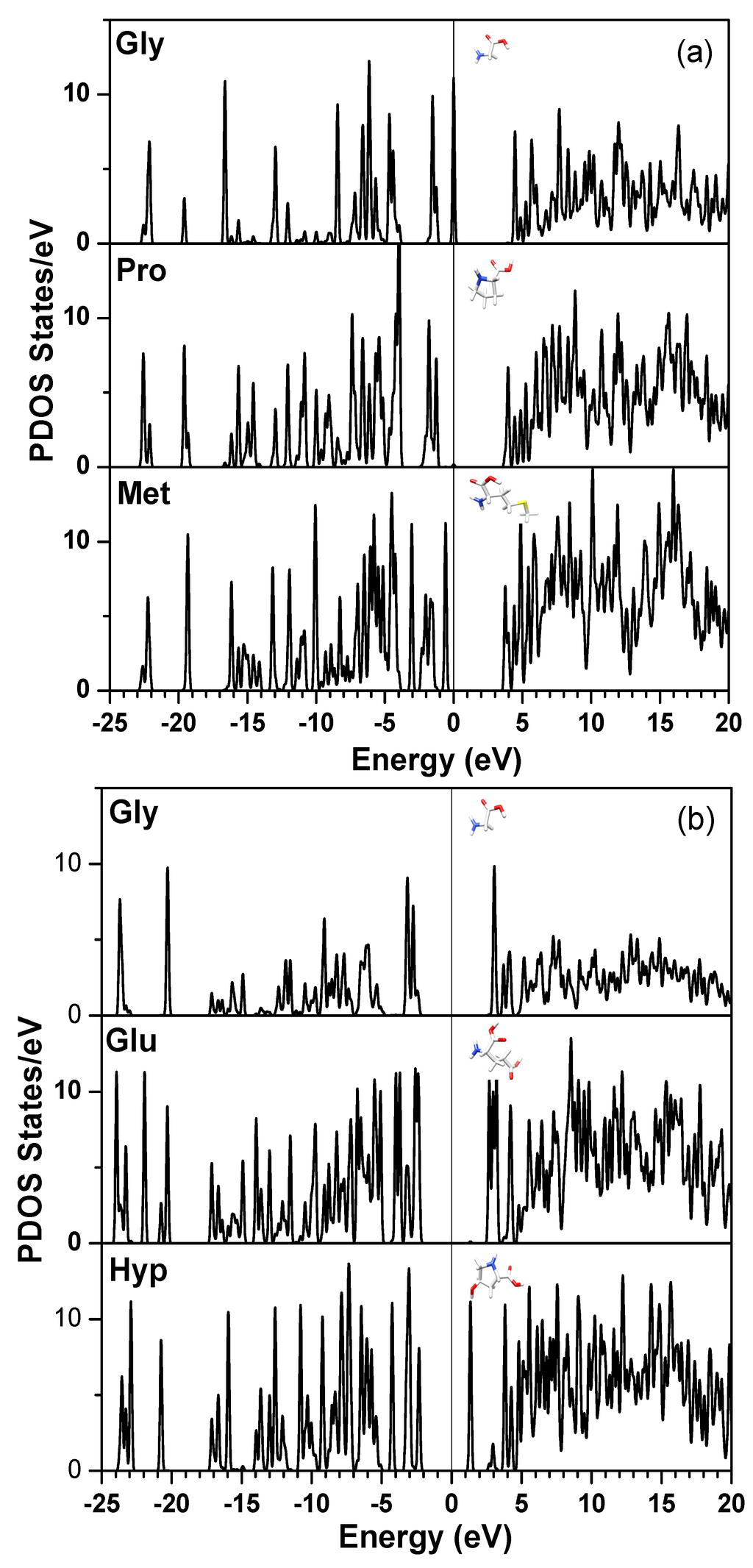
Figure 4.
(Color on-line) Calculated PDOS of: (a) three amino acids (Gly, Pro, Met) in the first triplet; and (b) Three amino acids (Gly, Glu, Hyp) in the last triplet of Figure 3.
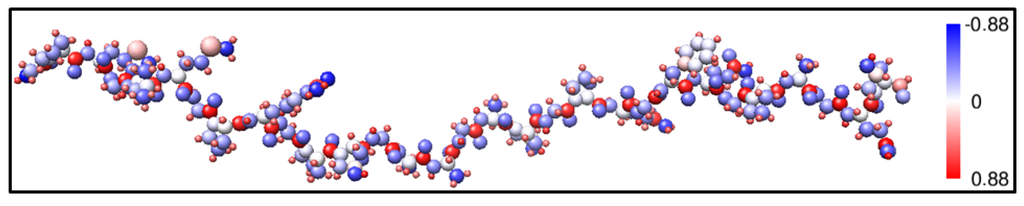
Figure 5.
(Color on-line) Ball and stick model of a single strand α2(I) of Figure 1 with the size of the atoms represented by their covalent radii. The color indicates the amount of charge transfer (Qα*, number of valence electrons) for each atom.
The nature of H-bonding may be the most important issue in the fundamental study of collagen and other proteins of biological interest in general. H-bond is a much weaker intermolecular bond than ionic or covalent bonds [73]. It is responsible for maintaining the triple helix structure in collagen. In the past, most of the discussion on H-bonding, especially for those with complex structures, was based on geometric considerations (interatomic bond distances and bond angles); instead of quantitative estimates from more rigorous quantum mechanical calculations. More recently, progress has been made in more rigorous calculations of various aspects of H-bonding and in the interpretation of experimental observations [74,75,76,77]. In the semi-empirical force field model, H-bonding is generally described by a Lennard-Jones type pair-potential [78]. As demonstrated in the case of a pure super-cooled water model [67], quantitative analysis of H-bonding using the OLCAO method is possible to elucidate the network structure in water. In the case of collagen, it is desirable to model the bridges between each of the polypeptide chains to estimate changes in H-bonding strength between different chains. It is desirable to add water molecules to the simulation cell to mimic the effect of solvents although no such effort is attempted in the present calculation.
In the present study, H-bonding is characterized by the calculation of the BO values between non-covalently bound H and O or N atoms. We identify and characterize the H-bonding in these complex macromolecules using the following procedure: (1) From the electronic structure calculations (obtained using the method given in Section 3.2.), the BO values for all interatomic pairs are collected in a large data file; (2) The specific BO values involving H–X (X = O or N) that are not covalently bonded (as judged from their separations) are identified; (3) These H-bonding BO values are graphically displayed and classified as being due to either intramolecular or intermolecular H-bonds; and (4) Those atomic pairs with higher than average BO values are analyzed by tracing which H and X atoms are involved and their local environments. Figure 6a shows a sketch of the intra- and inter-molecular H-bonds in the present 7-2 heterostructural model for collagen that have been identified and whose BO was calculated. In Figure 6b, we display these BO values vs. the H-bond length up to 3.5 Å. As can be seen, the intermolecular hydrogen bonds are mostly O–H, and with only one N–H at 3.0 Å. It can also be seen that the intra-molecular H-bonds (including O–H, N–H, C–H and H–H) always have larger bond lengths and smaller BO values than those of intermolecular hydrogen bonds with a bond length (BL) less than 2.3 Å. The presence of stronger intermolecular H-bonding in collagen molecules can be one of the possible reasons in providing the necessary cohesion between the three chains consistent with the general understanding about collagen stability [79]. The computed H-bonds between chains A, B and C are illustrated in Figure 7 with the BO shown as the associated bar height and the color of the bar indicating whether the bond is between the backbones of the chains or between the backbone of one chain and a residue’s side-chain from the other chain. Overall the BO remains relatively constant between chains along the length of the molecule with an approximately even distribution of H-bonds between the chains. However, in the central region of the molecule’s length there is a stretch where the only strong intermolecular bonds are those between chains A and B. This indicates that the C chain may have a more flexible conformation in this region. Additionally, there is little H-bonding between molecules at the end on the right. The results shown in Figure 7 are consistent with the interpretation of Brodsky and Persikov [5] on the role of interchain H-bonding between different amino acids. It should be pointed out that the presence of water molecules or solvents may alter these H-bonds and their BO values, but the technique and procedures used to quantify the H-bonding here can be applied equally well in these more complicated and demanding situations.
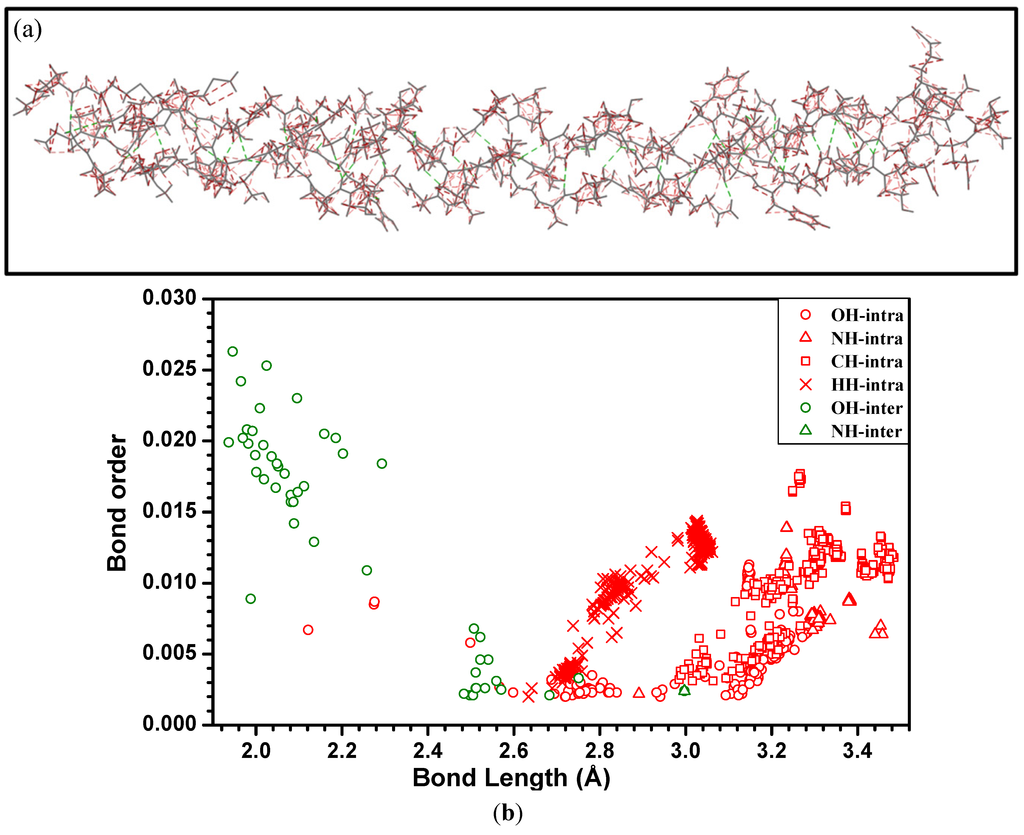
Figure 6.
(Color on-line) (a) Sketch of H-bonds within the 7-2 heterostructural model. Green dashed lines for intermolecular H-bonding and red dashed line for the intra-molecular H bonding; and (b) Distribution of the calculated BO values for H-bonds in the 7-2 heterostructural model. Different types of the H-bonding are marked and colored as indicated.
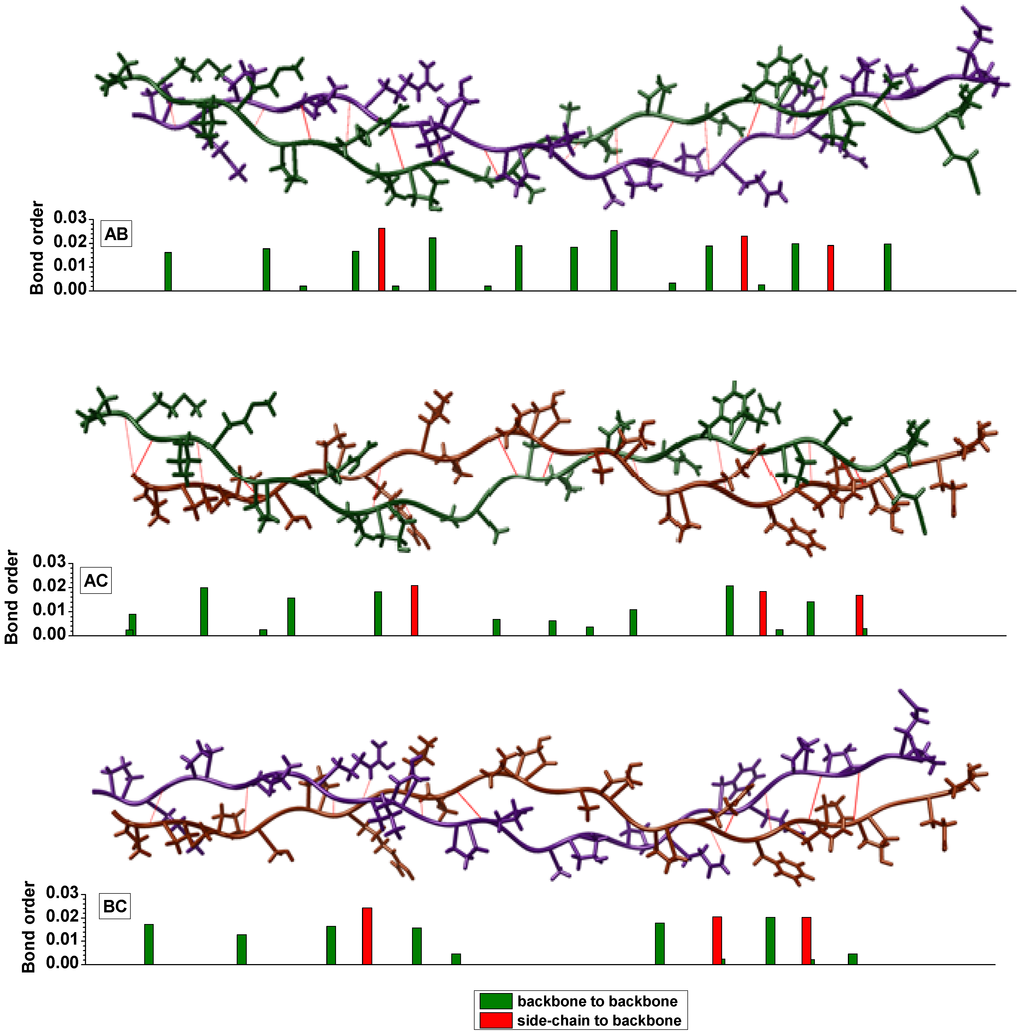
Figure 7.
(Color on-line) Calculated H-bond location and relative strength between pairs of chains [A (green), B (purple), and C (brown)].
3. Amino-Acid Potential Method for Large Proteins
3.1. Current Trends in Computational Biophysical Research
One of the main goals of performing large-scale ab initio calculations on biomolecular systems is to gain a fundamental understanding of the electronic structure. This can be used to quantify long-range forces between large biomolecular entities, e.g., proteins, and to design biomaterials built on the knowledge of organizing forces. In particular, partial charge and charge transfer on each atom or group of atoms (e.g., atoms in a particular amino acid) can be very useful for subsequent computation of the long-range electrostatic interaction between different particles or proteins made of amino acids. The electrostatic interaction is one of the three fundamental long-range interactions. The other two are the polar and van der Waals interactions which require different levels of theory to address [80].
Many different computational techniques have been applied to biomolecular systems ranging from small molecules to models of hundreds or thousands of atoms with very broad ranges of utility and accuracy [81]. Obviously, for large molecules the accuracy and the level of treatment could be limited. On the other hand, smaller molecules can be treated with more accurate quantum chemical methods based on DFT or beyond [82,83,84]. Thus, there is a tradeoff between the size of the system that can be handled and the level of the accuracy desired. Naturally, selecting which method or approach depends on the nature of the problem to be addressed and the resources available. It is highly desirable to have a viable method that can be applied to large biomolecular systems of at least several thousand atoms with accuracy close to DFT calculations presented in Section 2. In the case of collagen, no complete structure model is available for collagen due to its fibrous nature [85]. The result we presented in the previous section is based on a specific model which is only part of the 30-trimer structural domain of the collagen molecule in 7-2 helical symmetry [13,56]. The amino-acid sequence of this heterotrimer model has a distribution of residues commonly found in natural collagen [34]. The structures of many biological molecules fall under this intermediate range of 100–300 amino acids with up to 6000 atoms. Ribosomes and their protein conducting channels, membrane proteins, virus nano-particles such as cowpea mosaic virus (CPMV), tobacco mosaic virus (TMV), and brome mosaic virus (BMV), are some examples actively pursued by researchers [86,87]. For such systems, even with the highly efficient DFT-based OLCAO method, it is not feasible, and therefore a simplified method is needed. However, it should also be pointed out that new theoretical tools such as QM/QM and QM/MM, which are suitable for the investigation of large molecules including biomolecules, are starting to emerge [88,89].
3.2. Amino-Acid Potential Method for Large Proteins
We have developed a simplified method knowing that proteins are composed of a sequence of amino-acids and that their structures are usually available from the protein data bank (PDB). This is a “divide and conquer” strategy to lessen the computational burden while preserving the accuracy close to the full self-consistent field (SCF) calculations of the OLCAO method. In this approach, the SCF calculation is performed at the amino acid level which can be done very quickly because of the small size. The potential and charge density coefficients for each amino acid thus obtained (with proper boundary conditions for sequence connection) are then used for the whole protein without the need to perform the full SCF calculation for the much larger protein. Referring to the descriptions in Section 2.2., we first obtain the SCF charge density and potential function coefficients {Bj}, {Dj} and {Fj} for each atom in each individual amino acid in the protein sequence. Each SCF calculation for the amino acid will include two adjacent amino acids at the ends to provide correct connectivity, but only the coefficients of the central amino acid are collected and tabulated. This table is then used to construct the charge density and potential function for the whole protein and used for the electronic structure calculation without going through the SCF cycles. We call this an Amino-acid Potential Method (AAPM). The full self-consistent iteration procedure for the whole collagen model is avoided and the electronic structure is obtained by a single diagonalization of the secular Kohn-Sham equation. This resulted in a reduction of total time required by a factor of at least 10 in the case of the current 7-2 triple-helix model with 1135 atoms (see Table 2). The time saving will be even more dramatic as the size of the system increases. Since there are only 20 types of canonical amino acids for all proteins, the use of this AAPM implies that the electronic structure of large proteins can be obtained using the OLCAO method without being computationally prohibitive. In the following section, we will validate the AAPM method by comparing the calculated effective charges Q* on each atom and the DOS.
3.3. Validation of the AAPM
To test and validate the proposed AAPM method, we compare the results of effective charge Q* on each atom in the 7-2-heteral structural collagen model from three types of calculations: (1) A separate non-SCF calculation of each chain using the default atomic potential in the OLCAO database [51]. This is the lowest level of accuracy in the OLCAO method since the potential used was not obtained self-consistently; (2) Fully self-consistent LDA calculations of each individual chain in the model; and (3) A non-SCF calculation using AAPM for the same three chains. The Q* results for all atoms (N, O, C, S and H) in the α2(I) chain from the three approaches are shown in Figure 8 (similar results for the other two chains are not shown). As can be seen, the results from the non-SCF, full SCF, and AAPM calculations do differ, indicating the importance of SCF iterations. However, the results from the AAPM calculation are very close to those of the full SCF calculation, validating the simplified scheme. Note, that the dotted lines in Figure 8 are guides to the eye only. Also, atom numbers are shown in the order as they appear in the chain’s amino-acid sequence for different types of atoms. The calculated Q* obviously must fall within a narrow range of values for the same atomic species. For example, most values of Q* for N fall into a range centered around 5.5 electrons. In fact, for N and O, they gain about half an electron. We note several distinct peaks for Q* in the plot for N (atoms 1, 11, 12, 25, and 29). The peak for atom 1 is the first nitrogen that belongs to the N-terminal amino-acid Gly, atoms 11 and 12 belong to the side-chain of Arg, and atoms 25 and 29 belong to the side-chains in Gln. These peaks signify the sensitivity of the electronic structure in the OLCAO calculation as reflected in the Q* values which depend on the local atomic environment. Similar ranges of Q* values are obtained for the other two chains of the triple-helix (not shown). In general, H atoms gave up charge, N and O atoms gained charge, and C atoms both gain and lose charge, whereas S atoms lose very little charge since it is not very acidic in the side-chain of Met (not shown in Figure 8). The average absolute deviation of effective charges Q* for N, C, O, H and S are 0.012, 0.025, 0.021, 0.006 and 0.033 electron in the α2(I) chain with the corresponding maximum deviation of 0.036, 0.108, 0.054, 0.026, 0.033, respectively. It is gratifying to see that the AAPM retains more than 96% of the accuracy of the full SCF calculation on average. This level of accuracy is quite sufficient for the evaluation of partial charges of large proteins which has so far been derived either from educated guesses or inferred from indirect experimental observations.
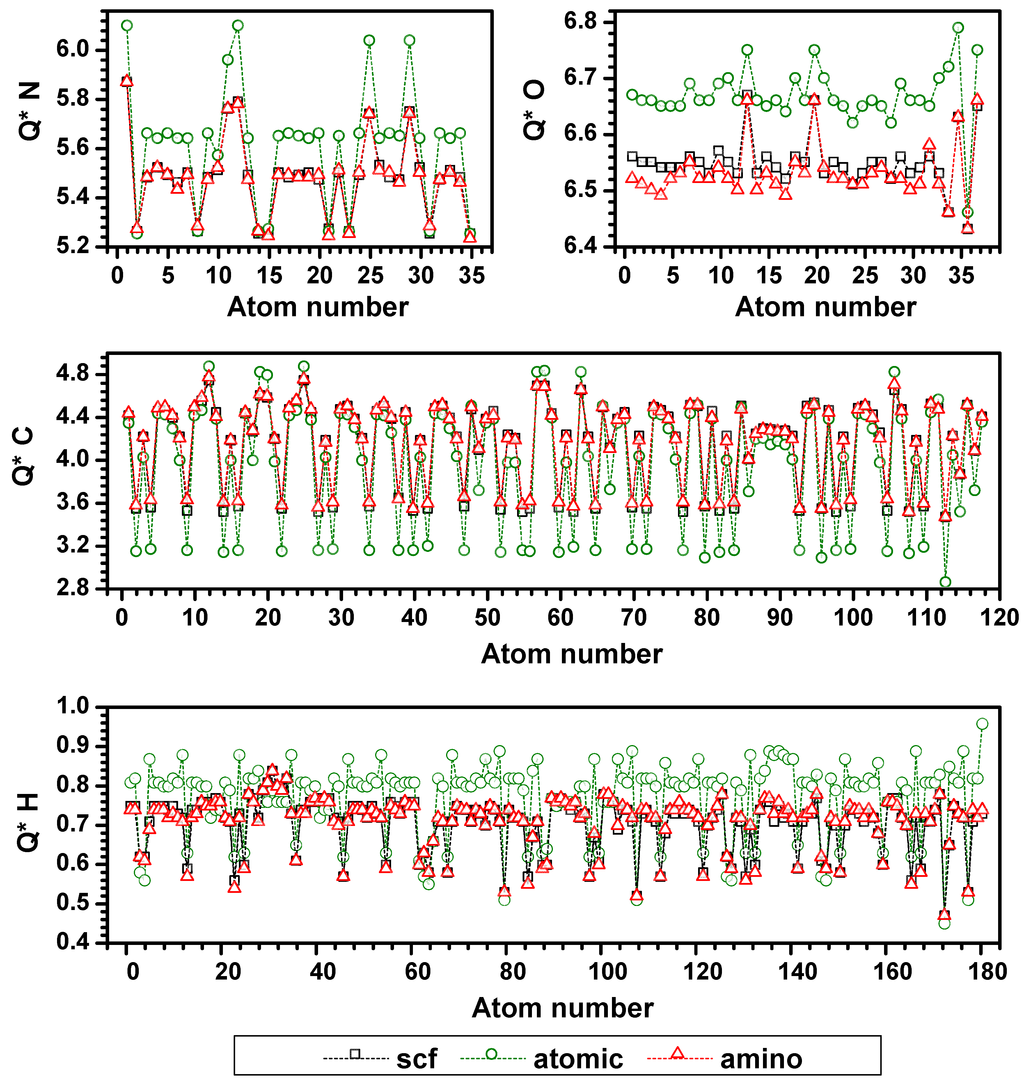
Figure 8.
(Color on-line) Comparison of effective charges Q* (electrons) for each atom in chain α2(I) among: Non-self-consistent field (SCF) calculation using atomic basis (green circles), Non-SCF calculation using an amino-acid-based potential method (AAPM) (red triangles), and Full SCF calculation (black squares).
3.4. Possible Application of the AAPM Approach
Now that the AAPM model has been demonstrated to be an effective tool, we will use it to study the electronic structure difference between the isolated chains and the complete molecule which is quite time-consuming.
Figure 9 shows the comparison of the Q* values between those from the full SCF calculation of the three individual chains (Figure 8) and those using the AAPM approach applied to the full triple helix heterostructural model with 1135 atoms including the six S atoms. The individual chain results are aligned so that atoms of a chain correspond correctly to atoms of the triple-helix. The Q* values are very close to each other, within 96% on average. Red circles are for the triple-helix and black crosses are for the individual molecules. A small difference is noticed between the two cases ranging from 0.0 to 0.18 electrons as a result of inter-molecular interaction now included in the AAPM calculation. Figure 10 shows the partial charge on the positively and negatively charged atoms of the 7-2 heterostructural model using the AAPM method. The sizes of the spheres based on the covalent radii of the atoms (in Å) and are: 0.77 for C, 0.75 for N, 0.73 for O, 0.37 for H, and 1.02 for S. Partial charges range from −0.85 electrons (darkest blue) to +0.85 electrons (darkest red) and the white color represents a charge neutral atom. More importantly, the distribution of partial charges within the structure has a mixture of colors indicating that there are no large groups of red or blue atoms other than those at the ends. The partial charge on a particular amino acid can be obtained from the totality of the partial charges of its atoms. Such results will be valuable in evaluating the electrostatic attraction or repulsion in long range intermolecular interactions. The ability to present partial charges based on realistically calculated values is a significant step forward from the current practice of using discrete and sometimes arbitrarily assumed values.
Figure 11 shows the calculated TDOS for the triple-helix and the sum of the DOS of the three individual collagen chains all obtained using AAPM. The difference of the two curves represents the number of states per energy range shows the effect of the intermolecular interactions. As can be seen, there are not many differences in the occupied VB region, indicating that the intermolecular interactions are fairly weak because they consist mostly of H-bonding (see Section 2). There are some discernible variations only in the unoccupied CB region where the state wave functions are more extended.
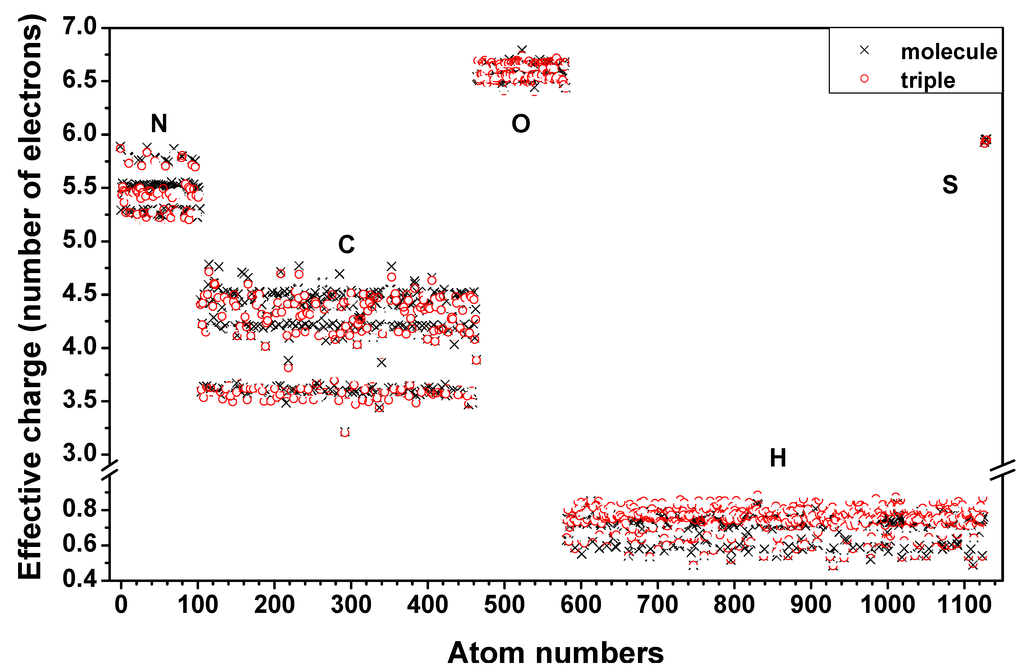
Figure 9.
(Color on-line) Comparison of effective charges Q* (electrons) from SCF calculation of three individual chains and the triple-helix using AAPM. Red circles represent triple-helix values and black x’s represent values from chain 1 (α2), 2 (α1) or 3 (α1) with atoms aligned with those of the triple-helix.
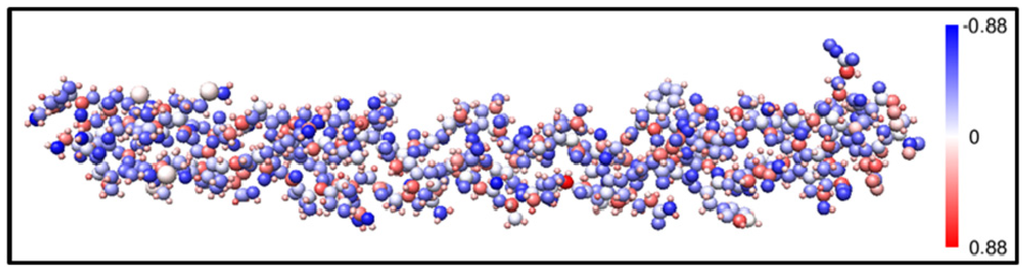
Figure 10.
(Color on-line) Partial charges on each atom in the 7-2 heterostructural model using. The size of the atoms is based on covalent radii used to compute an available surface area for the atom’s partial charge. Partial charge is negative (positive) for a gain (loss) in fractional electron charge and colored blue (red). White color indicates no charge transfer for the atom.
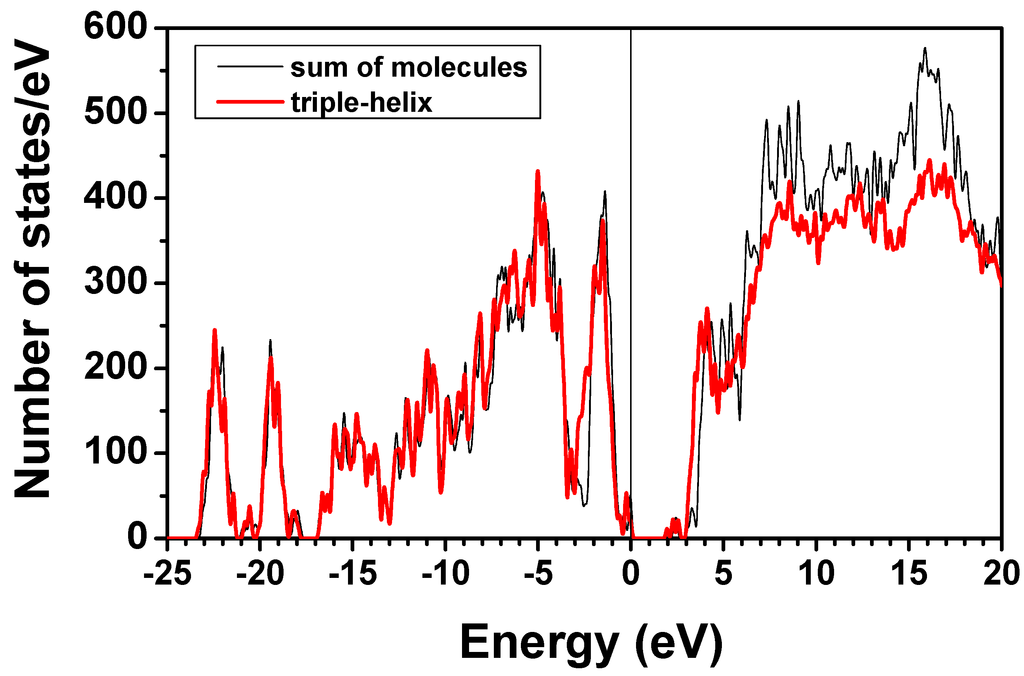
Figure 11.
(Color on-line) Comparison of total density of states for triple-helix and the sum of three individual molecules calculated using the AAPM.
4. Conclusions
In this paper, we presented the ab initio calculation of the electronic structure of a model of a complex collagen molecule. Analysis of the DOS, PDOS, and effective charges revealed many pertinent details. The quantitative evaluation of H-bonding and partial charges for long range electrostatic interactions are important issues in the fundamental study of collagen as well as for other proteins. Quantitative evaluation of bond order values for H-bonding reveals that the strength of H-bonding does not necessarily scale with the H–O or H–N separations. Based on the calculated electronic structures, it is possible to extend the calculation to optical absorption spectra of collagen molecules and those involving solvents. Such calculations will provide the dielectric response function which, so far, is only approximated by using the polarizable continuum model (PCM) [90,91]. The dielectric response function can be used as an input for the calculation of long-range van der Waals interactions between proteins in aqueous solution along the similar lines as recently successfully implemented for the single walled carbon nano-tubes of different chirality [92]. We believe that such an endeavor, which is now well within our current computational capability, can push collagen research to a much higher level of accuracy and sophistication. Of particular significance is the implementation and validation of a simpler AAPM that can be applied to much larger proteins at a modest cost. The present work represents the modeling at the lowest structural level (amino acids) and the next lowest structural level (collagen molecules) in the hierarchical levels of collagen. It provides the basis for the next level of modeling collagen such as microfibrils, larger collagen models, interfaces with bioceramics, etc. The success of the AAPM provides us with the confidence to apply it at the next higher level of complexity. We are tempted to speculate about similar calculations on other bio-related systems. A particularly attractive system is the viral nanoparticle or coated proteins such as the plant viruses BMV, CCMV, CMV (Cytomegalovirus), or TMV found either in dry form or in solution. The fundamental long range interactions among them can be related to their self-assembly abilities. This is an area where quantum mechanical treatment is completely lacking. Future work should include other models for collagen including replacement of Gly by other amino acids, and the addition of water with ions to represent physiological conditions in aqueous solution.
Acknowledgments
This work is supported by USA DOE-Office of BES, Division of Materials Science and Engineering under the grant DE-SC008176. This research used the resources of NERSC supported by the Office of Science of DOE under contract No. DE-AC03-76SF00098. W.Y.Ching acknowledges the help of Simone Vesentini in providing the initial structural models for type I collagen. Helpful discussions with R. Podgornik, R. French, A. Parsegian, and N. Steinmetz are gratefully acknowledged.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Fratzl, P. Collagen: Structure and Mechanics; Springer: New York, NY, USA, 2008; Volume 1. [Google Scholar]
- Maynes, R.; Burgeson, R. Structure and Function of Collagen Types; Academic Press: London, UK, 1987. [Google Scholar]
- Bateman, J.F.; Lamande, S.; Ramshaw, J.A.M. Collagen Superfamily; Comper, W.D., Ed.; Harwood Academic Publishers: Amsterdam, The Netherlands, 1996; Volume 2, pp. 22–67. [Google Scholar]
- Ottani, V.; Raspanti, M.; Ruggeri, A. Collagen structure and functional implications. Micron 2001, 32, 251–260. [Google Scholar]
- Brodsky, B.; Perishov, A.V. Molecular structure of the collagen triple helix. Adv. Protein Chem. 2005, 70, 301–339. [Google Scholar] [CrossRef]
- Rich, A.; Crick, F.H.C. The structure of collagen. Nature 1955, 176, 915–916. [Google Scholar] [CrossRef]
- Wess, T.J.; Hammersley, A.P.; Wess, L.; Miller, A. A consensus model for molecular packing of type I collagen. J. Struct. Biol. 1998, 122, 92–100. [Google Scholar]
- Ramshaw, J.A.M.; Shah, N.K.; Brodsky, B. Gly-X-Y tripeptide frequencies in collagen: A context for host-guest triple-helical properties. J. Struct. Biol. 1998, 122, 86–91. [Google Scholar]
- Kramer, R.Z.; Vitagliano, L.; Bella, J.; Berisio, R.; Mazzarelaa, L.; Brodsky, B.; Zagari, A.; Berman, H.M. X-ray crystallographic determination of a collagen-like peptide with repeating sequence (Por-Por-Gly). J. Mol. Biol. 1998, 280, 623–638. [Google Scholar] [CrossRef]
- Kramer, R.Z.; Venugopal, M.G.; Bella, J.; Mayville, P.; Brodsky, B.; Berman, H.M. Staggered molecular packing in crystals of a collagen-like peptide with a single charge pair. J. Mol. Biol. 2000, 301, 1191–1205. [Google Scholar]
- Kramer, R.Z.; Bella, J.; Mayville, P.; Brodsky, B.; Berman, H.M. The crystal and molecular structure of a collagen-like peptide with a biologically related sequence. J. Mol. Biol. 2001, 311, 131–147. [Google Scholar]
- Berisio, R.; Vitagliano, L.; Mazzarella, L.; Zagari, A. Crystal structure of a collagen-like polypeptide with repeating sequence Pro-Hyp-Gly at 1.4 Å resolution: Implication for collagen hydration. Biopolymers 2001, 56, 8–13. [Google Scholar]
- Berisio, R.; Vitagliano, L.; Mazzarella, L.; Zagari, A. Crystal structure of the collagen triple helix model [(Pro-Pro-Gly)10]3. Protein Sci. 2002, 11, 262–270. [Google Scholar]
- Ottani, V.; Martini, D.; Franchi, M.; Ruggeri, A.; Raspanti, M. Hierarchical structures in fibrillar collagens. Micron 2002, 33, 587–596. [Google Scholar]
- Christiansen, D.L.; Huang, E.K.; Silver, F.H. Assembly of type I collagen: Fusion of fibril subunits and the influence of fibril diameter on mechanical properties. Matrix Biol. 2000, 19, 409–420. [Google Scholar]
- Gautieri, A.; Vesentini, S.; Redealli, A.; Buehler, M.J. Hierarchical structure and nanomechanics of collagen microfibrils from the atomistic scale up. Nano Lett. 2011, 11, 757–766. [Google Scholar]
- Brodsky, B.; Ramshaw, J.A.M. The collagen triple-helix structure. Matrix Biol. 1997, 15, 545–554. [Google Scholar] [CrossRef]
- Persikov, A.V.; Ramshaw, J.A.M.; Kirkpatrick, A.; Brodsky, B. The collagen triple-helix structure. Biochemistry 2000, 39, 14960–14967. [Google Scholar] [CrossRef]
- Persikov, A.; Ramshaw, J.A.M.; Brodksy, B. Collagen model peptides: Sequence dependence of triple helix stability. Biopolymers 2000, 55, 436–450. [Google Scholar] [CrossRef]
- Almora-Barrios, N.; de Leeuw, N.H. Molecular dynamics simulation of the early stages of nucleation of hydroxyapatite at a collagen template. Cryst. Growth Des. 2012, 12, 756–763. [Google Scholar] [CrossRef]
- Kuibaniemi, H.; Tormp, G.; Prockop, D. Mutations in collagen genes: Causes of rare and some common diseases in humans. FASEB J. 1991, 5, 2052–2060. [Google Scholar]
- Scheuler-Furman, O.; Wang, C.; Bradeley, P.; Misura, K.; Baker, D. Progress in modeling of protein structures and interactions. Science 2005, 310, 638–642. [Google Scholar] [CrossRef]
- Butter, D.; Docherty, R.; Swart, R.M. The application of computational chemistry to the study of chemistry of collagen. J. Am. Leather Chem. Assoc. 1997, 92, 185–199. [Google Scholar]
- Klien, T.E.; Huang, C.C. Computational investigations of structure changes resulting from point mutation in a collegen-like peptide. Biopolymers 1999, 49, 167–183. [Google Scholar] [CrossRef]
- Mooney, S.D.; Huang, C.C.; Kollman, P.A.; Klein, T.E. Computed free energy differences between point mutations in a collagen-like peptide. Biopolymers 2001, 58, 347–353. [Google Scholar] [CrossRef]
- Vaidyanathan, J.; Vaidyanathan, T.K.; Yadav, P.; Linarus, C.E. Collagen-ligand interaction in dentinal adhesion: Computer visualization and analysis. Biomaterials 2001, 22, 2911–2920. [Google Scholar] [CrossRef]
- Madhan, B.; Thanikaivelan, P.; Subramanian, V.; Raghava, J.R.; Balachandran, U.N.; Ramasami, T. Molecular mechanics and dynamics on the interaction of gallic acid with collagen-like peptides. Chem. Phys. Lett. 2001, 346, 334–340. [Google Scholar] [CrossRef]
- Improta, R.; Freanca, M.; Crescenzi, O.; Benzi, C.; Barone, V. Understanding the role of stereoelectronic effects in determining collagen stability: 2. A quantum mechanical/molecular mechanical study of (Proline-Proline-Glycine)(n) polypeptides. J. Am. Chem. Soc. 2002, 124, 7857–7865. [Google Scholar] [CrossRef]
- Lorenzo, A.C.; Caffarena, W.R. Elastic properties, Young’s modulus determination and structural stability of the tropocollagen molecule: A computational study by steered molecular dynamics. J. Biomech. 2005, 38, 1527–1533. [Google Scholar] [CrossRef]
- Vesentini, S.; Fitie, C.F.C.; Montevecchi, F.M.; Redaelli, A. Molecular assessment of the elastic properties of collagen-like homotrimer sequences. Biomech. Model Mechan. 2005, 3, 224–234. [Google Scholar]
- Gautieri, A.; Vesentini, S.; Montevecchi, F.M.; Redaelli, A. Mechanical properties of physiological and pathological models of collagen peptides investigated via steered molecular dynamics simulations. J. Biomech. 2008, 41, 3073–3077. [Google Scholar] [CrossRef]
- Gautieri, A.; Uzel, S.; Vesentini, S.; Redaelli, A.; Buehler, M.J. Molecular and mesoscale mechanisms of osteogenesis imperfecta disease in collagen fibrils. Biophys. J. 2009, 97, 857–865. [Google Scholar] [CrossRef]
- Gautieri, A.; Russo, A.; Vesentini, S.; Redaelli, A.; Buehler, M.J. Coarse-grained model of collagen molecules using an extended MARTINI force field. J. Chem. Theory Comput. 2010, 6, 1210–1218. [Google Scholar]
- Rainey, J.K.; Goh, M.C. A statistically derived parameterization for the collagen triple-helix. Protein Sci. 2002, 11, 2748–2754. [Google Scholar] [CrossRef]
- Buehler, M.J. Nature designs tough collagen: Explaining the nanostructure of collagen fibrils. P Natl. Acad. Sci. 2006, 103, 12285–12290. [Google Scholar] [CrossRef]
- Gautieri, A.; Pate, M.I.; Vesentini, S.; Redaelli, A.; Buehler, M.J. Hydration and distance dependence of intermolecular shearing between collagen molecules in a model microfibril. J. Biomech. 2012, 45, 2079–2083. [Google Scholar]
- Rhys, N.H.; Dougan, L. The emerging role of hydrogen bond interactions in polyglutamine structure, stability and association. Soft Matter 2013, 9, 2359–2364. [Google Scholar] [CrossRef]
- Gautieri, A.; Vesentini, S.; Redaelli, A.; Buehler, M. Intermolecular slip mechanism in tropocollagen nanofibrils. Int. J. Mater. Res. 2009, 7, 921–925. [Google Scholar]
- Qin, Z.; Buehler, M.J. Molecular dynamics simulation of the α-helix to β-sheet transition in coiled protein filaments: Evidence for a critical filament length scale. Phys. Rev. Lett. 2010, 104, 198304:1–198304:4. [Google Scholar]
- Grant, C.A.; Phillips, M.A.; Thomson, N.H. Dynamic mechanical analysis of collagen fibrils at the nanoscale. J. Mech. Behav. Biomed. 2012, 5, 165–170. [Google Scholar] [CrossRef]
- Case, D.A.; Cheatham, T.E., III; Darden, T.; Gohlke, H.; Luo, R.; Merz, K.M., Jr; Onufriev, A.; Simmerling, C.; Wang, B.; Woods, R. The amber biomolecular simulation programs. J. Comput. Chem. 2005, 26, 1668–1688. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Parthasarathi, R.; Madhan, B.; Subramanian, V.; Ramasami, T. Ab initio and density functional theory based studies on collagen triplets. Theor. Chem. Acc. 2003, 110, 19–27. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry: III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Perdew, J.P.; Wang, Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 1988, 45, 13244–13249. [Google Scholar] [CrossRef]
- Jalkanen, K.J.; Olsen, K.; Knapp-Mohammady, M.; Bohr, J. First-principles structures for the close-packed and the 7/2 motif of collagen. Europhys. Lett. 2012, 100, 28003:1–28003:4. [Google Scholar] [CrossRef]
- Bohr, J.; Olsen, K. The close-packed triple helix as a possible new structural motif for collagen. Theor. Chem. Acc. 2011, 130, 1095–103. [Google Scholar] [CrossRef]
- Ching, W.Y. Theoretical studies of electronic properties of ceramic materials. J. Am. Ceram. Soc. 1990, 71, 3135–3160. [Google Scholar] [CrossRef]
- Ching, W.Y.; Rulis, P. Electronic Structure Methods for Complex Materials: The Orthogonalized Linear Combination of Atomic Orbitals; Oxford University Press: Oxford, UK, 2012. [Google Scholar]
- Okuyama, K.; Takayanagi, M.; Ashida, T.; Kakudo, M. A new structural model for collagen. Polym. J. 1977, 9, 341–343. [Google Scholar] [CrossRef]
- Rich, A.; Crick, F.H.C. The molecular structure of collagen. J. Mol. Biol. 1961, 3, 483–506. [Google Scholar] [CrossRef]
- Bella, J. A new method for describing the helical conformation of collagen: Dependence of the triple helical twist on amino acid sequence. J. Struct. Biol. 2010, 170, 377–391. [Google Scholar] [CrossRef]
- Okuyama, K.; Kawaguchi, T.; Shimura, M.; Noguchi, K.; Mizuno, K.; Bachinger, H.P. Crystal structure of the collagen model peptide (Pro-Pro-Gly) 4-Hyp-Asp-Gly-(Pro-Pro-Gly) 4 at 1.0 Å resolution. Biopolymers 2013, 99, 436–447. [Google Scholar] [CrossRef]
- Okuyama, K.; Miyama, K.; Mizuno, K.; Bachinger, H.P. Crystal structure of (Gly-Pro-Hyp) 9: Implications for the collagen molecular model. Biopolymers 2012, 97, 607–616. [Google Scholar] [CrossRef]
- Okuyama, K.; Xu, X.; Iguchi, M.; Noguchi, K. Revision of collagen molecular structure. Peptide Sci. 2006, 84, 181–191. [Google Scholar] [CrossRef]
- Vesentini, S.; Redaelli, A.; Montevecchi, F.M. Estimation of the binding force of the collagen molecule-decorin core protein complex in collagen fibril. J. Biomech. 2005, 38, 433–443. [Google Scholar] [CrossRef]
- Ching, W.Y.; Xu, Y.N.; Lou, Y.; Jean, Y.C. Electronic states and Fermi surfaces in the organic superconductor k-(ET)2CuN(CN)2Br. Phys. Rev. B 1997, 55, 2780–2783. [Google Scholar] [CrossRef]
- Caruso, A.N.; Pokhodyna, K.I.; Shum, W.W.; Ching, W.Y.; Anderson, B.; Bremer, M.T.; Vescovo, E.; Rulis, P.; Epstein, A.J.; Miller, J.S. Spin polarization from organic-based magnet [FeII(TCNE)(NCMe)2][FeIIICl4]. Phys. Rev. B 2009, 79, 195202–1. [Google Scholar]
- Ouyang, L.; Randaccio, L.; Rulis, P.; Kurmaev, E.Z.; Moewes, A.; Ching, W.Y. Electronic structure and bonding in Vitamin B12 cyanocobalamin. J. Mol. Struct. (Theo. Chem.) 2003, 622, 221–227. [Google Scholar] [CrossRef]
- Ouyang, L.; Rulis, P.; Ching, W.Y.; Nadin, G.; Randaccio, L. Electronic structure and bonding in adenosylcobalamin. Inorg. Chem. 2004, 43, 1235–1241. [Google Scholar]
- MacNaughton, J.B.; Moewes, A.; Lee, J.S.; Wetting, S.D.; Kraatz, H.-B.; Ouyang, L.; Ching, W.Y.; Kurmaev, E.Z. Dependence of the DNA electronic structure on environmental and structural variations. J. Phys. Chem. 2006, 110, 15742–15748. [Google Scholar]
- Liang, L.; Rulis, P.; Kahr, B.; Ching, W.Y. Theoretical study of the large linear dichroism of herapathite. Phys. Rev. B 2009, 80, 235132:1–235132:5. [Google Scholar]
- Ching, W.Y.; Rulis, P.; Misra, A. Ab initio elastic properties and tensile strength in hydroxyapatite crystal. Acta Biomater. 2009, 5, 3067–3075. [Google Scholar] [CrossRef]
- Liang, L.; Rulis, P.; Ching, W.Y. Mechanical properties, electronic structure and bonding of α- and β-tri-calcium phosphates with surface characterization. Acta Biomater. 2010, 6, 3763–3771. [Google Scholar]
- Liang, L.; Rulis, P.; Ouyang, L.; Ching, W.Y. Ab initio investigation of hydrogen bonding and network structure in a supercooled model of water. Phys. Rev. B 2011, 83, 024201:1–024201:7. [Google Scholar]
- Mulliken, R.S. Electron population analysis on LCAO-MO molecular wave functions I. J. Chem. Phys. 1955, 23, 1833–1840. [Google Scholar] [CrossRef]
- Pearson, R.G. Recent advances in the concept of hard and soft acids and bases. J. Chem. Educ. 1987, 64, 561–567. [Google Scholar] [CrossRef]
- Parr, R.G.; Chattaraj, P.K. Principle of maximum hardness. J. Am. Chem. Soc. 1991, 113, 1854–1855. [Google Scholar] [CrossRef]
- De Proft, F.; Geerling, P. Conceptual and computational DFT in the study of aromaticity. Chem. Rev. 2001, 101, 1451–1464. [Google Scholar] [CrossRef]
- Chattaraj, P.K.; Fuentealba, P.; Jaque, P.; Toro-Labbe, A. Validity of the minimal polarizability principle in molecular vibrations and internal rotations: An ab initio SCF study. J. Phys. Chem. A 1999, 103, 9307–9312. [Google Scholar]
- Jeffrey, G.A. An Introduction to H-Bonding (Topics in Physical Chemistry); Oxford University Press: Oxford, UK, 1997. [Google Scholar]
- Klamt, A.; Reinisch, J.; Eckert, F.; Graton, J.; le Questel, J. Interpretation of experimental hydrogen-bond enthalpies and entropies from COSMO polarisation charge densities. Phys. Chem. Chem. Phys. 2013, 15, 7147–7154. [Google Scholar]
- Devereux, M.; Popelier, P.; McLay, I. A refined model for prediction of hydrogen bond acidity and basicity parameters from quantum chemical molecular descriptors. Phys. Chem. Chem. Phys. 2009, 11, 1595–1603. [Google Scholar] [CrossRef]
- Kenny, P. Hydrogen bonding, electrostatic potential, and molecular design. J. Chem. Inf. Model 2009, 49, 1234–1244. [Google Scholar] [CrossRef]
- Nocker, M.; Handschuh, S.; Tautermann, C.; Liedl, K. Theoretical prediction of hydrogen bond strength for use in molecular modeling. J. Chem. Inf. Model 2009, 49, 2067–2076. [Google Scholar] [CrossRef]
- Foster, M.E.; Sohlberg, K. Empirically corrected DFT and semi-empirical methods for non-bonding interactions. Phys. Chem. Chem. Phys. 2010, 12, 307–322. [Google Scholar] [CrossRef]
- Brodsky, B. Hydrogen bonding in the triple-helix. Proc. Indian Acad. Sci. 1999, 111, 13–8. [Google Scholar]
- French, R.H.; Parsegian, V.A.; Podgornik, R.; Rajter, R.F.; Jagota, A.; Luo, J.; Asthagiri, D.; Chaudhury, M.K.; Chiang, Y.; Granick, S.; et al. Long range interactions in nanoscale science. Rev. Mod. Phys. 2010, 82, 1887–1944. [Google Scholar] [CrossRef]
- Tajkhorshi, E.; Aksimentiev, A.; Balabin, I.; Gao, M.; Isralewitz, B.; Phillips, J.C.; Zhu, F.; Schulten, K. Large scale simulation of protein mechanics and function. Adv. Protein Chem. 2003, 66, 195–247. [Google Scholar] [CrossRef]
- Enkovaara, J.; Rostgaard, C.; Mortensen, J.J.; Chen, J.; Dulak, M.; Ferrighi, L.; Gavnholt, J.; Glinsvad, C.; Haikola, V; Hansen, H.A.; et al. Electronic structure calculations with GPAW: A real-space implementation of the projector augmented-wave method. J. Phys. Condens. Matter 2010, 22, 253202:1–253202:24. [Google Scholar]
- Chaban, G.M.; Pizzarello, S. Ab initio calculations of 6- and 7-carbon meteoritic amino acids and their diastereomers. Meteor. Planet Sci. 2010, 45, 1053–1060. [Google Scholar] [CrossRef]
- Szalay, P.G.; Watson, T.; Perera, A.; Lotrich, V.F.; Bartlett, R.J. Benchmark studies on the building blocks of DNA: 1. Superiority of coupled cluster methods in describing the excited states of nucleobases in the Franck-Condon region. J. Chem. Phys. A 2012, 116, 6702–6710. [Google Scholar]
- Berisio, R.; DeSimone, A.; Ruggiero, A.; Importa, R.; Vitagliano, L. Role of side chains in collagen triple helix stabilization and partner recognition. J. Pept. Sci. 2009, 15, 131–140. [Google Scholar] [CrossRef]
- Yildiz, I.; Tvestkova, I.; Wev, A.W.; Shukla, S.; Masarapu, H.; Dragnea, B.; Steinmetz, N.F. Engineering brome mosaic virus for biomedical applications. RSC Adv. 2012, 2, 3670–3677. [Google Scholar]
- Al jabali, A.A.A.; Steinmetz, N.F.; Barclay, J.E.; Lomonossoff, G.P.; Evans, D.J. Controlled immobilisation of active enzymes on the cowpea mosaic virus capsid. Nanoscale 2012, 4, 4560–4564. [Google Scholar]
- Senn, H.; Thiel, W. QM/MM methods for biomolecular systems. Angew. Chem. Int. Ed. 2009, 48, 1198–1229. [Google Scholar]
- Menikarachchi, L.; Gascon, J. QM/MM approaches in medicinal chemistry research. Curr. Topics Med. Chem. 2010, 10, 46–54. [Google Scholar] [CrossRef]
- Floris, F.M.; Tomasi, J.; Ahuir, J.L.P. Dispersion and repulsion contributions to the solvation energy: refinements to a simple computational model in the continuum approximation. J. Comput. Chem. 1991, 12, 784–791. [Google Scholar] [CrossRef]
- Miertus, S.; Scrocco, E.; Tomasi, J. Electrostatic interaction of a solute with a continuum. A direct utilization of ab initio molecular potentials for the prevision of solvent effects. Chem. Phys. 1981, 55, 117–129. [Google Scholar] [CrossRef]
- Ratjer, F.; French, R.H.; Ching, W.Y.; Podgornik, R.; Parsegian, A. Chirality-dependent properties of carbon nanotube: Electronic structure, optical dispersion properties, Hamaker coefficients and van der Waals–London dispersion interactions. RSC Adv. 2013, 824, 823–842. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).