Abstract
Proteins are heteropolymers that play important roles in virtually every biological reaction. While many proteins have well-defined three-dimensional structures that are inextricably coupled to their function, intrinsically disordered proteins (IDPs) do not have a well-defined structure, and it is this lack of structure that facilitates their function. As many IDPs are involved in essential cellular processes, various diseases have been linked to their malfunction, thereby making them important drug targets. In this review we discuss methods for studying IDPs and provide examples of how computational methods can improve our understanding of IDPs. We focus on two intensely studied IDPs that have been implicated in very different pathologic pathways. The first, p53, has been linked to over 50% of human cancers, and the second, Amyloid-β (Aβ), forms neurotoxic aggregates in the brains of patients with Alzheimer’s disease. We use these representative proteins to illustrate some of the challenges associated with studying IDPs and demonstrate how computational tools can be fruitfully applied to arrive at a more comprehensive understanding of these fascinating heteropolymers.
1. Introduction
Proteins are heteropolymers that play essential roles in virtually all biological processes. Their vast importance in biochemistry and medicine explains why a great deal of effort has been directed at understanding their properties and function. Traditionally, proteins have been understood to have a well-defined three-dimensional structure that is inextricably linked to their function. Indeed, knowledge of the structure of a protein provides a great deal of information about that protein’s function (Figure 1) [1,2]. The importance of protein structure is underscored by the fact that amino acid mutations in a protein’s primary sequence which destabilize its tertiary structure often result in disease [3].
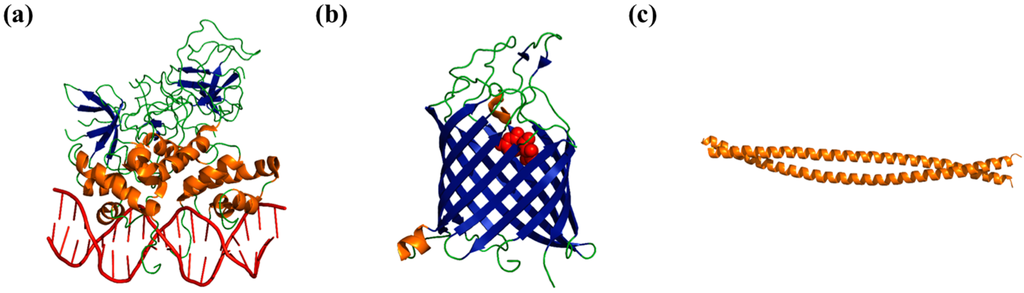
Figure 1.
Examples of the relationship between protein structure and function. (a) Crystal structure of the Lambda-phage repressor (Protein Data Bank (PDB) ID: 3bdn), which binds to its target DNA sequence (red) by making sequence-specific contacts through the grooves in the DNA double-helix [4]; (b) Crystal structure of Tsx (PDB ID: 1tlz [5]), a nucleoside transporter protein, that transports nucleosides (red) by creating pores in the membrane through a β-barrel motif (shown here in blue); and (c) Crystal structure of keratin (PDB ID: 3tnu), a fibrous structural protein whose toughness can be attributed to the helical coiled-coil structure it adopts in its fibers [6].
Although proteins are often depicted as having static three-dimensional structures, thermal fluctuations at body temperature enable them to sample different conformations throughout their biological lifetime [7]. Protein motions range from fast (~picoseconds) small amplitude (~Angstroms) fluctuations, to relatively slow (microseconds to seconds or longer), large scale motions that involve domain shifting and/or folding [8]. In general, all of these motions enable proteins to perform their prescribed functions. Given the essential role that protein motion plays in biology, discussions about protein structure should ideally revolve around the structural ensemble of thermally accessible states that a given protein can adopt [9].
For a number of proteins, the structural ensemble consisting of thermally accessible states contains structures that have relatively small deviations from the ensemble average structure. In general, such proteins are categorized as being “folded”. Structures of folded proteins, determined by experimental methods such as X-ray crystallography, correspond to the ensemble-averaged structures. Since the folded ensemble contains structures that have only small deviations from the ensemble average structure, the ensemble average itself captures many important features of the protein’s structure, and many insights into a protein’s function can be garnered from this ensemble average structure (Figure 1). By contrast, proteins within the class of intrinsically disordered proteins (IDPs) sample dissimilar conformations during their biological lifetime, and therefore the corresponding structural ensembles are heterogeneous. Given the vast number of structural states that are accessible to a disordered protein, the ensemble averaged structure for an IDP is typically not representative of any structure in the ensemble itself and therefore has little utility for understanding that protein’s function. Consequently, alternative methods are needed to understand the “structure” of these proteins.
Studying IDPs is important for a number reasons. First, they are quite prevalent in biology. It has been estimated that 25% of proteins encoded in the human genome are completely disordered and that 40% contain an intrinsically disordered region (IDR) of at least 30 amino acids in length [10,11,12]. These proteins have been found to play essential roles in many pathological processes. For example, aggregates of the IDP α-synuclein can be found in the brains of patients with Parkinson’s disease, and these aggregates have been linked to synaptic dysfunction in dopaminergic neurons [13]. Huntington’s disease, another IDP-associated neurodegenerative disease, is traceable to aggregation of the IDP Huntingtin protein [14,15,16,17]. Similarly, aggregation of the IDPs Amyloid-Beta peptide (Aβ) and tau protein are pathological hallmarks of Alzheimer’s disease [18,19,20,21,22]. In addition to diseases related to IDP aggregation, IDP malfunction can also cause pathogenic errors in signaling pathways. For example, mutations in IDPs involved in regulation of the cell cycle can disrupt gene regulation and cell signaling, mechanisms that are implicated in oncogenesis [23]. Tumor suppressor p53 is a largely disordered protein, which functions in cell cycle regulation [24]. Deactivating mutations of p53 can facilitate uncontrolled cell division and oncogenesis; e.g., mutations in the p53 are found in over 50% of cancers [25], including tumors of the colon, lung, ovaries, breast, liver, and brain [26,27].
While the importance of IDPs in human biology and pathology is unquestioned, their inherent structural heterogeneity makes them particularly challenging to study. In what follows, we first review protein structure in general, focusing on important differences between folded proteins and disordered proteins. We then introduce experimental and computational methods for studying intrinsically disordered proteins. Finally, we discuss examples of where these methods have been and could be applied to increase understanding of two IDPS, p53 and Aβ. While many IDPs have important functional roles in biology and are implicated in human diseases, we chose to focus on these two proteins because they typify two very different types of disordered proteins. P53 is a large (393 residues), intracellular, multi-domain protein that has a folded DNA binding domain in addition to several long intrinsically disordered regions (IDRs). These IDRs facilitate its role as a hub in cellular stress networks. By contrast, Aβ is a small (around 40 residues) fully disordered extracellular protein that may play a role in memory and learning [28] and does not contain any folded subdomains in its monomeric state. Although these proteins have very different structural properties, computational methods have been used to improve our understanding of both of these systems.
2. Folded Proteins versus Disordered Proteins—A Comparison
Proteins are heteropolymers consisting of covalent linkages between consecutive amino acid monomers. The amino acid sequence of a protein, termed its primary structure, confers chemical properties to the protein through the characteristic properties of the 20 amino acids. For traditional “folded” proteins, this chain folds into a unique structure. A central dogma of biochemistry is that a protein’s amino acid sequence determines its structure, which in turn determines its function [1,29]. While this paradigm has been often quoted in the literature, it is now recognized that conformational fluctuations in proteins play an essential role in protein function [30]. The inaccuracy of this paradigm is even more poignant for disordered proteins, which sample a variety of structurally dissimilar states during their biological lifetime [31].
The difference between folded proteins and disordered proteins can be understood based on an analysis of their potential energy landscapes (Figure 2). Folded proteins have a “funnel-shaped” global energy minimum, where the lowest energy state corresponds to the native structure [32,33], and the width of the unique global energy minimum determines the conformational entropy of the native state (Figure 2a). By contrast, disordered proteins have multiple local energy minima separated by small barriers (Figure 2b). Transitions between the different local energy minima occur quickly and often, leading to an ensemble consisting of a vast number of structurally dissimilar states, which have approximately equal energies. Thus, a comprehensive characterization of an IDP consists of an ensemble of states and the transition rates between them [34]. In practice, knowledge of the transition rates between conformers in an IDP ensemble is quite difficult to capture experimentally (or computationally). Consequently, in practice, studies of IDPs have focused on modeling the thermodynamically accessible states alone. As we outline below, while this represents an incomplete picture of these proteins, a great deal of information and insight has arisen from such studies.
While the above distinction between folded and disordered protein landscapes is instructive, it misses many of the nuances associated with discussions of protein structure. As we have alluded to above, thermal fluctuations cause both folded and disordered proteins to sample a variety of states during their lifetime. In this regard, we note that even proteins considered to be folded (and whose structures have been solved via X-ray crystallography), often contain both ordered regions and intrinsically disordered regions lacking a stable tertiary structure [35]. This means that the energy minimum of a folded protein with an IDR is actually not smooth, but is actually a rough surface with many smaller minima corresponding to different states sampled by the IDR within the native state (Figure 2c). Typical representations of folded and disordered proteins attempt to capture these inherent differences between the ensemble of states in a minimalist, yet informative manner. Folded proteins are often depicted as a single ensemble average structure (Figure 3a), while disordered proteins/regions are represented by an alignment (or overlay) of energetically favorable, yet structurally dissimilar states (Figure 3b).
Disorder imparts a number of properties to IDPs that would be difficult for folded proteins to realize. For example, the structural heterogeneity of IDPs (and IDRs) confers proteins the ability to be promiscuous in their choice of binding partners [36,37,38]. This property explains why IDPs are frequently found to be hubs in protein interaction networks and are specifically associated with signaling networks [37,39]. In fact, almost 70% of signaling proteins are predicted to contain an IDR of at least 30 consecutive residues [23]. The largely disordered tumor suppressor p53 (which we discuss further below), for example, is an important signaling hub, binding hundreds of proteins [39]. An additional strength of IDPs in signaling networks is their rapid turnover facilitated through an increased sensitivity to proteolytic degradation over folded proteins, allowing them to be quickly deactivated in response to changing cellular environments [40,41,42]. Outside of signaling, some structural features are enabled directly through the flexibility of IDPs, such as elasticity in elastin or enhanced flexibility in proteins that must pass through narrow tubes [43,44].
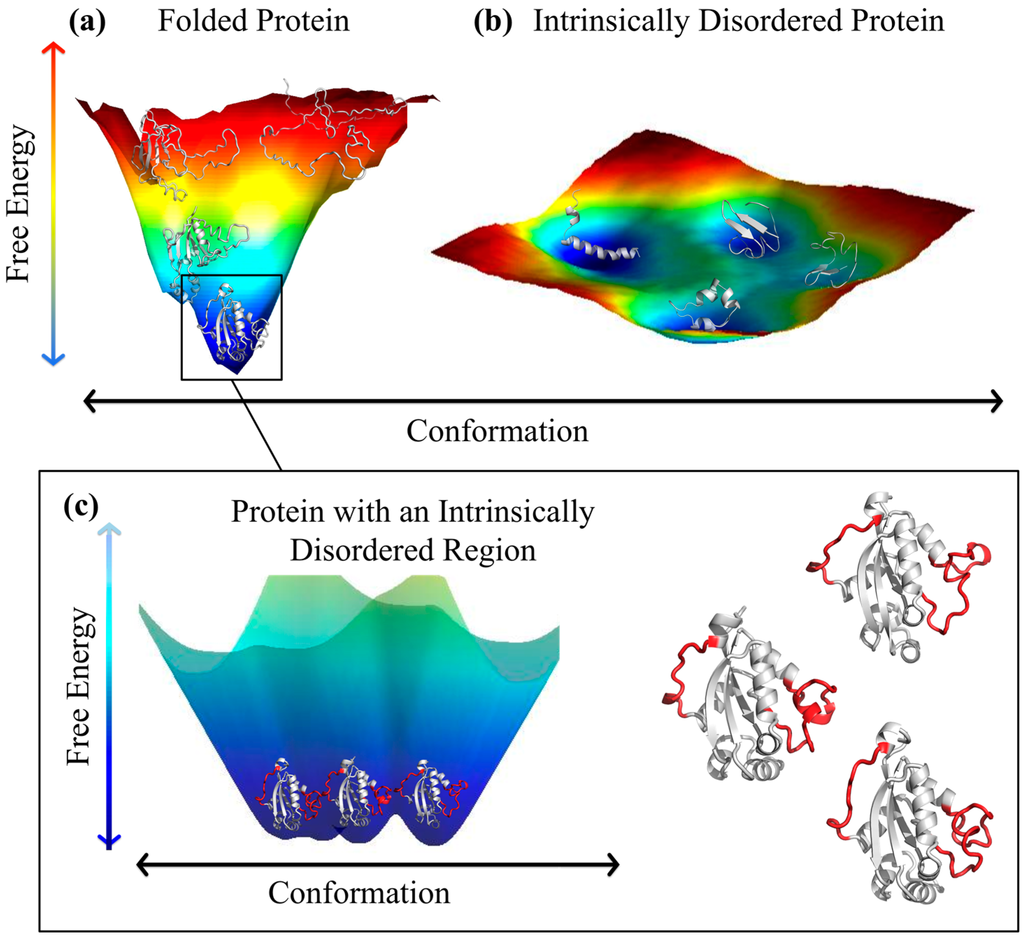
Figure 2.
Schematic of energy landscapes for (a) a folded protein (human nucleoside diphosphate kinase (NDPK), PDB ID: 1nsk) [45] and (b) an intrinsically disordered peptide (CcdA C-terminal, PDB ID: 3tcj) [46]; (c) close-up of the minimal free energy well in (a), where IDRs are shown in red and ordered regions are shown in white. The example NDPK conformations are shown again enlarged to the right for better visualization. In (a–c) lower free energy (dark blue) represents more probable conformations. Representative protein conformations were generated with molecular dynamics simulations in CHARMM using coordinates from the 1nsk and 3tcj PDB structures as initial states [47,48].
IDPs may obtain a folded structure upon binding their partners. Whether folding occurs before, during, or after contacting the partner is an oft-studied question, due to its implication in the design of molecules to potentially inhibit or stabilize IDP states. The conformational selection hypothesis proposes that unbound IDPs fluctuate through their bound conformations, and their partners selectively bind when the IDP is in the appropriate binding conformation [49]. Alternatively, the induced fit hypothesis proposes that IDPs first make low-affinity, non-specific contacts with their partners, and then fold as they bind [50,51]. Fly-casting, a related supposition that expands on this principle, states that extended IDP conformations result in IDPs possessing a relatively large capture radius which leads to fast association rates [52,53]. While this increased capture radius has not been shown to significantly increase the binding rate of IDPs over folded proteins, it has been shown for an IDP and its binding partner that weak encounter complexes initiated from an extended conformation of the IDP are more likely to evolve to the native complex than weak encounter complexes initiated from a folded form of the IDP [54]. This indicates that some IDPs may be more likely to have productive encounters with their partners than folded proteins, as they can more easily fold into their bound state after an initial non-native interaction with their partner. The conformational selection and induced fit hypotheses are not mutually exclusive, and may be used in different combinations by each IDP with each of its binding partners. Additionally, many IDPs remain disordered upon binding their partners, and this disorder may also have functional roles [55].
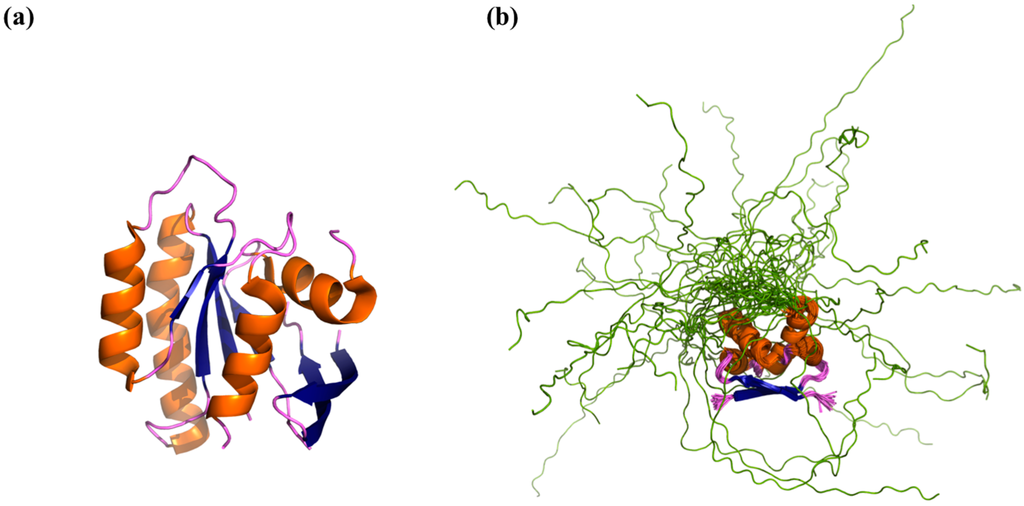
Figure 3.
Varied degree of order in proteins (a) Crystal structure of the protein H-Ras, solved in complex with GTPase-Activating Protein (not shown, PDB ID: 2x1v) [56]. H-Ras is a folded protein containing a number of loops (purple) that have well-defined B-factors. These loops have no regular secondary structure yet they are ordered in the sense that they have well defined three-dimensional coordinates. Ordered regions of the protein that have regular secondary structure are shown in orange (helices) and blue (sheets); (b) NMR ensemble of the CcdA dimer (PDB ID: 2h3a), a protein with both an ordered region and an IDR [57]. The intrinsically disordered C-terminal tail (shown in green) populates a large number of structurally dissimilar states. Each of the potential C-terminal conformations is depicted as a distinct backbone trace (green), and the ordered regions are shown in orange/blue/purple according to secondary structure.
3. Experimental Studies of IDP “Structure”
The ensemble average structure of a folded protein is usually determined using X-ray crystallography or nuclear magnetic resonance (NMR) spectroscopy (via the measurement of distance constraints between heavy atoms) [58]. These methods, however, cannot be used to obtain a comprehensive picture of the structural ensemble of IDPs, for the reasons mentioned in Section 2. Instead, experimental methods more appropriate for heterogeneous data can be used to find boundaries and distributions of measurable variables across the ensemble of conformational states sampled by the IDP.
Insights into aspects of an IDP ensemble are typically obtained using a number of experimental techniques. Two useful measurements are secondary chemical shifts and paramagnetic relaxation enhancement (PRE). Secondary chemical shifts, measured with NMR, quantify the deviation between measured chemical shifts and random coil chemical shifts for each residue, providing local information about secondary structure propensities in IDPs [59]. It is important to note that since IDPs typically fluctuate between dissimilar conformations on a time scale that is fast relative to the experimental time scale, the measured chemical shifts at each residue are ensemble averages [60].
While the ensemble average for chemical shifts is computed as a simple average, many measurements on protein structure scale exponentially (r−6) with the distance r. This has the particular consequence that measurements which scale exponentially with distance will be biased towards small distances. For example, NMR PREs measure long-range (up to 25 Angstrom) residual contacts within a protein by tagging a specific amino acid with a paramagnetic probe, thereby affecting the relaxation properties of nearby nuclei [60,61]. The distance dependency of PREs ensures that closer distances will have more weight, and thus these measurements are more sensitive to states with short inter-residue distances.
NMR measurements of the Nuclear Overhauser Effect (NOE) can also provide short-range distance constraints between different nuclei in a structure [58,60]. For example, NOEs are typically observed between nuclei separated by less than ~8 angstroms, and therefore provide valuable information about residues that are distant in the primary sequence but that are nearby in three-dimensional space [62]. Similar to PREs, observed NOE intensities depends exponentially on distance, and thus ensemble averages are biased toward a small subset of conformations that have close contacts. Moreover, rapid conformational fluctuations of IDPs lowers the intensities of observed NOEs in comparison to folded proteins. In short, NOEs are usually not observed between residues in an IDP that are far apart in the primary sequence [58,60,63]. Thus, while NOEs can be used to form distance constraints between residues for determining structure of folded proteins, they have not proven as useful for studying IDPs [64].
Residual dipolar coupling (RDC) measurements provide information about the relative orientation of two nuclei, which typically share a covalent bond, with respect to an external magnetic field. Prior to measuring residual dipolar couplings, the protein of interest is typically embedded in an alignment medium that reduces the effects of molecular tumbling, thereby maximizing the measured magnitude of the dipolar couplings. RDCs encode ensemble-averaged information about structured elements in IDPs where the average is complicated by the dependence on orientation angles [60,65,66].
Small angle X-ray scattering (SAXs) experiments provide information about the overall shape and size of molecules [67]. Although these data, again, correspond to ensemble average information, when combined with structural models, SAXs profiles can provide needed information that can be used to validate and refine models describing the thermodynamically accessible states of the IDP of interest.
Recently, high speed atomic force microscopy (HS-AFM) has allowed visualization of the topography of proteins at nanometer resolution through a time-series of topographic images with a frame rate of more than ten frames per second [68]. HS-AFM does not require labeling or staining of the molecule, but forms a topographic image of an entire system residing on a surface in a solution with minimal perturbation to the molecule in near physiological conditions [69]. In studies of the 1767 residue heterodimeric protein FACT (facilitates chromatin transcription), which contains two major IDRs consisting of approximately 200 residues each, a frame-rate of 5–12.5 frames per second was sufficient to visualize changes in the IDRs’ surface over time [70]. These data can be used as bounds on models of IDPs, for example, in the form of distributions of radii of gyration.
In sum, existing experimental techniques for studying protein structure can provide boundary conditions that can be quite useful for ensemble construction. Combining experimental measurements from different sources with computational studies has shown promise in generating conformational ensembles of IDPs [71,72,73]. In the following section, we discuss how computation can be used to gain further insight into the conformational ensemble of IDPs from experimentally garnered data.
4. Computational Methods for Describing IDP Ensembles
Molecular simulations can complement experimental methods, yielding structural models for the dominant thermodynamically accessible states of IDPs [74]. While experiment usually provides ensemble-averaged information, molecular simulations provide atomistic information that can clarify experimental observations and that can provide fodder for future experiments [31].
Molecular dynamics (MD) simulations, in particular, can generate trajectories for proteins using an underlying potential energy function, which is used to calculate the forces on each atom (and consequently the motion of each atom) in a protein [75,76]. The potential energy function includes terms describing the energy associated with bond lengths, bond angles, and torsion angles, as well as long range forces arising from the Coulombic energy and van der Waals interactions. The parameters defining each of these terms are learned either empirically or from ab Initio calculations [75,77]. Several issues arise when applying these methods to IDPs. First, most parameterized force fields were developed for folded proteins, and it is an open question as to whether all of the available energy functions are generally applicable to IDPs. While some more specific force fields have been developed with IDPs in mind (and fruitfully applied), it is not clear how generally applicable these methods are [78,79,80,81,82]. More importantly, the conformational heterogeneity of IDPs calls for extensive simulations to ensure that the relevant regions of conformational space have been adequately sampled. In general, this process is quite demanding from a computational standpoint.
Another method for conformational sampling, attractive due to its relative computational efficiency, is the statistical coil model approach where one samples from empirical potentials to quickly generate an ensemble of states [83]. The computational advantage of this approach stems from the fact that structures are typically constructed by independently sampling individual residue phi-psi conformations for each residue in the protein. In this regard the potentials used are much simpler than molecular dynamics potentials and usually seek to reproduce coarse-grained behaviors, such as empirical backbone dihedral angle distributions for each residue from the Protein Data Bank (PDB) [83,84,85]. Like molecular dynamics potentials, however, the empirical potentials used in statistical coil-based approaches are usually trained on conformational propensities of natively folded proteins; e.g., the phi–psi angles of residues designated as coil (e.g., regions not in strand or helical conformations) in the PDB. User-defined restraints can be included, such as done with the Flexible Mecanno tool [84], to adapt the potential to the particular protein in question.
While there is much merit in these approaches, generating an accurate structural ensemble using these methods alone is not tractable for systems of even modest size. Computational tools may therefore have their greatest utility when used in conjunction with experimental data. For example, experimental observables can be used to restrain molecular simulations to obtain ensembles that have calculated observables that agree with the corresponding experimental values [71,86]. Such ensemble-restrained simulations have been used to obtain conformational ensembles of alpha-synuclein by restraining molecular dynamics simulations with paramagnetic relaxation enhancement (PRE) measurements, which provide information about the long-range interatomic distances in the protein [63]. These studies find that alpha-synuclein populates an ensemble of states that have smaller hydrodynamic radii than random coils, suggesting some degree of residual structure driven by interactions between the charged C-terminus and the hydrophobic central region of the protein [63]. Other approaches first generate candidates for the thermally accessible states of the protein using an empirical potential energy function and then compare calculated ensemble averages from the molecular models to corresponding experimentally determined ensemble averages [87]. Correct models have calculated averages that agree with experiment [88]. One example of such an approach is ENSEMBLE, which takes as input a set of conformations and experimental data and prunes this large set of conformations to a smaller set. Each structure is assigned a weight such that their ensemble average measurements agree with the data, and structures that do not contribute to fitting the experimental data are discarded [89]. Another approach for creating an ensemble that agrees with experimental measurements involves generating structures using a statistical coil-like model (Flexible-Meccano), a subset of which are selected for the agreement between their backbone dihedral angles and NMR chemical shifts. The process is then iterated until no further improvement in the agreement between chemical shifts and backbone dihedral angles can be obtained [90]. These models and their associated experimental data can be deposited in an openly accessible database termed pE-DB [91].
It is important to note that since experimental observables typically correspond to ensemble averages, it is not clear how to combine experiment with the results of computational models to arrive at an unfolded ensemble. While the problem of generating an ensemble that agrees with experiment is mathematically well defined, it is inherently under-determined. More specifically, the number of experimental restraints one can obtain from any given experiment pales in comparison to the number of degrees of freedom associated with even the smallest IDP. In other words, one can generate many mutually exclusive structural ensembles that have ensemble averages that agree with any given set of experimental data [88,92,93,94].
Several methods have been developed to deal with the degeneracy issue. In the most straightforward approach, one generates a number of different ensembles for an IDP that all agree with experiment. Structural features that are in common to all of the ensembles are interpreted as being those that are most likely to be “true”; i.e., while one cannot unambiguously determine which ensemble is correct, features that are common to all of the ensembles are likely to be legitimate [93,95]. A second method bases the choice of ensemble on a maximum entropy or, equivalently, a minimal information approach [96,97,98]. The general principle ensures that the ensemble (1) yields calculated observables that agree with experiment; and (2) is as similar as possible to some pre-defined “prior” probability distribution. For example, if the prior distribution is given by the potential energy of the potential conformers, then the method yields an ensemble that agrees with experiment and that minimally differs from what the potential energy surface says are favorable conformations.
Another method that explicitly tackles the issue of degeneracy is Bayesian Weighting (BW) [92,99]. The BW method consists of constructing coarse-grained conformational ensembles, defined as a finite set of representative structures and an associated set of weights, , which specifies the relative stabilities of each structure in the ensemble. The method begins by first generating a set of structures, either through a statistical coil model or by sampling from a molecular dynamics potential energy function. In general, it is helpful to construct libraries that cover a wide range of structural parameters (e.g., secondary structure content, radius of gyration, etc.) [88,100]. Predicted experimental measurements for each of these structures are then obtained using a variety of available algorithms (e.g., SHIFTX for NMR chemical shifts [101]). Using a Bayesian formalism, a posterior distribution over all possible weights for each structure is then computed by maximizing the agreement between the conformational ensemble and the experimental data. The strength of this approach lies in the fact that it accounts for both uncertainty associated with the experimental measurements (i.e., measurement error), and uncertainty in the algorithms used to predict experimental data from a given structure (i.e., prediction error), when generating the posterior distribution. Furthermore, it provides a quantitative estimate of the uncertainty in the underlying ensemble in the form of an uncertainty parameter, which takes a value between 0 and 1 and represents the extent to which one can assign weights to the structures in differently to agree with the data [92]. This uncertainty parameter was found to correlate well with model correctness in a computational study [92]. Thus, the BW formalism allows the user to use quantitative experimental measurements, such as NMR or SAXS data, to construct conformational ensembles, and produces a measure of the model’s statistical uncertainty. Cross-validating an ensemble with independent experimental data provides an additional method for justifying an ensemble [72,73].
To illustrate how computational tools can be used to study IDPs, in the remaining sections we focus on two IDPs that have been implicated in human disease. For p53, mutations causing abnormal signaling lead to cancer, whereas for Aβ, aggregation of monomers is linked to Alzheimer’s disease. As the pathology of these diseases is dissimilar, different questions have guided research into the proper and improper functioning of these two IDPs. We discuss how the computational tools mentioned above can aid in the process of garnering detailed structural insights into their disease processes, which can in turn be applied to the rational design of novel compounds aimed at combating disease. Moreover, studying the mutations and malfunctions of IDPs that lead to disease will improve understanding of the structural and mechanistic properties of IDPs that are essential for their correct function.
5. p53
Tumor suppressor p53 has been dubbed the “guardian of the genome” due to its central role in cell cycle regulation in response to stress [102,103]. Once p53 is activated by cellular stress signals, it binds DNA to regulate transcription of genes involved in stress response pathways, including cell cycle arrest, senescence, apoptosis, and metabolism [104]. Depending on the type of stress, p53 can arrest cell division while initiating transcription of genes for DNA repair in order to prevent duplication of a cell with damaged DNA, or initiate apoptosis to destroy cells with irreparably damaged DNA. Thus, alterations in the function of p53 can disrupt its ability to respond to DNA damage, allowing damaged cells to multiply. Like many other IDPs functioning as transcription factors, p53 is a hub protein, regulating over 150 genes [39,105] and binding hundreds of partner proteins [106,107] in a complex regulatory network. Its involvement in so many cellular processes ensures that mutations in p53 have widespread effects. In fact, 50% of cancers involve an inactivating mutation of p53 [108], and the apoptotic pathways controlled by p53 are impaired in the remaining cancers [25,108].
p53 functions as a homo-tetramer where each monomer contains six major domains (Figure 4a). The N-terminal region of p53 contains the largely disordered transcription activation domain (TAD, residues 1–67) and the short proline rich domain (PRD, residues 67–98) [109]. This is followed by the structured DNA binding domain (DBD, residues 98–303). The C-terminal region contains the intrinsically disordered nuclear localization signaling domain (NLS, residues 303–323), the tetramerization domain (residues 323–363) [109,110], and the intrinsically disordered C-terminal negative regulatory domain (NRD, residues 364–393) [111]. The intrinsic disorder of the TAD and NRD enable binding of multiple partners with varied strengths. Moreover, the flexible nature of the entire p53 molecule and the intrinsic disorder of TAD and NRD domains assist p53’s binding partners in forming multi-point interactions with p53 in both the TAD and the NRD [25]. However, the disorder of these domains also limits the ability of traditional experimental methods to investigate the structure of p53 or its disordered domains, particularly when not bound to partners. Instead, structural data on individual domains has been obtained, often in the presence of different stabilizing binding partners.
In the following sections, we will describe how computational methods have been used to investigate the mechanisms of regulation of p53 activity through its binding partners. Specifically, we discuss how computational methods have been used to understand the mechanisms by which the TAD and NRD domains are able to bind multiple partners in different conformations. The mechanism of partner recognition and folding upon binding used by each of these IDRs is interesting for both design of potential drugs to inhibit or re-stabilize p53 in tumors, as well as to better understand the engineering of IDPs.
5.1. p53 Transcription Activation Domain (TAD)
The IDR p53 TAD interacts with proteins forming transcriptional machinery as well as inhibitor proteins (Figure 4b). For example:
- In the absence of cellular stress, p53 TAD is bound by its inhibitor MDM2 (mouse double minute 2 homolog), which both tags p53 for degradation and inhibits the binding site of p53 to transcriptional co-activator proteins (Figure 4b) [112,113]. The TAD region is phosphorylated in response to cellular stress; phosphorylation of the TAD disrupts the interaction between p53 and MDM2, thereby allowing p53 to act as a transcriptional regulator [114].
- In response to cellular stress signals, the TAD domain binds to the transcriptional co-activators CBP (CREB-binding protein; CREB is the cAMP-response element-binding protein) and p300, which function as scaffolds for assembling transcription factors on DNA that regulate genes for stress response pathways (Figure 4b). CBP and p53 additionally bind the NRD and perform post-translational modifications of NRD residues, leading to increased stabilization of the p53-DNA complex [113].
- P53 is also activated as a transcription factor through its interaction with High Mobility Group Protein B1 (HGMB1)), which forms part of the transcription machinery on DNA (Figure 4b). HGMB1 has two binding domains: one domain binds to p53 and the other domain binds and bends DNA, most likely into a more suitable conformation for binding of the p53 DBD [115].
- p53 TAD also interacts with its inhibitor Replication Protein A (RPA), which preferentially binds single-stranded DNA (ssDNA) (Figure 4b) [116]. If damaged DNA results in an increase in ssDNA, RPA will instead bind ssDNA, freeing p53 to activate transcription of stress response genes [116]. Hyperphosphorylation of RPA through UV radiation also disrupts the interaction between p53 and RPA, allowing p53 to initiate repair of DNA damaged by the UV radiation [116].
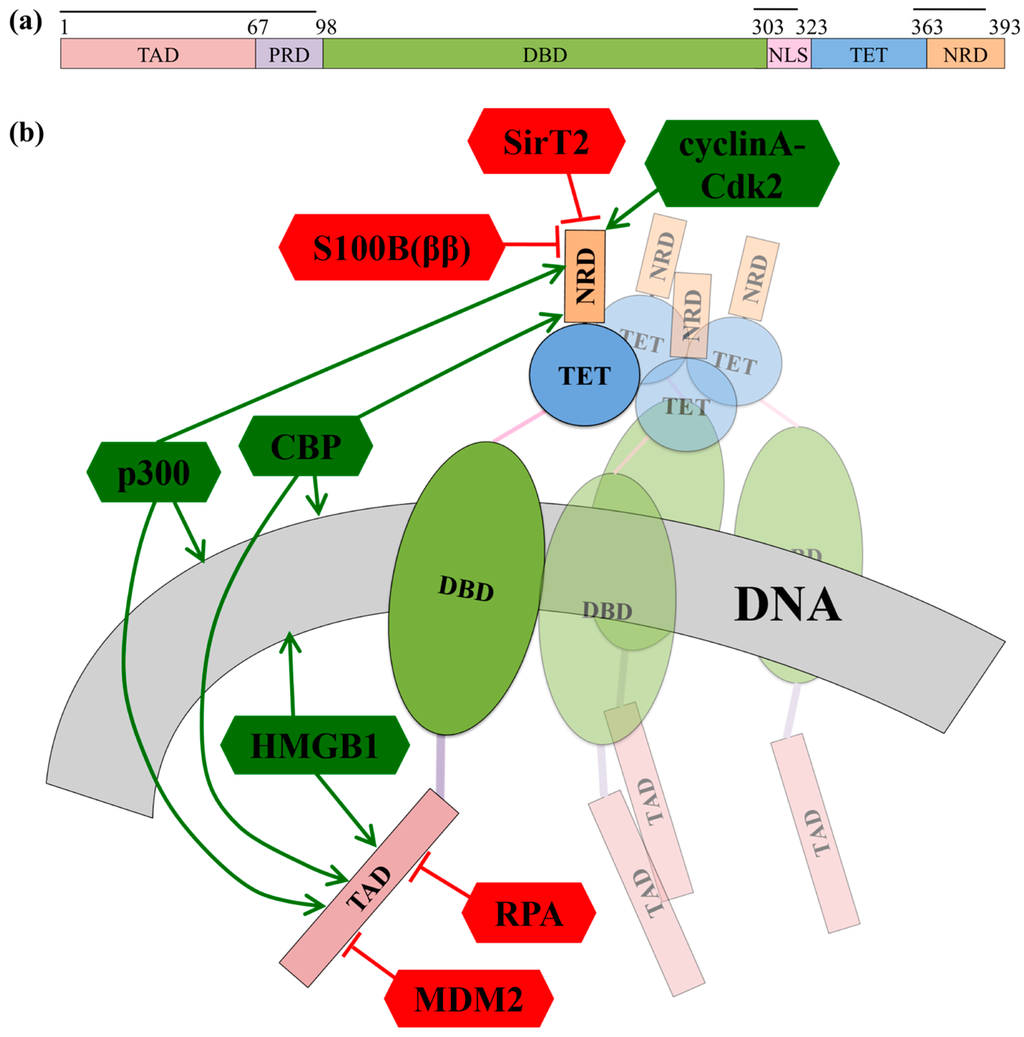
Figure 4.
p53 domains and interactions. (a) Primary sequence of p53, colored according to domains. Black lines are drawn over domains that are intrinsically disordered in the monomer; and (b) Schematic of interactions between p53 and the binding partners discussed in this review. A full p53 tetramer is shown bound to DNA. Interactions are shown along a single monomer; the remaining monomers are faded. Green and pointed arrows indicate interactions that promote transcription activity by p53; red and blocked arrows indicate interactions that repress transcription activity by p53.
The intrinsic disorder of p53 TAD provides it with flexibility to bind multiple partners using different residue subsets in different motifs (Figure 5b–f). The TAD domain has two subdomains; TAD1 is formed from residues 1–40 and TAD2 is formed from residues 41–67 [109,110,117]. The flexible nature of p53 TAD enables enhanced binding through the use of one or two subdomains, increasing the complexity of TAD’s interactions with its binding partners. For example, TAD mimics ssDNA when forming contacts with the DNA-binding protein RPA, as well as HGMB1, as part of a mechanism for detecting damaged DNA (Figure 5f,e) [115,116].
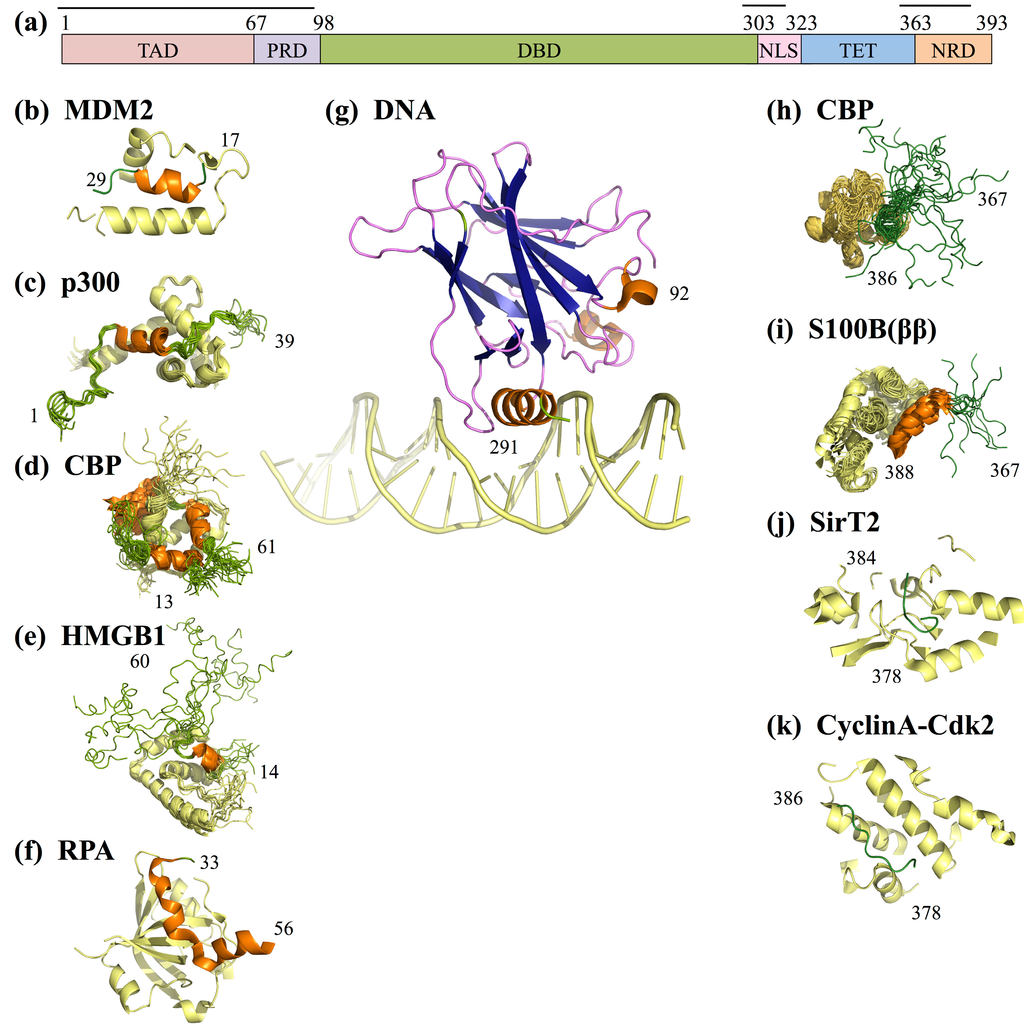
Figure 5.
p53 domains and interactions. (a) The primary sequence of p53, colored according to domains. Horizontal lines above sequence indicate disordered domains in the monomer; (b–k) A PDB structure/model for each p53 region discussed in the paper is shown beneath its corresponding domain in (a). Ordered regions of p53 are shown in orange (helices), blue (sheets), and purple (loops); IDRs are shown in green; DNA/regions of binding partners within 15 Å of p53 are shown in yellow. Multiple potential structures are shown superimposed for NMR ensembles, whereas a single structure is shown for crystal structures. Indices of first and last p53 residues included in each structure are provided. In order (b–k), the PDB IDs of the models shown are: 1ycr, 2k8f, 2l14, 2ly4, 2b3g, 4hje, 1jsp, 1dt7, 2h2f, and 1h26 [113,115,116,118,119,120,121,122,123,124].
Understanding how IDPs, which fold upon binding, obtain well-defined tertiary structures, in the presence of their binding partners, is central to understanding how these proteins function. Several hypotheses exist for how IDP folding and binding occurs. Molecular simulations, such as those described in the remainder of this section, have been used to model the conformational ensemble of the unbound p53 TAD to differentiate the roles played by conformational selection and induced fit in interactions between p53 TAD and its binding partners.
To investigate the structural details underlying the mechanism of MDM2 binding to p53 TAD, Xiong et al. performed ten one-microsecond long all-atom molecular dynamics simulations in explicit water of p53 residues 17–29, which are known to form a helical conformation when bound to MDM2 (Figure 5b) [125]. They observed that this helix is also sampled in the unbound state, suggesting that conformational selection may play a role in MDM2 binding. These MD simulations are in agreement with NMR results suggesting that p53 residues 18–26 sample alpha helical conformations [126], as well as with their UV resonance Raman spectroscopy results summarizing the distribution of backbone psi angles in the peptide [125]. Xiong et al. also examined the conformational preferences of a P27S mutation in TAD, which is associated with increased binding affinity to MDM2 [127], using MD simulations. They found that the unbound mutant peptide more heavily populates conformations similar to the MDM2-bound conformation of p53, due to increased alpha-helical content. The increased propensity for helicity in a mutant that has increased MDM2-affinity further supports the hypothesis that conformational selection guides the TAD–MDM2 interaction.
Much effort is being devoted to detecting pre-structured motifs in IDPs and in establishing their role in IDP binding, especially with respect to conformational selection [126,128]. For example, three pre-structured motifs have been detected in p53 TAD with NMR spectroscopy: a helix located in residues 18–26 and predicted to be present in 20% of the unbound population; a turn located in residues 40–44 that is predicted to be present in 5% of the population; and a turn in residues 48–53 that is predicted to be present in 15% of the population [126,129,130]. Each of these regions is flanked by a proline residue at the N-terminus and the C-terminus [130]. Prolines are known to terminate or cause kinks in helices, in part due to the phi/psi angles that they preferentially adopt in solution. Lee et al. observed that prolines are enhanced in regions flanking pre-structured motifs in IDPS, and used molecular dynamics simulations to investigate the role of prolines in these regions [130]. They generated short (10 ns) MD simulations of the wild-type peptides and mutants in which the flanking prolines were substituted with aspartic acid, histidine, alanine, or lysine [130]. Their simulations revealed that substitution of N-terminal prolines for other amino acids decreases the amount of helicity within the pre-structured motifs, and substitution of C-terminal prolines for other amino acids increases the amount of helicity within the pre-structured motifs. Based on these findings, Lee et al. argued that the location of prolines in regions flanking pre-structured motifs may have evolved to control the degree of pre-formed helicity within disordered regions, thereby regulating the degree of conformational selection by IDP partners [130]. Recently, Szöllősi et al. used molecular simulations to predict a number of pre-formed regions across a large set of IDPs [131], including the MDM2-binding region in p53. While the existence of pre-structured motifs in many IDPs is established, future studies should go past detection of folded conformations in the fully unbound state to explore the conformations sampled by IDPs when in the vicinity of or non-specifically bound to their partners, in order to further understand the role these motifs play in binding through induced fit.
Specific “anchor” residues within the binding regions may also drive the folding and binding process. Here, anchor residues in IDPs are defined as residues that are fully exposed to solvent when unbound, and become fully buried after binding [132]. Huang and Liu et al. investigated the role of anchor residues in IDP binding using short molecular dynamics simulations of the TAD peptide, which adopts distinct helices upon binding two of its receptors, MDM2 and p300 (Figure 5b,c) [132]. By simulating many complexes between the TAD peptide and its receptors, they concluded that binding by IDPs to targets is initiated by conformational selection, and completed by induced fit. For example, they observe through MD simulations of TAD peptides containing partial helical structure that the anchor residues will predominantly sample their bound-like configurations. In simulations of the encounter complex between TAD and MDM2, where the initial TAD conformation contained pre-formed partial helical structure and bound-like orientation of the anchor residues, it was observed that TAD will first insert its anchor residues into the receptor to stabilize the interaction, and then, through back-bone re-arrangements and induced fit, obtain its stable, bound structure within 1 ns simulation time. By contrast, in simulations of p53 TAD peptides in an encounter complex with MDM2, where the TAD peptides either had pre-formed partial helical structure, but with non-bound-like positioning of the anchor residues, or did not have pre-formed helical structure, p53 TAD did not form the bound state within the 10ns simulation time. The relatively short time frame of these simulations makes it difficult to exclude the possibility that the p53 TAD peptide eventually rearranges to form its bound state. Nevertheless, they suggest that bound-like anchor residue positions within partially pre-formed helices promote receptor binding. This study highlights the potential importance of anchor residues for IDP binding and demonstrates that specific residues within partially pre-formed motifs may control the folding upon binding process, as opposed to the entire pre-formed helix. That is, although the helix is accessible in the unbound state, only anchor residues may need to be fully pre-formed during the initial encounter to promote receptor binding. The exact role of anchor residues and pre-structured motifs is important to elucidate for design of specific inhibitors for interactions between IDPs and their partners [132]. If anchor residues could be identified that were unique to interactions between TAD and its different receptors, then therapeutic mechanisms could be designed to temper specific interactions by TAD, as opposed to all interactions. This would allow promotion or repression of specific pathways involving p53. The interplay between conformational sampling, pre-structured motifs and anchor residues should be further explored through molecular dynamics simulations of the protein in the presence of its binding partners.
The studies discussed above for p53 TAD [125,130,131,132] investigate the role of conformational selection in p53 IDRs using truncated p53 peptides. While the computational expense of these calculations often necessitate the use of short constructs and relatively short simulations times, it is important to recognize that the system of interest is the full-length protein. In this regard, it is always important to compare insights arising from these simulations to data obtained on the complete protein sequence. For example, previous work suggests that stability of the full MDM2-p53 complex is similar to that of the complex formed by a truncated TAD (residues 17–29) peptide [127]. Additionally, the N-terminal domain within the full p53 molecule behaves similarly to the isolated N-terminal residue 1–93 peptide and is not stabilized by contacts with folded regions of p53 [24,133]. The use of shorter peptides is not without its shortcomings however. Schon et al. show that the binding affinity of p53 to MDM2 is greatly affected by truncation of the p53 residue 15–29 peptide to shorter truncates [134]. This indicates that the shorter truncates sample conformations that bind MDM2 more readily than the full p53 molecule, and thus results for these peptides may not fully represent the physiological behavior of p53. Overall, while computational expense often restricts simulations to truncates or short time-scales, whenever possible, simulations of the biologically-active state should be used and questions should be pursued that can be addressed in affordable time periods and supported by experimental data.
5.2. p53 Negative Regulatory Domain (NRD)
The intrinsically disordered negative regulation domain of p53 binds many proteins that either hinder or promote the transcriptional regulatory activity of p53. Cellular signals received by the NRD in the form of post-translational modifications alter its conformation and binding, which in turn regulate the transcription activity of p53 [113,135]. Some of the NRD’s interactions include:
- Acetylation of p53NRD at Lysine 382 facilitates binding by the bromodomain of CBP (Figure 4b). This leads to recruitment of transcriptional co-activators essential for p53 to activate transcription of genes involved in cell cycle arrest [121]. Cell cycle arrest prevents division of the damaged cell, providing time for p53-initiated damage control pathways to repair the cell’s DNA before cell division is reinitiated.
- The protein s100B(ββ) binds NRD to both sterically block post-translational modification sites and disrupt p53 tetramerization (Figure 4b) [122].
- SirT2 binds NRD to de-acetylate its Lysine side-chains (Figure 4b) [136]. As NRD lysine acetylation is required for activation of p53 as a transcription factor [121], SirT2 deactivates p53.
- Cyclin A-CDk2 binds p53 NRD and phosphorylates Serine 315 after irradiation damage (Figure 4b), leading to activation of p53 [135]. Interestingly, both SirT2 and Cyclin A can regulate p53 in more roles than described here, alternately inhibiting or promoting p53’s transcriptional activation functions [137,138].
An eleven residue region (residues 376–386) contained in the NRD binding sites of each of the four interaction partners described above has been shown experimentally to adopt unique secondary structures upon binding each of its partners [37,39]. Residues 376–386 form a short bend within a mostly disordered region culminating in a turn when bound to the bromodomain of CBP (Figure 5h); a helix followed by a turn when bound to s100B(ββ) (Figure 5i); a turn followed by two short beta-bridges within a mostly disordered region when bound to SirT2 (Figure 5j); and a short turn followed by a mostly disordered region when bound to Cyclin A-Cdk2 (Figure 5k). As two of these proteins are known to promote p53’s tumor suppression activity, and two of these proteins are known to repress p53’s tumor suppression activity, the mechanism that p53 uses to obtain its unique bound structure for each partner is interesting for the design of therapeutic measures aiming to regulate p53’s activity.
Chen et al. investigated the role of conformational selection versus induced fit in binding of the NRD to its partner proteins [139]. While the presence of each of the bound structures in their MD simulations of the unbound p53 peptide could indicate that conformational selection enables binding, Chen proposed that a fly-casting mechanism [52] might be more favorable, in which non-specific binding of p53 to its partner occurs before folding. To investigate this hypothesis, Chen et al. computed a 2D potential of mean force for the 14-residue p53 peptide along reaction coordinates describing folding and binding of p53 to s100B(ββ), a partner protein with which it adopts a helical structure (Figure 5i). Specifically, Chen et al. used the center-of-mass distance between p53 and s100B(ββ) to represent binding. They generated eighteen 20ns implicit solvent replica exchange molecular dynamics production simulations of the p53 peptide and its binding site on s100B(ββ), where the center-of-mass distance between the two proteins was restrained to a distance varying from 11 Angstroms to 28 Angstroms across the simulations. Folding of the p53 peptide to a helical conformation was not explicitly biased, but was represented by the number of helical residues and the end-to-end distance. The s100B(ββ) atoms were held rigid except those in charged interface side-chains. The resulting PMF indicates that the peptide becomes less helical as it approaches s100B(ββ), before becoming more like its s100B(ββ)-bound structure, indicating that the peptide preferentially samples extended conformations when first contacting s100B(ββ), and initiates folding after it is in close proximity to s100B(ββ), in agreement with the fly-casting hypothesis [139].
Molecular dynamics simulations of the intrinsically disordered p53 NRD domain show that the isolated p53 peptides sample receptor bound conformations in their unbound states. For the NRD peptide [139], the conformational ensemble of an IDP may be different when it is searching for a receptor than when it is in close proximity to a receptor. To substantiate this hypothesis, longer or biased simulations, coupled with experimental data, and with an accurate measure of binding, would be necessary to sample a greater subset of the conformational space of p53 TAD as it contacts its partners. The atomistic resolution of MD enables questions such as these to be addressed in a straightforward manner.
6. Aβ
Common to many neurodegenerative disease-related proteins is not only the disordered nature of the monomeric state, but also a tendency to self-associate and form a diverse range of aggregate states. The most conspicuous of these aggregates comes in the form of amyloid fibrils that can be isolated from brain tissue of patients who have died from one of these diseases, either as intra-neuronal depositions or tangles (in the case of α-synuclein, polyglutamine and tau) or as extra-cellular inclusions (in the case of Aβ) [140]. An increasing body of evidence suggests that these fibrillar, amyloid structures are not the primary mediators of toxicity, but rather play secondary roles in the disease process, as either inert protein depositions at the end of the aggregation pathway or as secondary nucleation sites for the formation of smaller soluble aggregates [141]. While the mechanism of neurodegenerative disorders is likely multifactorial, a growing body of evidence suggests that lower molecular weight soluble oligomeric aggregates are the primary mediators of toxicity in Alzheimer’s and Parkinson’s diseases [13,20,142,143,144,145]. Whatever the precise disease causing species may be, it is clear that the aggregation process itself plays a pivotal role in the pathogenesis of these neurodegenerative disorders. A comprehensive understanding of the transition from a disordered state (an unfolded monomer) to an ordered, multimeric state (an oligomer or amyloid fibril), is therefore critical if one is to design novel therapeutics aimed at preventing or reversing this aggregation process (Figure 6).
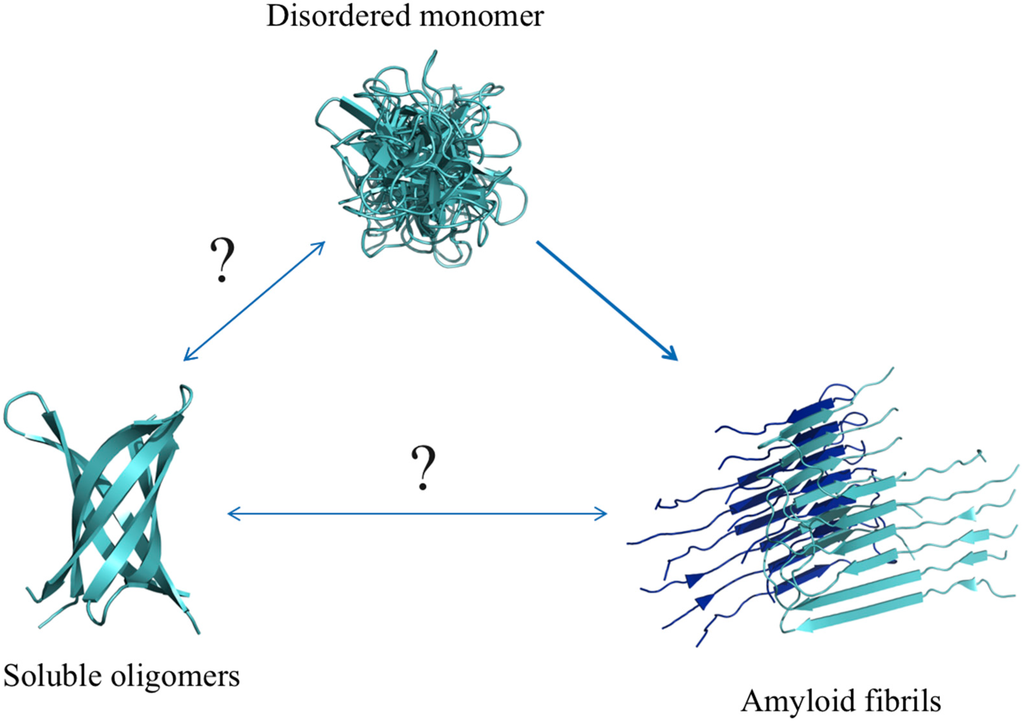
Figure 6.
Schematic of the different “structures” of the Aβ peptide. Monomers can form fibrils, which are highly stable and rarely dissociate back into monomers, but can also form meta-stable, soluble oligomers. A hypothetical structure of a soluble oligomer is shown on the right and a NMR model of Aβ fibrils (PDB ID: 2lmo) is shown on the right [146]. A double-headed arrow between oligomers and fibrils is shown to illustrate a potential, but relatively unknown, interplay between the two species.
6.1. Aβ Mutations and Aggregates
Post-mortem examinations of the brains of patients suffering from Alzheimer’s disease (AD) have led to the identification of extracellular plaques in the cerebral cortex that test positive for the presence of a small, 4 kDa peptide called amyloid β-protein (Aβ). Aβ was first purified from amyloid fibrils isolated from brain meninges in 1984 [147]. It is the product of targeted proteolysis of the β-amyloid precursor protein (APP), a large single-transmembrane glycoprotein that is widely expressed in both neural and non-neural cells [148]. APP is first cleaved in the extra-cellular lumen by β-secretase to produce a membrane-bound C-terminal fragment, along with an extra-cellular N-terminal fragment that is secreted. The membrane-bound APP portion is then cleaved by γ-secretase to release the final Aβ peptide, which in APP is partially buried within the membrane [149]. γ-secretase can cleave APP at multiple positions, resulting in Aβ peptides of different lengths. These peptides vary in the number of hydrophobic residues in their C-terminus, and as such have different aggregation propensities [150]. Several mutations have been identified as being related to AD pathology. A number of these mutations are found at, or directly flanking, the cleavage sites for the secretase enzymes, resulting in different distributions of cleavage products from the wild-type [151], and others are located within the central hydrophobic region of the cleaved Aβ sequence [152]. For example, comparison of the carboxyl-terminal peptides produced from cleavage of wild-type versus mutant APP, the particular mutations of which have been linked to familial AD, showed an increase in the fraction of “long” Aβ (particularly Aβ residues 1–42, or Aβ42 for short) relative to Aβ40 in the mutants [153]. Studies of various lengths of Aβ show that longer Aβ fragments (Aβ42 in particular) have an increased tendency to aggregate and form fibrils than the dominant form (Aβ40) in wild-type cells [150].
NMR studies suggest that Aβ exists predominantly as a disordered monomer [21,154]. However, as previously mentioned for aggregating IDPs in general, the disease process in Aβ is associated with a transition from this disordered monomeric state to more ordered multimeric states. Aβ has been observed, in vitro, to form aggregates of varying molecular weight, spanning the range from small, low molecular weight soluble oligomers, through protofibrils (small assemblies of Aβ that nucleate the formation of larger amyloid fibrils), all the way to insoluble amyloid fibrils consisting of thousands of monomers in a highly repetitive configuration.
In the remainder of this section, we first outline current knowledge of each aggregate state of Aβ, as well as open questions about each state and transitions between states. We then discuss how computation has addressed some of these questions.
6.2. Aβ Oligomers
It is proposed that the pathogenesis stems from a toxic gain of function when these multimeric states are formed [143,155,156]. Aβ appears to exist in a range of different oligomeric forms, presumably originating from disordered monomeric pools. Characterization of oligomeric species of Aβ is particularly nebulous, compared to other Aβ species, due to their polymorphic nature. Aβ oligomers have been known to adopt a variety of molecular weights, morphologies, and secondary structure content [143,145,148,157]. Central questions surrounding the different oligomeric species are whether or not they constitute toxic entities, and whether their formation is on the pathway towards amyloid fibril formation, or occurs through independent pathways. Answering these questions is central to understanding the mechanistic basis behind the disease, and in addition might provide clues as to how these pathways could be manipulated to prevent or reverse the disease process.
The mechanistic basis for the neurotoxicity of oligomeric structures remains unclear [148]. Early studies of Aβ suggest that it can form cylindrical, β-barrel type oligomers which resemble bacterial porins in electron micrographs [158]. It is thought that such oligomers can create channels in the cell membrane, leading to Ca2+ dysregulation and disruption of the membrane’s partitioning function [159]. An analysis of HypF-N oligomers, which have similar properties to their Aβ counterparts, found that toxic oligomers produced an influx of extracellular Ca2+ into the cytosol, in contrast to non-toxic oligomers produced under different conditions, despite having the same morphological and tinctorial features [160]. The same study found that the toxic forms differed in the packing of the hydrophobic interactions between adjacent monomers, suggesting that structural flexibility and hydrophobic exposure are critical determinants of an oligomer’s toxicity [160].
There are very little data pertaining to the conformation of individual monomers in the toxic oligomers. The formation of soluble oligomers was not disrupted by stabilizing monomeric Aβ in a β-hairpin state through the introduction of cysteine mutations in pairs of residues found to be in close contact in a solution NMR structure of the hairpin in complex with an Affibody, suggesting that these oligomeric species are composed of monomers in a similar hairpin state [161,162]. Amide-proton exchange NMR experiments have identified regions of the sequence that have the highest accessibility to the surrounding solvent when in a toxic oligomeric state. These regions are likely to correspond to turn conformations, and propose a configuration of strands arranged according to these turn regions [163]. These findings are all consistent with the formation of cylindrical oligomers composed of individual β-hairpins or sheets, much like the crystallographic structure of cylindrin, an oligomeric form of alpha-crystallin fragments [164]. Indeed, extrapolating from the structure of cylindrin, Laganowsky et al. propose a similar model of a trimeric Aβ oligomer [164]. Such a structural arrangement differs fundamentally from a pre-fibrillar oligomer (e.g., a small protofibril) in that it cannot be extended naturally to include more monomers. This is because many of the hydrogen bond donors and acceptors of the polypeptide backbone that are involved in fibrillar, inter-molecular hydrogen bonds are bonded to each other in an intra-molecular fashion in the hairpin state [162]. Thus, it is unlikely that these structures would form the basis for further aggregation without undergoing some structural changes to adopt the cross-β arrangement of a prototypical amyloid structure.
6.3. Aβ Fibrils
Histopathologic analyses of brain tissue derived from post-mortem examinations of patients that suffered from Alzheimer’s disease reveal large inclusions in the neural tissue that are composed of large quantities of amyloid fibrils [165,166]. It has been suggested that a propensity to form stable amyloid structures under the right conditions is wide-spread across the proteome [167]. These fibrillar structures are held together through intermolecular hydrogen bonds between the backbones of adjacent monomers arranged in β-strands perpendicular to the fibril axis, termed a cross-β structure [146,167,168]. They are ordered and highly structured, insoluble in nature, and have well-defined and highly repetitive structural cores. Amyloids thus have proved to be somewhat more yielding to structure determination techniques [146,169]. Structural models of Aβ fibrils derived from solid-state NMR restraints suggest a high degree of polymorphism in the different fibrillar structures. These models suggest that fibrils frequently contain more than one filament, such as the twofold and threefold symmetric fibrils of Aβ [146,168,170] which can be observed through scanning electron microscopy to be arranged in helical superstructures termed β-helices [171,172]. The solid-state NMR restraints used to create the twofold and threefold symmetric fibrils of Aβ were compatible with two mutually exclusive models for the relative height of anti-parallel β-strands within monomers in the fibril for both, termed positive and negative stagger [168]. Extensive molecular simulations conducted on fibrils containing the two types of stagger found that only negative stagger fibrils formed the left-handed helical suprastructures observed by electron microscopy [171,172]. Initially, two competing quaternary structure contacts between the C-terminal strands of the two filaments were proposed based on molecular simulations: parallel and anti-parallel [173]. Further solid-state NMR data indicated anti-parallel contacts between C-terminal strands [146]. When simulated using coarse-grained molecular simulations, Fawzi et al. found that both models for the quaternary contacts were stable, but the anti-parallel model was more likely to elongate [174].
The N-terminal region of Aβ appears disordered even in the fibrillar state, with the remaining residues adopting the fibril core cross-β structure [146,168,169]. This fibrillar conformation therefore suggests that, given the appropriate binding partner, there is a strong propensity for the formation of β-strands in the Aβ sequence.
6.4. Insight into Aβ Structure and Its Aggregation Mechanism through Computation
Several studies have applied brute-force, unbiased molecular dynamics simulations of the Aβ peptide to explore the conformational preferences of the disordered monomer. One study, which totaled over 200 μs of simulation time for each peptide, found that Aβ40 and Aβ42 have crudely similar characteristics, in that they can both adopt strand-based conformations, but that Aβ42 has an increased propensity to form hairpins in its C-terminus when compared to Aβ40 [175]. In another study, the conformational ensembles of the Aβ40 and Aβ42 monomers were constructed using BW with NMR data to learn the states sampled by each monomer [176]. A set of structures , generated through replica exchange molecular dynamics simulations of both full-length Aβ42 and overlapping Aβ42 peptide segments, was used to construct both ensembles (with the last two residues of Aβ42 truncated to form the Aβ40 structure set). Weights were computed for both ensembles using their respective NMR data [176]. Comparison of these two ensembles suggested a statistically significant, tenfold increase in the relative stability of a hairpin conformation in the Aβ42 isoform versus its shorter counterpart and correlates well with findings from unbiased molecular dynamics simulations of these two peptides [175].
While the strand segments within each hairpin correspond to segments that are also in a strand conformation in the fibrillar state, the tertiary structural arrangement of these strands is different since they are involved in intramolecular hydrogen bonds with each other [162], in contrast to the fibrillar conformations which contain intermolecular hydrogen bonds [146,168,169,170]. Hairpin-type structures containing intramolecular hydrogen bonds would therefore have to undergo structural rearrangements to form amyloid protofibrils. Nevertheless, a number of observations are consistent with the notion that hairpin structures are intermediate states in the fibrillization process. Indeed, sequestration of a β-hairpin conformation of Aβ40 slows aggregation [162], and stabilizing the bend between the two beta strands leads to a significant increase in the rate of fibrillogenesis [177]. Additional computational and experimental studies suggest that hairpin states are sparsely populated in the absence of fibril cores, and that stabilization of these states leads to an increase in the rate of fibril formation [177,178,179].
A number of computational studies have attempted to identify key molecular features involved in fibril or oligomer growth of Aβ40 or smaller amyloidogenic peptides derived from the Aβ40 sequence [180,181,182]. A common theme that arises from these simulations is that addition of monomer to a β-rich template representing either a soluble oligomer or a protofibril, occurs via a “dock-lock” mechanism that is similar to the scheme originally proposed by Esler et al. [183]. Docking consists of an incoming monomer loosely associating to the template in a manner such that it can readily dissociate. Locking involves the formation of hydrogen bonds to the template, yielding a structure where monomer dissociation is unlikely.
The relationship between soluble oligomers and fibril growth has also been explored using both experiment and simulation. Monitoring the aggregation of a di-cysteine mutant of Aβ40 in vitro by the selective binding of the latent fluorophore FlAsH to oligomers and fibrils showed that Aβ40 forms spherical oligomers that can slowly convert to amyloid fibrils through a nucleated conformational conversion mechanism [184]. Furthermore, discrete molecular dynamics simulations of both Aβ40 and Aβ42 showed assembly of elongated protofibrils from spherical oligomers [185]. These results are consistent with a number of studies having provided evidence for the formation of oligomers prior to the appearance of fibrils [145,186,187,188].
Computational studies have also complemented experiment, yielding additional insights into our understanding of oligomeric states in Aβ. Experimentally, an application of the technique of photo-induced cross-linking of unmodified proteins (PICUP) found that aggregate-free samples of Aβ40 contained monomers, dimers, trimers and tetramers in rapid equilibrium. In contrast, Aβ42 preferentially forms pentameric and hexameric “paranuclei” which assembled further into bead-like structures resembling protofibrils, arguing that the Aβ42 assembly pathway involves the formation of distinct intermediates that gradually rearrange into protofibrils [187,189]. This observation was also noted in a minimal self-assembly model for aggregation, which is in principle applicable to self-assembly processes in general, suggesting that the phenomenon may extend to other amyloidogenic proteins and beyond [190]. Further studies combining mutational experiments with PICUP suggest that the side-chain of residue 41 is important for paranucleus formation and further self-association into larger oligomers, while the side-chain of residue 42 primarily impacts paranucleus self-association [188]. A different study introducing the technique of ion mobility coupled with mass spectrometry analyzed the in vitro oligomer size distributions for both Aβ40 and Aβ42 and found that they differed considerably, lending further evidence to the notion that Aβ40 and Aβ42 self-assemble along different pathways [145]. In silico, coarse-grained simulations using a four-bead model that includes backbone hydrogen bonding, and residue-specific interactions due to effective hydropathy and charge, found that Aβ40 forms significantly more dimers than Aβ42, while Aβ42 forms more pentamers. Stable dimers were observed by X-ray crystallography for residues 17–41 [191]. Furthermore, they found that a turn centered around Gly-37-Gly-38 is formed in Aβ42 and not in Aβ40, and was found to be associated with initial contacts formed during monomer folding [192]. A later study using the same simulation technique on Arctic mutants of Aβ40 and Aβ42 was used to derive size-distributions in agreement with prior experimental data, and showed that the Aβ40 mutant was able to form paranuclei much like Aβ42, although the mutations prevented aggregation into higher order oligomers in both isoforms [185]. Using discrete molecular dynamics simulations of wild-type Aβ40 and, Urbanc et al. found that the region D1–R5 is more disordered and exposed to solvent in Aβ42 than Aβ40, suggesting that the N-terminal region is involved in mediating toxicity [193]. These results were subsequently found to be in agreement with all-atom simulations in explicit solvent [194].
While these studies illustrate that a synergistic relationship between experiment and computation can yield important insights into the structure and aggregation mechanism of Aβ, there are many unanswered questions that are ripe for the application of new techniques. Recently, kinetic studies of Aβ42 showed that the formation of toxic, soluble oligomers occurs as a secondary nucleation process, in which oligomers are formed in two phases: the first is in the absence of any amyloid aggregates, and the second in their presence [141]. The second phase results in an increased rate of oligomer formation, and radiolabeling experiments confirmed that oligomers formed were derived from the monomeric pool of Aβ42 rather than by breaking off fibrils directly. Thus, amyloid fibrils and toxic oligomers may sample distinct folding pathways under the right conditions, and the kinetics of oligomer formation is enhanced in the presence of fibrils. These data highlight the complex interplay between the monomeric, oligomeric and fibrillar pools of Aβ that is likely to underlie the disease state (Figure 6).
Further studies probing the conformational landscape of Aβ in the presence of additional Aβ molecules could provide insight to the role of induced-fit in the formation of oligomers or protofibrils. Furthermore, computational studies could be employed to investigate the role of flexibility in toxic oligomers, as well as the different pathways to oligomer and fibril formation.
7. Conclusions
IDPs play a central role in many cellular processes, as their disordered nature provides them with the ability to bind many partners, thereby regulating many biochemical processes. Because of this central role, the malfunction of IDPs can disrupt proper cellular function and lead to disease. Unfortunately, their disordered nature, which makes them so relevant in cellular networks, also makes them difficult to study with traditional experimental methods that were initially designed to study folded proteins. In this review, we discussed recent studies that have employed computational methods to analyze the conformational preferences and mechanisms of IDPs. We focused on two IDPs: p53, which is mutated in 50% of cancers, and Aβ, which is found in a toxic, aggregated state in the brains of patients with Alzheimer’s disease. While both of these proteins are commonly implicated in human disease, their mutated and/or aggregated states affect normal cell processes in different ways, and we chose these two proteins to highlight markedly different pathogenic pathways ascribed to IDP malfunction. Understanding the structural and functional preferences of these, and all, IDPs in their normal and pathologic states will allow for better understanding of disease pathways, and enable the intelligent design of therapeutics targeting IDPs.
The tumor suppressor p53 is a hub protein involved in hundreds of interactions, the majority of which occur within its disordered N- and C-termini. Computational studies of this protein have focused on the mechanism by which it forms a stable structure upon binding each of its partners, probing the roles that conformational selection and induced fit play in this process. Simulations of the unbound IDRs have established the presence of bound states in the unbound ensemble, supporting the hypothesis that binding is enabled through conformational selection, as the IDR is physically able to access its bound state in the absence of its partner. However, the preference for bound states may increase in the presence of a binding partner, in line with the induced fit hypotheses. Furthermore, the role that pre-structured motifs and anchor residues play in regulating binding have been probed for the N-terminal TAD region upon binding MDM2. These studies indicate that the placement of certain residues, such as prolines, within the IDR increase the stability of pre-formed structural motifs, and that pre-structured anchor residues may promote binding by initializing bound contacts with MDM2, while the remaining residues can fold after binding. The hybrid binding mechanism seen here of conformational selection of anchor residues followed by induced fit binding for the remaining IDR should be further demonstrated for other binding partners of p53 TAD to analyze how anchor residues may promote binding of IDPs to various partners. In general, additional simulations of the IDR in the presence of its binding partner would increase understanding of the cooperation between conformational selection, induced fit, and pre-structured motifs in IDP-binding. These analyses could be coupled with experiments to quantify the binding affinity of both wild-type IDPs and stabilized mutants to receptors. Hybrid experimental and computational studies would provide atomistic detail to the changes in binding mechanism that result in a change in binding affinity. Understanding the mechanism by which IDPs bind their partners could enable intelligent drug design for disease-causing mutations in IDPs. For instance, mutations, e.g., near anchor residues, or small molecule binders could alter the distribution of states across the unbound ensemble, thus altering the binding rate to particular partners as a therapeutic mechanism.
Understanding how Aβ transitions between disordered monomers and the different species mentioned in this review is a pre-requisite to controlling the early events of the Alzheimer’s disease processes. We have shown that computational tools can provide some measure of leverage when analyzing quantitative, experimental structural data about the disordered state. This can be achieved by using empirical molecular mechanics force fields to understand the unfolded state of these polymers, as well as by computing a distribution for the ways in which one can weight a given set of structures with experimental data to generate a conformational ensemble, as in the BW approach. Computational data are helpful in understanding the properties of the monomeric state and the mechanism of aggregation or abnormal signaling. We have discussed how current data suggest that hairpin-type conformations are present within the toxic oligomeric states of Aβ, thus distinguishing them from amyloid pathways due to the structural dissimilarity between hairpins and monomers in fibrillar conformations. Despite all of this, high-resolution information about the transition from a flexible monomer to a folded, relatively rigid oligomer or fibril has proved elusive so far. Part of the difficulty may stem from the fact that monomers and oligomers are in fast exchange with one-another, as suggested by data collected from multimeric alpha-synuclein, and computational studies could be targeted towards overcoming this obstacle.
One difficulty in characterizing IDPs stems from a lack of experimental and computational tools for studying folding events that occur on a timescale that is too fast to be probed with traditional experimental methods, and too slow to be tractable by traditional molecular simulations. A comprehensive understanding of this transition will therefore require improvements in the experimental methods available for structural characterization of short-lived intermediate states, coupled with a creative use of computational methods to obtain mechanistic insights into the transitions between these states.
Acknowledgments
This material is based upon work supported by the National Science Foundation Postdoctoral Research Fellowship in Biology under Grant No. 1309247.
Author Contributions
Virginia M. Burger, Thomas Gurry, and Collin M. Stultz all contributed to the writing content of this manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Petsko, G.A.; Ringe, D. Protein Structure and Function; New Science Press: London, UK, 2004. [Google Scholar]
- Richardson, J.S. The anatomy and taxonomy of protein structure. Adv. Protein Chem. 1981, 34, 167–339. [Google Scholar]
- Wang, Z.; Moult, J. SNPs, protein structure, and disease. Hum. Mutat. 2001, 17, 263–270. [Google Scholar] [CrossRef]
- Stayrook, S.; Jaru-Ampornpan, P.; Ni, J.; Hochschild, A.; Lewis, M. Crystal structure of the lambda repressor and a model for pairwise cooperative operator binding. Nature 2008, 452, 1022–1025. [Google Scholar] [CrossRef]
- Ye, J.; van den Berg, B. Crystal structure of the bacterial nucleoside transporter Tsx. EMBO J. 2004, 23, 3187–3195. [Google Scholar] [CrossRef]
- Lee, C.H.; Kim, M.S.; Chung, B.M.; Leahy, D.J.; Coulombe, P.A. Structural basis for heteromeric assembly and perinuclear organization of keratin filaments. Nat. Struct. Mol. Biol. 2012, 19, 707–715. [Google Scholar] [CrossRef]
- Vihinen, M. Relationship of protein flexibility to thermostability. Protein Eng. 1987, 1, 477–480. [Google Scholar] [CrossRef]
- Falke, J.J. A moving story. Science 2002, 295, 1480–1481. [Google Scholar] [CrossRef]
- Fisher, C.K.; Stultz, C.M. Protein structure along the order–disorder continuum. J. Am. Chem. Soc. 2011, 133, 10022–10025. [Google Scholar] [CrossRef]
- Oldfield, C.J.; Cheng, Y.; Cortese, M.S.; Brown, C.J.; Uversky, V.N.; Dunker, A.K. Comparing and combining predictors of mostly disordered proteins. Biochemistry 2005, 44, 1989–2000. [Google Scholar] [CrossRef]
- Uversky, V.N.; Dunker, A.K. Understanding protein non-folding. Biochim. Biophys. Acta 2010, 1804, 1231–1264. [Google Scholar] [CrossRef]
- Chouard, T. Structural biology: Breaking the protein rules. Nature 2011, 471, 151–153. [Google Scholar] [CrossRef]
- Conway, K.A.; Lee, S.-J.; Rochet, J.-C.; Ding, T.T.; Williamson, R.E.; Lansbury, P.T. Acceleration of oligomerization, not fibrillization, is a shared property of both alpha-synuclein mutations linked to early-onset Parkinson’s disease: Implications for pathogenesis and therapy. Proc. Natl. Acad. Sci. USA 2000, 97, 571–576. [Google Scholar] [CrossRef]
- Perutz, M.F. Glutamine repeats and neurodegenerative diseases: Molecular aspects. Trends Biochem. Sci. 1999, 24, 58–63. [Google Scholar] [CrossRef]
- Romero, P.; Obradovic, Z.; Li, X.; Garner, E.C.; Brown, C.J.; Dunker, A.K. Sequence complexity of disordered protein. Proteins Struct. Funct. Bioinf. 2001, 42, 38–48. [Google Scholar] [CrossRef]
- Crick, S.; Jayaraman, M.; Frieden, C.; Wetzel, R.; Pappu, R. Fluorescence correlation spectroscopy shows that monomeric polyglutamine molecules form collapsed structures in aqueous solutions. Proc. Natl. Acad. Sci. USA 2006, 103, 16764–16769. [Google Scholar] [CrossRef]
- Vitalis, A.; Lyle, N.; Pappu, R.V. Thermodynamics of β-sheet formation in polyglutamine. Biophys. J. 2009, 97, 303–311. [Google Scholar] [CrossRef]
- Hardy, J.; Selkoe, D.J. The amyloid hypothesis of Alzheimer’s disease: Progress and problems on the road to therapeutics. Science 2002, 297, 353–356. [Google Scholar] [CrossRef]
- Pitschke, M.; Prior, R.; Haupt, M.; Riesner, D. Detection of single amyloid beta-protein aggregates in the cerebrospinal fluid of Alzheimer’s patients by fluorescence correlation spectroscopy. Nat. Med. 1998, 4, 832–834. [Google Scholar] [CrossRef]
- El-Agnaf, O.M.A.; Mahil, D.S.; Patel, B.P.; Austen, B.M. Oligomerization and toxicity of β-amyloid-42 implicated in Alzheimer’s disease. Biochem. Biophys. Res. Commun. 2000, 273, 1003–1007. [Google Scholar]
- Zhang, S.; Iwata, K.; Lachenmann, M.J.; Peng, J.W.; Li, S.; Stimson, E.R.; Lu, Y.A.; Felix, A.M.; Maggio, J.E.; Lee, J.P. The Alzheimer’s peptide Aβ adopts a collapsed coil structure in water. J. Struct. Biol. 2000, 130, 130–141. [Google Scholar] [CrossRef]
- Schweers, O.; Schönbrunn-Hanebeck, E.; Marx, A.; Mandelkow, E. Structural studies of tau protein and Alzheimer paired helical filaments show no evidence for beta-structure. J. Biol. Chem. 1994, 269, 24290–24297. [Google Scholar]
- Iakoucheva, L.M.; Brown, C.J.; Lawson, J.D.; Obradovic, Z.; Dunker, A.K. Intrinsic disorder in cell-signaling and cancer-associated proteins. J. Mol. Biol. 2002, 323, 573–584. [Google Scholar] [CrossRef]
- Bell, S.; Klein, C.; Muller, L.; Hansen, S.; Buchner, J. p53 contains large unstructured regions in its native state. J. Mol. Biol. 2002, 322, 917–927. [Google Scholar] [CrossRef]
- Joerger, A.C.; Fersht, A.R. The tumor suppressor p53: From structures to drug discovery. Cold Spring Harb. Perspect. Biol. 2010, 2. [Google Scholar] [CrossRef]
- Lasky, T.; Silbergeld, E. P53 mutations associated with breast, colorectal, liver, lung, and ovarian cancers. Environ. Health Perspect. 1996, 104, 1324–1331. [Google Scholar] [CrossRef]
- Bogler, O.; Huang, H.J.; Kleihues, P.; Cavenee, W.K. The p53 gene and its role in human brain tumors. Glia 1995, 15, 308–327. [Google Scholar] [CrossRef]
- Koudinov, A.R.; Berezov, T.T. Alzheimer’s amyloid-beta (a beta) is an essential synaptic protein, not neurotoxic junk. Acta Neurobiol. Exp. 2004, 64, 71–79. [Google Scholar]
- Anfinsen, C.B. Principles that govern the folding of protein chains. Science 1973, 181, 223–230. [Google Scholar] [CrossRef]
- Bahar, I.; Lezon, T.R.; Yang, L.W.; Eyal, E. Global dynamics of proteins: Bridging between structure and function. Annu. Rev. Biophys. 2010, 39, 23–42. [Google Scholar] [CrossRef]
- Huang, A.; Stultz, C.M. Finding order within disorder: Elucidating the structure of proteins associated with neurodegenerative disease. Fut. Med. Chem. 2009, 1, 467–482. [Google Scholar] [CrossRef]
- Leopold, P.E.; Montal, M.; Onuchic, J.N. Protein folding funnels: A kinetic approach to the sequence-structure relationship. Proc. Natl. Acad. Sci. USA 1992, 89, 8721–8725. [Google Scholar] [CrossRef]
- Onuchic, J.N.; Wolynes, P.G. Theory of protein folding. Curr. Opin. Struct. Biol. 2004, 14, 70–75. [Google Scholar] [CrossRef]
- Chen, J. Towards the physical basis of how intrinsic disorder mediates protein function. Arch. Biochem. Biophys. 2012, 524, 123–131. [Google Scholar] [CrossRef]
- Tompa, P. Unstructural biology coming of age. Curr. Opin. Struct. Biol. 2011, 3, 419–425. [Google Scholar] [CrossRef]
- Uversky, V.N. Natively unfolded proteins: A point where biology waits for physics. Protein Sci. 2002, 11, 739–756. [Google Scholar] [CrossRef]
- Dunker, A.; Cortese, M.; Romero, P.; Iakoucheva, L.; Uversky, V. Flexible nets. The roles of intrinsic disorder in protein interaction networks. FEBS J. 2005, 272, 5129–5148. [Google Scholar] [CrossRef]
- Tompa, P.; Szasz, C.; Buday, L. Structural disorder throws new light on moonlighting. Trends Biochem. Sci. 2005, 30, 484–489. [Google Scholar] [CrossRef]
- Oldfield, C.; Meng, J.; Yang, J.; Yang, M.; Uversky, V.; Dunker, A. Flexible nets: Disorder and induced fit in the associations of p53 and 14-3-3 with their partners. BMC Genomics 2008, 9, S1. [Google Scholar] [CrossRef]
- Wright, P.E.; Dyson, H.J. Intrinsically unstructured proteins: Re-assessing the protein structure-function paradigm. J. Mol. Biol. 1999, 293, 321–331. [Google Scholar]
- Gsponer, J.; Futschik, M.E.; Teichmann, S.A.; Babu, M.M. Tight regulation of unstructured proteins: From transcript synthesis to protein degradation. Science 2008, 322, 1365–1368. [Google Scholar] [CrossRef]
- Tompa, P.; Prilusky, J.; Silman, I.; Sussman, J.L. Structural disorder serves as a weak signal for intracellular protein degradation. Proteins 2008, 71, 903–909. [Google Scholar] [CrossRef]
- Gross, M. Anarchy in the proteome. Chem. World 2011, 8, 42–45. [Google Scholar]
- Plaxco, K.W.; Gross, M. Cell biology. The importance of being unfolded. Nature 1997, 386, 657–659. [Google Scholar] [CrossRef]
- Webb, P.A.; Perisic, O.; Mendola, C.E.; Backer, J.M.; Williams, R.L. The crystal structure of a human nucleoside diphosphate kinase, NM23-H2. J. Mol. Biol. 1995, 251, 574–587. [Google Scholar] [CrossRef]
- Drobnak, I.; De Jonge, N.; Haesaerts, S.; Vesnaver, G.; Loris, R.; Lah, J. Energetic basis of uncoupling folding from binding for an intrinsically disordered protein. J. Am. Chem. Soc. 2013, 135, 1288–1294. [Google Scholar] [CrossRef]
- Brooks, B.R.; Bruccoleri, R.E.; Olafson, B.D.; States, D.J.; Swaminathan, S.; Karplus, M. Charmm-A program for macromolecular energy, minimization, and dynamics calculations. J. Comput. Chem. 1983, 4, 187–217. [Google Scholar] [CrossRef]
- Brooks, B.R.; Brooks, C.L., 3rd; Mackerell, A.D., Jr.; Nilsson, L.; Petrella, R.J.; Roux, B.; Won, Y.; Archontis, G.; Bartels, C.; Boresch, S.; et al. CHARMM: The biomolecular simulation program. J. Comput. Chem. 2009, 30, 1545–1614. [Google Scholar] [CrossRef]
- Monod, J.; Wyman, J.; Changeux, J.-P. On the nature of allosteric transitions: A plausible model. J. Mol. Biol. 1965, 12, 88–118. [Google Scholar] [CrossRef]
- Koshland, D.E. Application of a theory of enzyme specificity to protein synthesis. Proc. Natl. Acad. Sci. USA 1958, 44, 98–104. [Google Scholar] [CrossRef]
- Kumar, S.; Showalter, S.A.; Noid, W.G. Native-based simulations of the binding interaction between RAP74 and the disordered FCP1 peptide. J. Phys. Chem. B 2013, 117, 1–12. [Google Scholar]
- Shoemaker, B.A.; Portman, J.J.; Wolynes, P.G. Speeding molecular recognition by using the folding funnel: The fly-casting mechanism. Proc. Natl. Acad. Sci. USA 2000, 97, 8868–8873. [Google Scholar] [CrossRef]
- Levy, Y.; Onuchic, J.N.; Wolynes, P.G. Fly-casting in protein-DNA binding: Frustration between protein folding and electrostatics facilitates target recognition. J. Am. Chem. Soc. 2007, 129, 738–739. [Google Scholar] [CrossRef]
- Huang, Y.; Liu, Z. Kinetic advantage of intrinsically disordered proteins in coupled folding-binding process: A critical assessment of the “fly-casting” mechanism. J. Mol. Biol. 2009, 393, 1143–1159. [Google Scholar] [CrossRef]
- Tompa, P.; Fuxreiter, M. Fuzzy complexes: Polymorphism and structural disorder in protein-protein interactions. Trends Biochem. Sci. 2008, 33, 2–8. [Google Scholar] [CrossRef]
- Anand, K.; Parret, A.; Denayer, E.; Petrova, B.; Legius, E.; Scheffzek, K. Crystal structure of the activating H-Ras I163F mutant in costello syndrome, bound to Mg-Gdp. Available online: http://www.rcsb.org/pdb/explore/explore.do?pdbId=2X1V (accessed on 17 August 2014).
- Madl, T.; van Melderen, L.; Mine, N.; Respondek, M.; Oberer, M.; Keller, W.; Khatai, L.; Zangger, K. Structural basis for nucleic acid and toxin recognition of the bacterial antitoxin CcdA. J. Mol. Biol. 2006, 364, 170–185. [Google Scholar] [CrossRef]
- MacArthur, M.W.; Driscoll, P.C.; Thornton, J.M. NMR and crystallography—Complementary approaches to structure determination. Trends Biotechnol. 1994, 12, 149–153. [Google Scholar] [CrossRef]
- Redfield, C. Using nuclear magnetic resonance spectroscopy to study molten globule states of proteins. Methods 2004, 34, 121–132. [Google Scholar] [CrossRef]
- Kosol, S.; Contreras-Martos, S.; Cedeno, C.; Tompa, P. Structural characterization of intrinsically disordered proteins by NMR spectroscopy. Molecules 2013, 18, 10802–10828. [Google Scholar] [CrossRef]
- Gillespie, J.R.; Shortle, D. Characterization of long-range structure in the denatured state of staphylococcal nuclease. I. Paramagnetic relaxation enhancement by nitroxide spin labels. J. Mol. Biol. 1997, 268, 158–169. [Google Scholar]
- Tugarinov, V.; Choy, W.Y.; Orekhov, V.Y.; Kay, L.E. Solution NMR-derived global fold of a monomeric 82-kda enzyme. Proc. Natl. Acad. Sci. USA 2005, 102, 622–627. [Google Scholar] [CrossRef]
- Dedmon, M.M.; Lindorff-Larsen, K.; Christodoulou, J.; Vendruscolo, M.; Dobson, C.M. Mapping long-range interactions in alpha-synuclein using spin-label NMR and ensemble molecular dynamics simulations. J. Am. Chem. Soc. 2005, 127, 476–477. [Google Scholar] [CrossRef]
- Eliezer, D. Biophysical characterization of intrinsically disordered proteins. Curr. Opin. Struct. Biol. 2009, 19, 23–30. [Google Scholar] [CrossRef]
- Tjandra, N.; Bax, A. Direct measurement of distances and angles in biomolecules by NMR in a dilute liquid crystalline medium. Science 1997, 278, 1111–1114. [Google Scholar] [CrossRef]
- Jensen, M.R.; Markwick, P.R.; Meier, S.; Griesinger, C.; Zweckstetter, M.; Grzesiek, S.; Bernado, P.; Blackledge, M. Quantitative determination of the conformational properties of partially folded and intrinsically disordered proteins using NMR dipolar couplings. Structure 2009, 17, 1169–1185. [Google Scholar] [CrossRef]
- Bernado, P.; Svergun, D.I. Structural analysis of intrinsically disordered proteins by small-angle X-ray scattering. Mol. Biosyst. 2012, 8, 151–167. [Google Scholar] [CrossRef]
- Ando, T. High-speed atomic force microscopy. Microscopy 2013, 62, 81–93. [Google Scholar] [CrossRef]
- Katan, A.J.; Dekker, C. High-speed AFM reveals the dynamics of single biomolecules at the nanometer scale. Cell 2011, 147, 979–982. [Google Scholar] [CrossRef]
- Miyagi, A.; Tsunaka, Y.; Uchihashi, T.; Mayanagi, K.; Hirose, S.; Morikawa, K.; Ando, T. Visualization of intrinsically disordered regions of proteins by high-speed atomic force microscopy. Chemphyschem 2008, 9, 1859–1866. [Google Scholar] [CrossRef]
- Allison, J.R.; Varnai, P.; Dobson, C.M.; Vendruscolo, M. Determination of the free energy landscape of α-synuclein using spin label nuclear magnetic resonance measurements. J. Am. Chem. Soc. 2009, 131, 18314–18326. [Google Scholar] [CrossRef]
- Schwalbe, M.; Ozenne, V.; Bibow, S.; Jaremko, M.; Jaremko, L.; Gajda, M.; Jensen, M.R.; Biernat, J.; Becker, S.; Mandelkow, E.; et al. Predictive atomic resolution descriptions of intrinsically disordered htau40 and alpha-synuclein in solution from NMR and small angle scattering. Structure 2014, 22, 238–249. [Google Scholar] [CrossRef]
- Tompa, P.; Varadi, M. Predicting the predictive power of IDP ensembles. Structure 2014, 22, 177–178. [Google Scholar] [CrossRef]
- Rauscher, S.; Pomès, R. Molecular simulations of protein disorder. Biochem. Cell Biol. 2010, 88, 269–290. [Google Scholar] [CrossRef]
- Tuckerman, M.E. Statistical Mechanics: Theory and Molecular Simulation; Oxford University Press: Oxford, UK & New York, NY, USA, 2010. [Google Scholar]
- Karplus, M.; McCammon, J.A. Molecular dynamics simulations of biomolecules. Nat. Struct. Biol. 2002, 9, 646–652. [Google Scholar] [CrossRef]
- Leach, A.R. Molecular Modelling: Principles and Applications, 2nd ed.; Prentice Hall: Harlow, UK & New York, NY, USA, 2001. [Google Scholar]
- Vitalis, A.; Pappu, R.V. Absinth: A new continuum solvation model for simulations of polypeptides in aqueous solutions. J. Comput. Chem. 2009, 30, 673–699. [Google Scholar] [CrossRef]
- Vitalis, A.; Caflisch, A. Micelle-like architecture of the monomer ensemble of Alzheimer’s amyloid-beta peptide in aqueous solution and its implications for Abeta aggregation. J. Mol. Biol. 2010, 403, 148–165. [Google Scholar] [CrossRef]
- Meng, W.; Lyle, N.; Luan, B.; Raleigh, D.P.; Pappu, R.V. Experiments and simulations show how long-range contacts can form in expanded unfolded proteins with negligible secondary structure. Proc. Natl. Acad. Sci. USA 2013, 110, 2123–2128. [Google Scholar] [CrossRef]
- Wuttke, R.; Hofmann, H.; Nettels, D.; Borgia, M.B.; Mittal, J.; Best, R.B.; Schuler, B. Temperature-dependent solvation modulates the dimensions of disordered proteins. Proc. Natl. Acad. Sci. USA 2014, 111, 5213–5218. [Google Scholar] [CrossRef]
- Bottaro, S.; Lindorff-Larsen, K.; Best, R.B. Variational optimization of an all-atom implicit solvent force field to match explicit solvent simulation data. J. Chem. Theory Comput. 2013, 9, 5641–5652. [Google Scholar] [CrossRef]
- Jha, A.K.; Colubri, A.; Freed, K.F.; Sosnick, T.R. Statistical coil model of the unfolded state: Resolving the reconciliation problem. Proc. Natl. Acad. Sci. USA 2005, 102, 13099–13104. [Google Scholar] [CrossRef]
- Ozenne, V.; Bauer, F.; Salmon, L.; Huang, J.-R.; Jensen, M.R.; Segard, S.; Bernadó, P.; Charavay, C.; Blackledge, M. Flexible-meccano: A tool for the generation of explicit ensemble descriptions of intrinsically disordered proteins and their associated experimental observables. Bioinformatics 2012, 28, 1463–1470. [Google Scholar] [CrossRef]
- Bernstein, F.C.; Koetzle, T.F.; Williams, G.J.B.; Meyer, E.F., Jr.; Brice, M.D.; Rodgers, J.R.; Kennard, O.; Shimanouchi, T.; Tasumi, M. The protein data bank: A computer-based archival file for macromolecular structures. J. Mol. Biol. 1977, 112, 535–542. [Google Scholar] [CrossRef]
- Vendruscolo, M. Determination of conformationally heterogeneous states of proteins. Curr. Opin. Struct. Biol. 2007, 17, 15–20. [Google Scholar] [CrossRef]
- Daughdrill, G.W.; Kashtanov, S.; Stancik, A.; Hill, S.E.; Helms, G.; Muschol, M.; Receveur-Brechot, V.; Ytreberg, F.M. Understanding the structural ensembles of a highly extended disordered protein. Mol. Biosyst. 2012, 8, 308–319. [Google Scholar] [CrossRef]
- Fisher, C.K.; Stultz, C.M. Constructing ensembles for intrinsically disordered proteins. Curr. Opin. Struct. Biol. 2011, 21, 426–431. [Google Scholar] [CrossRef]
- Krzeminski, M.; Marsh, J.A.; Neale, C.; Choy, W.-Y.; Forman-Kay, J.D. Characterization of disordered proteins with ENSEMBLE. Bioinformatics 2013, 29, 398–399. [Google Scholar] [CrossRef]
- Jensen, M.R.; Salmon, L.; Nodet, G.; Blackledge, M. Defining conformational ensembles of intrinsically disordered and partially folded proteins directly from chemical shifts. J. Am. Chem. Soc. 2010, 132, 1270–1272. [Google Scholar] [CrossRef]
- Varadi, M.; Kosol, S.; Lebrun, P.; Valentini, E.; Blackledge, M.; Dunker, A.K.; Felli, I.C.; Forman-Kay, J.D.; Kriwacki, R.W.; Pierattelli, R.; et al. Pe-db: A database of structural ensembles of intrinsically disordered and of unfolded proteins. Nucleic Acids Res. 2014, 42, D326–D335. [Google Scholar] [CrossRef]
- Fisher, C.K.; Huang, A.; Stultz, C.M. Modeling intrinsically disordered proteins with bayesian statistics. J. Am. Chem. Soc. 2010, 132, 14919–14927. [Google Scholar] [CrossRef]
- Marsh, J.A.; Forman-Kay, J.D. Structure and disorder in an unfolded state under nondenaturing conditions from ensemble models consistent with a large number of experimental restraints. J. Mol. Biol. 2009, 391, 359–374. [Google Scholar] [CrossRef]
- Ganguly, D.; Chen, J.H. Structural interpretation of paramagnetic relaxation enhancement-derived distances for disordered protein states. J. Mol. Biol. 2009, 390, 467–477. [Google Scholar] [CrossRef]
- Huang, A.; Stultz, C.M. The effect of a Delta K280 mutation on the unfolded state of a microtubule-binding repeat in tau. PLoS Comput. Biol. 2008, 4, e1000155. [Google Scholar] [CrossRef]
- Pitera, J.W.; Chodera, J.D. On the use of experimental observations to bias simulated ensembles. J. Chem. Theory Comput. 2012, 8, 3445–3451. [Google Scholar] [CrossRef]
- Boomsma, W.; Ferkinghoff-Borg, J.; Lindorff-Larsen, K. Combining experiments and simulations using the maximum entropy principle. PLoS Comput. Biol. 2014, 10, e1003406. [Google Scholar] [CrossRef]
- Lane, J.L.; Schwantes, C.R.; Beauchamp, K.A.; Pande, V.S. Efficient inference of protein structural ensembles. Biol. Phys. 2014. 1408.0255. [Google Scholar]
- Fisher, C.K.; Ullman, O.; Stultz, C.M. Efficient construction of disordered protein ensembles in a bayesian framework with optimal selection of conformations. Pac. Symp. Biocomput. 2012, 17, 82–93. [Google Scholar]
- Gurry, T.; Ullman, O.; Fisher, C.K.; Perovic, I.; Pochapsky, T.; Stultz, C.M. The dynamic structure of alpha-synuclein multimers. J. Am. Chem. Soc. 2013, 135, 3865–3872. [Google Scholar] [CrossRef]
- Neal, S.; Nip, A.M.; Zhang, H.Y.; Wishart, D.S. Rapid and accurate calculation of protein H-1, C-13 and N-15 chemical shifts. J. Biomol. NMR 2003, 26, 215–240. [Google Scholar] [CrossRef]
- Lane, D.P. Cancer. p53, guardian of the genome. Nature 1992, 358, 15–16. [Google Scholar] [CrossRef]
- Pagano, B.; Jama, A.; Martinez, P.; Akanho, E.; Bui, T.T.T.; Drake, A.F.; Fraternali, F.; Nikolova, P.V. Structure and stability insights into tumour suppressor p53 evolutionary related proteins. PLoS One 2013, 8. [Google Scholar] [CrossRef]
- Vousden, K.H.; Prives, C. Blinded by the light: The growing complexity of p53. Cell 2009, 137, 413–431. [Google Scholar] [CrossRef]
- Zhao, R.; Gish, K.; Murphy, M.; Yin, Y.; Notterman, D.; Hoffman, W.H.; Tom, E.; Mack, D.H.; Levine, A.J. Analysis of p53-regulated gene expression patterns using oligonucleotide arrays. Genes Dev. 2000, 14, 981–993. [Google Scholar] [CrossRef]
- Braithwaite, A.W.; Del Sal, G.; Lu, X. Some p53-binding proteins that can function as arbiters of life and death. Cell Death Differ. 2006, 13, 984–993. [Google Scholar] [CrossRef]
- Maslon, M.M.; Hupp, T.R. Drug discovery and mutant p53. Trends Cell Biol. 2010, 20, 542–555. [Google Scholar] [CrossRef]
- Greenblatt, M.S.; Bennett, W.P.; Hollstein, M.; Harris, C.C. Mutations in the p53 tumor suppressor gene: Clues to cancer etiology and molecular pathogenesis. Cancer Res. 1994, 54, 4855–4878. [Google Scholar]
- Okorokov, A.L.; Orlova, E.V. Structural biology of the p53 tumour suppressor. Curr. Opin. Struct. Biol. 2009, 19, 197–202. [Google Scholar] [CrossRef]
- Silva, J.L.; Gallo, C.V.D.M.; Costa, D.C.F.; Rangel, L.P. Prion-like aggregation of mutant p53 in cancer. Trends Biochem. Sci. 2014, 39, 260–267. [Google Scholar] [CrossRef]
- Merrill, G.F.; Dowell, P.; Pearson, G.D. The human p53 negative regulatory domain mediates inhibition of reporter gene transactivation in yeast lacking thioredoxin reductase. Cancer Res. 1999, 59, 3175–3179. [Google Scholar]
- Moll, U.M.; Petrenko, O. The MDM2–p53 interaction. Mol. Cancer Res. MCR 2003, 1, 1001–1008. [Google Scholar]
- Lee, C.W.; Martinez-Yamout, M.A.; Dyson, H.J.; Wright, P.E. Structure of the p53 transactivation domain in complex with the nuclear receptor coactivator binding domain of CREB binding protein. Biochemistry 2010, 49, 9964–9971. [Google Scholar] [CrossRef]
- Lambert, P.F.; Kashanchi, F.; Radonovich, M.F.; Shiekhattar, R.; Brady, J.N. Phosphorylation of p53 serine 15 increases interaction with CBP. J. Biol. Chem. 1998, 273, 33048–33053. [Google Scholar] [CrossRef]
- Rowell, J.P.; Simpson, K.L.; Stott, K.; Watson, M.; Thomas, J.O. HMGB1-facilitated p53 DNA binding occurs via HMG-Box/p53 transactivation domain interaction, regulated by the acidic tail. Structure 2012, 20, 2014–2024. [Google Scholar] [CrossRef]
- Bochkareva, E.; Kaustov, L.; Ayed, A.; Yi, G.S.; Lu, Y.; Pineda-Lucena, A.; Liao, J.C.; Okorokov, A.L.; Milner, J.; Arrowsmith, C.H.; et al. Single-stranded DNA mimicry in the p53 transactivation domain interaction with replication protein A. Proc. Natl. Acad. Sci. USA 2005, 102, 15412–15417. [Google Scholar] [CrossRef]
- Chang, J.; Kim, D.H.; Lee, S.W.; Choi, K.Y.; Sung, Y.C. Transactivation ability of p53 transcriptional activation domain is directly related to the binding affinity to tata-binding protein. J. Biol. Chem. 1995, 270, 25014–25019. [Google Scholar] [CrossRef]
- Kussie, P.H.; Gorina, S.; Marechal, V.; Elenbaas, B.; Moreau, J.; Levine, A.J.; Pavletich, N.P. Structure of the MDM2 oncoprotein bound to the p53 tumor suppressor transactivation domain. Science 1996, 274, 948–953. [Google Scholar] [CrossRef]
- Feng, H.; Jenkins, L.M.; Durell, S.R.; Hayashi, R.; Mazur, S.J.; Cherry, S.; Tropea, J.E.; Miller, M.; Wlodawer, A.; Appella, E.; et al. Structural basis for p300 Taz2-p53 TAD1 binding and modulation by phosphorylation. Structure 2009, 17, 202–210. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, X.; Dantas Machado, A.C.; Ding, Y.; Chen, Z.; Qin, P.Z.; Rohs, R.; Chen, L. Structure of p53 binding to the BAX response element reveals DNA unwinding and compression to accommodate base-pair insertion. Nucleic Acids Res. 2013, 41, 8368–8376. [Google Scholar] [CrossRef]
- Mujtaba, S.; He, Y.; Zeng, L.; Yan, S.; Plotnikova, O.; Sachchidanand; Sanchez, R.; Zeleznik-Le, N.J.; Ronai, Z.; Zhou, M.M. Structural mechanism of the bromodomain of the coactivator CBP in p53 transcriptional activation. Mol. Cell 2004, 13, 251–263. [Google Scholar] [CrossRef]
- Rustandi, R.R.; Baldisseri, D.M.; Weber, D.J. Structure of the negative regulatory domain of p53 bound to S100B(betabeta). Nat. Struct. Biol. 2000, 7, 570–574. [Google Scholar] [CrossRef]
- Cosgrove, M.S.; Bever, K.; Avalos, J.L.; Muhammad, S.; Zhang, X.; Wolberger, C. The structural basis of sirtuin substrate affinity. Biochemistry 2006, 45, 7511–7521. [Google Scholar] [CrossRef]
- Lowe, E.D.; Tews, I.; Cheng, K.Y.; Brown, N.R.; Gul, S.; Noble, M.E.; Gamblin, S.J.; Johnson, L.N. Specificity determinants of recruitment peptides bound to phospho-CDK2/cyclin A. Biochemistry 2002, 41, 15625–15634. [Google Scholar] [CrossRef]
- Xiong, K.; Zwier, M.C.; Myshakina, N.S.; Burger, V.M.; Asher, S.A.; Chong, L.T. Direct observations of conformational distributions of intrinsically disordered p53 peptides using UV Raman and explicit solvent simulations. J. Phys. Chem. A 2011, 115, 9520–9527. [Google Scholar] [CrossRef]
- Lee, H.; Mok, K.H.; Muhandiram, R.; Park, K.H.; Suk, J.E.; Kim, D.H.; Chang, J.; Sung, Y.C.; Choi, K.Y.; Han, K.H. Local structural elements in the mostly unstructured transcriptional activation domain of human p53. J. Biol. Chem. 2000, 275, 29426–29432. [Google Scholar] [CrossRef]
- Zondlo, S.C.; Lee, A.E.; Zondlo, N.J. Determinants of specificity of MDM2 for the activation domains of p53 and p65: Proline27 disrupts the MDM2-binding motif of p53. Biochemistry 2006, 45, 11945–11957. [Google Scholar] [CrossRef]
- Fuxreiter, M.; Simon, I.; Friedrich, P.; Tompa, P. Preformed structural elements feature in partner recognition by intrinsically unstructured proteins. J. Mol. Biol. 2004, 338, 1015–1026. [Google Scholar] [CrossRef]
- Lee, S.H.; Kim, D.H.; Han, J.J.; Cha, E.J.; Lim, J.E.; Cho, Y.J.; Lee, C.; Han, K.H. Understanding pre-structured motifs (PreSMos) in intrinsically unfolded proteins. Curr. Protein Peptide Sci. 2012, 13, 34–54. [Google Scholar] [CrossRef]
- Lee, C.; Kalmar, L.; Xue, B.; Tompa, P.; Daughdrill, G.W.; Uversky, V.N.; Han, K.-H. Contribution of proline to the pre-structuring tendency of transient helical secondary structure elements in intrinsically disordered proteins. Biochim. Biophys. Acta 2014, 1840, 993–1003. [Google Scholar] [CrossRef]
- Szöllősi, D.; Horváth, T.; Han, K.-H.; Dokholyan, N.V.; Tompa, P.; Kalmar, L.; Hegedűs, T. Discrete molecular dynamics can predict helical prestructured motifs in disordered proteins. PLoS One 2014, 9. [Google Scholar] [CrossRef]
- Huang, Y.; Liu, Z. Anchoring intrinsically disordered proteins to multiple targets: Lessons from N-terminus of the p53 protein. Int. J. Mol. Sci. 2011, 12, 1410–1430. [Google Scholar] [CrossRef]
- Dawson, R.; Muller, L.; Dehner, A.; Klein, C.; Kessler, H.; Buchner, J. The N-terminal domain of p53 is natively unfolded. J. Mol. Biol. 2003, 332, 1131–1141. [Google Scholar] [CrossRef]
- Schon, O.; Friedler, A.; Bycroft, M.; Freund, S.M.; Fersht, A.R. Molecular mechanism of the interaction between MDM2 and p53. J. Mol. Biol. 2002, 323, 491–501. [Google Scholar] [CrossRef]
- Luciani, M.G.; Hutchins, J.R.; Zheleva, D.; Hupp, T.R. The C-terminal regulatory domain of p53 contains a functional docking site for cyclin A. J. Mol. Biol. 2000, 300, 503–518. [Google Scholar] [CrossRef]
- Hoffmann, G.; Breitenbucher, F.; Schuler, M.; Ehrenhofer-Murray, A.E. A novel sirtuin 2 (SIRT2) inhibitor with p53-dependent pro-apoptotic activity in non-small cell lung cancer. J. Biol. Chem. 2014, 289, 5208–5216. [Google Scholar] [CrossRef]
- Bosch-Presegue, L.; Vaquero, A. The dual role of sirtuins in cancer. Genes Cancer 2011, 2, 648–662. [Google Scholar] [CrossRef]
- Hsieh, J.K.; Yap, D.; O’Connor, D.J.; Fogal, V.; Fallis, L.; Chan, F.; Zhong, S.; Lu, X. Novel function of the cyclin A binding site of E2F in regulating p53-induced apoptosis in response to DNA damage. Mol. Cell. Biol. 2002, 22, 78–93. [Google Scholar] [CrossRef]
- Chen, J. Intrinsically disordered p53 extreme C-terminus binds to s100b(ββ) through “fly-casting”. J. Am. Chem. Soc. 2009, 131, 2088–2089. [Google Scholar] [CrossRef]
- Ross, C.A.; Poirier, M.A. Protein aggregation and neurodegenerative disease. Nat. Med. 2004, 10, S10–S17. [Google Scholar] [CrossRef]
- Cohen, S.I.A.; Linse, S.; Luheshi, L.M.; Hellstrand, E.; White, D.A.; Rajah, L.; Otzen, D.E.; Vendruscolo, M.; Dobson, C.M.; Knowles, T.P.J. Proliferation of amyloid-β42 aggregates occurs through a secondary nucleation mechanism. Proc. Natl. Acad. Sci. USA 2013, 110, 9758–9763. [Google Scholar] [CrossRef]
- Kayed, R.; Head, E.; Thompson, J.L.; McIntire, T.M.; Milton, S.C.; Cotman, C.W.; Glabe, C.G. Common structure of soluble amyloid oligomers implies common mechanism of pathogenesis. Science 2003, 300, 486–489. [Google Scholar] [CrossRef]
- Walsh, D.M.; Selkoe, D.J. Abeta oligomers—A decade of discovery. J. Neurochem. 2007, 101, 1172–1184. [Google Scholar] [CrossRef]
- Periquet, M.; Fulga, T.; Myllykangas, L.; Schlossmacher, M.G.; Feany, M.B. Aggregated alpha-synuclein mediates dopaminergic neurotoxicity in vivo. J. Neurosci. 2007, 27, 3338–3346. [Google Scholar] [CrossRef]
- Bernstein, S.L.; Dupuis, N.F.; Lazo, N.D.; Wyttenbach, T.; Condron, M.M.; Bitan, G.; Teplow, D.B.; Shea, J.-E.; Ruotolo, B.T.; Robinson, C.V.; et al. Amyloid-beta protein oligomerization and the importance of tetramers and dodecamers in the aetiology of Alzheimer’s disease. Nat. Chem. 2009, 1, 326–331. [Google Scholar] [CrossRef]
- Petkova, A.T.; Yau, W.-M.; Tycko, R. Experimental constraints on quaternary structure in Alzheimer’s beta-amyloid fibrils. Biochemistry 2005, 45, 498–512. [Google Scholar] [CrossRef]
- Glenner, G.G.; Wong, C.W. Alzheimer’s disease: Initial report of the purification and characterization of a novel cerebrovascular amyloid protein. Biochem. Biophys. Res. Commun. 1984, 120, 885–890. [Google Scholar] [CrossRef]
- Haass, C.; Selkoe, D.J. Soluble protein oligomers in neurodegeneration: Lessons from the Alzheimer’s amyloid beta-peptide. Nat. Rev. Mol. Cell Biol. 2007, 8, 101–112. [Google Scholar] [CrossRef]
- Haass, C. Take five—BACE and the gamma-secretase quartet conduct Alzheimer’s amyloid beta-peptide generation. EMBO J. 2004, 23, 483–488. [Google Scholar] [CrossRef]
- Burdick, D.; Soreghan, B.; Kwon, M.; Kosmoski, J.; Knauer, M.; Henschen, A.; Yates, J.; Cotman, C.; Glabe, C. Assembly and aggregation properties of synthetic Alzheimer’s Abeta amyloid peptide analogs. J. Biol. Chem. 1992, 267, 546–554. [Google Scholar]
- Citron, M.; Oltersdorf, T.; Haass, C.; McConlogue, L.; Hung, A.Y.; Seubert, P.; Vigo-Pelfrey, C.; Lieberburg, I.; Selkoe, D.J. Mutation of the beta-amyloid precursor protein in familial Alzheimer’s disease increases beta-protein production. Nature 1992, 360, 672–674. [Google Scholar] [CrossRef]
- Kassler, K.; Horn, A.C.; Sticht, H. Effect of pathogenic mutations on the structure and dynamics of Alzheimer’s Aβ42-amyloid oligomers. J. Mol. Model 2010, 16, 1011–1020. [Google Scholar] [CrossRef]
- Suzuki, N.; Cheung, T.; Cai, X.; Odaka, A.; Otvos, L.; Eckman, C.; Golde, T.; Younkin, S. An increased percentage of long amyloid beta protein secreted by familial amyloid beta protein precursor (beta APP717) mutants. Science 1994, 264, 1336–1340. [Google Scholar] [CrossRef]
- Kirkitadze, M.D.; Condron, M.M.; Teplow, D.B. Identification and characterization of key kinetic intermediates in amyloid beta-protein fibrillogenesis. J. Mol. Biol. 2001, 312, 1103–1119. [Google Scholar] [CrossRef]
- Glabe, C.G. Common mechanisms of amyloid oligomer pathogenesis in degenerative disease. Neurobiol. Aging 2006, 27, 570–575. [Google Scholar] [CrossRef]
- Selkoe, D.J. Folding proteins in fatal ways. Nature 2003, 426, 900–904. [Google Scholar] [CrossRef]
- Bartels, T.; Choi, J.G.; Selkoe, D.J. Alpha-synuclein occurs physiologically as a helically folded tetramer that resists aggregation. Nature 2011, 477, 107–110. [Google Scholar] [CrossRef]
- Lashuel, H.A.; Hartley, D.; Petre, B.M.; Walz, T.; Lansbury, P.T. Neurodegenerative disease: Amyloid pores from pathogenic mutations. Nature 2002, 418. [Google Scholar] [CrossRef]
- Demuro, A.; Mina, E.; Kayed, R.; Milton, S.C.; Parker, I.; Glabe, C.G. Calcium dysregulation and membrane disruption as a ubiquitous neurotoxic mechanism of soluble amyloid oligomers. J. Biol. Chem. 2005, 280, 17294–17300. [Google Scholar] [CrossRef]
- Silvia, C.; Benedetta, M.; Mariagioia, Z.; Anna, P.; Claudia, P.; Elisa, E.; Annalisa, R.; Massimo, S.; Christopher, M.D.; Cristina, C.; et al. A causative link between the structure of aberrant protein oligomers and their toxicity. Nat. Chem. Biol. 2010, 6, 140–147. [Google Scholar] [CrossRef]
- Sandberg, A.; Luheshi, L.M.; Söllvander, S.; Pereira de Barros, T.; Macao, B.; Knowles, T.P.J.; Biverstål, H.; Lendel, C.; Ekholm-Petterson, F.; Dubnovitsky, A.; et al. Stabilization of neurotoxic Alzheimer amyloid-β oligomers by protein engineering. Proc. Natl. Acad. Sci. USA 2010, 107, 15595–15600. [Google Scholar] [CrossRef]
- Hoyer, W.; Grönwall, C.; Jonsson, A.; Ståhl, S.; Härd, T. Stabilization of a beta-hairpin in monomeric Alzheimer’s amyloid-beta peptide inhibits amyloid formation. Proc. Natl. Acad. Sci. USA 2008, 105, 5099–5104. [Google Scholar] [CrossRef]
- Ahmed, M.; Davis, J.; Aucoin, D.; Sato, T.; Ahuja, S.; Aimoto, S.; Elliott, J.I.; van Nostrand, W.E.; Smith, S.O. Structural conversion of neurotoxic amyloid-beta1–42 oligomers to fibrils. Nat. Struct. Mol. Biol. 2010, 17, 561–567. [Google Scholar] [CrossRef]
- Laganowsky, A.; Liu, C.; Sawaya, M.R.; Whitelegge, J.P.; Park, J.; Zhao, M.; Pensalfini, A.; Soriaga, A.B.; Landau, M.; Teng, P.K.; et al. Atomic view of a toxic amyloid small oligomer. Science 2012, 335, 1228–1231. [Google Scholar] [CrossRef]
- Spillantini, M.G.; Schmidt, M.L.; Lee, V.M.-Y.; Trojanowski, J.Q.; Jakes, R.; Goedert, M. Alpha-synuclein in lewy bodies. Nature 1997, 388, 839–840. [Google Scholar] [CrossRef]
- Karran, E.; Mercken, M.; Strooper, B.D. The amyloid cascade hypothesis for Alzheimer’s disease: An appraisal for the development of therapeutics. Nat. Rev. Drug Discov. 2011, 10, 698–712. [Google Scholar] [CrossRef]
- Chiti, F.; Dobson, C.M. Protein misfolding, functional amyloid, and human disease. Annu. Rev. Biochem. 2006, 75, 333–366. [Google Scholar] [CrossRef]
- Paravastu, A.K.; Leapman, R.D.; Yau, W.-M.; Tycko, R. Molecular structural basis for polymorphism in Alzheimer’s beta-amyloid fibrils. Proc. Natl. Acad. Sci. USA 2008, 105, 18349–18354. [Google Scholar] [CrossRef]
- Lührs, T.; Ritter, C.; Adrian, M.; Riek-Loher, D.; Bohrmann, B.; Döbeli, H.; Schubert, D.; Riek, R. 3D structure of Alzheimer’s amyloid-β(1–42) fibrils. Proc. Natl. Acad. Sci. USA 2005, 102, 17342–17347. [Google Scholar] [CrossRef]
- Fitzpatrick, A.W.P.; Debelouchina, G.T.; Bayro, M.J.; Clare, D.K.; Caporini, M.A.; Bajaj, V.S.; Jaroniec, C.P.; Wang, L.; Ladizhansky, V.; Müller, S.A.; et al. Atomic structure and hierarchical assembly of a cross-beta amyloid fibril. Proc. Natl. Acad. Sci. USA 2013, 110, 5468–5473. [Google Scholar] [CrossRef]
- Rubin, N.; Perugia, E.; Goldschmidt, M.; Fridkin, M.; Addadi, L. Chirality of amyloid suprastructures. J. Am. Chem. Soc. 2008, 130, 4602–4603. [Google Scholar] [CrossRef]
- GhattyVenkataKrishna, P.K.; Uberbacher, E.C.; Cheng, X. Effect of the amyloid beta hairpin’s structure on the handedness of helices formed by its aggregates. FEBS Lett. 2013, 587, 2649–2655. [Google Scholar] [CrossRef]
- Buchete, N.-V.; Tycko, R.; Hummer, G. Molecular dynamics simulations of Alzheimer’s β-amyloid protofilaments. J. Mol. Biol. 2005, 353, 804–821. [Google Scholar] [CrossRef]
- Fawzi, N.L.; Okabe, Y.; Yap, E.-H.; Head-Gordon, T. Determining the critical nucleus and mechanism of fibril elongation of the Alzheimer’s aβ1–40 peptide. J. Mol. Biol. 2007, 365, 535–550. [Google Scholar] [CrossRef]
- Lin, Y.-S.; Bowman, G.R.; Beauchamp, K.A.; Pande, V.S. Investigating how peptide length and a pathogenic mutation modify the structural ensemble of amyloid beta monomer. Biophys. J. 2012, 102, 315–324. [Google Scholar] [CrossRef]
- Fisher, C.K.; Ullman, O.; Stultz, C.M. Comparative studies of disordered proteins with similar sequences: Application to Aβ40 and Aβ42. Biophys. J. 2013, 104, 1546–1555. [Google Scholar] [CrossRef]
- Sciarretta, K.L.; Gordon, D.J.; Petkova, A.T.; Tycko, R.; Meredith, S.C. Aβ40-lactam(d23/k28) models a conformation highly favorable for nucleation of amyloid. Biochemistry 2005, 44, 6003–6014. [Google Scholar] [CrossRef]
- Reddy, G.; Straub, J.E.; Thirumalai, D. Influence of preformed asp23−lys28 salt bridge on the conformational fluctuations of monomers and dimers of Aβ peptides with implications for rates of fibril formation. J. Phys. Chem. B 2009, 113, 1162–1172. [Google Scholar] [CrossRef]
- Tarus, B.; Straub, J.E.; Thirumalai, D. Dynamics of asp23−lys28 salt-bridge formation in aβ10–35 monomers. J. Am. Chem. Soc. 2006, 128, 16159–16168. [Google Scholar] [CrossRef]
- Nguyen, P.H.; Li, M.S.; Stock, G.; Straub, J.E.; Thirumalai, D. Monomer adds to preformed structured oligomers of a beta-peptides by a two-stage dock-lock mechanism. Proc. Natl. Acad. Sci. USA 2007, 104, 111–116. [Google Scholar] [CrossRef]
- Takeda, T.; Klimov, D.K. Probing energetics of Abeta fibril elongation by molecular dynamics simulations. Biophys. J. 2009, 96, 4428–4437. [Google Scholar] [CrossRef]
- Rojas, A.; Liwo, A.; Browne, D.; Scheraga, H.A. Mechanism of fiber assembly: Treatment of Abeta peptide aggregation with a coarse-grained united-residue force field. J. Mol. Biol. 2010, 404, 537–552. [Google Scholar] [CrossRef]
- Esler, W.P.; Stimson, E.R.; Jennings, J.M.; Vinters, H.V.; Ghilardi, J.R.; Lee, J.P.; Mantyh, P.W.; Maggio, J.E. Alzheimer’s disease amyloid propagation by a template-dependent dock-lock mechanism. Biochemistry 2000, 39, 6288–6295. [Google Scholar] [CrossRef]
- Lee, J.; Culyba, E.K.; Powers, E.T.; Kelly, J.W. Amyloid-β forms fibrils by nucleated conformational conversion of oligomers. Nat. Chem. Biol. 2011, 7, 602–609. [Google Scholar] [CrossRef]
- Urbanc, B.; Betnel, M.; Cruz, L.; Bitan, G.; Teplow, D.B. Elucidation of amyloid β-protein oligomerization mechanisms: Discrete molecular dynamics study. J. Am. Chem. Soc. 2010, 132, 4266–4280. [Google Scholar] [CrossRef]
- Teplow, D.B.; Lazo, N.D.; Bitan, G.; Bernstein, S.; Wyttenbach, T.; Bowers, M.T.; Baumketner, A.; Shea, J.-E.; Urbanc, B.; Cruz, L.; et al. Elucidating amyloid β-protein folding and assembly: A multidisciplinary approach. Acc. Chem. Res. 2006, 39, 635–645. [Google Scholar] [CrossRef]
- Bitan, G.; Kirkitadze, M.D.; Lomakin, A.; Vollers, S.S.; Benedek, G.B.; Teplow, D.B. Amyloid β-protein (Aβ) assembly: Aβ40 and Aβ42 oligomerize through distinct pathways. Proc. Natl. Acad. Sci. USA 2003, 100, 330–335. [Google Scholar] [CrossRef]
- Bitan, G.; Vollers, S.S.; Teplow, D.B. Elucidation of primary structure elements controlling early amyloid β-protein oligomerization. J. Biol. Chem. 2003, 278, 34882–34889. [Google Scholar] [CrossRef]
- Bitan, G.; Lomakin, A.; Teplow, D.B. Amyloid β-protein oligomerization: Prenucleation interactions revealed by photo-induced cross-linking of unmodified proteins. J. Biol. Chem. 2001, 276, 35176–35184. [Google Scholar] [CrossRef]
- Barz, B.; Urbanc, B. Minimal model of self-assembly: Emergence of diversity and complexity. J. Phys. Chem. B 2014, 118, 3761–3770. [Google Scholar] [CrossRef]
- Streltsov, V.A.; Varghese, J.N.; Masters, C.L.; Nuttall, S.D. Crystal structure of the amyloid-β p3 fragment provides a model for oligomer formation in Alzheimer’s disease. J. Neurosci. 2011, 31, 1419–1426. [Google Scholar] [CrossRef]
- Urbanc, B.; Cruz, L.; Yun, S.; Buldyrev, S.V.; Bitan, G.; Teplow, D.B.; Stanley, H.E. In silico study of amyloid β-protein folding and oligomerization. Proc. Natl. Acad. Sci. USA 2004, 101, 17345–17350. [Google Scholar] [CrossRef]
- Urbanc, B.; Betnel, M.; Cruz, L.; Li, H.; Fradinger, E.A.; Monien, B.H.; Bitan, G. Structural basis for aβ1–42 toxicity inhibition by Aβ c-terminal fragments: Discrete molecular dynamics study. J. Mol. Biol. 2011, 410, 316–328. [Google Scholar] [CrossRef]
- Barz, B.; Urbanc, B. Dimer formation enhances structural differences between amyloid β-protein (1–40) and (1–42): An explicit-solvent molecular dynamics study. PLoS One 2012, 7. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).