Abstract
Very few studies concern the isotropic phase of Side-Chain Liquid-Crystalline Polymers (SCLCPs). However, the interest for the isotropic phase appears particularly obvious in flow experiments. Unforeseen shear-induced nematic phases are revealed away from the N-I transition temperature. The non-equilibrium nematic phase in the isotropic phase of SCLCP melts challenges the conventional timescales described in theoretical approaches and reveal very long timescales, neglected until now. This spectacular behavior is the starter of the present survey that reveals long range solid-like interactions up to the sub-millimetre scale. We address the question of the origin of this solid-like property by probing more particularly the non-equilibrium behavior of a polyacrylate substituted by a nitrobiphenyl group (PANO2). The comparison with a polybutylacrylate chain of the same degree of polymerization evidences that the solid-like response is exacerbated in SCLCPs. We conclude that the liquid crystal moieties interplay as efficient elastic connectors. Finally, we show that the “solid” character can be evidenced away from the glass transition temperature in glass formers and for the first time, in purely alkane chains above their crystallization temperature. We thus have probed collective elastic effects contained not only in the isotropic phase of SCLCPs, but also more generically in the liquid state of ordinary melts and of ordinary liquids.
1. Introduction
Shear flow is used in solid mechanics as well as in fluid dynamics. The flow in liquids can be induced by the mechanical displacement of a surface in contact with the fluid (Figure 1).
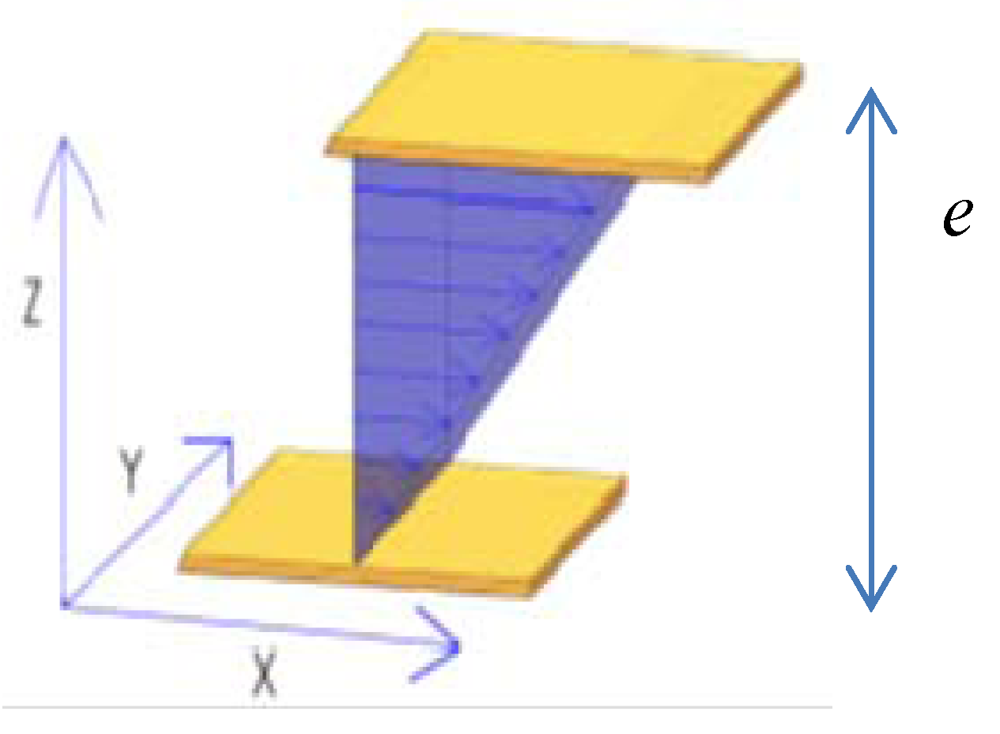
Figure 1.
Geometry of a simple shear flow. The liquid is placed between two surfaces separated by a gap “e”. The upper surface is moving whereas the lower one is fixed. When the translation motion is integrally transmitted to the liquid (no-slip boundary conditions), this latter is submitted to a shear gradient visualized by these arrows. The shear flow is defined by three main axes: velocity axis (X), gradient of velocity (Z), neutral axis (Y).
A splendid and unexpected birefringence emerges from the isotropic phase of side-chain liquid crystal polymer melts when they are sheared above a critical shear rate 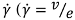 : ratio of the velocity ν of the moving surface to the gap thickness e in Figure 1). This birefringence (Figure 2) is the signature of the formation above the N-I transition temperature, of a non-equilibrium nematic phase oriented along the velocity axis. The first observation of shear-induced transition in the isotropic phase of thermotropic liquid crystal polymers was made by P. T. Mather in 1997 on a main-chain polymer [1]. The phenomenon was then identified a decade ago on a series of Side-Chain Liquid-Crystal Polymers (SCLCPs) evidencing the generic character of the shear-induced transition [2]. Small Angle neutron Scattering (SANS) experiments have shown that under flow, the mesogens adopt a specific orientation parallel to the chain in the shear-induced phase [2]. This specific non-equilibrium conformation excludes an interpretation in terms of a simple shift of the transition temperatures (for an overview of the chain conformation in liquid crystal phases at rest and under flow see [3,4,5,6,7]).
: ratio of the velocity ν of the moving surface to the gap thickness e in Figure 1). This birefringence (Figure 2) is the signature of the formation above the N-I transition temperature, of a non-equilibrium nematic phase oriented along the velocity axis. The first observation of shear-induced transition in the isotropic phase of thermotropic liquid crystal polymers was made by P. T. Mather in 1997 on a main-chain polymer [1]. The phenomenon was then identified a decade ago on a series of Side-Chain Liquid-Crystal Polymers (SCLCPs) evidencing the generic character of the shear-induced transition [2]. Small Angle neutron Scattering (SANS) experiments have shown that under flow, the mesogens adopt a specific orientation parallel to the chain in the shear-induced phase [2]. This specific non-equilibrium conformation excludes an interpretation in terms of a simple shift of the transition temperatures (for an overview of the chain conformation in liquid crystal phases at rest and under flow see [3,4,5,6,7]).
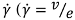 : ratio of the velocity ν of the moving surface to the gap thickness e in Figure 1). This birefringence (Figure 2) is the signature of the formation above the N-I transition temperature, of a non-equilibrium nematic phase oriented along the velocity axis. The first observation of shear-induced transition in the isotropic phase of thermotropic liquid crystal polymers was made by P. T. Mather in 1997 on a main-chain polymer [1]. The phenomenon was then identified a decade ago on a series of Side-Chain Liquid-Crystal Polymers (SCLCPs) evidencing the generic character of the shear-induced transition [2]. Small Angle neutron Scattering (SANS) experiments have shown that under flow, the mesogens adopt a specific orientation parallel to the chain in the shear-induced phase [2]. This specific non-equilibrium conformation excludes an interpretation in terms of a simple shift of the transition temperatures (for an overview of the chain conformation in liquid crystal phases at rest and under flow see [3,4,5,6,7]).
: ratio of the velocity ν of the moving surface to the gap thickness e in Figure 1). This birefringence (Figure 2) is the signature of the formation above the N-I transition temperature, of a non-equilibrium nematic phase oriented along the velocity axis. The first observation of shear-induced transition in the isotropic phase of thermotropic liquid crystal polymers was made by P. T. Mather in 1997 on a main-chain polymer [1]. The phenomenon was then identified a decade ago on a series of Side-Chain Liquid-Crystal Polymers (SCLCPs) evidencing the generic character of the shear-induced transition [2]. Small Angle neutron Scattering (SANS) experiments have shown that under flow, the mesogens adopt a specific orientation parallel to the chain in the shear-induced phase [2]. This specific non-equilibrium conformation excludes an interpretation in terms of a simple shift of the transition temperatures (for an overview of the chain conformation in liquid crystal phases at rest and under flow see [3,4,5,6,7]).This non-equilibrium behavior presents strong similarities with the shear-induced nematic phase, theoretically predicted by S. Hess [8,9] and P.D. Olmsted [10,11], later extended to lyotropic systems [12,13]. The scheme is a flow coupling to the life time of the orientational pre-transitional fluctuations. Despite an apparent similarity, the timescales involved by the shear flow are too slow to compete with the classical relaxation times [14,15]. The origin of the shear-induced phase is to be found elsewhere. Because it challenges the current state of the art, the discovery of the shear-induced nematic phase in the isotropic phase of SCLCPs has opened a new route for the understanding of the properties of the liquid state. It reveals elastic collective effects so far neglected in the liquid state and has permitted the identification of a solid-like response away from any phase transition.
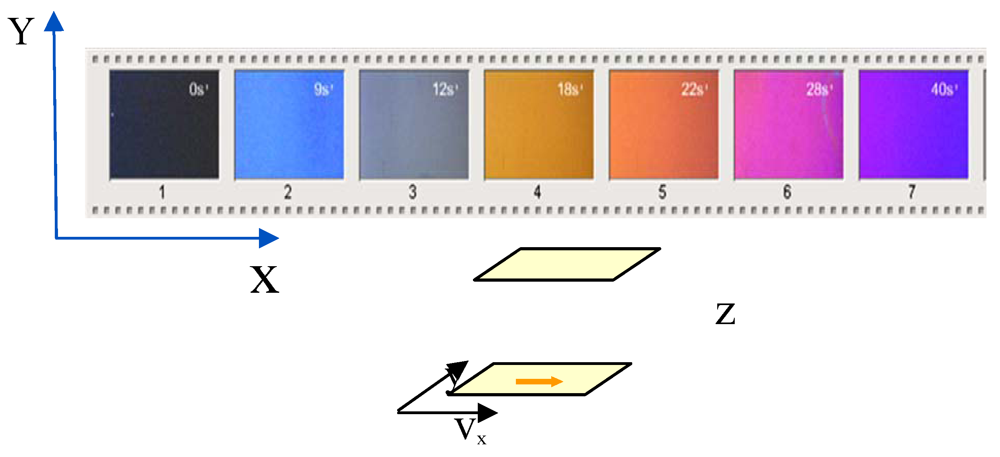
Figure 2.
Snapshots of the isotropic phase of SCLCP. A strong birefringence appears over a critical shear rate. The colors (observed between cross-polarizers) indicate from left to right an increase of the birefringence. The photographs view the plane containing the velocity/vorticity axis (X,Y). (A movie of the shear-induced transition is available on: http://www.youtube.com/watch?v=igo9hpo8Tzo.) Bottom: scheme of the specific polymer conformation in the shear-induced phase. Mesogens and chain are parallel to the velocity axis (X).
The treatment of the shear-induced transition in lyotropic systems benefited from an abundant body of literature, particularly because of the numerous experimental developments [16,17,18,19,20]. It is usually interpreted by a “nucleation-unidirectional growth” process assisted by the pre-transitional fluctuations [10,11,16,17,18,19,20,21,22] which leads to the coexistence of two defined shear bands related to the isotropic and the shear-induced phases. However, this scenario remains under debate, since the high shear branch of the flow curve, associated to the induced nematic phase, deviates from Newtonian fluid behavior [21,22] and the velocity cartography determined by NMR [23,24,25] suggests that the liquid moves rather as a gel. Finally, in SCLCPs, the coupling model to the pre-transitional fluctuations has to be definitely rejected since the lifetime of these fluctuations is about 103 to 104 times too short with respect to timescales of the flow [14]. The shear-induced birefringence in the isotropic phase of SCLCPs does not originate from orientational pre-transitional fluctuations. The present debate is thus to determine the origin of these extra long timescales.
In this manuscript, we first present a new series of shear experiments carried out in the isotropic phase of a nitro-biphenyl side-chain polyacrylate named PANO2. The monomer was synthesized at the Laboratory Léon Brillouin following the chemical protocol described in [26,27] and polymerized by controlled radical polymerization in collaboration with the Philipps-Universität Marburg (Germany). The transition temperatures of the polymer were determined by Calorimetry and Microscopy measurements and are tabulated in Table 1.
Asymptotic shear measurements have been carried out at different gap thicknesses or by changing the nature of the substrate. The dependence with respect to these two parameters confirms the non-relevance of a coupling with relaxation time as the lifetime of orientational pre-transitional fluctuations, but raises the question of possible interfacial and slippage states. The understanding of the shear-induced phase has thus to be related to a cohesive property hitherto neglected in the isotropic phase. Since 2005, we have been working on, and demonstrating, that improved dynamic measurements enable access to this cohesive property via the identification of a low frequency shear elasticity (solid-like character) in the liquid state in various glass formers away from any phase transition [28,29,30,31,32]. We apply this improved protocol first to the isotropic phase of the SCLCP, PANO2, compare it to an ordinary polymer chain (polybutylacrylate melt (PBuA)) of the same degree of polymerization, and finally examine the case of a short alkyl chain assimilated to a spacer: The heptadecane. In the three cases, a solid-like behavior is revealed in the liquid state. The characteristics of the samples are gathered in Table 1 of the Experimental part.

Table 1.
Characteristics of the 3 liquids.
| Samples | SCLCP: PANO2 | PBuA | Heptadecane |
|---|---|---|---|
| Chemical formula | 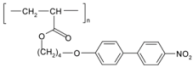 | 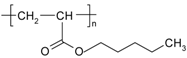 |  C17H36 |
| Supplier | LLB-Philipps-Univ. Marburg | Polymer Source Inc. | Sigma-Aldrich Co. |
| Molecular weightPolydispersity indexNumber of repetitive units | Mw = 54,000 g∙mol−1 I = Mw/Mn = 1.2 n = 160 | Mw = 20,000 g∙mol−1 I = Mw/Mn = 1.1 n = 160 | M = 240 g∙mol−1 n = 16 |
| Transition temperatures | Tg–33 °C–Nematic–94.5 °C–Isotropic | Tg = −64 °C Amorphous | Tm = 21 °C Crystalline |
2. Experimental
The rheo-microscopy experiments were performed in transmission mode under cross-polarized microscopy (Olympus BX60) in the (velocity, vorticity) plane with a magnification 100×. The cross-polarizers are oriented at 45° to the flow direction and a wavelength λ = 4,700Å ± 150 Å is used. Steady-state shear flow conditions were ensured using a home-improved CSS450 Linkam shear cell (with a temperature gradient <±0.05 °C) equipped with a quartz plate-plate fixture. The transmitted intensity I is measured with a photosensitive diode and normalized to the uncrossed polarizer intensity I0. The averaged birefringence <Δn> is measured as a function of the shear rate using the formula: I/I0 = sin²(<Δnx>.e.π/λ) where e is the gap thickness. <Δn> is measured as a function of the shear rate. It is averaged over the whole sample thickness (weighted by the fractions of isotropic and shear-induced phases). The gap is 0.060 mm.
The flow and dynamic relaxation measurements were carried out in steady-state and strain controlled dynamic modes respectively using a rheometer (ARESII from TA-Instrument). Simultaneously, a 7-digit voltmeter (Keitley-Rate: 300 data/s) measures the voltage of the motor imposing the oscillation (input wave), while another 7-digit voltmeter measures the voltage associated to the sensor (output wave). This setup permits the simultaneous access to the strain/stress signals and to the dynamic profile using the conventional viscoelastic formalism following the relationship: σ(ω) =G0.γ0.sin(ω.t + Δ 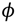 ) with G0, the shear modulus, γ0, the strain amplitude defined as the ratio of the displacement to the sample gap and Δ
) with G0, the shear modulus, γ0, the strain amplitude defined as the ratio of the displacement to the sample gap and Δ 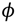 the phase shift between the input and the output waves, i.e., in terms of shear elastic (G′) and viscous (G″) moduli:σ (ω) = γ0. (G′(ω).sin(ω.t) + G″(ω).cos(ω.t)), with G′ the component in phase with the strain, and G″ the out-of-phase component and γ0 the strain amplitude. It should be stressed that the formalism in terms of G′ and G″ imposes that the resulting stress wave keeps the shape of the imposed strain wave (sinusoidal-like). Finally, the thermal environment (air-pulsed oven) ensures a temperature stability of ±0.05 °C. The sample was placed between plate-plate fixtures (10 mm diameter). Improved contacts between the liquid and the substrate are obtained by using wetting fixtures made of alumina [28,33].
the phase shift between the input and the output waves, i.e., in terms of shear elastic (G′) and viscous (G″) moduli:σ (ω) = γ0. (G′(ω).sin(ω.t) + G″(ω).cos(ω.t)), with G′ the component in phase with the strain, and G″ the out-of-phase component and γ0 the strain amplitude. It should be stressed that the formalism in terms of G′ and G″ imposes that the resulting stress wave keeps the shape of the imposed strain wave (sinusoidal-like). Finally, the thermal environment (air-pulsed oven) ensures a temperature stability of ±0.05 °C. The sample was placed between plate-plate fixtures (10 mm diameter). Improved contacts between the liquid and the substrate are obtained by using wetting fixtures made of alumina [28,33].
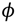 ) with G0, the shear modulus, γ0, the strain amplitude defined as the ratio of the displacement to the sample gap and Δ
) with G0, the shear modulus, γ0, the strain amplitude defined as the ratio of the displacement to the sample gap and Δ 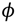 the phase shift between the input and the output waves, i.e., in terms of shear elastic (G′) and viscous (G″) moduli:σ (ω) = γ0. (G′(ω).sin(ω.t) + G″(ω).cos(ω.t)), with G′ the component in phase with the strain, and G″ the out-of-phase component and γ0 the strain amplitude. It should be stressed that the formalism in terms of G′ and G″ imposes that the resulting stress wave keeps the shape of the imposed strain wave (sinusoidal-like). Finally, the thermal environment (air-pulsed oven) ensures a temperature stability of ±0.05 °C. The sample was placed between plate-plate fixtures (10 mm diameter). Improved contacts between the liquid and the substrate are obtained by using wetting fixtures made of alumina [28,33].
the phase shift between the input and the output waves, i.e., in terms of shear elastic (G′) and viscous (G″) moduli:σ (ω) = γ0. (G′(ω).sin(ω.t) + G″(ω).cos(ω.t)), with G′ the component in phase with the strain, and G″ the out-of-phase component and γ0 the strain amplitude. It should be stressed that the formalism in terms of G′ and G″ imposes that the resulting stress wave keeps the shape of the imposed strain wave (sinusoidal-like). Finally, the thermal environment (air-pulsed oven) ensures a temperature stability of ±0.05 °C. The sample was placed between plate-plate fixtures (10 mm diameter). Improved contacts between the liquid and the substrate are obtained by using wetting fixtures made of alumina [28,33]. 3. Results and Discussion
3.1. Non-Monotonic Flow Curve: Characterisation of the Flow Birefringence
Figure 3(a) displays the evolution of the birefringence at several temperatures above TNI and also one temperature below. At T > TNI and low shear rates, the birefringence is close to zero and slightly shear rate-dependent. This regime corresponds to the so-called paranematic phase [10], or flow birefringence [34]. Above a critical shear rate 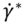 , one observes a strong departure of the birefringence. This non-linear behavior is interpreted, in the frame of the pre-transitional fluctuation coupling model [10] (Figure 3(b)), as a non-equilibrium, first-order phase transition, characterized by an alignment of the liquid crystal moieties along the velocity direction. The texture free from defects indicates a homogeneously aligned nematic phase (Figure 2). Figure 3(c) illustrates the critical shear rate corresponding to the onset of the emergence of the shear-induced birefringence. The (non-equilibrium) characteristic time
, one observes a strong departure of the birefringence. This non-linear behavior is interpreted, in the frame of the pre-transitional fluctuation coupling model [10] (Figure 3(b)), as a non-equilibrium, first-order phase transition, characterized by an alignment of the liquid crystal moieties along the velocity direction. The texture free from defects indicates a homogeneously aligned nematic phase (Figure 2). Figure 3(c) illustrates the critical shear rate corresponding to the onset of the emergence of the shear-induced birefringence. The (non-equilibrium) characteristic time 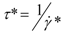 (Figure 3(c)) varies from 0.1 s up to 10−2 s. τ * is about 102 to 105 larger than the orientational order fluctuations’ lifetime [35], excluding a coupling with the shear flow, in agreement with the first observations carried out on other SCLCPs [14]. This shear-induced birefringence resembles the foreseen non-equilibrium N-I transition but it is not. Is there an equivalence between the birefringence timescales (τ *) and the characteristic timescales of the rheological behavior (stress-optical rule)?
(Figure 3(c)) varies from 0.1 s up to 10−2 s. τ * is about 102 to 105 larger than the orientational order fluctuations’ lifetime [35], excluding a coupling with the shear flow, in agreement with the first observations carried out on other SCLCPs [14]. This shear-induced birefringence resembles the foreseen non-equilibrium N-I transition but it is not. Is there an equivalence between the birefringence timescales (τ *) and the characteristic timescales of the rheological behavior (stress-optical rule)?
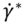 , one observes a strong departure of the birefringence. This non-linear behavior is interpreted, in the frame of the pre-transitional fluctuation coupling model [10] (Figure 3(b)), as a non-equilibrium, first-order phase transition, characterized by an alignment of the liquid crystal moieties along the velocity direction. The texture free from defects indicates a homogeneously aligned nematic phase (Figure 2). Figure 3(c) illustrates the critical shear rate corresponding to the onset of the emergence of the shear-induced birefringence. The (non-equilibrium) characteristic time
, one observes a strong departure of the birefringence. This non-linear behavior is interpreted, in the frame of the pre-transitional fluctuation coupling model [10] (Figure 3(b)), as a non-equilibrium, first-order phase transition, characterized by an alignment of the liquid crystal moieties along the velocity direction. The texture free from defects indicates a homogeneously aligned nematic phase (Figure 2). Figure 3(c) illustrates the critical shear rate corresponding to the onset of the emergence of the shear-induced birefringence. The (non-equilibrium) characteristic time 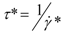 (Figure 3(c)) varies from 0.1 s up to 10−2 s. τ * is about 102 to 105 larger than the orientational order fluctuations’ lifetime [35], excluding a coupling with the shear flow, in agreement with the first observations carried out on other SCLCPs [14]. This shear-induced birefringence resembles the foreseen non-equilibrium N-I transition but it is not. Is there an equivalence between the birefringence timescales (τ *) and the characteristic timescales of the rheological behavior (stress-optical rule)?
(Figure 3(c)) varies from 0.1 s up to 10−2 s. τ * is about 102 to 105 larger than the orientational order fluctuations’ lifetime [35], excluding a coupling with the shear flow, in agreement with the first observations carried out on other SCLCPs [14]. This shear-induced birefringence resembles the foreseen non-equilibrium N-I transition but it is not. Is there an equivalence between the birefringence timescales (τ *) and the characteristic timescales of the rheological behavior (stress-optical rule)?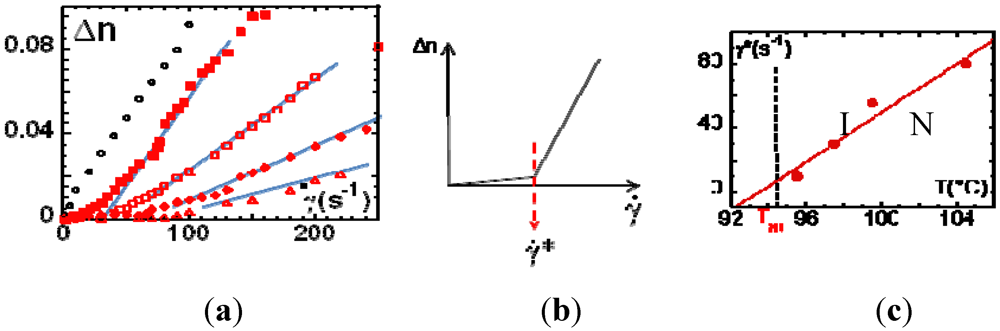
Figure 3.
(a) Evolution of the birefringence Δn of PANO2, measured in the (velocity, neutral axis) plane at 0.060 mm gap thickness as a function of the shear rate ( 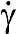 ) at different temperatures away from TNI: T-TNI: −2°C(○),+1°C(
) at different temperatures away from TNI: T-TNI: −2°C(○),+1°C(  ),+3°C(
),+3°C(  ),+5°C(
),+5°C(  ),+10°C(Δ). The wavelength is λ=4,700 Å; (b) Theoretically expected behavior: At low shear rates, the paranematic phase exhibits a flow birefringence proportional to the shear rate. Above a critical shear rate, the non-linear behavior indicates the onset of the shear-induced phase transition; (c) Critical shear rate versus temperature. The corresponding (non-equilibrium) characteristic time is defined by:
),+10°C(Δ). The wavelength is λ=4,700 Å; (b) Theoretically expected behavior: At low shear rates, the paranematic phase exhibits a flow birefringence proportional to the shear rate. Above a critical shear rate, the non-linear behavior indicates the onset of the shear-induced phase transition; (c) Critical shear rate versus temperature. The corresponding (non-equilibrium) characteristic time is defined by: 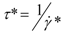 Sample: PANO2 at 0.060mm (
Sample: PANO2 at 0.060mm (  ) gap thickness.
) gap thickness.
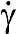 ) at different temperatures away from TNI: T-TNI: −2°C(○),+1°C(
) at different temperatures away from TNI: T-TNI: −2°C(○),+1°C(  ),+3°C(
),+3°C(  ),+5°C(
),+5°C(  ),+10°C(Δ). The wavelength is λ=4,700 Å; (b) Theoretically expected behavior: At low shear rates, the paranematic phase exhibits a flow birefringence proportional to the shear rate. Above a critical shear rate, the non-linear behavior indicates the onset of the shear-induced phase transition; (c) Critical shear rate versus temperature. The corresponding (non-equilibrium) characteristic time is defined by:
),+10°C(Δ). The wavelength is λ=4,700 Å; (b) Theoretically expected behavior: At low shear rates, the paranematic phase exhibits a flow birefringence proportional to the shear rate. Above a critical shear rate, the non-linear behavior indicates the onset of the shear-induced phase transition; (c) Critical shear rate versus temperature. The corresponding (non-equilibrium) characteristic time is defined by: 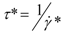 Sample: PANO2 at 0.060mm (
Sample: PANO2 at 0.060mm (  ) gap thickness.
) gap thickness.
3.2. Influence of the Gap Thickness and the Nature of the Substrate on the (Stationary) Flow Behavior
The second significant divergence with the prediction is the shape of the flow curve (stationary shear stress versus shear rate curve—for a description of the transient behavior, see [36,37]). The flow-induced phase transition is supposed to exhibit a 3-zone stress-shear rate curve (Figure 4(a)): at low shear rates, the paranematic phase corresponds to a Newtonian behavior, at intermediate strain rates, a stress plateau appears when the phase is induced and “phase-separates” into homogeneous bands flowing at strain rates 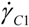 and
and 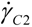 , to maintain the average imposed strain rate. Finally, at high shear rates, a new Newtonian branch should emerge corresponding to the induced nematic phase [10]. Concentrated systems of wormlike micelles [16,17,18,19,20,21,22,38,39] near a nematic transition are known to yield a non-monotonic flow curve of this form [10,16,17,18,19,20]; while more dilute systems exhibit a non-monotonic flow curve interpreted as an effect of flow on the reptation-reaction dynamics [40]. In this description, the stress plateau displayed upon applying an increasing shear rate is supposed to depend on the nature of the interface between the coexisting phases [10,12,13] but not on the nature of the substrate.
, to maintain the average imposed strain rate. Finally, at high shear rates, a new Newtonian branch should emerge corresponding to the induced nematic phase [10]. Concentrated systems of wormlike micelles [16,17,18,19,20,21,22,38,39] near a nematic transition are known to yield a non-monotonic flow curve of this form [10,16,17,18,19,20]; while more dilute systems exhibit a non-monotonic flow curve interpreted as an effect of flow on the reptation-reaction dynamics [40]. In this description, the stress plateau displayed upon applying an increasing shear rate is supposed to depend on the nature of the interface between the coexisting phases [10,12,13] but not on the nature of the substrate.
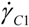 and
and 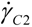 , to maintain the average imposed strain rate. Finally, at high shear rates, a new Newtonian branch should emerge corresponding to the induced nematic phase [10]. Concentrated systems of wormlike micelles [16,17,18,19,20,21,22,38,39] near a nematic transition are known to yield a non-monotonic flow curve of this form [10,16,17,18,19,20]; while more dilute systems exhibit a non-monotonic flow curve interpreted as an effect of flow on the reptation-reaction dynamics [40]. In this description, the stress plateau displayed upon applying an increasing shear rate is supposed to depend on the nature of the interface between the coexisting phases [10,12,13] but not on the nature of the substrate.
, to maintain the average imposed strain rate. Finally, at high shear rates, a new Newtonian branch should emerge corresponding to the induced nematic phase [10]. Concentrated systems of wormlike micelles [16,17,18,19,20,21,22,38,39] near a nematic transition are known to yield a non-monotonic flow curve of this form [10,16,17,18,19,20]; while more dilute systems exhibit a non-monotonic flow curve interpreted as an effect of flow on the reptation-reaction dynamics [40]. In this description, the stress plateau displayed upon applying an increasing shear rate is supposed to depend on the nature of the interface between the coexisting phases [10,12,13] but not on the nature of the substrate. 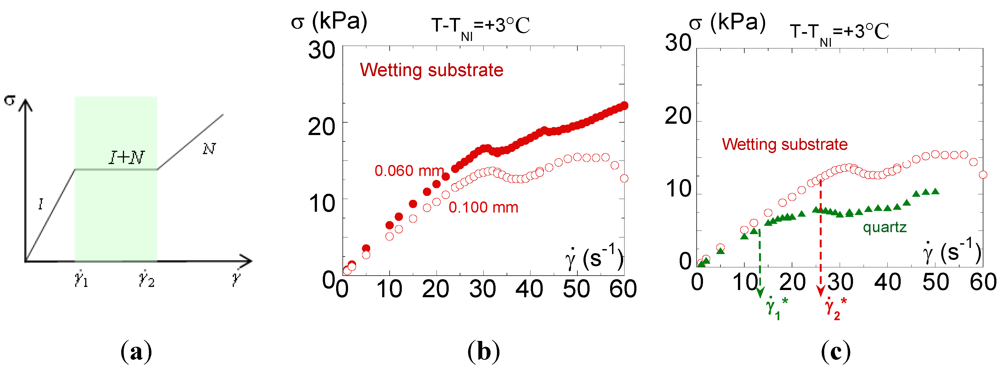
Figure 4.
(a) Constitutive relationship between stress σ and shear rate (flow curve). At low shear rates, the paranematic phase exhibits a Newtonian behavior. Above a critical shear rate, the stress plateau indicates the onset of the shear-induced phase transition and the coexistence of the isotropic and nematic phases. At high shear rates, another Newtonian branch emerges corresponding to the shear-induced nematic viscosity; (b) Steady-state measurements (flow curve): Evolution of the shear stress σ as a function of the shear rate at T - TNI = +3°C (plate-plate geometry: D = 10 mm, e = 0.100 mm with wetting surfaces at two different gap thicknesses: e = 0.100 mm (  ) e=0.060 mm (
) e=0.060 mm (  ); (c) Steady-state measurements (flow curve): Evolution of the shear stress σversus shear rate measured at the same thickness (e = 0.100 mm) and the same temperature (at T – TNI = +3°C) on a quartz surface (
); (c) Steady-state measurements (flow curve): Evolution of the shear stress σversus shear rate measured at the same thickness (e = 0.100 mm) and the same temperature (at T – TNI = +3°C) on a quartz surface (  : weak wetting) and a wetting surface (
: weak wetting) and a wetting surface (  : alumina) respectively (plate-plate geometry).
: alumina) respectively (plate-plate geometry).
 ) e=0.060 mm (
) e=0.060 mm (  ); (c) Steady-state measurements (flow curve): Evolution of the shear stress σversus shear rate measured at the same thickness (e = 0.100 mm) and the same temperature (at T – TNI = +3°C) on a quartz surface (
); (c) Steady-state measurements (flow curve): Evolution of the shear stress σversus shear rate measured at the same thickness (e = 0.100 mm) and the same temperature (at T – TNI = +3°C) on a quartz surface (  : weak wetting) and a wetting surface (
: weak wetting) and a wetting surface (  : alumina) respectively (plate-plate geometry).
: alumina) respectively (plate-plate geometry).
Figure 4(b,c) displays the shear stress versus steady-state shear rate curve of PANO2 at +3 °C above the NI transition temperature measured at two different gap thicknesses (using the same alumina substrate) or using two different substrates (the total wetting alumina and a partial wetting substrate quartz) respectively. In the isotropic phase, in absence of shear-induced phase, low degree of polymerization SCLCPs are expected to behave as Newtonian fluids, i.e., the viscosity (defined by the ratio: η = σ/ 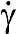 ) is constant. Both Figure 4(b) and Figure 4(c) display a non-Newtonian behavior indicating a coupling with the flow, i.e., the isotropic phase contains relaxation times of the order of the inverse of the shear rate (
) is constant. Both Figure 4(b) and Figure 4(c) display a non-Newtonian behavior indicating a coupling with the flow, i.e., the isotropic phase contains relaxation times of the order of the inverse of the shear rate ( 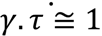 ). At low shear rates, the shear stress is nearly linear with the shear rate defining a quasi-Newtonian regime. At about 20–30 s−1, a second regime is identifiable by a slight overshoot followed by a lowering of the stress slope and even a stress plateau at 0.100 mm gap. The stress overshoot at about 20–30 s−1 seems to be coherent with the onset of the shear-induced birefringence (Figure 3(a)). The second regime seems to be coherent with the appearance of the shear-induced phase. A thickness dependence of the flow curve is clearly observable over 30 s−1, whereas the influence of the nature of the substrate (Figure 4(c)) is noticeable from the lowest shear rate (10 s−1). In the case of the quartz substrate (which provides a weak wetting), the shear stress is lower and the non-linear behavior appears earlier when a wetting substrate is used. The affinity of the liquid to the substrate is a necessary condition to transmit the shear motion (see [33] for a relationship between wetting and boundary conditions).
). At low shear rates, the shear stress is nearly linear with the shear rate defining a quasi-Newtonian regime. At about 20–30 s−1, a second regime is identifiable by a slight overshoot followed by a lowering of the stress slope and even a stress plateau at 0.100 mm gap. The stress overshoot at about 20–30 s−1 seems to be coherent with the onset of the shear-induced birefringence (Figure 3(a)). The second regime seems to be coherent with the appearance of the shear-induced phase. A thickness dependence of the flow curve is clearly observable over 30 s−1, whereas the influence of the nature of the substrate (Figure 4(c)) is noticeable from the lowest shear rate (10 s−1). In the case of the quartz substrate (which provides a weak wetting), the shear stress is lower and the non-linear behavior appears earlier when a wetting substrate is used. The affinity of the liquid to the substrate is a necessary condition to transmit the shear motion (see [33] for a relationship between wetting and boundary conditions).
 ) is constant. Both Figure 4(b) and Figure 4(c) display a non-Newtonian behavior indicating a coupling with the flow, i.e., the isotropic phase contains relaxation times of the order of the inverse of the shear rate (
) is constant. Both Figure 4(b) and Figure 4(c) display a non-Newtonian behavior indicating a coupling with the flow, i.e., the isotropic phase contains relaxation times of the order of the inverse of the shear rate ( 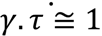 ). At low shear rates, the shear stress is nearly linear with the shear rate defining a quasi-Newtonian regime. At about 20–30 s−1, a second regime is identifiable by a slight overshoot followed by a lowering of the stress slope and even a stress plateau at 0.100 mm gap. The stress overshoot at about 20–30 s−1 seems to be coherent with the onset of the shear-induced birefringence (Figure 3(a)). The second regime seems to be coherent with the appearance of the shear-induced phase. A thickness dependence of the flow curve is clearly observable over 30 s−1, whereas the influence of the nature of the substrate (Figure 4(c)) is noticeable from the lowest shear rate (10 s−1). In the case of the quartz substrate (which provides a weak wetting), the shear stress is lower and the non-linear behavior appears earlier when a wetting substrate is used. The affinity of the liquid to the substrate is a necessary condition to transmit the shear motion (see [33] for a relationship between wetting and boundary conditions).
). At low shear rates, the shear stress is nearly linear with the shear rate defining a quasi-Newtonian regime. At about 20–30 s−1, a second regime is identifiable by a slight overshoot followed by a lowering of the stress slope and even a stress plateau at 0.100 mm gap. The stress overshoot at about 20–30 s−1 seems to be coherent with the onset of the shear-induced birefringence (Figure 3(a)). The second regime seems to be coherent with the appearance of the shear-induced phase. A thickness dependence of the flow curve is clearly observable over 30 s−1, whereas the influence of the nature of the substrate (Figure 4(c)) is noticeable from the lowest shear rate (10 s−1). In the case of the quartz substrate (which provides a weak wetting), the shear stress is lower and the non-linear behavior appears earlier when a wetting substrate is used. The affinity of the liquid to the substrate is a necessary condition to transmit the shear motion (see [33] for a relationship between wetting and boundary conditions). This dependence on the nature of the substrate indicates a slip mechanism which is delayed when the interaction to the substrate is improved by using wetting surfaces. The dependence on the thickness (Figure 4(b)) is also in agreement with a slip mechanism. In this case, the deviation from Newtonian behavior (in particular the “stress-plateau”) cannot fulfill a constitutive equation but results from a mechanical instability [41]. An estimation of slippage rate can be undertaken via the determination of a sliding velocity vs assuming that the flow can be modeled by a velocity gradient and that the slippage is located at both walls. This is a simplified model, but a detailed gradient and the location of the sliding zones are beyond the present scope.
In case of wall slip boundary conditions, the shear rate felt by the liquid is diminished from the applied one by a quantity: 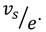 The effective shear rate is:
The effective shear rate is: 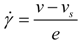 .
.
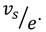 The effective shear rate is:
The effective shear rate is: 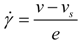 .
.
Figure 5.
(a) Illustration of a slip at the walls. νs is the sliding velocity; (b) Evolution of the sliding velocity νs (deduced from Figure 4(b)) versus shear stress for PANO2 at +3°C above the IN transition temperature.
The apparent shear rate is: 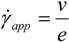 , then
, then 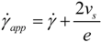 . In this scheme, the sliding process is outlined by a no-zero velocity νs with respect to the walls (Figure 5 (a)). The sliding velocity, νs can be extracted from the values at the same shear stress of the shear rates measured at two different thicknesses following the relationship:
. In this scheme, the sliding process is outlined by a no-zero velocity νs with respect to the walls (Figure 5 (a)). The sliding velocity, νs can be extracted from the values at the same shear stress of the shear rates measured at two different thicknesses following the relationship:
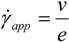 , then
, then 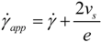 . In this scheme, the sliding process is outlined by a no-zero velocity νs with respect to the walls (Figure 5 (a)). The sliding velocity, νs can be extracted from the values at the same shear stress of the shear rates measured at two different thicknesses following the relationship:
. In this scheme, the sliding process is outlined by a no-zero velocity νs with respect to the walls (Figure 5 (a)). The sliding velocity, νs can be extracted from the values at the same shear stress of the shear rates measured at two different thicknesses following the relationship: 
Figure 5(b) displays the sliding velocity νs versus shear stress. It shows that from the lowest shear rates, νs is not zero. The extrapolation of νs to zero gives the stress threshold at which the sliding mechanism is supposed to occur: σ ≈ 2 kPa. The slip manifests itself very early in an apparent Newtonian regime ( 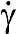 < 5 s−1; see Figure 4(b,c)). The three distinct zones in Figure 5(b) can be interpreted as different sliding regimes and thus an interpretation of the flow curve (σversus
< 5 s−1; see Figure 4(b,c)). The three distinct zones in Figure 5(b) can be interpreted as different sliding regimes and thus an interpretation of the flow curve (σversus 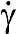 ) (Figure 4(b,c)) in terms of instabilities.
) (Figure 4(b,c)) in terms of instabilities.
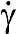 < 5 s−1; see Figure 4(b,c)). The three distinct zones in Figure 5(b) can be interpreted as different sliding regimes and thus an interpretation of the flow curve (σversus
< 5 s−1; see Figure 4(b,c)). The three distinct zones in Figure 5(b) can be interpreted as different sliding regimes and thus an interpretation of the flow curve (σversus 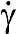 ) (Figure 4(b,c)) in terms of instabilities.
) (Figure 4(b,c)) in terms of instabilities.The evolution of the sliding velocity as a function of strain is very similar to what was predicted by F. Brochard and P.-G. de Gennes, in 1992 [42] who explored the flow of a polymer melt near a solid surface on which chains of identical chemical nature were grafted. The low stress zone was interpreted by a chain extension. Under the effect of friction, the chain deformation causes a restoring elastic force. There is a limit of deformation of the chain, beyond a critical stress for which the chain tangles and disentangles. When the sliding velocity increases, this regime cannot survive indefinitely, the chain stretches and loses its entanglements.
In the present case, the isotropic phase behaves similarly as entangled polymers but without an entanglement/disentanglement mechanism, since the PANO2 chain is too short to be entangled (see Table 1). In addition, the slippage phenomena occur at low shear rates (typically 10 s−1) as if the material was strongly entangled. It indicates that the intermolecular interactions play the role of entanglements. This cohesive or elastic property is inherent in the interactions in the isotropic state of SCLCPs. Therefore, the isotropic phase is a long-range correlated cohesive material.
3.3. Identification of a Finite Low Frequency Solid-Like Response
We quantitatively access the force of this cohesion by measuring a finite low frequency shear modulus (elastic modulus) in the isotropic phase of PANO2. This measurement is extended to an ordinary polymer melt (PBuA) and finally to a small molecule (alkyl chains) in the liquid state.
The linear dynamic relaxation experiment consists of applying a weak shear stress/strain to the fluid. The solicitation has to be sufficiently low to not modify the material under stress (causality-linearity principle). The liquid submitted to a small (linear) shear solicitation is scanned at a constant shear strain γ0, as a function of the frequency (ω), typically from 10−1 rad/s up to 102 rad/s. The liquid-like character is identifiable by a vanishing response on a long timescale, i.e., at low frequency (flow regime) whereas a solid-like behavior exhibits a no-vanishing response on a long timescale (solid-like response).
This method provides a dynamic profile in terms of elastic (or shear) modulus (G′) and viscous (or loss) modulus (G″). Experimental and theoretical literature illustrate the effect of the liquid crystal anchoring and its orientation on the dynamic response [43,44,45,46]. In the present study, the reinforcement of the boundary conditions is achieved by improving the wetting of the liquid to the substrate (alumina substrate) and by probing sub-millimetre gaps. By reinforcing the contacts, the total wetting guaranties a better dynamic transfer and small gaps reduce the strain-induced displacement [28,29].
We now examine the dynamic response of a thin but macroscopic (several tens of microns) thickness of the isotropic phase of PANO2. Figure 6(a) displays the frequency dependence of the elastic and of the viscous moduli of PANO2 at 3 °C above the NI transition temperature (70 °C above the glass transition temperature (Tg = 33 °C)). A non-measurable shear modulus (G′) and a ω-scaling of G″ are expected if PANO2 exhibits a liquid behavior in this frequency range. The experiment shows, by way of contrast, a non-negligible shear elastic response (G′(PANO2) 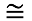 10,000 Pa) which is about one order of magnitude higher than the viscous response (G′ > G″). The viscous component being negligible, the primary response of the isotropic phase is elastic, i.e., solid-like. Moreover, the quasi-constant shear elastic and viscous moduli versus frequency attest to a solid-like response. Under weak solicitation, the liquid does not flow but resists with significant elasticity. These elastic interactions cannot be related to reminiscent liquid crystal properties (no birefringence is detectable in the isotropic phase under weak strain solicitation). The isotropic phase is thus a fragile but long-range, elastically-correlated “self-assembly”. The action of the flow is a shear-melting. Above a threshold (defined by the elastic modulus), the “self-assembly” collapses and flows. Rheological and birefringence curves displayed in Figure 3 and Figure 4 reflect therefore what is happening after the collapse. At this state, the system is more or less shear-molten, depending on the shear rate. The timescales in the non-linear regime can hardly be related to any characteristic time.
10,000 Pa) which is about one order of magnitude higher than the viscous response (G′ > G″). The viscous component being negligible, the primary response of the isotropic phase is elastic, i.e., solid-like. Moreover, the quasi-constant shear elastic and viscous moduli versus frequency attest to a solid-like response. Under weak solicitation, the liquid does not flow but resists with significant elasticity. These elastic interactions cannot be related to reminiscent liquid crystal properties (no birefringence is detectable in the isotropic phase under weak strain solicitation). The isotropic phase is thus a fragile but long-range, elastically-correlated “self-assembly”. The action of the flow is a shear-melting. Above a threshold (defined by the elastic modulus), the “self-assembly” collapses and flows. Rheological and birefringence curves displayed in Figure 3 and Figure 4 reflect therefore what is happening after the collapse. At this state, the system is more or less shear-molten, depending on the shear rate. The timescales in the non-linear regime can hardly be related to any characteristic time.
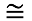 10,000 Pa) which is about one order of magnitude higher than the viscous response (G′ > G″). The viscous component being negligible, the primary response of the isotropic phase is elastic, i.e., solid-like. Moreover, the quasi-constant shear elastic and viscous moduli versus frequency attest to a solid-like response. Under weak solicitation, the liquid does not flow but resists with significant elasticity. These elastic interactions cannot be related to reminiscent liquid crystal properties (no birefringence is detectable in the isotropic phase under weak strain solicitation). The isotropic phase is thus a fragile but long-range, elastically-correlated “self-assembly”. The action of the flow is a shear-melting. Above a threshold (defined by the elastic modulus), the “self-assembly” collapses and flows. Rheological and birefringence curves displayed in Figure 3 and Figure 4 reflect therefore what is happening after the collapse. At this state, the system is more or less shear-molten, depending on the shear rate. The timescales in the non-linear regime can hardly be related to any characteristic time.
10,000 Pa) which is about one order of magnitude higher than the viscous response (G′ > G″). The viscous component being negligible, the primary response of the isotropic phase is elastic, i.e., solid-like. Moreover, the quasi-constant shear elastic and viscous moduli versus frequency attest to a solid-like response. Under weak solicitation, the liquid does not flow but resists with significant elasticity. These elastic interactions cannot be related to reminiscent liquid crystal properties (no birefringence is detectable in the isotropic phase under weak strain solicitation). The isotropic phase is thus a fragile but long-range, elastically-correlated “self-assembly”. The action of the flow is a shear-melting. Above a threshold (defined by the elastic modulus), the “self-assembly” collapses and flows. Rheological and birefringence curves displayed in Figure 3 and Figure 4 reflect therefore what is happening after the collapse. At this state, the system is more or less shear-molten, depending on the shear rate. The timescales in the non-linear regime can hardly be related to any characteristic time. 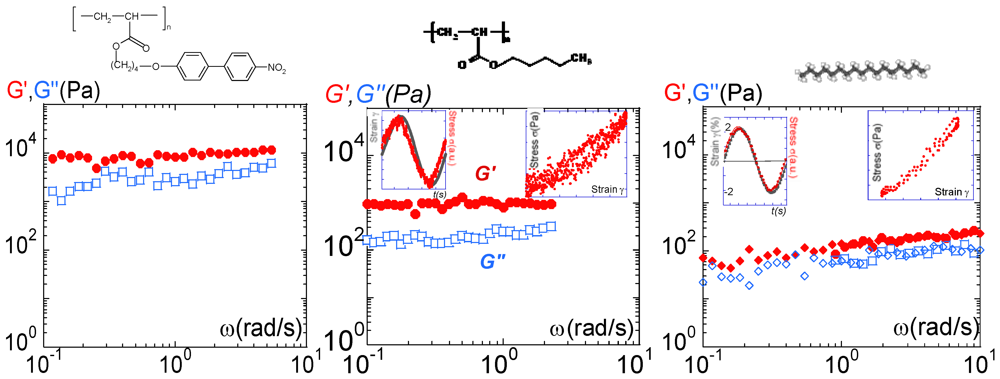
Figure 6.
(a) Frequency dependence of the elastic (G′:  ) and the viscous (G″:
) and the viscous (G″:  ) moduli of PANO2 at 3°C above the NI transition, 0.050 mm gap thickness and 0.3% strain amplitude; (b) Frequency dependence of the elastic (G′:
) moduli of PANO2 at 3°C above the NI transition, 0.050 mm gap thickness and 0.3% strain amplitude; (b) Frequency dependence of the elastic (G′:  ) and the viscous (G″:
) and the viscous (G″:  ) moduli of PBuA at room temperature (Tg = −63°C), 0.020 mm gap thickness and 0.5% strain amplitude (from reference [29]). Two insets have been added to illustrate the quasi-superposition of the strain input wave (
) moduli of PBuA at room temperature (Tg = −63°C), 0.020 mm gap thickness and 0.5% strain amplitude (from reference [29]). Two insets have been added to illustrate the quasi-superposition of the strain input wave (  ) and of the torque output wave (
) and of the torque output wave (  ), and the corresponding Lissajous cycle respectively; (c) Frequency dependence of the elastic (G′:
), and the corresponding Lissajous cycle respectively; (c) Frequency dependence of the elastic (G′:  : 0.5% strain,
: 0.5% strain,  : 1% strain) and the viscous (G″: □: 0.5% strain, ◊: 1% strain) moduli of the heptadecane at 3°C above the crystallization (Tf = 21°C) temperature and 0.058 mm gap thickness. Two insets illustrate the quasi-superposition of the strain input wave (
: 1% strain) and the viscous (G″: □: 0.5% strain, ◊: 1% strain) moduli of the heptadecane at 3°C above the crystallization (Tf = 21°C) temperature and 0.058 mm gap thickness. Two insets illustrate the quasi-superposition of the strain input wave (  ) and of the torque output wave (
) and of the torque output wave (  ) and to display the corresponding Lissajous cycle.
) and to display the corresponding Lissajous cycle.
 ) and the viscous (G″:
) and the viscous (G″:  ) moduli of PANO2 at 3°C above the NI transition, 0.050 mm gap thickness and 0.3% strain amplitude; (b) Frequency dependence of the elastic (G′:
) moduli of PANO2 at 3°C above the NI transition, 0.050 mm gap thickness and 0.3% strain amplitude; (b) Frequency dependence of the elastic (G′:  ) and the viscous (G″:
) and the viscous (G″:  ) moduli of PBuA at room temperature (Tg = −63°C), 0.020 mm gap thickness and 0.5% strain amplitude (from reference [29]). Two insets have been added to illustrate the quasi-superposition of the strain input wave (
) moduli of PBuA at room temperature (Tg = −63°C), 0.020 mm gap thickness and 0.5% strain amplitude (from reference [29]). Two insets have been added to illustrate the quasi-superposition of the strain input wave (  ) and of the torque output wave (
) and of the torque output wave (  ), and the corresponding Lissajous cycle respectively; (c) Frequency dependence of the elastic (G′:
), and the corresponding Lissajous cycle respectively; (c) Frequency dependence of the elastic (G′:  : 0.5% strain,
: 0.5% strain,  : 1% strain) and the viscous (G″: □: 0.5% strain, ◊: 1% strain) moduli of the heptadecane at 3°C above the crystallization (Tf = 21°C) temperature and 0.058 mm gap thickness. Two insets illustrate the quasi-superposition of the strain input wave (
: 1% strain) and the viscous (G″: □: 0.5% strain, ◊: 1% strain) moduli of the heptadecane at 3°C above the crystallization (Tf = 21°C) temperature and 0.058 mm gap thickness. Two insets illustrate the quasi-superposition of the strain input wave (  ) and of the torque output wave (
) and of the torque output wave (  ) and to display the corresponding Lissajous cycle.
) and to display the corresponding Lissajous cycle.
Figure 6(b) displays the dynamic behavior of a polybutylacrylate (PBuA) of molecular weight (Mw = 20,000 g∙mol−1). The study of a simple alkyl polyacrylate confirms that the elastic property is not specific to liquid crystal materials. This chain has the same architecture as PANO2. Only the terminal part of the liquid crystal moiety (the hard core) has been removed. This amorphous melt (PBuA) has been chosen with the same degree of polymerization as PANO2. At room temperature, i.e., at 90 °C above Tg, PBuA flows easily (the melt is below its entanglement regime 2. Me = 44,000 g∙mol−1 [47]). As already reported in [29], this unentangled melt displays a non-negligible elastic plateau with G′ and G″ constant and G′ larger than G″ within the frequency range (which is the conventional measurement range). The left inset in Figure 6(b) displays the two waves corresponding to the sinusoidal strain amplitude and the output torque respectively. The almost superimposed signals indicate that the melt response is quasi-instantaneous. This is confirmed by the right inset displaying the strain amplitude versus the torque (Lissajous curve). A perfectly solid-like response would be a narrow line oriented at 45° in the Lissajous representation. The experimental result is in agreement with a quasi-solid-like response (cycle tilted at 45°). The closure of the cycle guarantees the reliability of the measurement. The width of the cycle indicates a slight viscous contribution to the signal. The three representations (viscoelastic moduli, input and output waves, Lissajous curve) point to an elastic response, i.e., a solid-like behavior.
This elasticity cannot be related to some unknown property of liquid crystal moiety since the polymer is amorphous. Entanglements cannot be at the origin of the elasticity since the chain is unentangled. The second interesting point is that PBuA and PANO2 have the same polymerization degree; the influence of the liquid crystal moiety can be directly estimated from the strength of the elastic plateau. G′(PBuA) 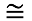 103 Pa whereas G′(PANO2)
103 Pa whereas G′(PANO2) 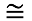 104 Pa. Clearly, the liquid crystal moieties have an important cohesive role interplaying as connectors. The reinforcement is about 10 times stronger when the polyacrylate chain is substituted by nitrobiphenyl groups. This observation confirms the assumption that the elasticity of the isotropic phase originates from intermolecular interactions. These intermolecular interactions are reinforced by polar and/or polar-induced interactions when the molecules possess liquid crystal moieties. The intermolecular interactions of PBuA are essentially governed by weak van der Waals interactions.
104 Pa. Clearly, the liquid crystal moieties have an important cohesive role interplaying as connectors. The reinforcement is about 10 times stronger when the polyacrylate chain is substituted by nitrobiphenyl groups. This observation confirms the assumption that the elasticity of the isotropic phase originates from intermolecular interactions. These intermolecular interactions are reinforced by polar and/or polar-induced interactions when the molecules possess liquid crystal moieties. The intermolecular interactions of PBuA are essentially governed by weak van der Waals interactions.
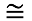 103 Pa whereas G′(PANO2)
103 Pa whereas G′(PANO2) 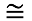 104 Pa. Clearly, the liquid crystal moieties have an important cohesive role interplaying as connectors. The reinforcement is about 10 times stronger when the polyacrylate chain is substituted by nitrobiphenyl groups. This observation confirms the assumption that the elasticity of the isotropic phase originates from intermolecular interactions. These intermolecular interactions are reinforced by polar and/or polar-induced interactions when the molecules possess liquid crystal moieties. The intermolecular interactions of PBuA are essentially governed by weak van der Waals interactions.
104 Pa. Clearly, the liquid crystal moieties have an important cohesive role interplaying as connectors. The reinforcement is about 10 times stronger when the polyacrylate chain is substituted by nitrobiphenyl groups. This observation confirms the assumption that the elasticity of the isotropic phase originates from intermolecular interactions. These intermolecular interactions are reinforced by polar and/or polar-induced interactions when the molecules possess liquid crystal moieties. The intermolecular interactions of PBuA are essentially governed by weak van der Waals interactions.Figure 6(c) displays the dynamic response of the liquid heptadecane. The heptadecane presents an abrupt first transition from crystalline state to liquid state at Tf = 21 °C. With 17 atoms of carbon, the heptadecane (above Tf) is an ordinary molecular liquid. This alkyl liquid presents the practical advantage of having a low vapor tension, and therefore a very weak evaporation. This is useful when the measurement requires long integration times. The spectrum displayed in Figure 6(c) has been carried out at 3 °C above the crystallization temperature. Any effect of the crystallization is excluded, since a short temperature gap away from Tf makes it integrally lose its crystalline properties (first order transition) in contrast to glass formers and possible glass transition effects. Figure 6(c) and the two insets indicate a (linear) solid-like response; the left inset in Figure 6(c) shows that the wave corresponding to the sinusoidal strain amplitude is quasi-superposed to the output torque, in agreement with the right inset displaying the Lissajous curve. The shear modulus G′ dominates the viscous component and both are weakly dependent on the frequency. This delicate elastic response obtained at low strain amplitude using total wetting surfaces shows for the first time that the elastic property can be also found on simple molecules. It excludes any glass transition effect. With a shear modulus of about G′ 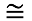 80–100 Pa, i.e., 10 times smaller than the one of PBuA and about 100 times weaker than PANO2, we demonstrate that the solid-like property is a generic character inherent to the liquid state.
80–100 Pa, i.e., 10 times smaller than the one of PBuA and about 100 times weaker than PANO2, we demonstrate that the solid-like property is a generic character inherent to the liquid state.
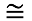 80–100 Pa, i.e., 10 times smaller than the one of PBuA and about 100 times weaker than PANO2, we demonstrate that the solid-like property is a generic character inherent to the liquid state.
80–100 Pa, i.e., 10 times smaller than the one of PBuA and about 100 times weaker than PANO2, we demonstrate that the solid-like property is a generic character inherent to the liquid state. 4. Conclusions
An unforeseen shear-induced, isotropic-to-nematic phase transition was identified 10 years ago in Side-Chain Liquid Crystal Polymers. Different polymers of various molecular weights and of various liquid crystal moieties have proven the generic character of this non-equilibrium phase. The confrontation of the timescales involved in the shear-induced phase has revealed that the scheme proposed by the ad hoc theoretical models based on a flow coupling to the lifetime of the orientational pre-transitional fluctuations is not valid. The shear-induced nematic phase occurs at extremely low shear rates with time scales from one to three decades slower that any known timescale (pre-transitional life time or polymer relaxation time...). The understanding of the shear-induced phase of SCLCPs is of utmost importance since it challenges the current description of the isotropic phase by evidencing very long timescales.
In this paper, we first focus on the isotropic phase of a low molecular weight nitro-biphenyl side-chain polyacrylate (PANO2). The shear-induced birefringence is observable up to at least 10 °C away from TNI (Figure 3(a)). This birefringence can hardly be coupled with pre-transitional fluctuations since they are supposed to persist only close to the (weak) first order N-I transition. The flow curve of PANO2 is also examined in the isotropic phase. The shear stress versus shear rate curve exhibits non-linear behavior that coincides, at the same gap thickness, with the emergence of the shear-induced birefringence. However, by varying the gap thickness or the nature of the substrate (Figure 4(b,c)), the flow curve is not invariant, and therefore cannot be interpreted as a constitutive phase transition related to the coexistence of two liquids [10,16,17,18,19,20], but as a sliding transition. The slip phenomenon is identified at the lowest shear rates in a regime considered as Newtonian. The SCLCP PANO2 inherently contains in its isotropic phase a macroscopic cohesion inclined to slip macroscopic mechanisms. This cohesion is not related to a polymer property (no entanglements). The strength of the cohesive property is quantitatively determined by dynamic relaxation. A finite elastic modulus is measured in the isotropic phase revealing the solid-like response to a weak solicitation (G′ and G″ are relatively not frequency-dependent within this frequency range with G′ > G″). This observation is in agreement with previous results reported on other SCLCPs [14]. The solid-like response shows that intermolecular interactions are macroscopically correlated. The side-chain groups seem to act as connectors creating a three-dimensional physical network. To evaluate the contribution of the liquid crystalline moieties to the elasticity, the measurement is extended to an ordinary melt (PBuA) of identical polymerization degree as PANO2 and to a molecular liquid made of alkyl chains (heptadecane).
PBuA also exhibits a low frequency elastic plateau but its elastic modulus is about 10 times weaker than PANO2. The “connector” effect of the liquid crystal groups provides, via polar and polar-induced interactions, additional cohesion, compared to polymers substituted with short alkyl (butyl) chains.
The study of the heptadecane reveals for the first time that a molecular liquid also possesses finite shear elasticity (Figure 6(c)). Its shear modulus is about 10 times lower than the one measured for the polymer PBuA, consequently about 100 times lower than the SCLCP. Only van der Waals interactions contribute to the intermolecular cohesion of the liquid heptadecane.
These important results confirm that the solid-like character, first identified in the isotropic phase of SCLCPs, originate neither from reminiscent liquid crystal properties, nor from the polymer properties, or nor from glass transition pre-transitional effects. Clearly the low frequency elasticity is a condensed matter property. They meet a series of various works reporting on a non-vanishing elasticity. In 1983, B.V. Derjaguin and Co. [48,49,50] reported on an elastic response in various liquids at the micron scale. The measurement was performed at one frequency (73 Hz) using the vibration of a piezoelectric system (resonator). In liquid-crystal polymers, the earlier works are due to Martinoty and co-authors, in 1994 reporting on “abnormal” gel-like behavior in the isotropic phase [51,52] attributed to clusters assisted by liquid crystal properties. In 2003, a low frequency gel behavior was identified by the same group up to 50 µm thickness on a low molecular weight polystyrene melt attributed to pre-transitional glass transition clusters [53]. In 2004, McKinley et al. reported on a 3–4 µm thickness elasticity on a polystyrene solution but attributed it to trapped dust particles [54]. In 2005, L. Noirez and co-authors reported on elastic behaviors in the isotropic phase of SCLCPs using a conventional rheometer and at the millimeter scale [14]. Then, solid-like behaviors (G′ and G″ constant with G′ >G ″) were identified using the total wetting protocol [28] in various glass formers (glycerol, o-terphenyl) and ordinary polymers [29,30,31,32]. In 2007, S-Q Wang [55] reproduced the results of [15] using the same protocol. Other techniques, such as X-ray photon correlation spectroscopy [56], evidence relaxation modes in glass formers much slower than those conventionally described. These converging results indicate that an elastic state has so far been missed in the description of the liquid state. Liquids are actually not so “liquid” but contain a delicate and breakable solid-like component at the macroscopic scale that is the signature of the strength and of the long-range character of intermolecular interactions. These interactions are clearly reinforced in the presence of liquid crystalline moieties via the contribution of dipolar or polar-induced interactions. In molecular liquids, noteworthy approaches consider a solid-like continuum [57,58,59] and even predict a low frequency shear elasticity the strength of which depends on the network size [60]. But, to our knowledge, very few theoretical developments concerning polymers set the role of the intermolecular forces as predominant [61,62].
This identification of the shear-induced isotropic-nematic transitions in very basic SCLCPs has brought the unambiguously proof of extremely long timescale away from phase transition temperature. This spectacular transition was the starting point of the search for a finite low frequency solid-like response (absence of flow behavior), first in SCLCPs, then in polymer melts, and finally in molecular liquids. Side-Chain Liquid Crystal Polymers are exceptional tools to probe the condensed properties of liquids.
Acknowledgments
The authors (HM, LN, PB) are very grateful to the late P. G. de Gennes for his interest in our developments. We would like also to thank P. D. Olmsted, G. Marrucci, and P. Martinoty for fruitful debates. The SCLCP PANO2 was synthesised by controlled radical polymerization in the Laboratory of J. H. Wendorff in collaboration with C. Stillings and the group of A. Studer “Organisch Chemisches-Institut, Westfälische Wilhelms-Universität Münster” in Germany.
References and Notes
- Mather, P.T.; Romo-Uribe, A.; Han, C.D.; Chang, S.S. Rheo-optical evidence of a flow-induced isotropic-nematic transition in a thermotropic liquid-crystalline polymer. Macromolecules 1997, 30, 7977–7989. [Google Scholar]
- Pujolle-Robic, C.; Noirez, L. Observation of shear-induced nematic-isotropic transition in side-chain liquid crystal polymers. Nature (London) 2001, 409, 167–171. [Google Scholar] [CrossRef]
- Noirez, L.; Keller, P.; Cotton, J.P. On the structure and the chain conformation of side-chain liquid-crystal polymers. Liq. Cryst. 1995, 18, 129–148. [Google Scholar]
- Pépy, G.; Noirez, L.; Keller, P.; Lambert, M.; Moussa, F.; Cotton, J.P.; Strazielle, C.; Lapp, A.; Hardouin, F.; Mauzac, M.; et al. Observation of the conformation and structure of some liquid-crystal polymers by small-angle neutron scattering. Makromol. Chem.-Macromol. Chem. Phys. 1990, 191, 1383–1392. [Google Scholar] [CrossRef]
- Noirez, L.; Pépy, G.; Benguigui, L. Smectic order and backbone anisotropy of a side chain liquid-crystalline polymer by small-angle neutron scattering. J. Phys. II 1991, 1, 821–830. [Google Scholar]
- Noirez, L.; Lapp, A. Shear flow induced transition from liquid-crystalline to polymer behavior in side-chain liquid crystal polymers. Phys. Rev. Lett. 1997, 78, 70–73. [Google Scholar] [CrossRef]
- Noirez, L. Shear induced smectic-A-smectic-C transition in side-chain liquid-crystalline polymers. Phys. Rev. Lett. 2000, 84, 2164–2167. [Google Scholar]
- Hess, S. Pre- and post-transitional behavior of the flow alignment and flow- induced phase transition in liquid crystals. Naturforsch. Z. 1976, 31a, 1507–1513. [Google Scholar]
- Hess, S.; Ilg, P. On the theory of the shear-induced isotropic-to-nematic phase transition of side chain liquid-crystalline polymers. Rheol. Acta 2005, 44, 465–477. [Google Scholar]
- Olmsted, P.D.; Goldbart, P. Theory of the nonequilibrium phase transition for nematic liquid crystals under shear flow. Phys. Rev. A 1990, 41, 4578–4581. [Google Scholar]
- Olmsted, P.D.; Goldbart, P. Isotropic-nematic transition in shear flow: State selection, coexistence, phase transitions, and critical behavior Phys. Rev. A 1992, 46, 4966–4993. [Google Scholar] [CrossRef]
- Olmsted, P.D.; David Lu, C.-Y. Coexistence and phase separation in sheared complex fluids Phys. Rev. E 1999, 60, 4397–4415. [Google Scholar]
- Cates, M.E.; Fielding, S.M. Rheology of giant micelles. Adv. Phys. 2006, 55, 799–879. [Google Scholar]
- Noirez, L. Origin of shear-induced phase transitions in melts of liquid-crystal polymers. Phys. Rev. E 2005, 72, 51701–51704. [Google Scholar]
- Mendil, H.; Baroni, P.; Grillo, I.; Noirez, L. The frozen state in the liquid phase of side-chain liquid-crystal polymers. Phys. Rev. Lett. 2006, 96, 077801–077804. [Google Scholar]
- Schmitt, V.; Lequeux, F.; Pousse, A.; Roux, D. Flow behavior and shear induced transition near an isotropic/nematic transition in equilibrium polymers. Langmuir 1994, 10, 955–961. [Google Scholar]
- Berret, J.F.; Roux, D.C.; Porte, G.; Linder, P. Shear-induced isotropic-to-nematic phase transition in equilibrium polymers. Europhys. Lett. 1994, 25, 521–526. [Google Scholar]
- Decruppe, J.P.; Cressely, R.; Makhloufi, R.; Cappelaere, E. Flow birefringence experiments showing a shear-banding structure in a CTAB solution. Colloid Polym. Sci. 1995, 273, 346–351. [Google Scholar]
- Cappelaere, E.; Cressely, R.; Decruppe, J.P. Linear and non-linear rheological behavior of salt-free aqueous CTAB solutions. Colloid Surf. A 1995, 104, 353–374. [Google Scholar]
- Cappelaere, E.; Berret, J.F.; Decruppe, J.P.; Cressely, R.; Lindner, P. Rheology, birefringence, and small-angle neutron scattering in a charged micellar system: Evidence of a shear-induced phase transition. Phys. Rev. E 1997, 56, 1869–1878. [Google Scholar] [CrossRef]
- Salmon, J.B.; Colin, A.; Manneville, S. Velocity profiles in shear-banding wormlike micelles. Phys. Rev. Lett. 2003, 90, 2283031–2283034. [Google Scholar]
- Lettinga, M.P.; Manneville, S. Competition between shear banding and wall slip in worm-like micelles. Phys. Rev. Lett. 2009, 103, 2483021–2283024. [Google Scholar]
- Fisher, E.; Callaghan, P.T. Is a birefringence band a shear band? Europhys. Lett. 2000, 50, 803809. [Google Scholar]
- Fisher, E.; Callaghan, P.T. Shear banding and the isotropic-to-nematic transition in wormlike micelles. Phys. Rev. E 2001, 64, 11501–11515. [Google Scholar]
- Feindel, K.; Callaghan, P.T. Anomalous shear banding: Multidimensional dynamics under fluctuating slip conditions. Rheol. Acta 2010, 49, 1003–1013. [Google Scholar]
- Finkelmann, H. Synthesis, Structure and Properties of Liquid Crystalline Side Chain Polymers. In Handbook of Liquid Crystals: High Molecular Weight Liquid Crystals; Dietrich, D., John, W.G., George, W.G., Hans, W.S., Volkmar, V., Eds.; Academic Press: Salt Lake, UT, USA, 2008; Part II, Chapter 3. [Google Scholar]
- Decobert, G.; Soyer, F.; Dubois, J.C. Chiral liquid crystalline side chain polymers. Polym. Bull. 1985, 14, 179–185. [Google Scholar]
- Baroni, P.; Mendil, H.; Noirez, L. Méthode de détermination des propriétés dynamiques d'un matériau fluide ou solide déformable. France Patent 05 10988, 27 November 2005. [Google Scholar]
- Mendil, H.; Baroni, P.; Noirez, L. Solid-like rheological response of non-entangled polymers in the molten state. Eur. Phys. J. E 2006, 19, 77–86. [Google Scholar]
- Noirez, L.; Baroni, P.; Mendil-Jakani, H. The missing parameter in rheology: Hidden solid-like correlations in viscous liquids, polymer melts and glass formers. Polym. Int. 2009, 58, 962–968. [Google Scholar]
- Noirez, L.; Baroni, P. Revealing the solid-like nature of glycerol at ambient temperature. J. Mol. Struct. 2010, 972, 16–21. [Google Scholar]
- Noirez, L.; Mendil-Jakani, H.; Baroni, P. Identification of finite shear-elasticity in the liquid state of molecular and polymeric glass-formers. Philos. Mag. 2011, 91, 1977–1986. [Google Scholar]
- The following equation (Tolstoi theory 1952) links the wetting property (determined via the contact angle θ method) to the slippage ability (via the slippage length b defined as the distance from the surface corresponding to the origin of the velocity gradient as shown): b~ exp(σ2.γ(1-cos θ)/kT)-1, θ=0 in the case of total wetting (σ is related to the molecule size and γ to the surface tension).
- de Gennes, P.G.; Prost, J. The Physics of Liquid Crystals; Oxford University Press: New York, NY, USA, 1974. [Google Scholar]
- Reys, V.; Dormoy, Y.; Gallani, J.L.; Martinoty, P.; Le Barny, P.; Dubois, J.C. Short-range-order effects in the isotropic phase of a side-chain polymeric liquid crystal. Phys. Rev. Lett. 1988, 61, 2340–2343. [Google Scholar]
- Pujolle-Robic, C.; Olmsted, P.D.; Noirez, L. Transient and stationary flow behavior of side chain liquid-crystalline polymers: Evidence of a shear-induced isotropic-to-nematic phase transition. Europhys. Lett. 2002, 59, 364–369. [Google Scholar]
- Pujolle-Robic, C.; Noirez, L. Identification of nonmonotonic behaviors and stick-slip transition in liquid crystal polymers. Phys. Rev. E 2003, 68, 0617061–0617065. [Google Scholar]
- Berret, J.F.; Roux, D.C.; Porte, G. Isotropic-to-nematic transition in wormlike micelles under shear. J. Phys. II 1994, 4, 1261–1279. [Google Scholar]
- Berret, J.F.; Porte, G. Metastable versus unstable transients at the onset of a shear-induced phase transition. Phys. Rev. E 1990, 60, 4268–4271. [Google Scholar] [CrossRef]
- Spenley, N.A.; Cates, M.E.; McLeish, T.C.B. Nonlinear rheology of wormlike micelles. Phys. Rev. Lett. 1993, 71, 939–942. [Google Scholar]
- Larson, R.G. The Structure and Rheology of Complex Fluids; Oxford University Press: New York, NY, USA, 1999. [Google Scholar]
- Brochard, F.; de Gennes, P.G. Shear-dependent slippage at a polymer/solid interface. Langmuir 1992, 8, 3033–3037. [Google Scholar]
- Jérome, B. Surface effects and anchoring in liquid crystals. Rep. Prog. Phys. 1991, 54, 391–451. [Google Scholar]
- Jérôme, B.; Commandeur, J.; de Jeu, W.H. Backbone effects on the anchoring of side-chain polymer liquid crystals. Liq. Cryst. 1997, 22, 685–692. [Google Scholar]
- Choate, E.P.; Cui, Z.; Forest, M.G. Effects of strong anchoring on the dynamic moduli of heterogeneous nematic polymers. Rheol. Acta 2008, 47, 223–236. [Google Scholar]
- Choate, E.P.; Forest, M.G. A classical problem revisited: Rheology of nematic polymer monodomains in small amplitude oscillatory shear Rheol. Acta 2006, 46, 83–94. [Google Scholar]
- Lakrout, H.; Creton, C.; Ahn, D.; Shull, K.R. Influence of molecular features on the tackiness of acrylic polymer melts. Macromoleculars 2001, 34, 7448–7458. [Google Scholar]
- Badmaev, B.B.; Bazaron, U.B.; Derjaguin, B.V.; Budaev, O.R. Measurement of the shear elasticity of polymethylsiloxane liquids. Phys. B 1983, 122, 241–246. [Google Scholar]
- Derjaguin, B.V.; Bazaron, U.B.; Zandanova, K.T.; Budaev, O.R. The complex shear modulus of polymeric and small-molecule liquids. Polymer 1989, 30, 97–103. [Google Scholar]
- Badmaev, B.B.; Dembelova, T.; Damdinov, B.; Makarova, D.; Budaev, O. Influence of surface wettability on the accuracy of measurement of fluids effective shear modulus. Colloids Surf. A Physicochem. Eng. Asp. 2011, 383, 90–94. [Google Scholar]
- Gallani, J.L.; Hilliou, L.; Martinoty, P.; Keller, P. Abnormal viscoelastic behavior of side-chain liquid-crystal polymers. Phys. Rev. Lett 1994, 72, 2109–2112. [Google Scholar]
- Martinoty, P.; Hilliou, L.; Mauzac, M.G.; Benguigui, L.; Collin, D. Side-chain liquid crystal polymers: Gel-like behavior below their gelation points. Macromoleculars 1999, 32, 1746–1752. [Google Scholar]
- Collin, D.; Martinoty, P. Dynamic macroscopic heterogeneities in a flexible linear polymer melt. Phys. A 2002, 320, 235–248. [Google Scholar]
- Clasen, C.; McKinley, G.H. Gap-dependent microrheoetry of complex liquids. J. Non-Newton. Fluid Mech. 2004, 124, 1–10. [Google Scholar] [CrossRef]
- Wang, S.-Q.; Ravindranath, S.; Wang, Y.; Boukany, P. New theoretical considerations in polymer rheology: Elastic breakdown of chain entanglement network. J. Chem. Phys. 2007, 127, 064903:1–064903:14. [Google Scholar]
- Chushkin, Y.; Caronna, C.; Madsen, A. Low-frequency elastic behavior of a supercooled liquid. EPL 2008. [Google Scholar]
- Granato, A.V. The shear modulus of liquids. J. Phys. IV 1996, 6, C8-1–C8-9. [Google Scholar]
- Granato, A.V. Mechanical properties of simple condensed matter. Mater. Sci. Eng. A 2009, 521, 6–11. [Google Scholar]
- Dyre, J.C. Solidity of viscous liquids. III. α relaxation. Phys. Rev. E 2005, 72, 011501:1–011501:7. [Google Scholar]
- Volino, F. Théorie visco-élastique non-extensive VI. Application à un liquide formant une phase vitreuse : L’orthoterphényl (OTP). Ann. Phys. 1997, 22, 181–231. [Google Scholar] [CrossRef]
- Ibar, J.P. Do we need a new theory in polymer physics? J.M.S.-Rev. Macromol. Chem. Phys. 1997, C37, 389–457. [Google Scholar]
- Guenza, M. Intermolecular effects in the center-of-mass dynamics of unentangled polymer fluids. Macromolecules 2002, 35, 2714–2722. [Google Scholar]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).