Modeling the Kinetics of Polyethylene Terephthalate and Polyesters with Terminal Hydroxyl Groups Transesterification Reactions
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Synthesis of Oligoesters with Terminal Hydroxyl Groups
2.3. PET and Oligoesters with Terminal Hydroxyl Groups Interchain Exchange
2.4. Characterization of PET, Oligoesters and Transesterification Products
2.4.1. Fourier Transform Infrared (FTIR) Spectroscopy
2.4.2. Viscosimetry
2.4.3. Differential Scanning Calorimetry (DSC)
2.4.4. Gel Permeation Chromatography (GPC)
2.4.5. Oligoester Synthesis Conversion
2.4.6. Nuclear Magnetic Resonance (NMR) Spectroscopy
3. Results
3.1. PET Flakes Characterization
3.2. Oligoesters Characterization
3.3. Kinetic Model Development
- Polyesters within the same source (PET or other polyester) are assumed to be in equilibrium.
- Antimony trioxide was used as a catalyst, with the concentration of the catalyst [ccat] in the reaction mixture being constant.
- All reactions of the same type proceeded at the same rate, regardless of the chain lengths. It is assumed that polymer chain effects, such as steric or neighbor effects, are included in the selected reaction rate constants. The pre-exponential factors and activation energies used were determined [21,28,31] to describe the kinetics of transesterification in polyethylene terephthalate in the presence of the antimony trioxide catalyst. The reaction types and their corresponding rate constants are given in Table 3.
- 4.
- The plug flow reactor model is used, including all assumptions.
- 5.
- It is assumed that all terminal groups of polyethylene terephthalate, other polyesters and their reaction products are hydroxyl. Side reactions are not taken into account.
- Reactions 1–11, occurring between two bound glycols.
- Reactions 12–35, occurring between the terminal units of glycols with hydroxyl groups and bound glycols.
- Reactions 36–49, occurring between the bound units of glycols and free glycols.
- Reactions 50–63, occurring between two terminal units of glycols.
- Reactions 64–67, occurring between the terminal units of glycols and free glycols.
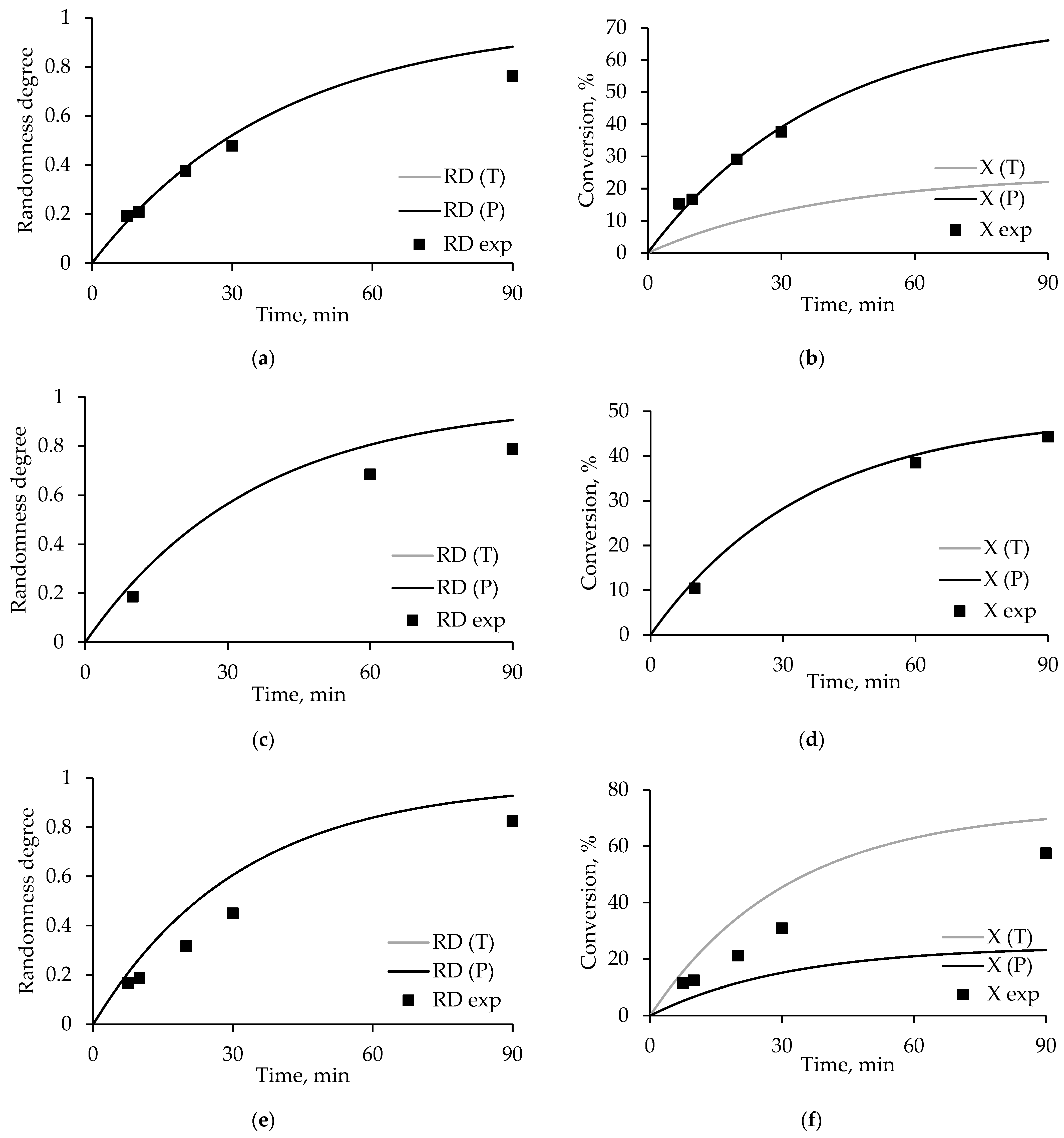
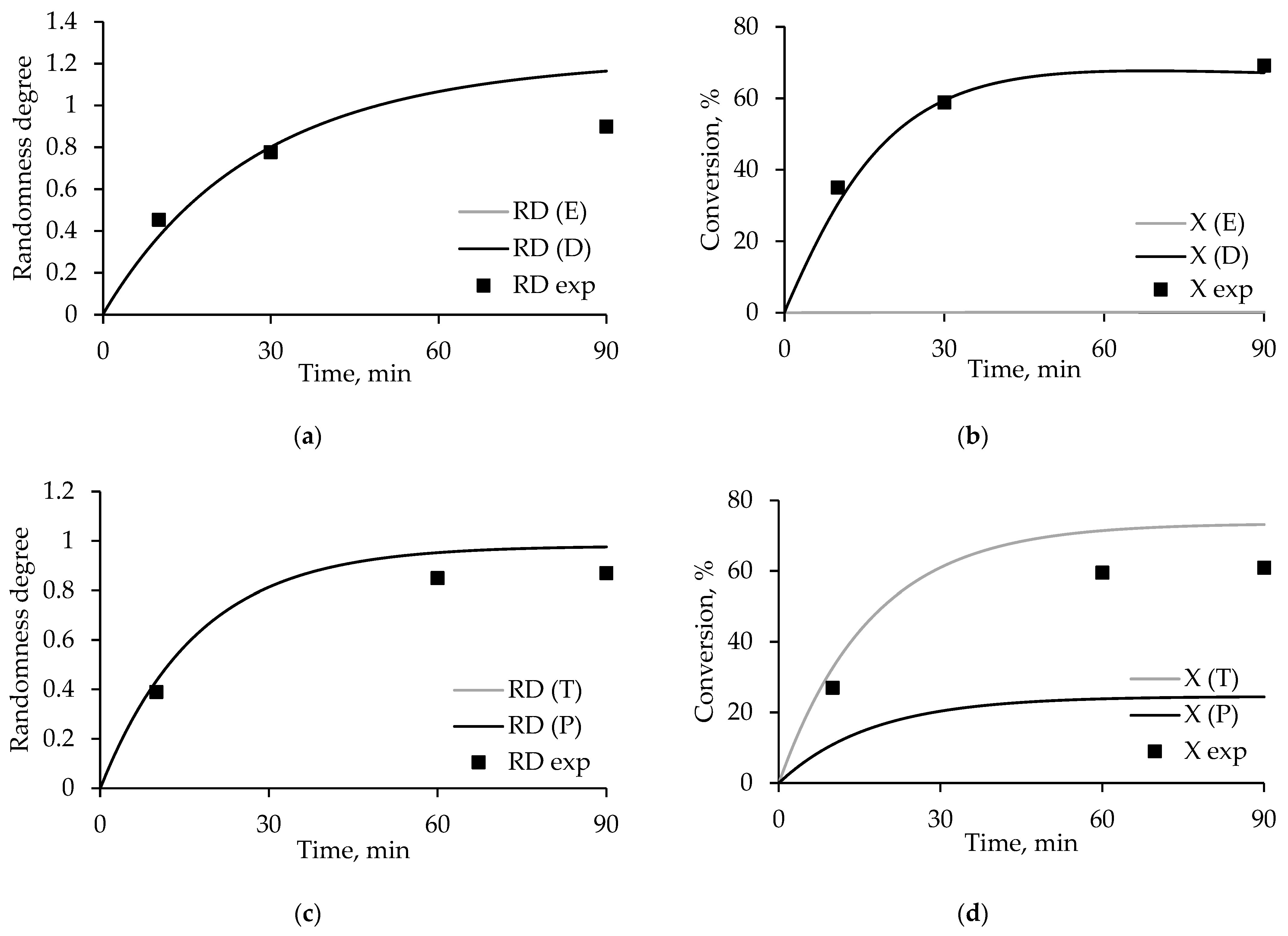
3.4. Degree of Randomness and Conversion Model Calculations
- E ≠ D, T = P.
- E = D, T ≠ P.
- E ≠ D, T ≠ P.
3.5. Molecular Weight Characteristics Model Calculations
3.6. Conversion and Degree of Randomness in PET/ODET Blends
3.7. Molecular Weight Characteristics of PET/Oligoester Transesterification Products
3.8. Interpretation of Reactions in PET/PEN Blends
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PET | Polyethylene terephthalate |
| PEN | Polyethylene naphthalate |
| ODET | Oligodiethylene terephthalate |
| OEP | Oligoethylene phthalate |
| OPT | Oligopropyl-ene terephthalate |
| OPP | Oligopropylene phthalate |
| ODEET | Oligo(diethylene-co-ethylene terephthalate |
| OEPT | Oligo(ethylene phthalate-co-terephthalate |
| OPET | Oligo(propylene-co-ethylene terephthalate |
| OPEPT | Oligo(propylene-co-ethylene phthalate-co-terephthalate |
| FTIR | Fourier transform infrared spectroscopy |
| DSC | Differential scanning calorimetry |
| GPC | Gel permeation chromatography |
| NMR | Nuclear magnetic resonance spectroscopy |
References
- Bhanderi, K.K.; Joshi, J.R.; Patel, J.V. Recycling of Polyethylene Terephthalate (PET Or PETE) Plastics—An Alternative to Obtain Value Added Products: A Review. J. Indian Chem. Soc. 2023, 100, 100843. [Google Scholar] [CrossRef]
- Muringayil Joseph, T.; Azat, S.; Ahmadi, Z.; Moini Jazani, O.; Esmaeili, A.; Kianfar, E.; Haponiuk, J.; Thomas, S. Polyethylene Terephthalate (PET) Recycling: A Review. Case Stud. Chem. Environ. Eng. 2024, 9, 100673. [Google Scholar] [CrossRef]
- Kirshanov, K.; Toms, R.; Aliev, G.; Naumova, A.; Melnikov, P.; Gervald, A. Recent Developments and Perspectives of Recycled Poly(Ethylene Terephthalate)-Based Membranes: A Review. Membranes 2022, 12, 1105. [Google Scholar] [CrossRef]
- Abedsoltan, H. A Focused Review on Recycling and Hydrolysis Techniques of Polyethylene Terephthalate. Polym. Eng. Sci. 2023, 63, 2651–2674. [Google Scholar] [CrossRef]
- Xu, Y.; Cui, R.; Han, Y.; Jiang, J.; Hu, D.; Zhao, L.; Xi, Z. Efficient Alcoholysis of Poly(Ethylene Terephthalate) by Using Supercritical Carbon Dioxide as a Green Solvent. Polymers 2024, 16, 1564. [Google Scholar] [CrossRef]
- Brivio, L.; Meini, S.; Sponchioni, M.; Moscatelli, D. Chemical Recycling of Polyethylene Terephthalate (PET) to Monomers: Mathematical Modeling of the Transesterification Reaction of Bis(2-Hydroxyethyl) Terephthalate to Dimethyl Terephthalate. Chem. Eng. Sci. 2024, 284, 119466. [Google Scholar] [CrossRef]
- Kirshanov, K.; Toms, R.; Melnikov, P.; Gervald, A. Investigation of Polyester Tire Cord Glycolysis Accompanied by Rubber Crumb Devulcanization. Polymers 2022, 14, 684. [Google Scholar] [CrossRef]
- Wei, X.; Zheng, W.; Chen, X.; Qiu, J.; Sun, W.; Xi, Z.; Zhao, L. Chemical Upcycling of Poly(Ethylene Terephthalate) with Binary Mixed Alcohols toward Value-Added Copolyester by Depolymerization and Repolymerization Strategy. Chem. Eng. Sci. 2024, 294, 120103. [Google Scholar] [CrossRef]
- Kirshanov, K.A.; Gervald, A.Y.; Toms, R.V.; Lobanov, A.N. Obtaining Phthalate Substituted Post-Consumer Polyethylene Terephthalate and Its Isothermal Crystallization. Fine Chem. Technol. 2022, 17, 164–171. [Google Scholar] [CrossRef]
- Peng, X.; Shin, Y.; Zervoudakis, A.J.; Nomura, K.; Lindenmeyer, K.M.; Miller, K.M.; Ellison, C.J. Poly(Ethylene Terephthalate)-polyethylene Block Copolymer Architecture Effects on Interfacial Adhesion and Blend Compatibilization. J. Polym. Sci. 2024, 62, 753–765. [Google Scholar] [CrossRef]
- Mikhailov, P.A.; Kalita, A.G.; Zuev, K.V.; Kramarev, D.V.; Ushakova, O.B.; Kulichikhin, V.G. Synthesis of Poly(Ethylene Terephthalate)–4′-Hydroxybiphenyl-4-Carboxylic Acid Copolymers by Transesterification. Polym. Sci. Ser. B 2021, 63, 745–753. [Google Scholar] [CrossRef]
- Kuété, M.A.; Van Velthem, P.; Ballout, W.; Klavzer, N.; Nysten, B.; Ndikontar, M.K.; Pardoen, T.; Bailly, C. Eco-Friendly Blends of Recycled PET Copolymers with PLLA and Their Composites with Chopped Flax Fibres. Polymers 2023, 15, 3004. [Google Scholar] [CrossRef]
- Leung, W.H.; Leitao, E.M.; Verbeek, C.J.R. Copolymerization of Polyethylene Terephthalate and Polycaprolactone Using Catalytic Transesterification. Polymer 2023, 284, 126297. [Google Scholar] [CrossRef]
- Kirshanov, K.; Toms, R.; Melnikov, P.; Gervald, A. Unsaturated Polyester Resin Nanocomposites Based on Post-Consumer Polyethylene Terephthalate. Polymers 2022, 14, 1602. [Google Scholar] [CrossRef] [PubMed]
- Bórquez-Mendivil, A.; Hurtado-Macías, A.; Leal-Pérez, J.E.; Flores-Valenzuela, J.; Vargas-Ortíz, R.Á.; Cabrera-Covarrubias, F.G.; Almaral-Sánchez, J.L. Hybrid Coatings of SiO2–Recycled PET Unsaturated Polyester Resin by Sol-Gel Process. Polymers 2022, 14, 3280. [Google Scholar] [CrossRef]
- Babaei, M.; Jalilian, M.; Shahbaz, K. Chemical Recycling of Polyethylene Terephthalate: A Mini-Review. J. Environ. Chem. Eng. 2024, 12, 112507. [Google Scholar] [CrossRef]
- Bohre, A.; Jadhao, P.R.; Tripathi, K.; Pant, K.K.; Likozar, B.; Saha, B. Chemical Recycling Processes of Waste Polyethylene Terephthalate Using Solid Catalysts. ChemSusChem 2023, 16, e202300142. [Google Scholar] [CrossRef]
- Puglisi, C.; Samperi, F. Exchange Reaction Mechanisms in the Reactive Extrusion of Condensation Polymers. In Reactive Extrusion; Wiley: Hoboken, NJ, USA, 2017; pp. 133–177. [Google Scholar]
- Devaux, J.; Godard, P.; Mercier, J.P. Bisphenol-A Polycarbonate–Poly(Butylene Terephthalate) Transesterification. I. Theoretical Study of the Structure and of the Degree of Randomness in Four-component Copolycondensates. J. Polym. Sci. Polym. Phys. Ed. 1982, 20, 1875–1880. [Google Scholar] [CrossRef]
- Mikhaylov, P.A.; Filatova, M.P.; Kulichikhin, V.G. New Insights into Transreaction Mechanism between Poly (Ethylene Terephthalate) and Bisphenol A Polycarbonate in Melt. Polym. Int. 2024, 74, 346–352. [Google Scholar] [CrossRef]
- Mahjub, A.; Jafari, S.H.; Khonakdar, H.A.; Wagenknecht, U.; Heinrich, G. Monte–Carlo Simulation of Ester Exchange Reactions in PET/PEN Blends. Macromol. Theory Simul. 2013, 22, 207–216. [Google Scholar] [CrossRef]
- Geyer, B.; Röhner, S.; Lorenz, G.; Kandelbauer, A. Synthesis of Ethylene Terephthalate and Ethylene Naphthalate (PET-PEN) Block- Co -polyesters with Defined Surface Qualities by Tailoring Segment Composition. J. Appl. Polym. Sci. 2014, 131, 40731. [Google Scholar] [CrossRef]
- Tharmapuram, S.R.; Jabarin, S.A. Processing Characteristics of PET/PEN Blends, Part 1: Extrusion and Transesterification Reaction Kinetics. Adv. Polym. Technol. 2003, 22, 137–146. [Google Scholar] [CrossRef]
- Collins, S.; Peace, S.K.; Richards, R.W.; Macdonald, W.A.; Mills, P.; King, S.M. Transesterification in Poly(Ethylene Terephthalate). Molecular Weight and End Group Effects. Macromolecules 2000, 33, 2981–2988. [Google Scholar] [CrossRef]
- Collins, S.; Kenwright, A.M.; Pawson, C.; Peace, S.K.; Richards, R.W.; MacDonald, W.A.; Mills, P. Transesterification in Mixtures of Poly(Ethylene Terephthalate) and Poly(Ethylene Naphthalene-2,6-Dicarboxylate): An NMR Study of Kinetics and End Group Effects. Macromolecules 2000, 33, 2974–2980. [Google Scholar] [CrossRef]
- Golriz, M.; Khonakdar, H.A.; Jafari, S.H.; Oromiehie, A.; Abedini, H. An Improved Non-Isothermal Kinetic Model for Prediction of Extent of Transesterification Reaction and Degree of Randomness in PET/PEN Blends. Macromol. Theory Simul. 2008, 17, 241–251. [Google Scholar] [CrossRef]
- Krentsel’, L.B.; Makarova, V.V.; Kudryavtsev, Y.V.; Govorun, E.N.; Litmanovich, A.D.; Markova, G.D.; Vasnev, V.A.; Kulichikhin, V.G. Interchain Exchange and Interdiffusion in Blends of Poly(Ethylene Terephthalate) and Poly(Ethylene Naphthalate). Polym. Sci.-Ser. A 2009, 51, 1241–1248. [Google Scholar] [CrossRef]
- Kim, I.S.; Woo, B.G.; Choi, K.Y.; Kiang, C. Two-phase Model for Continuous Final-stage Melt Polycondensation of Poly(Ethylene Terephthalate). III. Modeling of Multiple Reactors with Multiple Reaction Zones. J. Appl. Polym. Sci. 2003, 90, 1088–1095. [Google Scholar] [CrossRef]
- Chicheva, D.S.; Krasnykh, E.L.; Shakun, V.A. Kinetic Regularities of Neopentyl Glycol Esterification with Acetic and 2-Ethylhexanoic Acids. Fine Chem. Technol. 2024, 19, 28–38. [Google Scholar] [CrossRef]
- Javed, S.; Fisse, J.; Vogt, D. Optimization and Kinetic Evaluation for Glycolytic Depolymerization of Post-Consumer PET Waste with Sodium Methoxide. Polymers 2023, 15, 687. [Google Scholar] [CrossRef]
- Kirshanov, K.A.; Toms, R.V.; Balashov, M.S.; Golubkov, S.S.; Melnikov, P.V.; Gervald, A.Y. Modeling of Poly(Ethylene Terephthalate) Homogeneous Glycolysis Kinetics. Polymers 2023, 15, 3146. [Google Scholar] [CrossRef]
- ASTM D4603-18; Standard Test Method for Determining Inherent Viscosity of Poly(Ethylene Terephthalate) (PET) by Glass Capillary Viscometer. ASTM International: West Conshohocken, PA, USA, 2018.
- Aliev, G.; Toms, R.; Melnikov, P.; Gervald, A.; Glushchenko, L.; Sedush, N.; Chvalun, S. Synthesis of L-Lactide from Lactic Acid and Production of PLA Pellets: Full-Cycle Laboratory-Scale Technology. Polymers 2024, 16, 624. [Google Scholar] [CrossRef] [PubMed]
- ASTM D1544-10; Standard Test Method for Color of Transparent Liquids (Gardner Color Scale). ASTM International: West Conshohocken, PA, USA, 2010.
- de Ilarduya, A.M.; Muñoz-Guerra, S. Chemical Structure and Microstructure of Poly(Alkylene Terephthalate)s, Their Copolyesters, and Their Blends as Studied by NMR. Macromol. Chem. Phys. 2014, 215, 2138–2160. [Google Scholar] [CrossRef]
- Rieckmann, T.; Volker, S. Poly(ethylene terephthalate) polymerization –Mechanism, catalysis, kinetics, mass transfer and reactor design. In Modern Polyesters: Chemistry and Technology of Polyesters and Copolyesters; Scheirs, J., Long, T.E., Eds.; John Wiley & Sons: London, UK, 2003; pp. 31–116. [Google Scholar]
- Yamadera, R.; Murano, M. The Determination of Randomness in Copolyesters by High Resolution Nuclear Magnetic Resonance. J. Polym. Sci. A-1 1967, 5, 2259–2268. [Google Scholar] [CrossRef]
- de la Campa, J.G.; Guzmán, J.; de Abajo, J.; Riande, E. Glass Transition Temperatures of Copolymers (Ethylene Glycol/Diethylene Glycol) Terephthalates. Die Makromol. Chem. 1981, 182, 3163–3168. [Google Scholar] [CrossRef]
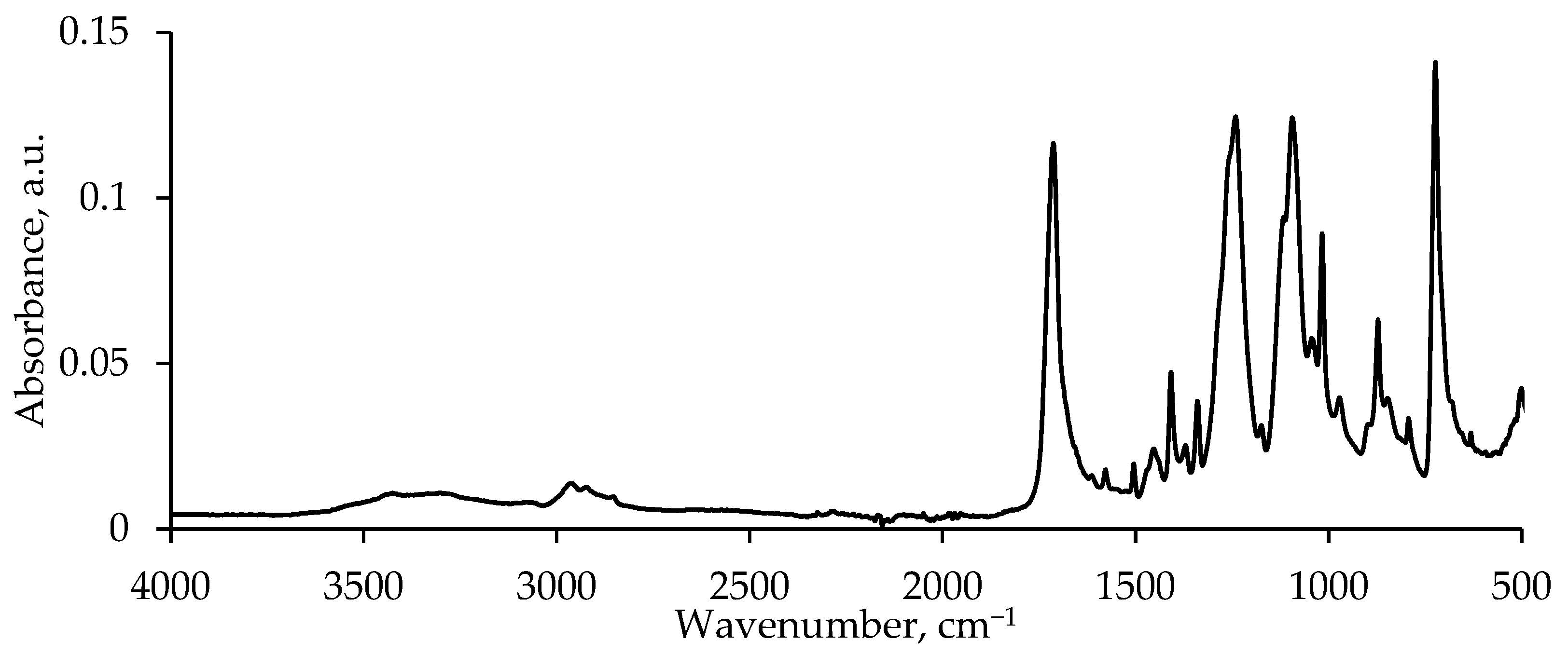
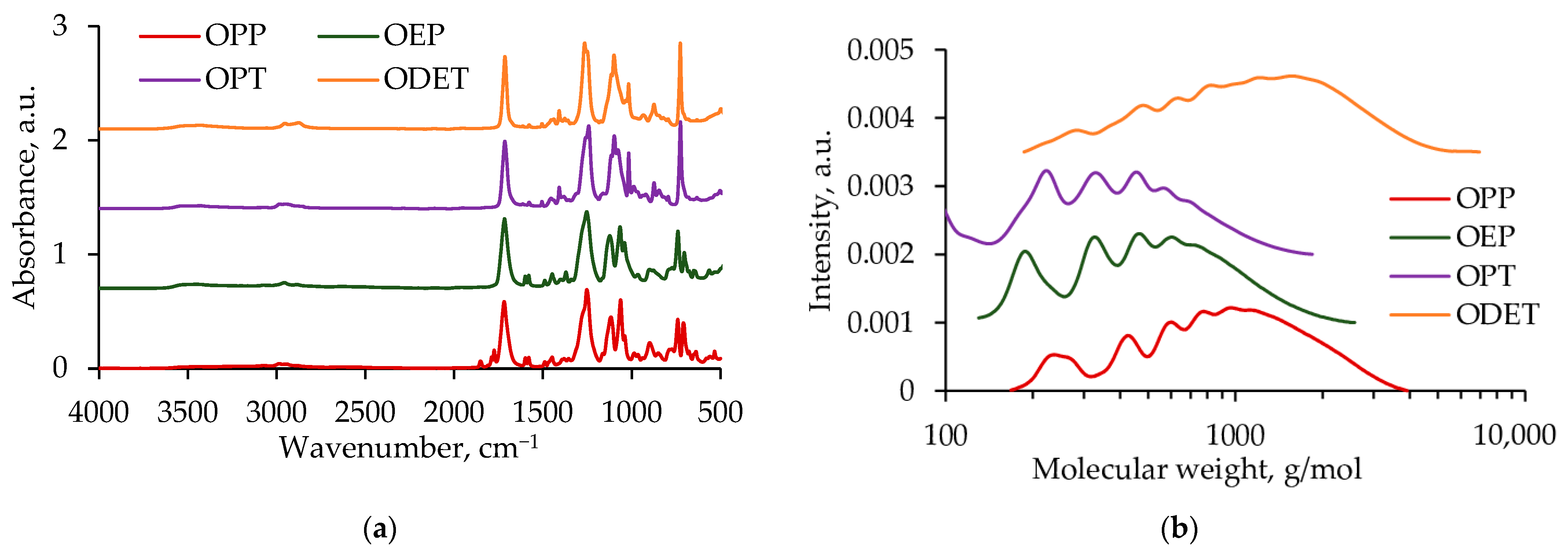

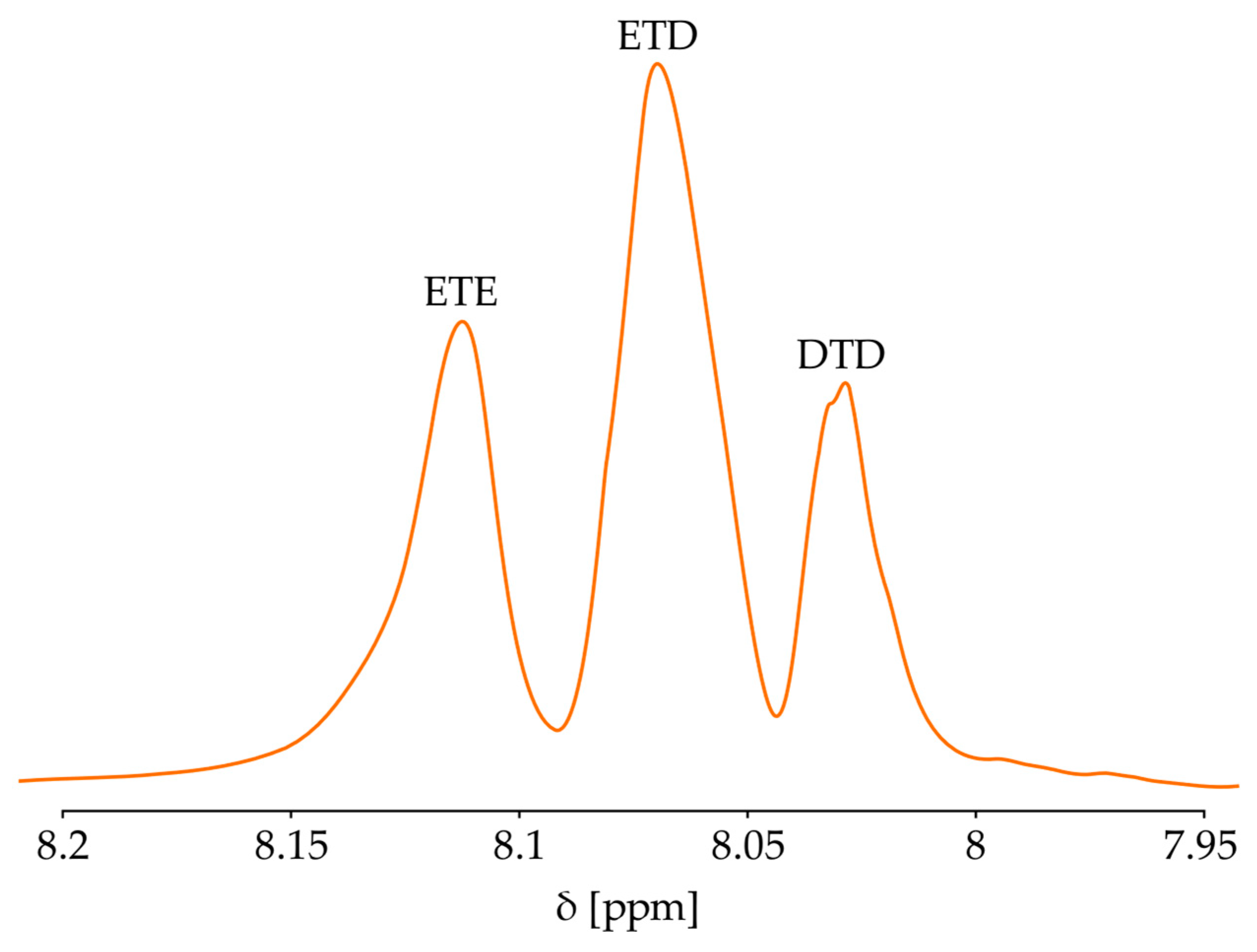
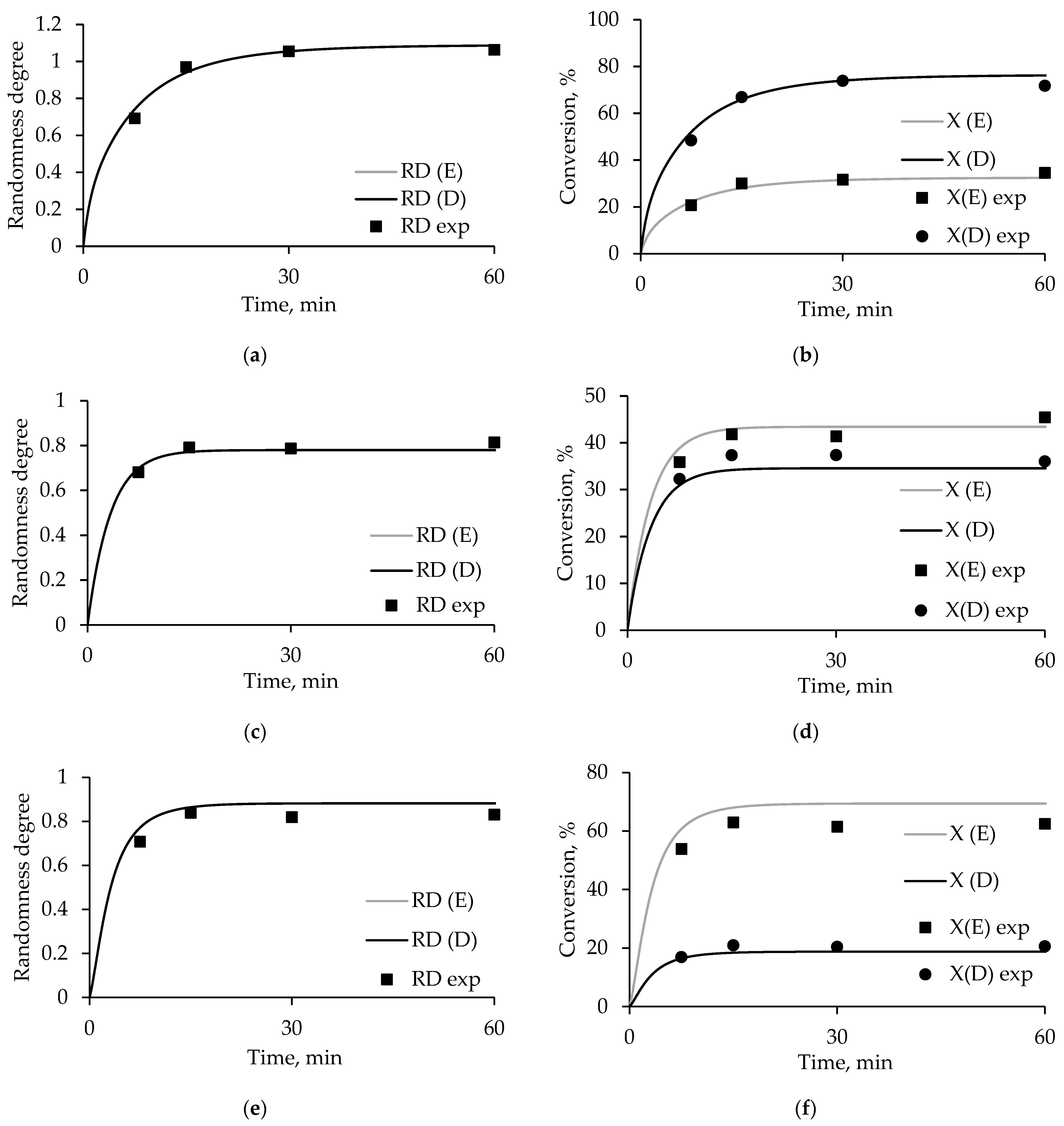
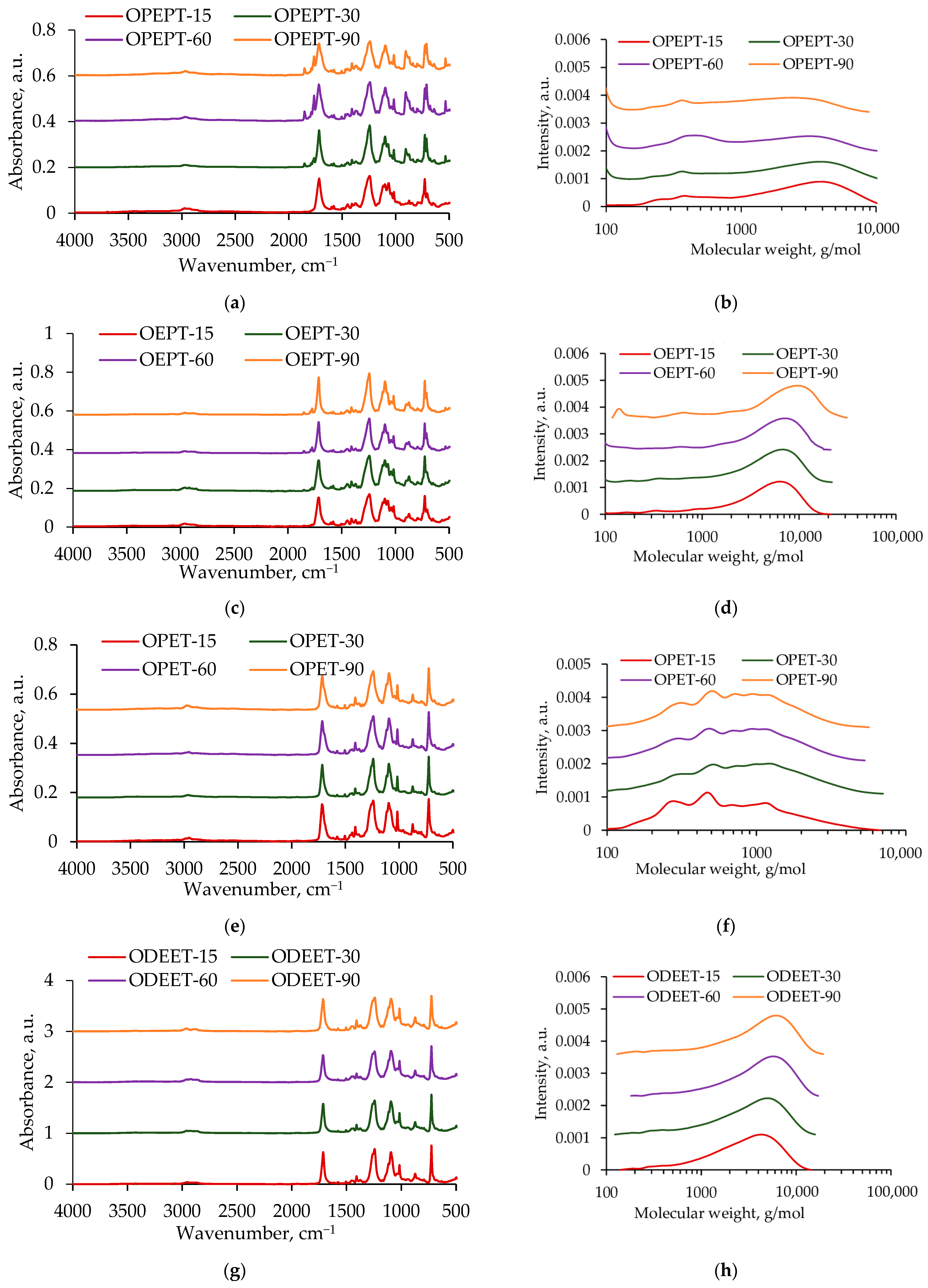
| Sample | Mn, g/mol | Mw, g/mol | PDI | Conversion, % | Color |
|---|---|---|---|---|---|
| OPP | 667 | 1096 | 1.64 | 95.80 | 1 |
| OEP | 648 | 1100 | 1.70 | 96.66 | 3 |
| OPT | 611 | 932 | 1.53 | 94.34 | 1 |
| ODET | 857 | 1366 | 1.59 | 97.22 | 2 |
| Name of the Reacting Component | Abbreviation | Concentration, g/L |
|---|---|---|
| Bonded ethylene glycol | TET | c1 |
| Bonded glycol | TDT | c2 |
| Bonded ethylene glycol | TEP | c3 |
| Bonded glycol | TDP | c4 |
| Bonded ethylene glycol | PEP | c5 |
| Bonded glycol | PDP | c6 |
| Terminal ethylene glycol | TE | c7 |
| Terminal glycol | TD | c8 |
| Terminal ethylene glycol | PE | c9 |
| Terminal glycol | PD | c10 |
| Free ethylene glycol | E | c11 |
| Free glycol | D | c12 |
| Reaction | Reaction Rate Constant |
|---|---|
| Between two bonded glycols | |
| Between terminal glycol and terminal or bonded glycol | |
| Between free glycol and terminal or bonded glycol |
| № | Reaction | Reaction Rate Equation |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 8 | ||
| 9 | ||
| 10 | ||
| 11 | ||
| 12 | ||
| 13 | ||
| 14 | ||
| 15 | ||
| 16 | ||
| 17 | ||
| 18 | ||
| 19 | ||
| 20 | ||
| 21 | ||
| 22 | ||
| 23 | ||
| 24 | ||
| 25 | ||
| 26 | ||
| 27 | ||
| 28 | ||
| 29 | ||
| 30 | ||
| 31 | ||
| 32 | ||
| 33 | ||
| 34 | ||
| 35 | ||
| 36 | ||
| 37 | ||
| 38 | ||
| 39 | ||
| 40 | ||
| 41 | ||
| 42 | ||
| 43 | ||
| 44 | ||
| 45 | ||
| 46 | ||
| 47 | ||
| 48 | ||
| 49 | ||
| 50 | ||
| 51 | ||
| 52 | ||
| 53 | ||
| 54 | ||
| 55 | ||
| 56 | ||
| 57 | ||
| 58 | ||
| 59 | ||
| 60 | ||
| 61 | ||
| 62 | ||
| 63 | ||
| 64 | ||
| 65 | ||
| 66 | ||
| 67 |
| Sample Code | Concentration, g/L | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| c1 | c2 | c3 | c4 | c5 | c6 | c7 | c8 | c9 | c10 | c11 | c12 | |
| ODEET-75:25 | 5.12 | 0 | 0 | 0 | 0 | 1.17 | 0.08 | 0 | 0 | 1.07 | 0 | 0 |
| ODEET-50:50 | 3.41 | 0 | 0 | 0 | 0 | 2.34 | 0.05 | 0 | 0 | 2.14 | 0 | 0 |
| ODEET-25:75 | 1.71 | 0 | 0 | 0 | 0 | 3.52 | 0.03 | 0 | 0 | 3.21 | 0 | 0 |
| Sample Code | Concentration, g/L | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| c1 | c2 | c3 | c4 | c5 | c6 | c7 | c8 | c9 | c10 | c11 | c12 | |
| OPEPT | 3.41 | 0 | 0 | 0 | 0 | 2.22 | 0.05 | 0 | 0 | 2.38 | 0 | 0 |
| OEPT | 3.41 | 0 | 0 | 0 | 0 | 2.29 | 0.05 | 0 | 0 | 2.23 | 0 | 0 |
| OPET | 3.41 | 0 | 0 | 0 | 0 | 2.10 | 0.05 | 0 | 0 | 2.63 | 0 | 0 |
| ODEET | 3.41 | 0 | 0 | 0 | 0 | 2.34 | 0.05 | 0 | 0 | 2.14 | 0 | 0 |
| Sample Code | Mn | Mw | PDI | ||
|---|---|---|---|---|---|
| OPEPT | 15 | Experimental data | 1170 | 2820 | 2.41 |
| 30 | 1520 | 3430 | 2.26 | ||
| 60 | 1210 | 2600 | 2.15 | ||
| 90 | 1200 | 2540 | 2.12 | ||
| Simulation result | 1493 | 2630 | 1.76 | ||
| OEPT | 15 | Experimental data | 1450 | 4990 | 3.44 |
| 30 | 1250 | 5220 | 4.18 | ||
| 60 | 1520 | 5700 | 3.75 | ||
| 90 | 1700 | 7590 | 4.46 | ||
| Simulation result | 1567 | 2778 | 1.77 | ||
| ODEET | 15 | Experimental data | 1750 | 3550 | 2.03 |
| 30 | 1800 | 4000 | 2.22 | ||
| 60 | 2000 | 4900 | 2.45 | ||
| 90 | 2600 | 5000 | 1.92 | ||
| Simulation result | 1621 | 2883 | 1.78 | ||
| OPET | 15 | Experimental data | 1020 | 2180 | 2.14 |
| 30 | 1780 | 3250 | 1.83 | ||
| 60 | 1270 | 4010 | 3.16 | ||
| 90 | 1752 | 4911 | 2.80 | ||
| Simulation result | 1383 | 2410 | 1.74 | ||
| Sample Code | Concentration, g/L | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| c1 | c2 | c3 | c4 | c5 | c6 | c7 | c8 | c9 | c10 | c11 | c12 | |
| PET/PEN-75:25 | 5.19 | 0 | 0 | 0 | 0 | 1.73 | 0.05 | 0 | 0 | 0.03 | 0 | 0 |
| PET/PEN-50:50 | 3.46 | 0 | 0 | 0 | 0 | 3.46 | 0.04 | 0 | 0 | 0.06 | 0 | 0 |
| PET/PEN-25:75 | 1.73 | 0 | 0 | 0 | 0 | 5.19 | 0.02 | 0 | 0 | 0.09 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kirshanov, K.A.; Toms, R.V.; Aliev, G.S.; Ismaylov, D.A.; Shagina, N.Y.; Sokolovskiy, P.V.; Nizameeva, G.R.; Gervald, A.Y. Modeling the Kinetics of Polyethylene Terephthalate and Polyesters with Terminal Hydroxyl Groups Transesterification Reactions. Polymers 2025, 17, 992. https://doi.org/10.3390/polym17070992
Kirshanov KA, Toms RV, Aliev GS, Ismaylov DA, Shagina NY, Sokolovskiy PV, Nizameeva GR, Gervald AY. Modeling the Kinetics of Polyethylene Terephthalate and Polyesters with Terminal Hydroxyl Groups Transesterification Reactions. Polymers. 2025; 17(7):992. https://doi.org/10.3390/polym17070992
Chicago/Turabian StyleKirshanov, Kirill A., Roman V. Toms, Gadir Sh. Aliev, Daniil A. Ismaylov, Natalya Yu. Shagina, Pavel V. Sokolovskiy, Guliya R. Nizameeva, and Alexander Yu. Gervald. 2025. "Modeling the Kinetics of Polyethylene Terephthalate and Polyesters with Terminal Hydroxyl Groups Transesterification Reactions" Polymers 17, no. 7: 992. https://doi.org/10.3390/polym17070992
APA StyleKirshanov, K. A., Toms, R. V., Aliev, G. S., Ismaylov, D. A., Shagina, N. Y., Sokolovskiy, P. V., Nizameeva, G. R., & Gervald, A. Y. (2025). Modeling the Kinetics of Polyethylene Terephthalate and Polyesters with Terminal Hydroxyl Groups Transesterification Reactions. Polymers, 17(7), 992. https://doi.org/10.3390/polym17070992









